1 Introduction

It is believed that the heavy ion collisions at Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) have produced a new state of matter, the so-called quark gluon plasma (QGP) [1,2,3]. At a qualitative level, the QGP can be described very well by relativistic hydrodynamics with a very small \(\eta /s\) [4], with \(\eta /s\) the shear viscosity to entropy density ratio. This indicates that the QGP is strongly coupled, and thus calculational tools beyond the perturbative QCD are called for. Such tools are now available via the AdS/CFT duality.

AdS/CFT [5,6,7], the duality between a string theory in the AdS space and a conformal field theory in the physical space-time, provides a helpful tool to explore properties of strong coupling systems. Thanks to this duality, challenging questions about dynamics in quantum phases of matter in strong coupling regime can be mapped to processes in theories of gravity that are tractable. In the past two decades, this duality has been used to study various quantities with respect to QGP [8], such as jet quenching parameter and the drag force.

The jet quenching parameter has the meaning of the average squared transverse momentum transferred from the medium to the traversing parton, per unit mean free path [9, 10]. In field theory, this parameter can be calculated from a Wilson line in the adjoint representation along a light-cone direction. Meanwhile, in the gravity dual description, it can be obtained from the minimal surface of a world-sheet which ends on an orthogonal Wilson loop lying along two light-like lines. The first calculations of the jet quenching parameter for \({\mathcal {N}} = 4\) SYM plasma was carried out by Liu, Rajagopal and Wiedemann in [11]. They find that

$$\begin{aligned} {\hat{q}}_{SYM}=\frac{\pi ^{\frac{3}{2}}\Gamma (\frac{3}{4})}{\Gamma (\frac{5}{4})}\sqrt{\lambda }T^3, \end{aligned}$$
(1)

where T is the temperature and \(\lambda \) is the ’t Hooft coupling with \(\lambda =g_{YM}^2N_c=\frac{R^4}{{\alpha ^\prime }^2}\). Here R and \(\alpha ^\prime \) are the AdS radius and the reciprocal of the string tension, respectively. Interestingly, the magnitude of the parameter in (1) turns out to be closer to the value extracted from RHIC data [12, 13] than pQCD result for the typical value of the \(\lambda =6\pi \) of QCD. Later, the work of [11] has been extended to various cases. For instance, the chemical potential effect on \({\hat{q}}\) is discussed in [14,15,16]. The anisotropy effect on \({\hat{q}}\) is studied in [17]. The effect of electromagnetic field on \({\hat{q}}\) have been analyzed in [18, 19]. Also, this parameter has been addressed in some AdS/QCD models [20, 21]. For related results, see [22,23,24,25,26,27,28,29,30].

Another observable quantity sensitive to the in-medium energy loss is the drag force. This quantity is related to the damping rate \(\mu \) (or friction coefficient), defined by Langevin equation, \(dp/dt = -\mu p+f\), subject to a driving force f. For constant speed trajectory (\({\dot{p}}=0\)), f is equivalent to a drag force. The first AdS/CFT calculation of the drag force appeared in [31, 32]. The results show that

$$\begin{aligned} f_{SYM}=-\frac{\pi \sqrt{\lambda }T^2}{2}\frac{v}{\sqrt{1-v^2}}, \end{aligned}$$
(2)

where v is the quark velocity. Subsequently, there were many attempts to address the drag force in this direction. For example, the effect of the chemical potential on f is studied in [33, 34]. The effect of non-commutativity on f is analyzed in [35]. The \(R^2\) corrections to f is discussed in [36]. Also, this quantity has been studied in some AdS/QCD models [37, 38]. Other interesting results, can be found, for example, in [39,40,41,42,43,44,45,46].

The purpose of this paper is to study the effect of gluon condensate on the jet quenching parameter and the drag force. It was argued [47,48,49] that the gluon condensate, serving as an order parameter for (de)confinement, is useful to study the nonperturbative nature of the QGP (for the role of the gluon condensate in RHIC physics, see [50]). On the other hand, lattice results [51] indicate that the value of the gluon condensate reveals a drastic drop around \(T_c\), regardless of the number of quark flavors. For those reasons, it would be interesting to investigate the possible effects that the gluon condensate might cause on various quantities. Already, some good work has been done in this direction. For example, the gluon condensate dependence of the heavy quark potential has been studied in [52] and the results show that the potential becomes deeper as the gluon condensate decreases in the deconfined phase and the mass of the quarkonium drops near \(T_c\). Here motivated by [52], we study the effect of the gluon condensate on the jet quenching parameter and the drag force. More specifically, we would like to see how the gluon condensate affects the two quantities and the energy loss. On the other hand, the jet quenching parameter and the drag force represent two different mechanisms for the in-medium energy loss. By definition, the former is related to the momentum fluctuation \({\hat{q}}\propto <\vec {p}_\perp ^2>\) and the latter is related to an averaged momentum loss escaping to the medium \(<{\dot{p}}>\). Evaluations of the same effect on the two quantities could be regarded as a simple comparison between the two mechanisms.

The structure of this paper is as follows. In the next section, we briefly review the deformed AdS background with backreaction due to the gluon condensate given in [53]. In Sects. 3 and 4, we study the effect of gluon condensate on the jet quenching parameter and the drag force, in turn. The last part is devoted to our conclusion and a discussion.

2 Background geometry

To begin with, we introduce the 5-dimensional (5D) gravity action in Minkowski with a dilaton coupled [54],

$$\begin{aligned} I=\frac{1}{2\kappa ^2}\int d^5x\sqrt{g}\left( {\mathcal {R}}+\frac{12}{R^2}-\frac{1}{2}\partial _M\phi \partial ^M\phi \right) , \end{aligned}$$
(3)

where \(\kappa ^2\) is the 5D Newtonian constant. \({\mathcal {R}}\) represents the Ricci scalar. R denotes the AdS radius. The index M runs from 0 to 4. Moreover, the dilaton \(\phi \) is a massless scalar and it will couple to the gluon operator. The fact that there is a non-vanishing gluon condensate in QCD is expressed by the fact that the dilaton will have a non-trivial background. Hence, one can find the most general backgrounds by solving the coupled system of the dilaton equation of motion and the Einsteins equation. As discussed in [53], there are two relevant solutions for the action (3). The first is the dilaton-wall solution [55, 56],

$$\begin{aligned} ds^2=\frac{1}{z^2}\left( \sqrt{1-c^2z^8}(d\vec {x}^2-dt^2)+dz^2\right) , \end{aligned}$$
(4)

with

$$\begin{aligned} \phi (z)=\sqrt{\frac{3}{2}}\log \left( \frac{1+cz^4}{1-cz^4}\right) +\phi _0, \end{aligned}$$
(5)

where, for simplicity, we have set \(R=1\). In the above metric, \(\vec {x}=x_1,x_2,x_3\) denotes the boundary coordinates. z is the coordinate of the 5th dimension with \(z=0\) the boundary. c represents the gluon condensation. \(\phi _0\) refers to a constant.

The second is the dilaton black hole solution [57],

$$\begin{aligned} ds^2=\frac{1}{z^2}[A(z)d\vec {x}^2-B(z)dt^2+dz^2], \end{aligned}$$
(6)

with

$$\begin{aligned} A(z)= & {} (1+fz^4)^{(f+a)/{2f}}(1-fz^4)^{(f-a)/{2f}},\nonumber \\ B(z)= & {} (1+fz^4)^{(f-3a)/{2f}}(1-fz^4)^{(f+3a)/{2f}},\nonumber \\ f^2= & {} a^2+c^2, \end{aligned}$$
(7)

and the corresponding dilaton profile is

$$\begin{aligned} \phi (z)=\frac{c}{f}\sqrt{\frac{3}{2}}\log \left( \frac{1+fz^4}{1-fz^4}\right) +\phi _0. \end{aligned}$$
(8)

Note that the solution (6) is well defined only in the range \(0<z<f^{-1/4}=z_c\), where f determines the position of the singularity and \(z_c\) behaves as an infrared (IR) cut-off. Although it does not allow us to define the temperature by requiring the absence of a conical singularity as long as \(c\ne 0\). one could associate a with a temperature by \(a=(\pi T)^4/4\) [53]. Moreover, the solution (6) reduces to solution (4) for \(a=0\) and becomes the Schwarzschild black hole solution for \(c=0\). Also, there is a Hawking–Page transition between (4) and (6) at some critical value of a. Hence, the background (4) is for the confined phase, while the background (6) is for the deconfined phase. For more details as regards the two backgrounds, see [53].

Next, if one works with \(r=\frac{1}{z}\) as the radial coordinate, then the metric (6) becomes

$$\begin{aligned} ds^2=r^2A(r)d\vec {x}^2-r^2B(r)dt^2+\frac{dr^2}{r^2}, \end{aligned}$$
(9)

with

$$\begin{aligned} \phi (r)=\frac{c}{f}\sqrt{\frac{3}{2}}\log \left( \frac{1+fr^{-4}}{1-fr^{-4}}\right) +\phi _0; \end{aligned}$$
(10)

now the range is \(r_f<r<\infty \) with \(r_f=f^{1/4}\). Note that (6) and (9) are equivalent but only with different coordinate systems.

3 Jet quenching parameter

In this section, we follow the argument in [11] to study the behavior of the jet quenching parameter for the background metric (9). In the proposal of [11], \({\hat{q}}\) can be extracted from the following expression:

$$\begin{aligned} <W^{\mathbb {A}}[{{{\mathcal {C}}}}]> \ \approx \exp \left[ -\frac{1}{4\sqrt{2}}{\hat{q}}L_-L_k^2\right] , \end{aligned}$$
(11)

where \({\mathcal {C}}\) refers to the null-like rectangular contour of size \(L_k\times L_-\) with \(L_->>L_k\). Here \(L_k\) is the small transverse separation and \(L_-\) is the length related to the partons moving at relativistic velocities.

In the holographic set up, the Wilson loop in the fundamental representation is evaluated as

$$\begin{aligned} <W^{\mathbb {F}}[{{{\mathcal {C}}}}]> \ \approx \exp [-S_I],\quad S_I=S-S_0 , \end{aligned}$$
(12)

where \(S_I\), S and \(S_0\) are the normalized action, total energy of the heavy quark pair, and the self-energy of the two single quarks, respectively.

Using the relation \(<W^{\mathbb {A}}[{\mathcal {C}}]> \ = \ <W^{\mathbb {F}}[{\mathcal {C}}]>^2\), one gets

$$\begin{aligned} {\hat{q}}=8\sqrt{2}\frac{S_I}{L_-L_k^2}. \end{aligned}$$
(13)

To proceed, one uses the following light-cone coordinates:

$$\begin{aligned} dt=\frac{dx^++dx^-}{\sqrt{2}},\quad dx_1=\frac{dx^+-dx^-}{\sqrt{2}}, \end{aligned}$$
(14)

to rewrite the metric (9) as

$$\begin{aligned} ds^2= & {} \frac{1}{2}(r^2A-r^2B)[(dx^+)^2+(dx^-)^2]+r^2A(dx_2^2+dx_3^2)\nonumber \\&-(r^2A+r^2B)dx^+dx^-+\frac{dr^2}{r^2}, \end{aligned}$$
(15)

where \(A\equiv A(r)\) and \(B\equiv B(r)\).

Consider a heavy quark moving along the \(x^-\) direction. In this case, the world-sheet ansatz for the string configuration is

$$\begin{aligned}&x^-=\tau , \quad x_2=\sigma , \quad x^+=constant, \nonumber \\&\quad x_3=constant, \quad r=r(\sigma ), \end{aligned}$$
(16)

where the boundary condition is \(r(\pm \frac{L_k}{2})=\infty \).

Plugging (16) into (15), one gets

$$\begin{aligned} ds^2=\frac{1}{2}(r^2A-r^2B)d\tau ^2+\left( r^2A+\frac{{\dot{r}}^2}{r^2}\right) d\sigma ^2, \end{aligned}$$
(17)

with \({\dot{r}}=dr/d\sigma \).

The string action can reduce to the Nambu–Goto action, given by

$$\begin{aligned} S=-\frac{1}{2\pi \alpha ^\prime }\int d\tau d\sigma \sqrt{-det g_{\alpha \beta }}, \end{aligned}$$
(18)

with

$$\begin{aligned} g_{\alpha \beta }=G_{\mu \nu }\frac{\partial X^\mu }{\partial \sigma ^\alpha } \frac{\partial X^\nu }{\partial \sigma ^\beta }, \end{aligned}$$
(19)

where \(G_{\mu \nu }\) and \(X^\mu \) represent the metric and the target space coordinates, respectively.

By virtue of (10) and (17), the Nambu–Goto action in (18) reads

$$\begin{aligned} S=\frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _0^{L_k/2} d\sigma e^{\phi /2}\sqrt{r^4A(A-B)+(A-B){\dot{r}}^2}.\nonumber \\ \end{aligned}$$
(20)

Since (20) does not depend explicitly on \(\sigma \), the corresponding Hamiltonian is a constant,

$$\begin{aligned} {\mathcal {L}}-\frac{\partial \mathcal L}{\partial {\dot{r}}}{\dot{r}}= & {} \frac{e^{\phi /2} r^4A(A-B)}{\sqrt{r^4A(A-B)+(A-B){\dot{r}}^2}}\nonumber \\= & {} constant=C, \end{aligned}$$
(21)

which leads to

$$\begin{aligned} {\dot{r}}^2=\frac{r^4A}{C^2}[e^\phi r^4A(A-B)-C^2]. \end{aligned}$$
(22)

The above equation involves determining the zeros and the region of positivity of the right-hand side. It was shown [15] that \(r_0\) (\(r_0\ge r_f\)) is an extremal point with \({\dot{r}}=0\), yielding

$$\begin{aligned} C=e^{\frac{\phi (r_0)}{2}}r_0^2\sqrt{A_0(A_0-B_0)}, \end{aligned}$$
(23)

where \(A_0=A(r)|_{r=r_0}\), \(B_0=B(r)|_{r=r_0}\) and \(\phi (r_0)=\phi (r)|_{r=r_0}\).

Thus, (22) can be integrated to leading order of \(C^2\) for the low energy limit (\(C\rightarrow 0\)),

$$\begin{aligned} L_k=2\int _{r_0}^\infty dr\frac{d\sigma }{dr}\simeq 2C\int _{r_0}^\infty dr\frac{1}{e^{\phi /2} r^4A\sqrt{A-B}}. \end{aligned}$$
(24)

In Fig. 1 we plot \(L_k\) versus \(r_0\) for \(c=0.02 GeV^4\) and \(T=200 MeV\). Other cases with different values of c and T show a similar picture.

Fig. 1
figure 1

\(L_k\) versus \(r_0\). Here we take \(c=0.02 \ \mathrm{GeV}^4\) and \(T=200 \) MeV

Full size image
Fig. 2
figure 2

Left: \({\hat{q}}/{\hat{q}}_a\) versus T. Right: \({\hat{q}}/{\hat{q}}_0\) versus c

Full size image

On the other hand, plugging (22) into (20), one gets

$$\begin{aligned} S= & {} \frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _{r_0}^\infty dr\frac{e^\phi r^4A(A-B)}{C}\nonumber \\&\times \frac{1}{\sqrt{\frac{r^4A}{C^2}[e^\phi r^4A(A-B)-C^2]}},\nonumber \\= & {} \frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _{r_0}^\infty dr\frac{e^\phi \sqrt{r^4A(A-B)^2}}{\sqrt{e^\phi r^4A(A-B)-C^2}}. \end{aligned}$$
(25)

Similarly, one expands (25) to leading order of \(C^2\) as

$$\begin{aligned} S=\frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _{r_0}^\infty dr\sqrt{e^\phi (A-B)}\left[ 1+\frac{C^2}{2e^\phi r^4A(A-B)}\right] ;\nonumber \\ \end{aligned}$$
(26)

note that the action S is divergent and needs to be subtracted by the self-energy of the two free quarks, given by

$$\begin{aligned} S_0= & {} \frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _{r_0}^\infty dre^{\phi /2}\sqrt{g_{--}g_{rr}},\nonumber \\= & {} \frac{\sqrt{2}L_-}{2\pi \alpha ^\prime }\int _{r_0}^\infty dre^{\phi /2}\sqrt{(A-B)}. \end{aligned}$$
(27)

Then the normalized action is obtained:

$$\begin{aligned} S_I=S-S_0=\frac{\sqrt{2}L_-C^2}{4\pi \alpha ^\prime }\int _{r_0}^\infty dr \frac{1}{e^{\phi /2}r^4A\sqrt{A-B}}. \end{aligned}$$
(28)

Using (13), (24) and (28), one ends with the jet quenching parameter in the dilaton black hole background as

$$\begin{aligned} {\hat{q}}=\frac{I(c)^{-1}}{\pi \alpha ^\prime }, \end{aligned}$$
(29)

with

$$\begin{aligned} I(c)=\int _{r_0}^\infty dr \frac{1}{e^{\phi /2}r^4A\sqrt{A-B}}. \end{aligned}$$
(30)

Before going further, we discuss the range of T and c. First, to attempt a comparison to implications of experimental data, we choose T not far above the QCD phase transition, \(T_c\); here we take \(T_c=170\) MeV [58]. Second, we set \(0\le c\le 0.9~\mathrm{GeV}^4\), as follows from [52].

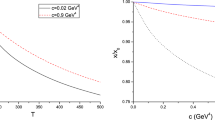
Let us discuss the results. In the left panel of Fig. 2, we plot \({\hat{q}}/{\hat{q}}_a\) as a function of T with fixed c, where \({\hat{q}}_a={\hat{q}}|_{T=170 MeV}\). One finds that increasing T leads to increasing \({\hat{q}}/{\hat{q}}_a\), implying that the jet quenching parameter increases as the temperature increases, as expected.

To study how c affects \({\hat{q}}\), we plot \({\hat{q}}/{\hat{q}}_0\) as a function of c for different T, where \({\hat{q}}_0={\hat{q}}|_{c=0}\). From these figures, one can see that at fixed temperature \({\hat{q}}/{\hat{q}}_0\) increases as c increases. In other words, the inclusion of the gluon condensation enhances the jet quenching parameter. Interestingly, it was argued [29] that the D-instanton density (closely related to the chiral condensation and the gluon condensation) also enhances the jet quenching parameter.

Moreover, one finds that, as T increases, the slope of the curve decreases, which means that c has stronger effect on \({\hat{q}}\) at low temperature. On the other hand, it was shown [51] that the value of the gluon condensate drops near \(T_c\) of the deconfinement transition. Thus, one notices that the jet quenching parameter decreases as the gluon condensate decreases in the deconfined phase.

Fig. 3
figure 3

Left: \(f/f_a\) versus a. Right: \(f/f_0\) versus c. Here we take the speed of light as unity

Full size image

4 Drag force

Next, we follow the calculations in [31, 32] to investigate the behavior of the drag force for the background metric (9). Since the gluon condensate does not distinguish the \(\vec {x}\) coordinates, without loss of generality, one can discuss the quark moving in one of \(\vec {x}\) directions. Here we consider a heavy quark moving along the \(x_1\) direction. For this case, the parametrization is

$$\begin{aligned} t=\tau ,\quad x_1=vt+\xi (r),\quad x_2=0,\quad x_3=0,\quad r=\sigma . \end{aligned}$$
(31)

The relevant string dynamics is described by the Nambu–Goto action,

$$\begin{aligned} S=-\frac{1}{2\pi \alpha ^\prime }\int d\tau d\sigma \sqrt{-det g_{\alpha \beta }}. \end{aligned}$$
(32)

Plugging (31) into (9), the induced metric reads

$$\begin{aligned} g_{tt}=-r^2B, \quad g_{xx}=r^2A,\quad g_{rr}=\frac{1}{r^2}; \end{aligned}$$
(33)

then the Lagrangian density reads

$$\begin{aligned} {\mathcal {L}}= & {} e^{\phi /2}\sqrt{-g_{rr}g_{tt}-g_{rr}g_{xx}v^2-g_{xx}g_{tt}{\xi ^\prime }^2}\nonumber \\= & {} e^{\phi /2}\sqrt{B-Av^2+r^4AB{\xi ^\prime }^2}, \end{aligned}$$
(34)

where \(\xi ^\prime =d\xi /d\sigma \). Now that this action does not depend on \(\xi \) explicitly, the corresponding momentum is a constant,

$$\begin{aligned} \Pi _\xi =\frac{\partial {\mathcal {L}} }{\partial \xi ^\prime }=\xi ^\prime \frac{e^{\phi /2}r^4AB}{\sqrt{B-Av^2+r^4AB{\xi ^\prime }^2}}=constant, \end{aligned}$$
(35)

resulting in

$$\begin{aligned} {\xi ^\prime }^2=\frac{{\Pi _\xi }^2(B-Av^2)}{ r^4AB(e^\phi r^4AB-{\Pi _\xi }^2)}. \end{aligned}$$
(36)

Notice that in the right-hand side of (36), the denominator and numerator are both positive for large r and negative for small r. Moreover, \({\xi ^\prime }^2\) should be everywhere positive. Given these conditions, the denominator and numerator should change sign at the same point. For the numerator, the critical point \(r_c\) satisfies

$$\begin{aligned} B(r_c)=A(r_c)v^2, \end{aligned}$$
(37)

with \(A(r_c)=A(r)|_{r=r_c}\).

Also, the denominator changes sign at \(r_c\), yielding

$$\begin{aligned} {\Pi _\xi }^2=e^{\phi (r_c)}r_c^4A(r_c)B(r_c), \end{aligned}$$
(38)

where \(B(r_c)=B(r)|_{r=r_c}\) and \(\phi (r_c)=\phi (r)|_{r=r_c}\).

On the other hand, the current density for the momentum \(p_1\) (along the \(x_1\) direction) is

$$\begin{aligned} \pi _x^r=-\frac{1}{2\pi \alpha ^\prime }\xi ^\prime \frac{g_{tt}g_{xx}}{-g}, \end{aligned}$$
(39)

and the drag force is

$$\begin{aligned} f=\frac{dp_1}{dt}=\sqrt{-g}\pi _x^r. \end{aligned}$$
(40)

As a result, the drag force in the dilaton black hole background is obtained:

$$\begin{aligned} f=-\frac{1}{2\pi \alpha ^\prime }e^{\frac{\phi (r_c)}{2}}r_c^2A(r_c)v, \end{aligned}$$
(41)

where the minus sign indicates that the direction of the drag force is against the movement.

Furthermore, the rate of energy loss is found to be

$$\begin{aligned} \frac{dE}{dt}=\vec {f}\cdot \vec {v}=-\frac{1}{2\pi \alpha ^\prime }e^{\frac{\phi (r_c)}{2}}r_c^2A(r_c)v^2. \end{aligned}$$
(42)

In the left panel of Fig. 3, we plot \(f/f_a\) versus T for different quark velocities, where \(f_a=f|_{T=170 MeV}\). From these plots, one sees that as T increases \(f/f_a\) increases. Also, as v increases \(f/f_a\) increases, similar to the behavior of the jet quenching parameter. On the other hand, we show \(f/f_0\) as a function c for different temperatures in the right panel, where \(f_0=f|_{c=0}\). One finds that c enhances the drag force and this effect is stronger at low temperature, consistent with the findings of the jet quenching parameter.

However, one might notice one difference between the right panel of Figs. 2 and 3: for \(T=170\) MeV, the slope of \(f/f_0\) is bigger than that of \({\hat{q}}/{\hat{q}}_0\), which means that, near \(T_c\), the gluon condensate has a stronger effect on the drag force than the jet quenching parameter.

5 Conclusion and discussion

The gluon condensate is a useful quantity to characterize the QCD deconfinement transition. In this paper, we studied the jet quenching parameter and the drag force in a deformed AdS background with backreaction due to the gluon condensate, respectively. It is shown that, as the gluon condensate decreases in the deconfined phase, the two quantities both decrease, implying that the energy loss is reduced near \(T_c\) due to the drop of the gluon condensate. Also, we observe that near \(T_c\) the gluon condensate has a stronger effect on the drag force than the jet quenching parameter.

However, it should be admitted that this study could not give a concrete conclusion on the energy loss further above \(T_c\) because it is unknown at this stage how the gluon condensate and temperature vary with respect to each other at high temperature. Thus, it is essential to study the temperature dependence of the gluon condensate in detail. We hope we can report on this issue in the near future.