Analysis of $D_s D K^*$ and $D_s D^{*} K^*$ vertices and branching ratio of $B^+\rightarrow {K^*}^0 \pi ^+$

Abstract

In this paper, the strong form factors and coupling constants of $D_sDK^*$ and $D_sD^*K^*$ vertices are investigated within the three-point QCD sum rules method with and without the $SU_{f}(3)$ symmetry. In this calculation, the contributions of the quark–quark, quark–gluon, and gluon–gluon condensate corrections are considered. As an example of specific application of these coupling constants, the branching ratio of the hadronic decay $B^+\rightarrow {K^*}^0 \pi ^+$ is analyzed based on the one-particle-exchange which is one of the phenomenological models. In this model, B decays into a $D_s D^*$ intermediate state, and then these two particles exchange a $D (D^*)$ producing the final $K^*$ and $\pi$ mesons. In order to compute the effect of these interactions, the $D_s D K^*$ and $D_s D^* K^*$ form factors are needed.

1 Introduction

In high energy physics, investigation of meson interactions depends on information about the proper functional form of strong form factors. Among all vertices, the charmed meson ones, which play an important role in understanding the final-state re-scattering effects in the hadronic B decays, are much more significant. They are related to the basic parameters $\beta$ and $\lambda$ in the heavy quark effective Lagrangian [1]. Therefore, researchers have concentrated on computing the strong form factors and coupling constants connected to these vertices. Until now, the vertices involving charmed mesons such as $D^* D^* \rho$ [2], $D^* D \pi$ [3, 4], $D D \rho$ [5], $D^* D \rho$ [6], $D D J/\psi$ [7], $D^* D J/\psi$ [8], $D^*D_sK$, $D^*_sD K$, $D^*_0 D_s K$, $D^*_{s0} D K$ [9], $D^*D^* P$, $D^*D V$, DDV [10], $D^* D^* \pi$ [11], $D_s D^* K$, $D_s^* D K$ [12], $D D \omega$ [13], $D_s D_s V$, $D^{*}_s D^{*}_s V$ [14, 15], and $D_1D^*\pi , D_1D_0\pi , D_1D_1\pi$ [16] have been studied within the framework of the QCD sum rules.

The effective Lagrangians for the interaction $D_sDK^*$ and $D_sD^*K^*$ vertices are as follows: [17]:

$$\begin{aligned} \mathcal{L}_{D_s D K^*}= & {} i g_{D_s D K^*}~{K^*}^\alpha (\bar{D}_s \partial _\alpha D -\partial _\alpha \bar{D}_s D),\nonumber \\ \mathcal{L}_{D_s D^* K^*}= & {} -g_{D_s D^* K^*} \epsilon ^{ \alpha \beta \rho \sigma }\partial _{\alpha } D^*_{\beta }(\partial _{\rho } K^{*}_{\sigma } \bar{D}_s \nonumber \\&+D_s \partial _{\rho } \bar{K}^{*}_{\sigma }), \end{aligned}$$

(1)

where $g_{D_s D K^*}$ and $g_{D_s D^* K^*}$ are the strong form factors. From these Lagrangians, the elements related to the $D_sDK^*$ and $D_sD^*K^*$ vertices can be derived in terms of the strong form factors as:

$$\begin{aligned}&\langle D(p) K^*(q, \varepsilon ^{_K}) |D_s(p') \rangle \nonumber \\&\quad = -g_{D_sD K^*}(q^2)\times (p^\mu +p'^\mu )\varepsilon ^{_K}_{\mu } (q),\nonumber \\&\langle D^*(p,\varepsilon ^{_D}) K^*(q,\varepsilon ^{_K}) | D_s(p') \rangle \nonumber \\&\quad = i g_{D_s D^* K^*}(q^2)\times \epsilon ^{ \alpha \beta \mu \nu } p'_\alpha q_{_\beta } \varepsilon ^{_D}_\mu (p) {\varepsilon ^{_K}_\nu }(q), \end{aligned}$$

(2)

where $q=p-p'$.

In this work, we decide to calculate the strong form factors and coupling constants associated with the $D_sDK^*$ and $D_sD^*K^*$ vertices in the frame work of the three-point QCD sum rules (3PSR). As an example of specific application of these coupling constants can be pointed out to branching ratio calculations of hadronic B decays. In this paper, we would like to consider the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay according to the coupling constants of the $D_sDK^*$ and $D_sD^*K^*$ vertices.

The plan of the present paper is as follows: In Sect. 2, the strong form factor calculation of the $D_{s} D K^*$ vertex is derived in the framework of the 3PSR; computing the quark–quark, quark–gluon and gluon–gluon condensate contributions in the Borel transform scheme. Using necessary changes in the expression obtained for the $g_{D_{s} D K^*}$, the strong form factor $g_{ D_{s} D^{*} K^*}$ is presented. In Sect. 3, we analyze the strong form factors as well as the coupling constants with and without the $SU_{f}(3)$ symmetry. For a better analysis, a comparison is made between our results and the predictions of other methods. Finally, we consider the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay using the coupling constants of the $D_sDK^*$ and $D_sD^*K^*$ vertices.

2 Strong form factors of $D_sDK^*$ and $D_sD^*K^*$ vertices

To compute the strong form factors of the $D_sDK^*$ and $D_sD^*K^*$ vertices via the 3PSR, we start with the following correlation functions as

$$\begin{aligned}&\Pi ^{K^*}_{\mu }(p, p')= i^2 \int d^4x d^4y\nonumber \\&\quad \times e^{ip'x}e^{-i(p'-p)y}\left\langle 0 \left| \mathcal {T}\left\{ j^{D_s}(x) {j_\mu ^{K^*}}^{\dagger }(y) {j^{D}}^{\dagger }(0)\right\} \right| 0 \right\rangle ,\nonumber \\&\Pi ^{K^*}_{\mu \nu }(p, p')= i^2 \int d^4x d^4y\nonumber \\&\quad \times e^{ip'x}e^{-i(p'-p)y}\left\langle 0 \left| \mathcal {T}\left\{ j^{D_s}(x) {j_\mu ^{K^*}}^{\dagger }(y) {j^{D^*}_{\nu }}^{\dagger }(0)\right\} \right| 0 \right\rangle ,\nonumber \\ \end{aligned}$$

(3)

where $K^*$ is supposed as an off-shell meson. For off-shell charmed mesons, the correlation functions are:

$$\begin{aligned}&\Pi ^{D}_{\mu }(p, p') = i^2 \int d^4x d^4y\nonumber \\&\quad \times e^{ip'x}e^{-i(p'-p)y}\left\langle 0 \left| \mathcal {T}\left\{ j^{D_s}(x) {j^{D}}^{\dagger }(y) {j_{\mu }^{K^*}}^{\dagger }(0) \right\} \right| 0 \right\rangle ,\nonumber \\&\Pi ^{D^*}_{\mu \nu }(p, p') = i^2 \int d^4x d^4y\nonumber \\&\quad \times e^{ip'x}e^{-i(p'-p)y}\left\langle 0 \left| \mathcal {T}\left\{ j^{D_s}(x) {j^{D^*}_{\nu }}^{\dagger }(y) {j_{\mu }^{K^*}}^{\dagger }(0) \right\} \right| 0 \right\rangle ,\nonumber \\ \end{aligned}$$

(4)

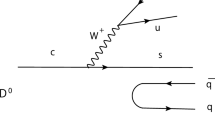
where $j^{D_{s}}=\bar{c} \gamma _5 s,~j^{D}=\bar{c} \gamma _5 u,~j^{D^*_{\mu }}=\bar{c} \gamma _{\mu } u$, and $j^{K^*}_{\mu }=\bar{u} \gamma _{\mu } s$ are interpolating currents with the same quantum numbers of $D_{s},~D,~D^*$, and $K^*$ mesons, respectively. Also, $\mathcal {T}$ is time ordering product, p and $p'$ are the four momentum of the initial and final mesons, respectively, as depicted in Fig. 1.

To calculate the strong form factor of the $D_{s} D K^*$ vertex in the framework of the 3PSR, the correlation functions in Eqs. (3) and (4) are calculated in two different ways. First, they are calculated in the space-like region in terms of quark–gluon language like quark–quark, gluon–gluon condensate, etc. using the Wilson operator product expansion (OPE). It is called the QCD or theoretical side of the QCD sum rules. Second, in the hadronic representation, they are calculated in the time-like region in terms of hadronic parameters such as the form factors, decay constants and masses. It is named the phenomenological or physical side.

In order to calculate the phenomenological part of the correlation functions in Eqs. (3) and (4), three complete sets of intermediate states with the same quantum number should be inserted in these equations. Performing the Fourier transformation, for the phenomenological parts, we have:

$$\begin{aligned} \Pi ^{K^*}_{\mu }= & {} -\frac{\langle 0|j^{D_s }|D_s(p')\rangle \langle D_s(p')|K^*(q,\varepsilon ^{_K}) D(p)\rangle \langle K^* (q,\varepsilon ^{_K})|{j^{K^*}_{\mu }}^{\dagger }|0\rangle \langle D(p)|{j^{D}}^{\dag }|0\rangle }{(p^2-m^2_{D})(p'^2-m^2_{D_s})(q^2-m^2_{K^*})}+\hbox {higher and continuum states,}\nonumber \\ \Pi ^{D}_{\mu }= & {} -\frac{\langle 0|j^{D_s }|D_s(p')\rangle \langle D_s(p')|D(q)K^*(p,\varepsilon ^{_K})\rangle \langle D (q)|{j^{D}}^{\dagger }|0 \rangle \langle K^*(p,\varepsilon ^{_K})| {j_{\mu }^{K^*}}^{\dagger }|0\rangle }{(p^2-m^2_{K^*})(p'^2-m^2_{D_s})(q^2-m^2_{D})}+\hbox {higher and continuum states.} \end{aligned}$$

(5)

The matrix elements $\langle 0 | j_{\mu }^{K^*} | K^*(q,\varepsilon ^{_K}) \rangle$, and $\langle 0 | j^{D_{(s)}} | D_{(s)}(p) \rangle$ are defined as:

$$\begin{aligned} \langle 0 | j_{\mu }^{K^*} | K^*(q,\varepsilon ^{_K}) \rangle= & {} m_{K^*} f_{K^*} \varepsilon ^{*{_K}}_{\mu }(q), \nonumber \\ \langle 0 | j^{D_{(s)}} | D_{(s)}(p) \rangle= & {} \frac{ m^2_{D_{(s)}} f_{D_{(s)}}}{m_c+m_{u(s)}}, \end{aligned}$$

(6)

where $m_{K^*}$, $m_{D_{(s)}}$, $f_{K^*}$, and $f_{D_{(s)}}$ are the masses and decay constants of mesons $K^*$ and $D_{(s)}$, respectively. $\varepsilon _\mu$ is the polarization vector of the vector meson $K^*$.

We should choose one of the Lorentz structures appearing in Eq. (2) and compute $\Pi _{\mu }^{K^*}$ and $\Pi _{\mu }^{D}$ in terms of the strong form factors. As can be seen in Eq. (2), the form factor $g_{D_s D K^*}$ is the same for two the Lorentz structures $p_\mu$ and $p'_\mu$, and thus can be extracted from sum rules for each of them. But we must choose the Lorentz structure which has fewer ambiguities in the 3PSR approach, which means, less influence of the condensates of higher dimension, and a better stability as a function of the Borel mass parameter [3]. With these conditions, we choose the $p_\mu$ structure. However, our calculations show that the results for the $p'_\mu$ structure is exactly the same as this for $p_\mu$. Therefore in this case, we could work with any of the structures appearing in Eq. (2).

Fig. 1

Perturbative diagrams for off-shell $K^*$ (a) and off-shell D meson (b)

Inserting Eqs. (2) and (6) in Eq. (5) and after some calculations, we obtain $\Pi _{\mu }^{K^*}$ and $\Pi _{\mu }^{D}$ in terms of the strong form factors $g^{K^*}_{D_s D K^* }$ and $g^{D}_{D_s D K^* }$ as:

$$\begin{aligned} \Pi _{\mu }^{K^*}= & {} -g^{K^*}_{D_s D K^* }(q^2)\nonumber \\&\times \frac{ m_{K^*}m_{D}^2 m_{D_s}^2 f_{K^*}f_{D} f_{D_s} }{m_c(m_c+m_s)(p^2-m^2_{D})(p'^2-m^2_{D_s})(q^2-m^2_{K^*})}p_{\mu }\nonumber \\&+\hbox {higher and continuum states,}\,\nonumber \\ \Pi _{\mu }^{D}= & {} -g^{D}_{ D_s D K^* }(q^2)\nonumber \\&\times \frac{m_{D_s}^2m_D^2 f_{K^*}f_{D}f_{D_s}(q^2-m_{D}^2-m_{K^*}^2)}{2~m_c(m_c+m_s)m_{K^*} (p^2-m_{K^*}^2)(p'^2-m_{D_s}^2)(q^2-m_{D}^2)}p_{\mu }\nonumber \\&+\hbox {higher and continuum states}\,. \end{aligned}$$

(7)

In the theoretical side, the three-point correlation function contains the perturbative and non-perturbative parts as

$$\begin{aligned} \Pi ^{K^*(D)}_{\mu }=(\Pi ^{K^*(D)}_{per}+\Pi ^{K^*(D)}_{nonper}) ~p_\mu +\hbox {other structures.}\, \end{aligned}$$

(8)

According to the 3PSR method, we can estimate the perturbative part of the correlation function, using the double dispersion relation, as

$$\begin{aligned} \Pi _{per}^{K^*(D)}= & {} -\frac{1}{4 \pi ^2} \int ds\int ds'\frac{\rho ^{K^*(D)}}{(s-p^2)(s'-p'^2)}\nonumber \\&+\hbox {subtraction terms}\,, \end{aligned}$$

(9)

where $\rho ^{K^*(D)}$ is spectral density. The spectral density is calculated in terms of the usual Feynman integrals by the help of the Cutkosky rules, where the quark propagators are replaced by Dirac-delta functions, i.e., $\frac{1}{p^2-m^2}\rightarrow (-2\pi i)\delta (p^2-m^2)$. The diagrams corresponding to the perturbative part (bare loop) are depicted in Fig. 1. Using Fig. 1 and after some straightforward calculations, we have:

$\bullet$ For the off-shell $K^*$ (Fig. 1a):

$$\begin{aligned} \rho ^{K^*}_{ D_s D K^* }= & {} 6I_0[2 m_cm_s-2m_c^2\nonumber \\&+\Delta '+ C'_1 (2 m_cm_s-2m_c^2+u) ]. \end{aligned}$$

$\bullet$ For the off-shell D (Fig. 1b):

$$\begin{aligned} \rho ^{D}_{ D_s D K^*}= & {} 6I_0[2m_cm_s-2m_s^2+\Delta \nonumber \\&+ C_1 (2m_cm_s-2m_s^2+2\Delta + u) ]. \end{aligned}$$

The explicit expressions of the coefficients in the spectral densities are given in Appendix A.

Now, the non-perturbative part contributions to the correlation function are discussed. In QCD, the correlation function can be evaluated by OPE in the deep Euclidean region. Using the expansion of it in terms of a series of local operators with increasing dimension, we get:

$$\begin{aligned} \Pi _{\mu }= & {} C_{\mu }^{(0)}\mathrm{I}+C_{\mu }^{(3)}\langle 0|\bar{\Psi }\Psi |0\rangle \nonumber \\&+C_{\mu }^{(4)}\langle 0|G^{a}_{\rho \nu }G_{a}^{\rho \nu }|0\rangle +C_{\mu }^{(5)}\langle 0| \bar{\Psi } \sigma _{\rho \nu } T^a G_a^{\rho \nu } \Psi | 0\rangle \nonumber \\&+ C_{\mu }^{(6)}\langle 0|\bar{\Psi }\Gamma \Psi \bar{\Psi }\Gamma '\Psi |0\rangle +\cdots , \end{aligned}$$

(10)

where $C_{\mu }^{(i)}$ are the Wilson coefficients, I is the unit operator, $\bar{\Psi }$ is the local fermion field operator and $G^{\rho \nu }$ is the gluon strength tensor. The Wilson coefficient $C_{\mu }^{(0)}$ is the contribution of the perturbative part of QCD ( i.e., $\Pi ^{K^*(D)}_{per}$), and the other coefficients are contributions of the non-perturbative part ($\Pi ^{K^*(D)}_{nonper}$). It is important to note that in above equation, $C_{\mu }^{(5)} \langle 0| \bar{\Psi } \sigma _{\rho \nu } T^a G_a^{\rho \nu } \Psi | 0\rangle \equiv m^2_0 C_{\mu }^{(5)} \langle 0|\bar{\Psi }\Psi |0\rangle$ [18]. Therefore, we can collect the coefficients $C^{(3)}_{\mu }$ and $C^{(5)}_{\mu }$ as $(C^{(3)}_{\mu }+m_0^2~ C^{(5)}_{\mu }) \langle 0|\bar{\Psi }\Psi |0\rangle$, where $m_0^2=0.8\pm 0.2~ \mathrm {GeV}^2$ [18].

In Eq. (10), the Wilson coefficients $C_{\mu }^{(3)}$, $C_{\mu }^{(4)}$ and $C_{\mu }^{(5)}$ of dimensions 3, 4 and 5 are related to contributions of the quark–quark, gluon–gluon and quark–gluon condensate, respectively. Also, $C_{\mu }^{(6)}$ is connected to contribution of the four-quark condensate of dimension six. For the calculation of the condensate terms, we consider these points:

• (a) Our calculations show that the contributions of the four-quark condensate are less than a few percent, therefore the condensate terms of dimensions 3, 4 and 5 are more important than the other terms in OPE.

• (b) In the 3PSR, when the light quark is a spectator, the gluon–gluon condensate contributions can be easily ignored [18].

• (c) The quark condensate contribution of the light quark which is a non spectator, is zero after applying the double Borel transformation with respect to the both variables $p^2$ and $p'^{2}$, because only one variable appears in the denominator.

• (d) In the 3PSR, when the heavy quark is a spectator, the quark–quark condensate contributions are suppressed by inverse of the heavy quark mass, and can be safely omitted [18].

Therefore, to compute the contribution of the non-perturbative part of the correlation function for the off-shell D meson, three diagrams of dimensions 3 and 5, shown in Fig. 2, are considered. In this case, the quark–quark and quark–gluon diagrams are more important than the other terms in the OPE since the light quark s is a spectator.

Fig. 2

Non-perturbative diagrams for the off-shell D meson

For a better analysis, we compare the contributions of the quark–quark plus quark–gluon condensates with the gluon–gluon condensate for the off-shell D meson, by applying the Borel transformation, in the interval $5~\mathrm {GeV}^2 \le Q^2\le 16~\mathrm {GeV}^2$  $(Q^4=-q^2)$ in Fig. 3. As can be seen, the gluon–gluon condensate contributions can be easily ignored.

Fig. 3

The quark–quark (QQ) plus quark–gluon (QG) condensate contributions (solid line) and also gluon–gluon (GG) condensate (dash-dot line) on $Q^2$ for the off-shell D meson

When $K^*$ is an off-shell meson, the gluon–gluon diagrams of dimension 4 are more important than the quark–quark and quark–gluon condensates since the heavy quark c is a spectator. Figure 4 shows these diagrams related to the gluon–gluon condensate.

Fig. 4

Non-perturbative diagrams for the off-shell $K^*$ meson

After some straightforward but lengthy calculations and applying the double Borel transformations [19], the results for the gluon–gluon condensate contributions (Fig. 4), and quark–quark as well as quark–gluon contributions (Fig. 2) are obtained as

$$\begin{aligned} \Pi ^{K^*}_{nonper}=- i\frac{C^{K^*}_{D_sDK^*}}{12} \left\langle \frac{\alpha _s}{\pi } G^2 \right\rangle , \; \Pi ^{D}_{nonper}= \frac{C^{D}_{D_sDK^*}}{12}\langle s\bar{s}\rangle ,\nonumber \\ \end{aligned}$$

(11)

where the explicit expressions for $C_{D_sDK^*}^{K^*}$ and $C_{D_sDK^*}^{D}$ are given in Appendix B. It should be noted that in order to obtain the gluon–gluon condensate contributions, we followed the same procedure as stated in Ref. [19].

The strong form factors are calculated by equating two representations of the correlation function and applying the Borel transformations [20] with respect to the $p^2(p^2\rightarrow M^2_1)$ and $p'^2(p'^2\rightarrow M^2_2)$ on the phenomenological as well as the perturbative and non-perturbative parts of the correlation function in order to suppress the contributions of the higher states and continuum. The equations for the strong form factors are obtained as follows:

$$\begin{aligned} g^{K^*}_{D_sDK^* }(q^2)= & {} \Lambda ^{K^*}_{D_sDK^*} \left\{ -\frac{1}{4\pi ^2}\int ^{s_0^{D_s}}_{(m_c+m_s)^2}ds' \int ^{s_0^D}_{s_1}\right. \nonumber \\&\times ds~ \rho ^{K^*}_{D_sDK^*}(s,s',q^2) e^{-\frac{s}{M_1^2}} e^{-\frac{s'}{M_2^2}}\nonumber \\&\left. - i\frac{M^{2}_{1}M^{2}_{2}}{12} \left\langle \frac{\alpha _s}{\pi } G^2 \right\rangle \times C^{K^*}_{D_sDK^*} \right\} ,\nonumber \\ g^{D}_{D_sDK^*}(q^2)= & {} \Lambda ^{D}_{D_sDK^*} \left\{ -\frac{1}{4\pi ^2}\int ^{s^{D_s}_0}_{(m_c +m_s)^2}ds' \int ^{s^{K^*}_0}_{s_2}\right. \nonumber \\&\times ds~ \rho ^{D}_{ D_sDK^*}(s,s',q^2) e^{-\frac{s}{M_1^2}} e^{-\frac{s'}{M_2^2}}\nonumber \\&\left. +\frac{M_1^2 M_2^2}{12}\langle s\bar{s}\rangle \times C^{D}_{D_sDK^*} \right\} , \end{aligned}$$

(12)

where $\langle \frac{\alpha _s}{\pi } G^2 \rangle =0.012~ \mathrm {GeV}^{4}$ [21], $\langle s \bar{s}\rangle =(0.8\pm 0.2)\langle u \bar{u}\rangle$, and $\langle u \bar{u}\rangle =-{(0.24\pm 0.01 ~\mathrm {GeV})}^3$ [22]. In these relations, $s^{K^*}_0$ and $s^{D(D_s)}_0$ are the continuum thresholds in $K^*$ and $D(D_s)$ mesons, respectively. Also, $s_1$ and $s_2$ are the lower limits of the integrals over s as

$$\begin{aligned} s_{1}=\frac{m_c^2(m_c^2-s'+q^2)}{m_{c}^{2}-s'}\,,\quad \quad \quad s_{2}=\frac{m_s^2(m_s^2-s'+q^2)}{m_{s}^{2}-s'}\,. \end{aligned}$$

The phrases $\Lambda ^{K^*}_{D_sDK^*}$ and $\Lambda ^{D}_{D_sDK^*}$ are defined as:

$$\begin{aligned} \Lambda ^{K^*}_{D_sDK^*}= & {} -\frac{m_c(m_c+m_s)(q^2-m_{K^*}^{2})}{m_{K^*} m_{D}^2m_{D_s}^2 f_{K^*}f_{D}f_{D_s}}~ e^{\frac{m_{D}^2}{M_1^2}}e^{\frac{m_{D_s}^2}{M_2^2}},\nonumber \\ \Lambda ^{D}_{D_sDK^*}= & {} -\frac{2~m_c(m_c+m_s)m_{K^*}(q^2-m_{D}^{2})}{ m_{D}^2m_{D_s}^2 f_{K^*}f_{D} f_{D_s}(q^2-m_{D_s}^2-m_{K^*}^2)}\nonumber \\&\times e^{\frac{m_{K^*}^2}{M_1^2}} e^{\frac{m_{D_s}^2}{M_2^2}}. \end{aligned}$$

(13)

Following the previous steps, relations similar to Eq. (12) can be obtained for the strong form factors of the $D_{s} D^{*} K^*$ vertex via the 3PSR. It should be noted that in this case, calculations are done for the Lorentz structure $\epsilon ^{ \alpha \beta \mu \nu }p_{\alpha }p'_{\beta }$. In order to have the correct relations for the strong form factors of the $D_{s} D^{*} K^*$ vertex, the appropriate terms of $\Lambda$, the spectral density $\rho$, and quark–gluon condensate coefficients $C_{D_sD^*K^*}^{K^*}$ and $C_{D_sD^*K^*}^{D^*}$ should be replaced in Eq. (12). The explicit expressions for $C_{D_sD^*K^*}^{K^*}$ and $C_{D_sD^*K^*}^{D^*}$ are given in Appendix B. In addition, proper expressions for $\Lambda$ related to the strong form factors $g^{K^*}_{D_{s} D^{*} K^*}$ and $g^{D^*}_{D_{s} D^{*} K^*}$ are as follows:

$$\begin{aligned} \Lambda ^{K^*}_{D_{s}D^{*}K^*}= & {} -\frac{(m_c+m_s)(q^2-m^2_{K^*})}{m_{K^*}m_{D^{*}}m^{2}_{D_{s}} f_{K^*}f_{D^{*}}f_{D_{s}}}~ e^{\frac{m_{D^*}^2}{M_1^2}}e^{\frac{m_{D_s}^2}{M_2^2}},\nonumber \\ \Lambda ^{D^{*}}_{D_{s}D^{*}K^*}= & {} -\frac{(m_c+m_s)(q^2-m^2_{D^*})}{m_{K^*}m_{D^{*}}m^{2}_{D_{s}} f_{K^*}f_{D^{*}}f_{D_{s}}}~e^{\frac{m_{K^*}^2}{M_1^2}} e^{\frac{m_{D_s}^2}{M_2^2}}. \end{aligned}$$

(14)

Also, the spectral densities are calculated as

$$\begin{aligned} \rho ^{K^*}_{ D_s D^* K^* }= & {} -12I_0[C'_1m_c+C'_2(m_c-m_s)+m_c],\nonumber \\ \rho ^{D^*}_{ D_s D^* K^*}= & {} 12I_0[C_1m_s+C_2(m_s-m_c)+m_s]. \end{aligned}$$

(15)

3 Numerical analysis

In this section, the strong form factors and coupling constants for the $D_{s} D K^*$ and $D_s D^* K^*$ vertices as well as the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay are considered. For this aim, the values of quark and meson masses are chosen as: $m_s = 0.14 \pm 0.01~\mathrm GeV$, $m_c=1.26 \pm 0.02 ~\mathrm GeV$, $m_{D^*}=2.01~ \mathrm GeV$, $m_{K^*}=0.89~ \mathrm GeV$, $m_{D_{s}}=1.97~\mathrm GeV$, and $m_{D}=1.87~\mathrm GeV$ [23]. Moreover, the leptonic decay constants are presented in Table 1.

Table 1 The leptonic decay constants in $\mathrm MeV$

Fig. 5

$M_1^2$ and $M_2^2$ dependence of $g_{D_s D K^*}^{K^*}$ and $g_{D_s D K^*}^{D}$ for three values of the continuum thresholds

Fig. 6

The strong form factor $g^{D}_{D_sDK^*}$ on $Q^2$ for different values of the Borel parameters

There are four auxiliary parameters containing the Borel mass parameters $M_1$ and $M_2$, and continuum thresholds $s^{K^*}_{0}$, $s_{0}^{D(D_s)}$ and $s^{D^*}_{0}$ in Eq. (12). The strong form factors and coupling constants are the physical quantities, and should be independent of them. However the continuum thresholds are not completely arbitrary; these are related to the energy of the first exited state. The values of the continuum thresholds are taken to be $s^{K^*}_{0}=(m_{K^*}+\delta )^2$, $s_{0}^{D(D_s)}=(m_{D(D_s)}+\delta ')^2$ and $s_{0}^{D^*}=(m_{D^*}+\delta ')^2$ . We use $0.40 ~\mathrm{GeV}\le \delta \le 0.60~\mathrm{GeV}$ and $0.30 ~\mathrm{GeV}\le \delta ' \le 0.70~\mathrm{GeV}$ [2,3,4]. Our results should be almost insensitive to the intervals of the Borel parameters. On the other hand, the intervals of the Borel mass parameters must suppress the higher states, continuum and contributions of the highest-order operators. In other words, the sum rule for the strong form factors must converge. We get a very good stability for the form factors as a function of the two independent Borel parameters in the regions $6 ~\mathrm{GeV^2}< M_1^2 < 8 ~\mathrm{GeV^2}$ and $6 ~\mathrm{GeV^2}< M_2^2 < 8 ~\mathrm{GeV^2}$ when $K^*$ is an off-shell meson, and also $6 ~\mathrm{GeV^2}< M_1^2 < 8 ~\mathrm{GeV^2}$ and $8 ~\mathrm{GeV^2}< M_2^2 < 10 ~\mathrm{GeV^2}$ when D ($D^*$) meson is an off-shell. Figure 5 shows the dependence of the form factors $g_{D_s D K^*}^{K^*}$ and $g_{D_s D K^*}^{D}$ on the Borel mass parameters $M_1^2$ and $M_2^2$ for three values of the continuum thresholds $s_0^{K^*}$ and $s_0^D$.

As previously mentioned, these intervals of $M_1^2$ and $M_2^2$ must suppress the higher states, continuum and contributions of the highest-order operators. For instance, Fig. 6 shows the strong form factor $g^{D}_{D_sDK^*}$ with respect to $Q^2$ for different values of the Borel parameters. In addition, this figure displays perturbative contribution of the form factor $g^{D}_{D_sDK^*}$. As can be seen, the important contribution of the form factor comes from the perturbative part, i.e., the contributions of the quark–quark and quark–gluon condensates, as the most important terms of the condensates in this case, are less than the perturbative part. Therefore, the obtained regions for the Borel parameters can suppress the higher order condensates.

It should be noted that, from now on, to calculate the strong form factors $g_{D_s D K^*}^{K^*}$ and $g_{D_s D^* K^*}^{K^*}$, we get $[M_1^2, M_2^2]=[7, 7]~\mathrm GeV^2$, and for $g_{D_s D K^*}^{D}$ and $g_{D_s D^* K^*}^{D^*}$, we get $[M_1^2, M_2^2]=[7, 9]~\mathrm GeV^2$.

The numerical results for the strong form factors calculated via the 3PSR in Eq. (12) have a cut-off. Therefore, we look for a parametrization of the form factors in such that in the validity region of the 3PSR, this parametrization coincides with the sum rules prediction. Our numerical calculations show that the sum rule predictions for the form factors in Eq. (12) are well fitted to the following function:

$$\begin{aligned} g(Q^2)=A~e^{-Q^2/B}. \end{aligned}$$

The values of the parameters A and B are given in Table 2 for various $(\delta , \delta ')$.

The dependence of the strong form factors $g^{D}_{D_sDK^*}(Q^2)$, $g^{K^*}_{D_sDK^*}(Q^2)$, $g^{D^*}_{D_sD^*K^*}(Q^2)$ and $g^{K^*}_{D_sD^*K^*}(Q^2)$ in $Q^2$ are shown in Fig. 7. The boxes and circles in Fig. 7 show the results of the numerical evaluation via the 3PSR for the form factors $g^{K^*}_{ D_sDK^*} (g^{K^*}_{ D_sD^*K^*})$ and $g^{D}_{ D_sDK^*}(g^{D^*}_{ D_sD^*K^*})$, respectively. As can be seen, the form factors and their fit functions coincide together, well.

The value of the strong form factors at $Q^2 = -m_m^2$, where $m_m$ is the mass of the off-shell meson, is defined as coupling constant. Coupling constant results of the two vertices, ${D_sDK^*}$ and ${D_sD^*K^*}$, are presented in Table 3. It should be mentioned that the coupling constant $g_{D_sDK^*}$ is the dimensionless quantity and the coupling constant $g_{D_sD^*K^*}$ is in the unit of $\mathrm GeV^{-1}$. The errors are estimated by variation of the Borel parameters, variation of the continuum thresholds, the leptonic decay constants and uncertainties in the values of the other input parameters. It should be noted that the main uncertainty comes from the continuum thresholds and the decay constants.

Table 4 shows a comparison between our results with the values predicted by the light-cone sum rules (LCSR) method. The results of Ref. [26] have been rescaled according to the strong form factor definitions in Eq. (2). It should be reminded that the value of $g_{D_sDK^*} (g_{D_sD^*K^*})$ in Table 4 is an average of the two coupling constant values $g^{K^*}_{D_sDK^*}(g^{K^*}_{D_sD^*K^*})$ and $g^{D}_{D_sDK^*}(g^{D}_{D_sD^*K^*})$ in Table 3.

In order to investigate the strong coupling constant values via the $SU_{f}(3)$ symmetry, the mass of the s quark is ignored in all calculations. In view of the $SU_{f}(3)$ symmetry, the values of the parameters A and B for the $g_{D_sDK^*}$ and $g_{D_sD^*K^*}$ strong form factors are given in Table 5 with $(\delta ,\delta ')=(0.50,0.50)~{\mathrm{GeV}}$. In addition, considering the $SU_{f}(3)$ symmetry, we obtain the values of the coupling constants of the vertices ${D_sDK^*}$ and ${D_sD^*K^*}$ as shown in Table 6. It is possible to compare the coupling constant values of $g_{D_sDK^*}$ and $g_{D_sD^*K^*}$ with $g_{DD\rho }$ and $g_{D^*D^*\rho }$ respectively, in the $SU_{f}(3)$ symmetry consideration. Table 7 shows a comparison between our results with the values predicted by the LCSR and 3PSR methods.

Table 2 Parameters appearing in the fit functions for the $D_sDK^*$ and $D_sD^*K^*$ vertices for various $(\delta , \delta ')$, where $(\delta _1,\delta '_1)=(0.40,0.30),$ $~(\delta _2,\delta '_2)=(0.50,0.50)$ and $(\delta _3,\delta '_3)=(0.60,0.70) ~\mathrm GeV$

Fig. 7

The strong form factors $g^{D}_{D_sDK^*}$, $g^{K^*}_{D_sDK^*}$, $g^{D^*}_{D_sD^*K^*}$ and $g^{K^*}_{D_sD^*K^*}$ on $Q^2$

An example of specific application of these coupling constants is in branching ratio calculations of B meson decays. It is reminded that re-scattering effects play an important role in the hadronic B decays. It is not easy to take them into account in a systematic way due to the non-perturbative nature of the multi-particle dynamics. In practical calculations, the phenomenological models can be used to overcome the difficulty [26]. The one-particle-exchange is one of these phenomenological models. In this model, the soft re-scattering of the intermediate states in two-body channels with one-particle exchange makes the main contributions. The phenomenological Lagrangian contains many input parameters, which describe the strong couplings among the charmed mesons in the hadronic B decays.

For instance, we would like to consider the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay according to the method of Refs. [27, 28]. It should be noted that our main goal in this investigation is to illustrate the use of the coupling constants $g_{D_sDK^*}$ and $g_{D_sD^*K^*}$ in branching ratio calculations of B decays. Therefore, we do not discuss the methods of calculation, which are presented here.

According to Refs. [27, 28], the $B \rightarrow K^* \pi$ decay amplitude, $A_{K^* \pi }$ contains the short-distance (SD) and the long-distance (LD) contributions:

$$\begin{aligned} {\mathcal {M}}_{K^* \pi } = {\mathcal {M}}_{SD} + {\mathcal {M}}_{LD}. \end{aligned}$$

(16)

Using the effective Hamiltonian for non-leptonic B decays [29,30,31,32,33] in the factorization approximation, the value of the SD amplitude is ${\mathcal {M}}_{SD}=1.52\times 10^{-8}$, which is evaluated by the following formula [27]:

$$\begin{aligned}&{\mathcal {M}}_{SD}(B^+ \rightarrow {K^*}^0 \pi ^+)\nonumber \\&\quad = G_F \sqrt{2} F_1^{B\rightarrow \pi }(m_{K^*}^2) f_{K^*} m_{K^*} V_{tb}^*V_{ts}\nonumber \\&\qquad \times \left[ a_4-\frac{ a_{10} }{ 2 } \right] \left( \varepsilon ^*\cdot p_B\right) . \end{aligned}$$

(17)

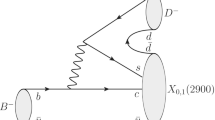
Figure 8 shows diagrams, for the $B\rightarrow K^* \pi$ decay with $D_s, D^*$ intermediate states, used to calculate the ${\mathcal {M}}_{LD}$ part of the amplitude. As can be seen in Fig. 8, the $B\rightarrow {K^*} \pi$ decay may be occur in two steps. First, the B decays into a $D_s D^*$ intermediate state ($B\rightarrow D_s D^*$), and then these two particles exchange a $D (D^*)$ producing the final $K^*$ and $\pi$. In order to compute the effect of these interactions in the final decay rate, we need the $D_s D K^* (D_s D^* K^*)$ and $D^* D \pi (D^* D^* \pi )$ form factors.

Table 3 The coupling constant of the vertices ${D_sDK^*}$ and ${D_sD^*K^*}$

Table 4 Values of the strong coupling constant using the 3PSR (ours) and LCSR approaches

Table 5 Parameters appearing in the fit functions for the $g_{D_sDK^*}$ and $g_{D_sD^*K^*}$ form factors in $SU_{f}(3)$ symmetry with $(\delta ,\delta ')=(0.50,0.50)~\mathrm GeV$

Table 6 The coupling constants of the vertices ${D_sDK^*}$ and ${D_sD^*K^*}$, in $SU_{f}(3)$ symmetry

Table 7 Values of the coupling constant using the LCSR, and 3PSR

Fig. 8

Diagrams for the $B\rightarrow K^* \pi$ decay with $D_s, D^*$ intermediate states

The ${\mathcal {M}}_{LD}$ consists of two parts, real and imaginary:

$$\begin{aligned} {\mathcal {M}}_{LD}={\mathcal {R}}_{LD}+i\, {\mathcal {I}}_{LD}. \end{aligned}$$

(18)

The computation of the imaginary part of the charming penguin diagrams contributing to $B\rightarrow K^*\pi$ decay gives

$$\begin{aligned} {\mathcal {I}_{LD}}= & {} \frac{m_D}{32 \pi ^2 m_B} \sqrt{\omega ^{*2}-1} \int d\mathbf{n}~ \mathcal{M}(B\rightarrow D_s D^{*}) \nonumber \\&\times \mathcal{M}(D_s D^{*}\rightarrow K^* \pi ) , \end{aligned}$$

(19)

where the integration is over the solid angle. Using the following kinematics:

$$\begin{aligned}&p_B^\mu ~=~m_B v^\mu =(m_B,{\vec {0}} )\ ,\ ~~~~ p^\mu _{D^{*}}~=~m_{D^*}v^{\prime \mu } ,\nonumber \\&q~=~p_B-p_{D^{*}} , \end{aligned}$$

(20)

the amplitude for the decay $B\rightarrow D_s D^{*}$ is computed by factorization as:

$$\begin{aligned} \mathcal{M}(B(v)\rightarrow D_s(q) D^{*}(\epsilon , v^\prime ))= & {} - K \,(m_B+m_{D^*})\,\epsilon ^{*}\cdot v\,,\nonumber \\ \end{aligned}$$

(21)

where $K =\sqrt{2} \frac{G_{F}}{1+\omega ^*}V_{cb}^* V_{cs}\ a_2 \sqrt{m_B m_{D^*}} f_{D_s}$, and $\omega ^* = \frac{m_B^2+m_{D^*}^2-m^2_{D_s}}{2 m_{D^*} m_B}$. Using the heavy quark effective lagrangian, the calculation of the amplitude $D_s \,D^{*}\rightarrow K^*\pi$ leads to [27]:

$$\begin{aligned}&\mathcal{M}(D_s(q) D^{*}(\epsilon , v^\prime )\rightarrow K^*(p_K,\hat{\epsilon })\pi (p_\pi ))\nonumber \\&\quad = - \frac{2 g\, F^2(|\mathbf {p}_\pi |) }{f_\pi } \frac{g_V}{\sqrt{2}}\sqrt{ \frac{m_{D^*}}{m_{D_s}}} \epsilon _\lambda \hat{\epsilon }^*_\sigma \nonumber \\&\qquad \times \left[ \frac{2\beta \, m_D\, q^\sigma p_\pi ^\lambda }{ (m_{D}v^\prime -p_\pi )^2-m^2_{D} }\right. \nonumber \\&\qquad + \left. \frac{4 \lambda \, m_{D^*}\, G^{\sigma \lambda }(p_\pi ,p_K, v^\prime )}{ (m_{D^*}v^\prime -p_\pi )^2-m^2_{D^*} }\right] , \end{aligned}$$

(22)

where

$$\begin{aligned} G^{\sigma \lambda }(p_\pi ,p_K, v^\prime )= & {} -\, (v^\prime \cdot q) \biggl (g^{\sigma \lambda }(p_K\cdot p_\pi ) -p_\pi ^\sigma p_K^\lambda \biggr ) \nonumber \\&- \,(q\cdot p_\pi )\biggl (v^{\prime \sigma }p_K^\lambda -g^{\sigma \lambda }(v^\prime \cdot p_K)\biggr )\nonumber \\&-\, q^\lambda \biggl (p_\pi ^\sigma (p_K\cdot v^\prime ) - v^{\prime \sigma } (p_K\cdot p_\pi )\biggr ).\nonumber \\ \end{aligned}$$

(23)

Eq. (22) is calculated based on the three parameters $F(|\mathbf {p}_\pi |)$, g and $g_V$. $F(|\mathbf {p}_\pi |)$ is a form factor taking into account that in the vertex $DD^*\pi$ the pion is not soft and therefore the coupling constant should be corrected. Its central value is $F(|\mathbf {p}_\pi |)\, = \,0.065$ determined by a quark potential model and discussed in Ref. [28]. The definition of g is related to the coupling $G_{D^*D\pi }$, which can be written in general as $G_{D^*D\pi }=\frac{2 g~ m_D }{f_\pi }$. The parameter g is predicted to have the value $g = 0.59 \pm 0.07 \pm 0.01$ [35]. The definition of $g_V$ is expressed in Ref. [34] and its value is $g_V\simeq 5.8$. The basic parameters $\beta$ and $\lambda$ in the heavy quark effective Lagrangian can be related to the strong coupling constants $g_{D_s D K^*}$ and $g_{D_s D^* K^*}$ as [1, 26]:

$$\begin{aligned} \beta = \frac{\sqrt{2}\, g_{D_sDK^*}}{2\,g_V},~~~~~~~ \lambda =\frac{\sqrt{2}\, g_{D_sD^*K^*}}{2\,g_V}. \end{aligned}$$

(24)

Our numerical values for the $g_{D_s D K^*}$ and $g_{D_s D^* K^*}$ have been presented in Table 4. Using Eqs. (21) and (22) in Eq. (19) and straightforward calculations, our numerical value for the imaginary part of the LD amplitude of two diagrams (a) and (b) in Fig. 8 is ${\mathcal {I}}^{(a, b)}_{LD}=-2.46\times 10^{-8}$.

A similar method of the imaginary part is used to calculate the real part of the LD amplitude [27]. The result for ${\mathcal {R}}^{(a, b)}_{LD}=2.34\times 10^{-8}$, which is the same order of the imaginary part.

The branching ratio of the non-leptonic process $B^+\rightarrow K^{*0} \pi ^+$ is given by

$$\begin{aligned}&\mathcal {BR}(B^+\rightarrow K^{*0} \pi ^+) \nonumber \\&\quad =\frac{\tau _B}{16 \pi m^3_B}|\mathcal {M}_{K^*\pi }|^2 \sqrt{\lambda (m_B^2, m_K^2, m_{\pi }^2)}, \end{aligned}$$

(25)

where $\lambda (m_B^2, m_K^2, m_{\pi }^2)=m_B^4+m_K^4+m_{\pi }^4-2m_B^2m_K^2-2m_B^2m_{\pi }^2-2m_K^2m_{\pi }^2$. Our results for the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay are presented in Table 8. These results are obtained for only the short distance amplitude $({\mathcal {M}}_{SD})$, and also for the total amplitude (${\mathcal {M}}_{SD}+{\mathcal {M}}_{LD}$). Furthermore, this table contains the experimental value for the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$. Considering the error in the experimental value, our estimation for the branching ratio value of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay with the total amplitude is in consistent agreement with the experimental data.

Table 8 Branching ratio values (units $10^{-5}$) of the $B^+\rightarrow {K^*}^0 \pi ^+$ mode

In summary, taking into account the contributions of the quark–quark, quark–gluon and gluon–gluon condensate corrections, the strong form factors $g_{D_sDK^*}$ and $g_{D_sD^*K^*}$ were estimated within the 3PSR with and without the $SU_{f}(3)$ symmetry. A comparison was made between our results and the predictions of other methods. Finally, the branching ratio of the $B^+\rightarrow {K^*}^0 \pi ^+$ decay was estimated using the coupling constants of the $D_sDK^*$ and $D_sD^*K^*$ vertices.

Appendices

Appendix A

In this appendix, the explicit expressions of the coefficients in the spectral densities are given as:

$$\begin{aligned} I_0(s,s',q^2)= & {} \frac{1}{4\lambda ^\frac{1}{2}(s,s',q^2)},\nonumber \\ \lambda (a,b,c)= & {} a^2+ b^2+ c^2- 2ac- 2bc- 2ac ,\nonumber \\ \Delta= & {} s'+m_s^2-m_c^2,\nonumber \\ \Delta '= & {} s'+m_c^2-m_s^2,\nonumber \\ \Delta ''= & {} s+m_s^2,\nonumber \\ u= & {} s+s'-q^2,\nonumber \\ C_1= & {} \frac{1}{\lambda (s,s',q^2)}[2 s' \Delta '' -u \Delta ],\nonumber \\ C_2= & {} \frac{1}{\lambda (s,s',q^2)}[2 s \Delta -u \Delta '' ],\nonumber \\ \end{aligned}$$

also $C'_1={C_1}_{|_{m_c\leftrightarrow m_s}}$ and $C'_2={C_2}_{|_{m_c\leftrightarrow m_s}}$.

Appendix B

In this appendix, the explicit expressions of the coefficients of the quark and gluon condensate contributions of the strong form factor in the Borel transform scheme is presented.

$$\begin{aligned} C_{D_{s}DK^*}^{D}= & {} \Bigg (3\,\frac{m_{{s}}{m_{{c}}}^{2}}{M_{1}^{4} M_{2}^{2}}-3\,{\frac{m_{{s}}{q} ^{2}}{M_{1}^{4} M_{2}^{2}}}+3\,{\frac{m_{{c}}{m_{{s}}}^{2}}{M_{1}^{4} M_{2}^{2}}}\\&-\frac{5}{2}\,{\frac{{m_{{0}}}^{2}m_{{c}}}{M_{1}^{4} M_{2}^{2}}}+3\,{\frac{m_{{s}} {m_{{c}}}^{2}}{M_{1}^{2} M_{2}^{4}}}-3\,{\frac{{m_{{0}}}^{2}m_{{c}}}{M_{1}^{2} M_{2}^{4}}}\\&-\frac{1}{2}\,{\frac{{m_{{0}}}^{2}{m_{{c}}}^{3}}{M_{1}^{4}M_{2 }^{4}}}+\frac{1}{2}\,{\frac{{m_{{0}}}^{2}m_{{c}}{q}^{2}}{M_{1}^{4}M_{2 }^{4}}}+3\,{\frac{{m_{{c}}}^{3}{m_{{s}}}^{2}}{M_{1}^{2}M_{2}^{6}}}\\&-\frac{3}{2} \,{\frac{{m_{{0}}}^{2}{m_{{c}}}^{3}}{M_{1}^{2}M_{2}^{6}}}\Bigg )\times e^{-\frac{m_c^2}{M_2^2}},\\ C_{D_{s}D^* K^*}^{D^*}= & {} \Bigg ( 6\,{\frac{m_{{s}}m_{{c}}}{M_{1}^{2}M_{2}^{4}}}-6\,{\frac{{q}^{2}{m_{{s}} }^{2}}{M_{1}^{4}M_{2}^{4}}}+2\,{\frac{{m_{{0}}}^{2}{q}^{2}}{ M_{1}^{4}M_{2}^{4}}}\\&+6\,{\frac{{m_{{c}}}^{2}{m_{{s}}}^{2}}{M_ {1}^{4}M_{2}^{4}}}-2\,{\frac{{m_{{0}}}^{2}{m_{{c}}}^{2}}{M_{ 1}^{4}M_{2}^{4}}}+6\,{\frac{{m_{{c}}}^{2}{m_{{s}}}^{2}}{M_{1}^{2}M_{2}^{6}}}\\&-3\,{\frac{{m_{{0}}}^{2}{m_{{c}}}^{2}}{M_{1}^{2}M_{2}^{6}}}\Bigg )\times e^{-\frac{m_c^2}{M_2^2}}, \\ C_{D_sDK^*}^{K^*}= & {} -\hat{I}_0(3,2,2)m_c^6-\hat{I}_1(3,2,2)m_c^5 m_s\\&+\hat{I}_2(3,2,2)m_c^5m_s+2\hat{I}_0(3,2,2)m_c^5m_s \\&-\hat{I}_1(3,2,2)m_c^4m_s^2+\hat{I}_2(3,2,2)m_c^4m_s^2\\&-2\hat{I}_0(3,2,2)m_c^3m_s^3-\hat{I}_2(3,1,2)m_c^4\\ \end{aligned}$$

$$\begin{aligned}&-\hat{I}_0^{[0,1]}(3,2,2)m_c^4+3\hat{I}_1(2,2,2)m_c^4\\&-3\hat{I}_2(2,2,2)m_c^4+\hat{I}_1(3,1,2)m_c^4 \\&-3\hat{I}_0(3,2,1)m_c^4+2\hat{I}_2(2,2,2)m_c^3m_s\\&+2\hat{I}_0(3,2,1)m_c^3m_s+2\hat{I}_0^{[1,0]}(3,2,2)m_c^3m_s \\&-2\hat{I}_1(2,2,2)m_c^3m_s+\hat{I}_2^{[1,0]}(3,2,2)m_c^3m_s\\&+6\hat{I}_0(4,1,1)m_c^3m_s+4\hat{I}_0(2,2,2)m_c^3m_s \\&+\hat{I}_2(3,2,1)m_c^3m_s-\hat{I}_1(3,2,1)m_c^3m_s\\&+\hat{I}_0(3,1,2)m_c^3m_s+\hat{I}_1^{[1,0]}(3,2,2)m_c^3m_s \\&-2\hat{I}_0(2,2,2)m_c^2m_s^2+2\hat{I}_1(3,1,2)m_c^2m_s^2\\&-3\hat{I}_0(4,1,1)m_c^2m_s^2-2\hat{I}_2(3,1,2)m_c^2m_s^2 \\&-2\hat{I}_0^{[0,1]}(3,2,2)m_c^2m_s^2+5\hat{I}_0(3,1,2)m_cm_s^3\\&+2\hat{I}_2(2,1,3)m_cm_s^3+2\hat{I}_2(3,1,2)m_cm_s^3 \\&-2\hat{I}_1(2,1,3)m_cm_s^3-2\hat{I}_1(3,1,2)m_cm_s^3\\&-\hat{I}_0(2,2,2)m_s^4+\hat{I}_0^{[1,0]}(3,2,2)m_s^4 \\&-5\hat{I}_1^{[1,1]}(3,2,2)m_c^2+2\hat{I}_0^{[0,1]}(3,1,2)m_c^2\\&-5\hat{I}_2^{[1,1]}(3,2,2)m_c^2+3\hat{I}_2^{[1,0]}(3,2,1)m_c^2 \\&+2\hat{I}_0^{[0,1]}(2,2,2)m_c^2+3\hat{I}_1(1,3,1)m_c^2\\&-2\hat{I}_0(1,2,2)m_c^2+3\hat{I}_1^{[1,0]}(3,2,1)m_c^2 \\&-3\hat{I}_2(1,3,1)m_c^2-12\hat{I}_0(1,1,3)m_cm_s\\&+\hat{I}_2^{[1,1]}(3,2,2)m_cm_s-3\hat{I}_1^{[1,0]}(3,2,1)m_cm_s \\&-9\hat{I}_0(2,1,2)m_cm_s+3\hat{I}_1(1,3,1)m_cm_s\\ \end{aligned}$$

$$\begin{aligned}&-2\hat{I}_1^{[0,1]}(2,1,3)m_cm_s-\hat{I}_2(2,2,1)m_cm_s \\&-3\hat{I}_2^{[1,0]}(3,2,1)m_cm_s+\hat{I}_1(2,2,1)m_cm_s\\&+4\hat{I}_1(2,1,2)m_cm_s-2\hat{I}_2^{[0,1]}(2,1,3)m_cm_s \\&-4\hat{I}_2(2,1,2)m_cm_s-3\hat{I}_2(1,3,1)m_cm_s\\&+\hat{I}_1^{[1,1]}(3,2,2)m_cm_s-2\hat{I}_0(3,1,1)m_s^2 \\&+\hat{I}_2(2,1,2)m_s^2-\hat{I}_1(2,1,2)m_s^2\\&+2\hat{I}_0^{[1,0]}(2,2,2)m_s^2+3\hat{I}_0(1,1,3)m_s^2 \\&+\hat{I}_2^{[1,0]}(2,2,2)m_s^2-2\hat{I}_0(2,2,1)m_s^2\\&+\hat{I}_1^{[1,0]}(2,2,2)m_s^2+2\hat{I}_0^{[0,1]}(2,2,2)m_s^2 \\&+3\hat{I}_0(2,1,2)m_s^2-2\hat{I}_0^{[1,1]}(2,2,2)\\&-2\hat{I}_0^{[0,2]}(3,1,2)-2\hat{I}_1(1,2,1)\\&+2\hat{I}_0^{[0,1]}(2,2,1) \\&+\hat{I}_0^{[0,1]}(1,2,2)+2\hat{I}_2(1,2,1)\\&-3\hat{I}_0^{[1,1]}(3,2,1)-3\hat{I}_0^{[0,1]}(1,1,3)+\hat{I}_0(2,1,1) \\&+2\hat{I}_2(1,1,2)+\hat{I}_0^{[0,1]}(2,1,2)-2\hat{I}_1(1,1,2),\\ C_{D_{s}D^*K^*}^{K^*}= & {} 2\hat{I}_{2}(3,2,2)m_{c}^{5}+2\hat{I}_{0}(3,2,2)m_{c}^{5}\\&+2\hat{I}_{1}(3,2,2)m_{c}^{5}-2\hat{I}_{2}(3,2,2)m_{c}^{4}m_{s}\\&-2\hat{I}_{0}(3,2,2)m_{c}^{3}m_{s}^{2}-2\hat{I}_{2}(3,2,2)m_{c}^{3}m_{s}^{2}\\&-2\hat{I}_{1}(3,2,2)m_{c}^{3}m_{s}^{2}+2\hat{I}_{2}(3,2,2)m_{c}^{2}m_{s}^{3}\\&+4\hat{I}_{2}(2,2,2)m_{c}^{3}+2\hat{I}_0^{[0,1]}(3,2,2)m_{c}^{3}\\ \end{aligned}$$

$$\begin{aligned}&+6\hat{I}_{1}(4,1,1)m_{c}^{3}+2\hat{I}_2^{[1,0]}(3,2,2)m_{c}^{3}\\&+6\hat{I}_{0}(4,1,1)m_{c}^{3}+4\hat{I}_{0}(2,2,2)m_{c}^{3}\\&+2\hat{I}_{0}(3,2,1)m_{c}^{3}+2\hat{I}_0^{[1,0]}(3,2,2)m_{c}^{3}\\&+2\hat{I}_1^{[0,1]}(3,2,2)m_{c}^{3}+2\hat{I}_2^{[0,1]}(3,2,2)m_{c}^{3}\\&-2\hat{I}_{1}(3,1,2)m_{c}^{3}+2\hat{I}_{1}(3,2,1)m_{c}^{3}\\&+2\hat{I}_1^{[1,0]}(3,2,2)m_{c}^{3}+4\hat{I}_{1}(2,2,2)m_{c}^{3}\\&+6\hat{I}_{2}(4,1,1)m_{c}^{3}-4\hat{I}_{2}(2,2,2)m_{c}^{2}m_{s}\\&-2\hat{I}_2^{[1,0]}(3,2,2)m_{c}^{2}m_{s}+8\hat{I}_{0}(2,1,3)m_{c}^{2}m_{s}\\&+2\hat{I}_{1}(3,1,2)m_{c}^{2}m_{s}-2\hat{I}_{0}(3,1,2)m_{c}^{2}m_{s}\\&+4\hat{I}_{2}(2,1,3)m_{c}^{2}m_{s}-2\hat{I}_{2}(3,1,2)m_{c}^{2}m_{s}\\&-6\hat{I}_{2}(4,1,1)m_{c}^{2}m_{s}-2\hat{I}_2^{[0,1]}(3,2,2)m_{c}^{2}m_{s}\\&+4\hat{I}_{1}(3,1,2)m_{c}m_{s}^{2}+4\hat{I}_{0}(3,1,2)m_{c}m_{s}^{2}\\ \end{aligned}$$

$$\begin{aligned}&-2\hat{I}_1^{[1,0]}(3,2,2)m_{c}m_{s}^{2}+12\hat{I}_{1}(1,1,4)m_{c}m_{s}^{2}\\&-2\hat{I}_2^{[1,0]}(3,2,2)m_{c}m_{s}^{2}+12\hat{I}_{2}(1,1,4)m_{c}m_{s}^{2}\\&-2\hat{I}_0^{[1,0]}(3,2,2)m_{c}m_{s}^{2}+6\hat{I}_{2}(3,1,2)m_{c}m_{s}^{2}\\&+12\hat{I}_{0}(1,1,4)m_{c}m_{s}^{2}-4\hat{I}_{2}(3,1,2)m_{s}^{3}\\&+2\hat{I}_2^{[1,0]}(3,2,2)m_{s}^{3}-12\hat{I}_{2}(1,1,4)m_{s}^{3}\\&-4\hat{I}_{2}(2,1,3)m_{s}^{3}-2\hat{I}_{2}(2,2,2)m_{s}^{3}\\&+2\hat{I}_{2}(3,1,1)m_{c}-4\hat{I}_2^{[1,0]}(3,2,1)m_{c}\\&-4\hat{I}_1^{[0,1]}(3,1,2)m_{c}+4\hat{I}_{0}(1,2,2)m_{c}\\&-2\hat{I}_1^{[1,0]}(3,1,2)m_{c}+4\hat{I}_{2}(1,2,2)m_{c}\\&+8\hat{I}_{0}(2,1,2)m_{c}+8\hat{I}_{2}(2,1,2)m_{c}\\&+2\hat{I}_{0}(3,1,1)m_{c}+4\hat{I}_{1}(1,2,2)m_{c}\\ \end{aligned}$$

$$\begin{aligned}&-6\hat{I}_1^{[1,0]}(3,2,1)m_{c}+2\hat{I}_{0}(2,2,1)m_{c}\\&-4\hat{I}_0^{[0,1]}(3,1,2)m_{c}-4\hat{I}_2^{[0,1]}(3,1,2)m_{c}\\&+2\hat{I}_2^{[1,1]}(3,2,2)m_{c}+2\hat{I}_1^{[1,1]}(3,2,2)m_{c}\\&+2\hat{I}_{1}(2,2,1)m_{c}+6\hat{I}_{1}(2,1,2)m_{c}\\&+2\hat{I}_0^{[1,1]}(3,2,2)m_{c}-6\hat{I}_0^{[1,0]}(3,2,1)m_{c}\\&-2\hat{I}_{1}(3,1,1)m_{c}+8\hat{I}_1^{[1,0]}(2,1,3)m_{s}\\&+4\hat{I}_2^{[1,0]}(3,2,1)m_{s}+12\hat{I}_{1}(1,1,3)m_{s}\\&-4\hat{I}_{2}(1,2,2)m_{s}+2\hat{I}_2^{[0,1]}(2,2,2)m_{s}\\&-2\hat{I}_{2}(2,2,1)m_{s}+4\hat{I}_2^{[0,1]}(3,1,2)m_{s}\\&-2\hat{I}_2^{[1,1]}(3,2,2)m_{s}+4\hat{I}_{1}(2,1,2)m_{s}\\&+4\hat{I}_{2}(1,1,3)m_{s}+4\hat{I}_{0}(2,1,2)m_{s}\\&-10\hat{I}_{2}(2,1,2)m_{s}+2\hat{I}_2^{[1,0]}(2,2,2)m_{s}\\&+4\hat{I}_2^{[0,1]}(2,1,3)m_{s}+20\hat{I}_{0}(1,1,3)m_{s}, \end{aligned}$$

where

$$\begin{aligned} \hat{I}_{\mu }^{[\alpha ,\beta ]} (a,b,c)= & {} [M_1^2]^{\alpha }[M_2^2]^{\beta }\frac{d^\alpha }{d(M_1^2)^{\alpha }} \frac{d^\beta }{d(M_2^2)^{\beta }}\\&\times {[}M_1^2]^{\alpha }[M_2^2]^{\beta }\hat{I}_{\mu } (a,b,c), \\ \hat{I}_k(a,b,c)= & {} i \frac{(-1)^{a+b+c+1}}{16 \pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)} (M_1^2)^{1-a-b+k}\\&\times (M_2^2)^{4-a-c-k} \, {U}_0(a+b\\&+c-5,1-c-b),\\ \hat{I}_m(a,b,c)= & {} i \frac{(-1)^{a+b+c+1}}{16 \pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)} (M_1^2)^{-a-b-1+m}\\&\times (M_2^2)^{7-a-c-m} \, {U}_0(a+b\\&+c-5,1-c-b),\\ \hat{I}_6(a,b,c)= & {} i \frac{(-1)^{a+b+c+1}}{32 \pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)} (M_1^2)^{3-a-b}\\&\times (M_2^2)^{3-a-c} \, {U}_0(a+b\\&+c-6,2-c-b), \\ \hat{I}_n(a,b,c)= & {} i \frac{(-1)^{a+b+c}}{32 \pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)} (M_1^2)^{-4-a-b+n}\\&\times (M_2^2)^{11-a-c-n} \, {U}_0(a+b\\&+c-7,2-c-b), \end{aligned}$$

where $k=1, 2$, $m=3, 4, 5$ and $n=7, 8$. We can define the function $U_0(a,b)$ as:

$$\begin{aligned} U_0 (a, b)= & {} \int _0^{\infty } dy (y + M_1^2 + M_2^2)^ay^b \\&\times \exp \left[ -\frac{B_{-1}}{y} - B_0 - B_1y \right] , \end{aligned}$$

where

$$\begin{aligned} B_{-1}= & {} \frac{1}{M_2^2M_1^2}(m_s^2(M_1^2 +M_2^2)^2 -M_2^2M_1^2Q^2), \\ B_{0}= & {} \frac{1}{M_1^2M_2^2}(m_s^2 + m_c^2)(M_1^2+M_2^2) ,\\ B_{1}= & {} \frac{m_c^2}{M_1^2M_2^2}. \end{aligned}$$