Theoretical study of the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction

Abstract

We develop a model to study the $D^0 \rightarrow K^- \pi ^+ \eta$ weak decay, starting with the color favored external emission and Cabibbo favored mode at the quark level. A less favored internal emission decay mode is also studied as a source of small corrections. Some pairs of quarks are allowed to hadronize producing two pseudoscalar mesons, which posteriorly are allowed to interact to finally provide the $K^- \pi ^+ \eta$ state. The chiral unitary approach is used to take into account the final state interaction of pairs of mesons, which has as a consequence the production of the $\kappa$ ($K^*_0(700)$) and the $a_0(980)$ resonances, well visible in the invariant mass distributions. We also introduce the $\bar{K}^{*0} \eta$ production in a phenomenological way and show that the s-wave pseudoscalar interaction together with this vector excitation mode are sufficient to provide a fair reproduction of the experimental data. The model provides the relative weight of the $a_0(980)$ to the $\kappa$ excitation, and their strength is clearly visible in the low energy part of the $K \pi$ spectrum.

1 Introduction

The weak decay of heavy mesons into several mesons has received much attention in the past and continues to draw attention nowadays. In particular, three meson decays of D mesons already captured attention in early days, looking at the topology of the decay at the quark level and the posterior hadronization of pairs of quarks into mesons [1,2,3]. More recently the emphasis is put in the valuable information that these processes contain on the final state interaction of pairs of mesons and the production of resonances [4]. The existence of three particles in the final state gives much flexibility to play with the invariant mass of pairs of particles, providing ranges where several resonances appear. The Dalitz plot and the projected invariant mass distributions are thus very rich, containing much information on the dynamics of mesons. In this direction, the data on the $D^+ \rightarrow \pi ^+ \pi ^- \pi ^+$ reaction are used in [5] to determine parameters for the $f_0(980)$ and $f_0(1370)$. Further steps in this direction analyzing the invariant mass spectra in the $D^+$ and $D_s^+$ decay into three pions are given in [6] using the K-matrix approach to deal with the $\pi -\pi$ interaction. The same Dalitz plot distributions are analyzed in [7] using different partial wave analysis within the K-matrix approach, trying to extract information on different scalar meson states. An interesting feature appears in the $D^0 \rightarrow \pi ^+ \pi ^- \pi ^0$ reaction measured by the BaBar collaboration [8, 9] where the final pion pairs are surprisingly dominated by isospin $I=0$, but this feature, rather than being tied to a dynamical property of the final state interaction, was found to be a consequence of subtle cancellations between different topological decay modes entering the reaction [10]. The $D^+ \rightarrow K^- \pi ^+ \pi ^+$ ($D^0 \rightarrow K^0_s \pi ^+ \pi ^+$) decay mode [11, 12] was also instrumental in this direction, showing a clear signal for the $\kappa$ resonance ($K^*_0(700)$) in the $\pi K$ channel, which was analyzed in detail in [13] within the chiral unitary approach, and later on in [14]. A different approach to that reaction is followed in [15, 16] by means of dispersion relations, and input of experimental phase shifts and a few subtraction constants fitted to the data, as a way to take into account the final state interaction of the meson components. In a different formalism as the one followed here, also the rescattering with the third particle is taken into account in Refs. [15, 16] and shown to be relevant in some kinematical regions. The related $D^0 \rightarrow K^0 \pi ^+ \pi ^-$ reaction was also the object of a detailed study considering the final state interaction by means of amplitudes tested in other reactions [17]. Similarly, the $D^+ \rightarrow K^+ K^- K^+$ has been also thoroughly studied in [18], and more recently in Ref. [19] with the aim of obtaining information on the $K \bar{K}$ interaction.

The advent of the chiral unitary approach for the meson meson interaction [20,21,22,23,24] has brought new tools to analyze these reactions, allowing one to make predictions for mass distributions with a minimum input. The agreement found with the data serves in most cases to support the dynamical character of some resonances, which appear as a consequence of the meson meson interaction and are not of $q \bar{q}$ nature. In this line the $D^0$ decays to $K^0_S$ plus $f_0(500)$, $f_0(980)$ or $a_0(980)$ were studied in [25], and the relative strength for the excitation of these resonances was predicted in that scheme, showing agreement with experiment in the ratios available. In [26] the $D_s^+ \rightarrow \pi ^+ \pi ^- \pi ^+$ and $\pi ^+ K^+ K^-$ decays were studied and the role of the $f_0(980)$ resonance in the $\pi ^+ \pi ^-$ and $K^+ K^-$ mass distributions was established. In [27] the $D_s^+ \rightarrow \pi ^+ \pi ^0$ plus $a_0(980)$ or $f_0(980)$ reactions were studied and, thanks to the presence of a triangle singularity, an abnormal isospin violation was found with large mixing of the two scalar resonances. One of the findings of the chiral unitary approach in the meson sector is the existence of two $K_1(1270)$ resonances [28, 29], much in resemblance with the two $\Lambda (1405)$ states [30,31,32,33,34]. Taking this into account, predictions for the production of these two resonances were done in [35] in the decay of $D^0 \rightarrow \pi ^+$ plus $\rho K$ or $K^* \pi$. Finally, in [36] the $D_s^+ \rightarrow \pi ^+ \pi ^0 \eta$ reaction measured by the BESIII collaboration [37] was studied and a good agreement with data was found, showing that the mechanism for production was internal emission rather than annihilation as suggested in the experimental paper.

The reaction that we study here, the $D^0 \rightarrow K^- \pi ^+ \eta$ decay, measured by the Belle collaboration [38], is similar to the latter one mentioned above in a related Cabibbo suppressed channel, $D^0 \rightarrow \pi ^+ \pi ^0 \eta$ [39]. In addition to the $\pi \eta$ interaction which leads to the $a_0(980)$ resonance, here one also has the $K \pi$ interaction, which shows as a p-wave resonance in the form of a $K^*$, and also in s-wave, giving rise to the $\kappa$ ($K^*_0(700)$), both of them well visible in the data. Our study, using the chiral unitary approach, shows how the two s-wave signals are related in the theoretical scheme and comparison with the data allows a theoretical interpretation of the results, showing the value of the reaction to provide information on the meson meson interaction and indirectly on the nature of the $a_0(980)$ and $K^*_0(700)$ resonances.

2 Formalism

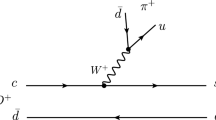
As usual when studying a weak decay, we start from the most favored Cabibbo mechanism at the quark level. For the $D^0 \rightarrow K^- \pi ^+ \eta$ reaction we start with the external emission mechanism [40] shown in Fig. 1.

Fig. 1

External emission of $D^0$ creating a $\pi ^+$ and a $s\bar{u}$ pair, followed by hadronization of the $s\bar{u}$ pair

It is not trivial to see how the $a_0(980)$ resonance, which shows a large strength in the reaction [38], can appear with this mechanism. The first step is to hadronize the $s\bar{u}$ component to form a pair of mesons. This is accomplished, as usual, introducing a $q\bar{q}$ pair with the quantum numbers of the vacuum. Here we are concerned about the flavor and then proceed as follow: A hadronic state H is formed as

$$\begin{aligned} H= \sum _i s \bar{q}_i q_i \bar{u}= \left( M M \right) _{31} \end{aligned}$$

(1)

where M is the $q\bar{q}$ matrix. We then write the M matrix in terms of the pseudoscalar mesons as

$$\begin{aligned} M \rightarrow P \equiv \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}+\frac{\eta ^\prime }{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}+\frac{\eta ^\prime }{\sqrt{6}} &{} K^0 \\ K^- &{} \bar{K}^0 &{} -\frac{\eta }{\sqrt{3}}+\sqrt{\frac{2}{3}}\eta ^\prime \end{array} \right) \ \end{aligned}$$

(2)

where the standard $\eta -\eta ^\prime$ mixing has been assumed [41]. In terms of the SU(3) octet and singlet one has [41, 42]

$$\begin{aligned} \eta = \frac{1}{3} \eta _1 + \frac{2 \sqrt{2}}{3} \eta _8,~~~~~ \eta ' = \frac{2\sqrt{2}}{3} \eta _1 - \frac{1}{3} \eta _8, \end{aligned}$$

(3)

which shows that the largest component of the $\eta$ is the octet, while for the $\eta '$ the singlet is the largest component.

We find then

$$\begin{aligned} H= & {} K^- \left( \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}+\frac{\eta ^\prime }{\sqrt{6}} \right) + \bar{K}^0 \pi ^-\nonumber \\&+ \left( -\frac{\eta }{\sqrt{3}}+\sqrt{\frac{2}{3}}\eta ^\prime \right) K^- \end{aligned}$$

(4)

$$\begin{aligned}\rightarrow & {} K^- \frac{\pi ^0}{\sqrt{2}} + \bar{K}^0 \pi ^-. \end{aligned}$$

(5)

In the last step above we see that the $K^-\eta$ term cancels. This is a consequence of the $\eta$, $\eta ^\prime$ mixing that we are taking. In subsection 2.3 we discuss what one gets with a more general mixing. In addition we eliminate the $K^-\eta ^\prime$ channel which is too far away for the relevant $K^*_0(700)$ resonance.

The $K^- \eta$ state has disappeared from the tree level but we could obtain it through rescattering, $\bar{K} \pi \rightarrow \bar{K}\eta$. Let us first try with p-wave. The $\bar{K} \pi$ can produce the $\bar{K}^{*0}$ that can decay into $\bar{K} \eta$, which is dynamically allowed. However, the threshold of $\bar{K} \eta$ is about 150 MeV above the nominal $K^*$ mass, that has a width of 50 MeV. The tail of the $K^*$ resonance at these energies gives a negligible contribution and we disregard this possible mechanism. We can try with s-wave. However, the $\bar{K}\eta$ threshold is around 1041 MeV, far away from the $K^*_0(700)$ peak, even considering the large $\kappa$ width. In addition, the coupling of the $\kappa$ to $K\eta$ is about half that of the $K\pi$ [43]. All these things together indicate that the hadronization in this way, followed by rescattering to produce $K^-\eta$, is an inefficient mechanism to produce the desired final state and this is corroborated by the experimental partial wave analysis which gives a very small contribution from $\bar{K}\eta$ in s-wave.

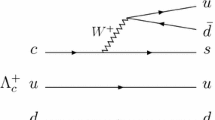
Next we resort to allowing the hadronization on the $d\bar{u}$ component as seen in Fig. 2, and use the $s\bar{u}$ component to produce the $K^-$. Following the same steps as before we find now:

$$\begin{aligned} H= & {} \sum _i u \bar{q}_i q_i \bar{d}= \left( P^2 \right) _{12}\nonumber \\= & {} \left( \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}+\frac{\eta ^\prime }{\sqrt{6}} \right) \pi ^+\nonumber \\&+ \pi ^+ \left( -\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}+\frac{\eta ^\prime }{\sqrt{6}}\right) + K^+\bar{K}^0 \nonumber \\\rightarrow & {} \frac{2}{\sqrt{3}} \eta \pi ^+ + K^+\bar{K}^0 \end{aligned}$$

(6)

Here we see that the $\pi ^0\pi ^+$ channel has cancelled but not the $\eta \pi ^+$, hence, together with the $K^-$ from the $s\bar{u}$ pair we have the hadronic final state

$$\begin{aligned} H^\prime = \frac{2}{\sqrt{3}} \eta \pi ^+K^- + K^+\bar{K}^0 K^- \end{aligned}$$

(7)

and we already have the $\eta \pi ^+K^-$ final state. The cancellation of the $\pi ^0 \pi ^+$ channel must necessarily occur since the $\pi ^0 \pi ^+$ $s-wave$ has $I=2$ which is not contained in the original $u \bar{d}$ state, which has $I=1$.

Fig. 2

$D^0$ decay to $\bar{d} u K^-$, followed by hadronization of the $u\bar{d}$ pair

The next step consists on taking into account the interaction of the meson pairs, which is depicted in Fig. 3.

Fig. 3

Final state interaction of the meson pairs

Fig. 4

Internal emission for $D^0$ decay followed by hadronization

We can have rescattering of the $K^-\pi ^+$, which will produce the $\kappa$ and of the $K^+\bar{K}^0 \rightarrow \eta \pi ^+$ which will produce the $a_0^+(980)$. For the reasons discussed above, we neglect the $\eta K^-$ scattering. Analytically we have:

$$\begin{aligned} t&=C&\left\{ h_{\eta \pi ^+K^-} + h_{\eta \pi ^+K^-} \left[ G_{K^-\pi ^+}\left( M_{inv}\left( {K^-\pi ^+}\right) \right) \right. \right. \nonumber \\&\quad t_{K^-\pi ^+,K^-\pi ^+}\left( M_{inv}\left( {K^-\pi ^+}\right) \right) \nonumber \\&\left. + G_{\pi ^+\eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \ t_{\pi ^+\eta ,\pi ^+\eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \right] \nonumber \\&+h_{K^+ \bar{K}^0 K^-} G_{K^+\bar{K}}\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \nonumber \\&\quad \left. \ t_{K^+ \bar{K}^0,\pi ^+\eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \right\} \end{aligned}$$

(8)

where C is a global constant that will be taken from the normalization of the data and $h_i$ are the weights of the components in Eq. (7)

$$\begin{aligned} h_{\eta \pi ^+K^-}=\frac{2}{\sqrt{3}}\equiv h_1; \ \ h_{K^+ \bar{K}^0 K^-}=1\equiv h_3 \end{aligned}$$

(9)

The function $G_i$ and $t_i$ are the loop functions and scattering matrices respectively, which we take from [20, 25] for the $\pi \eta$, $K\bar{K}$ channels and from [44,45,46] for the $K\pi$, $K\eta$ channels. As in [25, 45], the G functions are regularized with a cut off, the maximum three momentum in the loop, with a value of $q_{max}\approx 600$ MeV that has been fitted to data. We shall use our approach up to $K\pi$ and $\pi \eta$ invariant masses around 1.1 GeV, where the $\pi$ momenta for these systems at rest are 426 MeV/c and 398 MeV/c, respectively, low enough compared to $q_{max}$ to make the cut method reasonable.

Since in [20, 25] one studies the neutral states, we mention here that, since in our isospin convention the $\pi ^+$ is the $-|11>$ isospin state, then

$$\begin{aligned} t_{K^+ \bar{K}^0,\pi ^+\eta }=-t_{K \bar{K},\pi \eta }^{I=1}; \ \ t_{K^+ \bar{K}^0,\pi ^+\eta }=\sqrt{2} t_{K^+ K^-,\pi ^0\eta } \end{aligned}$$

(10)

As to the $K \pi$, $K \eta$ channels, we also take advantage to note that [45, 46] contain small correction terms with respect to [47] and for completeness we give the detailed functions in the Appendix.

So far we have relied on the most favored mechanism, color enhanced, external emission. There is also a possibility to reach the final state with internal emission, which is color suppressed, as depicted in Fig. 4.

We should first note that without hadronization we can produce $\bar{K}^{*0} \eta$ with $\bar{K}^{*0} \rightarrow \pi ^+ K^-$ to which we shall come back. The $\pi ^+K^-$ will be there in p-wave.

We can go back and see if the $K^- \pi ^+ \eta$ state could be formed through the $K^*$ via the mechanism of external emission of Fig. 1 (prior to hadronization). The $s \bar{u}$ component could give rise to a $K^{*-}$ and we would have $K^{*-} \pi ^+$ produced in the first step. Through decay of $K^{*-} \rightarrow K^- \eta$ we would have the final $K^- \pi ^+ \eta$ state.

However, as we mentioned in the discussion after Eq. (5), the $K^-\eta$ threshold is about 150 MeV above the nominal $K^*$ mass, which has a width of 50 MeV. Hence, this contribution is negligible. On the other hand, the $K^{*-}$ shows up experimentally in the $\pi K$ mass distribution, which indicates that the mechanism for production of $K^- \pi ^+ \eta$ via the $K^*$ is the one based on internal emission that we have visualized before.

For s-wave production we recur to hadronization. In the hadronization of the mechanism of Fig. 4(a) we will have the final state (omitting $\eta ^\prime$)

$$\begin{aligned} H= & {} \sum _i s \bar{q}_i q_i \bar{d}= \left( P^2 \right) _{32}\nonumber \\= & {} K^- \pi ^+ + \bar{K}^0 \left( -\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}\right) -\frac{\eta }{\sqrt{3}} \bar{K}^0 \nonumber \\= & {} K^- \pi ^+ -\bar{K}^0 \frac{\pi ^0}{\sqrt{2}} \end{aligned}$$

(11)

where the $\bar{K}^0 \eta$ channel has also cancelled. Including the $u\bar{u}$ state which is $\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}$, as seen in Eq. (2), we have

$$\begin{aligned} H^\prime =\left( K^-\pi ^+ -\bar{K}^0 \frac{\pi ^0}{\sqrt{2}}\right) \left( \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}\right) \end{aligned}$$

(12)

The mechanism of Fig. 4(b) leads to the hadronized state

$$\begin{aligned} H^\prime= & {} \bar{K}^0 \sum _i u \bar{q}_i q_i \bar{u}= \bar{K}^0 \left( P^2 \right) _{11}\nonumber \\= & {} \bar{K}^0 \left( \left( \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{3}}\right) ^2 + \pi ^+\pi ^- + K^+ K^- \right) \end{aligned}$$

(13)

We can see that several channels are produced with both mechanisms and we add the two contributions

$$\begin{aligned} H^\prime= & {} K^-\pi ^+ \frac{\pi ^0}{\sqrt{2}} +K^- \pi ^+ \frac{\eta }{\sqrt{3}} +\bar{K}^0 \frac{\pi ^0 \eta }{\sqrt{6}} +\bar{K}^0 \frac{\eta \eta }{3}\nonumber \\&+\bar{K}^0\pi ^+\pi ^- +\bar{K}^0 K^+ K^- \end{aligned}$$

(14)

The $\bar{K}^0\pi ^0\pi ^0$ combination disappears in the sum. We see that we have a tree level contribution in $K^- \pi ^+ \eta$, and several other terms from where we can obtain the final state $K^- \pi ^+ \eta$ with rescattering. But some of these channels are useless to produce the final state. For instance, the $K^- \pi ^+\pi ^0$ term. The $\pi ^+\pi ^0$ in s-wave can be in $I=2$ ($I=0$ is not allowed because $I_3 = 1$), but not in $I=1$, and hence cannot create the $\pi ^+\eta$. The $K^-\pi ^0 \rightarrow K^- \eta$ only sees the tail of the $\kappa$, as we have discussed previously, and hence, we disregard this channel. The $\bar{K}^0\eta \eta$ is equally unsuited since $K^0\eta \rightarrow K^- \pi ^+$ will also only see the tail of the $\kappa$. Indeed, the $K \eta$ threshold appears at 1041 MeV very far away from the normal mass of the $K^{*}_0 (700)$ peak, even considering the large width. As we pointed out after Eq. (9), $K \pi$ and $K \eta$ are considered as coupled channels in the chiral unitary approach. The $K \eta$ channel helps building up strength for the $\kappa$ state, but the amplitudes $K \pi \rightarrow K \eta$, above the $K \eta$ threshold are already very small. For the same reason $\bar{K}^0 \pi ^+\pi ^-$ is also unsuited since $K^0\pi ^- \rightarrow K^- \eta$ will also only see the $\kappa$ resonance tail. Hence for practical purposes we are left with a hadronic state

$$\begin{aligned} H^\prime _{int} = \bar{h}_1 K^-\pi ^+ \eta + \bar{h}_2 \bar{K}^0 \pi ^0 \eta + \bar{h}_3 \bar{K}^0 K^+ K^- \end{aligned}$$

(15)

with

$$\begin{aligned} \bar{h}_1=\frac{1}{\sqrt{3}}; \ \ \bar{h}_2=\frac{1}{\sqrt{6}}; \ \ \bar{h}_3=1 \end{aligned}$$

(16)

We see that the states $K^- \pi ^+ \eta$ and $\bar{K}^0 K^+ K^-$ also appeared in external emission Eq. (7). There is a new term $\bar{h}_2 \bar{K}^0 \pi ^0 \eta$ and we can have $\bar{K}^0 \pi ^0 \rightarrow K^- \pi ^+$ reaching the final $K^- \pi ^+\eta$ state, see Fig. 5. The internal emission term should have a different weight, $C\beta$, with the modulus of $\beta$ smaller than 1.

Fig. 5

Final state interaction of the $\bar{K}^0 \pi ^0$ pair in the $\bar{K}^0 \pi ^0 \eta$ term

The amplitude for the $K^-\pi ^+ \eta$ production process including rescattering of the different terms is then given by ( see Eqs. (9) and (16) for the $h_i$ and $\bar{h}_i$ coefficients)

$$\begin{aligned} t&=C&\left\{ h_1 + \beta \bar{h}_1 + G_{K\pi }\left( M_{inv}\left( {K^-\pi ^+}\right) \right) \right. \nonumber \\&\quad \left[ \left( h_1 + \beta \bar{h}_1\right) \ t_{K^-\pi ^+,K^-\pi ^+}\left( M_{inv}\left( {K^-\pi ^+}\right) \right) \right. \nonumber \\&\left. + \beta \bar{h}_2 \ t_{\bar{K}^0\pi ^0,K^-\pi ^+}\left( M_{inv}\left( {K^-\pi ^+}\right) \right) \right] \nonumber \\&+ \left( h_1 + \beta \bar{h}_1\right) \ G_{\pi \eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \ t_{\pi ^+\eta ,\pi ^+\eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \nonumber \\&\left. +\left( h_3 + \beta \bar{h}_3\right) \ G_{K\bar{K}}\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \ t_{K^+ \bar{K}^0,\pi ^+\eta }\left( M_{inv}\left( {\pi ^+\eta }\right) \right) \right\} \nonumber \\ \end{aligned}$$

(17)

As in [48] (see Eq. (19) of Ref. [48]) we smoothly extrapolate the Gt amplitude above an energy $M_{cut}=1100$ MeV, and the results barely change for different sensible extrapolations. We should note that in the chiral unitary approach the $t_{\bar{K} \pi , \bar{K} \pi }$ amplitudes are obtained from the $\bar{K} \pi , \bar{K} \eta$ coupled channels, where the $\kappa$ is generated from the interaction. On the other hand the $t_{\pi \eta , \pi \eta }$ and $t_{K \bar{K}, \pi \eta }$ amplitudes are obtained with the coupled channels $K \bar{K}$ and $\pi \eta$, and the $a_0(980)$ is generated from the interaction.

2.1 The $D^0 \rightarrow \eta \bar{K}^{*0} \rightarrow \pi ^+ K^- \eta$ contribution

We saw in connection with Fig. 1 that we could produce $\pi ^+ K^{*-}$ with external emission. Then the $K^{*-}$ could decay to $K^-\eta$ in p-wave, but the process was inefficient since it involved the tail of the $K^*$ far away from the nominal $K^*$ mass. However, the mechanisms of internal emission in Fig. 4 can both produce ${\bar{K}}^{*0} \eta$, and the ${\bar{K}}^{*0}$ can decay to $K^- \pi ^+$. We derive here the amplitude for the $D^0 \rightarrow \eta \bar{K}^{*0} \rightarrow \pi ^+ K^- \eta$ process, which will add coherently to the s-wave contributions that we have studied before, producing interference with the s-wave terms in the $\pi \eta$ and $\bar{K} \eta$ mass distributions. The mechanism of production is depicted in Fig. 6.

Fig. 6

Diagram for $D^0 \rightarrow \bar{K}^{*0} \eta \rightarrow K^- \pi ^+ \eta$. The momenta of the particles are written in parenthesis and $q\equiv p_K + p_\pi$

Up to an unknown constant D, which we will fit to the experimental strength, the full relativistic amplitude, needed to see the contribution of the mechanism in a large invariant mass span, is given by

$$\begin{aligned} \mathcal {M}= & {} \tilde{D} (p_D+ p_\eta )^\mu \left( -g_{\mu \nu }+ \frac{q_\mu q_\nu }{M_{K^*}^2}\right) \left( p_K\right. \\&\left. -p_\pi \right) ^\nu \frac{1}{q^2- M_{K^*}^2 + i M_{K^*} \Gamma _{K^*}}\\= & {} \frac{ \tilde{D}}{q^2- M_{K^*}^2 + i M_{K^*} \Gamma _{K^*}} \left[ -\left( p_D+ p_\eta \right) \cdot \left( p_K-p_\pi \right) \right. \\&\left. + \frac{\left( p_K+ p_\pi \right) \cdot \left( p_K-p_\pi \right) }{M_{K^*}^2} \left( p_D+ p_\eta \right) \cdot \left( p_K + p_\pi \right) \right] . \end{aligned}$$

Using $(p_K+ p_\pi )\cdot (p_K-p_\pi )=m_K^2-m_\pi ^2$ and labeling the particles $K^-(1)$, $\pi ^+(2)$, $\eta (3)$, we write $s_{13}=(p_K+ p_\eta )^2$; $s_{23}=(p_\pi + p_\eta )^2$ and the transition matrix $\mathcal {M}$ can be written as

$$\begin{aligned} \mathcal{M}= & {} \frac{ \tilde{D} }{q^2- M_{K^*}^2 + i M_{K^*} \Gamma _{K^*}} \left[ \left( m_K^2\right. \right. \nonumber \\&\left. \left. -m_\pi ^2\right) \frac{\left( m_D^2-m_\eta ^2\right) }{M_{K^*}^2} - s_{13}+ s_{23} \right] , \end{aligned}$$

(18)

with $\tilde{D} = D \ e^{i \phi }$.

2.2 Full mechanism with s- and p-waves

We define

$$\begin{aligned} t^\prime = t + M, \end{aligned}$$

(19)

and then $t^\prime$ depends on $s_{12}=M_{inv}^2(K^-\pi ^+) = q^2$, $s_{13}=M_{inv}^2(K^-\eta )$, $s_{23}=M_{inv}^2(\pi ^+\eta )$, although only two of these variables are independent since

$$\begin{aligned} s_{12}+s_{13}+s_{23}=m_D^2+m_K^2+m_\pi ^2+m_\eta ^2. \end{aligned}$$

(20)

Then we use the formula of the PDG for three body decay [49]

$$\begin{aligned} \frac{d^2 \Gamma }{dM_{inv}^2(12) dM_{inv}^2(23)}=\frac{1}{(2\pi )^3} \frac{1}{32 m_D^3} |t^\prime |^2 , \end{aligned}$$

(21)

and we integrate over either of the invariant masses to obtain the single invariant mass distributions. Permuting the indices 123 and using Eq. (20) we easily find $d\Gamma /dM^{2}_{inv}(13)$.

The data of Ref. [38] are not efficiency corrected. The efficiency factors for the Dalitz plot are not published, but we have obtained the efficiencies for the projected three mass distributions from the corresponding author of Refs. [38, 50]. Since this is not the place to publish these data, we just mention that normalizing the correction factors to an average value common to all distributions, which appears at $m^2_{K\pi }=0.90$ GeV$^2$, $m^2_{\pi \eta }=1.55$ GeV$^2$, $m^2_{K\eta }=2.5$ GeV$^2$, the normalized correction coefficient raises smoothly from 0.975 at $m^2_{K\pi }=0.40$ GeV$^2$ till 1.05 at $m^2_{K\pi }=0.65$ GeV$^2$ and decreases smoothly till 0.65 a $m^2_{K\pi }=1.7$ GeV$^2$. Similarly, the coefficient for the $\pi \eta$ distribution decreases smoothly from 1.03 at threshold till 0.90 at $M^2_{\pi \eta }=1.0$ GeV$^2$ and increases smoothly from this mass till 1.05 at 1.80   GeV$^2$. The coefficient for the $K \eta$ mass distribution increases from 0.775 at 1.1  GeV$^2$ till 1.05 at 2.8 GeV$^2$ and decreases smoothly till 0.85 at 2.9 GeV$^2$. Our results contain global normalization factors C, D and we fit to the data our results multiplied by these efficiency correction factors.

2.3 General $\eta -\eta ^\prime$ mixing scheme

In a general case we have the mixing between $\eta$ and $\eta ^\prime$ in terms of the singlet and octet $q\bar{q}$ SU(3) terms

$$\begin{aligned} \eta =\cos \theta _p \eta _8 - \sin \theta _p \eta _1 \ ; \ \eta ^\prime =\sin \theta _p \eta _8 + \cos \theta _p \eta _1, \end{aligned}$$

(22)

and the world average of this angle has been obtained in Ref. [51] as $\theta _p=-14.34^\circ$. The mixing from [41] that we are taking corresponds to $\cos \theta _p=2\sqrt{2}/3$, very close to $\cos (14.34^\circ )$. Inverting Eqs. (22) we have

$$\begin{aligned} \eta _1=\cos \theta _p \eta ^\prime - \sin \theta _p \eta \ ; \ \eta _8 =\sin \theta _p \eta ^\prime + \cos \theta _p \eta , \end{aligned}$$

(23)

Noting that

$$\begin{aligned} \eta _1= & {} \frac{1}{\sqrt{3}}\left( u\bar{u}+d\bar{d}+s\bar{s}\right) \\ \eta _8= & {} \frac{1}{\sqrt{6}}\left( u\bar{u}+d\bar{d}-2s\bar{s}\right) \\ \pi ^0= & {} \frac{1}{\sqrt{2}}\left( u\bar{u}-d\bar{d}\right) \end{aligned}$$

we can write

$$\begin{aligned} u\bar{u}= & {} \frac{1}{\sqrt{6}}\eta _8 + \frac{1}{\sqrt{3}} \eta _1+ \frac{1}{\sqrt{2}} \pi ^0 \\ d\bar{d}= & {} \frac{1}{\sqrt{6}}\eta _8 + \frac{1}{\sqrt{3}} \eta _1- \frac{1}{\sqrt{2}} \pi ^0\\ s\bar{s}= & {} \frac{1}{\sqrt{3}}\eta _1 - \frac{2}{\sqrt{6}} \eta _8 \end{aligned}$$

Substituting now $\eta _1$, $\eta _8$ in terms of $\eta$, $\eta ^\prime$ of Eq. (23) we obtain

$$\begin{aligned} u\bar{u}= & {} \left( \frac{\cos \theta _p}{\sqrt{6}}-\frac{\sin \theta _p}{\sqrt{3}} \right) \eta + \left( \frac{\sin \theta _p}{\sqrt{6}}+\frac{\cos \theta _p}{\sqrt{3}} \right) \eta ^\prime + \frac{\pi ^0}{\sqrt{2}} \\ d\bar{d}= & {} \left( \frac{\cos \theta _p}{\sqrt{6}}-\frac{\sin \theta _p}{\sqrt{3}} \right) \eta + \left( \frac{\sin \theta _p}{\sqrt{6}}+\frac{\cos \theta _p}{\sqrt{3}} \right) \eta ^\prime - \frac{\pi ^0}{\sqrt{2}} \\ s\bar{s}= & {} \left( -\frac{2}{\sqrt{6}}\cos \theta _p - \frac{\sin \theta _p}{\sqrt{3}} \right) \eta +\left( \frac{\cos \theta _p}{\sqrt{3}} - \frac{2\sin \theta _p}{\sqrt{6}} \right) \eta ^\prime \end{aligned}$$

which substitute the diagonal terms in Eq. (2). As a consequence the $K^-\eta \pi ^+$ term of $(P^2)_{31}$, that cancelled in Eq. (5), now does not cancel and we get an extra term for the mechanism of Fig. 1 which is

$$\begin{aligned} -\left( \frac{\cos \theta _p}{\sqrt{6}} + \frac{2\sin \theta _p}{\sqrt{3}} \right) K^-\eta \pi ^+ \end{aligned}$$

(24)

Similarly, we revaluate $(P^2)_{12}$ for the the diagram of Fig. 2 and we see that the term $2\eta \pi ^+K^-/\sqrt{3}$ of Eq. (7) is substituted by

$$\begin{aligned} \left( \frac{2\cos \theta _p}{\sqrt{6}} - \frac{2\sin \theta _p}{\sqrt{3}} \right) \eta \pi ^+K^- \end{aligned}$$

(25)

We can add the terms of Eqs. (24) and (25) and we have the global term

$$\begin{aligned} \left( \frac{\cos \theta _p}{\sqrt{6}} - \frac{4\sin \theta _p}{\sqrt{3}} \right) K^-\eta \pi ^+ \end{aligned}$$

(26)

replacing $2K^-\eta \pi ^+/\sqrt{3}$ in Eq. (7). There is a 15% difference between these two numbers, which anticipates small changes with respect to the results obtained with the standard mixing. Due to the small changes found we do not consider the changes in the subdominant internal emission terms. The small decrease of 15% between Eq. (26) and $2K^-\eta \pi ^+/\sqrt{3}$ of the standard mixing, can be compensated with an increase of 15% in the coefficient C in Eq. (8), while keeping $C\beta$ the same, and the final results are practically indistinguishable.

Fig. 7

$M_{K\pi }$ distribution. Individual contributions. The total s-wave contains the tree level, the $a_0(980)$ and the $\kappa$ rescattering terms

Fig. 8

$M_{K\pi }$ distribution. Combined contributions. The total s-wave contains the tree level plus the $a_0(980)$ and the $\kappa$ rescattering terms

Fig. 9

$M_{\pi \eta }$ distribution

Fig. 10

$M_{K\eta }$ distribution

3 Results

We have four parameters at our disposal to fit the data C, $D\exp (i \phi )$, and $\beta$. C and D are uncorrelated since C determines the absolute strength of the width and D controls the strength of the $K^*$ excitation. The parameter $\beta$ gives the relative weight of the subdominant internal emission mechanism. We perform a best fit to the three mass distributions of Figs. 7, 9, 10. We should note that since C and D are related to the global strength and the strength of the $K^*$ peak, we only have the phase $\phi$ and the subdominant term to determine the non trivial shapes of the different mass distributions. In Figs. 7, 8, 9, 10 we show the results obtained for the three invariant mass distributions with the parameters shown in Table 1.

Table 1 Values of the parameters from the fit. An extra global factor $3.0 \times 10^7$ is applied to all distributions to compare with the number of events in the data (the different binning for the distributions is considered when comparing to the data)

We can see that we get a good reproduction of the data at a qualitative level. We reproduce, because it is an input, the peak of the $m_{K\pi }$ mass distribution. What is a consequence of our theoretical formalism is the accumulated strength below the peak of the $\bar{K}^{*0}$ resonance and the $a_0(980)$ strength, which are correlated in our theoretical framework.

In Fig. 7 we show the contributions of the $a_0(980)$ (the two terms of Eq. (8) involving the $t_{\pi ^+\eta ,\pi ^+\eta }$ and $t_{K^+ \bar{K}^0,\pi ^+\eta }$ amplitudes) and $\kappa$ (term of Eq. (8) involving $t_{K^-\pi ^+,K^-\pi ^+}$). We should note that the $t_{K^-\pi ^+,K^-\pi ^+}$ amplitude contains contributions from $I=1/2$ (the $\kappa$) and $I=3/2$, but the $I=1/2$ is dominant and we shall call this the $\kappa$ contribution. As we see, both the $a_0(980)$ and $\kappa$ contributions are small compared to the contribution of the tree level (first term of Eq. (8)). However, upon interference with the tree level, the effect of the $a_0(980)$ and $\kappa$ get reinforced. This is better seen in Fig. 8, where we show separately the contributions, tree$+a_0(980)$, tree$+\kappa$, and tree$+a_0(980)+\kappa$ (s-wave). What the two figures tell us is the importance of the tree level term, enhancing the contributions of the $a_0(980)$ and $\kappa$ through interference. It is thus clear that a proper analysis of the data requires the explicit consideration of the tree level in order to extract the s-wave $\pi K$ and $\pi \eta$ amplitude from them. It is also striking that the prominent role of the $a_0(980)$ in the $\pi \eta$ mass distribution is obtained in our approach without introducing it in the formalism, unlike the $\bar{K}^{*0}$ contribution which is put by hand. This comes as a consequence of the rescattering of $\pi ^+\eta$ and $K^+\bar{K}^{0}$, as seen in Fig. 3. The scattering amplitudes $\pi ^+\eta \rightarrow \pi ^+\eta$ and $K^+\bar{K}^{0} \rightarrow \pi ^+\eta$ in the chiral unitary approach contain the $a_0(980)$ resonance, which comes as a consequence of the interaction of the mesons and is also not introduced by hand in the approach. We should stress the cusp like shape of this resonance both in the theory and in the experiment, something already noted in the high statistics BESIII experiment on the $\chi _{c1} \rightarrow \eta \pi ^+\pi ^-$ reaction [52] accurately described theoretically in [53] along similar lines as shown here. It is also interesting to see the curious effect that the $\bar{K}^{*0}$ contribution has in the $M_{\pi \eta }$ and $M_{K\eta }$ distributions, giving rise to two broad peaks at lower and higher invariant masses. These peaks, correctly interpreted in the experimental analysis of [37] to the light of our different formulation, are typical examples of replicas in some invariant mass distributions of resonant peaks of one particular invariant mass. It is important to identify them correctly to avoid claims of new resonances. We can see in these plots that the effect of the $a_0(980)$ and $\kappa$ resonances are instead rather smooth and structureless in the non resonant invariant plots.

Finally, since the C coefficient governs the absolute normalization and the D coefficient the strength of the $\bar{K}^{*0}$, the relative strength between the $a_0(980)$ peak and the low energy $\bar{K}\pi$ bump is a prediction of the theory with no free parameters.

We should note that we have added the s-wave (tree level, $a_0(980)$ and $\kappa$) and p-wave ($\bar{K}^{*0}$) amplitudes coherently. This is important because while in the $\bar{K}\pi$ invariant mass distribution the $\kappa$ and $K^+\bar{K}^{*0}$ do not interfere after the integration over $s_{23}$ in Eq. (21), this is not the case in the other mass distributions. Also in the $\bar{K}\pi$ invariant mass distribution there is interference between the $a_0(980)$ and the $\bar{K}^{*0}$ amplitudes. One can see, indeed, that the incoherent sum of the s-wave and p-wave in Fig. 7 at low invariant masses does not give the total mass distribution. It is also interesting to see in Fig. 7 that the $\kappa$ contribution is quite small and the strength at low invariant $\bar{K}\pi$ is mostly due to the tree level contribution together with the $a_0(980)$ and its interference with the $\bar{K}^{*0}$.

Fig. 11

Effect on the three mass distributions of the different extrapolations of Eq. (27) in the chiral amplitudes

Fig. 12

Effect on the three mass distributions of the different phase $\phi$

An inspection to our results shows that the $K\pi$ and $\pi \eta$ mass distributions in Figs. 7, 8, 9 are fairly well obtained. The worse case is the $K \eta$ mass distribution in Fig.10, where the qualitative features are well reproduced, but the agreement with the data is not as good as in the other mass distributions. This is not surprising since we deliberately ignored the $K \eta$ interactions because they occur at higher invariant masses. The $K \pi$ mass distribution around 1 GeV above the $K^*$ peak is also not well described by our model. This region is not improved with changes of the parameters in our model. Yet, it is not our purpose to describe that region, but to see the role played by the scalar resonances. In the fit of Ref. [38] the $a_0(980)$ and $\kappa$ resonances are included explicitly (note that we do not introduce neither the $a_0(980)$ nor the $\kappa$ by hand) and, in addition to the resonances considered in our work, they introduce the $a_2(1320)^+$, $\bar{K^*}(1410)^0$, $K^*(1680)^-$, and $K_2^*(1980)^-$, by means of which a better agreement with the data is obtained. Our results indicate that the role played by these extra resonances is small, and so is the case in [38]. The aim of our work concentrates on the role played by the $a_0(980)$ and $\kappa$ resonances, which appear in our approach as a consequence of final state interaction of meson meson components. Their role is shown in the low invariant mass part of the $K \pi$ distribution, below $M_{K\pi }^2= 0.7$ GeV$^2$ in Figs. 7, 8 and the peak around 1 GeV in Fig. 9. As mentioned before, this is accomplished basically by means of a phase, $\phi$, and a subdominant term that goes with $\beta$, and the agreement with the data is fair, considering that the $a_0(980)$ and the $\kappa$ resonances are generated in the approach and their strength is fixed. The approach serves then to back the picture where these resonances are obtained from the meson meson interaction. However, one should note that unlike other reactions, like the $D_s^+ \rightarrow \pi ^+ \pi ^0 \eta$ [36], where the $a_0(980)$ contribution could be isolated and provided the driving mechanism of the reaction, here the clear bump at low $K \pi$ invariant masses in Fig. 7 comes from a subtle mixture of $a_0(980)$, $\kappa$, tree level and even some interference between $\bar{K}^{*0}$ contribution and the $a_0(980)$ as we pointed out before. It is good to see that we can interpret that region within our model. However, the same nature of the solution obtained indicates that in a standard partial wave analysis it could be difficult to disentangle the role played by each mechanism.

To finalize the discussion we show now in Figs. 11, 12 the effects of the smooth extrapolation of the amplitudes and the phase of the $K^*$. In Fig. 11 we show the results obtained using three different extrapolations which were used in Ref. [48]. We take

$$\begin{aligned} Gt\left( M_\mathrm{inv}\right) = Gt\left( M_\mathrm{cut} \right) \ \mathrm {e}^{-\alpha \left( M_\mathrm{inv} - M_\mathrm{cut}\right) } ~~~ \mathrm{for }~~ M_\mathrm{inv} > M_\mathrm{cut}, \end{aligned}$$

(27)

with $M_\mathrm{cut}$= 1100 MeV, with $\alpha =0.0037$ MeV$^{-1}$, 0.0054 MeV$^{-1}$, 0.0077 MeV$^{-1}$, which reduce Gt by about a factor 3, 5, 10, respectively, at $M_\mathrm{cut}$+300 MeV. The former results were obtained using $\alpha =0.0037$ MeV$^{-1}$. Figure 11 shows the results using one or another extrapolation and the results barely change in the three mass distributions.

In Fig. 12 we show the results of using a different phase, $\phi$, of the $K^*$. All the other parameters are taken the same. What we see is that the $K \pi$ mass distribution barely changes. In particular, this is the case in the low energy part of the spectrum, which is well reproduced by our model, what makes our results there basically independent of this parameter and, hence, our approach more predictive. On the other hand, the phase has repercussion on the $K \eta$ mass distribution, the one which we already admitted is not so tied to our input of the chiral unitary approach. The phase also does not change much the strength at the peak of the $a_0(980)$ in the $\pi \eta$ mass distribution, however, it changes it at low and high invariant $\pi \eta$ masses to the point of distorting somewhat the shape of the $a_0(980)$ in the lower part of the spectrum. This feature is interesting to note. To see the genuine $a_0(980)$ shape that can be compared to the scattering amplitudes it is better to use other reactions, like the $\chi _{c1} \rightarrow \pi ^+ \pi ^- \eta$ [53], because the $\chi _{c1}$ has isospin $I=0$ and then the $\pi ^+ \pi ^-$ cannot form the $\rho$. Then the genuine shape of the $a_0(980)$ shows up clearly as seen in the experimental work of BESIII [52], which has the cleanest signal of the $a_0(980)$ so far in our opinion.

4 Conclusions

We have studied the $D^0 \rightarrow K^- \pi ^+ \eta$ decay, recently measured by the Belle collaboration, and found that it provides valuable information on the scalar mesons $a_0(980)$ and $\kappa$ ($K^*_0(700)$). The analysis is done studying first how the primary quark production proceeds and then hadronizing pairs of quarks to provide two pseudoscalar mesons. We find that while the $K^- \pi ^+ \eta$ state can be produced in a primary stage, prior to any final state interaction consideration, the interaction of mesons, and not only the final ones, gives rise to two resonances, the $\kappa$ in the final $\bar{K} \pi$ channel and the $a_0(980)$ in the final $\pi ^+ \eta$ channel. Our formalism, which uses the chiral unitary approach to account for the interaction of pairs of pseudoscalar mesons, is well suited for these kind of reactions. It produces simultaneously the two resonances and provides their relative strength with no free parameters in the dominant mode of decay, based on external emission. A small fraction of internal emission is also taken into account in the approach, and shows up in the fit to the data with a strength in agreement with what one expects from a subdominant mechanism. Including empirically the $\bar{K}^{*0} \eta$ production we find a relatively good agreement with the data in the three invariant mass distributions and all the range of masses. The agreement found with the data gives support to our theoretical scheme, where the final state interaction is responsible for the main features, and indirectly to the nature of the resonances $\kappa$ and $a_0(980)$, which do not qualify as $q \bar{q}$ states, but come as a consequence of the interaction of the mesons pairs in coupled channels. We found that the features of the reaction come from subtle interference of terms involving $a_0(980)$, $\kappa$, tree level and $K^{*0}$ excitation, which makes this reaction not as clean, concerning the role of the scalar resonances, as other related reactions. However, together with the success obtained in other reactions using the same idea, the information favoring that picture is piling up, revealing the different nature of the low lying scalar mesons from the ordinary $q \bar{q}$ mesons.

Appendix: Scattering amplitude in the \(K\pi \), \(K\eta \) channels

The T matrix is taken in matrix form as

$$\begin{aligned} T= [ 1- V G]^{-1} V \end{aligned}$$

(A.1)

with the $\pi ^- K^+(1)$, $\pi ^0 K^0(2)$, $\eta K^0 (3)$ channels and we have

$$\begin{aligned} V_{11}= & {} \frac{-1}{6f^2} \left( \frac{3}{2}s- \frac{3}{2s}\left( m_\pi ^2-m_K^2\right) ^2 \right) \end{aligned}$$

(A.2)

$$\begin{aligned} V_{12}= & {} \frac{1}{2 \sqrt{2}f^2} \left( \frac{3}{2}s- m_\pi ^2-m_K^2- \frac{\left( m_\pi ^2-m_K^2\right) ^2}{2s} \right) \end{aligned}$$

(A.3)

$$\begin{aligned} V_{22}= & {} \frac{-1}{4f^2} \left( -\frac{s}{2}+ m_\pi ^2+m_K^2- \frac{\left( m_\pi ^2-m_K^2\right) ^2}{2s} \right) \end{aligned}$$

(A.4)

$$\begin{aligned} V_{13}= & {} \frac{1}{2\sqrt{6}f^2} \left( \frac{3}{2}s- \frac{7}{6}m_\pi ^2-\frac{1}{2}m_\eta ^2-\frac{1}{3}m_K^2\right. \nonumber \\&\left. + \frac{3}{2s}\left( m_\pi ^2-m_K^2\right) \left( m_\eta ^2-m_K^2\right) \right) \end{aligned}$$

(A.5)

$$\begin{aligned} V_{23}= & {} -\frac{1}{4\sqrt{3}f^2} \left( \frac{3}{2}s- \frac{7}{6}m_\pi ^2-\frac{1}{2}m_\eta ^2-\frac{1}{3}m_K^2\right. \nonumber \\&\left. + \frac{3}{2s}\left( m_\pi ^2-m_K^2\right) \left( m_\eta ^2-m_K^2\right) \right) \end{aligned}$$

(A.6)

$$\begin{aligned} V_{33}= & {} -\frac{1}{4f^2} \left( - \frac{3}{2}s- \frac{2}{3}m_\pi ^2+m_\eta ^2+ 3m_K^2\right. \nonumber \\&\left. - \frac{3}{2s}\left( m_\eta ^2-m_K^2\right) ^2 \right) \end{aligned}$$

(A.7)

where f is the pion decay constant, $f=93$ MeV, and s the square of the center of mass energy.