1 Introduction

The 2012 discovery at Large Hadron Collider experiments [1, 2] of a resonance that has measured properties compatible with those of a \(\text {SM}\) Higgs boson, raises some expectations. Should the language of quantum field theory be interpreted correctly by most of the research community, huge corrections to the Higgs boson mass are expected, rendering its measured value [3] of

$$\begin{aligned} M_h = 125.09\pm 0.32~\text {GeV} \end{aligned}$$
(1)

untenable unless its value is finely tuned with unrelated contributions cancelling to a suspiciously large degree. This technical hierarchy problem can be solved by new physics that appears around the TeV scale, the foremost example being TeV scale supersymmetry. TeV scale supersymmetry predicts that the masses of new hitherto undiscovered sparticles are not much higher than the TeV scale. These to date have not been discovered, and the most natural portion of supersymmetry parameter space is being heavily squeezed by experimental constraints.

It is possible that there is some misunderstanding in the way that quantum field theory generates such huge corrections and that the technical hierarchy problem should be taken cum grano salis. It is also possible that supersymmetry is simply a little late to the LHC party, is a little heavier than expected and isn’t quite as natural as was originally thought. It is therefore crucial to try to discover superparticles. Within the simplest supersymmetric extension of the \(\text {SM}\), the \({\text {MSSM}}\), there is a lot of parameter space where h appears to be essentially \(\text {SM}\) like. Its mass, which is \(M_{h}= M_Z \cos 2\beta \) at tree level in the decoupling limit (\(M_Z\) being the mass of the Z boson and \(\tan \beta =v_u/v_d\) is the ratio of the two neutral CP-even \({\text {MSSM}}\) Higgs field vacuum expectation values (VEVs)), receives large corrections at the loop level. It has been known for some time that the largest corrections to its mass (squared) come from top/stop corrections, which are enhanced by the large value of the top mass [4]:

$$\begin{aligned} M_{h}^2 = M_Z^2 \cos ^2 2 \beta + \frac{3}{2 \pi ^2} \frac{m_t^4}{v^2} \left[ \ln \frac{M^2}{m_t^2} + \frac{X_t^2}{M^2} - \frac{X_t^4}{12 M^4}\right] ,\nonumber \\ \end{aligned}$$
(2)

where \(M=\sqrt{m_{{\tilde{t}}_1} m_{{\tilde{t}}_2}}\), \(m_{{\tilde{t}}_i}\) is the running \(i{\text {th}}\) stop mass, \(m_t\) is the running top mass, \(X_t= A_t - \mu /\tan \beta \) is the running stop mixing parameter and \(v\sim 246~\text {GeV}\) is the running SM-like Higgs VEV. Each quantity on the right hand side of Eq. (2) is evaluated at some \(\overline{\text {DR}}'\) [5,6,7] renormalisation scale Q. The stops play a crucial rôle in bringing the value of \(M_h\) predicted up to the measured value from the tree-level value. The measured value of \(M_{h}\) in Eq. (1) prefers those parts of parameter space that have larger stop masses and/or large mixing between the two stops.

The truncation of perturbation theory at a finite order generates a theoretical uncertainty on the prediction of \(M_{h}\). This then leads to an associated uncertainty in the inferred masses and mixings of stops that agree with the experimentally inferred value of \(M_{h}\). The allowed range of stop parameter space depends very sensitively on the accuracy of the \(M_{h}\) prediction. Equation (2) shows that the stop mass scale depends roughly exponentially upon \(M_h\) in the high \(m_{{\tilde{t}}_i}\) limit.Footnote 1 Achieving the most precise prediction for \(M_h\) is then of paramount importance. In order to predict \(M_{h}\) with higher accuracy and greater precision, higher-order contributions and large log re-summation are required. To date, terms up to two-loop order have been computed in the on-shell scheme [8,9,10,11,12,13,14,15,16,17,18,19] and up to three-loop order in the \(\overline{\text {DR}}\)/\(\overline{\text {DR}}'\) scheme [4, 13,14,15, 20,21,22,23,24,25,26,27,28,29,30,31,32].

Currently, ATLAS and CMS perform many different searches for stops. They depend upon various \({\text {MSSM}}\) parameters, but in the more constraining and direct cases, the searches rule out lightest stop masses up to around \(1~\text {TeV}\) [33, 34]. Ideally, it would be useful to determine exactly how heavy the stops might be so that it can be judged how much of the viable parameter space has been excluded and so that one may inform the utility of future higher energy colliders such as the Future Circular Collider (FCC) [35,36,37]. However, it was shown in Refs. [38,39,40,41,42] that stops far heavier than the 100 TeV putative centre of mass energy of the FCC are compatible with Eq. (1), provided that one is willing to accept the tuning in v implied by the technical hierarchy problem.Footnote 2 We shall repeat this calculation taking our more precise estimates of the theoretical uncertainties in \(M_h\) into account.

Fig. 1
figure 1

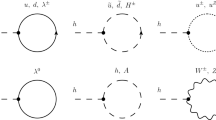
Schematics of different MSSM approximation schemes: fixed order \(\overline{\text {DR}}'\) and EFT. In the fixed order \(\overline{\text {DR}}'\) scheme the MSSM is matched to effective \(\text {QCD}\times \text {QED}\) at the scale \({Q_\text {match}}\). In the EFT scheme the MSSM is matched to an effective \(\text {SM}\) at the supersymmetric scale \(M_S\). Horizontal lines show the matching scales

Full size image

There are several current publicly available MSSM spectrum calculator computer programs on the market. These calculate the spectrum consistent with weak-scale data on the gauge couplings and the masses of SM states. Each employs an approximation scheme. The two approximation schemes examined here are called the fixed order \(\overline{\text {DR}}'\) scheme and the EFT scheme, depicted in Fig. 1. The fixed order \(\overline{\text {DR}}'\) scheme matches effective QED\(\times \)QCD to the \({\text {MSSM}}\) at a single scale \({Q_\text {match}}\). The values \({Q_\text {match}}=M_Z\) or \({Q_\text {match}}=M_t\) are commonly taken, and data on gauge couplings and quark, lepton and electroweak boson masses are input at this scale \({Q_\text {match}}\) (see Ref. [43] for a more detailed description). These couplings are then run using \({\text {MSSM}}\) renormalisation group equations (RGEs) to M, where the Higgs potential minimisation conditions are imposed and supersymmetric physical observables including \(M_h\) are calculated. \(M_h\) is calculated using the known higher order diagrammatic corrections, up to three loops, of the order \(o \in \{{\alpha _{\text {s}}}{\alpha _t}\), \({\alpha _{\text {s}}}{\alpha _b}\), \({\alpha _t}^2\), \({\alpha _t}{\alpha _b}\), \({\alpha _b}^2\), \({\alpha _\tau }^2\), \({\alpha _{\text {s}}}^2{\alpha _t}\}\), where \({\alpha _{\text {s}}}= {g_{3}}^{2}/(4\pi )\), \(\alpha _{t,b,\tau } = y_{t,b,\tau }^2/(4\pi )\) and \(y_t\), \(y_b\), \(y_\tau \) are the top, bottom and tau Yukawa couplings, respectively, and \(g_3\) is the QCD gauge coupling. These fixed-order corrections include two-loop terms which are proportional to \(o \ln ^2 (M_S/M_Z)/(4 \pi )^2\) as well as terms of order \(o M_Z^2 / M_S^2 / (4 \pi )^2\). However, some three-loop terms, for example of order \(\{{\alpha _t}^{2}{\alpha _{\text {s}}}, {\alpha _t}^{3}\}\) \(\times \) \(\ln ^3 (M_S/M_Z) / (4 \pi )^3\), are missed. As \(M_S\) becomes larger (for example as motivated by the negative results of sparticle searches), such missing logarithmic higher order terms become numerically more important, and missing them will imply a larger uncertainty in the fixed order \(\overline{\text {DR}}'\) prediction of \(M_h\). This has motivated the approximation scheme which we call the EFT scheme, where the heavy SUSY particles are decoupled at the SUSY scale \(M_S\) and the RGEs are used to re-sum the large logarithmic corrections. However, the EFT scheme neglects terms of order \({M_{Z}}^{2}/M_S^2\) at the tree level and therefore is less accurate the closer \(M_S\) is to \(M_Z\). Which scheme is the most accurate for various different physical predictions is not obvious beforehand and depends on the MSSM parameters. It is one of our goals to determine in which domain of \(M_S\) the fixed-order scheme becomes less accurate than the EFT scheme.

The preceding paragraph has been greatly simplified for clarity of discussion. In the \({\text {MSSM}}\) there are many gauge and Yukawa couplings and one-loop corrections from all of these are included in the fixed order \(\overline{\text {DR}}'\) calculations. Also, we have used \(M_S\) as a catch-all supersymmetric scale, but really the individual sparticles contribute to the logarithms and finite terms with their own masses, not with some universal value of \(M_S\).

The programs used for our \(M_{h}\) predictions are the fixed order \(\overline{\text {DR}}'\) spectrum generators SOFTSUSY 4.1.1 [43, 44], FlexibleSUSY 2.1.0 [45, 46] and HSSUSY 2.1.0 [46], which uses the EFT approach. We include the three-loop corrections that are available in Himalaya 1.0.1 [47].

In Ref. [48], the hybrid fixed order \(\overline{\text {DR}}'\)EFT calculation of FeynHiggs [49, 50] was compared to the purely EFT calculation of SUSYHD [42]. The observed numerical differences between the (mostly) on-shell hybrid calculation of FeynHiggs and the \(\overline{\text {DR}}'\) calculation of SUSYHD were found to be mainly caused by renormalisation scheme conversion terms, the treatment of higher-order terms in the determination of the Higgs boson pole mass and the parametrisation of the top Yukawa coupling. When these differences are taken into consideration, excellent agreement was found between the two programs for SUSY scales above \(1~\text {TeV}\). This finding confirms that above this scale the terms neglected in the EFT calculation are in fact negligible and the EFT calculation yields an accurate prediction of the Higgs boson mass. Similarly, in Ref. [51] the \(\overline{\text {DR}}'\) hybrid fixed order/EFT calculation implemented in FlexibleSUSY (denoted as FlexibleEFTHiggs) was compared to the \(\overline{\text {DR}}'\) fixed order calculation available in FlexibleSUSY. A prescription for an uncertainty estimation of both calculations was given and it was found that (based on that uncertainty estimate) above a few TeV the hybrid and the pure EFT calculations are more precise than the fixed order \(\overline{\text {DR}}'\) calculation.

Our work differs from Refs. [48, 51] in that we perform a comparison between the \(\overline{\text {DR}}'\) fixed order and the pure EFT predictions. Our \(\overline{\text {DR}}'\) fixed order calculation is also a loop higher in order than the previous work. We shall give a prescription for the estimation of the theoretical uncertainties of the two \(M_h\) predictions in the \(\overline{\text {DR}}'\) scheme based on the procedures described in Refs. [40, 42, 51]. Based on our uncertainty estimates we derive an \(M_S\) region in that scheme, above which the EFT prediction becomes more precise than the fixed order one.

In Sect. 2, we estimate and dissect theoretical uncertainties in state-of-the art predictions of the lightest \(CP\) even Higgs boson pole mass in the \(\overline{\text {DR}}'\) scheme. Then, in Sect. 3, we update the upper bounds on the lightest stop mass from the experimental determination of the Higgs boson mass and from the stability of an appropriate vacuum by our detailed quantification of the theoretical uncertainties and state-of-the-art calculation of \(M_h\). We summarise in Sect. 4.

2 Higgs boson mass prediction uncertainties

Sources of uncertainty in the \(\overline{\text {DR}}'\) fixed-order calculation of the lightest \(CP\)-even Higgs boson pole mass prediction can be divided into two classes:

  • Missing higher order contributions to the Higgs self energy and to the electroweak symmetry breaking (EWSB) conditions.

  • Missing higher order corrections in the determination of the running \(\overline{\text {DR}}'\) gauge and Yukawa couplings and the VEVs from experimental quantities.

The prescription presented in Ref. [51] to estimate these missing higher order contributions is sensitive to leading and subleading logarithmic as well as non-logarithmic terms. An analysis of how these different kinds of higher order terms enter the uncertainty estimate can be found in that reference. In the \(CP\)-conserving \({\text {MSSM}}\) the known two- and three-loop contributions to the \(CP\) even Higgs self energy and EWSB conditions are included. The currently unknown (subleading) logarithmic higher order corrections can be estimated by varying the renormalisation scale at which the Higgs boson mass is calculated, \(Q_\text {pole}\). We estimate this uncertainty as in Ref. [51],

$$\begin{aligned} \varDelta M_h^{(Q_\text {pole})}= \max _{Q_\text {pole}\in [M_S/2,2M_S]}\left| M_h(Q_\text {pole}) - M_h(M_S)\right| ,\nonumber \\ \end{aligned}$$
(3)
Fig. 2
figure 2

Individual sources of uncertainty of the three-loop fixed order \(\overline{\text {DR}}'\) Higgs boson mass prediction of SOFTSUSY

Full size image

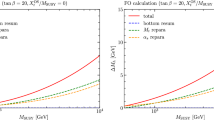
where \(M_S\) is the SUSY scale, usually set to \(M_S= \sqrt{m_{\tilde{t}_1}m_{\tilde{t}_2}}\). In Fig. 2 we show this uncertainty as the blue dashed line for a scenario with degenerate \(\overline{\text {DR}}'\) mass parameters (aside from the Higgs mass parameters, which are fixed in order to achieve successful EWSB), \(\tan \beta = 20\) and maximal stop mixing, \(X_t = -\sqrt{6}M_S\). For this scenario \(\varDelta M_h^{(Q_\text {pole})}\) varies between 0.5–\(1~\text {GeV}\), depending on the SUSY scale. In Ref. [51] this uncertainty is larger, because the three-loop contribution to the Higgs boson mass was not included. The kink at \(M_S\approx 700~\text {GeV}\) is due to a switch in the approximation scheme being used in the calculation of the three-loop contribution of Himalaya: the integrands of the three-loop integrals were expanded in different sparticle “mass hierarchies” where different sparticles were approximated as being massless [31]. As \(M_S\) changes, Himalaya switches from one mass hierarchy to another one that fits better to the given parameter point, resulting in the kink. We note that \(\varDelta M_h^{(Q_\text {pole})}\) is approximately independent of \(M_S\) as \(M_S\) becomes large. The dominant \(Q_\text {pole}\) dependence comes from the first term on the right-hand side of Eq. (2): from the running Z mass, at one-loop order. This will be cancelled by to leading order in \(\log (Q_\text {pole})\) by the one-loop electroweak corrections that are added to \(M_h\) by the spectrum generators that we employ. However, higher order logarithms (formally at the two-loop order) in the electroweak gauge couplings remain. These remaining pieces have no explicit dependence at leading order on \(M=M_S\). In the limit of large \(M_S\), the first term in the square brackets of Eq. (2) contains both a dependence on a large \(M_S\) and \(Q_\text {pole}\) through renormalisation of the running top Yukawa coupling \(y_t = \sqrt{2} m_t / (v \sin \beta )\). The \(Q_\text {pole}\) dependence of leading logarithm terms due to this are cancelled by the explicit two-loop terms of order \(\alpha _t^2/(4 \pi )^2\) in the \(M_h\) calculation that the spectrum generators employ, but higher powers of the logarithms do not cancel. The \(Q_\text {pole}\) dependence from this term is then formally of three-loop order, but is boosted somewhat by the large value of \(y_t\). For \(\tan \beta =20\) and large \(M_S\), the \(Q_\text {pole}\) dependence is small, partly aided by cancellations in the beta function of \(y_t\). However, for \(\tan \beta =5\), as is the case in Ref. [51], for example, one can see an increase in scale uncertainty with a larger \(M_S\) due to a larger value of \(y_t\) (and consequently a larger beta function/scale dependence).

The size of the missing (subleading) logarithmic higher order contributions to the running \({\text {MSSM}}\) \(\overline{\text {DR}}'\) gauge and Yukawa couplings can be estimated in a similar way to that of \(Q_\text {pole}\) by varying the renormalisation scale \({Q_\text {match}}\), at which the said parameters are determined. We define this uncertainty as

$$\begin{aligned} {\varDelta M_h^{({Q_\text {match}})}}= \max _{Q\in [{Q_\text {match}}/2,2{Q_\text {match}}]}\left| M_h(Q) - M_h({Q_\text {match}})\right| \nonumber \\ \end{aligned}$$
(4)

where \({Q_\text {match}}\) is the scale at which these parameters are determined, usually set to \(M_Z\) or \(M_t\). The uncertainty \({\varDelta M_h^{({Q_\text {match}})}}\) is shown as blue dashed-dotted line in Fig. 2 and is below \(0.2~\text {GeV}\) for the scenario shown.

Besides the logarithmic higher order corrections there are also ‘non-logarithmic’ higher corrections, which are important and should be taken into account in any robust uncertainty estimate [51]. We estimate these non-logarithmic corrections by changing the calculation of the running \({\text {MSSM}}\) parameters \(m_t\), \({\alpha _{\text {s}}}\) and \(\alpha _{\text {e.m.}}\) by higher orders: the running \(\overline{\text {DR}}'\) top mass \(m_t\) is calculated in two different ways, similar to Ref. [51]:

$$\begin{aligned} m_t^{(1)}&= M_t + \widetilde{\varSigma }_t^{(1),S} + M_t \left[ \widetilde{\varSigma }_t^{(1),L} + \widetilde{\varSigma }_t^{(1),R} \right] \nonumber \\&\phantom {={}} + M_t \left[ \widetilde{\varSigma }_t^{(1),\text {SQCD}} + \widetilde{\varSigma }_t^{(2),\text {SQCD}} + \left( \widetilde{\varSigma }_t^{(1),\text {SQCD}}\right) ^2 \right] \nonumber \\ \end{aligned}$$
(5)

and

$$\begin{aligned} m_t^{(2)}&= M_t + \widetilde{\varSigma }_t^{(1),S} + m_t \left[ \widetilde{\varSigma }_t^{(1),L} + \widetilde{\varSigma }_t^{(1),R} \right] \nonumber \\&\phantom {={}} + m_t \left[ \widetilde{\varSigma }_t^{(1),\text {SQCD}} + \widetilde{\varSigma }_t^{(2),\text {SQCD}} \right] , \end{aligned}$$
(6)

where \(M_t\) denotes the top pole mass, \(\widetilde{\varSigma }_t^{(1),S}\), \(\widetilde{\varSigma }_t^{(1),L}\) and \(\widetilde{\varSigma }_t^{(1),R}\) denote the scalar, left-handed and right-handed part of the one-loop top self energy without SUSY-QCD contributions and \(\widetilde{\varSigma }_t^{(1,2),\text {SQCD}}\) denote the one-loop and two-loop SUSY-QCD contributions from Refs. [52,53,54].Footnote 3 Note, that in Ref. [51] the two-loop SM-QCD contribution has been used on the right hand side of Eqs. (5) and (6), while here we use the full two-loop SUSY-QCD contribution of \(\mathcal {O}(\alpha _s^2)\). Since the latter is significantly larger, the difference between \(m_t^{(1)}\) and \(m_t^{(2)}\) is larger in our case. Equations (5) and (6) are equivalent at \(\mathcal {O}({\alpha _{\text {s}}}^2)\), but differ at \(\mathcal {O}(\alpha _{\text {e.m.}}{\alpha _{\text {s}}})\), for example. Since the difference contains both logarithmic and non-logarithmic terms, it can be used as an uncertainty estimate. Similar to Ref. [51] we define

$$\begin{aligned} \varDelta M_h^{(m_t)}= \left| M_h(m_t^{(1)}) - M_h(m_t^{(2)})\right| . \end{aligned}$$
(7)

In Ref. [51] four different top mass calculations are combined, whilst we combine only two. The size of \(\varDelta M_h^{(m_t)}\) is shown in Fig. 2 as a green dotted line. Since \(\varDelta M_h^{(m_t)}\) contains terms of the form \(\log (m_t/m_{\tilde{t}_i})\), the uncertainty increases logarithmically with the SUSY scale. It therefore serves as an estimate of both (leading) logarithmic and non-logarithmic higher order corrections and is a reasonable measure to express the fact that the fixed-order calculation suffers from a large theoretical uncertainty for multi-TeV stop masses.

We estimate the effect of unknown higher order logarithmic and non-logarithmic threshold corrections to \({\alpha _{\text {s}}}\) and \(\alpha _{\text {e.m.}}\) in a similar way to our approach for estimating \(\varDelta M_h^{(m_t)}\):

$$\begin{aligned} {\alpha _{\text {s}}}^{(1)}= & {} \frac{{\alpha _{\text {s}}}^{\text {SM}(5)}}{1 - \varDelta ^{(1)}{\alpha _{\text {s}}}- \varDelta ^{(2)}{\alpha _{\text {s}}}}, \end{aligned}$$
(8)
$$\begin{aligned} {\alpha _{\text {s}}}^{(2)}= & {} {\alpha _{\text {s}}}^{\text {SM}(5)} \left[ 1 + \varDelta ^{(1)}{\alpha _{\text {s}}}+ (\varDelta ^{(1)}{\alpha _{\text {s}}})^2 + \varDelta ^{(2)}{\alpha _{\text {s}}}\right] , \end{aligned}$$
(9)

and

$$\begin{aligned} \alpha _{\text {e.m.}}^{(1)}= & {} \frac{\alpha _{\text {e.m.}}^{\text {SM}(5)}}{1 - \varDelta ^{(1)}\alpha _{\text {e.m.}}- \varDelta ^{(2)}\alpha _{\text {e.m.}}}, \end{aligned}$$
(10)
$$\begin{aligned} \alpha _{\text {e.m.}}^{(2)}= & {} \alpha _{\text {e.m.}}^{\text {SM}(5)} \Big [1 + \varDelta ^{(1)}\alpha _{\text {e.m.}}+ ( \varDelta ^{(1)}\alpha _{\text {e.m.}})^2 \nonumber \\&+\,\varDelta ^{(2)}\alpha _{\text {e.m.}}\Big ] \end{aligned}$$
(11)

and take the difference as an uncertainty estimate,

$$\begin{aligned} \varDelta M_h^{({\alpha _{\text {s}}})}= & {} \left| M_h({\alpha _{\text {s}}}^{(1)}) - M_h({\alpha _{\text {s}}}^{(2)}) \right| , \end{aligned}$$
(12)
$$\begin{aligned} \varDelta M_h^{(\alpha _{\text {e.m.}})}= & {} \left| M_h(\alpha _{\text {e.m.}}^{(1)}) - M_h(\alpha _{\text {e.m.}}^{(2)}) \right| . \end{aligned}$$
(13)

Note that the uncertainties estimated by \(\varDelta M_h^{({\alpha _{\text {s}}})}\) and \(\varDelta M_h^{(\alpha _{\text {e.m.}})}\) were not included in Ref. [51]. Their respective sizes are shown in Fig. 2 as yellow dashed and brown double-dotted lines, respectively. Due to the logarithmic contributions of the form \(\log (m_t/m_{\tilde{t}_i})\) to the threshold corrections of \({\alpha _{\text {s}}}\) and \(\alpha _{\text {e.m.}}\), the two uncertainties increase logarithmically with the SUSY scale. However, since \(\alpha _{\text {e.m.}}\) is very small, the uncertainty \(\varDelta M_h^{(\alpha _{\text {e.m.}})}\) is negligible. The magnitude of \(\varDelta M_h^{({\alpha _{\text {s}}})}\) can be around \(20\%\) of \(\varDelta M_h^{(m_t)}\) for large \(M_S\).

There are some inter-dependencies between the different sources of uncertainty and it is practically impossible to exactly take these into account unless the higher order corrections are explicitly calculated. However, the quantification of theoretical uncertainties is an inexact pursuit and it serves us well enough to combine the different sources of uncertainty linearly

$$\begin{aligned} \varDelta M_h^{(\texttt {SS+H})}= & {} \varDelta M_h^{(Q_\text {pole})}+ {\varDelta M_h^{({Q_\text {match}})}}+ \varDelta M_h^{(m_t)}\nonumber \\&+\,\varDelta M_h^{({\alpha _{\text {s}}})}+ \varDelta M_h^{(\alpha _{\text {e.m.}})}\, \end{aligned}$$
(14)

in order to have some kind of reasonable estimate of the total level of theoretical uncertainty in the prediction. The combination \(\varDelta M_h^{(\texttt {SS+H})}\) is shown in Fig. 2 as a red solid line. As expected, due to logarithmic contributions of the form \(\log (m_t/m_{\tilde{t}_i})\), the combined uncertainty of the fixed-order calculation of SOFTSUSY increases with the SUSY scale and reaches \(\varDelta M_h^{(\texttt {SS+H})}\sim 4~\text {GeV}\) for \(M_S\sim 10~\text {TeV}\). The size of the individual uncertainties show that the prescription proposed in Ref. [51] is reasonable, because the additional uncertainties \({\varDelta M_h^{({Q_\text {match}})}}\), \(\varDelta M_h^{({\alpha _{\text {s}}})}\) and \(\varDelta M_h^{(\alpha _{\text {e.m.}})}\) that we have introduced here are small. However, compared to the combined uncertainty estimate of Ref. [51] our combined uncertainty is smaller by about \(40\%\) for SUSY scales of around \(M_S\sim 1~\text {TeV}\) and about \(25\%\) smaller for \(M_S\sim 10~\text {TeV}\). The main reasons are the reduced scale uncertainty \(\varDelta M_h^{(Q_\text {pole})}\) due to the three-loop Higgs boson mass corrections that are included here and our different definition of \(\varDelta M_h^{(m_t)}\).

In the following we compare the fixed-order Higgs boson mass prediction for this scenario to the pure EFT calculation of HSSUSY [46]. HSSUSY is a spectrum generator from the FlexibleSUSY package, which implements the high-scale SUSY scenario, where the quartic \(\text {SM}\) Higgs coupling \(\lambda (M_S)\) is predicted from matching to the \({\text {MSSM}}\) at a high SUSY scale \(M_S\). It provides a prediction of the Higgs pole mass in the \({\text {MSSM}}\) in the pure EFT limit, \(v^2 \ll M_S^2\), up to the two-loop level \(\mathcal {O}({\alpha _{\text {s}}}({\alpha _t}+{\alpha _b}) + ({\alpha _t}+{\alpha _b})^2 + {\alpha _\tau }{\alpha _b}+ {\alpha _\tau }^2)\) [40, 55,56,57], including next-to-next-to-leading-log (NNLL) re-summation [58, 59]. Additional pure \(\text {SM}\) three- and four-loop corrections [60,61,62,63,64,65] can be taken into account on demand.

To estimate the Higgs boson mass uncertainty of HSSUSY we use the procedure developed in Ref. [66], which is an extension of the methods used in Refs. [40, 42]. The sources of uncertainty of HSSUSY are divided into the following three categories:

  • \(\text {SM}\) uncertainty from missing higher order corrections in the determination of the running \(\text {SM}\) \(\overline{\text {MS}}\) parameters

  • EFT uncertainty from neglecting terms of order \(\mathcal {O}(v^2/M_S^2)\)

  • SUSY uncertainty from missing higher order contributions from SUSY particles

As in the fixed order \(\overline{\text {DR}}'\) calculation, we divide the \(\text {SM}\) uncertainty into a logarithmic and non-logarithmic part. However, since large logarithmic corrections to the Higgs mass are re-summed in the EFT calculation, for the ‘logarithmic part’, we refer specifically to smaller logarithms of the form \(\ln ({Q_\text {match}}/m_{\tilde{t}_1})\) or \(\ln (Q_\text {pole}/M_t)\). These small logarithmic higher order corrections are estimated by varying the renormalisation scale \(Q_\text {pole}\), at which the Higgs boson mass is calculated in the effective \(\text {SM}\):

$$\begin{aligned} \varDelta M_h^{(Q_\text {pole})}= \max _{Q_\text {pole}\in [M_t/2,2M_t]}\left| M_h(Q_\text {pole}) - M_h(M_t)\right| . \end{aligned}$$
(15)

The non-logarithmic part is estimated by switching the three-loop QCD contributions [60, 61] on or off in the extraction of the running \(\text {SM}\) top Yukawa coupling from the top pole mass,

$$\begin{aligned} \varDelta M_h^{(y_t^\text {SM})}= \left| M_h(y_t^{\text {SM},2\ell }(M_Z)) - M_h(y_t^{\text {SM},3\ell }(M_Z)) \right| . \end{aligned}$$
(16)

Although this difference is sensitive to non-logarithmic higher order contributions to the Higgs boson mass, it shows an additional dependence on the separation of the electroweak scale and the SUSY scale (as was observed in Refs. [42, 67] and shown in the green dotted line of Fig. 3). The main reason for this dependence is that the running top Yukawa coupling (the largest dimensionless parameter in the MSSM) enters the RGEs of the other MSSM parameters, thus affecting their running below \(M_S\). The effect is stronger for more separated scales.

The EFT uncertainty is estimated by Ref. [42] by multiplying the one-loop contribution of each individual SUSY particle to the quartic Higgs coupling \(\lambda (M_S)\) at the SUSY scale by the factor \((1 + v^2/M_S^2)\). We use the resulting change in the Higgs boson pole mass prediction as an estimate for the EFT uncertainty,

$$\begin{aligned} \varDelta M_h^{(v^2/M_S^2)}= \left| M_h - M_h(v^2/M_S^2) \right| , \end{aligned}$$
(17)

where \(M_h(v^2/M_S^2)\) is the predicted Higgs boson mass with the additional \(v^2/M_S^2\) terms. In Ref. [57] it was shown that this uncertainty estimate is very conservative.

The SUSY uncertainty is also divided into a logarithmic and a ‘non-logarithmic’ part. We estimate the (leading) logarithmic part again by varying the scale \({Q_\text {match}}\), at which the matching of the MSSM to the effective \(\text {SM}\) is performed, similar to Ref. [42],

$$\begin{aligned} {\varDelta M_h^{({Q_\text {match}})}}= \max _{Q\in [M_S/2,2M_S]}\left| M_h(Q) - M_h(M_S)\right| . \end{aligned}$$
(18)

Like \(\varDelta M_h^{(y_t^\text {SM})}\), \({\varDelta M_h^{({Q_\text {match}})}}\) also shows an additional dependence on the separation of the electroweak scale and the SUSY scale due to the dependence of the RGEs on the running parameters. The non-logarithmic part is estimated by re-parametrising the threshold correction for \(\lambda (M_S)\) in terms of the MSSM top Yukawa coupling at the SUSY scale, \({y_{t}}^{\text {MSSM}}(M_S)\), and we take the resulting shift in the Higgs boson mass as an estimate for the uncertainty

$$\begin{aligned} {\varDelta M_h^{(y_t^{\text {MSSM}})}}= \left| M_h - M_h(y_t^{\text {MSSM}}(M_S)) \right| . \end{aligned}$$
(19)

A similar uncertainty was defined in Ref. [51], where the loop order of the calculation of \(y_t^{\text {MSSM}}(M_S)\) was switched between tree- and one-loop level. Our uncertainty \({\varDelta M_h^{(y_t^{\text {MSSM}})}}\) is significantly smaller than the one used in Ref. [51], because we are working at one loop higher order and the uncertainty there contains large two-loop next-to-leading logarithms (see the discussion in Ref. [46]).

Fig. 3
figure 3

Individual sources of uncertainty of the two-loop EFT Higgs boson mass prediction of HSSUSY

Full size image

Analogously to our procedure with the fixed order \(\overline{\text {DR}}'\) calculation, we combine all individual HSSUSY uncertainties linearly,

$$\begin{aligned} \varDelta M_h^{(\texttt {HSSUSY})}= & {} \varDelta M_h^{(Q_\text {pole})}+ {\varDelta M_h^{({Q_\text {match}})}}+ \varDelta M_h^{(y_t^\text {SM})}\nonumber \\&+\, {\varDelta M_h^{(y_t^{\text {MSSM}})}}+ \varDelta M_h^{(v^2/M_S^2)}. \end{aligned}$$
(20)

Figure 3 shows the individual uncertainties of HSSUSY from these three categories. For low SUSY scales, \(M_S\lesssim 1~\text {TeV}\), the combined uncertainty estimate of HSSUSY, \(\varDelta M_h^{(\texttt {HSSUSY})}\), (red solid line) is dominated by the EFT uncertainty \(\varDelta M_h^{(v^2/M_S^2)}\) (brown dashed-double-dotted line) due to the fact that the neglected terms of \(\mathcal {O}(v^2/M_S^2)\) are not negligible in this region. For \(M_S\gtrsim 2~\text {TeV}\) the EFT uncertainty drops below \(0.1~\text {GeV}\) and the remaining sources dominate. For even higher scales of \(M_S\gtrsim 10~\text {TeV}\), the two components of the SUSY uncertainty, \({\varDelta M_h^{({Q_\text {match}})}}\) and \({\varDelta M_h^{(y_t^{\text {MSSM}})}}\), become smaller because the dimensionless running couplings become smaller at higher SUSY scales in this scenario. For high scales of \(M_S\gtrsim 10~\text {TeV}\) the combined uncertainty is dominated by the \(\text {SM}\) uncertainty, in particular by the uncertainty \(\varDelta M_h^{(y_t^\text {SM})}\) in the extraction of the running \(\text {SM}\) top Yukawa coupling at the electroweak scale, which remains at \(\varDelta M_h^{(y_t^\text {SM})}\sim 0.5~\text {GeV}\).

Fig. 4
figure 4

Higgs boson mass predictions at fixed three-loop order with SOFTSUSY (red solid line) and FlexibleSUSY (blue dashed line) and in the EFT (black dashed line). The coloured regions show the estimated composite theoretical uncertainties in the different predictions of \(M_h\). The FlexibleSUSY uncertainty is very similar to the SOFTSUSY one, and so is not shown for reasons of clarity. The orange band shows the experimentally measured Higgs boson mass with the experimental uncertainty

Full size image

In Fig. 4 the \(M_h\) prediction in the fixed-order and the EFT approximation schemes are shown, together with their uncertainties.Footnote 4 We see from the figure that the allowed \(M_S\) range depends sensitively on the approximation scheme: 1.3–\(3.0~\text {TeV}\) for fixed-order and 2.5–\(4.6~\text {TeV}\) for EFT. The Higgs mass increases as a function of the SUSY scale due to the logarithmic enhancement from heavy SUSY particles. As discussed above, the combined uncertainty of the fixed-order calculations (red band) tends to increase with increasing \(M_S\), while the uncertainty of the EFT calculation (grey band) decreases. The point where the fixed-order and the EFT calculation have the same estimated uncertainty is \(M_S^\text {equal}=1.2~\text {TeV}\). To improve the prediction near this point, a “hybrid” calculation should be used, where the large logarithms are re-summed and \(\mathcal {O}(v^2/M_S^2)\) terms are included [46, 48, 50, 51, 57, 68, 69].

3 Upper bound on the lightest stop mass

The logarithmic enhancement of the loop corrections to the Higgs boson mass from heavy stops suggests that there is an upper limit on the mass of the lightest stop from the requirement of predicting \(M_h = 125.09~\text {GeV}\) and a stable and appropriate (i.e. colour and charge preserving) vacuum. As was already shown in Ref. [40], the maximum lightest stop mass is around \(10^{11}\) GeV. At very large stop masses, EWSB is fine-tuned, despite the fact that the Higgs mass in our spectrum generators comes out to be small. This is because the generators implicitly tune parameters in order to obtain the measured central value of the Z boson mass \(M_Z=91.1876\) GeV (or equivalently, the inferred value of \(v \sim 246~\text {GeV}\)). We see this in the MSSM EWSB equation [70] which predicts \(M_Z\):

$$\begin{aligned} \frac{M_{Z}^2}{2}= \frac{m_{\bar{H}_1}^2(Q) - m_{\bar{H}_2}^2(Q) \tan ^2 \beta (Q)}{\tan ^2 \beta (Q) - 1} - \frac{1}{2} \mathfrak {R}\varPi _{ZZ}^T(Q) - \mu ^2\nonumber \\ \end{aligned}$$
(21)

where \(m_{\bar{H}_i}^2 = m_{H_i}^2 - t_i/v_i\), \( \mathfrak {R}\varPi _{ZZ}^T(Q)\) is the Z self-energy and \(t_i\) are the tadpole contributions from loops. Q is the scale at which EWSB is calculated: usually around the TeV scale and \(v_i\) are the two Higgs VEVs of the \(CP\) even electrically neutral \({\text {MSSM}}\) Higgs fields. When the stop masses are huge, they contribute to huge values of \(m_{\bar{H}_i}^2\) through the MSSM RGEs, which at one loop order are [71]:

$$\begin{aligned} \frac{1}{\kappa } \frac{d m_{H_1}^2}{d t}= & {} 6\, y_b^2 \left( m_{H_1}^2 + m_{{\tilde{Q}}_3}^2 + m_{{\tilde{d}}_3}^2 +A_b^2\right) \nonumber \\&-\, 6 g_2^2 M_2^2 - \frac{6}{5}g_1^2M_1^2 + \frac{3}{5}g_1^2\Big [m_{H_2}^2 - m_{H_1}^2\nonumber \\&+\,\text {Tr}(m_{\tilde{Q}}^2 - m_{\tilde{L}}^2 - 2 m_{\tilde{u}}^2 + m_{\tilde{d}}^2 + m_{\tilde{e}}^2)\Big ], \end{aligned}$$
(22)
$$\begin{aligned} \frac{1}{\kappa } \frac{d m_{H_2}^2}{d t}= & {} 6\, y_t^2 \left( m_{H_2}^2 + m_{{\tilde{Q}}_3}^2 + m_{{\tilde{u}}_3}^2 +A_t^2\right) \nonumber \\&-\, 6 g_2^2 M_2^2 - \frac{6}{5}g_1^2M_1^2 + \frac{3}{5}g_1^2\Big [m_{H_2}^2 - m_{H_1}^2\nonumber \\&+\,\text {Tr}(m_{\tilde{Q}}^2 - m_{\tilde{L}}^2 - 2 m_{\tilde{u}}^2 + m_{\tilde{d}}^2 + m_{\tilde{e}}^2)\Big ], \end{aligned}$$
(23)

where t is the natural logarithm of the renormalisation scale and \(M_i\), \(m_i\) are soft supersymmetry breaking mass parameters of order \(M_S\), as defined in Ref. [71]. In order for the left-hand side of Eq. (21) to obtain the experimental value, the first and the last term must cancel to a very large degree. There is no fundamental reason why this is the case and the terms must be tuned.

In practice, HSSUSY inverts the Higgs minimisation equations, taking \(\mu (M_S)\) and the value of the \(CP\)-odd Higgs boson mass \(m_A(M_S)\) as input values. In this scheme, \(m_{\bar{H}_i}^2\) are implicitly tuned in order to give \(M_Z^2\) at the experimental central value. Once this single tuning has been achieved, there are no more large corrections to \(M_{h}\) from heavy sparticles: they are all proportional to \(M_Z \propto v\), which has already been tuned.

Fig. 5
figure 5

Higgs boson mass prediction with the EFT calculation HSSUSY as a function of the lightest \(\overline{\text {DR}}'\) stop mass and the \(\overline{\text {DR}}'\) stop mixing parameter for degenerate SUSY mass parameters and \(\tan \beta (M_S) = 1\). The solid lines show the central value of \(M_{h}\) according to Eq. (1) plus or minus the theoretical uncertainty. The dark regions at the top and bottom of the plot display regions of parameter space which have charge and colour breaking minima. Hatched regions have \(\lambda (M_S) < 0\)

Full size image

We estimate the upper bound on the lightest \(\overline{\text {DR}}'\) stop mass \(m_{\tilde{t}_1}\) in Fig. 5 by scanning over \(M_S\) and the relative \(\overline{\text {DR}}'\) stop mixing parameter \(X_t/M_S\) in a scenario with degenerate SUSY breaking mass parameters (except for \(m_{H_i}^2\)) set equal to \(M_S\), \(\mu (M_S)=m_A(M_S)=M_S\) and \(\tan \beta = 1\) to make the tree-level Higgs mass vanish. This should then be the limiting case where we require the largest correction from stops in order to predict \(M_h\) in the correct range to satisfy the experimental measurement. The Higgs boson mass has been calculated with the pure EFT calculation HSSUSY, because it has a smaller uncertainty than the fixed-order calculations in the limit of large stop masses. The black lines show the contours of \(M_h = 125.09~\text {GeV}\pm \varDelta M_h^{(\texttt {HSSUSY})}\), where \(\varDelta M_h^{(\texttt {HSSUSY})}\) is the estimate of the theory uncertainty from HSSUSY, as described in Sect. 2. In the red hatched region the quartic Higgs coupling is negative at the SUSY scale, \(\lambda (M_S) < 0\), pointing to a potentially unstable electroweak vacuum.Footnote 5\(^{,}\)Footnote 6 In order to tell whether a point with \(\lambda (M_S)<0\) really is excluded, one should examine the full MSSM scalar potential. We consider this to be beyond the scope of the present work, and so for now, we simply leave it as a point of interest. We also display regions which are excluded because they would lead to charge and colour breaking minima which are deeper than the electroweak vacuum, outside the region [40]

$$\begin{aligned} \frac{X_t^2}{m_{\tilde{Q}_3} m_{\tilde{u}_3}} < \left( 4 - \frac{1}{\sin ^2\beta }\right) \left( \frac{m_{\tilde{Q}_3}}{m_{\tilde{u}_3}} + \frac{m_{\tilde{u}_3}}{m_{\tilde{Q}_3}}\right) . \end{aligned}$$
(24)

Applying Eq. (24) at \(Q=M_S\) with our boundary conditions on the quantities within it leads to

$$\begin{aligned} -2< X_t/M_S< 2, \end{aligned}$$
(25)

which corresponds to the non-darkened region in the horizontal middle band of Fig. 2. From regions with a stable electroweak vacuum based on the criterion in Eq. (25) and where Eq. (1) is satisfied including the theoretical uncertainty, we estimate an upper bound of \(m_{\tilde{t}_1} < 3.7 \times 10^{11}~\text {GeV}\).

4 Summary

By using the state-of-the-art EFT Higgs boson mass prediction of HSSUSY we derived an estimate for the upper bound of the lightest running stop mass that is compatible with the measured value of the Higgs boson mass of \(M_h = 125.09\) GeV, taking into account the uncertainty estimate of the EFT calculation. Our estimate for the range of the lightest stop mass is

$$\begin{aligned} m_{{\tilde{t}}_1} < 3.7 \times 10^{11} ~\text {GeV}, \end{aligned}$$
(26)

provided the sparticle spectrum is not split so that some sparticles are much lighter than \(m_{{\tilde{t}}_1}\), as this would invalidate the assumptions implicit within the EFT calculation that all sparticles are around \(M_S\). Our more precise estimate of theoretical uncertainties in the prediction of \(M_h\) does not qualitatively change the conclusion of the previous study in Ref. [40]. Unfortunately, such a bound is very much higher than the potential energies of conceivable terrestrial particle accelerators.

We also compared the precision of the Higgs boson mass predictions of the state-of-the-art \(\overline{\text {DR}}'\) fixed-order and EFT spectrum generators SOFTSUSY, FlexibleSUSY and HSSUSY in the \({\text {MSSM}}\). We estimated the uncertainties of the Higgs boson mass of the fixed-order and the EFT calculation by considering unknown logarithmic and non-logarithmic higher-order corrections. As part of our work, we have provided a scheme to estimate the theoretical uncertainties in fixed-order \(\overline{\text {DR}}'\) calculations, based on the prescription used in Ref. [51]. Our prescription is an extension of Ref. [51], which takes further sources of uncertainty into account. By comparing the precision of the predictions of the two methods, we concluded that for SUSY masses below \(M_S^\text {equal}=1.2~\text {TeV}\), the fixed-order calculation is more precise, while above that scale the EFT method is more precise. To estimate this scale, we took the maximal mixing case where all soft supersymmetry breaking masses are set to be degenerate at \(M_S\) (except for \(m_{H_i}\), which are fixed in order to achieve successful EWSB) and where \(\tan \beta =20\). The precise value of \(M_S^\text {equal}\) will change depending upon the scenario and can vary between \(M_S= 1.0~\text {TeV}\) and \(1.3~\text {TeV}\) for minimal/maximal stop mixing and small/large values of \(\tan \beta \). However, once one imposes the experimental measurement upon \(M_h\), \(M_S\ge 1.3~\text {TeV}\) according to the fixed-order calculationFootnote 7 and \(2 ~\text {TeV}\) according to the EFT calculation, as Fig. 4 shows. For \(M_S\ge 1.3~\text {TeV}\), the EFT has smaller uncertainties and so one is likely to be in a régime where \(M_h\) is better approximated by EFT methods. It is unclear as yet, however, whether details of the \({\text {MSSM}}\) spectrum other than \(M_h\) are better approximated by EFT methods. One question which we have not addressed is: which approximation scheme (fixed order \(\overline{\text {DR}}'\) or EFT) is more accurate when there is a hierarchical sparticle spectrum? It is quite possible, for example, that the stops are heavy but several of the other \({\text {MSSM}}\) sparticles are significantly lighter. For such scenarios the precision of the fixed order \(\overline{\text {DR}}'\) calculation would have to be compared with the precision of an appropriate EFT that contains the light sparticles. We leave such a study for future work.