1 Introduction

Existence of topological defects have been reported in various aspects of the physics and their important roles in physical properties of the systems have been highlighted. From gravitational/cosmological point of view, the effects and importance of the topological defects could be related to their role as a possible dark matter source [1, 2], their role in large scale structure of the universe [3,4,5] anisotropy in the Cosmic Microwave Background (CMB) [6, 7] and their lensing properties [8] (which are due to existence of deficit angle). Essentially, the topological defects in cosmology are produced due to symmetries that are broken in phase transition that has taken place in the early universe [3,4,5]. Depending on the number and type of the symmetries that are broken, these topological defects are categorized into domain walls (a discrete symmetry is broken and it divides the universe into blocks), cosmic strings (axial or cylindrical symmetry is broken and have applications in regard to grand unified particle physics models/electroweak scale), monopoles (a spherical symmetry is broken) and textures (several symmetries are broken). Since these topological defects may be formed during the early universe, they may also carry valuable information of this era which highlights yet another importance of studying them. The topological defects are located at the boundaries of regions which have chosen different minima during the early universe phase transition. So far, these topological defects have inspired a large number of publications which among them one can point out; cosmic strings in the presence of Maxwell theory [9, 10], their superconducting property in the presence of different models of gravity (such as Einstein [11], Brans–Dicke [12] and dilaton gravity [13]), the QCD [14] and quantum [15] applications of the magnetic strings, limits on the cosmic string tension using CMB temperature anisotropy maps [16], gravitational waves produced by cosmic strings [17] and decaying domain walls [18] and localization of fields and chiral spinor on domain walls [19]. (For further studies regarding topological defects, we refer the reader to an incomplete list of Refs. [20,21,22,23,24,25]). Motivated by these studies and their interesting results, here we investigate a type of topological defects which are known as magnetic branes (generalization of magnetic string), in the presence of two generalizations; massive gravity and nonlinear electromagnetic field which are generalizations in gravitational and matter field sectors, respectively.

Although the Maxwell electrodynamics (linear electrodynamics) is one of the most successful theories in the history of physical science, it does not provide very precise results in some scales. On the other hand, due to the fact that the most physical systems are nonlinear in the nature, the generalization of linear electrodynamics to nonlinear ones seems to be logical. In addition, owing to specific properties of nonlinear electrodynamics in the gauge/gravity coupling, the relations between the general relativity (GR) and nonlinear electrodynamics attract significant attention. Nonlinear electrodynamic theories have some interesting results and predictions, and therefore, various nonlinear models of electrodynamics have been introduced by many authors. For typical examples, one may look at the Born-Infeld theory [26], logarithmic form [27], exponential Lagrangian [28], arcsin nonlinear electrodynamics [29, 30] and etc. Black hole and magnetic solutions by considering these nonlinear electrodynamics have been investigated in Refs [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. Also, other aspects of these nonlinear models have been studied in the context of quantum level [53,54,55,56] and astrophysical area [57,58,59] as well. The extensive usages of these nonlinear theories provide the validity of their authenticity.

Taking into account the conformal invariance, one may find that it plays an important role in the structure of the some interesting models of string theory. In other words, conformal invariance is a kind of criterion for obtaining covariant equations of motion for the on-shell classical background in the low energy effective of string theory [60, 61]. Regarding the equations of motion in the classical Einstein gravity, one finds the conformal invariance is equivalent to the existence of a traceless stress-energy tensor. It is evident that the Maxwell theory enjoys the conformal invariance only in 4-dimensions. But in three or higher dimensional spacetime, the conformal symmetry will be broken. In other words, the stress-energy tensor of Maxwell theory is traceless only for 4-dimensions. In order to keep the conformal invariance symmetry in arbitrary dimensions, one should generalize the Maxwell field to the so-called power Maxwell invariant (PMI) theory. PMI theory is one of the interesting branches of nonlinear electrodynamics in which its Lagrangian is an arbitrary power of Maxwell Lagrangian (\(\mathcal {L}_{PMI}(\mathcal {F} )\propto \mathcal {F}^{s}\), where \(\mathcal {F}\) is the Maxwell invariant) [62,63,64,65]. This theory of nonlinear electrodynamics has more interesting properties with regard to linear electrodynamics (Maxwell case), and for the case of \(s=1\), it reduces to the Maxwell theory. Another attractive property is related to conformal invariance property. In other words, when the power of the Maxwell invariant is a quarter of spacetime dimensions (\(s=d/4\), where d is dimensions), this theory enjoys conformal invariance, and therefore, its energy-momentum tensor will be traceless. In this case one may obtain the Reissner-Nordström like solutions in higher dimensions [62]. The effects of considering PMI source for the classical black hole solutions in various gravities have been studied in literature, for example; Lovelock and Lifshitz black holes with PMI field have been investigated in [65,66,67,68], BTZ black holes in the Einstein and F(R) gravities with this nonlinear electrodynamic model have been studied in Refs. [42, 69, 70], the effects of PMI for BTZ black hole with a scalar hair in the Einstein gravity are reported in [71]. Thermodynamics of topological black holes in the Brans–Dicke theory in the presence PMI field has been studied before [72]. Geometrical thermodynamics and the van der Waals like phase transition of black holes in higher dimensional spacetimes with PMI theory have been evaluated in Einstein and dilaton gravity [73,74,75,76]. Moreover, holographic superconductors and magnetic branes (string) supported by PMI source have been investigated in Refs. [77,78,79].

Although most of physicists believe that we should respect to conformal invariance symmetry, they believe that Lorentz invariance symmetry should be broken in high energy regimes. Considering a nonzero mass for the gravitons may leads to such breaking symmetry. Recent observations of gravitational waves from a binary black hole merger provided a firmly evidence of Einstein theory [80]. However, graviton in Einstein gravity is a massless particle, whereas there are several arguments that state graviton may be a massive object [80]. Therefore, GR can be generalized to include massive gravitons. The first attempt for such generalization was done by Fierz and Pauli [81] by using a linear theory. However, propagators of this theory do not reduce to those of GR in limit of vanishing graviton mass, \(m=0\) (van Dam, Veltman and Zakharov discontinuity). In order to remove this substantial problem, Vainshtein introduced a mechanism which requires the system to be considered in a nonlinear regime [82]. Nonetheless, we encounter with Boulware–Deser ghost in the generalization of Fierz and Pauli massive theory to the nonlinear regime [83]. To solve such problem, another class of massive gravity was proposed by de Rham, Gabadadze and Tolley (dRGT) [84, 85]. dRGT massive theory is free of Boulware–Deser ghost and it can be used in higher dimensions with admissible validity [86, 87]. It is noteworthy that, in order to obtain exact solutions with massive terms, an additional metric (called the reference metric) is invariably needed. The reference metric is required due to the fact that the interaction terms that can be formed from the metric alone, cannot be used to construct a mass term. In addition, this is an unphysical metric that does not have a direct influence on the geometrical nature of spacetime and it just helps us to find exact solutions and get rid of Boulware–Deser ghost instability. Considering the suitable reference metric, one finds various interesting publications in the context of dRGT massive gravity. Relativistic stars and black object solutions in dRGT massive gravity with interesting results have been investigated in [88,89,90,91,92]. On the other hand, it was shown that massive gravity can be expressible on an arbitrary reference metric [87]. Therefore, a modification on the reference metric could lead to another dRGT like massive theory. In this respect, Vegh has introduced a new reference metric with broken translational symmetry property [93]. In this massive gravity, similar to dRGT theory, massive terms are built by using this kind of reference metric which have an additional property. Also, in this theory, graviton may behave like a lattice and exhibits a Drude peak [93], and it is stable and free of ghost [94]. Neutron stars have been studied in this theory and it was found that the maximum mass of the neutron stars can be more than \( 3M_{\odot }\) (\(M_{\odot }\) is mass of the Sun) [95]. Black hole solutions and their thermodynamic properties have been investigated in Refs. [96,97,98]. Besides, the generalizations of this massive theory to include higher derivative gravity [99], and gravity’s rainbow extension [100] have been studied as well. In addition, black hole and magnetic solutions with (non)linear electrodynamics have been explored in the context of massive gravity [101, 102].

In this paper, we want to study the magnetic solutions of Einstein-massive gravity with linear and nonlinear electrodynamics in four and higher dimensions. This paper is one of interesting papers for considering the effects of massive gravitons on the horizonless solutions of nonsingular spacetime. Before proceeding, we provide some brief motivations for considering arbitrary higher dimensional spacetimes. In the 20th century, Kaluza and Klein introduced a new theory of gravity in five dimensions which unified gravitation and electromagnetism [103, 104]. In addition, development of string and M-theories led to further progresses in higher dimensional gravity. Another motivation originates from the anti de Sitter/conformal field theory (AdS/CFT) correspondence which relates the properties of d-dimensional black holes with quantum field theory in (\(d-1\) )-dimensional hypersurface [105]. On the other hand, with respect to gravitational researches, one often considers the number of spacetime dimensions as a free parameter of the theory and investigates its effects. Studying the effects of this parameter on various aspects of each theory, may lead to new insights (for example we refer the reader to the effects of various dimensions in PMI theory [62,63,64,65]).

The outline of the paper is as follow; in Sect. 2, we introduce the massive gravity with Maxwell and PMI theories and related field equations, briefly. In Sect. 3, we obtain the solutions in Einstein-Maxwell-massive gravity and show that these solutions are not black holes, but they contain a conic singularity. Then, we investigate the effects of all parameters on the deficit angle. In the next section, we extend the Maxwell source to nonlinear PMI theory and study the properties of the obtained solutions in this case, extensively. The last section is devoted to some closing remarks.

2 Basic field equations

The d-dimensional action in Einstein-massive gravity coupled to electromagnetic field is given by

$$\begin{aligned} \mathcal {I}_{G}&=-\frac{1}{16\pi }\int _{\mathcal {M}}d^{d}x\sqrt{-g}\Bigg [ \mathcal {R}-2\Lambda \nonumber \\&\quad +\mathcal {L}(\mathcal {F})+m^{2}\sum _{i=1}^{4}c_{i} \mathcal {U}_{i}(g,f)\Bigg ] , \end{aligned}$$
(1)

where \(\mathcal {R}\) is the scalar curvature, \(\Lambda =\pm (d-1)(d-2)/2l^{2} \) is the negative/positive cosmological constant for asymptotically AdS/dS solutions, and \(\mathcal {L}(\mathcal {F})\) is an arbitrary Lagrangian of electrodynamics. In addition, f is a fixed symmetric tensor, \(c_{i}\)’s are massive coefficients, and \(\mathcal {U}_{i}\) ’s are symmetric polynomials of the eigenvalues of matrix \(\mathcal {K}_{\nu }^{\mu }=\sqrt{g^{\mu \alpha }f_{\alpha \nu }}\)

$$\begin{aligned} \mathcal {U}_{1}&=\left[ \mathcal {K}\right] ,\;\;\;\;\;\mathcal {U}_{2}= \left[ \mathcal {K}\right] ^{2}-\left[ \mathcal {K}^{2}\right] ,\;\;\;\;\;\\ \mathcal {U}_{3}&=\left[ \mathcal {K}\right] ^{3}-3\left[ \mathcal {K}\right] \left[ \mathcal {K}^{2}\right] +2\left[ \mathcal {K}^{3}\right] , \\ \mathcal {U}_{4}&=\left[ \mathcal {K}\right] ^{4}-6\left[ \mathcal {K}^{2} \right] \left[ \mathcal {K}\right] ^{2}\\&\quad +8\left[ \mathcal {K}^{3}\right] \left[ \mathcal {K}\right] +3\left[ \mathcal {K}^{2}\right] ^{2}-6\left[ \mathcal {K} ^{4}\right] . \end{aligned}$$

Now, we can obtain the field equations by using variational principle. Varying the action (1) with respect to both metric tensor and gauge potential, one can obtain the following field equations

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }\left( \mathcal {R}-2\Lambda \right) +m^{2}\chi _{\mu \nu }=T_{\mu \nu }, \end{aligned}$$
(2)
$$\begin{aligned}&\partial _{\mu }\left( \sqrt{-g}\mathcal {L}_{\mathcal {F}}F^{\mu \nu }\right) =0, \end{aligned}$$
(3)

where \(\mathcal {L}_{\mathcal {F}}=d\mathcal {L}(\mathcal {F})/d\mathcal {F}\) and \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) is the Maxwell invariant in which \( F_{\mu \nu }\) \(=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the Faraday tensor and \(A_{\mu }\) is the gauge potential. In addition, \(\chi _{\mu \nu }\) is the massive term with the following form

$$\begin{aligned} \chi _{\mu \nu }&=-\frac{c_{1}}{2}\left( \mathcal {U}_{1}g_{\mu \nu }- \mathcal {K}_{\mu \nu }\right) \nonumber \\&\quad -\frac{c_{2}}{2}\left( \mathcal {U}_{2}g_{\mu \nu }-2\mathcal {U}_{1}\mathcal {K}_{\mu \nu }+2\mathcal {K}_{\mu \nu }^{2}\right) \nonumber \\&\quad -\frac{c_{3}}{2}(\mathcal {U}_{3}g_{\mu \nu }-3\mathcal {U}_{2} \mathcal {K}_{\mu \nu } \nonumber \\&\quad +6\mathcal {U}_{1}\mathcal {K}_{\mu \nu }^{2}-6\mathcal {K}_{\mu \nu }^{3})- \frac{c_{4}}{2}(\mathcal {U}_{4}g_{\mu \nu }-4\mathcal {U}_{3}\mathcal {K}_{\mu \nu }\nonumber \\&\quad +12\mathcal {U}_{2}\mathcal {K}_{\mu \nu }^{2}-24\mathcal {U}_{1}\mathcal {K }_{\mu \nu }^{3}+24\mathcal {K}_{\mu \nu }^{4}). \end{aligned}$$
(4)

and the energy-momentum tensor of electromagnetic source in Eq. (2) can be introduced as

$$\begin{aligned} T_{\mu \nu }=\frac{1}{2}g_{\mu \nu }\mathcal {L}(\mathcal {F})-2\mathcal {L}_{ \mathcal {F}}F_{\mu \lambda }F_{\nu }^{\lambda }. \end{aligned}$$
(5)

3 Magnetic solutions in Einstein-massive gravity with Maxwell field

Here, we are going to study the magnetic solutions of Eqs. (2) and (3) by considering the Maxwell electromagnetic field, namely \(\mathcal {L}(\mathcal {F})=-\mathcal {F}\). To do so, we consider the metric of d-dimensional spacetime in the following explicit form

$$\begin{aligned} ds^{2}= & {} -\frac{\rho ^{2}}{l^{2}}dt^{2}+\frac{d\rho ^{2}}{g(\rho )} +l^{2}g(\rho )d\varphi ^{2}\nonumber \\&+\frac{\rho ^{2}}{l^{2}} h_{ij}dx_{i}dx_{j},~~~~~i,j=1,2,3,\ldots ,n, \end{aligned}$$
(6)

where \(g(\rho )\) is an arbitrary function of radial coordinate \(\rho \) which should be determined, \(h_{ij}dx_{i}dx_{j}\) is the Euclidean metric on the (\( d-3\))-dimensional submanifold, and the scale length factor l is related to the cosmological constant \(\Lambda \). In addition, the angular coordinate \( \varphi \) is dimensionless and ranges in \(0\le \varphi \le 2\pi \) while \( x_{i}\)’s range is \((-\infty ,+\infty )\). The motivation of considering the metric gauge [\(g_{tt}\varpropto -\rho ^{2}\) and \(\left( g_{\rho \rho }\right) ^{-1}\varpropto g_{\varphi \varphi }\)] instead of the usual Schwarzschild like gauge [\(\left( g_{\rho \rho }\right) ^{-1}\varpropto g_{tt}\) and \(g_{\varphi \varphi }\varpropto \rho ^{2}\)] comes from the fact that we are looking for the magnetic solutions instead of electric ones. In addition, one can obtain such magnetic metric with local transformations of \( t\rightarrow il\varphi \) and \(\varphi \rightarrow it/l\) in the horizon flat Schwarzschild like metric, \(ds^{2}=-g(\rho )dt^{2}+\frac{d\rho ^{2}}{g(\rho ) }+\rho ^{2}d\varphi ^{2}+\frac{\rho ^{2}}{l^{2}}h_{ij}dx_{i}dx_{j}\). In other words, using such transformation, the metric (6) can be mapped to d-dimensional Schwarzschild like spacetime locally, but not globally, and therefore, both spacetimes are distinct.

In order to obtain exact solutions, we should make a suitable choice for the reference metric. Regarding the mentioned local transformation, we consider the following ansatz for the reference metric

$$\begin{aligned} f_{\mu \nu }=diag(-\frac{c^{2}}{l^{2}},0,0,\frac{c^{2}}{l^{2}}h_{ij}), \end{aligned}$$
(7)

where c in the above equation is a positive constant. Before we go on, we discuss the reason for considering such a reference metric (7 ). In case of d dimensional black holes, the metric with \((-,+,\ldots ,+)\) signature is given by

$$\begin{aligned} ds^{2}= & {} -g(\rho )dt^{2}+\frac{d\rho ^{2}}{g(\rho )}+\rho ^{2} d\varphi ^{2}\nonumber \\&\quad + \frac{\rho ^{2}}{l^{2}}h_{ij}dx_{i}dx_{j},~~~~~i,j=1,2,3,\ldots ,n. \end{aligned}$$
(8)

The black hole solutions in massive gravity are obtained using the ansatz metric \(f_{\mu \nu }=diag(0,0,c^{2},\frac{c^{2}}{l^{2}}h_{ij})\) for reference metric. In electrical black hole solutions, the metric function, \( g(\rho )\), is coupled with radial and temporal coordinates whereas in magnetic spacetime metric (Eq. 6), it is coupled with radial and spatial coordinates. Therefore, to obtain exact solutions in an axially symmetric spacetime with the form (6), reference metric \(f_{\mu \nu }=diag(0,0,c^{2},\frac{c^{2}}{l^{2}}h_{ij})\) should be modified into \( f_{\mu \nu }=diag(\frac{-c^{2}}{l^{2}},0,0,\frac{c^{2}}{l^{2}}h_{ij})\). It should be noted that using the reference metric (\(f_{\mu \nu }=diag(\frac{ -c^{2}}{l^{2}},0,0,\frac{c^{2}}{l^{2}}h_{ij})\)), results into a new class of nontrivial solutions. In addition, it is worth mentioning that this choice for reference metric, first, cannot produce any infinite value for the bulk action, since the bulk action contains non-negative powers of \(f_{\mu \nu }\) , and second, it does not preserve general covariance in the transverse coordinates t, \(x_{1}\), \(x_{2}\), \({\ldots .}\)

Using the metric ansatz (7), \(\mathcal {U}_{i}\)’s can be calculated in the following forms

$$\begin{aligned} \mathcal {U}_{1}= & {} \frac{d_{2}c}{\rho },\;\;\mathcal {U}_{2}=\frac{ d_{2}d_{3}c^{2}}{\rho ^{2}}, \nonumber \\ \mathcal {U}_{3}= & {} \frac{d_{2}d_{3}d_{4}c^{3}}{ \rho ^{3}}, \nonumber \\ \mathcal {U}_{4}= & {} \frac{d_{2}d_{3}d_{4}d_{5}c^{4}}{\rho ^{4}}, \end{aligned}$$
(9)

where \(d_{i}=d-i\). Due to our interest to investigate the magnetic solutions, we should assume a suitable gauge potential which leads to consistent field equations

$$\begin{aligned} A_{\mu }=h(\rho )\delta _{\mu }^{\varphi }. \end{aligned}$$
(10)

Using the Maxwell equation (3) with \(\mathcal {L}( \mathcal {F})=-\mathcal {F}\), and the metric (6), one finds the following differential equation

$$\begin{aligned} d_{2}F_{\varphi \rho }+\rho F_{\varphi \rho }^{\prime }=0, \end{aligned}$$
(11)

where \(F_{\varphi \rho }=h^{\prime }(\rho )\) and “prime” denotes differentiation with respect to \(\rho \). The solution of Eq. (11) is

$$\begin{aligned} F_{\varphi \rho }=\frac{q}{\rho ^{d_{2}}}, \end{aligned}$$
(12)

where q is an integration constant which may be related to electric charge. Substituting Eqs. (6) and (10) in the field Eq. (2), one can obtain

$$\begin{aligned}&\frac{l^{2}}{2}g^{\prime }(\rho )+\frac{\rho }{d_{2}}F_{\varphi \rho }^{2}- \frac{d_{3}l^{2}}{2}\left\{ m^{2}\left( \frac{cc_{1}}{d_{3}}+\frac{c_{2}c^{2} }{\rho }+\frac{d_{4}c_{3}c^{3}}{\rho ^{2}}\right. \right. \nonumber \\&\quad \left. \left. +\frac{d_{4}d_{5}c_{4}c^{4}}{\rho ^{3}}\right) -\frac{\left( g(\rho )+\frac{2\Lambda \rho ^{2}}{d_{2}d_{3}} \right) }{\rho }\right\} =0, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{l^{2}}{2}g^{\prime \prime }(\rho )+\frac{d_{3}l^{2}}{\rho }g^{\prime }(\rho )\nonumber \\&\quad -F_{\varphi \rho }^{2}-\frac{d_{3}l^{2}}{2}\left\{ m^{2}\left( \frac{ cc_{1}}{\rho }+\frac{d_{4}c_{2}c^{2}}{\rho ^{2}}+\frac{d_{4}d_{5}c_{3}c^{3}}{ \rho ^{3}}\nonumber \right. \right. \\&\left. \left. \quad +\frac{d_{4}d_{5}d_{6}c_{4}c^{4}}{\rho ^{4}}\right) -\frac{ d_{4}g(\rho )}{\rho ^{2}}-\frac{2\Lambda }{d_{3}}\right\} =0. \end{aligned}$$
(14)

Using the above equations, one can calculate the metric function \(g(\rho )\) as

$$\begin{aligned} g(\rho )&=\frac{m_{0}}{\rho ^{d_{3}}}-\frac{2\Lambda \rho ^{2}}{d_{1}d_{2}}\nonumber \\&\quad + \frac{2d_{3}q^{2}}{d_{2}\rho ^{2d_{3}}}+m^{2}\left( c_{2}c^{2}+\frac{ cc_{1}\rho }{d_{2}}\nonumber \right. \\&\left. \quad +\frac{d_{3}c_{3}c^{3}}{\rho }+\frac{d_{3}d_{4}c_{4}c^{4} }{\rho ^{2}}\right) , \end{aligned}$$
(15)

which \(m_{0}\) is an integration constant related to the mass. It is worthwhile to mention that in the absence of massive parameter (\(m=0\)), the metric function (15) reduces to the Einstein-standard Maxwell [10].

3.1 Geometric properties

In order to discuss the geometric properties of spacetime, we should focus on special points of spacetime (such as roots of the metric function) and boundary of radial coordinate (both \(\rho \rightarrow 0\) and \(\rho \rightarrow \infty \)) as well.

Since the second term (\(\Lambda \) term) of the metric function is dominant for large values of \(\rho \), the asymptotical behavior of the solution (15) is adS or dS provided \(\Lambda <0\) or \(\Lambda >0\).

In order to find the location of curvature singularities (6), one can calculate the Kretschmann scalar as

$$\begin{aligned} R_{\mu \nu \lambda \kappa }R^{\mu \nu \lambda \kappa }&=\left( \frac{ d^{2}g(\rho )}{d\rho ^{2}}\right) ^{2}\nonumber \\&\quad +2d_{2}\left( \frac{1}{\rho }\frac{ dg(\rho )}{d\rho }\right) ^{2}+2d_{2}d_{3}\left( \frac{g(\rho )}{\rho ^{2}} \right) ^{2}. \nonumber \\ \end{aligned}$$
(16)

Using the metric function (15), it is easy to show that the Kretschmann scalar (16) diverges at \(\rho =0\), and therefore, one may guess that there is a curvature singularity located at \( \rho =0\), but as we will show, the spacetime will never achieve \(\rho =0\). There are two possible cases for the metric function: first, the metric function has no root which is interpreted as naked singularity, and second, the metric function has one or more roots. We assume that \(r_{+}\) is the largest real positive root of the metric function \(g(\rho )\). Therefore the metric function \(g(\rho )\) will be negative for \(\rho <r_{+}\) and positive for \(\rho >r_{+}\). This indicates that signature of the metric at this root changes from \((-,+,+,+,\ldots ,+)\) change to \((-,-,-,+,\ldots ,+)\). In general relativity and gravity, although the field equations are metric dependent, they must not depend on the signature of metric [106,107,108,109]. The mentioned change in the signature of metric indicates that field equations for \(\rho >r_{+}\) and \(\rho <r_{+}\) are different resulting into two sets of different metric functions. To avoid such inconsistency, the possibility of extending the spacetime to \(\rho <r_{+}\) must be removed. To do so, we introduce a new radial coordinate r as

$$\begin{aligned} r^{2}=\rho ^{2}-r_{+}^{2}\Longrightarrow d\rho ^{2}=\frac{r^{2}}{ r^{2}+r_{+}^{2}}dr^{2}, \end{aligned}$$
(17)

where \(\rho \ge r_{+}\) leads to \(r\ge 0\). Applying this coordinate transformation, the metric (6) should be written as

$$\begin{aligned} ds^{2}&=-\frac{r^{2}+r_{+}^{2}}{l^{2}}dt^{2}\nonumber \\&\quad +\frac{r^{2}}{\left( r^{2}+r_{+}^{2}\right) g(r)}dr^{2}+l^{2}g(r)d\varphi ^{2}\nonumber \\&\quad +\frac{ r^{2}+r_{+}^{2}}{l^{2}}dX^{2}, \end{aligned}$$
(18)

in which the coordinate \(\varphi \) assumes the value \(0\le \varphi <2\pi \) , as usual. The metric function g(r) (Eq. (15)) is now given by

$$\begin{aligned} g(r)&=\frac{m_{0}}{r^{d_{3}}}-\frac{2\Lambda \left( r^{2}+r_{+}^{2}\right) }{ d_{1}d_{2}}+\frac{2d_{3}q^{2}}{d_{2}r^{2d_{3}}}\nonumber \\&\quad +m^{2}\left( c_{2}c^{2}+\frac{ cc_{1}\sqrt{r^{2}+r_{+}^{2}}}{d_{2}}+\frac{d_{3}c_{3}c^{3}}{\sqrt{ r^{2}+r_{+}^{2}}}\nonumber \right. \\&\left. \quad +\frac{d_{3}d_{4}c_{4}c^{4}}{\left( r^{2}+r_{+}^{2}\right) } \right) , \end{aligned}$$
(19)

The nonzero component of the electromagnetic field in the new coordinates can be given by

$$\begin{aligned} F_{\varphi r}=\frac{q}{\left( r^{2}+r_{+}^{2}\right) ^{d_{2}/2}}. \end{aligned}$$
(20)

One can show that all curvature invariants are functions of \(g^{\prime \prime }\), \(g^{\prime }/r\), and \(g/r^{2}\). Since these terms do not diverge in the range \(0\le r<\infty \), one finds that all curvature invariants are finite. Therefore, this spacetime has no curvature singularity and no horizon. However, the spacetime (18) has a conic geometry with a conical singularity at \(r=0\), because the limit of the ratio “circumference/radius” is not \(2\pi \),

$$\begin{aligned} \lim _{r\longrightarrow 0}\frac{1}{r}\sqrt{\frac{g_{\varphi \varphi }}{g_{rr}} }\ne 1. \end{aligned}$$
(21)

The conical singularity can be removed if one exchanges the coordinate \( \varphi \) with the following period

$$\begin{aligned} Period_{\varphi }=2\pi \left( \lim _{r\longrightarrow 0}\frac{1}{r}\sqrt{ \frac{g_{\varphi \varphi }}{g_{rr}}}\right) ^{-1}=2\pi \left( 1-4\mu \right) , \end{aligned}$$
(22)

where \(\mu \) is given by

$$\begin{aligned} \mu =\frac{1}{4}\left[ 1-\frac{1}{2lr_{0}\left. g^{\prime \prime }(r)\right| _{r=0}}\right] , \end{aligned}$$
(23)

in which \(\left. g(r)\right| _{r=0}=\left. g^{\prime }(r)\right| _{r=0}=0\), and \(\left. g^{\prime \prime }(r)\right| _{r=0}\) is

$$\begin{aligned} \left. g^{\prime \prime }(r)\right| _{r=0}= & {} \frac{-2\Lambda }{d_{2}}- \frac{2(d_{3})^{2}q^{2}}{d_{2}r_{+}^{d_{1}}}+m^{2}\nonumber \\&\quad \left( \frac{cc_{1}}{r_{+}}+\frac{d_{3}c^{2}c_{2}}{r_{+}^{2}}+\frac{d_{3}d_{4}c_{3}c^{3}}{r_{+}^{3}}+ \frac{d_{3}d_{4}d_{5}c_{4}c^{4}}{r_{+}^{4}}\right) ,\nonumber \\ \end{aligned}$$
(24)

where shows that the metric (18) describes a spacetime which is locally flat, but has a conical singularity at \(r=0\) with a deficit angle as

$$\begin{aligned} \delta \phi =8\pi \mu . \end{aligned}$$
(25)

Here, we skip investigation of physical properties of the obtained results. After obtaining the consequences of nonlinear case, we give a detailed discussion with comparison.

4 Magnetic solutions in the Einstein-massive gravity with PMI field

In this section, we are going to obtain d-dimensional magnetic brane solutions in the presence of PMI field. Therefore, we consider the PMI Lagrangian with the following form

$$\begin{aligned} \mathcal {L}_{PMI}(\mathcal {F})=(-\kappa \mathcal {F})^{s}, \end{aligned}$$
(26)

where \(\kappa \) and s are coupling and positive arbitrary constants, respectively. Since the Maxwell invariant is negative in static spacetimes, hereafter, we set \(\kappa =1\) without loss of generality to obtain real solutions. Also, it is easy to show that when s goes to 1, the PMI Lagrangian (26) reduces to the standard Maxwell Lagrangian (\(\mathcal { L}_{Maxwell}(\mathcal {F})=- \mathcal {F}\)) which we have investigated in the previous section. It is easy to show that for the case of \(power=dimension/4\) , one can obtain \(T^{\mu }_{\mu }=0\) in PMI theory, which is confirmation of its conformal invariance properties in this case.

Considering Eq. (26), the electromagnetic field equation (3) reduces to

$$\begin{aligned} (2s-1)\rho h^{\prime \prime }(\rho )+d_{2}h^{\prime }(\rho )=0, \end{aligned}$$
(27)

with the following solutions

$$\begin{aligned} F_{\varphi \rho }=h^{\prime }(\rho )=\left\{ \begin{array}{ll} \frac{q}{\rho }, &{}\quad s=d_{1}/2 \\ \frac{(2s-d_{1})q}{(2s-1)\rho ^{d_{2}/(2s-1)}}, &{}\quad otherwise \end{array} \right. . \end{aligned}$$
(28)

where q is an integration constant. Using Eqs. (6) and (28), one can show that the gravitational field equation (2) reduces to

$$\begin{aligned}&\frac{d_{3}d_{4}g(\rho )}{\rho ^{2}}+\frac{2d_{3}g\prime (\rho )}{\rho } +g^{\prime \prime }(\rho )+2\Lambda \nonumber \\&\quad +\left( 2F_{\varphi \rho }^{2}\right) ^{s}-\frac{d_{3}m^{2}}{\rho ^{4}}\left( c_{1}c\rho ^{3}+d_{4}c_{2}c^{2}\rho ^{2}+d_{4}d_{5}c_{3}c^{3}\rho \nonumber \right. \\&\left. \quad +d_{4}d_{5}d_{6}c_{4}c^{4}\right) =0, \end{aligned}$$
(29)
$$\begin{aligned}&\frac{d_{2}d_{3}g(\rho )}{\rho ^{2}}+\frac{d_{2}g\prime (\rho )}{\rho } \nonumber \\&\quad +2\Lambda +(1-2s)\left( 2F_{\varphi \rho }^{2}\right) ^{s}-\frac{d_{2}m^{2}}{ \rho ^{4}}\left( c_{1}c\rho ^{3}\nonumber \right. \\&\quad \left. +d_{3}c_{2}c^{2}\rho ^{2}+d_{3}d_{4}c_{3}c^{3}\rho +d_{3}d_{4}d_{5}c_{4}c^{4}\right) =0. \end{aligned}$$
(30)
Fig. 1
figure 1

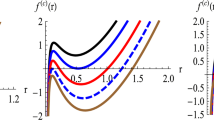
PMI solutions: \(\delta \left( \phi \right) \) versus \(r_{+}\) for \(q=0.1\), \(c=c_{1}=c_{2}=c_{3}=c_{4}=l=1\), \(d=5\) , \(s=0.9\), \(m=0\) (continuous line), \(m=0.4\) (dotted line), \(m=0.8\) (dashed line) and \(m=1\) (dashed-dotted line). Left diagram: \(\Lambda =-1\); Right diagram: \(\Lambda =1\)

Full size image

Substituting Eq. (28) in the above equations, it is straightforward to show that the metric function \(g(\rho )\) has the following form

$$\begin{aligned} g(\rho )= & {} \frac{m_{0}}{\rho ^{d_{3}}}-\frac{2\Lambda \rho ^{2}}{d_{1}d_{2}} +m^{2}\left( c_{2}c^{2}+\frac{cc_{1}\rho }{d_{2}}\nonumber \right. \\&\left. \quad +\frac{d_{3}c_{3}c^{3}}{ \rho }+\frac{d_{3}d_{4}c_{4}c^{4}}{\rho ^{2}}\right) +\mathbf {A}, \end{aligned}$$
(31)

in which

$$\begin{aligned} \mathbf {A}=\left\{ \begin{array}{ll} \frac{\left( \sqrt{2}q\right) ^{d_{1}}}{\rho ^{d_{3}}}\ln \left( \frac{\rho }{l}\right) , &{}\quad s=d_{1}/2 \\ \frac{2^{s}\rho ^{2}(2s-1)^{2}}{d_{2}(2s-d_{1})}\left( \frac{\left( 2s-d_{1}\right) q}{\left( 2s-1\right) \rho ^{d_{2}/(2s-1)}}\right) ^{2s}, &{}\quad otherwise \end{array} \right. . \end{aligned}$$

It is worthwhile to mention that in the absence of massive parameter (\(m=0\) ), the metric function (31) is just like the metric function which was obtained before in Ref. [110].

Considering the Kretschmann scalar (16), one can show that the metric (6) with the metric function (31), like the Maxwell case, has a singularity at \(\rho =0\). However, as we mentioned before, it is not possible to extend the spacetime to \(\rho <r_{+}\) because of signature changing (see Ref. [79], for more details). Also, one can apply the coordinate transformation (17) to the metric (6) and find the metric function as

$$\begin{aligned} g(r)&=\frac{m_{0}}{r^{d_{3}}}-\frac{2\Lambda \left( r^{2}+r_{+}^{2}\right) }{d_{1}d_{2}} \nonumber \\&\quad +m^{2}\left( c_{2}c^{2}+\frac{cc_{1}\sqrt{r^{2}+r_{+}^{2}}}{ d_{2}}+\frac{d_{3}c_{3}c^{3}}{\sqrt{r^{2}+r_{+}^{2}}}\nonumber \right. \\&\quad \left. +\frac{ d_{3}d_{4}c_{4}c^{4}}{\left( r^{2}+r_{+}^{2}\right) }\right) \nonumber \\&+\left\{ \begin{array}{ll} \frac{\left( \sqrt{2}q\right) ^{d_{1}}}{\left( \sqrt{r^{2}+r_{+}^{2}}\right) ^{d_{3}}}\ln \left( \frac{\sqrt{r^{2}+r_{+}^{2}}}{l}\right) , &{}\quad s=d_{1}/2 \\ \frac{2^{s}\left( r^{2}+r_{+}^{2}\right) (2s-1)^{2}}{d_{2}(2s-d_{1})}\left( \frac{\left( 2s-d_{1}\right) q}{\left( 2s-1\right) \left( \sqrt{ r^{2}+r_{+}^{2}}\right) ^{d_{2}/(2s-1)}}\right) ^{2s}, &{}\quad otherwise, \end{array} \right. \end{aligned}$$
(32)

and the electromagnetic field in the new coordinate is

$$\begin{aligned} F_{\varphi r}=\left\{ \begin{array}{ll} \frac{q}{\sqrt{r^{2}+r_{+}^{2}}}, &{}\quad s=(d-1)/2 \\ \frac{(2s-d_{1})q}{(2s-1)\left( \sqrt{r^{2}+r_{+}^{2}}\right) ^{d_{2}/(2s-1)} }, &{}\quad otherwise \end{array} \right. . \end{aligned}$$
(33)

In this case, like the Maxwell case, this spacetime has a conical singularity at \(r=0\) with the deficit angle \(\delta \left( \phi \right) =8\pi \mu \) where \(\mu \) is modified due to the nonlinear electrodynamics with the following form

$$\begin{aligned} \left. g^{\prime \prime }(r)\right| _{r=0}&=\frac{-2\Lambda }{d_{2}} +m^{2}\left( \frac{cc_{1}}{r_{+}} \nonumber \right. \\&\left. \quad +\frac{d_{3}c^{2}c_{2}}{r_{+}^{2}}+\frac{ d_{3}d_{4}c_{3}c^{3}}{r_{+}^{3}}+\frac{d_{3}d_{4}d_{5}c_{4}c^{4}}{r_{+}^{4}} \right) \nonumber \\&+\left\{ \begin{array}{ll} \frac{2^{d_{1}/2}q^{d_{1}}}{r_{+}^{d_{1}}}, &{}\quad s=d_{1}/2 \\ \frac{2^{s}(2s-1)}{d_{2}}\left( \frac{q^{2}\left( d_{1}-2s\right) ^{2}}{ (2s-1)^{2}r_{+}^{d_{2}/(2s-1)}}\right) ^{s}, &{}\quad otherwise \end{array} \right. . \nonumber \\ \end{aligned}$$
(34)

Due to complexity of obtained relation in Eq. (34), it is not possible to calculate the root and divergence points of deficit angle analytically, therefore, we study them in some graphs.

Fig. 2
figure 2

PMI solutions: \(\delta \left( \phi \right) \) versus \(r_{+}\) for \(c=c_{1}=c_{2}=c_{3}=c_{4}=m=l=1\), \(d=5\), \( s=0.9 \), \(q=0\) (continuous line), \(q=0.007\) (dotted line), \(q=0.0122\) (dashed line) and \(q=0.1\) (dashed-dotted line). Left diagram: \(\Lambda =-1\); right diagram: \(\Lambda =1\)

Full size image
Fig. 3
figure 3

PMI solutions: \(\delta \left( \phi \right) \) versus \(r_{+}\) for \(q=0.1\), \(c=c_{2}=c_{3}=c_{4}=m=l=1\), \(d=5\), \( s=0.9\), \(c_{1}=-10\) (continuous line), \(c_{1}=-7.87\) (dotted line), \( c_{1}=-6.5\) (dashed line), \(c_{1}=-5.855\) (dashed-dotted line) and \(c_{1}=-5\) (bold line). Left diagram: \(\Lambda =-1\); right diagram: \(\Lambda =1\)

Full size image
Fig. 4
figure 4

PMI solutions: \(\delta \left( \phi \right) \) versus \(r_{+}\) for \(q=0.1\), \(c=c_{1}=c_{2}=c_{3}=c_{4}=m=l=1\), \( d=5 \), \(s=0.8\) (continuous line), \(s=1\) (dotted line) and \(s=1.1\) (dashed line). Left diagram: \(\Lambda =-1\); right diagram: \(\Lambda =1\)

Full size image
Fig. 5
figure 5

PMI solutions: \(\delta \left( \phi \right) \) versus \(r_{+}\) for \(q=0.1\), \(c=c_{1}=c_{2}=c_{3}=c_{4}=m=l=1\), \( s=0.9\), \(d=5\) (continuous line), \(d=6\) (dotted line), \(d=7\) (dashed line) and \(d=8\) (dashed-dotted line). Left diagram: \(\Lambda =-1\); right diagram: \(\Lambda =1\)

Full size image

Before starting, we should point it out that we have an upper limit of \( -\infty <\delta \phi \le 2\pi \) on the values that deficit angle can acquire. This limit is marked with a horizontal dotted line in plotted diagrams. The value of deficit angle determines the geometrical structure of solutions. Depending on geometrical properties, gravitational effects and lensing properties of the magnetic solutions, hence topological defects will be different. Here, we see that depending on choices of different parameters, deficit angle could be positive/negative and it may have roots and divergence points. In order to highlight the effects of background spacetime, we have plotted two series of diagrams for AdS (left panels of Figs. 1, 2, 3, 4, 5) and dS (right panels of Figs. 1, 2, 3, 4, 5).

Evidently, for AdS case, depending on the choices of different parameters, deficit angle could have: (1) two roots in which between roots, the deficit angle negative valued whereas before smaller and after larger roots, it is positive. (2) one extreme root in which the deficit angle is always positive valued. (3) two roots with one divergency where between smaller/larger root and divergency the deficit angle is negative and everywhere else, it is positive valued. (4) finally, two roots with two divergencies in which the divergencies are located between the roots. In this case, between smaller (larger) root and smaller (larger) divergency, the deficit angle is negative valued. Between divergencies, it is positive but its values are not in permitted area. Only before (after) smaller (larger) root, the deficit angle is positive valued and within permitted area.

On contrary, for dS case, plotted diagrams show existence of a root and a divergency for deficit angle. Before root and after divergency, the deficit angle is positive where only before root, permitted values of the deficit angle exists whereas after divergency its values are not within permitted ones.

The number of roots are a decreasing function of mass of graviton (m) (left panel of Fig. 1), electric charge (left panel of Fig. 2), \(c_{1}\) (left panel of Fig. 3), nonlinearity parameter (left panel of Fig. 4) and dimensions (left panel of Fig. 5 ) for AdS case. On the other hand, for dS case, the places of root and divergency are increasing functions of m (right panel of Fig. 1), q (right panel of Fig. 2), \(c_{1}\) (right panel of Fig. 3 ), s (right panel of Fig. 4) and dimensions (right panel of Fig. 5).

The existence of positive valued deficit angle results into conic like geometrical structure for our astrophysical objects, hence topological defects are known as horizonless magnetic solutions. On contrary, the existence of negative values of deficit angle leads to a saddle-like cone structure for the solutions. These two different structures for magnetic solutions could be related to different second fundamental form of spacetime. On the other hand, it was argued that positivty/negativity of the deficit angle results into attractive-type/repulsive-type gravitational potentials (furthers details could be found in Refs. [111,112,113,114]).

Considering different geometrical structure depending on the sign of deficit angle, one can conclude that the root of deficit angle is where magnetic solutions have phase transition-like behavior. In other words, since there is a change of sign at the root of deficit angle, magnetic solutions go under a typical topological phase transition in these points. It could be pointed out that there are cases in which roots are extreme ones. In these cases, although no change of sign takes place, the total geometrical structure of the solutions presents diverse different comparing to the non-zero deficit angle (absence of conic like singularity for zero deficit angle). Therefore, it could be stated that extreme roots are also marking phase transition points. Another point which carries the properties of phase transition for magnetic solutions is divergency of the deficit angle. In other words, divergencies of the deficit angle could be interpreted as places in which magnetic solutions go under a phase transition. This is due to the fact that deficit angle has smooth behavior everywhere except at divergencies which are discontinuities. Usually, around these divergence points, the sign of deficit angle is changed. In other words, there is a change in the sign of deficit angle before and after divergence point.

Although different parameters have specific contributions in existence/absence of root and divergency for deficit angle, the highest effects belong to the \(\Lambda \) term, hence structure of the background spacetime.

For dS spacetime (positive \(\Lambda \)), existence of both points (root and divergence) irrespective of different parameters is evident. Before the divergency, the values of deficit angle are within permitted area while after it, the values are in forbidden region. The root of deficit angle in this case is located at the permitted area. Therefore, one can state that for dS case, the existence of deficit angle is limited to region before its divergency and in this region, deficit angle enjoys a phase transition related to the existence of root. The length of permitted region for deficit angle is a function of massive parameters, electric charge, dimensions and nonlinearity parameter.

For AdS spacetime, the situation is different. Existence of divergency depends on positivity and negativity of massive coefficient \(c_{1}\) and it is found for sufficiently small and negative values of this parameter. Interestingly, contrary to dS case, AdS spacetime could enjoy the existence of up to two divergencies in its deficit angle (for sufficiently small and negative \(c_{1}\)). In the case of one divergence point, the divergency exists between two roots and signature of the deficit angle around it is the same (it is negative). In this case, the deficit angle enjoys two roots and one divergency. For the case of two divergencies, the divergence points are between two roots. Around divergencies the sign of deficit angle changes. Between the divergencies, the deficit angle is positive valued but within prohibited region. Therefore, the magnetic solutions have phase transition over a region which is marked with divergencies. This shows that in this case, the deficit angle has two roots and one divergency with a prohibited region. The study here showed that generalization to massive gravity introduces some new phase transitions into magnetic solutions. This highlights the effects of the massive gravity in geometrical structure of the solutions, hence their physical properties.

5 Conclusions

The paper was dedicated to study the nonlinearly charged magnetic brane solutions in the presence of massive gravity. The exact solutions were obtained and the absence of black hole solutions was confirmed. The existence of conic like singularity was shown and it was pointed out that geometrical, hence, physical/gravitational properties of the solutions depend on a value known as deficit angle.

This property of the solutions (deficit angle) determines the total structure of magnetic branes. It was shown that there is a diverse difference in the geometrical properties of the solutions with positive deficit angle comparing to negative ones. These geometrical properties are providing guidelines for how phenomena such as lensing property would be different. That being said, roots and divergencies could be interpreted as topological phase transition points. In roots, the transition is being done smoothly while in the divergencies, system jumps between different deficit angles, hence geometrical structure.

In general, it was shown that existence of the divergencies for deficit angle were the background spacetime and massive gravity dependent. If the massive coefficients are positive valued, only for dS background, deficit angle could acquire divergency whereas, the AdS case enjoys only root in its deficit angle. On the contrary, if the massive coefficients could be negative, for both AdS and dS backgrounds, it is possible to introduce multi geometrical phase transition and a prohibited region. Existence of the prohibited regions indicates that our magnetic solutions are bounded by specific limits. These limited areas and the conditions for them are rooted in massive gravity and its coefficients. Despite the effects of other parameters on limiting areas and the conditions, in the absence of massive coefficients, these limited areas would rather vanish or significantly be modified. The effect of nonlinearity nature of the solutions in the case of AdS spacetime was in level of modifying the number of roots. Whereas for dS spacetime, it was only in level of modifying the prohibited/permitted region for deficit angle.

The obtained solutions here contain magnetic brane ones. Considering the AdS nature of the solutions and their phase transitions, it is possible to conduct studies in the context of AdS/CFT correspondence. Furthermore, one can investigate trajectory of the particles and lensing properties of these solutions in more details to understand the effects of massive gravity and nonlinear electromagnetic fields. In addition, it is notable that our solutions are static and independent of time. One may modify these solutions in the case of dynamic time dependent for investigating the “self-acceleration” properties [115, 116]. We leave these subjects for the future works.