The $f(R,T^\phi )$ gravity models with conservation of energy–momentum tensor

Abstract

In this paper, we have derived a spatially flat homogeneous and isotropic cosmological model in $f(R,T^\phi )$ gravity with a scalar field. In addition to a minimally coupled scalar field with self interacting potential, we also have a contribution from the coupling of the geometry and the field. We have reconstructed a form of $f(R,T^\phi )$ by requiring the conservation of energy–momentum tensor of the scalar field. The behavior of the reconstructed $f(R,T^\phi )$ gravity is examined for a flat potential as well as a massless scalar field model. The evolution of the universe is studied via the deceleration and equation of state parameters. The promising feature of the model is the transition behavior of the universe from deceleration to the present acceleration.

1 Introduction

In recent years, the observations of H(z) data from Ia supernova [1,2,3], cosmic microwave background (CMB) [4], large scale structures (LSS) [5], Wilkinson microwave anisotropy probe (WMAP) [6], baryon acoustic oscillations (BAO) [7], PLANCK [8], etc, have generated strong theoretical and observational evidence that the present expansion of the universe is in an accelerated phase. These observations also suggest that about two thirds of the critical energy density in the universe seems to be stored in a form of an unknown component. The late time cosmic acceleration is usually assumed to be driven by such a mysterious fluid or field which is generally known as ‘dark energy’ (DE) [9]. Some hypothetical candidates for DE are the cosmological constant [10, 11], quintessence [12], phantom [13], k-essence [14], tachyons [15, 16], Chaplygin gas [17] and the quintom [18]. The big-bang model of Einstein’s general relativity (GR) with a cosmological constant ${\varLambda }$, called the ${\varLambda }$CDM model [19], is the most acceptable model amongst the scientific community to explain the observed late time accelerated expansion, except its fine-tuning at the Planck scale [20]. The fine-tuning problem confronts the fundamental theories with great challenges, and makes research on this problem a major endeavour in modern astrophysics and cosmology.

The fine-tuning and coincidence problems [21] of the ${\varLambda }$CDM model have led to a search for dynamical DE models [22,23,24]. One of the most common candidates for dynamical DE is ‘quintessence’ (see [12] and references therein). The concept of quintessence basically uses a scalar particle field which is used as the responsible agent for driving a super-fast expansion during the inflationary phase [25,26,27,28,29,30,31]. Due to the remarkable qualitative similarity between the present DE and the primordial DE that is supposed to drive inflation in the early universe, scalar field models have also been successfully implemented for the description of late-time cosmic acceleration [32,33,34,35,36]. However, constructing viable scaling models which can start the universe with inflation followed by the radiation- and matter-dominated epochs, and finally which can allow the universe to enter into the present accelerating phase, is still a challenging task [37, 38]. Keeping in mind that scalar fields play an important role in explaining early and late-time cosmic acceleration, one of the motivations of the present work is to study FRW models with a scalar field.

Another perspective to understand the problem of DE is the reconstruction of the gravitational field theory or modification of Einstein’s GR which could be capable of reproducing late time cosmic acceleration. However, the idea of modification of GR was not born just after the discovery of the accelerating universe. Many modified theories of gravitation exist since a long time due to the combined motivation coming from cosmology, astrophysics and high-energy physics. The attention in modified theories has just accelerated with the discovery of the accelerating expansion of the universe. The possibility that the modification of GR at galactic and cosmological scales can explain dark matter (DM) and DE has been become an active area of research since the beginning of the 21st century [39,40,41,42,43]. At present, there exist numerous proposals which are the modifications in some way or another of the Einstein-Hilbert (EH) gravitational action, namely, f(R) theories [44,45,46], Gauss–Bonnet, f(G) gravity [47, 48], brane world theory [49], f(T) theory [50] etc. Although, these modified theories have already given qualitative answers to a number of fundamental questions, none of them satisfactorily explain the greatest mystery gifted to the scientific community in the 20th century [51]. Therefore, there is still a resurgence of interest in these modified theories to seek the answer of several cosmological problems such as the singularity problem, inflation, DE, DM, late-time cosmic acceleration and the cosmological constant problem.

In the beginning, interest in modified theories was focused on the modification of the geometric part of the EH action. In 2011, Harko et al. [52] have proposed a general non-minimal coupling between matter and geometry in the framework of an effective gravitational Lagrangian consisting of an arbitrary function of the Ricci scalar R and the trace T of the energy–momentum tensor, and introduced f(R, T) gravitational theory. The authors have justified choosing T as an argument for the Lagrangian from exotic imperfect fluids or quantum effects (conformal anomaly). The new matter and time-dependent terms in the gravitational field equations play the role of an effective cosmological constant. A strange behavior of f(R, T) gravity is the non-vanishing covariant derivative of the stress-energy tensor. As a consequence, the equations of motion show the presence of an extra-force acting on a test particle, and consequently the motion is non-geodesic. The authors have applied this theory to analyse the Newtonian limit of the equations of motion and provided a constraint on the magnitude of the extra acceleration by studying the perihelion precession of Mercury. They conclude that the extra acceleration in f(R, T) gravity results not only from a geometrical contribution, but also from the matter content. This extraordinary behavior of f(R, T) gravity has attracted many researchers to explore this theory in different contexts of cosmology and astrophysics [53,54,55,56,57,58,59,60]. One of the interesting issues in cosmology is the reconstruction of modified theories of gravity. Therefore, many authors have reconstructed f(R, T) gravity in different frameworks [61,62,63,64].

The study of different phenomena in f(R, T) gravity may also provide some significance signatures and effects which could distinguish and discriminate between various gravitational models. So far, a serious shortcoming of f(R, T) theory is the non-vanishing covariant derivative of the energy–momentum tensor and, consequently, the standard continuity equation does not hold in this theory, in general. Similarly, the Klein–Gordon equation does not hold if the matter is taken as the scalar field. Therefore, an interesting problem is to search out the form of f(R, T) for which the standard continuity and Klein–Gordon equations hold. This issue has been undertaken firstly by Chakraborty [65] who has shown that a part of an arbitrary function of f(R, T) theory can be determined by taking into account conservation of the stress-energy tensor. Later on, Alvarenga and collaborators [66] have also circumvented this problem by showing that the functions of f(R, T) theory can always be constructed that gives a guarantee of the standard continuity equation. The authors also have shown that for a well motivated f(R, T) Lagrangian, the quasi-static approximation leads to very different results as compared to the concordance ${\varLambda }$CDM model. Recently, Baffou et al. [67] have obtained a model by imposing the conservation of the energy–momentum tensor. The authors have studied the dynamics and stability of the model using de Sitter and power-law solutions. Very recently, Moraes et al. [68] have considered a new approach of the conservation of the effective energy–momentum tensor in the f(R, T) gravity formalism. The results obtained in all these works are quite reasonable due to the choice of the ordinary matter content. Thus, there is a need to explore f(R, T) gravity taking into account the consideration of the continuity equations of some other matter sources such as a scalar field. The theoretical and observational investigation of scalar field models is an essential task in cosmology. Recently, Singh and Singh [69] have reconstructed flat scalar and exponential potential models of f(R, T) gravity in scalar field cosmology.

In the present work, we extend the work carried out by Singh and Singh [69] by taking into account the Klein–Gordon equation for the scalar field. We reconstruct the $f(R,T^\phi )=R+2f(T^\phi )$ gravity model in scalar field cosmology with a self interacting scalar potential in the framework of a flat FRW space-time; here $T^\phi$ refers to the trace of the energy–momentum tensor of the scalar field. We investigate the features of a reconstructed form of $f(R,T^\phi )$ gravity by considering a flat potential and a massless scalar field model. The paper is organised as follows. The model and field equations of $f(R,T^\phi )$ gravity in scalar field cosmology are presented in the next Sect. 2. A flat potential model is studied in Sect. 3. In Sect. 4, we study a massless scalar field model and we also differentiate this model from the flat potential model studied in Sect. 3. The sum up of the findings are accumulated in the concluding Sect. 5.

2 The model and field equations in $f(R,T^\phi )$ gravity

Harko et al. [70] have presented several exact cosmological solutions with a scalar field as the only matter source in GR. Many researchers have studied some of the most intriguing aspects of our universe containing a self-interacting scalar field possessing an interaction potential as the only matter source in modified gravity [69, 71, 72]. In [52], the authors also have introduced a version of f(R, T) gravity for scalar field cosmology, namely, $f(R,T^\phi )$ gravity by considering in the action an algebraic function $F(R,\phi )$ of the Ricci curvature R and scalar field $\phi$. The authors have expressed $\phi$ as a function of R and $T^\phi$, where $T^\phi$ is the trace of the energy momentum tensor of the scalar field. Thus, they have formulated the gravitational action of $f(R,T^\phi )$ by considering a function ${\tilde{F}}(R,T^\phi )\equiv F\left[ R,\phi (R,T^\phi )\right]$ plus matter fields in the gravitational action. In an example, the authors have presented the gravitational action for a particular model where $f(R,T^\phi )=R+f(T^\phi )$, which, under the consideration of massless scalar fields, leads to the gravitational action of k-essence models [14]. Further, they have shown that an exponential form of $F(R,\phi )$ for a massless scalar field model leads to a power-law solution.

Singh and Singh [69] have reconstructed a particular form of $f(R,T^\phi )=R+f(T^\phi )$ for a flat scalar potential model and exponential potential model without taking into account the Klein–Gordon equation. Since the covariant derivative of the stress-energy tensor does not vanish in general in $f(R,T^\phi )$ gravity, in the present study we reconstruct $f(R,T^\phi )=R+f(T^\phi )$ for which the covariant derivative of the stress-energy tensor of the scalar field vanishes. In other words, we find the above said form of $f(R,T^\phi )$ for which the Klein–Gordon equation holds.

We consider a minimally coupled scalar field $\phi$ self interacting with a scalar potential $V(\phi )$ in the gravitational action of $f(R,T^\phi )$ theory of gravity, i.e.,

$$\begin{aligned} S=\frac{1}{2}\int \left[ f(R,T^\phi )+ 2{\mathcal {L}}_\phi \right] \sqrt{-g}d^4x, \end{aligned}$$

(1)

where $f(R,T^\phi )$ is an arbitrary function of the Ricci scalar curvature R and the trace $T^\phi$ of the energy–momentum tensor, and $\mathcal {L_\phi }$ corresponds to the matter Lagrangian of the scalar field. We use the system of units in which $8\pi G=1=c$. The energy–momentum tensor of the matter source is defined as

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\;{\mathcal {L}}_\phi )}{\delta g^{\mu \nu }}, \end{aligned}$$

(2)

where $g_{\mu \nu }$ is the metric tensor. We consider the matter Lagrangian ${\mathcal {L}}_\phi$ to depend only on the metric tensor $g_{\mu \nu }$, and not on its derivatives. Therefore, the energy–momentum tensor in Eq. (2) simplifies to

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu }{\mathcal {L}}_\phi -2\frac{\partial {\mathcal {L}}_\phi }{\partial g^{\mu \nu }}. \end{aligned}$$

(3)

The variation of action (1) with respect to the metric tensor $g_{\mu \nu }$, yields the field equations of $f(R,T^\phi )$ gravity

$$\begin{aligned}&f_R(R,T^\phi )R_{\mu \nu }-\frac{1}{2}f(R,T^\phi )g_{\mu \nu }\nonumber \\&\quad +\,(g_{\mu \nu }\square -\nabla _\mu \nabla _\nu )f_R(R,T^\phi )= T_{\mu \nu }\nonumber \\&\quad -\,f_T(R,T^\phi )(T_{\mu \nu }+\circleddash _{\mu \nu }), \end{aligned}$$

(4)

where $f_R$ and $f_{T^\phi }$ denote the partial derivatives of $f(R,T^\phi )$ with respect to R and $T^\phi$, respectively. As per usual notation, $\triangledown _\mu$ is the covariant derivative, $\square \equiv \triangledown _\mu \triangledown ^\mu$ is the d’Alembert operator and $\circleddash _{\mu \nu }$ is defined by

$$\begin{aligned} \circleddash _{\mu \nu }\equiv g^{\alpha \beta }\frac{\delta T^\phi _{\alpha \beta }}{\delta g^{\mu \nu }}, \end{aligned}$$

(5)

which by use of (3) becomes

$$\begin{aligned} \circleddash _{\mu \nu }=-2T^\phi _{\mu \nu }+g_{\mu \nu }{\mathcal {L}}_\phi -2g^{\alpha \beta }\frac{\partial ^2{\mathcal {L}}_\phi }{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. \end{aligned}$$

(6)

Since we are interested in constructing a form of $f(R,T^\phi )$ for which the scalar field satisfies the Klein–Gordon equation, we take the covariant derivative of Eq. (4), which results in

$$\begin{aligned}&f_R(R,T^\phi )\nabla ^\mu R_{\mu \nu }+R_{\mu \nu }\nabla ^\mu f_R(R,T^\phi )\nonumber \\&\qquad -\,\frac{1}{2}g_{\mu \nu }\left( f_R(R,T^\phi )\nabla ^\mu R+f_{T^\phi }(R,T^\phi )\nabla ^\mu T^\phi \right) \nonumber \\&\qquad +\,(g_{\mu \nu }\nabla ^\mu \square -\nabla ^\mu \nabla _\mu \nabla _\nu )f_R(R,T^\phi )\nonumber \\&\quad =\nabla ^\mu T^\phi _{\mu \nu }-f_{T^\phi }(R,T^\phi )(\nabla ^\mu T^\phi _{\mu \nu }+\nabla ^\mu \circleddash _{\mu \nu })\nonumber \\&\qquad -\,(T^\phi _{\mu \nu }+\circleddash _{\mu \nu })\nabla ^\mu f_{T^\phi }(R,T^\phi ). \end{aligned}$$

(7)

The above equation can be simplified as

$$\begin{aligned} \nabla ^\mu T^\phi _{\mu \nu }= & {} \frac{1}{1-f_{T^\phi }(R,T^\phi )}\left[ \phantom {\frac{1}{2}}f_{T^\phi }(R,T^\phi )\nabla ^\mu \circleddash _{\mu \nu }\right. \nonumber \\&\left. +\,(T^\phi _{\mu \nu }+\circleddash _{\mu \nu })\nabla ^\mu f_{T^\phi }(R,T^\phi )\right. \nonumber \\&\left. -\,\frac{1}{2}g_{\mu \nu }f_{T^\phi }(R,T^\phi )\nabla ^\mu T^\phi \right] . \end{aligned}$$

(8)

The outcomes from different observational data also show a possibility for the existence of some strange kind of fields in the universe such as phantom fields having negative kinetic energy as proposed by Caldwell [13]. We consider that the universe is filled with the scalar field (quintessence or phantom) minimally coupled to gravity. The energy–momentum tensor of a scalar field $\phi$ with self-interacting scalar potential $V(\phi )$, reads as

$$\begin{aligned} T^\phi _{\mu \nu }=\epsilon \phi ,_{\,\mu }\;\phi ,_{\,\nu }- g_{\mu \nu }\left[ \frac{\epsilon }{2}g^{\varrho \sigma }\phi ,_{\,\varrho }\,\phi _{,\,\sigma }-V(\phi ) \right] , \end{aligned}$$

(9)

where $\epsilon =\pm \, 1$ correspond to quintessence and phantom scalar fields, respectively.

We consider a spatially flat homogeneous and isotropic Friedmann–Robertson–Walker (FRW) model of the universe which is given by the line-element

$$\begin{aligned} ds^{2} =dt^{2}-a^2(t)\left[ dr^2+r^2(d\theta ^2+sin^2\theta d\vartheta ^2)\right] , \end{aligned}$$

(10)

where a(t) is the scale factor.

The trace of the energy–momentum tensor (9) is defined as $T^\phi =g^{\mu \nu }T^\phi _{\mu \nu }$ which becomes, for the above line element

$$\begin{aligned} T^\phi =-\epsilon {\dot{\phi }}^2(t)+4V(\phi ), \end{aligned}$$

(11)

where a dot denotes the derivative with respect to cosmic time t.

Since the field equations of $f(R,T^\phi )$ theory depend on $\circleddash _{\mu \nu }$, i.e., on the physical nature of the matter source, a number of models corresponding to different forms of $f(R,T^\phi )$ may be generated for different kinds of matter source. We choose the matter Lagrangian of the scalar field as

$$\begin{aligned} {\mathcal {L}}_\phi =-\left[ \frac{1}{2}\epsilon {\dot{\phi }}^2(t)-V(\phi )\right] . \end{aligned}$$

(12)

Using (12) in (6), we get

$$\begin{aligned} \circleddash _{\mu \nu }= -2T^\phi _{\mu \nu }-g_{\mu \nu }\left[ \frac{1}{2}\epsilon {\dot{\phi }}^2(t)-V(\phi )\right] . \end{aligned}$$

(13)

Consequently, Eq. (8) takes the form

$$\begin{aligned} \nabla ^\mu T^\phi _{\mu \nu }= & {} \frac{{\dot{\phi }}(t)}{1+f_{T^\phi }(R,T^\phi )}\nonumber \\&\left[ \phantom {\left( \frac{1}{2}\epsilon {\dot{\phi }}^2(t)-V(\phi )\right) }2\left( \epsilon \ddot{\phi }(t)-2V'(\phi )\right) f_{T^\phi T^\phi }(R,T^\phi )\right. \nonumber \\&\left. \left\{ T^\phi _{\mu \nu }+g_{\mu \nu }\left( \frac{1}{2}\epsilon {\dot{\phi }}^2(t)-V(\phi )\right) \right\} \right. \nonumber \\&\left. -g_{\mu \nu }V'(\phi )f_{T^\phi }(R,T^\phi )\phantom {\left( \frac{1}{2}\epsilon {\dot{\phi }}^2(t)-V(\phi )\right) }\right] . \end{aligned}$$

(14)

Here, a prime denotes a derivative with respect to the argument.

Equation (14) for the energy–momentum tensor (9), yields

$$\begin{aligned}&\epsilon {\ddot{\phi }}(t)+3\epsilon \left( \frac{\dot{a}}{a}\right) {\dot{\phi }}(t)+\frac{dV(\phi )}{d\phi }=2\epsilon {\dot{\phi }}^2(t)\left[ \epsilon \ddot{\phi }(t)-2V'(\phi )\right] \nonumber \\&\quad f_{T^\phi T^\phi }(R,T^\phi )+V'(\phi )f_{T^\phi }(R,T^\phi ). \end{aligned}$$

(15)

The Klein–Gordon equation for a scalar field is given as

$$\begin{aligned} \epsilon {\ddot{\phi }}(t)+3\epsilon \left( \frac{\dot{a}}{a}\right) {\dot{\phi }}(t)+\frac{dV(\phi )}{d\phi }=0, \end{aligned}$$

(16)

Now, in order to hold the Klein–Gordon equation, the r.h.s of Eq. (15) has to vanish, i.e.,

$$\begin{aligned}&2\epsilon {\dot{\phi }}^2(t)\left[ \epsilon {\ddot{\phi }}(t) -2V'(\phi )\right] f_{T^\phi T^\phi }(R,T^\phi )\nonumber \\&\quad -\,V'(\phi )f_{T^\phi }(R,T^\phi )=0. \end{aligned}$$

(17)

In general, it is not possible to find the explicit solution of Eq. (17). However, a number of forms of $f(R,T^\phi )$, e.g., $f(R,T^\phi )= R+2f(T^\phi )$, $f(R,T^\phi )$= $\mu f_1(R)+\nu f_2(T^\phi )$, where $f_1(R)$ and $f_2(T^\phi )$ are arbitrary functions of R and $T^\phi$, and $\mu$ and $\nu$ are real constants, respectively and $f(R,T^\phi )=R\;f(T^\phi )$ etc., have been proposed in [52]. We choose the most popular one, viz.,

$$\begin{aligned} f(R,T^\phi )=R+2f(T^\phi ), \end{aligned}$$

(18)

where R is a function of t and $f(T^\phi )$ is an arbitrary function of the trace $T^\phi$ of the energy–momentum tensor.

Equation (18) shows that the action is given by the same EH action of GR plus a function of $T^\phi$. The term $2f(T^\phi )$ in the gravitational action modifies the gravitational interaction between matter and curvature. Equation (17), by use of Eq. (18), reduces to

$$\begin{aligned}&2\epsilon {\dot{\phi }}^2(t)\left[ \epsilon {\ddot{\phi }}(t) -2V'(\phi )\right] f_{T^\phi T^\phi }(T^\phi )\nonumber \\&\quad -\,V'(\phi )f_{T^\phi }(T^\phi )=0. \end{aligned}$$

(19)

The most general solution of the above equation is given as

$$\begin{aligned}&f(T^\phi )= T_0\nonumber \\&\quad +\,\frac{2T_1\epsilon \beta {\dot{\phi }} ^2(t) \left[ \epsilon {\ddot{\phi }}(t) -2 V'(\phi )\right] \exp \left[ \frac{T^\phi V'(\phi )}{2 \epsilon {\dot{\phi }}^2(t) \left( \epsilon {\ddot{\phi }}(t)-2 V'(\phi ) \right) }\right] }{V'(\phi )},\nonumber \\ \end{aligned}$$

(20)

where $T_0$ and $T_1$ are integration constants. It is not possible to draw any physical conclusion from the above form of $f(T^\phi )$ as it cannot be written explicitly in terms of its argument. Therefore, in what follows, we consider a flat potential model and a massless scalar field model.

3 Flat potential model

Let us assume a constant potential $V(\phi )=V_0$ for which Eq. (19) has the solution

$$\begin{aligned} f(T^\phi )=\alpha T^\phi +\beta , \end{aligned}$$

(21)

where $\alpha$ and $\beta$ are constants of integration. Consequently, we have

$$\begin{aligned} f(R,T^\phi )=R+2(\alpha T^\phi +\beta ), \end{aligned}$$

(22)

which is the reconstructed form of $f(R,T^\phi )$ for which the Klein–Gordon equation is satisfied for a flat potential. Further, one can rewrite the Klein–Gordon equation for $V(\phi )=V_0$ as

$$\begin{aligned} \frac{{\ddot{\phi }}(t)}{{\dot{\phi }}(t)}=-3\left( \frac{\dot{a}}{a}\right) . \end{aligned}$$

(23)

Now, we look for the field equations to study the evolution of the universe in the framework of a form of $f(R,T^\phi )$ gravity as obtained in Eq. (22). Using Eq. (22) in Eq. (4), the field equations become

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu }=T^\phi _{\mu \nu }-2 (T^\phi _{\mu \nu }+\circleddash _{\mu \nu })\alpha +(\alpha T^\phi +\beta ) g_{\mu \nu }.\nonumber \\ \end{aligned}$$

(24)

In $f(R,T^\phi )$ gravity, the cosmic acceleration can be shown to be a result of geometry-matter coupling. The presence of coupling terms in the gravitational action may even be understood as the introduction of an effective fluid for which the usual energy conditions may not hold. Therefore, they may even lead to the cosmological constant, quintessence or a phantom model at late times. Houndjo and Piattella [63] have considered the matter-geometry coupling terms in f(R, T) gravity as exotic matter which represents quintessence and phantom DE. Therefore, in order to compare the gravitational field equations (24) with Einstein’s, we recast these in such a way that the corrections coming from the coupling between the scalar field and geometry of $f(R,T^\phi )$ gravity describes an effective source. Moreover, in the present scenario the contribution due to the coupling of geometry and scalar field may be taken as the “matter” component which is responsible for accelerating the universe. Now from hereon, we call this contribution the matter due to $f(R,T^\phi )$ gravity [64, 69].

Let $\rho _f$ and $p_f$ be, respectively, the energy density and pressure of the DE coming from the coupling of the scalar field and the geometry. Thus, the field equations (24) in the background of the FRW metric (10) yield, the Friedmann equations

$$\begin{aligned} 3\left( \frac{\dot{a}}{a}\right) ^2= & {} \rho _{\phi }+\rho _f, \end{aligned}$$

(25)

$$\begin{aligned} \frac{2{\ddot{a}}}{a}+\left( \frac{\dot{a}}{a}\right) ^2= & {} -(p_\phi +p_f), \end{aligned}$$

(26)

where $\rho _{\phi }$ and $p_{\phi }$ are the energy density and pressure of the scalar field, respectively, and are given as

$$\begin{aligned} \rho _\phi= & {} \frac{1}{2}\epsilon {\dot{\phi }}^2+V(\phi ), \end{aligned}$$

(27)

$$\begin{aligned} p_\phi= & {} \frac{1}{2}\epsilon {\dot{\phi }}^2-V(\phi ), \end{aligned}$$

(28)

and

$$\begin{aligned} \rho _f= & {} 2(\rho _{\phi }+p_{\phi })\alpha +\alpha T^\phi +\beta = \alpha (\epsilon {\dot{\phi }}^2+4V_0) + \beta , \nonumber \\\end{aligned}$$

(29)

$$\begin{aligned} p_f= & {} -\, f(T^\phi )= \alpha (\epsilon {\dot{\phi }}^2-4V_0) - \beta . \end{aligned}$$

(30)

where $\rho _f$ is computed from the 00-component of $2(T_{\mu \nu }+\circleddash _{\mu \nu })f^{\prime }(T)+f(T) g_{\mu \nu }$ of Eq. (24) and $p_f$ is computed from the 11-component of the same expression.

Since we have three equations, namely, the Klein–Gordon equation (16) and, Friedmann equations (25) and (26) with three unknowns a(t), $\phi (t)$ and V(t). But as we have already considered the potential as flat in the reconstruction of $f(R,T^\phi )$ (to get the solution of Eq. (19)), in order to obtain the exact solution of the remaining two physical unknowns a(t) and $\phi (t)$, we can use only two independent equations. We select the Klein–Gordon (23) for the flat potential and the Friedmann equation (25). One may readily verify that the Eq. (26) must satisfy all solutions.

From Eqs. (23) and (25), we have

$$\begin{aligned} \left( \frac{{\ddot{\phi }}}{{\dot{\phi }}}\right) ^2 =A\epsilon {\dot{\phi }}^2+B, \end{aligned}$$

(31)

where $A=3(\frac{1}{2}+\alpha )$ and $B=3V_0(1+4\alpha )+3\beta$. We observe that Eq. (31) does not have any real solution for a phantom scalar field ($\epsilon =-\,1$) but for a quintessence scalar field ($\epsilon =1$), we obtain

$$\begin{aligned} \phi (t)= & {} \phi _0+\frac{2 }{\sqrt{A}}\tanh ^{-1}\left( \sqrt{AB} e^{\sqrt{B} t}\right) , \end{aligned}$$

(32)

$$\begin{aligned} \phi (t)= & {} \phi _0-\frac{2 }{\sqrt{A}}\tanh ^{-1}\left( \frac{ e^{\sqrt{B} t}}{\sqrt{AB}}\right) , \end{aligned}$$

(33)

where $\phi _0$ is an integration constant. Another integration constant is taken zero without any loss of generality. We observe that Eq. (32) leads to an imaginary solution. Therefore, we shall proceed with Eq. (33) which possesses real solutions provided $A>0$ and $B>0$, i.e, $\alpha >-\frac{1}{2}$ and $\beta > -V_0(1+ 4 \alpha )$. Using Eq. (33) in Eq. (25), we have

$$\begin{aligned} 9 \left( \frac{\dot{a}}{a}\right) ^2=\frac{4 A B^2 e^{2 \sqrt{B} \;t}}{\left( 1-A B e^{2 \sqrt{B}\;t}\right) ^2}+B. \end{aligned}$$

(34)

On integrating, the above equation gives two solutions for the scale factor:

$$\begin{aligned} a(t)= & {} a_0e^{\frac{\sqrt{B} }{3}t} \left( e^{2 \sqrt{B} \;t}-AB\right) ^{-\frac{1}{3}}, \end{aligned}$$

(35)

$$\begin{aligned} a(t)= & {} a_0e^{-\frac{\sqrt{B} }{3}t} \left( e^{2 \sqrt{B} \;t}-AB\right) ^{\frac{1}{3}}, \end{aligned}$$

(36)

where $a_0$ is an integration constant. The scale factor given by Eq. (35) corresponds to a contracting model, whereas the scale factor in Eq. (36) describes an expanding universe. Since we are living in an expanding universe, we discard Eq. (35) here. Thus, the evolution of the universe is governed by Eq. (36). Real solutions exist when one has $t\ge \frac{log\left( AB\right) }{2\sqrt{B}}$. It is to be noted that $a(t)=a_0(1-AB)^{\frac{1}{3}}$ at $t=0$. This model avoids the Big-Bang singularity provided $1-AB>0$, i.e., $\beta <\frac{2-(8 \alpha ^2 -6 \alpha -\,1)V_0}{2 \alpha +1}$. Otherwise an initial singularity occurs at $t=\frac{log\left( AB\right) }{2\sqrt{B}}$.

Table 1 The present values of $q_0$ from some observational outcomes and the corresponding values of $\gamma$

Figures 1 and 2 plot the scale factor a(t) versus t which describes the evolution of the universe for singular and non-singular models, respectively. The significance of $f(R,T^\phi )$ gravity and the potential $V_0$ of the scalar field is shown in these figures. One may see that larger values of $\alpha$, $\beta$ and $V_0$ enhance the rate of expansion of the universe throughout its evolution. A higher value of $\alpha$ allows expansion faster than a higher value of $\beta$, whereas a large scalar field potential dominates over both $\alpha$ and $\beta$, and it gives rise to the fastest cosmological expansion as shown in Fig. 1. The effect of these parameters is quiet different for negative values of $\alpha$ as shown in Fig. 2. For negative values of $\alpha$, the parameter $\beta$ dominates both $\alpha$ and $V_0$ and it enhances the expansion fastest. However, some small negative values of $\alpha$ dominate over higher scalar potentials, but these are dominated by higher values of $\beta$. From Fig. 2 we note that the singularity free models are not only possible for negative $\alpha$, but also for positive ones.

Fig. 1

a(t) versus t with $a_0=1$

Fig. 2

a(t) versus t with $a_0=1$

The scale factor in terms of red shift is defined by

$$\begin{aligned} a=\frac{a_0}{1+z}. \end{aligned}$$

(37)

The deceleration parameter is defined as $q=-\frac{a \ddot{a}}{\dot{a}^2}$ which by the use of (36) and (37) can be written in terms of z as

$$\begin{aligned} q(z)=2-\frac{3}{1+4 \gamma (1+z)^6}, \end{aligned}$$

(38)

where $\gamma =AB$ and we have chosen $e^{-\frac{\sqrt{B}}{3}t_0}(e^{2\sqrt{B}t_0}-\gamma )^\frac{1}{3}$ as unity. The present value of deceleration parameter is $q(z=0)=2-\frac{3}{1+4\gamma }$. As we know, the positive values of deceleration parameter ($q>0$) describe the decelerated phases of the universe, whereas the negative values ($q<0$) describe the accelerated phases of the universe. For a negative deceleration parameter at $z=0$, i.e., $2-\frac{3}{1+4\gamma }<0$, we must have $-\frac{1}{4}<\gamma <\frac{1}{8}$ which implies that $-\frac{1}{4 B}<A<\frac{1}{8 B}$, thus, we have the constraint $-\frac{1+6 B}{12 B}<\alpha <\frac{1-6 B}{12 B}$ to accommodate late time acceleration of the universe.

Since the deceleration parameter given by (38) is a single parameter expression, so the value of $\gamma$ can be determined for the present value of deceleration parameter, consistent with the various observational data. In Table 1 we borrow some of the present values of deceleration parameter from various observational outcomes and calculate the corresponding values of $\gamma$.

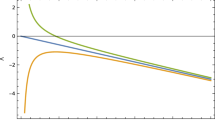
Figure 3 plots q versus z for different values of $\gamma$ calculated in Table 1. We see that q transits from $q=2$ to some negative values $q\le -\,1$. The universe enters into present accelerated phase from a decelerated phase at a red shift somewhere around $0.2 \le z \le 1.3$. The exact numerical values of transition red shift is listed in Table 1 in each case. In the first two cases, i.e., $\gamma =0.05$ and $\gamma =0.028$, the universe enters into the accelerating phase very recently, i.e., $z= 0.2$ and $z= 0.3$, respectively. For $\gamma =0.009$ the transition occurs at $z= 0.6$ while for $\gamma =0.001$ the transition takes place quite a long back at $z= 1.3$. The red shift where the transition of the universe from deceleration to acceleration takes place for the first three cases fall in interval $0.2\le z\le 0.6$ which is consistent with many observational outcomes (see Ref. [78] and references therein).

Fig. 3

q versus z with different values of $\gamma$ calculated in Table 1

The expressions for energy density and pressure of the scalar field become

$$\begin{aligned} \rho _{\phi }= & {} \frac{2 B^2 e^{2 \sqrt{B} \;t}}{\left( e^{2 \sqrt{B} \;t}-\gamma \right) ^2}+V_0, \end{aligned}$$

(39)

$$\begin{aligned} p_{\phi }= & {} \frac{2 B^2 e^{2 \sqrt{B} \;t}}{\left( e^{2 \sqrt{B} \;t}-\gamma \right) ^2}-V_0, \end{aligned}$$

(40)

respectively.

The recent results from Planck Collaboration [8], and first Panoramic Survey Telescope & Rapid Response System [79] give the motivation to concentrate especially on the present value of the EoS parameter. We study the EoS parameters of the scalar field and matter due to $f(R,T^\phi )$ gravity which are defined as $\omega _{\phi }=\frac{p_{\phi }}{\rho _{\phi }}$ and $\omega _{f}=\frac{p_f}{\rho _f}$, respectively. We also consider that the scalar field and matter due to $f(R,T^\phi )$ gravity are non-interacting and together represent an effective matter, i.e, $\rho _{eff}=\rho _\phi +\rho _f$ and $p_{eff}=p_\phi +p_f$. Therefore, the EoS parameter of effective matter can be defined as $\omega _{eff}=\frac{\rho _{eff}}{p_{eff}}$.

The EoS parameter of the scalar field in terms of red shift gives

$$\begin{aligned} \omega _\phi (z)=-\frac{V_0-2 B^2 (1+z)^6}{V_0+2 B^2 (1+z)^6}. \end{aligned}$$

(41)

Considering the case $\gamma =0.05$ corresponding to the best fit current value $q_0=-\,0.5$ with the recent observational data [73,74,75] and assuming the present age of the universe $t_0=13.7\;Gyr$ [80], we calculate B from the expression $e^{-\frac{\sqrt{B}}{3}t_0}(e^{2\sqrt{B}t_0}-\gamma )^\frac{1}{3}=1$, which gives $B=0.000012$. The behavior of $\omega _\phi$ versus z with $B=0.000012$ and some physically consistent values of potential is shown in Fig. 4.

Fig. 4

$\omega _\phi$ versus z with $B=0.000012$ and different values of $V_0$ (vertical lines are grid)

We see that $\omega _\phi$ transits from $\omega _\phi =1$ to some negative values $\omega _\phi \le -\,1$. It crosses the quintessence dividing line $\omega _\phi =-\frac{1}{3}$ somewhere between $0.1 \le z \le 1.4$ depending on the scalar potential. Therefore, the scalar field acts as ordinary matter at early times whereas it acts like quintessence at late times. It means that the scalar field behaves like an ordinary matter in the decelerated phases, and eventually becomes the candidate for quintessence DE at late times for lower scalar potential. However, the scalar field behaves as a cosmological constant at late times for higher scalar potential. Thus, the scalar field describes all kinds of matter represented by the EoS $-\,1\le \omega _\phi \le 1$. One must note that the term $\frac{2 B^2 e^{2 \sqrt{B} \;t}}{\left( e^{2 \sqrt{B} \;t}-AB\right) ^2}$ in (40) remains always positive, which shows that it is only the scalar field potential which generates the negative pressure to accelerate the universe at late times.

The energy density and pressure of the matter due to $f(R,T^\phi )$ gravity become

$$\begin{aligned} \rho _f= & {} \beta +4\alpha \left[ V_0+\frac{B^2 e^{2\sqrt{\beta }\;t}}{\left( e^{2 \sqrt{B} \;t}-\gamma \right) ^2}\right] , \end{aligned}$$

(42)

$$\begin{aligned} p_f= & {} -\beta -4\alpha \left[ V_0-\frac{B^2 e^{ 2\sqrt{\beta }\;t}}{\left( e^{2 \sqrt{B} \;t}-\gamma \right) ^2}\right] , \end{aligned}$$

(43)

respectively. Consequently, the EoS parameter of the matter due to $f(R,T^\phi )$ gravity in terms of red shift can be expressed as

$$\begin{aligned} \omega _{f}=-\frac{\beta +4\alpha \left[ v_{0}-B^{2}(1+z)^6\right] }{\beta +4\alpha \left[ v_{0}+B^{2}(1+z)^6\right] }. \end{aligned}$$

(44)

If $\alpha =0$, we have $\omega _f=-\,1$, which shows that the constant $\beta$ in the reconstructed form $f(R,T^\phi )$ gravity is nothing but a cosmological constant. Since we are interested to analyze the behavior of $f(R,T^\phi )$ gravity without a cosmological constant, therefore, we consider $\beta =0$. The behavior of $\omega _{f}$ with $B=0.000012$ and different values of $V_0$ is shown in Fig. 5.

Fig. 5

$\omega _{f}$ versus z with $\beta =0$, $B=0.000012$ and different values of $V_0$ (vertical lines are grid)

Table 2 A comparison of effective EoS parameter with some observational outcomes

We observe that $\omega _{f}$ transits from $\omega _{f}=1$ to some negative values for lower potential, whereas it approaches to $\omega _{f}=-\,1$ for higher potential. Therefore, at early times, $\omega _{f}$ describes ordinary matter, whereas it describes quintessence at late times for small values of potential. However, a higher scalar potential is required for $\omega _{f}$ to describe the behavior of a cosmological constant at late times. Thus, the matter due to $f(R,T^\phi )$ gravity can also describe all kinds of matter given by the EoS $-\,1\le \omega _{f}\le 1$.

It is to be noted that if one chooses $\alpha =0$ and $\beta ={\varLambda }$, i.e., $f(R,T^\phi )=R+2{\varLambda }$, the solutions of the GR model with a cosmological constant can be recovered. Further, when $\beta =0$ then $\omega _{f}\rightarrow -\,1$ as $t\rightarrow \infty$, the term $4\alpha V_0$ plays the role of a cosmological constant at late times. If $\alpha =0$ and $\beta =0$, then $\rho _f=0=p_f$ which shows that the matter due to $f(R,T^\phi )$ gravity vanishes.

Now it is of worthwhile to study the nature of effective matter. The effective energy density and pressure are obtained as

$$\begin{aligned} \rho _{eff}= & {} \frac{1}{3} \left[ B+\frac{A B^2 e^{2 \sqrt{B}\; t}}{\left( e^{2 \sqrt{B}\; t}-\gamma \right) ^2}\right] , \end{aligned}$$

(45)

$$\begin{aligned} p_{eff}= & {} \frac{1}{3} \left[ -\,B+\frac{A B^2 e^{2 \sqrt{B}\; t}}{\left( e^{2 \sqrt{B}\; t}-\gamma \right) ^2}\right] . \end{aligned}$$

(46)

Note that instead of $\omega _{f}$, if we consider the effective EoS parameter $\omega _{eff}$, then

$$\begin{aligned} w_{eff}= \frac{p_{\phi }+p_f}{\rho _{\phi }+\rho _f}=-\frac{1-4\gamma (1+z)^6}{1+4\gamma (1+z)^6}. \end{aligned}$$

(47)

In Fig. 6, the behavior of $\omega _{eff}$ is shown for values of $\gamma$ calculated in Table 1. The effective matter describes transitions within the EoS $-\,1\le \omega _{eff}\le 1$. We see that $\omega _{eff}$ starts from $\omega _{eff}=1$, and after crossing the quintessence diving line $\omega _{eff}=-\frac{1}{3}$, it finally attains some negative values nearby $\omega _{eff}=-\,1$ at $z=0$.

Fig. 6

$\omega _{eff}$ versus z with different values $\gamma$ calculated in Table 1 (vertical lines are grid)

One may note that when the transition from decelerating to accelerating universe takes place, then the effective matter also exhibits a transition from ordinary matter to quintessence somewhere between $0.2 \le z \le 1.3$, and finally approaches towards $\omega _{eff}\approx -\,1$ at $z=0$. Thus, the transiting behavior of effective matter from baryonic to quintessence causes the transition of the universe from decelerating to accelerating.

A comparison of present values of effective EoS parameter corresponding to different values of $\gamma$ with some observational outcomes is presented in Table 2. It is to be noted that the present values $\omega _{eff}=-0.67_{\gamma =0.05}$, $\omega _{eff}=-0.80_{\gamma =0.028}$, and $\omega _{eff}=-0.931_{\gamma =0.009}$, are consistent with the various observational outcomes mentioned in Table 2. The value $\omega _{eff}=-\,0.992_{\gamma =0.001}$ is quite near to a cosmological constant which is consistent with many observational data [82,83,84,85,86]. The viability of the model proves from the fact that we borrow the current values of deceleration from some set of observational outcomes mentioned in Table 1 but the effective EoS parameter for those values comes out to be consistent with the other observational data mentioned in Table 2.

The dimensionless density parameter ${\varOmega }_\phi =\frac{\rho _\phi }{3H^2}$ of the scalar field gives

$$\begin{aligned} {\varOmega }_\phi =\frac{3 \left[ \frac{2 B^2 e^{2 \sqrt{B} t}}{\left( e^{2 \sqrt{B} t}-A B\right) ^2}+{V_0}\right] }{B \left( 1+\frac{2 A B}{e^{2 \sqrt{B} t}-A B}\right) ^2}. \end{aligned}$$

(48)

The density parameter of the matter due to $f(R,T^\phi )$ gravity ${\varOmega }_{f}=\frac{\rho _f}{3H^2}$ yields

$$\begin{aligned} {\varOmega }_{f}=\frac{3 \left[ 4 \alpha \left( \frac{B^2 e^{2 \sqrt{B} t}}{\left( e^{2 \sqrt{B} t}-A B\right) ^2}+{V_0}\right) +\beta \right] }{B \left( 1+\frac{2 A B}{e^{2 \sqrt{B} t}-A B}\right) ^2}. \end{aligned}$$

(49)

Thus, in the present model, we have ${\varOmega }_{eff}={\varOmega }_\phi +{\varOmega }_{f}=1$, which not only ensures that the model is effectively flat but also confirms the validity of the solutions.

4 Massless scalar field model

The massless scalar field model corresponds to zero potential, i.e., $V_0=0$. One may observe that Eq. (19) gives the same form of $f(R,T^\phi )$ for a massless scalar field as we have obtained for a non-vanishing scalar potential in Eq. (22). Therefore, we can express all physical quantities just by substituting $B=3\beta$ and $V_0=0$ in the solutions of the flat potential model. However, we shall rewrite all physical quantities in terms of $\alpha$ and $\beta$ by dropping the constants A and B which were taken in the flat potential model for the sake of convenience.

The scale factor (36) can be written as

$$\begin{aligned} a(t)=a_0e^{-\sqrt{\frac{\beta }{3} }t} \left[ e^{2 \sqrt{3\beta } \;t}-9\beta \left( \frac{1}{2}+\alpha \right) \right] ^{\frac{1}{3}}. \end{aligned}$$

(50)

For real solutions one must have $\beta >0$ and $t\ge \frac{log\left[ 3\beta \left( \alpha +\frac{1}{2}\right) \right] }{2\sqrt{3\beta }}$. An initial singularity occurs at $t=\frac{log\left[ 3\beta \left( \alpha +\frac{1}{2}\right) \right] }{2\sqrt{3\beta }}$. However, since $a(t)=a_0\left[ 1-9\beta \left( \frac{1}{2}+\alpha \right) \right] ^{\frac{1}{3}}$ at $t=0$, the massless scalar field model also avoids the Big-Bang singularity provided $1-3\beta \left( \frac{1}{2}+\alpha \right) >0$, i.e., $\beta <\frac{2}{1+2 \alpha }$. Here, we would like to differentiate the present model with the model discussed by Harko et al. [52] as a particular example. In [52], the authors considered an exponential form of $F(R,\phi )$ for a massless scalar field, which leads to a power-law solution. Moreover, the authors have not incorporated the covariant divergence of the energy momentum tensor. As we have mentioned earlier, the covariant derivative of the energy momentum tensor does not vanish in f(R, T) gravity in general. Consequently, the matter in f(R, T) gravity does not satisfy the standard continuity equation. In the present study we have reconstructed a particular form of $f(R,T^\phi )$ considered in Eq. (18), taking into account that the covariant derivative of the energy momentum tensor of the scalar field is equal to zero. For the reconstructed form of $f(R,T^\phi )$ given in Eq. (22), the Klein–Gordon equation holds as well. One may also observe that the evolution of the scale factor given by Eq. (50) is different from the power-law expansion which was obtained in [52].

Figure 7 plots a(t) versus t for a massless scalar field which shows singular and non-singular models for different values of $\alpha$ and $\beta$. Let us explain that how the massless scalar field model is different from the model with non-zero scalar potential. We observe that the parameter $\alpha$ of $f(R,T^\phi )$ gravity affects only the early evolution of the massless scalar field model, whereas the behavior of the parameter $\beta$ is similar to the non-vanishing scalar potential model. In fact, $\alpha$ decides the origin of the universe on the time scale. Therefore, suitable choices of $\alpha$ under the constraint $\beta <\frac{2}{1+2 \alpha }$ give rise to singularity free models. However, the late time evolution asymptotically coincides for all values of $\alpha$ if $\beta$ is fixed. On the other hand, the parameter $\beta$ affects the entire cosmological evolution. A large value of $\beta$ enhances the expansion rate of the universe, whereas a small value slows it down. The significance of $f(R,T^\phi )$ gravity of the massless scalar field model in the context of decelerating or accelerating universe can be understood in better a way by studying the deceleration parameter.

Fig. 7

a(t) versus t with $a_0=1$ and different values of $\alpha$ and $\beta$

Table 3 The present values of $q_0$ from some observational outcomes and the corresponding values of $\lambda$

Fig. 8

q versus z for different values of $\lambda$ calculated in Table 3

The deceleration parameter for the massless scalar field in terms of red shift reads as

$$\begin{aligned} q(z)=2-\frac{3}{1+36\lambda (1+z)^6}, \end{aligned}$$

(51)

where $\lambda =\beta \left( \alpha +\frac{1}{2}\right)$ and $e^{-\sqrt{\frac{ \beta }{3}}t_0}(e^{2\sqrt{3\beta } t_0}-9\lambda )^\frac{1}{3}$ is taken to be unity. For a negative value of deceleration parameter at present, i.e., $q(z=0)=2-\frac{3}{1+36\lambda }<0$, we must have $-\frac{1}{36}\le \lambda <\frac{1}{72}$ which implies that $\frac{-36 \beta -1}{18 \beta }<\alpha <\frac{1-72 \beta }{36 \beta }$, this is the constraint on $\alpha$ for attaining an accelerating universe at present time. It is to be noted that $q=-\,1$ as $\alpha \rightarrow -\frac{1}{2}$ or $\beta =0$, therefore, the massless scalar field model can also exhibit an ever accelerating universe in $f(R,T^\phi )$ gravity.

The deceleration parameter is a single parameter expression in $\lambda$. The values of $\lambda$ are calculated in Table 3 using some present values of deceleration parameter consistent with observations.

Figure 8 plots q versus z for different values of $\lambda$ calculated in Table 3. The deceleration parameter starts from a positive value, and evolves up to some negative values $q<-\,1$. Hence, the massless scalar field model also exhibits transitions from decelerating to accelerating universe at a red shift somewhere between $0.2 \le z \le 1.3$. The exact values of red shift where the transition from deceleration to acceleration takes place in mentioned in Table 3. We note that the transition red shift for the first three cases occur between $0.2\le z \le 0.6$, which is consistent with many observational outcomes (see Ref. [78] and references therein). Thus, the massless scalar field model is self sufficient to describe the cosmological evolution without encountering an initial singularity. In what follows, we shall see that it is the parameter $\beta$ of $f(R,T^\phi )$ gravity which plays the role of the scalar field potential in the massless scalar field model. Moreover, it is only the parameter $\beta$ which provides negative pressure for driving acceleration of the universe at late times.

The energy density and pressure of the massless scalar field are equal, having the expression

$$\begin{aligned} \rho _{\phi }=\frac{18 \beta ^2 e^{2 \sqrt{3\beta } \;t}}{\left[ e^{2 \sqrt{3\beta } \;t}-9\beta (\frac{1}{2}+\alpha )\right] ^2}=p_\phi . \end{aligned}$$

(52)

The EoS parameter for the massless scalar field has the constant value $\omega _\phi =1$. Therefore, the massless scalar field acts similarly to stiff matter.

The energy density and pressure of the matter due to $f(R,T^\phi )$ gravity become

$$\begin{aligned} \rho _f= & {} \beta +\frac{36\alpha \beta ^2 e^{2 \sqrt{3\beta } \;t}}{\left[ e^{2 \sqrt{3\beta } \;t}-9\beta (\frac{1}{2}+\alpha )\right] ^2}, \end{aligned}$$

(53)

$$\begin{aligned} p_f= & {} -\,\beta +\frac{36\alpha \beta ^2 e^{2 \sqrt{3\beta } \;t}}{\left[ e^{2 \sqrt{3\beta } \;t}-9\beta (\frac{1}{2}+\alpha )\right] ^2}. \end{aligned}$$

(54)

Consequently, the EoS parameter of the matter due to $f(R,T^\phi )$ gravity in terms of red shift can be read as

$$\begin{aligned} \omega _{f}=-\frac{1-36\alpha \beta (1+z)^6}{1+36\alpha \beta (1+z)^6}. \end{aligned}$$

(55)

Now for the best fit value $\lambda =0.02$ with the observational data [73,74,75], we calculate $\beta$ from the expression $e^{-\sqrt{\frac{ \beta }{3}}t_0}(e^{2\sqrt{3\beta } t_0}-9\lambda )^\frac{1}{3}=1$, which gives $\beta =4.52\times 10^{-6}$. The behavior of $\omega _{f}$ with $\beta =4.52 \times 10^{-6}$ and different physically consistent values of $\alpha$ is shown in Fig. 9. We see that $\omega _{f}$ exhibits transition from ordinary matter to quintessence like behavior at late times for higher values of $\alpha$ while it becomes the cosmological constant for small values of $\alpha$.

Fig. 9

$\omega _{f}$ versus z with $\beta =4.52 \times 10^{-6}$ and different values of $\alpha$ (vertical lines are grid)

Table 4 A comparison of effective EoS parameter with some observational outcomes

Since $\omega _{f}=-\,1$ for $\alpha =0$, the matter due to $f(R,T^\phi )$ gravity behaves like a cosmological constant. This follows from the fact that if $\alpha =0$ and $\beta ={\varLambda }$ then $f(R,T^\phi )=R+2{\varLambda }$, i.e., $f(R,T^\phi )$ gravity becomes equivalent to the ${\varLambda }$CDM model of GR. Hence, $\beta$ can be understood as a cosmological constant in $f(R,T^\phi )$ gravity. However, if $\beta =0$ then $\rho _f=0=p_f$, i.e., the matter due to $f(R,T^\phi )$ gravity vanishes even when $\alpha \ne 0$. Here, one must understand the significance of the parameter $\beta$ in $f(R,T^\phi )$ gravity. The $f(R,T^\phi )$ gravity contributes nothing to the massless scalar field model if $\beta =0$. Moreover, from Eqs. (52) and (54), we have $p_f=-\beta +2\alpha p_\phi$, and from Eq. (52) it is also clear that $p_\phi \ge 0$, which implies that $2\alpha p_\phi \ge 0$. Therefore, it is only the parameter $\beta$ which provides negative pressure for accelerating the universe at late times. Hence, we can say that the parameter $\beta$ of $f(R,T^\phi )$ gravity mimics the scalar field potential in the massless scalar field model which becomes responsible for the acceleration of the universe at late times.

The effective EoS parameter as a function of z takes the form

$$\begin{aligned} \omega _{eff}= -\frac{1-36 \lambda (1+z)^6}{1+36 \lambda (1+z)^6}. \end{aligned}$$

(56)

Fig. 10

$\omega _{eff}$ versus z with different values of $\lambda$ calculated in Table 3 (vertical lines are grid)

The behavior of $\omega _{eff}$ is shown in Fig. 10 for observationally consistent values of $\lambda$ calculated in Table 3. We see that $\omega _{eff}$ shows a transition from $\omega _{eff}=1$ to some negative values $\omega _{eff}\le -\,1$. If $\lambda \rightarrow 0$, i.e., $\alpha \rightarrow -\frac{1}{2}$ or $\beta \rightarrow 0$ then $\omega _{eff}\rightarrow -\,1$.

Thus, the effective matter describes transition from stiff matter to quintessence ($\lambda =0.006$, $\lambda =0.003$ and $\lambda =0.001$) or cosmological constant ($\lambda =0.0001$) at late times. The transiting behavior of effective matter causes the transition of the universe from decelerating to accelerating in these cases.

A comparison of present values of effective EoS corresponding to different values of $\gamma$ with some observational outcomes is presented in Table 4. It is to be noted that the present values $\omega _{eff}=-0.65_{\gamma =0.006}$, $\omega _{eff}=-0.81_{\gamma =0.003}$, and $\omega _{eff}=-0.93_{\gamma =0.001}$, are consistent with the various observational outcomes mentioned in Table 4. The value $\omega _{eff}=-0.993_{\gamma =0.0001}$ is very near to a cosmological constant which is consistent with many recent observational data [82,83,84,85,86].

The density parameter of the scalar field is

$$\begin{aligned} {\varOmega }_\phi =\frac{18 \beta e^{2 \sqrt{3\beta } \;t}}{\left[ 9 \beta ( \frac{1}{2}+\alpha )+ e^{2 \sqrt{3\beta }\; t}\right] ^2}. \end{aligned}$$

(57)

Similarly, the density parameter of the matter due to $f(R,T^\phi )$ gravity is

$$\begin{aligned} {\varOmega }_{f}=1-\frac{18 \beta e^{2 \sqrt{3\beta } \;t}}{\left[ 9 \beta ( \frac{1}{2}+\alpha )+ e^{2 \sqrt{3\beta }\; t}\right] ^2}. \end{aligned}$$

(58)

From (56) and (57), we have ${\varOmega }_f+{\varOmega }_\phi =1$. Hence, the model is effectively flat. We have also checked that the obtained solutions for this model and the flat potential model satisfy the equation (26) which we have not used to obtain the solutions.

5 Conclusion

In this paper, we have studied modified $f(R,T^\phi )$ gravity with a minimally coupled scalar field with self interacting potential in a flat FRW model. We have reconstructed a particular form $f(R,T^\phi )= R+2f(T^\phi )$ by requiring the Klein–Gordon equation to be satisfied for the scalar field. The solutions are consistent with a quintessence model for the scalar field. The reconstructed form is $f(R,T^\phi )=R+2(\alpha T^\phi +\beta )$ which leads to the field equations equivalent to the Einstein field equations with an effective energy momentum tensor containing the sum of a scalar field, and matter due to $f(R,T^\phi )$ gravity. We have investigated the behavior of the reconstructed form of $f(R,T^\phi )$ gravity in two models, namely, a flat potential ($V_0$) model, and a massless scalar field model. Each model has been intensely examined via the deceleration and EoS parameters. Both models may avoid the big-bang singularity under some constraints. Both models are found consistent with many observational outcomes. The findings of both models are summarized in the following points:

• In the first model where we have considered a flat potential, the scale factors with positive and negative values of $\alpha$ show that $f(R,T^\phi )$ gravity and the scalar field potential both enhance the expansion rate of the universe.

• The deceleration parameter shows a transition from decelerating to accelerating universe. The transition from deceleration to acceleration occurs between $0.2 \le z \le 0.6$ with the best fit present values of deceleration parameter.

• The scalar field and matter due to $f(R,T^\phi )$ gravity behave as ordinary matter at early times and eventually start acting as DE (quintessence) or a cosmological constant at late times. The matter due to $f(R,T^\phi )$ gravity can describe all matter governed by an EoS $-\,1\le \omega _f\le 1$, i.e, quintessence, baryonic matter, stiff matter, DE and a cosmological constant.

• The constant $\beta$ in reconstructed form of f(R, T) gravity plays the role of a cosmological constant. If $\beta =0$ then the term $4\alpha V_0$ serves the role of a cosmological constant at late times.

• The transition of the effective matter from ordinary matter to quintessence causes the transition of the universe from decelerating to accelerating.

• In the massless scalar field model, the parameter $\alpha$ affects only the early evolution of the universe, whereas the late time evolution asymptotically coincides if $\beta$ is fixed. The parameter $\beta$ affects the whole cosmological evolution and a large value of $\beta$ enhances the expansion rate of the universe, whereas a small value slows down the expansion. Singularity free models are possible under the constraint $\beta <\frac{2}{2\alpha +1}$.

• The massless scalar field model also shows a transition from a decelerating to an accelerating universe.

• If $\beta =0$ then $\rho _f=0=p_f$, i.e., the matter due to $f(R,T^\phi )$ vanishes. The parameter $\beta$ mimics a scalar field potential in the massless scalar field model which accelerates the universe at late times.

• The effective matter in the massless scalar field model also describes transition from ordinary matter to quintessence which causes the transition from decelerated to accelerated universe.

As final concluding remarks, we can say that $f(R,T^\phi )$ gravity with conservation of energy momentum tensor is capable of describing a suitable cosmological model in which a transition from a decelerated to an accelerated phase occurs. Hence, the $f(R,T^\phi )$ gravity plays an essential role in the evolution of the universe.