1 Introduction

Extra dimensions provide an approach to modify gravity without abandoning the form of the action proposed in Einstein’s general relativity. From a phenomenological point of view we can avoid constraints coming from standard model observations, by considering a brane-world scenario, that is, we are living in a hypersurface (3-D) in a higher-dimensional spacetime. From the theoretical point of view, string theory predicts a boundary layer, a brane, on which edges of open strings stand [1]. The possibility that we may be living in a brane generates many questions as to how gravity looks like. Also in an attempt to solve the much debated hierarchy problem, various problems were studied, but also in order to understand the cosmology, such as inflation and dark energy. In this contribution to study of the consequences of the brane world in 4-D, we study one of the most famous models, the DGP (Dvali, Gabadadze, Porrati) [2] model. Even if the DGP model has been ruled out by the observations [3] and we have the presence of a ghost [4,5,6], it remains an interesting laboratory for brane models and their consequences. In that direction, the galileon models [7] have been derived from it by integrating out the extra dimension and obtaining an effective field theory on the boundary, where the additional scalar field, the galileon, represents the brane-bending mode or tells how the brane bends in the extra dimension. This extra degree of freedom has a very interesting phenomenology, like for example producing a screening mechanism through the non-linearities of it, the Vainshtein mechanism. In that direction, we would like to study the black hole solution, which means we have the full exact solution and not only a linearized version of the theory.

We know that the physics of black holes and gravitational collapse is complicated, especially because of the matter localized on the brane, while the gravitational field can access the extra dimension. This is also because of the non-local effects of the bulk which can backreact on the brane.

Our first aim will be to reduce the theory to an effective theory on the brane and find an exact solution. We cannot necessarily embed this solution into a bulk but some information of the global solution can be understood, and some intuition can be developed. The solution can be smoothly continued into the bulk via the ADM formalism, where the solution on the brane can be considered as an initial data. At least a local solution of the bulk exists, even if the global solution is not guaranteed. Hence, we analyze the solution, the existence of a horizon and the stability of it under odd and even perturbations.

2 DGP model

The model is defined as an empty five-dimensional space (not necessarily Minkowski) and all the energy-momentum is localized on the four-dimensional brane. The theory is described by the following action in vacuum:

$$\begin{aligned} \mathcal {S}&=M_{(5)}^3\int {\text {d}^5X} \sqrt{-g} R^{(5)}-2 M_{(5)}^3\int {\text {d}^4x}\sqrt{-h}K\nonumber \\&\quad +\frac{M_{(4)}^2}{2}\int {\text {d}^4x}\sqrt{-h} R^{(4)}, \end{aligned}$$
(1)

where (g, h) are, respectively, the metric of the bulk and the brane, (\(X^A,x^\mu \)) the coordinates in the bulk, and over the brane K is the extrinsic curvature (the Gibbons–Hawking term), \((R^{(5)},R^{(4)})\) the intrinsic curvature in 5-D and 4-D, respectively, and \((M_{(5)},M_{(4)})\) are the coupling constants.

Variation of the action gives

$$\begin{aligned} \delta S&=M_{(5)}^3\int {\text {d}^5X}\sqrt{-g}\Bigl [R_{AB}^{(5)}-\frac{1}{2}R^{(5)}g_{AB}\Bigr ]\delta g^{AB}\nonumber \\&\quad -M_{(5)}^3\int {\text {d}^4x}\sqrt{-h}\Bigl [K_{\mu \nu }-K h_{\mu \nu }\Bigr ]\delta h^{\mu \nu }\nonumber \\&\quad +\frac{M_{(4)}^2}{2}\int {\text {d}^4x}\sqrt{-h} \Bigl [R_{\mu \nu }^{(4)}-\frac{1}{2}R^{(4)}h_{\mu \nu }\Bigr ]\delta h^{\mu \nu } \end{aligned}$$
(2)

and therefore we have

$$\begin{aligned} \text {Bulk equation:}\quad R_{AB}^{(5)}-\frac{1}{2}R^{(5)}g_{AB}&=0, \end{aligned}$$
(3)
$$\begin{aligned} \text {Brane equation:}\quad R_{\mu \nu }^{(4)}-\frac{1}{2}R^{(4)}h_{\mu \nu }&=\frac{1}{r_c}\Bigl (K_{\mu \nu }-Kh_{\mu \nu }\Bigr ), \end{aligned}$$
(4)

where \(r_c=M_{(4)}^2/2M_{(5)}^3\) is the crossover scale that governs the transition between four-dimensional behavior and five-dimensional behavior. The bulk equation implies \(R_{AB}^{(5)}=0\) and \(R^{(5)}=0\), which implies

$$\begin{aligned} R_{ABCD}^{(5)}=W_{ABCD}^{(5)} \end{aligned}$$
(5)

where W is the bulk Weyl tensor. To obtain the equation on the brane, we follow the formalism defined in [8]. For that, we define the spacelike unit vector to the brane \(n^A\) and the projection tensor over the brane \(q_{AB}=g_{AB}-n_A n_B\) which reduces to the brane metric \(h_{\mu \nu }\) when the bulk coordinates \(X^A\) reduces to the brane coordinates \(x^\mu \). Projecting indices of the Riemann tensor, we can find a relation between the Ricci tensor in 4D and the Riemann tensor in 5D, known as the Gauss equation,

$$\begin{aligned} R_{\mu \rho \nu \sigma }^{(4)}=R_{ABCD}^{(5)}q^A_\mu q^B_\rho q^C_\nu q^D_\sigma +K_{\mu \nu }K_{\rho \sigma }-K_{\mu \sigma } K_{\rho \nu }. \end{aligned}$$
(6)

Contracting the indices \(\rho \) and \(\sigma \), we get

$$\begin{aligned} R_{\mu \nu }^{(4)}=R_{ABCD}^{(5)}q^A_\mu q^B_\rho q^C_\nu q^D_\sigma h^{\rho \sigma }+K K_{\mu \nu }-K_{\mu \sigma } K_{\nu }^\sigma . \end{aligned}$$
(7)

But because n is orthogonal to the brane, its projection is zero \((n^A q_{A B}=0)\), and we have

$$\begin{aligned} q^B_\rho q^D_\sigma h^{\rho \sigma }&=(\delta ^B_\rho -n^B n_\rho )(\delta ^D_\sigma -n^D n_\sigma )h^{\rho \sigma }\nonumber \\&=q^{BD}=g^{BD}-n^B n^D, \end{aligned}$$
(8)

which gives

$$\begin{aligned} R_{\mu \nu }^{(4)}&=R_{AC}^{(5)}q^A_\mu q^C_\nu - R_{ABCD}^{(5)}q^A_\mu q^C_\nu n^B n^D + K K_{\mu \nu }- K_{\mu \sigma } K_{\nu }^\sigma \nonumber \\&=-\,R_{ABCD}^{(5)}q^A_\mu q^C_\nu n^B n^D+K K_{\mu \nu }-K_{\mu \sigma } K_{\nu }^\sigma , \end{aligned}$$
(9)

because \(R_{AC}^{(5)}=0\). Finally, we can write it as

$$\begin{aligned} R_{\mu \nu }^{(4)}&=- W_{ABCD}^{(5)}q^A_\mu q^C_\nu n^B n^D+K K_{\mu \nu }-K_{\mu \sigma } K_{\nu }^\sigma \end{aligned}$$
(10)
$$\begin{aligned}&=-E_{\mu \nu }+K K_{\mu \nu }-K_{\mu \sigma } K_{\nu }^\sigma \end{aligned}$$
(11)

where we defined \(E_{\mu \nu }=W_{ABCD}^{(5)}q^A_\mu q^C_\nu n^B n^D\), known as the electric part of the Weyl tensor. One generally has to solve the bulk equations of motion first in order to evaluate it. Therefore it represents a non-local term from a brane point of view. Notice also that it is traceless, \(E_\mu ^\mu =0\).

Contracting this equation, we get

$$\begin{aligned} R^{(4)}&=K^2-K_{\rho \sigma } K^{\rho \sigma } \end{aligned}$$
(12)

and therefore

$$\begin{aligned} R_{\mu \nu }^{(4)}-\frac{1}{2}R^{(4)}h_{\mu \nu }&=-E_{\mu \nu }+K K_{\mu \nu }-K_{\mu \sigma } K_{\nu }^\sigma \nonumber \\&\quad -\frac{1}{2}h_{\mu \nu }\Bigl (K^2-K_{\rho \sigma } K^{\rho \sigma }\Bigr ). \end{aligned}$$
(13)

Therefore we end with two coupled equations on the brane,

$$\begin{aligned} G_{\mu \nu }&=\frac{1}{r_c}\Bigl (K_{\mu \nu }-Kh_{\mu \nu }\Bigr ), \end{aligned}$$
(14)
$$\begin{aligned} G_{\mu \nu }&=-E_{\mu \nu }+ K K_{\mu \nu }- K_{\mu \sigma } K_{\nu }^\sigma -\frac{1}{2}h_{\mu \nu }\Bigl (K^2- K_{\rho \sigma } K^{\rho \sigma }\Bigr ), \end{aligned}$$
(15)

where we dropped the index \(^{(4)}\) because from now on all quantities will be defined in the four-dimensional brane.

Following the idea developed in [9], we define the tensor

$$\begin{aligned} L_{\mu \nu }=K_{\mu \nu }-\frac{K}{2}h_{\mu \nu }+\frac{1}{2r_c}h_{\mu \nu } \end{aligned}$$
(16)

and rewrite Eq. (14) as

$$\begin{aligned} G_{\mu \nu }+\frac{3}{2r_c^2}h_{\mu \nu }=\frac{1}{r_c}\Bigl ( L_{\mu \nu }+\frac{L}{2}h_{\mu \nu }\Bigr ), \end{aligned}$$
(17)

where L is solution of the following algebraic equation, obtained by equating Eqs. (14) and (15):

$$\begin{aligned} L_\mu ^{~\alpha }L_{\alpha \nu }-\frac{L^2}{4}h_{\mu \nu } +\frac{3}{4r_c^2}h_{\mu \nu }=-E_{\mu \nu }. \end{aligned}$$
(18)

3 Solution on the brane

In the following, we will focus on static spherically solutions in the vacuum of the form

$$\begin{aligned} \mathrm{d}s^2=-A(r)\mathrm{d}t^2+\frac{\mathrm{d}r^2}{B(r)}+r^2\mathrm{d}\varOmega ^2. \end{aligned}$$
(19)

As shown in [10, 11], the electric part of the Weyl tensor can be decomposed. In fact, we can define a unit timelike vector \(u^\mu \) and define the projection tensor associated \(f_{\mu \nu }=h_{\mu \nu }+u_\mu u_\nu \). Therefore we can write in a spherically symmetric background

$$\begin{aligned} E_{\mu \nu }=\rho (r)\Bigl (u_{\mu }u_{\nu }+\frac{1}{3}f_{\mu \nu }\Bigr ) +P(r)\Bigl (r_{\mu }r_{\nu }-\frac{1}{3}f_{\mu \nu }\Bigr ), \end{aligned}$$
(20)

where \((\rho ,P)\) are, respectively, an effective energy density and anisotropic stress on the brane arising from the 5-D gravitational field, and \(r_\mu \) is a unit radial vector.

Also it is easy to see from (17) and (19) that L is diagonal, hence we write \(L^\mu _{~\nu }=\text {diag} \Bigl (L_0,L_1,L_2,L_3\Bigr )\), which from Eqs. (18) and (20) give

$$\begin{aligned} L_1&=\pm \sqrt{L_0^2-\frac{2}{3}(2\rho +P)}, \end{aligned}$$
(21)
$$\begin{aligned} L_2&=L_3=\pm \sqrt{L_0^2-\frac{1}{3}(4\rho -P)}. \end{aligned}$$
(22)

Also from the brane equation (17), we have

$$\begin{aligned} -A\frac{\mathrm{d}}{\text {d} r}\Bigl (\frac{B}{A}\Bigr )=\frac{r}{r_c}\Bigl (L_1-L_0\Bigr ). \end{aligned}$$
(23)

Hereafter, we will assume that radial photons should experience no acceleration, the velocity of light in the radial direction should remain constant. Therefore we have [12] \(A=B\), which implies \(L_1=L_0\); hence from (21) we have \(2\rho +P=0\). This constraint between the density and the pressure is the same as in the absence of the induced curvature term [11].

Finally, we have from (18)

$$\begin{aligned} 4L_0^2+2P\pm 8L_0\sqrt{L_0^2+P}=\frac{3}{r_c^2}. \end{aligned}$$
(24)

To solve this equation, we define [9] \(v=2\pm \sqrt{L_0^2+P}/L_0\) and obtain

$$\begin{aligned} L_0^2&=\frac{3}{2r_c^2(v^2-3)}, \end{aligned}$$
(25)
$$\begin{aligned} P&=\frac{3}{2r_c^2}\frac{(v-1)(v-3)}{v^2-3}. \end{aligned}$$
(26)

We see that we need \(v^2>3\). The only undetermined function is v, all the other quantities as \((\rho ,P,K_{\mu \nu })\) are related to v.

Considering now the Bianchi identity derived from Eq. (17),

$$\begin{aligned} \nabla _\mu L^\mu _{~\nu }+\frac{1}{2}\nabla _\nu L=0, \end{aligned}$$
(27)

we can close the system of equations and get an equation for v,

$$\begin{aligned} \frac{\mathrm{d}v}{\mathrm{d} r}+\frac{2}{3r}(v-3)(v^2-3)=0, \end{aligned}$$
(28)

which gives after integration

$$\begin{aligned} \frac{r^4}{r_c^2}=Q^2 \frac{|v-\sqrt{3}|^{(\sqrt{3}+1)/2}}{|v+\sqrt{3}|^{(\sqrt{3}-1)/2}|v-3|}, \end{aligned}$$
(29)

where Q is an integration constant.

Equation (29) gives v(r), which from (25) gives \(L_0(r)\), and therefore we can solve Eq. (17),

$$\begin{aligned} \frac{rB'(r)+B(r)-1}{r^2}=-\frac{3}{2r_c^2}\pm \frac{\sqrt{3/2}}{r_c^2}\frac{v}{\sqrt{v^2-3}}, \end{aligned}$$
(30)

where the sign ± is because of the sign of \(L_0\).

We have found three different solutions depending on the range of v. In the first solution we have \(v<-\sqrt{3}\), the second solution corresponds to \(\sqrt{3}<v<3\) and the last one to \(v>3\). Accordingly the range for r will be, respectively, \(r>\sqrt{Qr_c}\), \(r>0\) and \(r>\sqrt{Qr_c}\). The second and the third solutions are identical except the range for r; hence we keep only the second solution which covers the full spacetime (brane). The first solution does not cover the full spacetime \(r>\sqrt{Qr_c}\) and therefore cannot describe a black hole. This solution will not be studied in this paper. Hence we have two branches of the solution,

$$\begin{aligned} A\equiv B=1-\frac{2m}{r}-\frac{r^2}{2r_c^2}\pm \frac{r^2}{2r_c^2}f(v), \end{aligned}$$
(31)

where m is an integration constant, v is solution of the algebraic equation (29) and f can be written in terms of Gauss’ hypergeometric function,

$$\begin{aligned} f(v)&=\sqrt{6}\frac{v-2}{\sqrt{v^2-3}}\nonumber \\&\quad -\frac{4\sqrt{2}(\sqrt{3}-1)(v-3)^2}{5(v-\sqrt{3})^{3/2}(v+\sqrt{3})^{1/2}}~_2 \nonumber \\&\quad \quad F_1\Bigl [1,\frac{3(3-\sqrt{3})}{8},\frac{9}{4},(\sqrt{3}-1)\frac{v-3}{v-\sqrt{3}}\Bigr ]. \end{aligned}$$
(32)

f is a concave down monotonically increasing function of r. It is negative for \(r\lesssim 0.78 \sqrt{Qr_c}\) and positive otherwise and \(\lim _{r\rightarrow \infty } f=1\).

In conclusion to this section, we found for the first time the exact static spherically symmetric solution of the DGP model on the brane by assuming only \(A=B\). The solution is given in a parametric form Eqs. (29), (31), and (32).

We will continue with this parametric form of the solution but, of course, we can write the metric by considering the change of coordinates \((r\rightarrow v)\) where

$$\begin{aligned} r=\sqrt{Q r_c}\frac{(v-\sqrt{3})^{\frac{\sqrt{3}+1}{8}}}{(v+\sqrt{3})^{\frac{\sqrt{3}-1}{8}}(3-v)^{1/4}}, \end{aligned}$$
(33)

and we have

$$\begin{aligned} \mathrm{d}s^2=-A(r(v))\mathrm{d}t^2+\frac{r'(v)^2}{A(r(v))}\mathrm{d}v^2+r(v)^2\mathrm{d}\varOmega ^2. \end{aligned}$$
(34)

4 Structure of the solution

The horizon structure of the black hole on the brane depends on the branch considered. The negative branch (negative sign in Eq. (31)) has a black hole horizon and a cosmological horizon because of the de Sitter structure at large distances, while the positive branch, which is asymptotically flat, has a single horizon.

It is interesting to study the asymptotic behavior of this solution. We have at large distances

$$\begin{aligned} f(r)= 1-\frac{2q^2r_c^2}{r^4}+\frac{2q^4r_c^4}{5r^8}-\frac{4q^6r_c^6}{9r^{12}}+O\left( \frac{1}{r^{16}}\right) , \end{aligned}$$
(35)

where we have redefined the integration constant \(q=\sqrt{3/2}(3-\sqrt{3})^{(\sqrt{3}-1)/4}(3+\sqrt{3})^{-(\sqrt{3}+1)/4} Q\). Therefore we have at large distances

$$\begin{aligned}&\text {positive branch: }A=1-\frac{2m}{r}-\frac{q^2}{r^2}+\frac{q^4r_c^2}{5r^3}+\cdots , \end{aligned}$$
(36)
$$\begin{aligned}&\text {negative branch: }A=1-\frac{2m}{r}-\frac{r^2}{2r_c^2}+\frac{q^2}{r^2}-\frac{q^4r_c^2}{5r^3}+\cdots . \end{aligned}$$
(37)

We see that only the positive branch has a smooth limit as \(r_c\rightarrow 0\) (Randall–Sundrum limit) and as such we will refer to it as the RS branch. In contrast the negative branch is not smooth as \(r_c\rightarrow 0\) and it represents a distinct new feature of DGP, the DGP branch also being known as the self-accelerating branch. The RS branch converges to \(A=1-2m/r-q^2/r^2\), but it should not be confused with the Reissner–Nordström spacetime. In fact the tidal charge (\(q^2\)) has always the same sign and it is physically more natural for a brane solution [11]; the tidal charge strengthens the gravitational field. This is why our solution does not have a Cauchy horizon, even in the limit \(r_c\rightarrow 0\). Also as \(r_c\rightarrow \infty \), we recover the Schwarzschild solution (\(1-2m/r\)) for the two branches, and the solution is the same as in Einstein theory, therefore there is no van Dam–Veltman–Zacharov (vDVZ) [13,14,15] discontinuity. The continuity of the theory is restored because the nonlinear effects were taken into account, while we would conclude to a discontinuity if we use the linearized solution at large distances (35). It is clearly a realization of the Vainshtein mechanism.

In the other limit, at small distances, we have

$$\begin{aligned} f(r)\simeq -\,\delta \frac{(r_c q)^{3/2}}{r^3}, \end{aligned}$$
(38)

with

$$\begin{aligned} \delta =2 \sqrt{2}\frac{\varGamma \left( \frac{5}{4}\right) \varGamma \left( \frac{1}{8} \left( 3 \sqrt{3}-1\right) \right) }{3^{3/8}\varGamma \left( \frac{3}{8} \left( 3+\sqrt{3}\right) \right) }\simeq 3.11, \end{aligned}$$

which gives

$$\begin{aligned} A=1-\frac{2M}{r} +\cdots \,,~\text {with}~M=m\pm \delta \frac{q^{3/2}}{4\sqrt{r_c}}. \end{aligned}$$
(39)

We see that even in the case of a massless black hole (\(m=0\)), we have a “mass term” because of the fifth dimension. Hence we recover a standard result; even for a massless black hole, the behavior of the solution is 1 / r at small distances and \(1/r^2\) at large distances.

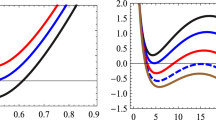
In order to keep the effective mass positive, in the DGP branch, we impose \(\bar{q}<\frac{4}{\delta }\bar{m}\), where \((\bar{m}=m/\sqrt{q r_c},\bar{q}=q/r_c)\). The existence of the black hole is constrained in Fig. 1. From this we see that, for a fixed parameter \(\bar{q}\), the mass of the black hole has an upper bound but also a lower bound. We would have a naked singularity for the lightest black holes; this can be seen as an instability of the branch.

Fig. 1
figure 1

Existence of the black hole for the DGP branch: The blue part represents the range of the parameters \((\bar{m},\bar{q})\) for which the black hole has two horizons. In the gray region, the metric is always negative and the white region corresponds to a black hole with only a cosmological horizon, because of the negativity of the effective mass, hence inside the cosmological horizon the solution would be a naked singularity

Full size image

The RS branch is much simpler, we have a black hole for all positive parameters \((\bar{m},\bar{q})\); also these parameters play the same role, they increase the position of the horizon and hence its entropy. At large distances, the Newtonian potential is dominant. Depending on the parameters, the situation can be the same for all distances, the solution will be very close to the Schwarzschild solution, except for large values of \(\bar{q}\) where the mass of the black hole will be renormalized at small distances. But in the case of the DGP branch, we do not have the same behavior at large and small distances; hence we have a new distance scale \(r_\star \) dubbed the Vainshtein radius,

$$\begin{aligned} r_\star \simeq (mr_c^2)^{1/3}. \end{aligned}$$
(40)

As we said previously, the mass of the black hole is bounded from below. The existence of the horizon is constrained by \(m> \bar{q}^2 r_c^2/r_\star \simeq \bar{q}^2 10^{28} M_{\odot }\) if we assume the Vainshtein radius to be of the order of the galaxy scale and the crossover scale of the order of the Hubble scale. A stellar black hole exists if \(\bar{q}<10^{-14}\). Otherwise it will be a naked singularity.

The extrinsic curvature and therefore the curvature constant can be easily derived from (25) and (26),

$$\begin{aligned} R=\frac{3}{r_c^2}\Bigl (2\mp \sqrt{6}\frac{v-1}{\sqrt{v^2-3}}\Bigr ), \end{aligned}$$
(41)

which is singular at \(r=0\) (\(v=\sqrt{3}\)). Also we can see that \(R>0\) for the DGB branch and it converges to \(12/r_c^2\), while we have \(R<0\) for the RS branch and it goes to zero at infinity. A non-vanishing curvature outside the source leads usually to a screening mechanism and we have shown previously the absence of the vDVZ discontinuity. On the physical stability of the solutions, it is interesting to study the violation of the energy conditions if we consider the tensor \(K_{\mu \nu }-Kh_{\mu \nu }\) as a source term, and the positivity of the gravitational mass of this spacetime. These particular problems should be addressed separately.

5 Stability

In order to study the linear stability of this solution, we use the Regge–Wheeler formalism [16, 18] and we decompose the metric perturbations according to their transformation properties under two-dimensional rotations. They are classified as odd (or axial) and even (or polar) perturbations.

5.1 Odd perturbations

In this section, we consider the odd perturbations. For that we assume an infinitesimal perturbation \(\epsilon _{\mu \nu }\) of the background metric \(\bar{h}_{\mu \nu }\) in the form \(h_{\mu \nu }=\bar{h}_{\mu \nu }+\epsilon _{\mu \nu }\). Each perturbation component can be decomposed into spherical harmonics and also we can remove some of the perturbations by a change of coordinates. We will assume the Regge–Wheeler gauge [16]. Finally, because of the symmetries of the background, we can always fix the azimuthal number m to zero. For more details, see e.g. [17]. In conclusion, odd-mode perturbations can be written as

$$\begin{aligned} \epsilon _{\mu \nu }^\text {odd}= \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad h_0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad h_1\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ h_0 &{}\quad h_1 &{}\quad 0 &{}\quad 0\\ \end{pmatrix} \sin \theta P'_l(\cos \theta )\,, \end{aligned}$$
(42)

where \(P_l\) are Legendre polynomials and \((h_0,h_1)\) are functions of (t, r).

Using Eqs. (14) and ( 15), we obtain

$$\begin{aligned}&G_{\mu \nu }+r_c^2 S_{\mu \nu }=-E_{\mu \nu }, \end{aligned}$$
(43)
$$\begin{aligned}&S_{\mu \nu }=R_{\mu \sigma }R^\sigma _\nu +\frac{R^2}{4}h_{\mu \nu }-\frac{1}{2}R_{\rho \sigma }R^{\rho \sigma }h_{\mu \nu }-\frac{2}{3}RR_{\mu \nu }. \end{aligned}$$
(44)

Therefore, the perturbations are

$$\begin{aligned} \delta G_{\mu \nu }+r_c^2 \delta S_{\mu \nu }=-\delta E_{\mu \nu }. \end{aligned}$$
(45)

But unfortunately, because \(E_{\mu \nu }\) is a non-local term, we need to know the geometry and the perturbations of the bulk to determine it. Therefore, we will assume that there is no backreaction of the perturbations of the bulk on the brane.

From the equation \(\delta G_{2 3}+r_c^2\delta S_{2 3}=0\), we obtain

$$\begin{aligned} \dot{h}_0=A A' h_1+A^2h_1' \end{aligned}$$
(46)

where \((\dot{~} ~,~')\) are derivatives w.r.t. time and r, respectively. Using this equation in \(\delta G_{1 3}+r_c^2\delta S_{1 3}=0\) and the redefinition \(h_1=rQ(t,r)/A(r)\), we obtain

$$\begin{aligned}&\frac{\partial ^2 Q}{\partial t^2}-\frac{\partial ^2 Q}{\partial r^{*2}}+V_{RW} Q=0, \end{aligned}$$
(47)
$$\begin{aligned}&V_{RW}=A(r)\Bigl [\frac{l(l+1)}{r^2}-\frac{6m}{r^3}\pm \frac{H(r)}{r_c^2}\Bigr ]\,, \end{aligned}$$
(48)
$$\begin{aligned}&H=6f(r)+\frac{3}{2}r f'(r)-\frac{6\Bigl (3+(3f+rf')^2\Bigr )}{12f+8rf'+r^2f''}, \end{aligned}$$
(49)

where \(\text {d}r^*=\text {d}r/A\), the tortoise coordinate.

From the form of the effective potential, see Fig. 2, we can conclude to the stability of odd perturbations because the potential is always positive.

Fig. 2
figure 2

Effective potential for odd perturbations in DGP branch (upper graph) and RS branch (lower graph). \(R_H\) represents the position of the event horizon and \(R_C\) the cosmological horizon. We see that both branches have always a positive effective potential

Full size image

5.2 Even perturbations

Following the same philosophy for even-parity perturbations in the so-called Zerilli gauge, we have

$$\begin{aligned} \epsilon _{\mu \nu }^\text {even}= \begin{pmatrix} A(r)H_0 &{} H_1 &{} 0 &{} 0\\ H_1 &{} \frac{H_2}{A(r)} &{} 0 &{} 0\\ 0 &{} 0 &{} r^2K &{} 0\\ 0 &{} 0 &{} 0 &{} r^2\sin ^2\theta K\\ \end{pmatrix} P_l(\cos \theta ) \end{aligned}$$
(50)

where \((H_0,H_1,H_2,K)\) are functions of (t, r). First, it is easy to find \(H_0=H_2\), then we can find an algebraic equation between \((H_0,H_1,K)\) that we can use to eliminate \(H_0\). We are then left with two first order equations for the variables \((H_1,K)\). To diagonalize the equations, we need to define the change of variables

$$\begin{aligned} H_1(t,r)&= h(r) R(t,r)+ k(r) S(t,r)\nonumber \\ K(t,r)&= f(r) R(t,r)+ g(r) S(t,r) \end{aligned}$$
(51)

where (h, k, f, g) are free functions defined in such a way that we end with

$$\begin{aligned} \frac{\partial R}{\partial r^*}&= S, \end{aligned}$$
(52)
$$\begin{aligned} \frac{\partial S}{\partial r^*}&= (V_Z+\frac{\partial ^2}{\partial t^2})R, \end{aligned}$$
(53)

which gives

$$\begin{aligned} \frac{\partial ^2 R}{\partial t^2}-\frac{\partial ^2 R}{\partial r^{*2}}+V_Z R=0 \end{aligned}$$
(54)

where \(V_Z\) has the same form as in general relativity. Very surprisingly, all the terms \(r_c\) which indicate the modification to general relativity cancel;

$$\begin{aligned} V_Z&=\frac{A\Bigl [2\lambda ^2(1+\lambda )r^3+a_1 \lambda ^2+a_2 \lambda +a_3\Bigr ]}{r^3\Bigl (\lambda r+\frac{r^2}{2}A'-rA+1\Bigr )^2}, \end{aligned}$$
(55)
$$\begin{aligned} a_1&=\frac{r^3}{2}\Bigl (r^2A''+2rA'-6A+6\Bigr ), \end{aligned}$$
(56)
$$\begin{aligned} a_2&=-\,\frac{r^3}{4}\Bigl [r^3 A A'''+r^2 A A''-4 r^2 A''-2 r^2 A'^2+6 r A A'\nonumber \\&\quad -8 r A'-6 A^2+22 A-16\Bigr ], \end{aligned}$$
(57)
$$\begin{aligned} a_3&=-\,\frac{r^3}{16}\Bigl [-4 r^3 A^2 A'''+4 r^3 A A'''-3 r^4 A A''^2-4 r^2 A^2 A''\nonumber \\&\quad +12 r^2 A A''-8 r^2 A''-4 r^3 A'^3+8 r^2 A A'^2-12 r^2A'^2\nonumber \\&\quad -8 r A^2 A'+24 r A A'-16 r A'+2 r^4 A A''' A'+2 r^4 A'^2 A''\nonumber \\&\quad +4 r^3 A A' A''+4 A^3-24 A^2+36 A-16\Bigr ]. \end{aligned}$$
(58)

The graph of the Zerilli potential is similar to the Regge–Wheeler potential for the same parameters. Therefore we can conclude to the stability of both perturbations.

The positivity of the potential indicates the stability of the spacetime under linear perturbations [19] for the two branches. It is important to notice that we did not consider the source term in order to study the stability of the theory. In this case, the source term is much more complicated than in general relativity. In fact it is not localized, the source is a function of the electric part of the Weyl tensor which is a non-local term.

6 Conclusion

In conclusion, we have derived an exact black hole solution on the brane for the DGP model. This solution recovers the standard results at small and large distances but also covers the intermediate regime which was not known. The two branches depend on three parameters, the mass of the black hole, the tidal charge and the cross scale parameter. We have shown than if we do not consider the perturbations of the bulk (the source term), the solutions are stable under linear perturbations. But as is well known, the DGP branch has a ghost which looks inconsistent with this result. The first possibility which might explain the result is that we have a ghost (negative kinetic term) or laplacian instability which can be derived from the action which exists even if the black hole is stable. But it seems very unfortunate to reach a spacetime with a ghost being stable. See for example [20] for how to study the presence of a ghost. The second possibility might be that the instability comes from the bulk and not from the brane. This means that we would need to incorporate the perturbations of the bulk term \((\delta E_{\mu \nu })\) to see the instability. This is a difficult task because we do not have access to the bulk solution but it could be found numerically by integrating the equations from ADM formalism where the solution on the brane will be our initial condition, our Cauchy surface.