1 Introduction

The idea of the astrophysical object namely a Black hole, has been conceived long back theoretically. The interest in black hole grew only after the advent of the theory of general relativity (GR) by Einstein. In 1916, Schwarzschild first obtained the exact vacuum solution of Einstein’s field equation in GR, which is a static black hole solution. The Schwarzschild static black hole solution is simple and the Weyl tensor calculated with the Schwarzschild spacetime is identical to the Riemann tensor i.e., \( C_{\mu \nu \gamma \delta }= R_{\mu \nu \gamma \delta } \) because both the Ricci tensor and Ricci scalar vanishes. Consequently, one obtains \(C_{\mu \nu \gamma \delta } C^{\mu \nu \gamma \delta }= R_{\mu \nu \gamma \delta } R^{\mu \nu \gamma \delta }= \frac{48\,G^2\,M^2}{c^4 r^6}\) (where M is the mass of a Schwarzschild black hole) [1, 2]. The curvature becomes infinite at the origin \(r=0\), indicating the existence of a singularity. The Schwarzschild metric cannot be extended smoothly because the Kretschmann scalar invariant \((R_{\mu \nu \gamma \delta } R^{\mu \nu \gamma \delta })\) involves second derivatives of the metric and the spacetime is no longer well-defined. The presence of the central singularity underlines the inadequacy of GR as a theory of spacetime below some length scale.

The discovery of gravitational waves in 2015 by LIGO and VIRGO collaborations [3,4,5,6,7,8] made it clear that the detected gravitational waves were produced from the coalescence of two massive black holes. The first image of a black hole discovered by the Event Horizon Telescope (EHT) collaboration in 2019 pointed out that a black hole exists in nature. It is now generally accepted that supermassive black holes exist. The discovery of the supermassive black hole at the center of the M87 galaxy led to a spurt in activities to investigate compact objects, particularly black holes (BHs) in the framework of GR and beyond GR. BH is the final stage of a massive collapsing star, and the study of BHs is an active field of research in relativistic astrophysics many decades [9]. The geometric approaches developed to analyze black holes, the presence of their singularity, in the relativistic solutions, and their extreme density because of high compactness provided a good natural laboratory for testing theories of quantum gravity. In general, it is known that there is a scope for modification in the gravitational or matter sector in Einstein’s field equation, leading to modification of the Friedmann equation. While the modified gravity sector is considered with a linear combination of scalar curvatures, the geometrical modifications are usually expressed as an effective modification in the matter sector, namely, f(R), f(R, T), f(Q), etc., which reflects back into the Einstein’s field equation with effective energy density and pressure. A modification of the matter sector does not modify the gravity, instead, it adds new contributions of matter-energy within the GR. Many alternative theories of gravity have come up in recent times to avoid the singularity problem of the standard Big Bang model that exists in GR, proposing emergent universe [10,11,12,13,14,15,16,17,18,19,20] and bouncing [21,22,23,24,25,26,27,28,29,30,31,32,33] universes.

In GR, it is known that any singularity occurring at the event horizon can be removed by a coordinate transformation [34,35,36], but the singularity at the centre of the black hole is a curvature singularity which cannot be removed by a coordinate transformation [37, 38]. The idea of regular black hole (singularity-free) solution originated in mid-sixties with Sakharov’s proposal to begin with a vacuum equation of state (\(p=-\rho \)) at very high densities [39]. Sakharov [39] and Gliner [40] demonstrated that the essential singularity would not occur when the vacuum is replaced by a vacuum like medium described by a de Sitter metric. In relativistic astrophysics, the first regular black hole (RBH) (i.e., non-singular black hole) having an event horizon was obtained by Bardeen [41]. RBH in GR is constructed by modifying the mass of Schwarzschild BHs with a r-dependent function. Subsequently, a number of black hole solutions in four dimensions have been obtained [42,43,44,45,46,47,48,49]. Ay\(o'\)n-Beato and Garcia [50] interpreted the Bardeen BH in the framework of field theory with a magnetic monopole as a source in the non-linear electrodynamics. In the literature [51,52,53,54,55], the above approach has been extended to describe the RBH with spherical symmetry.

In 1999, Randall and Sundrum (RS) proposed their first brane-world model [56] (RS-1) consisting of a positive and a negative brane tension to resolve the hierarchy problem in particle physics. In the proposed brane world scenario, we live on a (3+1) dimensional hypersurface embedded in a higher dimensional spacetime called bulk. The observed forces and particles in particle physics are confined on the (3+1) dimensional brane while gravity propagates freely in the bulk. Subsequently, Randall and Sundrum proposed another model [57] (RS-2) by sending the negative tension brane to infinity. In the RS-2 model, the Newtonian gravity can be recovered at a low energy limit.The single brane RS-2 scenario is extremely useful for addressing cosmological issues and probing astrophysical objects. The motivation of the paper is to investigate non-singular black holes in the RS-2 brane world gravity [57] framework inspired by non-commutative geometry which are known as “Gaussian black holes” (GBH). In the paper, we obtain GBH solutions in the RS-2 brane-world and investigate the shadow of the GBH.

The paper is organized as follows: in Sect. 2, mathematical formalism and modified field equations in brane world gravity are presented. In Sect. 3, Gaussian Black hole (GBH) Solutions are obtained, and different features of GBH are discussed. The cosmological constant \(\Lambda \) to get de Sitter inner core of GBH is determined. In Sect. 4, we present an analytical setup of the GBH solution to investigate the shadow of the black hole. The effective potential and the shadow behaviour of the black holes are analyzed in Sect. 5. Finally we briefly describe the new results in Sect. 6.

2 Mathematical formalism and modified field equation

We consider the modified Einstein’s field equation (EFE) on the RS-2 [57] three brane is given by

$$\begin{aligned} G_{\alpha \beta } = \kappa ^2 \, T^{eff}_{\alpha \beta } \end{aligned}$$
(1)

where \(\kappa ^2=8 \pi G\), G is Newton’s gravitational constant, \(\alpha \), and \( \beta \) are four dimensional indices, and the effective energy-momentum tensor is

$$\begin{aligned} T^{eff}_{\alpha \beta } = T_{\alpha \beta } + \frac{6}{\lambda } S_{\alpha \beta } - \frac{1}{\kappa ^2} {{\mathcal {E}}_{\alpha \beta }} \end{aligned}$$
(2)

where \(T_{\alpha \beta }\) is the energy momentum tensor for the isotropic fluid on the brane and \(\lambda \) is the brane tension, which corresponds to the vacuum energy density on the brane. The bulk corrections at a very high energy scale [58, 59] led to nonlocal quadratic terms in the energy momentum tensor (\(S_{\alpha \beta } \)) and the projection of the Weyl tensor on the brane (\({\mathcal {E}}_{\alpha \beta } \)) in eq. (2), are given by

$$\begin{aligned}{} & {} S_{\alpha \beta }=\frac{1}{12} T_{\alpha \beta } \,T - \frac{1}{4} T_{ \alpha \delta } T^{\delta }_{\beta }+\frac{1}{24} \; g_{\alpha \beta } \;(3 T_{\gamma \delta } T^{\gamma \delta } -T^2), \nonumber \\ \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {\mathcal {E}}_{\alpha \beta }= - \frac{6}{\kappa ^2 \lambda } \left[ U u_{\alpha } u_{\beta } + P r_{\alpha } r_{\beta } + \frac{1}{3} h_{\alpha \beta } (U-P) \right] , \end{aligned}$$
(4)

where T is the trace of the energy-momentum tensor, \(\rho \) and p are energy density and pressure, \(u_{\alpha }\) is the 4-velocity and \(r_{\alpha }\) is a unit radial vector on the brane, U and P are the nonlocal energy dark density and nonlocal pressure on the brane of the 5-dimensional embedding space and the tensor \({\mathcal {E}}_{\alpha \beta }\) is traceless. It is evident that \({\mathcal {E}}_{\alpha \beta } \rightarrow 0\) for the limiting condition the inverse of brane tension \(\frac{1}{\lambda } \rightarrow 0\). Consequently, at this limit, \(T_{\alpha \beta }^{eff}= T_{\alpha \beta }\), therefore, one recovers the standard 4D general relativity. The equation of state (EoS) for U and P is \(P=\omega U\), and the EoS parameter lies in the range \(-3<\omega <2\) [59]. The stress-energy tensor on the brane is

$$\begin{aligned} T_{\alpha \beta }= \rho \; u_{\alpha } u_{\beta } + p \;h_{\alpha \beta }, \end{aligned}$$
(5)

where \(h_{\alpha \beta }= g_{\alpha \beta } +u_{\alpha } u_{\beta } \) is the projection of the 5-dimensional metric on the brane and \(U=A \rho +C\) where A and C are constant model parameters. However, the conservation equation can be written as

$$\begin{aligned} \frac{dp}{dr} = - \frac{1}{2} \frac{d\nu }{dr} ( \rho + p ). \end{aligned}$$
(6)

We consider a static, spherically symmetric line element on the brane as

$$\begin{aligned} ds^{2}= - e^{\nu (r)} dt^{2} + e^{\mu (r)} \;dr^{2} + r^2 (d\theta ^2 + sin^2 \theta \; d\phi ^2) \end{aligned}$$
(7)

where \(\mu (r)\) and \(\nu (r)\) are the metric potential. Using the above metric given by Eq. (7) in Eq. (1) the components of the modified Einstein field equations [50, 60, 61] yields

$$\begin{aligned} e^{-\mu } \left( \frac{\mu '}{r} - \frac{1}{r^2} \right) + \frac{1}{r^2} = \kappa ^2 \rho ^{eff}. \end{aligned}$$
(8)
$$\begin{aligned} e^{-\mu } \left( \frac{\nu '}{r} +\frac{1}{r^2}\right) - \frac{1}{r^2} = \kappa ^2 p_r^{eff} \end{aligned}$$
(9)
$$\begin{aligned} e^{-\mu } \left( \frac{ \nu '' }{2} - \frac{\mu ' \nu '}{4} + \frac{\nu '^2}{4} + \frac{\nu '-\mu '}{2r} \right) = \kappa ^2 p_t^{eff}. \end{aligned}$$
(10)

The effective energy density, radial pressures and transverse pressure are given by

$$\begin{aligned}{} & {} \rho ^{eff}= \rho (r) \left( 1+\frac{1}{2\lambda } \rho (r) \right) + \frac{6U}{ \kappa ^4 \lambda }, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} p_r^{eff}= p(r) + \frac{1}{\lambda } \rho (r) \left( p(r) + \frac{1}{2} \rho (r) \right) + \frac{2U}{ \kappa ^4 \lambda } + \frac{4P}{ \kappa ^4 \lambda }, \nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned}{} & {} p_t^{eff}= p(r) + \frac{1}{\lambda } \rho (r) \left( p(r) + \frac{1}{2} \rho (r) \right) + \frac{2U}{ \kappa ^4 \lambda } - \frac{2P}{ \kappa ^4 \lambda }\nonumber \\ \end{aligned}$$
(13)

where \(()'\) represents derivative w.r.t. r. The effective radial pressure and the transverse pressure are not same, it leads to pressure anisotropy. From Eqs. (11) and (12) we obtain

$$\begin{aligned} \rho ^{eff} + p_r^{eff}= (\rho +p(r) ) \left( 1+ \frac{\rho }{\lambda } \right) +\frac{4}{ \kappa ^4 \lambda } (P+2U). \nonumber \\ \end{aligned}$$
(14)

The radial null vector \(l^{\alpha }\) is selected as \(l^0= e^{\alpha /2} \), \(l^{r}= \pm e^{\beta /2} \) and \(l^i= 0 \) (i represents other spatial coordinates index). We determine \(R_{\alpha \beta } l^{\alpha }l^{\beta }= e^{\alpha }R_{00} +e^{\beta } R_{rr}= \frac{(e^{\mu +\nu })'}{ e^{\mu +\nu }}\) which vanishes when

$$\begin{aligned} \mu (r)+\nu (r) = g(t) \end{aligned}$$
(15)

The Schwarzschild metric property can be recovered by rescaling the time coordinate given by Eq. (15), and for simplicity it really makes earlier considerations

$$\begin{aligned} \mu (r)+ \nu (r)=0. \end{aligned}$$
(16)

The above equation yields BH solution with an effective energy density and radial pressure that satisfies: \(\rho ^{eff}+p_r^{eff}=0\) which yields

$$\begin{aligned} (\rho +p) \left( 1+ \frac{\rho }{\lambda } \right) +\frac{4}{ \kappa ^4 \lambda } (P+2U)=0. \end{aligned}$$
(17)

Considering the equation of state \(P=\omega \; U\) and using \(U=A \rho +C\), one obtains

$$\begin{aligned} \frac{p}{\rho } = -1 - \frac{4(A\rho +C) (\omega +2)}{ \kappa ^4 \rho (\rho + \lambda )}. \end{aligned}$$
(18)

Therefore it is evident from the Eq. (18) that the vacuum configuration \(\rho +p=0\) is possible when

$$\begin{aligned} (\omega +2) (A\rho +C)=0 \end{aligned}$$
(19)

unless \(\lambda \rightarrow \infty \). Thus we obtain the following: Case I: \(\omega = -2\) and Case II: \(U=0\) which will be discussed in the next section.

3 Gaussian black hole solutions and different features

For simplicity we define

$$\begin{aligned} f(r) = e^{- \mu (r)} \end{aligned}$$
(20)

in Eqs. (12)–(13) and the components of the energy momentum tensors can be expressed as

$$\begin{aligned} \kappa ^2 p_r^{eff} = - \kappa ^2 \rho ^{eff} = f(r) \left( \frac{1}{r^2} + \frac{f'}{rf(r)} \right) - \frac{1}{r^2} \end{aligned}$$
(21)
$$\begin{aligned} \kappa ^2 p_t^{eff} = \frac{f(r)}{2}\left[ \frac{f''}{f(r)} + \frac{2 f'}{rf(r)} \right] \end{aligned}$$
(22)

Black hole solutions are permitted when the components of the energy momentum tensor follow

$$\begin{aligned} T^0_0=T^r_r, \; \; \; and \;\;\; T^{\theta }_{\theta } = T^{\phi }_{\phi }. \end{aligned}$$
(23)

We consider the distribution of matter density by a Gaussian source [62, 63] in the next para.

The mass of a black hole in a spherically symmetric spacetime is

$$\begin{aligned} M = 4\pi \int _0^{\infty } r^2 \rho (r) dr. \end{aligned}$$
(24)

The density profile \(T^t_t=-\rho \), is exponentially decreasing from a constant value which is given by

$$\begin{aligned} \rho =-T^t_t=\frac{M}{(4\pi l_0^2)^{3/2}}\; e^{- \frac{r^2}{4 l_o^2}} \end{aligned}$$
(25)

where \(l_0\) represents the Gaussian distribution free parameter and M represents the total mass per unit energy of a Gaussian black hole. Nicolini et al. [62, 63] first conceived the idea of a Gaussian black hole employing the parameter \(\theta \) that characterize the coordinate of non-commutativity. In the paper, we use a length scale-free parameter \(l_0\) related to the non-commutative parameter \(\theta \) as was used in Ref. [64].

The fluid satisfies the equation of state as follows

$$\begin{aligned} p= - \rho \end{aligned}$$
(26)

which at a short distance reproduces the “vacuum” state equation i.e., at \(r=0\) as \(\rho (0)= -p(0)\) but finite, and emanates from the condition that the effective radial pressure and density also follow: \(p_r^{eff} = - \rho ^{eff}\). The following cases are obtained:

Case I: The effective tangential pressure is given by

$$\begin{aligned} p_t^{eff}= \rho \left[ \frac{2}{\kappa ^4 \lambda }(1-\omega ) A -1 -\frac{1}{2} \rho \right] , \end{aligned}$$
(27)

for \(U= A \rho \) and \(C=0\). We note the following

$$\begin{aligned}{} & {} (i) \; p_t^{eff} \ge 0 \;\; for \; \rho< \frac{4}{\kappa ^4 \lambda } (1-\omega ) A -2 \nonumber \\{} & {} (ii) \; p_t^{eff}< 0 \;\;\ for \; \rho < \frac{4}{\kappa ^4 \lambda } (1-\omega ) A -2. \end{aligned}$$
(28)

Case II: \(P=U=0\) leads to the transverse effective pressure given by

$$\begin{aligned} p_t^{eff}= - \rho \left[ 1+ \frac{1}{2} \rho \right] , \end{aligned}$$
(29)

which is negative.

We consider here the first case with \(U\ne 0\). The effective tangential pressure is anisotropic in the brane world scenario, but as \(\lambda \rightarrow \infty \), we get isotropic effective pressure as \( p_t^{eff} = - \rho \) and \(p_r^{eff}= -\rho \). On integrating Eq. (11) once using Eqs. (21) and (25) we obtain

$$\begin{aligned} f(r)= & {} 1 - \frac{B_o}{r}- \frac{\kappa ^2 M}{ 2\pi ^{3/2} \; r} \left[ \left( 1+ \frac{6A}{\kappa ^4 \lambda } \right) \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2} \right) \right. \nonumber \\{} & {} \left. + \frac{ \sqrt{2}M}{64 \pi ^{3/2} l_0^3 \lambda } \; \gamma \left( \frac{3}{2}, \frac{r^2}{2l_0^2} \right) \right] \end{aligned}$$
(30)

where \(B_o\) is an integration constant and the lower incomplete \(\gamma \) function is \(\gamma (s,x) = \int _0^{x} t^{s-1} e^{-t} dt \). The metric potential \(f(r) \rightarrow 1\) as \(r\rightarrow \infty \). For point like source we set \(B_o=0\), thus the metric function becomes

$$\begin{aligned} f(r)= & {} 1 - \frac{\kappa ^2 M}{ 2\pi ^{3/2} \; r} \left[ \left( 1+ \frac{6A}{\kappa ^4 \lambda } \right) \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2} \right) \right. \nonumber \\{} & {} \left. + \frac{ \sqrt{2}M}{64 \pi ^{3/2} l_0^3 \lambda } \; \gamma \left( \frac{3}{2}, \frac{r^2}{2l_0^2} \right) \right] \end{aligned}$$
(31)

The BH solution in the brane-world scenario is represented by the metric potential asymptotically approaches the Schwarzschild BH solution because the incomplete Gamma function at infinity attains the value: \(\gamma (\frac{3}{2}, \frac{r^2}{4l_0^2}) \rightarrow \sqrt{\frac{\pi }{2}} \). The metric potential f(r) is a function of the following model parameters, namely, (i) the brane tension (\(\lambda \)), (ii) the non-commutative length (\(l_0\)), (iii) the equation of state parameter of the bulk (A) and (iv) mass of the black hole (M). In Fig. 1, we plot the variation of f(r) with \(\frac{r}{2l_0}\) for different masses, for a given set of \(l_0\), \(\lambda \) and A and found the following: (i) two horizons exist and they correspond to an extremal black hole for \(M>M_{r_H}=1.5\), (ii) degenerate horizons for \(M=1.15 \), and (iii) for \(M< 1.15\), there is no horizon. The radial variation of f(r) plotted in Fig. 2 with different non-commutative parameters \(l_0\) for a set of model parameter, and no variation is observed. The radial variations of f(r) drawn in Fig. 3 with different A for a given set of parameters, \(l_0\), mass (M) and \(\lambda \), show that as A increases, the depth of the minimum in f(r) increases. It is also evident that the differences between the two zeros of \(g^{tt} \) also increases.

Fig. 1
figure 1

Radial variation of f(r) with masses \(M=1\) (red), 1.15 (blue), 2 (dashed) and 2.5 (green) taking \(l_0=10\), \(\lambda =100\) and \(A=1\)

Full size image
Fig. 2
figure 2

Radial variation of f(r) with \(l_0= 1\), 10,100 for \(M=2\), \(\lambda =1\) and \(A=1\)

Full size image
Fig. 3
figure 3

Radial variation of f(r) with \(A=-1 \) (green), 0 (blue), 10 (red), 18 (dashed) for \(M=2\), \(\lambda =1\) and \(l_0=1\)

Full size image
Fig. 4
figure 4

Radial variation of effective transverse pressure \(p^{eff}_t\) in the unit of \(l_0^2\) with \(A=-1, \; l_0=0.05 \) for the following cases of \(\frac{M}{2l_o} \) and \( \lambda \) (i) 100 and 0.01 (dashed) (ii) 50 and 0.01 (blue) (iii) 1 and 0.001 (cyan) (iv) 10 and 0.001 (red)

Full size image

The variation of the transverse pressure plotted in Fig. 4 for massive BH with different brane tension and mass of GBH. It is noted that as the brane tension negative but for lower brane tension it is positive. Thus the strong energy condition for the fluid for higher brane tension and lower mass transverse pressure is negative, but it is positive with larger brane tension and massive GBH. It is found that \(SEC = \rho ^{eff}+p_r^{eff} + 2 p_t^{eff}\) is negative in the latter case, which requires exotic matter, but in the former case, the effect of bulk on the transverse effective pressure of the fluid indicates the presence of normal matter. However, in the absence of the effect of brane world gravity, the effective transverse pressure is always found negative.

We obtain here the noncommutative geometry inspired Schwarzschild black hole in brane world and the metric potential is given by

$$\begin{aligned} f(r)= 1 - \frac{\kappa ^2 M}{ 4\pi \; r} \left[ \left( 1+ \frac{6A}{\kappa ^4 \lambda } \right) + \frac{ \sqrt{2}M}{64 \pi ^{3/2} l_0^3 \lambda } \right] \end{aligned}$$
(32)

The following are the properties of the matter density \(\rho \) in the framework of brane world gravity:

  1. 1.

    Near the origin, \( i.e., r< l_0\), \(\frac{d\rho }{dr} \simeq 0 \rightarrow \rho \simeq \rho (0)\).

  2. 2.

    Away from the origin for \( i.e., r> l_0\), \(\frac{d\rho }{dr} \simeq 0 \rightarrow \rho \simeq const. \ll \rho (0)\).

  3. 3.

    Asymptotically far away \( i.e., r \gg \frac{\kappa ^2\,M}{4 \pi } \Bigg ( \bigg (1+ \frac{6A}{\kappa ^4 \lambda } \bigg ) + \frac{ \sqrt{2} M}{ 64 \pi ^{3/2} l_0^3 \, \lambda } \Bigg )\), \(\rho \rightarrow 0\).

The four dimensional GR counter part of the Schwarzschild solution in non-commutative geometry on the brane is obtained for the limiting case \(\lambda \rightarrow \infty \). The Eq. (31) yields

$$\begin{aligned} f(r)=1- \frac{4 M}{r \sqrt{\pi } } \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2}\right) , \end{aligned}$$
(33)

where we substitute \(\kappa ^2= 8 \pi \) in the gravitational unit \(G=1\). It reduces to the Schwarzschild solution in GR i.e., for a commutative geometry \(f(r) = 1- \frac{2M}{r}\) as \( \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2}\right) \rightarrow \Gamma ( \frac{3}{2})\). In Eq. (32), the extra term is a particular feature of the Gaussian density profile for a Gaussian Black hole in Brane scenario, which further reduces to that in GR given by Eq. (33). The event horizon radius is determined from the vanishing of the \(g_{tt}\), which yields

$$\begin{aligned} r_H= & {} 2M \left[ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{2}{\sqrt{\pi }} \gamma \left( \frac{3}{2}, \frac{r_{H}^2}{4l_0^2} \right) \right. \nonumber \\{} & {} \left. + \frac{M}{16\sqrt{2} \pi ^{2} l_0^3 \lambda } \gamma \left( \frac{3}{2}, \frac{r^2_H}{2l_0^2} \right) \right] . \end{aligned}$$
(34)

The event horizon [65] expressed in terms of the upper incomplete gamma function becomes

$$\begin{aligned} r_H= & {} 2M \left[ 1+ \frac{3A}{32 \pi ^2 \lambda } \right] \nonumber \\{} & {} - 2 M \left[ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{2}{\sqrt{\pi }} \Gamma \left( \frac{3}{2}, \frac{r_{H}^2}{4l_0^2} \right) \right. \nonumber \\{} & {} \left. - \frac{M}{16 \sqrt{2} \pi ^2 l_0^3 \lambda } \gamma \left( \frac{3}{2}, \frac{r_{H}^2}{2 l_0^2} \right) \right] \end{aligned}$$
(35)

The first term is the Schwarzschild solution obtained in the brane world gravity and the second term is the non-commutative corrections that originated here. In the ”large radius” regime \(\frac{r_H^2}{4l_0^2} \gg 1\), it can be solved by iteration method. The first order in \(\left( \frac{M}{l_0}\right) \) is given by

$$\begin{aligned} r_H&=2 M_{SB} \left[ 1- \frac{M}{\sqrt{\pi } l_0^2} e^{- \frac{M^2}{l_0^2} }\right] \nonumber \\&\quad + 2M_{*} \left( 1- \frac{M}{\sqrt{\pi } l_0^2} e^{-\frac{2M^2}{l_0^2} } \right) \end{aligned}$$
(36)

where \(M_{*}=M^2 \frac{1}{16 \sqrt{2} \pi ^2 l_0^3 \lambda } \gamma \left( \frac{3}{2}, \frac{r_{H}^2}{2 l_0^2} \right) \) and the the Schwarz schild mass becomes, \(M_{SB}= 2\,M\left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \). However, as \(\lambda \rightarrow \infty \) one recovers GR limiting value of the mass: \(M_{SB}=M\).

3.1 de Sitter core

In this section, we discuss de Sitter geometry near the origin of the GBH solution Eq. (31). As the non-commutative property does not allow us to reach the centre \(r=0\), we use the incomplete gamma function for a short distance (as permitted in theory determined by the length scale \(l_0\)) which is

$$\begin{aligned} \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2}\right) = \frac{r^3}{12l_0^3} - \frac{r^5}{80 l_0^5} \;... \;... \end{aligned}$$
(37)

using the above expansion in Eq. (31), we get

$$\begin{aligned} f(r)= 1- M (\alpha +\beta M) r^2 + O(r^4) \end{aligned}$$
(38)

where \(\alpha = \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{1}{3\sqrt{\pi } l_0}\), \(\beta =\frac{1}{16 \pi ^2l_0^6 \lambda }\). The Ricci scalar becomes

$$\begin{aligned} R=12 M (\alpha +\beta M) \end{aligned}$$

which is non-zero at the centre that can be used to describe a BH without singularity. Consequently, one obtains the de Sitter line element characterised by an effective cosmological constant, which is given by

$$\begin{aligned} \Lambda = 3 M \left[ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{1}{3\sqrt{\pi } l_0} + \frac{M}{16 \pi ^2l_0^6 \lambda } \right] \end{aligned}$$
(39)

and the equivalent Ricci scalar in GR is a finite constant quantity \(R= 4 \Lambda \) in de Sitter spacetime.

The effect of non-commutativity exponentially decreases at a short distance \(r_H l_0<<1\), and for this, the quantum effect is important. The Eq. (35) is used to determine the mass of a compact object, which is given by

$$\begin{aligned} M= \frac{ \sqrt{\pi } r_ H}{ 2\left[ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \left( \frac{r_H^3}{12 l_0^3} - \frac{r_H^5}{80 l_0^5 }\right) + \frac{M}{32 \sqrt{2} \pi ^{3/2} l_0^3 \lambda } \left( \frac{r_H^3}{3\sqrt{2} l_0^3} - \frac{r_H^5}{10 \sqrt{2} l_0^5} \right) \right] }. \end{aligned}$$
(40)

The corresponding GBH mass given by Eq. (40) in the limiting case is defined as

$$\begin{aligned} M_0= \lim _{r_H \rightarrow 2l_0} M \end{aligned}$$

consequently a quadratic equation in M is obtained as follows:

$$\begin{aligned} M_0 \left[ \frac{M_0}{120 \pi ^{3/2} l_0^3 \lambda } -\frac{8}{15} \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \right] = -2\sqrt{\pi } l_0. \end{aligned}$$

We note the following:

Case 1: for \(\frac{1}{\lambda } \rightarrow 0\), \(\;\;\;\;\;\; M_0=\frac{15 \sqrt{2} l_0}{4}\).

Case 2: for \(\lambda \rightarrow 0\), \(\;\;\;\;\; M_0=\frac{2 l_0^3}{\sqrt{\pi }} (3A+16 \pi ^2)\).

At a very high energy scale in the brane world framework, the mass of GBH will be more compared to that in GR when \(l_0^2 > \frac{15 \sqrt{2} \pi }{8(3A +16 \pi ^2)}\) and alternatively, the GBH mass will be less compared to that of GR when \(l_0^2 < \frac{15 \sqrt{2} \pi }{8(3A +16 \pi ^2)}\). Thus, the brane tension is playing a significant role for a massive GBH.

The black hole temperature or the Hawking temperature [65] is given by

$$\begin{aligned} T_H \equiv - \left( \frac{1}{4 \pi } \frac{dg_{tt}}{dr} \right) _{r=r_H}. \end{aligned}$$
(41)

Using Eqs. (31) and (34) in Eq. (41) we derive an expression for Hawking temperature which is

$$\begin{aligned} \hspace{-20.5pc}T_H= & {} - \left( \frac{1}{4 \pi } \frac{df(r)}{dr} \right) _{r=r_H} = \frac{1}{4\pi r_H} \left[ 1- \frac{r_H^3}{4l_0^3} \frac{ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{2}{\sqrt{\pi }} \;e^{- \frac{r_H^2}{4l_0^2}} + \frac{M}{8 \pi ^{2} \lambda } \;e^{- \frac{r_H^2}{2l_0^2}}}{\left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \frac{2}{\sqrt{\pi }} \; \gamma \left( \frac{3}{2}, \frac{r_{H}^2}{4l_0^2} \right) + \frac{M}{16 \sqrt{2} \pi ^{2} l_0^3 \lambda } \; \gamma \left( \frac{3}{2}, \frac{r_{H}^2}{2l_0^2} \right) }\right] . \end{aligned}$$
(42)

For low energy limit, \(\frac{1}{\lambda } \rightarrow 0\), it reduces to the four dimensional GR Hawking temperature for non-commutative inspired BH [63].

4 Analytical set up

The spacetime metric for the regular BH is given by

$$\begin{aligned} ds^{2}= - f(r) \; dt^{2} + f(r)^{-1} \; dr^{2}+ r^2 ( d\theta ^2+ \sin ^2 \theta \; d\phi ^2 ) \end{aligned}$$
(43)

where \( f(r)= 1 - \frac{\kappa ^2\,M}{ 2\pi ^{3/2} \; r} \Bigg [ \bigg (1+ \frac{6A}{\kappa ^4 \lambda }\bigg ) \gamma \bigg (\frac{3}{2}, \frac{r^2}{4l_0^2}\bigg ) + \frac{ \sqrt{2}M}{64 \pi ^{3/2} l_0^3 \lambda } \gamma \bigg (\frac{3}{2}, \frac{r^2}{2l_0^2}\bigg )\Bigg ]\). The Lagrangian for a free particle will be used to determine the radius of photon sphere which is

$$\begin{aligned} {\mathcal {L}} = \frac{1}{2} g_{\mu \nu } {\dot{x}}^{\mu } {\dot{x}}^{\nu }. \end{aligned}$$
(44)

where \(\dot{(}) = \frac{d}{d\tau }\) and \(\tau \) is the affine parameter. Expanding Eq. (44) we get

$$\begin{aligned} 2{\mathcal {L}} = -f(r) {\dot{t}}^2 + \frac{1}{f(r)}{\dot{r}}^{2} + ( r^2 {\dot{\theta }}^2 + \sin ^2 \theta {\dot{\phi }}^2 ) \end{aligned}$$
(45)

To obtain trajectory of the light path of the photon around the GBH, we consider \(\theta \) and \(\phi \) as free parameters, and set \(\theta =\frac{\pi }{2}\). The momenta are given by

$$\begin{aligned}{} & {} P_t= \frac{\partial {\mathcal {L}} }{\partial {\dot{t}}}= -f(r) {\dot{t}}, \; \; \; P_r= \frac{\partial {\mathcal {L}} }{\partial {\dot{r}}}= \frac{1}{f(r)} {\dot{r}}, \nonumber \\{} & {} P_{\theta } = \frac{\partial {\mathcal {L}} }{\partial {\dot{\theta }}}= r^2{\dot{\theta }}, \; \; P_{\phi }= \frac{\partial {\mathcal {L}} }{\partial {\dot{\phi }}}= r^2 \sin ^2 \theta {\dot{\phi }}. \end{aligned}$$
(46)

Now as defined above, \(\theta =\frac{\pi }{2}\), and at the equatorial plane, we get

$$\begin{aligned} \frac{\partial {\mathcal {L}} }{\partial {\dot{t}}}=constant, \end{aligned}$$
(47)

the energy (E) and angular momentum (J) at \(r\rightarrow \infty \) are obtained from

$$\begin{aligned} f(r) \; {\dot{t}}=E, \;\; P_{\phi }= r^2 {\dot{\phi }} = J. \end{aligned}$$
(48)

The Hamilton–Jacobi equation is the most general method to find the geodesic equation of motion of photon (photon orbit) around NSBH. In higher dimensions

$$\begin{aligned} \frac{\partial S}{\partial \tau } ={\mathcal {H}} = - \frac{1}{2} g^{\mu \nu } \frac{\partial S}{\partial x^{\mu }} \frac{\partial S}{\partial x^{\nu }} \end{aligned}$$
(49)

where \(g^{\mu \nu } \) is the inverse of the metric and S is the Jacobian given by

$$\begin{aligned} S= \frac{1}{2} m^2 \tau - E + J \phi +S_r(r) + S_{\phi } (\phi ) \end{aligned}$$
(50)

where \(S_r(r)\) and \(S_{\phi } (\phi )\) are functions of r and \(\phi \) and m is the mass of the test particle, it is zero for photon. The Hamilton–Jacobi Eq. (49) can be rewritten as

$$\begin{aligned}{} & {} r^4 f^2(r) \left( \frac{\partial S}{\partial \tau } \right) = E^2 r^4 -r^2 f(r) ({\mathcal {K}}+J^2) \end{aligned}$$
(51)
$$\begin{aligned}{} & {} \frac{1}{\sin ^2 \phi } \left( \frac{\partial S_{\phi }}{\partial \phi } \right) ^2 ={\mathcal {K}} - J^2 cot^2 \phi \end{aligned}$$
(52)

where \({\mathcal {K}}\) is the Carter constant [66] and f(r) is given in Eq. (31). Using the above Eq. (46) in Eq. (49) we get the following

$$\begin{aligned}{} & {} {\dot{t}} = \frac{ E}{f(r)}, \;\;\;\; {\dot{\phi }}= \frac{J}{r^2 \sin ^2 \phi }; \nonumber \\{} & {} r^2{\dot{r}} = \pm \sqrt{{\mathcal {R}}}, \; \; \; (r^2 \sin ^2 \phi ) \; {\dot{\phi }}= \pm \sqrt{\Theta _i } \end{aligned}$$
(53)

where “+” and “−” sign corresponds to motion of photon either in outgoing or, incoming radial direction. For the null curves the Eqs. (52) yields

$$\begin{aligned} {\mathcal {R}}(r)= E^2r^4 -r^2 f(r) \; ( {\mathcal {K}}^2 + J^2), \end{aligned}$$
(54)
$$\begin{aligned} \Theta (\phi ) = {\mathcal {K}} - J^2 \cot ^2 \phi . \end{aligned}$$
(55)

The characteristics of photons near the black hole can be defined by two impact parameters, which are functions of the constants E, J and \( {\mathcal {K}}\). For general orbit we define the impact parameters \(\xi = \frac{J}{E} \) and \(\eta = \frac{{\mathcal {K}}}{E^2}\). The photon captured by the gravitational field of the GBH will orbit around it. It forms a boundary of the GBH. The boundary of the shadow of a GBH can be estimated from the effective potential. The radial null geodesic from Eqs. (50) and (53) combined to obtain the following equation:

$$\begin{aligned} \left( \frac{dr}{d\tau } \right) ^2 + V_{eff}= 0, \end{aligned}$$
(56)

where \( V_{eff}\) is the effective potential. For the radial motion we obtain

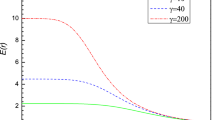
$$\begin{aligned} V_{eff}= & {} \frac{f(r)}{r^2} ( {\mathcal {K}}+ J^2) - E^2 \nonumber \\{} & {} = \left[ \frac{1}{r^2} - \frac{\kappa ^2 M}{ 2\pi ^{3/2} \; r^3} \left( \left( 1+ \frac{6A}{\kappa ^4 \lambda } \right) \gamma \left( \frac{3}{2}, \frac{r^2}{4l_0^2} \right) \right. \right. \nonumber \\{} & {} \left. \left. + \frac{ \sqrt{2}M}{64 \pi ^{3/2} l_0^3 \lambda } \; \gamma \left( \frac{3}{2}, \frac{r^2}{2l_0^2} \right) \right) \right] ( {\mathcal {K}}+ J^2) - E^2. \nonumber \\ \end{aligned}$$
(57)

The effective potential is identical to the classical equation describing the motion of a massless particle in a 1-dimensional potential V(r) with its energy \(\frac{1}{2} E^2\). The potential V(r) is a function of a set of physical quantities, namely, Mass (M), angular momentum (J), Carter constant \({\mathcal {K}}\), energy (E), brane tension (\(\lambda \)), A, and the noncommutative parameter (\(l_0\)). The radial variation of the potential V(r) in Fig. 5 is drawn for different masses of the BHs; the potential depth is found to increase with the increase in energy. The Fig. 6 is drawn for different energy for a given mass of BHs, the particles approaching the BH are trapped, and for less massive BH the particles will follow an unstable trajectory. However, it is evident from Fig. 7 that as the angular momentum (J) of the incoming particles increases, the particles will be trapped in the stable orbit for lower (J) and in the unstable circular orbits for higher J, around the black hole. It is evident that the separation between the two zeros of the potential is not altered for different angular momentum (J), but the minimum of the potential depth gradually increases with an increase in the angular momentum (J) i.e., for higher energy particles. There is a maximum of \(V_{eff}(r)\) for every value of the angular momentum, but the height of the maxima diminishes with the decrease in angular momentum (J). Thus orbits of the photons are different for different J. The particles are bounded for a radius \(r<r_{min}\) and unbounded in the range \(r_{min}<r<r_{max}\). The range of values can be determined from the sketch. It is found that \(r_{min}\) increases as the angular momentum (J) increases. The photons will fly away from the Gaussian BH and a lower bound on the angular momentum J exists, which originates a photon sphere around the BH. In the next paragraph, we analyze the shadow of a static Gaussian Black hole (assuming a very slow rotation of BH).

The photon orbits are circular and unstable for a maximum value of the effective potential. The unstable circular orbit determines the boundary of the apparent shape of the shadow. The maximal value of the effective potential corresponds to a circular orbit, and we note that an unstable photon satisfy

$$\begin{aligned} V_{eff}{\Big |}_{r=r_p}= \frac{dV_{eff}}{dr}{\Big |}_{r=r_p} = 0, \; \; \; {\mathcal {R}}(r)= \frac{d {\mathcal {R}}(r)}{dr}{\Big |}_{r=r_p}=0 \nonumber \\ \end{aligned}$$
(58)

Using Eqs. (57) and (58), we get

$$\begin{aligned}{} & {} \frac{f(r_p)}{r_p^2} ({\mathcal {K}} + J^2) - E^2 =0 \nonumber \\{} & {} \frac{r_p f'(r_p) -2 f(r_p)}{r_p^3} ({\mathcal {K}} + J^2) =0. \end{aligned}$$
(59)

The photon radius is obtained from

$$\begin{aligned} r_pf'(r_p)-2f(r_p)=0 \end{aligned}$$

which is

$$\begin{aligned} r_p= & {} 6 M \left[ \left( 1+ \frac{3A}{32 \pi ^2 \lambda } \right) \left( \sqrt{\pi }-\frac{M}{l_0^2} e^{- \frac{M}{l_0^2}} \right) \right. \nonumber \\{} & {} + \left. \frac{\sqrt{2} M}{64\pi ^2l_0^3 \lambda } \left( 1- \frac{M}{\sqrt{\pi }l_0^2 } e^{- \frac{M}{l_0^2}} \right) \right] \end{aligned}$$
(60)

obtained by iteration.

Fig. 5
figure 5

Radial variation of the effective potential for \(M = \)10 (red), 5 (blue), 2 (dashed) in the unit of in the unit of \(2l_0\)

Full size image
Fig. 6
figure 6

Radial variation of the effective potential for \(E^2\)= 1 (dashed), 2 (blue), 3 (red) for \(M= 10\) in the unit of \(2l_0\)

Full size image
Fig. 7
figure 7

Radial variation of the effective potential for J= 10 (dashed), 8 (blue), 5 (red), 4 (cyan) for \(M= 5\) in the unit of \(2l_0\)

Full size image

5 Effective potential and shadow behaviour of GBH

We define the impact parameters \(\eta \) and \(\xi \) that are functions of the energy E, angular momentum (J) and the Carter constant (\({\mathcal {K}}\)) respectively as

$$\begin{aligned} \xi = \frac{J}{E}, \; \; \; \; \eta = \frac{{\mathcal {K}}}{E^2}. \end{aligned}$$
(61)

Using Eq. (58) with \(\frac{V_{eff}}{E^2}=0 \) and \(\frac{{\mathcal {R}}}{E^2}=0 \), we get

$$\begin{aligned} \eta +\xi ^2=\frac{r_p^2}{f(r_p)}, \; \; \eta +\xi ^2=\frac{4r_p^2}{r f'(r_p)+ 2f(r_p)}. \end{aligned}$$
(62)

The above equations yield,

$$\begin{aligned} \eta +\xi ^2=\frac{5 r_p^2}{r_p f'(r_p)+ 3f(r_p)}, \end{aligned}$$
(63)

where the right hand side is also \(\frac{r_p^2}{f(r_p)}\), in the observer’s frame the shadow can be described properly making use of the celestial coordinates \(\alpha \) and \(\beta \) [67]. Following the definition introduced by Chandrasekhar [68] we get

$$\begin{aligned} \alpha = \lim _{r_p \rightarrow \infty } \left( \frac{ r_p P^{\phi }}{P^t}\right) , \;\; \beta _i= \lim _{r_p \rightarrow \infty } \left( \frac{ r_p P^{r}}{P^t} \right) . \end{aligned}$$
(64)

For an observer on the equatorial plane, these equations can be written as

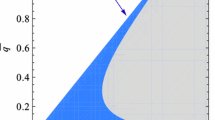
$$\begin{aligned} \eta +\xi ^2= \alpha ^2+\beta ^2= \frac{r_p^2}{f(r_p)} \end{aligned}$$
(65)

the radius of the shadow is \(R_{bhs}=\frac{r_p}{\sqrt{f(r_p)} }\). The form of f(r) is complex and therefore, we study numerically. Figure 7 shows that as the mass increases, the radius of the shadow also increases. However, the shadow of the photon orbit around the BGBH will be studied elsewhere with non negligible rotation.

Fig. 8
figure 8

Shadow of GBH with M= 3 and \(l_0\)= 0.1 (red), 5 (black), 0.5 (blue)

Full size image
Fig. 9
figure 9

Shadow of GBH with mass \(M=3\) with \(l_0\)= 0.1 (red), 4 (blue), 1.0 (green)

Full size image

We plot shadow of GBH with a given mass \(M=3 \; units\) for \(l_0=0.1 \) (red), 0.5 (blue), 5 (black) in Fig. 8, and \(l_0=\)0.1 (red), 4.0 (blue), 1.0 (green) in Fig. 9. It is evident that for \(l_0= 4 \; unit\) or greater the radii decreases.

6 Discussion

In the paper, we present a Gaussian black hole (GBH) in the framework of brane world gravity with a Gaussian distribution of the energy density. GBHs obtained here are regular spherical black holes inspired by non-commutative geometry. The radial variation of the GBH metric potential is found to depend on the model parameters, namely, E, J, \({\mathcal {K}}\), \(l_0\), A and \(\lambda \). We consider a given set of values of the model parameters to describe GBH with properties that are acceptable. We note from Figs. 1, 2 and 3, that there is a minimum mass of the GBH (say \(M_{r_H}\)) for a given set of model parameters below which BH does not exist, one event horizon exists for BH mass \(M=M_{r_H}\) (where \(M_{r_H}\) is the critical mass) and two event horizons exist for \(M> M_{r_H}\). The lower limit on the critical mass of GBH (\(M_{r_H}\)) is found to be determined by Brane world model parameters. For the interior fluid with isotropic pressure on the brane, it is evident that in the RS-2 brane scenario, the matter part of the modified Einstein field equation can be described by an effective anisotropic matter distribution. The effective energy density, radial pressure, and transverse pressure are determined, and we determine the condition for a black hole solution in the RS-2 brane model, which also satisfy, \(\rho ^{eff}+p_r^{eff} =0\). The above constraint that emerges in the brane world coincides with the vacuum condition of an isotropic fluid \(p= -\rho \) in GR. However, the effective transverse pressure in Brane world is different from the isotropic pressure (p) in GR. The effective transverse pressure \( p_{t}^{eff}\), for GBH in Fig. 4 shows that near the black hole \( p_t^{eff} \ne 0\). It is evident that for a massive GBH, the effective transverse pressure is negative (shown by blue and dashed curves) and for GBH with lower mass, the transverse effective pressure is positive (shown by cyan and red curves in Fig. (4)). The latter result for the effective transverse pressure obtained in Brane world scenario is new and interesting as it indicates existence of normal matter in GBH, this is not possible in GR. The event horizon is determined in Eq. (35). The de Sitter inner core of a GBH is determined near the centre of the GBH and the corresponding value of the cosmological constant. We determined the limiting black hole mass (\(M_0\)) for the following two cases: (i) \(\frac{1}{\lambda } \rightarrow 0 \) and (ii) \(\lambda \rightarrow 0 \) and found that at a very high energy scale, the limiting mass of GBH is more than that of the mass of the GBH at low energy. Thus a massive GBH is permitted in the Brane world scenario compared to that of a GBH in GR inspired by non-commutative geometry in a restrictive domain of the brane tension. We also determine the Hawking temperature of GBH and found the temperature is smaller than that of GR in a non-commutative inspired BH [63]. The non-commutative inspired BH in the brane world does not end up with a singularity at the end stage of the black hole evaporation.

We also studied the shadow of the GBH (with slow rotation) in detail. The effective potentials are drawn with the radial coordinates away from the centre of GBH and found that as the mass of GBH increases, the event horizon size diminishes (Fig. 5). The event horizon does not depend on the parameter \(E^2\) (Fig. 6), particles with negative energy can reach very near the GBH as evident from Figs. 5 and 6 for a set of model parameters. The radius of the photon sphere around the GBH is determined. Two distinct horizons are observed for different angular velocities (J) in Fig. 7; the horizon near the GBH is independent of J, but the horizon size at the farthest distance increases with the decrease of J. The trajectories of the particles having large spin values can be derived from Fig. 7. The photons from a source while grazing a GBH will be trapped and the photons orbit around the GBH with definite radii depending on its energy and angular velocity. There are stable and unstable orbits that produces the photon sphere around the GBH. The two dimensional diagram of the photon sphere is drawn in Fig. 8, it is found the radius of the sphere of photons will be more for a massive GBH. The existence of a massive GBH with no singularity inspired by non-commutative geometry is found in the Brane world scenario, and the mass of GBH depends on the brane tension. In the GBH, the energy density, the pressures are all finite at the centre with a finite mass determined by the brane tension (\(\lambda \)). GBH formed with a small brane tension is found to have a large mass, may be a superrmassive black hole can be accommodated here. Thus GBHs that are formed in the brane world gravity are exciting astrophysical objects as the current detection of gravitational waves supports such black holes. It is also interesting to investigate in other modified theories of gravity. The shadow of a black hole will be distorted in the presence of rotation of the GBH, which will be presented elsewhere.