Regge trajectories for heavy quarkonia from the quadratic form of the spinless Salpeter-type equation

Abstract

In this paper, we present one new form of the Regge trajectories for heavy quarkonia which is obtained from the quadratic form of the spinless Salpeter-type equation (QSSE) by employing the Bohr-Sommerfeld quantization approach. The obtained Regge trajectories take the parameterized form $M^2={\beta }({c_l}l+{\pi }n_r+c_0)^{2/3}+c_1$, which are different from the present Regge trajectories. Then we apply the obtained Regge trajectories to fit the spectra of charmonia and bottomonia. The fitted Regge trajectories are in good agreement with the experimental data and the theoretical predictions.

1 Introduction

The Regge theory [1, 2] is based on Lorentz invariance, unitary and analyticity of the scattering matrix and has nothing with quarks and gluons. Due to its generality, the Regge theory is still an indispensable tool in phenomenological studies. The Regge theory is concerned with almost all aspects of strong interactions. One of the most distinctive features of the Regge theory is the Regge trajectory which is one of the effective approaches for studying hadron spectra [3,4,5,6,7].

It is known that the Regge trajectories for the hadrons constituting of light quarks are approximately linear [8,9,10,11,12,13,14,15,16], that is, the mass M is related to the spin J and the principle quantum number n by

$$\begin{aligned} M^2={\alpha }J+{\beta }n+{\mathrm{const}}., \end{aligned}$$

(1)

where $\alpha$ and $\beta$ are the Regge slopes which are almost equal for light mesons. For heavy mesons, $\alpha$ will be smaller than $\beta$ [6, 17,18,19]. In Ref. [20], the authors show that the Regge trajectories are nonlinear in case of both fixed and running coupling constants by using the perturbative QCD. In Ref. [21], the authors show by analyzing the data from the UA8 and ISR experiments at CERN that the effective Pomeron Regge trajectories require a term quadratic in t. In Ref. [22], the authors scrutinize the hadronic Regge trajectories in the framework of the string model and the potential model, and recognize that the Regge trajectories for mesons and baryons are not straight and parallel lines in general in the current resonance region both experimentally and theoretically. In Ref. [23], the authors show that meson trajectories are nonlinear and intersecting by fitting experimental data. In Ref. [6], the authors argue that the hadronic Regge trajectories are essentially nonlinear and can be well approximated by a specific square-root form. In Refs. [24, 25], the quasilinear Regge trajectories for heavy mesons are discussed. In Refs. [26,27,28], the authors obtain an interpolating mass formula which gives the nonlinear Regge trajectories.

The idea of nonlinear Regge trajectories is not new [29,30,31,32,33,34,35]. Different models and different potentials will effect the Regge trajectories [6, 36, 37]. Different from the massless string model which produces the linear Regge trajectories, the relativistic string with massive ends will result in the complicated behavior of the Regge trajectories [38,39,40,41]. In Ref. [42], the authors obtain the nonlinear Regge trajectories from the gauge/string correspondence. In Ref. [6], the authors present a phenomenological string model for square-root Regge trajectories. In Refs. [43,44,45], the square-root trajectory is obtained by combining both Regge poles and cuts. The Schrödinger equation with the Cornell potential produces the Regge trajectories $M^2{\sim }{\beta }l^{4/3}$, and the linear Regge trajectories demands the confining potential rising as $r^{2/3}$ [46]. In Ref. [47], the authors show that the Regge trajectories become linear for the Dirac equation with the linear confinement for large orbital angular momenta. The Regge trajectories for the Klein-Gordon equation are considered in Refs. [48,49,50]. In Ref. [51], the authors obtained the linear, non-intersecting and parallel Regge trajectories by calculating the numerical solutions of the relativistic Thompson equation. In Ref. [52], the authors obtain the nonlinear Regge trajectories by including spin dependent terms in a three-dimensional reduction of the Bethe-Salpeter equation. In case of the spinless Salpeter equation, the Cornell potential or the linear potential can yield linear Regge trajectories [53, 54]. In Ref. [55], the authors find straight Regge trajectories in case of light-light quarkonia starting from a first principle Salpeter equation. In Ref. [56], the authors discuss the Regge trajectories by solving the eigenvalue equation with the quadratic mass operator. In this paper, we obtain one new form of the Regge trajectories from the quadratic form of the spinless Salpeter-type equation (QSSE) [57,58,59,60] with the Cornell potential or the linear potential. As the obtained new Regge trajectories employed to the spectra of charmonia and bottomonia, the fitted data are in very good agreement with the experimental data and theoretical predictions.

This paper is organized as follows. In Sect. 2, the new form of the Regge trajectories is obtained from the quadratic form of the spinless Salpeter-type equation with the Cornell potential and the power-law potentials. In Sect. 3, the obtained Regge trajectory is applied to fit the spectra of bottomonia and charmonia. We conclude in Sect. 4.

2 Regge trajectories from the quadratic form of the spinless Salpeter-type equation

In this section, we review briefly the QSSE at first. Then we present the orbital and radial Regge trajectory formulas obtained from the QSSE by employing the Bohr-Sommerfeld quantization approach [5, 61], which are different from the known Regge trajectories.

2.1 QSSE

The Bethe-Salpeter equation [62, 63] is based on the relativistic field theory and is an appropriate tool to deal with bound states. In Ref. [64], a first principal Bethe-Salpeter equation is obtained by using the only assumption that $\ln W$ (W being the Wilson loop correlator) can be written in QCD as the sum of its perturbative expression and an area term. By means of a three dimensional reduction, the Bethe-Salpeter equation becomes the eigenvalue equation for the square mass operator [56,57,58, 64, 65]

$$\begin{aligned} M^2=M_0^2+U, \end{aligned}$$

(2)

where

$$\begin{aligned} M_0= & {} \omega _1+\omega _2=\sqrt{m_1^2 + \mathbf{p}^2}+\sqrt{m_2^2 + \mathbf{p}^2},\nonumber \\ \langle \mathbf{p} \vert U \vert \mathbf{p}^\prime \rangle= & {} {1\over (2 \pi )^3 } \sqrt{ w_1 + w_2 \over 2 w_1 w_2}\, \hat{I}^{\mathrm{inst}}_{ab}( \mathbf{p} , \mathbf{p}^\prime ) \sqrt{ w_1^\prime + w_2^\prime \over 2 w_1^\prime w_2^\prime }\sigma _1^a\sigma _2^b.\nonumber \\ \end{aligned}$$

(3)

Fig. 1

The radial Regge trajectory of $\pi$

Fig. 2

Choice of parameters for various models incorporating the linear potential or the screened linear potential. The joined black line (Ours) is for $\sigma =\beta ^{3/2}/(12m_b)$ ($\beta =5.1$ ${\mathrm{GeV}}^2$) which is from Eq. (24). $\sigma$ is the string tension, $m_b$ is the mass of the bottom quark

Fig. 3

Radial Regge trajectories for bottomonia. Open squares are predicted masses by the fitted Regge trajectories. The well-established states are given by solid dots and the unsigned states are given by circles

Fig. 4

Same as Fig. 3 except for the orbital Regge trajectories

Table 1 Bottomonium masses (in units of ${\mathrm{MeV}}$) fitted by the radial Regge trajectories [Eq. (26)]. The experimental masses are from PDF [90]. The fitted results by using the Regge trajectories [Eq. (26)] are shown in comparison with the theoretical values of EFG13 [91], GM15 [92], SOEF16 [93] and DLGZ17 [94]. ? denotes the possible candidates for the unwell-established states

Table 2 Bottomonium masses (in units of ${\mathrm{MeV}}$) fitted by the orbital Regge trajectories [Eq. (26)]. The experimental masses are from PDF [90]. The fitted results by using the Regge trajectories [Eq. (26)] are shown in comparison with the theoretical values of EFG13 [91], GM15 [92], SOEF16 [93] and DLGZ17[94]

In the above equations, M is the bound state mass, $\mathbf{p}$ the c.m. momentum of quarks, $m_1$ and $m_2$ their constituent masses, $\omega '_1=\sqrt{m_1^2+\mathbf{p}'^2}$ and $\omega '_2=\sqrt{m_2^2+\mathbf{p}'^2}$. $\hat{I}_{ab}^{\mathrm{inst}}(\mathbf{p} , \mathbf{p}^\prime )$ is the instantaneous kernel. Neglecting any reference to the spin degrees of freedom of the involved bound-state constituents, Eq. (2) reduces to the quadratic form of the spinless Salpeter-type equation which is written in configuration space as [52, 57,58,59,60]

$$\begin{aligned} M^2\varPsi (\mathbf{r}) =\left[ \omega _1+\omega _2 \right] ^2\varPsi (\mathbf{r}) +{\mathcal {U}}\varPsi (\mathbf{r}), \end{aligned}$$

(4)

where $\omega _i$ is the square-root operator of the relativistic kinetic energy of constituent

$$\begin{aligned} \omega _i=\sqrt{m_i^2 -\varDelta }. \end{aligned}$$

(5)

$m_i$ are effective masses in the phenomenological model. The relativistic corrections with ${\mathcal {U}}$ are small for heavy constituents and will make calculations complicated. Just like the case of the spinless Salpeter equation [66,67,68,69,70], we assume that ${\mathcal {U}}$ in Eq. (4) can be taken to be nonrelativistic for simplicity although the kinetic energies of the constituents are taken to be relativistic. In the nonrelativistic limit, the configuration-space ${\mathcal {U}}$ reduces to

$$\begin{aligned} {\mathcal {U}} = 2(m_1+m_2)V(r), \end{aligned}$$

(6)

where V(r) is the usual nonrelativistic potential. In this paper, the Cornell potential [71, 72] and the power-law potentials are considered,

$$\begin{aligned} V(r)=-{\alpha \over r} + {\sigma }r,\quad {\sigma }r^a. \end{aligned}$$

(7)

In Ref. [55], the authors find straight Regge trajectories for the light-light case starting from a first principle Salpeter equation. As a well-defined standard approximation to the Bethe-Salpeter equation, the spinless Salpeter equation [73,74,75] yields the linear Regge trajectories for the linear potential. In Ref. [56], the Regge trajectories for the light-light quarkonium systems are calculated by using both the linear mass operator and the quadratic mass operator, respectively. The authors notice the differences between two kinds of Regge trajectories. In the following, we will propose one kind of nonlinear Regge trajectories from the QSSE [Eq. (4)] which has a quadratic mass operator.

2.2 Bohr-Sommerfeld quantization approach

In this subsection, we follow Ref. [5] to employ the Bohr-Sommerfeld quantization approach [61] to obtain the orbital Regge trajectories and the radial Regge trajectories from the QSSE.

In case of equally massive constituents ($m_1=m_2=m$), the quadratic mass operator of the QSSE with the Cornell potential reads from Eq. (4)

$$\begin{aligned} M^2=4\left( \mathbf{p}^2+m^2\right) +{\mathcal {U}}(r), \end{aligned}$$

(8)

where

$$\begin{aligned} \mathbf{p}^2=p_r^2+\frac{p_{\phi }^2}{r^2},\quad {\mathcal {U}}=4m\left[ -{\alpha \over r} + \sigma r\right] . \end{aligned}$$

(9)

Due to the central interaction, the orbital angular momentum $p_{\phi }=L$ is a constant of the motion. From the conservation of the total energy M of the bound state, the radial momentum $p_r$ can be written as

$$\begin{aligned} p_{r}= & {} \pm \, \frac{1}{2r}\, \sqrt{(M^2-4m^2)r^2-4L^2+4{\alpha }mr-4m{\sigma }r^3}\nonumber \\= & {} \pm \,\frac{1}{2r}\, \sqrt{g(r)}. \end{aligned}$$

(10)

Solving $g(r)=0$ gives the three roots of g(r). $r_j$ ($j=0,1,2$) are

$$\begin{aligned} r_j = 2\, \sqrt{\frac{-P}{3}}\, \cos \left( \frac{\theta + 2 {\pi } j}{3}\right) +\frac{E}{3{\sigma }}, \end{aligned}$$

(11)

where

$$\begin{aligned} E= & {} \frac{M^2-4m^2}{4m},\nonumber \\ P= & {} -\frac{1}{3 {\sigma ^2}}\left( E^2+3{\sigma }{\alpha } \right) , \quad \cos \theta = -\frac{Q}{2} \sqrt{\frac{27}{-P^3}},\nonumber \\ Q= & {} -\frac{1}{27 {\sigma ^3}}\left( 2E^3 +9{\sigma }{\alpha } E-27\frac{{\sigma ^2}}{m}L^2 \right) . \end{aligned}$$

(12)

As $r_1 \le 0 \le r_2 \le r_0$, the turning points are $r_{-}=r_2$ and $r_{+}=r_0$. The radial motion takes place between two turning points, $r_{-}$ and $r_{+}$.

The action variables in the Bohr-Sommerfeld quantization approach [61] read

$$\begin{aligned} J_s=\oint p_s\, dq_s, \end{aligned}$$

(13)

where s is the degrees of freedom of the bound state, $q_s$ and $p_s$ are the coordinates and conjugate momenta. The integral is performed over one cycle of the motion. The action variables should be quantized,

$$\begin{aligned} J_s=(n_s+c_s)\, h, \end{aligned}$$

(14)

where h is the Planck constant, $n_s$ ($\ge 0$) is an integral quantum number. $c_s$ is a real constant, $c_s=1/2$ [76]. Using Eqs. (13) and (14) to quantize $J_{\phi }$ gives $L=l+c_{\phi }$, $c_{\phi }=1/2$. Quantization of $J_r$ yields

$$\begin{aligned}&m\, r_{+}\, (E r_1+2\alpha )\, K(\eta )+m\, E\, r_{+}\,(r_{+}-r_{1})\, E(\eta )\nonumber \\&-3L^2\, \varPi (\pi /2,\gamma ,\eta )-\frac{3}{2}\pi \, n r_{+}\sqrt{r_{+}-r_{1}}\, \sqrt{m\sigma }=0, \end{aligned}$$

(15)

where

$$\begin{aligned} n=n_r+c_{r}=n_r+\frac{1}{2},\quad \eta =\frac{r_{+}-r_{-}}{r_{+}-r_{1}}, \quad \gamma =1-\frac{r_{-}}{r_{+}}. \end{aligned}$$

(16)

In the above equation, $n_r$ is the radial quantum number. K(x), E(x) and $\varPi (\pi /2,x,y)$ are the complete elliptic integrals of the first, second and third kind, respectively [77].

As angular momenta becomes large, $l \gg n_r$, $r_{-} \approx r_{+}$ and $\eta \approx 0$. Then, $\theta = \pi$, $K(\eta )=E(\eta )=\varPi (\pi /2,\gamma ,\eta )=\pi /2$. Keeping the leading terms in Eq. (15), the Regge trajectories can be obtained

$$\begin{aligned} M^2 \sim {\beta _l}l^{2/3},\quad \beta _l= 6\left( 2m^2\sigma ^2\right) ^{1/3}. \end{aligned}$$

(17)

As the radial quantum number becomes large, i.e., $n_r \gg l$, $r_1 \approx r_{-} \approx 0$, $\eta \approx 1$. Substituting $r_1 = r_{-} = 0$ into Eq. (13) yields

$$\begin{aligned} M^2 \sim {\beta _{n_r}} n_r^{2/3},\quad \beta _{n_r}=\left( 12m{\pi }\sigma \right) ^{2/3}. \end{aligned}$$

(18)

In case of the power-law potential $V(r)={\sigma }r^{a}$ ($a > 0$), the orbital Regge trajectories for large l are

$$\begin{aligned} M^2 \sim {\beta _l(a)}l^{2a/(a+2)} \quad (l \gg n), \end{aligned}$$

(19)

where $\beta _l(a)$ reads

$$\begin{aligned} \beta _l(a)=4(m\sigma )^{2/(a+2)} \left( 1+\frac{a}{2}\right) \left( \frac{2}{a}\right) ^{a/(a+2)}. \end{aligned}$$

(20)

In Ref. [52], the Regge trajectories similar to Eq. (19) are obtained under the semiclassical limit, however, the authors did not discuss in detail the linear potential case. As $n_r$ becomes large, we have the radial Regge trajectories from Eq. (13)

$$\begin{aligned} M^2 \sim {\beta _{n_r}}(a) n_r^{2a/(a+2)}\quad (n_r \gg l). \end{aligned}$$

(21)

The Regge slope is

$$\begin{aligned} {\beta _{n_r}}(a)=4\left( m\sigma \right) ^{2/(a+2)}\left[ \frac{a \pi }{B(1/a,3/2)}\right] ^{2a/(a+2)}, \end{aligned}$$

(22)

where B(x, y) is the beta function [77].

Fig. 5

Choice of parameters for various models incorporating the linear potential or the screened linear potential. The joined black line (Ours) is for $\sigma =\beta ^{3/2}/(12m_c)$ ($\beta =2.02$ ${\mathrm{GeV}}^2$) which is from Eq. (24). $\sigma$ is the string tension, $m_c$ is the mass of the charm quark

Fig. 6

Radial Regge trajectories for charmonia. The well-established states are given by solid dots and the candidate states are given by circles. Open squares are predicted masses by the fitted Regge trajectories

Fig. 7

Same as Fig. 6 except for the orbital Regge trajectories

The new form of the Regge trajectories [Eqs. (17) and (18)] are obtained from the QSSE (4) by taking the nonrelativistic approximation (6) and neglecting the spin dependent interactions. If higher corrections are considered, the form of the Regge trajectories will become complicated. Moreover, the employed Bohr-Sommerfeld quantization approach is a semiclassical method and is used as an approximation method. Therefore, the obtained Regge trajectories are approximate. For simplicity, we assume the heavy quarkonium Regge trajectories take the simple form. The radial Regge trajectory Eq. (18) can be extended to be of a more general form

$$\begin{aligned} M^2=\beta {\pi }^{2/3}\left( n_r+c'_0\right) ^{2/3}+c'_1,\;\; \end{aligned}$$

(23)

where

$$\begin{aligned} \beta =(12m\sigma )^{2/3}. \end{aligned}$$

(24)

And the orbital Regge trajectories (17) can be extended to be

$$\begin{aligned} M^2={\beta }3^{1/3}\left( l+c''_0\right) ^{2/3}+c''_1. \end{aligned}$$

(25)

By considering Eqs. (23) and (25) and fitting experimental data, we assume that the heavy quarkonium Regge trajectory take the parameterized form

$$\begin{aligned} M^2=\beta \left( {c_l}l+{\pi }n_r+c_0\right) ^{2/3}+c_1. \end{aligned}$$

(26)

In Eq. (26), $\beta$ is an universal parameter which has a theoretical value according to Eq. (24). The fitted $\beta$ for both the bottomonium Regge trajectories and the charmonium Regge trajectories agree well with Eq. (24). $c_l$ is also an universal parameter. The fitted $c_l$ for the bottomonium Regge trajectories ($c_l=\sqrt{6}$) and for the charmonium Regge trajectories ($c_l=\sqrt{5.34}$) deviate from the corresponding theoretical value $c_l=\sqrt{3}$. $c_0$ and $c_1$ vary with different trajectories.

The obtained new form of the Regge trajectory [Eq. (26)] is an approximation to the exact unknown one. Out of expectation, by fitting the theoretical values of the $\varUpsilon$ ($\varUpsilon (1S)$, $\varUpsilon (2S)$, $\varUpsilon (3S)$, $\varUpsilon (4S)$, $\varUpsilon (5S)$ and $\varUpsilon (6S)$) and $\psi$ ($J/\psi (1S)$, $\psi (2S)$, $\psi (3S)$ and $\psi (4S)$), we find the obtained Regge trajectory [Eq. (26)] is in good agreement with the theoretical values obtained by solving the eigenvalue equation for a squared bound state mass [65]. It suggests that the new Regge trajectories [Eq. (26)] can be applicable not only to QSSE but also to Eq. (2). Moreover, the new form of the Regge trajectories agree well with the experimental data, see Sect. 3.

2.3 Regge trajectories from the Schrödinger equation, the spinless Salpeter equation and the QSSE

There are many discussions on the Regge trajectories in the framework of the Bethe-Salpeter equation and many reductions of it (see the Introduction), however, most of these discussions rely on the numerical solutions and the explicit formula of the Regge trajectories is not given due to the complexity of these equations. In this subsection, we list the explicit formulas of the Regge trajectories for the equations which can be handled easily.

For simplicity, the power-law potentials are considered in this subsection, see Eq. (7). The nonrelativistic Schrödinger equation reads

$$\begin{aligned} E\psi (\mathbf{r})=\frac{\mathbf{p}^2}{2\mu }\psi (\mathbf{r})+{\sigma }r^a\psi (\mathbf{r}). \end{aligned}$$

(27)

The radial and orbital Regge trajectories obtained from Eq. (27) read [5, 46], respectively,

$$\begin{aligned}&M^2{\sim }l^{4a/(a+2)},\;\;\;\; {\text {for large }}l,\nonumber \\&M^2{\sim }n_r^{4a/(a+2)},\;\;\; {\text {for large }}n_r, \end{aligned}$$

(28)

where $M=m_1+m_2+E$. As a relativistic expansion of the Schrödinger equation and a well-defined standard approximation to the Bethe-Salpeter equation, the semirelativistic spinless Salpeter equation reads

$$\begin{aligned} M\psi (\mathbf{r})=\left[ \sqrt{\mathbf{p}_1^2+m_1^2}+\sqrt{\mathbf{p}_2^2+m_2^2}\right] \psi (\mathbf{r})+{\sigma }r^a\psi (\mathbf{r}). \end{aligned}$$

(29)

The radial and orbital Regge trajectories obtained from Eq. (29) read [5, 53, 54], respectively,

$$\begin{aligned}&M^2{\sim }l^{2a/(a+1)},\;\;\;\; {\text {for large }}l,\nonumber \\&M^2{\sim }n_r^{2a/(a+1)},\;\;\; {\text {for large }}n_r. \end{aligned}$$

(30)

In case of the QSSE, the radial and orbital Regge trajectories read from Eqs. (19) and (21), respectively,

$$\begin{aligned}&M^2{\sim }l^{2a/(a+2)},\;\;\;\; {\text {for large }}l,\nonumber \\&M^2{\sim }n_r^{2a/(a+2)},\;\;\; {\text {for large }}n_r. \end{aligned}$$

(31)

For the Schrödinger equation, the linear Regge trajectories need the confining potential rising as $r^{2/3}$; for the spinless Salpeter equation, the linear Regge trajectories demand the linear confining potential; for the QSSE, the linear Regge trajectories need the harmonic-oscillator-type potential.

Table 3 Charmonium masses (in units of ${\mathrm{MeV}}$) fitted by the radial Regge trajectories [Eq. (26)]. The experimental masses are from PDG [90]. The fitted results by using the Regge trajectories [Eq. (26)] are shown in comparison with the theoretical values of GI85 [131], BGS05 [119], EFG13 [91] and LC09 [120]. ? denotes the possible candidates for the unwell-established states

Table 4 Charmonium masses (in units of ${\mathrm{MeV}}$) fitted by the orbital Regge trajectories [Eq. (26)]. The experimental masses are from PDG [90]. The fitted results by using the Regge trajectories [Eq. (26)] are shown in comparison with the theoretical values of GI85 [131], BGS05 [119], EFG13 [91] and LC09 [120]

From Eqs. (28), (30) and (31), we can see that the exponents in the radial and orbital Regge trajectories diminish as the bound-state equations vary from the Schrödinger equation to the spinless Salpeter equation and then to the QSSE. Eqs. (28), (30) and (31) show that different dynamic equations will result in different Regge trajectories although both Eqs. (8) and (29) are reduced from the Bethe-Salpeter equation and the Schrödinger equation can be obtained from Eqs. (8) and (29) by nonrelativistic approximation. The good agreement of the fitted data with the experimental data (see Sect. 3) suggests that the QSSE and the eigenvalue equation for the square mass operator [Eq. (2)] will be better than the Schrödinger equation and the spinless Salpeter equation for heavy quarkonia.

3 Regge trajectories and mass spectra of heavy quarkonia

In this section, we employ the obtained new form of the Regge trajectories to fit the spectra of charmonium and bottomonium. Experimental data are used as inputs to determine the parameters of the Regge trajectories. Then the fitted Regge trajectories can predict the masses of the unobserved states. In this work, the linear Regge trajectories are also fitted by the experimental data and we find that the new form of the Regge trajectories are better than the linear ones.

3.1 Nonlinear Regge trajectories

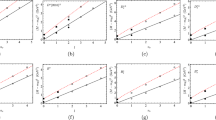
For light mesons, the Regge trajectories are suggested to be linear although the parameters take different values [78,79,80,81,82,83]. By fitting the experimental data, we find that the new Regge trajectory is better than the linear one even for $\pi$ mesons, see Fig. 1 [84]. For heavy quarkonia especially for bottomonia, the Regge trajectories deviate significantly from the linearity. The differences between the results obtained by the linear and the results obtained by the nonlinear Regge trajectories are shown in Figs 3, 4, 6 and 7.

For the baryon Regge trajectories within the quark-diquark models [85], the radial Regge trajectories for the heavy, light vector mesons [86], the Regge-like relation for the heavy-light systems [87], and the light meson Regge trajectories [8, 9, 88], the linear confining potential plays dominant role. Similarly, the linear confining potential also dominates the new form of the nonlinear Regge trajectories (26), which can be seen from the derivation in the subsection 2.2. The good fitting of the experimental data by the Regge trajectory (26) confirms this observation and suggests that the contributions of the color Coulomb potential to the heavy quarkonium Regge trajectories is subordinate.

3.2 Masses of Bottomonia

Using the experimental data of the well-established states, the parameters of the radial Regge trajectories, the orbital Regge trajectories and the linear Regge trajectories are determined. Using the masses of pseudoscalar mesons $\eta _b(nS)$ and the masses of the vector mesons $\varUpsilon (nS)$, the universal parameter $\beta$ is calculated, $\beta =5.1$ ${\mathrm{GeV}}^2$ for bottomonia which is consistent with the theoretical value. According to Eq. (24), there is a relation between the heavy quark mass m and the string tension $\sigma$. The chosen value of $\beta$ for bottomonium is reasonable because the fitted $\beta$ can be obtained by reasonable $m_b$ and $\sigma$, see Fig. 2. (In Fig. 2, the data are from various models with various potentials which incorporating the linear potential or the screened linear potential.)

The universal parameter $c_l$ is calculated by fitting the orbital Regge trajectories for $\eta _b(1S)$ and $\varUpsilon (1S)$, $c_l=\sqrt{6}$ for bottomonia. $c_0$ and $c_1$ vary with different Regge trajectories. The fitted Regge trajectories are shown in Figs 3 and 4. The fitted and predicted masses of bottomonia by the Regge trajectories are listed in Tables 1 and 2 and they are in good agreement with other theoretical predictions.

The mass of $\varUpsilon (10860)$ resonance is $10891.1\pm 3.2^{+1.2}_{-2.0}$ [90]. $\varUpsilon (10860)$ is usually assigned as $\varUpsilon (5S)$ [113,114,115,116] while it is regarded as one of the strong candidates for the exotic hadron in Ref. [117] due to the unexpectedly large partial widths which disagree with the expectation for a pure $b\bar{b}$ state. The mass of $\varUpsilon (11020)$ resonance is $10987.5^{+6.4+9.1}_{-2.5-2.3}$. And $\varUpsilon (11020)$ is signed as $\varUpsilon (6S)$ [113, 114, 116]. In Ref. [118], the authors propose that $\varUpsilon (10580)$, $\varUpsilon (10860)$ and $\varUpsilon (11020)$ are likely mixtures of conventional $b\bar{b}$ bottomonia and pairs of $B\bar{B}$ or $B_s\bar{B}_s$ mesons.

3.3 Masses of charmonia

The universal parameter $\beta$ for the radial charmonium Regge trajectories is determined by the masses of pseudoscalar mesons $\eta _c(nS)$ and the masses of the vector mesons $\psi (nS)$, $\beta =2.02$ ${\mathrm{GeV}}^2$ for charmonia. According to Eq. (24), the possible values of the charm quark mass $m_c$ and the string tension $\sigma$ are reasonable, see Fig. 5.

The universal parameter $c_l$ is calculated by fitting the orbital Regge trajectories for $\eta _c(1S)$ and $J/\psi (1S)$, $c_l=\sqrt{5.34}$ for charmonia. $c_0$ and $c_1$ vary with different Regge trajectories. The fitted Regge trajectories are in Figs 6 and 7. The fitted and predicted masses of charmonia by the Regge trajectories are listed in Tables 3 and 4 and they are in agreement with other theoretical predictions.

The X(3940) is proposed as the $\eta _c(3S)$ charmonium state [125,126,127,128] and X(4160) as the $\eta _c(4S)$ state [129]. In Refs. [119, 120, 130], the authors argue that the above assignments would imply anomalously large $\varPsi (nS)-\eta _c(nS)$ mass splittings .

X(4040) is a hopeful candidate for $\psi (3S)$ [132,133,134,135]. Y(4260) is assigned as a normal $c\bar{c}$ state $\psi (4S)$ [136, 137]. In Refs. [138, 139], the authors argue that Y(4260) is a molecular state. In Refs. [120, 121], Y(4660) is taken as a candidate for canonical charmonium state. In Refs. [140, 141], Y(4660) is taken as tetraquark state candidate. In Refs. [142, 143], Y(4660) is regarded as a $\psi 'f_0(980)$ molecule. Y(4660) was also suggested to a baryonium state [144]. The mass of Y(4660) is $4664{\pm }12$ ${\mathrm{MeV}}$, which is about equal to the predicted mass [4679 ${\mathrm{MeV}}$] by the fitted Regge trajectory of charmonium state $6^3S_1$, see Fig. 6b and Table 3.

X(3915) is usually identified as the $\chi _{c0}(2p)$ of charmonium based on its mass and likely $J^{PC}$ [130, 145] and this assignment has some problems [146].

X(3872) is a candidate for $\chi _{c1}(2P)$ [130]. In Ref. [145], X(3872) is excluded as being the yet-unobserved conventional charmonium state $\chi _{c1}(2P)$. X(3872) is also discussed in the $D^0\bar{D}^{{*}0}$ hadronic molecular scenario [147].

In Fig 6c and d, masses of X(3915) and X(3872) are used to fit the Regge trajectories. In Fig. 6a, X(3940) and X(4160) lie on the pseudoscalar Regge trajectory. X(4040), X(4260) and Y(4660) lie on the vector Regge trajectory, see Fig. 6b.

4 Conclusions

In this paper, one new form of the Regge trajectories is proposed based on the quadratic form of the spinless Salpeter-type equation and the Bohr-Sommerfeld quantization method. The obtained Regge trajectories for the Cornell potential or for the linear potential take the parameterized form $M^2=\beta \left( {c_l}l+{\pi }n_r+c_0\right) ^{2/3}+c_1$. The parameters $\beta$ and $c_l$ and the coefficient $\pi$ before $n_r$ are universal for bottomonia and charmoniua, respectively. It is shown that the experimental data are very well described by the radial Regge trajectories and the orbital Regge trajectories for both bottomonia and charmonia. The good agreement of the fitted data with the experimental data suggests that the QSSE and the eigenvalue equation for the square mass operator [Eq. (2)] will be good for heavy quarkonia.

One distinctive feature of the new form of the Regge trajectories is that the new form of the heavy quarkonium Regge trajectories and the curvature are determined by the quadratic form of mass operator and the linear potential for long distances which has been validated by lattice QCD calculations, while the contributions of the color Coulomb potential for short distances to the Regge trajectories for heavy quarkonia will be subordinate to that of the linear confining potential.