1 Introduction

There is a vast amount of experimental data on the spectra of different types of hadrons [1]. One of the widely used approaches in studying the hadron spectra is the Regge trajectory [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. The study of Regge trajectories of hadron spectra is beneficial for gaining insights into the strong interactions from various perspectives [22,23,24,25,26,27,28,29,30,31]. Clearly, an unified dynamic mechanism will lead to the universal description of Regge trajectories for hadrons [25,26,27].

The meson Regge trajectories exhibit structures that vary in different energy regions [32, 33]. This variability is expected to hold true for other hadrons with a similar dynamic mechanism, such as baryons and tetraquarks in the diquark picture. For the light-light systems, it is well-known that they can be well described by the renowned linear Regge trajectories [3, 4]. In case of the heavy-heavy systems, an universal description is presented in Refs. [34, 35]. Regarding the heavy-light systems, the authors provide an universal description of the orbitally excited heavy-light mesons and baryons in Ref. [28]. In Ref. [36], we present the heavy-light diquark Regge trajectories. The proposed Regge trajectory relations can universally describe the heavy-light mesons and the heavy-light diquarks. In this study, we apply the Regge trajectory relationsFootnote 1 newly proposed in Ref. [36] to the heavy-light baryons composed of a heavy quark and a light diquark or composed of a light quark and a heavy diquark, as well as to the heavy-light tetraquarks consisting of one heavy (light) diquark and one light (heavy) antidiquark.

This paper is organized as follows: In Sect. 2, the Regge trajectory relations are obtained from the spinless Salpeter equation (SSE). In Sect. 3, the universal description of the heavy-light diquarks, mesons, baryons and tetraquarks is investigated. Discussions on concavity of the Regge trajectories are given in Sect. 4 and the conclusions are in Sect. 5.

2 Regge trajectory relations for the heavy-light systems

2.1 SSE

The spinless Salpeter equation (SSE) [37,38,39,40,41,42,43] reads as

$$\begin{aligned} M\Psi _{d,m,b,t}({\textbf{r}})=M_0\Psi _{d,m,b,t}({\textbf{r}})+V_{d,m,b,t}\Psi _{d,m,b,t}({\textbf{r}}), \end{aligned}$$
(1)

where \(M_0=\omega _1+\omega _2\). M is the bound state mass (diquark, meson, baryon and tetraquark). \(\Psi _{d,m,b,t}({\textbf{r}})\) are the diquark wave function, the meson wave function, the baryon wave function, and the tetraquark wave function, respectively. \(V_{d,m,b,t}\) are the diquark potential, the meson potential, the baryon potential, and the tetraquark potential, respectively. \(\omega _1\) is the relativistic energy of constituent 1, and \(\omega _2\) is of constituent 2,

$$\begin{aligned} \omega _i=\sqrt{m_i^2+\textbf{p}^2}=\sqrt{m_i^2-\Delta }\;\; (i=1,2). \end{aligned}$$
(2)

\(m_1\) and \(m_2\) are the effective masses of heavy constituent 1 and light constituent 2, respectively.

In the present work, the Cornell-like potential is considered [37, 38, 44, 45],

$$\begin{aligned} V_{d,m,b,t}=-\frac{3}{4}\left[ V_c+{\sigma }r+C\right] (\mathbf{{F}}_i\cdot \mathbf{{F}}_j)_{d,m,b,t}, \end{aligned}$$
(3)

where \(V_c\,{\propto }\,1/r\) is the color Coulomb potential or a Coulomb-like interaction for different hadrons [37, 44]. The second term is the linear confining potential and \(\sigma \) is the string tension. C is a fundamental parameter [46, 47]. \(\mathbf{{F}}_i\cdot \mathbf{{F}}_j\) is the color-Casmir,

$$\begin{aligned} \langle (\mathbf{{F}}_i\cdot \mathbf{{F}}_j)_{d}\rangle =-\frac{2}{3},\quad \langle (\mathbf{{F}}_i\cdot \mathbf{{F}}_j)_{m,b,t}\rangle =-\frac{4}{3}. \end{aligned}$$
(4)

From Eqs. (1) and (3), we see that the heavy-light diquarks, the heavy-light mesons, the heavy-light baryons, and the heavy-light tetraquarks are described in an unified approach [37, 38]. Therefore, it is expected that these heavy-light systems can be described universally by the Regge trajectory approach.

2.2 Regge trajectory relations

The mass of the light constituent is assumed to approach zero, \(m_2\rightarrow 0\) in Refs. [15, 28] or is considered by correction term in Refs. [16, 27, 48,49,50]. In the limit \(m_1\rightarrow \infty \) and \(m_2\rightarrow 0\), Eq. (1) is reduced to be

$$\begin{aligned} M\Psi _{d,m,b,t}({\textbf{r}})=\left[ m_1+{{|\textbf{p}|}}+V_{d,m,b,t}\right] \Psi _{d,m,b,t}({\textbf{r}}). \end{aligned}$$
(5)

By employing the Bohr-Sommerfeld quantization approach [51, 52], we have from Eq. (5)

$$\begin{aligned} M{\sim }2\sqrt{\sigma '}\sqrt{l},\;M{\sim }\sqrt{2{\pi }\sigma '}\sqrt{n_r}, \end{aligned}$$
(6)

where

$$\begin{aligned} \sigma '=\left\{ \begin{array}{ll} \sigma /2, &{} \text {diquarks}, \\ \sigma , &{} \text {mesons, baryons, tetraquarks}. \end{array}\right. \end{aligned}$$
(7)

Using Eq. (6), the parameterized formula can be written as [36]

$$\begin{aligned} M=m_R+\beta _x\sqrt{x+c_{0x}},\,(x=l,\,n_r). \end{aligned}$$
(8)

The parameter in Eq. (8) reads as [32]

$$\begin{aligned} \beta _x=c_{fx}c_xc_{c}. \end{aligned}$$
(9)

The constants \(c_{x}\) [\(c_{n_r}\) and \(c_l\)] and \(c_{c}\) are

$$\begin{aligned} c_{c}=\sqrt{\sigma '},\quad c_l=2,\quad c_{n_r}=\sqrt{2\pi }. \end{aligned}$$
(10)

Both \(c_{fl}\) and \(c_{fn_r}\) are theoretically equal to one and are fitted in practice. For the heavy-light mesons, the common choice of \(m_R\) is [15, 28, 32, 48,49,50, 53]

$$\begin{aligned} m_R=m_1. \end{aligned}$$
(11)

\(m_R\), \(c_x\) and \(\sigma \) are universal for the heavy-light systems. \(c_{fx}\) and \(c_{0x}\), which vary with different Regge trajectories, are determined by fitting the given Regge trajectory.

The usual Regge trajectory Eq. (8) with (11), which is obtained in the limit \(m_1\rightarrow \infty \) and \(m_2\rightarrow 0\), cannot give agreeable results of the heavy-light diquarks. Corresponding to different ways to include the light constituent’s mass, two modified formulas are proposed in Ref. [36], which can describe universally both the heavy-light mesons and the heavy-light diquarks. One is Eq. (8) with

$$\begin{aligned} m_R=m_1+m_2+C', \end{aligned}$$
(12)

where

$$\begin{aligned} C'=\left\{ \begin{array}{ll} C/2, &{} \text {diquarks}, \\ C, &{} \text {mesons, baryons, tetraquarks}. \end{array}\right. \end{aligned}$$
(13)

Another reads

$$\begin{aligned} M=m_R+\sqrt{\beta _x^2(x+c_{0x})+\kappa _{x}m^{3/2}_2(x+c_{0x})^{1/4}} \end{aligned}$$
(14)

if \(m_2{\ll }M\), where

$$\begin{aligned} m_R=m_1+C',\quad \kappa _x=\frac{4}{3}\sqrt{{\pi }\beta _x}, \end{aligned}$$
(15)

where \(\beta _x\) is in (9). (8) with (12) is an extension of \(M=m_1+m_2+\sqrt{a(n_r+{\alpha }l+b)}\) [16], while (14) with (15) is based on the results in [27, 48]. As \(m_2=0\), these two modified formulas, formulas (8) with (12) and (14) with (15), become identical. As \(m_2=0\) and C is neglected, these two modified formulas reduce to the usual Regge trajectory formula for the heavy-light mesons, i.e., (8) with (11). In this work, we apply these two modified formulas to the heavy-light systems: diquarks, mesons, baryons, tetraquarks.

3 Universal description of the heavy-light systems

In this section we present the universal description of different types of heavy-light systems by employing (8) with (12) and (14) with (15). The Regge trajectories for the heavy-light systems are fitted individually.

3.1 Parameters

The parameters are [54,55,56]

$$\begin{aligned}&m_u=m_d=0.33\, {\textrm{GeV}},\quad m_s=0.50\, {\textrm{GeV}},\nonumber \\&m_c=1.55\, {\textrm{GeV}},\quad m_b=4.88\, {\textrm{GeV}},\nonumber \\&\sigma =0.18\,{\textrm{GeV}^2},\quad C=-0.3\,{\textrm{GeV}}, \nonumber \\&m_{[ud]}=0.710\,{\textrm{GeV}},\quad m_{\{ud\}}=0.909\,{\textrm{GeV}},\nonumber \\&m_{[us]}=0.948\,{\textrm{GeV}},\quad m_{\{us\}}=1.069\,{\textrm{GeV}},\nonumber \\&m_{\{cc\}}=3.226\,{\textrm{GeV}},\quad m_{\{bb\}}=9.778\,{\textrm{GeV}},\nonumber \\&m_{\{cb\}}=6.526\,{\textrm{GeV}},\quad m_{\{ss\}}=1.203\,{\textrm{GeV}}, \end{aligned}$$
(16)

where \(\{\;\}\) denotes the axial-vector diquark and \([\;]\) the scalar diquark. \(c_{0x}\) and \(c_{fx}\) vary with different Regge trajectories.

The values in Eq. (16) are used to calculate the masses of tetraquarks [54], baryons [55] and mesons [56]. In Ref. [28], the values are used to give an universal description of the heavy-light mesons and baryons. The values are also used to discuss diquarks [35, 36].

3.2 Heavy-light diquarks

Diquarks have been discussed by various approaches, for example, the QCD sum rules [57,58,59,60,61,62,63,64]. In Ref. [36], we show that the Regge trajectories for the heavy-light diquarks can be well described by (8) with (12) and (14) with (15). The spectra of the heavy-light diquarks (cu), (cs), (bu) and (bs) obtained by using the Regge trajectory approach agree with other theoretical predictions. See [36] for more details.

In case of Eq. (8) with (12), the heavy-light diquarks satisfy the universal description irrespective of both mass of the light constituents and mass of the heavy constituent. In case of Eq. (14) with (15), the heavy-light diquarks satisfy the universal description irrespective of mass of the heavy constituents.

3.3 Heavy-light mesons

Table 1 The experimental values [1] and the theoretical values (EFG) [56] for the charmed and bottom mesons. The values are in GeV
Full size table
Table 2 The fitted values of parameters \(c_{fn_r}\), \(c_{fl}\), \(c_{0n_r}\), and \(c_{0l}\) by employing formulas (8) with (12) (Fit1) and (14) with (15) (Fit2). The used data are in Tables 1, 3, 4 and 5
Full size table
Fig. 1
figure 1

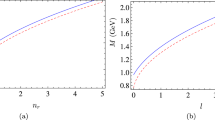
The radial and orbital Regge trajectories for the heavy-light mesons by employing formulas (8) with (12) (the black lines) and (14) with (15) (the red dashed lines). The PDG data (the dots and the filled squares) and the theoretical data (the circles and the empty squares) are listed in Table 1. \(m_R\) for the black lines and for the red dashed lines are different, see (12) and (15)

Full size image
Fig. 2
figure 2

The heavy-light mesons are ploted in the \(((M-m_1-m_2-C)^2,\,x)\) plane (Fit1) and in the \(((M-m_1-C)^2,\,x)\) plane (Fit2), respectively. \(x=l,\,n_r\). \(m_1\) is the mass of the heavy constituent and \(m_2\) the mass of the light constituent. C is in (3). The used data are listed in Table 1

Full size image

By using Eqs. (8) with (12) and (14) with (15) and data in Table 1, the radial and orbital Regge trajectories for the heavy-light mesons \(D^{*}\), \(D_s^{*\pm }\), \(B^{*}\) and \(B^{*}_s\) are obtained, see Fig. 1. The fitted values are listed in Table 2. In Fig. 1, the Regge trajectories (the red dashed lines) obtained by employing (14) with (15) lie above the Regge trajectories (the black lines) obtained by applying (8) with (12). It is because \(m_R\) for these two Regge trajectories are different, see Eqs. (12) and (15). The figures show that the heavy-light mesons satisfy both of these two Regge trajectory relations.

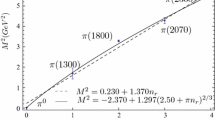
From Fig. 2 and the fitted values in Table 2, we can see that both of the radial and orbital Regge trajectories in the \(((M-m_1-m_2-C)^2,\,x)\) planes almost overlap with each other irrespective of both the light quark flavor and heavy quark flavor. It shows an universal description of these heavy-light mesons. For the heavy-light mesons, the Regge trajectories in the \(((M-m_1-C)^2,\,x)\) plane are universal only irrespective of heavy quark flavor.

As employing Eq. (8) with (12), the average values of \(c_{fn_r}\) and \(c_{fl}\) are 1.026 and 1.026 for the heavy-light mesons, respectively. When applying Eq. (14) with (15), the average values of \(c_{fn_r}\) and \(c_{fl}\) are 1.108 and 1.114, respectively.

From Table 2, we can see that the fitted values of \(c_{fn_r}\) and \(c_{fl}\) decrease in the majority of cases as the masses of the constituents increase when employing (8) with (12). However, the fitted values of \(c_{fn_r}\) and \(c_{fl}\) obtained by using (14) with (15) frequently decrease with the increase of the masses of the heavy constituent and rise with the increase of the masses of the light constituent. This trend aligns with the results in [28].

3.4 Heavy-light baryons

Table 3 The experimental and theoretical data for the radially excited states \(\frac{1}{2}^+\) of baryons \(\Lambda _c^+\) and \(\Lambda _b^0\). Q denotes the heavy quark. The values are in GeV
Full size table

In the diquark picture, the baryons consisting of one light quark and one heavy diquark or consisting of one heavy quark and one light diquark are denoted as the heavy-light baryons and belong to the heavy-light systems. Employing (8) with (12) and (14) with (15) to the heavy-light baryons, the Regge trajectories are fitted. The used data are listed in Table 3 and the fitted values are in Table 2. The fitted Regge trajectories are in Fig. 3.

The difference of \(m_R\) for two Regge trajectory relation leads to that the Regge trajectories (the red dashed lines) obtained by employing (14) with (15) lie above the Regge trajectories (the black lines) obtained by applying (8) with (12), see Fig. 3. From Fig. 4 and the fitted values in Table 2, we can see that the heavy-light baryons satisfy both of these two Regge trajectory relations. We also notice that some fitted Regge trajectories by employing (8) with (12) are better than the fitted Regge trajectories by applying (8) with (12), for example, the Regge trajectory for \(\Omega _c\), see Fig. 3m.

Similar to the meson case, from Fig. 4 and the fitted values in Table 2, we can see that both of the radial and orbital Regge trajectories for the heavy-light baryons plotted in the \(((M-m_1-m_2-C)^2,\,x)\) planes almost overlap with each other irrespective of both the light constituent and the heavy constituent. This shows an universal description of these heavy-light baryons. For the heavy-light baryons, the Regge trajectories in the \(((M-m_1-C)^2,\,x)\) plane are universal only irrespective of heavy constituent.

As employing Eq. (8) with (12), the average values of \(c_{fn_r}\) and \(c_{fl}\) are 0.794 and 0.749 for the heavy-light baryons, respectively. When applying Eq. (14) with (15), the average values of \(c_{fn_r}\) and \(c_{fl}\) are 0.896 and 0.855, respectively. The fitted \(c_{fn_r}\) and \(c_{fl}\) for the heavy-light baryons are smaller than that for the heavy-light mesons. The fitted values for the doubly heavy baryons approximate the fitted values for the heavy-light mesons because the doubly heavy baryons strongly resemble the heavy-light mesons.

Table 4 The theoretical values (EFG) [55, 65] for the heavy-light baryons. The values are in GeV
Full size table
Fig. 3
figure 3

Same as Fig. 1 except for the heavy-light baryons and Tables 3 and 4

Full size image
Fig. 4
figure 4

Same as Fig. 2 except for the heavy-light baryons and Tables 3 and 4

Full size image

3.5 Heavy-light tetraquarks

The heavy-light tetraquarks denote tetraquarks consisting of one heavy diquark and one light antidiquark or consisting of one light diquark and one heavy antidiquark. The tetraquarks composed of a diquark and antidiquark in color \(\bar{3}\) and 3 configurations are considered.

Applying Eqs. (8) with (12) and (14) with (15) and using data in Table 5, the radial and orbital Regge trajectories for the heavy-light tetraquarks are obtained, see Fig. 5. The fitted values are listed in Table 2. Similar to the heavy-light mesons and the heavy-light baryons, the Regge trajectories (the red dashed lines) obtained by employing (14) with (15) lie above the Regge trajectories (the black lines) obtained by applying (8) with (12), see Fig. 5.

From Fig. 6 and the fitted values in Table 2, we can see that the heavy-light tetraquarks satisfy both of these two Regge trajectory relations. Moreover, we can see that the universal description of the heavy-light tetraquarks approximately holds. We notice that the fitted results are not reliable enough because the experimental data is lack and the theoretical data on the \(\lambda \)-excited states are scarce. [The theoretical data on the \(\lambda \)-excited states of the tetraquarks are scarce because the masses of these states lie above the corresponding thresholds.]

As employing Eq. (8) with (12), the average values of \(c_{fn_r}\) and \(c_{fl}\) are 0.553 and 0.579 for the heavy-light tetraquarks, respectively. When applying Eq. (14) with (15), the mean values of \(c_{fn_r}\) and \(c_{fl}\) are 0.647 and 0.676, respectively. The fitted \(c_{fn_r}\) and \(c_{fl}\) for the heavy-light tetraquarks are smaller than that for the heavy-light mesons and the heavy-light baryons.

Table 5 The theoretical values (KOS) [66] for the doubly heavy tetraquarks. The values are in GeV
Full size table
Fig. 5
figure 5

Same as Fig. 1 except for the heavy-light tetraquarks and Table 5

Full size image
Fig. 6
figure 6

Same as Fig. 2 except for the heavy-light tetraquarks and Table 5

Full size image

4 Concavity of the Regge trajectories

The Regge trajectories take different forms in different energy regions [32, 33]. In this section, the Regge trajectories are depicted in the \((M^2,\,x)\) \((x=n_r,\,l)\) planes. In Refs. [35, 36, 67], it is shown that the Regge trajectories for all types of diquarks (including the doubly heavy diquarks, the heavy-light diquarks and the light diquarks) are concave downwards.

In Ref. [68], it is shown that the meson Regge trajectories are concave downwards for the doubly heavy mesons and the heavy-light mesons. In the case of the light mesons, the Regge trajectories assume a linear form when the masses of the light quark and antiquark are taken as zero. However, upon taking into account the masses of the light quark and antiquark, the Regge trajectories for the light mesons also adopt a concave shape, see Refs. [27, 48].

In Ref. [34], we show that the Regge trajectories for the heavy-heavy baryons and tetraquarks are also concave downwards. In this work, we observe that the Regge trajectories for the heavy-light baryons and the heavy-light tetraquark also display a concave shape. Taking into account the masses of the light constituent, it is expected that the Regge trajectories for the light baryons and the light tetraquarks will similarly be concave.

The curvature of the Regge trajectories holds significant importance [68]. In potential models, the curvature is related to the dynamic equation and the confining potential. Based on the discussions in this section, we assume that, when considering the mass of the light constituent, all Regge trajectories for the diquarks, mesons, baryons and tetraquarks are concave downwards in the \((M^2,\,n_r)\) and \((M^2,\,l)\) planes. Future experimental data will either validate or challenge the concavity conjecture. It will improve understanding of hadron dynamics and promote the study of hadron spectra.

5 Conclusions

We apply two newly proposed Regge trajectory relations (8) along with (12) and (14) along with (15) to analyze the heavy-light systems, presenting the numerical plots for clarity. We find that the heavy-light diquarks, the heavy-light mesons, the heavy-light baryons and the heavy-light tetraquarks satisfy these two formulas.

In the scenario where Eq. (8) is combined with (12), the heavy-light systems conform to the universal description regardless of the masses of the light constituents and the heavy constituent. When considering Eq. (14) alongside (15), the heavy-light systems adhere to the universal description regardless of the masses of the heavy constituents. It is observed that the fitted slopes for the radial Regge trajectories are greater than those for the orbital Regge trajectories across all heavy-light systems.

The fitted slopes exhibit distinctive differences among the heavy-light mesons, baryons and tetraquarks, respectively. When employing Eq. (8) with (12), the average values of \(c_{fn_r}\) (\(c_{fl}\)) are 1.026, 0.794 and 0.553 (1.026, 0.749 and 0.579) for the heavy-light mesons, the heavy-light baryons and the heavy-light tetraquarks, respectively. When applying Eq. (14) with (15), the average values of \(c_{fn_r}\) (\(c_{fl}\)) are 1.108, 0.896 and 0.647 (1.114, 0.855 and 0.676) for the heavy-light mesons, baryons and tetraquarks, respectively.

Furthermore, the fitted results indicate that the Regge trajectories for the heavy-light systems exhibit concave downward shapes in the \((M^2,\,n_r)\) and \((M^2,\,l)\) planes. It is expected that, when considering the mass of the light constituent, all Regge trajectories for the diquarks, mesons, baryons and tetraquarks are concave downwards in the \((M^2,\,n_r)\) and \((M^2,\,l)\) planes. Future experimental data will either validate or refute the concavity conjecture. It will improve understanding of hadron dynamics and promote the study of hadron spectra.