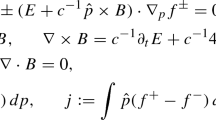Abstract
In this work, the hydrogen’s ionization energy was used to constrain the free parameter b of three Born–Infeld-like electrodynamics namely Born–Infeld itself, Logarithmic electrodynamics and Exponential electrodynamics. An analytical methodology capable of calculating the hydrogen ground state energy level correction for a generic nonlinear electrodynamics was developed. Using the experimental uncertainty in the ground state energy of the hydrogen atom, the bound \(b>5.37\times 10^{20}K\frac{V}{m}\), where \(K=2\), \(4\sqrt{2}/3\) and \(\sqrt{\pi }\) for the Born–Infeld, Logarithmic and Exponential electrodynamics respectively, was established. In the particular case of Born–Infeld electrodynamics, the constraint found for b was compared with other constraints present in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nonlinear electrodynamics (NLED) are extensions of Maxwell’s electromagnetism which arise when self-interaction in field equations is allowed. From the axiomatic point of view, they can be built from a Lagrangian of a vector field that respects three conditions: invariance under the Lorentz group, invariance under the U(1) gauge group and the Lagrangian depending only on combinations of the field and its first derivative, i.e. \(\mathcal {L}=\mathcal {L}\left( A_{\mu },\partial _{\nu }A_{\mu }\right) \).
The first two NLED proposals emerged in the 1930s in two very different contexts. In 1934, Born and Infeld proposed the Born–Infeld electrodynamics (BI) in order to deal with the divergence of the self-energy of a point charge [1, 2]. The BI electrodynamics was originally conceived as a fundamental theory for electromagnetism, but later it was found that it was not renormalizable and therefore should be considered as an effective theory.Footnote 1 In 1936, W. Heisenberg and H. Euler showed that, for energies below the electron mass, the self-coupling of the electromagnetic field induced by virtual pairs of electron-positrons can be treated as an effective field theory [4]. This theory is known as Euler–Heisenberg electrodynamics and it provided the first description of the vacuum polarization effect present in the QED [5].
Due to different motivations, other nonlinear electrodynamics were proposed – e.g. Logarithmic and Exponential electrodynamics [6,7,8,9] – and the NLED became a class of electromagnetic theories [10]. This class of theories has applications in several branches of physics being particularly interesting in systems where the NLED are minimally coupled with gravitation as in the cases of charged black holes [11,12,13,14,15,16,17] and cosmology [18,19,20,21,22].
Nonlinear electrodynamics have some different features with respect to Maxwell’s electrodynamics. Among these features, the most interesting is its non-trivial structure for radiation propagation. Due to nonlinearity of the field equations, the electromagnetic field self-interacts generating deformities in the light cone [23]. Thus, in the NLED context, the introduction of a background field affects the propagation velocity of the electromagnetic waves and generates the birefringence phenomenon. This phenomenon is present in all physically acceptable NLED with the exception of BI electrodynamics [24].
Excluding the Euler–Heisenberg electrodynamics and its variations [5], all other NLED have at least one free parameter which must be experimentally constrained [25]. These constraints can be directly obtained from measurements of atomic transitions [26, 27] and photon-photon scattering [28, 29] associated with self-interaction of NLED. Another possibility occurs in the astrophysical context where bounds to the NLED are imposed through photon splitting process present in magnetars spectra [30]. Moreover, for NLED where the birefringence effect is not negligible, bounds can be established through measurements of vacuum magnetic birefringence generated by the passage of a polarized laser beam through a magnetic dipole field (PVLAS collaboration – see [31] and references therein).
The purpose of this paper is to build a procedure capable of constraining nonlinear electrodynamics and to apply this procedure to three Born–Infeld-like electrodynamics. In Sect. 2, an introduction to the NLED is presented with emphasis on three specific nonlinear electrodynamics: Born–Infeld NLED, Logarithmic NLED and Exponential NLED. The procedure based on the hydrogen’s ionization energy which constrains NLED is developed in Sect. 3. In this section, bounds on the free parameters of each NLED are established and the results obtained are compared with those present in the literature. The final remarks are discussed in Sect. 4.
2 Nonlinear electrodynamics
The nonlinear electrodynamics in vacuum are described by the Lagrangian
where
are the contractions of the electromagnetic field strength tensor \(F^{\mu \nu }\) with its dual \(\tilde{F}^{\mu \nu }=\frac{1}{2}\varepsilon ^{\mu \nu \alpha \beta }F_{\alpha \beta }\). The variation of (1) with respect of \(A_{\mu }\) and Bianchi identity result in the nonlinear field equations
where \(\mathcal {L}_{F}\) e \(\mathcal {L}_{G}\) are the Lagrangian partial derivatives with respect to the invariants. This set of equations completely describe the system. The electric system displacement vector, from which nonlinear effects can be interpreted as a polarization of the medium, are given by \(D^{i}\equiv h^{0i}\) or, in terms of the Lagrangian derivatives, by
Usually, the system of Eqs. (2) and (3) is very difficult to be analytically solved. An exception is the electrostatic case where \(\vec {E}\) only depends on one variable. In this situation, Eq. (3) is automatically satisfied and (2) reduces to
Since the solution of (5) is identical to the Maxwell case, the problem becomes an algebraic problem associated with the inversion of the equation
2.1 Born–Infeld-like electrodynamics
An important sub-class of the NLED arises when (1) is an analytical function of the F and G. In this case, the Lagrangian can be written as a series of the invariants
where the linear coefficient in G can be neglected because of Bianchi identity. The main NLED (Born–Infeld, Euler–Heisenberg, etc) have this structure. For instance, the first coefficients for Born–Infeld electrodynamics [1] are
Any NLED which can be expanded as (7) with the first coefficients given by (8) is said a Born–Infeld-like electrodynamics [32, 33]. Any two Born–Infeld-like NLED are fundamentally different, but in the weak field limit, when the nonlinearities are small corrections to Maxwell electrodynamics, they exhibit the same properties. Three examples of Born–Infeld-like NLED are the Born–Infeld itself, the Logarithmic and the Exponential electrodynamics.
2.1.1 Born–Infeld electrodynamics
The Born–Infeld NLED was first proposed in 1934 by Born and Infeld [1, 2] and its Lagrangian is given by
This electrodynamic was created with the main purpose of avoiding the divergence of a point-like particle self-energy, but it shows other interesting features such as the absence of birefringence in vacuum [23, 24].
The electric displacement vector associated with (9) is given by
In the weak field regime, \(\mathcal {L}_{BI}\) can be approximated as
and (10) results in
where
is the relative permittivity tensor. For the pure electrostatic case,
The \(\chi =E^{2}/2b^{2}\) term is identified as the electric susceptibility which is associated with the medium’s polarization. Note that, because \(\chi >0\), the vacuum behaves as a medium which resists to the formation of an electric field.
The displacement vector generated by the nucleus of a hydrogen-like atom (a point particle system) is given by
where e is the electron charge and Z is the atomic number. The substitution of this expression into (10), with \(\vec {B}=0\), results in the electric field given by
where \(a_{0}\) is the Bohr radius and \(x=Z\frac{r}{a_{0}}\) and \(\varepsilon =\sqrt{\frac{Z^{3}e}{a_{0}^{2}b}}\) are dimensionless parameters. The parameter \(\varepsilon \) measures how much the electric field deviates from Maxwell’s electrodynamics.
2.1.2 Logarithmic and Exponential electrodynamics
The Logarithmic and Exponential electrodynamics belong to a special class, called Born–Infeld-like NLED, which was proposed in order to study topics such as inflation [6] and exact solutions of spherically symmetric static black holes [7, 8]. These electrodynamics are characterized by having a finite self-energy solution for a point-like charge but, unlike Born–Infeld NLED, they predict a birefringence effect in the presence of an electromagnetic background field.
The Lagrangians for Logarithmic and Exponential NLED are given by [32, 33]
where \(X=F+\frac{G^{2}}{2b^{2}}\). In the weak field limit, both Lagrangians can be approximated by (11) and the electric displacement vectors for pure electrostatic case are given by (12).
Following the same steps used in Born–Infeld case, we can calculate the electric fields generated by the nucleus of a hydrogen-like atom:
where x and \(\varepsilon \) are defined as in (14). The function \(W\left( z\right) \) is the Lambert functionFootnote 2 defined as the inverse function of \(z\left( W\right) =We^{W}\). When \(\varepsilon \rightarrow 0\), both electric fields reduce to the Maxwell case. Besides, \(\vec {E}_{Ex}\) diverges at the origin but slower than Maxwell, and \(\vec {E}_{Lg}\) is bounded from above in a similar way such as Born–Infeld field.
The behavior of the electric fields (14), (17) and (18) are shown in Fig. 1.
3 Testing NLED using hydrogen’s ionization energy
The theory about the energy levels of a hydrogen-like atom is described by the quantization of Dirac equation and subject to several correction factors such as the relativistic-recoil of the nucleus, electron self-energy, vacuum polarization due to the creation of virtual electron-positron pairs, etc (for details see [34, 35] and references therein). This theoretical structure in the context of Maxwell electrodynamics establishes a theoretical experimental agreement for the hydrogen’s ionization (HI) energy of 2 parts per \(10^{10}\) [36]. Thus, any correction to HI energy generated by modifications in the Maxwell potential must be a small correction and it can be treated perturbatively.
The Hamiltonian for a hydrogen-like atom in the context of NLED is given by
where \(\hat{K}\) is the kinetic term, \(\hat{V}_{M}\) is the Maxwell potential and \(\hat{V}_{G}\) is the potential energy of the NLED. Thus, \(\hat{H}_{0}\) is the usual hydrogen atom Hamiltonian and \(\hat{H}_{p}\) is a perturbation of this Hamiltonian.
The first order correction for HI energy due a Hamiltonian \(\hat{H}_{p}\) is given by
where \(\Psi _{100}\) is the ground state wave function
and
\(E_{G}\left( r\right) \) is the electric field absolute value generated by a NLED and \(E_{M}\left( r\right) =Ze/r^{2}\).
Defining the dimensionless variables \(r=\frac{a_{0}y}{Z}\) and \(r^{\prime }=\frac{a_{0}}{Z}x\), expression (19) is rewritten as
Since we are working in a perturbative regime where \(E_{G}\) provides small corrections to Maxwell’s case we might be tempted to expand \(E_{G}\) into a Laurent series and to keep only the first correction term. This approximation, however, is not valid at the lower limit of the integral since all terms neglected become relevant as \(x\le 1\). This is a crucial point in the determination of \(E_{HI_{1}}\) because this implies that each electrodynamic will produce a different correction even though, in the weak field limit, they are identical.
The term \(E_{M}\left( x\right) \) in (20) can be explicitly worked out and the \(E_{HI_{1}}\) results in
This expression will be the starting point to calculate the correction to the hydrogen’s ionization energy.
3.1 Hydrogen’s ionization energy for Born–Infeld electrodynamics
The substitution of Born–Infeld electric field (14) in (21) leads to
with
where \(G_{pq}^{mn}\left( \left. z\right| _{\vec {b}_{q}}^{\vec {a}_{p} }\right) \) are the MeijerG functions [37].
For small corrections to Maxwell’s potential \(\varepsilon \ll 1\), the MeijerG functions can be approximated byFootnote 3
Thus, the two first corrections for HI energy due the Born–Infeld electrodynamics are given by
with \(\varepsilon =\sqrt{\frac{Z^{3}e}{a_{0}^{2} b}}\). It is noteworthy that the first term in expression (23) was first obtained in [38]. A positive \(E_{HI_{1}}^{BI}\) indicates a reduction in the ionization energy. This is consistent with a susceptibility \(\chi >0\) which reduces the value of the electric field generated by the nucleus.
Comparison of the numerical results for \(\frac{a_{0}}{\left( Ze\right) ^{2} }E_{HI_{1}}^{BI}\) and the leading order approximation for different values of \(\varepsilon \) is shown in Table 1.
3.2 Hydrogen’s ionization energy for Logarithmic electrodynamics
The correction for the HI energy due the Logarithmic NLED is obtained using the electric field (17) in (21):
with
In the limit \(\varepsilon \ll 1\), the expressions above can be approximated by
Thus, up to leading order, expression (24) results in
This result is very similar to the first order Born–Infeld correction (23) differing only by a numerical factor of \(\mathcal {O}\left( 1\right) \).
Comparison of the numerical results for \(\frac{a_{0}}{\left( Ze\right) ^{2} }E_{HI_{1}}^{Lg}\) and the leading order approximation is presented in Table 2.
3.3 Hydrogen’s ionization energy for Exponential electrodynamics
The substitution of the Exponential NLED electric field (18) in (21) leads to
where
and
Integral \(I_{1}^{Ex}\) was calculated using the properties of the Lambert function W after the change of variable \(ue^{u}=\frac{\varepsilon ^{4}}{x^{4}}\). The other three integrals do not have analytical solutions. However, approximated solutions can be achieved following the steps described in Appendix A. The leading order correction for HI energy due the Exponential electrodynamics is obtained substituting (27), (A2), (A3) and (A4) into (26):
Comparison of the numerical results for \(\frac{a_{0}}{\left( Ze\right) ^{2} }E_{HI_{1}}^{Ex}\) and the leading order approximation is presented in Table 3.
3.4 Constraining parameter b
The ground state energy level correction calculated in the previous sections is generically given by
where \(K=2\), \(4\sqrt{2}/3\) and \(\sqrt{\pi }\) for the Born–Infeld, Logarithmic and Exponential electrodynamics respectively. The experimental value of hydrogen atom ionization energy in frequency units is [36]
It is important to emphasize that this value measured by the National Institute of Standards and Technology (NIST) is a purely experimental result which does not assume any theoretical background. The same does not occur with other measurements available in the literature – e.g. Particle Data Group [39] – which provide the ionization energy already assuming Maxwell’s electrostatic potential.
Imposing that the energy correction must be smaller than 3 times the experimental error \(\sigma _{\nu }\) i.e. \(E_{HI_{1}}<3h\sigma _{\nu }\), parameter b (with \(Z=1\)) is constrained by the expression
Restoring SI units and using values given by [40] we obtain
which in terms of the dimensionless parameter \(\varepsilon \) corresponds to
The last result is consistent with the approximation \(\varepsilon \ll 1\) used in the previous theoretical calculations.
For the particular Born–Infeld case, the expression (30) results in
Historically, the first estimation for \(b_{BI}\) was done by Born and Infeld [1] relating in an oversimplified manner the mass of the electron with its self-energy. The value found by those authors was \(b_{BI}>1.2\times 10^{20}\frac{V}{m}\). Forty years later Soft et al. [26] obtained \(b_{BI}>1.7\times 10^{22}\frac{V}{m}\) through a theoretical-experimental comparison involving muonic spectral transitions in lead atoms \(_{82}Pb\). Although an order of magnitude more precise than (32), the theoretical modeling presented in [26] is questionable because it does not take into account the loss of spherical symmetry due to the presence of the remaining leptons. This kind of approach is particularly problematic in NLED where the loss of spherical symmetry implies in \(\vec {\nabla }\times \vec {D}\ne 0\) [27] and consequently invalidates the expression (6) used in [26]. More recently in the 21st century it was suggested by Dávila et al. [30] that \(b_{BI}\) can be bound from the magnetars spectrum due to the effect of photon splitting. Following this approach, the authors of [30] estimated \(b_{BI}>2.0\times 10^{19}\frac{V}{m}\). Finally, at the end of 2016 ATLAS collaboration announced the first direct measurement of photon-photon scattering in ultra-peripheral heavy-ion collisions [28, 41]. Based on this measure, Ellis et al. [29] constrained Born–Infeld parameter to \(b_{BI}>4.3\times 10^{27}\frac{V}{m}\). This last result is six orders of magnitude larger than (32), but it was obtained from a much more complex theoretical-experimental arrangement [42] and therefore subject to greater uncertainty. In this sense, the treatment adopted here provides a simpler laboratory, and a mathematical method adaptable without difficulty to a great variety of NLED such as, for instance, the Logarithmic and Exponential electrodynamics.
4 Final remarks
In this work the ground state energy level correction \(E_{HI_{1}}\) for the hydrogen atom generated by three Born–Infeld-like electrodynamics was obtained. More specifically, a general expression for the correction \(E_{HI_{1}}\) was derived through a perturbative approach, then this correction was calculated for the Born–Infeld, Logarithmic and Exponential electrodynamics. Using the experimental uncertainty for HI energy, the free parameters b’s of each of these NLED were lower bounded, and for the particular Born–Infeld case the result found was compared with other constraints present in the literature. It is worth mentioning that the method developed here based on the expression (21) and the techniques of the Appendix A can easily be extended to constrain other nonlinear electrodynamics.
An important point in the derivation of \(E_{HI_{1}}\) concerns the need to know the electric field exactly (see discussion below Eq. (20)). This point can be observed by the distinct values obtained for \(E_{HI_{1}}^{BI}\), \(E_{HI_{1}}^{Lg}\) and \(E_{HI_{1}}^{Ex}\). Although different, these values are similar and we can wonder if the expression (30) could be used to constrain a more general class of NLED. The necessary and sufficient condition to apply the result (30) to others NLED is related to the behavior of the electric field. Observing Fig. 1 and the values of K (\(K_{BI}=2\), \(K_{Lg}=4\sqrt{2}/3\) and \(K_{Ex}=\sqrt{\pi }\)) we see that the greater is the difference between the Maxwell and Born–Infeld-like NLED electric fields the higher is the K value. Thus, we can state that any NLED whose electric field absolute value \(E_{NLED}\) fulfills the condition \(E_{BI}<E_{NLED}<E_{Ex}\) will have \(b_{Ex}<b_{NLED}<b_{BI}\). Also, since K slightly varies from \(K_{Ex}\) to \(K_{BI}\) we can estimate that any NLED which has an \(E_{NLED}\) near to \(E_{BI}\) or \(E_{Ex}\) will have its free parameter bounded by \(b_{NLED} \gtrsim 10^{21}V/m\). Thus, we can impose limits on a broad class of NLED only by knowing the behavior of its electric field.
Finally, it is important to discuss the possibility of application involving the electrodynamics of Euler–Heisenberg (EH) [4, 5]. EH electrodynamics is an effective description of the self-interaction process due the electron-positron virtual pairs present in QED (vacuum polarization). Thus, starting from EH NLED one could think of using the procedure developed in this work to obtain, in an alternative way, the vacuum polarization correction for the hydrogen’s ionization energy [34, 43]. The problem with this approach is that the EH electrodynamics is built assuming a slowly varying electromagnetic field in distances of the order of the electron Compton wavelength \(\lambda _{e}\), and this requirement is not satisfied in the calculation of \(E_{HI_{1}}\). The essential part of the integral \(E_{HI_{1}}\) is in the range [0,1[ (see Appendix A), and within this range the EH electric field rapidly varies at distances of order \(\lambda _{e} \). Therefore, the vacuum polarization effect associated with the hydrogen atom can not be described by the Euler–Heisenberg effective electrodynamics [43].
Notes
This kind of approach was explicitly performed when Fradkin and Tseytlin showed that BI electrodynamics appears as an effective theory of low energies in open string theories [3].
For \(z\in \mathbb {R} \) and \(z\ge 0\), \(W\left( z\right) \ge 0\) and it is monotonically increasing. Besides, \(\lim _{z\rightarrow 0}\frac{W\left( z\right) }{z}=1\) and \(\lim _{z\rightarrow \infty }W\left( z\right) =\infty \).
The \(\gamma _{E}\) is the Euler–Mascheroni constant.
References
M. Born, L. Infeld, Proc. R. Soc. Lond. A 144, 852 (1934)
M. Born, L. Infeld, Proc. R. Soc. Lond. A 147, 522 (1934)
E.S. Fradkin, A.A. Tseytlin, Phys. Lett. B 163, 123 (1985)
W. Heisenberg, H. Euler, Z. Phys. 98, 714 (1936)
M. Shifman, A. Vainshtein, J. Wheater (eds.), From Fields to Strings: circumnavigating theoretical physics, Ian Kogan Memorial Collection (World Scientific, Singapore, 2005), p. 445
B.L. Altshuler, Class. Quantum Gravity 7, 189 (1990)
H. Soleng, Phys. Rev. D 52, 6178 (1995)
S.H. Hendi, J. High Energy Phys. 03, 065 (2012)
S.H. Hendi et al., Eur. Phys. J. C 76, 150 (2016)
J. Plebansky, Lectures on Non-linear Electrodynamics (Nordita, Copenhagen, 1968)
E. Ayon-Beato, A. Garcia, Phys. Rev. Lett. 80, 5056 (1998)
J. Diaz-Alonso, D. Rubiera-Garcia, Phys. Rev. D 81, 064021 (2010)
J. Diaz-Alonso, D. Rubiera-Garcia, Phys. Rev. D 82, 085024 (2010)
R. Ruffini, Y.-B. Wu, S.-S. Xue, Phys. Rev. D 88, 085004 (2013)
R.R. Cuzinato, C.A.M. de Melo, K.C. de Vasconcelos, L.G. Medeiros, P.J. Pompeia, Astrophys. Space Sci. 359, 59 (2015)
S.H. Hendi, B. Eslam Panah, S. Panahiyan, J. High Energy Phys. 11, 157 (2015)
S.H. Hendi et al., Eur. Phys. J. C 76, 571 (2016)
V.A. De Lorenci, R. Klippert, M. Novello, J.M. Salim, Phys. Rev. D 65, 063501 (2002)
V.V. Dyadichev, D.V. Galtsov, A.G. Zorin, M.Y. Zotov, Phys. Rev. D 65, 084007 (2002)
M. Novello, S.E.P. Bergliaffa, J. Salim, Phys. Rev. D 69, 127301 (2004)
M. Novello, A.N. Araujo, J.M. Salim, Int. J. Mod. Phys. A 24, 5639 (2009)
L.G. Medeiros, Int. J. Mod. Phys. D 21, 1250073 (2012)
C.A.M. de Melo, L.G. Medeiros, P.J. Pompeia, Mod. Phys. Lett. A 30, 1550025 (2015)
G. Boillat, J. Math. Phys. 11, 941 (1970)
M. Fouché, R. Battesti, C. Rizzo, Phys. Rev. D 93, 093020 (2016)
G. Soff, Phys. Rev. A 7, 903 (1973)
H. Carley, M.K.-H. Kiessling, Phys. Rev. Lett. 96, 030402 (2006)
ATLAS Collaboration, Nat. Phys. 13, 852 (2017)
J. Ellis, N. Mavromatos, T. You, Phys. Rev. Lett. 118, 261802 (2017)
J.M. Davila, C. Schubert, M.A. Trejo, Int. J. Mod. Phys. A 29, 1450174 (2014)
F. Della Valle et al., Eur. Phys. J. C 76, 24 (2016)
P. Gaete, J. Helayël-Neto, Eur. Phys. J. C 74, 2816 (2014)
P. Gaete, J. Helayël-Neto, Eur. Phys. J. C 74, 3182 (2014)
P.J. Mohr, B.N. Taylor, Rev. Mod. Phys. 77, 1 (2005)
M.I. Eides, H. Grotch, V.A. Shelyuto, Phys. Rep. 342, 63 (2001)
A.E. Kramida, A critical compilation of experimental data on spectral lines and energy levels of hydrogen, deuterium, and tritium. Atom. Data Nucl. Data Tables 96(6), 586–644 (2010)
D. Zwillinger, Table of Integrals, Series, and Products (Elsevier Science, Amsterdam, 2014)
G. Heller, L. Motz, Phys. Rev. 46, 502 (1934)
K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38, 090001 (2014)
P.J. Mohr, D.B. Newell, B.N. Taylor, Rev. Mod. Phys. 88, 035009 (2016)
ATLAS Collaboration, ATLAS-CONF-2016-111 (2016)
M. Kłusek-Gawenda, P. Lebiedowicz, A. Szczurek, Phys. Rev. C 93, 044097 (2016)
E.A. Uehling, Phys. Rev. 48, 55 (1935)
Acknowledgements
The authors acknowledge A. E. Kramida and R. R. Cuzinatto for their useful comments. They are also grateful to CNPq-Brazil for financial support.
Author information
Authors and Affiliations
Corresponding author
Appendix A: \(I_{2}^{Ex}\), \(I_{3}^{Ex}\) and \(I_{4}^{Ex}\) approximate solutions
Appendix A: \(I_{2}^{Ex}\), \(I_{3}^{Ex}\) and \(I_{4}^{Ex}\) approximate solutions
The first step to calculate \(I_{2}^{Ex}\) is split the integral in the ranges [0, 1) and \(\left[ 1,\infty \right) \).
As \(\varepsilon \ll 1\) (small corrections to Maxwell’s case), the W function can be approximated by
which for the second integral is a great approximation and thus results in
where
is the exponential integral function.
The next step is to work out with the first integral. Performing the variable substitution \(ue^{u}=\frac{\varepsilon ^{4}}{x^{4}}\), the integral A leads to:
where the exponential of exponential was expanded in a Taylor series. The term \(e^{-\frac{u}{4}}\) ensures the convergence of the integral at the limit \(u\rightarrow \infty \) when \(n=0\). It is important to emphasize that although \(\varepsilon \ll 1\) the sum can not be truncated in the first terms. This occurs because the lower bound of integration depends on \(\varepsilon \). Thus, all terms of the sum will contribute to \(\varepsilon ^{2}\), \(\varepsilon ^{3}\), etc.
The third step is to rewrite A in terms of exponential integral functions and expanding these functions up to order \(\varepsilon ^{4}\):
The first two terms in the r.h.s. of A above cancel out for \(n=1\) (although they separately diverge). This can be seen by expanding \(\Gamma \left( \frac{1-n}{4}\right) \) around \(n=1\),
Thus,
where it was used the relation
By substituting A into (A1) we obtain the final expression for \(I_{2}^{Ex}\):
The computation procedure for the integrals \(I_{3}^{Ex}\) and \(I_{4}^{Ex}\) follows the same steps described above. For \(I_{3}^{Ex}\) we have:
Using \(\frac{\varepsilon ^{4}}{x^{4}}=ue^{u}\), the integral B is rewritten as
Thus,
And for the integral \(I_{4}^{Ex}\) we have:
Once more using the substitution \(\frac{\varepsilon ^{4}}{x^{4}}=ue^{u}\), the integral C is rewritten as:
Thus,
Results (A2), (A3) and (A4) are necessary to obtain Eq. (28) appearing in the main text.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Akmansoy, P.N., Medeiros, L.G. Constraining Born–Infeld-like nonlinear electrodynamics using hydrogen’s ionization energy. Eur. Phys. J. C 78, 143 (2018). https://doi.org/10.1140/epjc/s10052-018-5643-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5643-1