1 Introduction

Nowadays, it is a general belief that there should be some deep connection between gravity and thermodynamics. Bekenstein [1, 2] was the first who disclosed that a black hole can be regarded as a thermodynamic system with entropy and temperature proportional, respectively, to the horizon area and surface gravity [1,2,3,4]. The temperature T and entropy S together with the energy (mass) of the black holes satisfy the first law of thermodynamics \(\mathrm{d}M=T\mathrm{d}S\) [1,2,3,4]. Historically, Hawking and Page were the first who reported the existence of a certain phase transition in the phase space of the Schwarzschild anti-de Sitter (AdS) black hole [5]. In recent years, the studies on the phase transition of gravitational systems have got renewed interest. It has been shown that one can extend the thermodynamic phase space of a Reissner–Nordstrom (RN) black holes in an AdS space, by considering the cosmological constant as a thermodynamic pressure, \(P=-\Lambda /8\pi \) and its conjugate quantity as a thermodynamic volume [6,7,8,9,10,11]. In particular, it was argued that indeed there is a complete analogy for RN–AdS black holes with the van der Walls liquid–gas system with the same critical exponents [12]. The studies were also extended to nonlinear Born–Infeld electrodynamics [13]. In this case, one needs to introduce a new thermodynamic quantity conjugate to the Born–Infeld parameter, which is required for consistency of both the first law of thermodynamics and the corresponding Smarr relation [13]. Extended phase space thermodynamics and P–V criticality of the black holes with power-Maxwell electrodynamics were investigated in [14]. When the gauge field is in the form of logarithmic and exponential nonlinear electrodynamics, critical behavior of black hole solutions in Einstein gravity has also been explored [15]. Treating the cosmological constant as a thermodynamic pressure, the effects of higher curvature corrections from Lovelock gravity on the phase structure of asymptotically AdS black holes have also been explored. In this regard, critical behavior and phase transition of higher curvature corrections such as Gauss–Bonnet [16, 17] and Lovelock gravity have also been investigated [18, 19]. The studies were also extended to the rotating black holes, where phase transition and critical behavior of Myers–Perry black holes have been investigated [20]. Other studies on the critical behavior of the black hole spacetimes in an extended phase space have been carried out in [21,22,23,24,25,26].

Although Maxwell theory is able to explain a variety of phenomena in electrodynamics, it suffers some important problems such as then divergence of the electric field of a point-like charged particle or infinity of its self energy. In order to solve these problems, one may get help from the nonlinear electrodynamics [27,28,29,30]. Inspired by developments in string/M-theory, the investigation on the nonlinear electrodynamics has got a lot of attention in recent years.

On the other side, a scalar field called dilaton emerges in the low energy limit of string theory [31]. Breaking of spacetime supersymmetry in ten dimensions leads to one or more Liouville-type potentials, which exist in the action of dilaton gravity. In addition, the presence of the dilaton field is necessary if one couples the gravity to other gauge fields. Therefore, the dilaton field plays an essential role in string theory and it has attracted extensive attention in the literature [32,33,34,35,36,37,38,39,40,41,42,43,44]. Critical behavior of the Einstein–Maxwell-dilaton black holes has been studied in [45]. In the context of Born–Infeld and power-Maxwell nonlinear electrodynamics coupled to the dilaton field, critical behavior of \((n+1)\)-dimensional topological black holes in an extended phase space has been explored in [46, 47], respectively. Although the asymptotic behavior of these solutions [46, 47] are neither flat nor anti-de Sitter (AdS), it was found that the critical exponents have the universal mean field values and do not depend on the details of the system, while the thermodynamic quantities depend on the dilaton coupling constant, nonlinear parameter and the dimension of the spacetime. In the present work, we would like to extend the study of the critical behavior of the black holes, in an extended phase space, to other nonlinear electrodynamics in the context of dilaton gravity such as exponential and logarithmic nonlinear electrodynamics. Following [13, 47], and in order to satisfy the Smarr relation we shall extend the phase space to include a nonlinear parameter as a thermodynamic variable and consider its conjugate quantity as polarization. We will complete the analogy of the nonlinear dilaton black holes with a Van der Waals liquid–gas system and work in the canonical ensemble. In addition, we calculate the critical exponents and show that they are universal and are independent of the dilaton and nonlinearity parameters. Finally, we shall explore the phase transition of dilaton black holes coupled to nonlinear electrodynamics by considering the discontinuity in the Gibss free energy of the system. We will see that in addition to the first- and second-order phase transition in charged black holes, the presence of the dilaton field admits a zeroth-order phase transition in the system. This phase transition is occurred due to a finite jump in the Gibbs free energy which is generated by dilaton–electromagnetic coupling constant, \(\alpha \), for a certain range of pressure. This novel behavior indicates a small/large black hole zeroth-order phase transition in which the response functions of the black holes thermodynamics diverge, e.g. the isothermal compressibility.

This paper is outlined as follows. In the next section, we present the action, basic field equations and our metric ansatz for dilaton black holes. In Sect. 3, we explore the critical behavior of dilaton black holes coupled to exponential nonlinear (EN) electrodynamics. In Sect. 4, we investigate P–V criticality of dilaton black holes when the gauge field is in the form of logarithmic nonlinear (LN) electrodynamics. In Sect. 5, we investigate the effects of nonlinear gauge field parameter in the strong nonlinear regime on the critical behavior of the system. In Sect. 6, we explore the phase transition of nonlinear dilaton black holes. We finish with closing remarks in Sect. 7.

2 Basic field equations

We examine the following action of Einstein-dilaton gravity which is coupled to nonlinear electrodynamics:

$$\begin{aligned} S= & {} \frac{1}{16\pi }\int \mathrm{d}^{4}x\sqrt{-g}\left( \mathcal {R}\right. \nonumber \\&\left. -\,2 g^{\mu \nu } \partial _{\mu } \Phi \partial _{\nu }\Phi -V(\Phi ) +L(F,\Phi )\right) , \end{aligned}$$
(1)

where \({\mathcal {R}}\) is the Ricci scalar curvature, \(\Phi \) is the dilaton field and \(V(\Phi )\) is the potential for \(\Phi \). We assume the dilaton potential to have the form of two Liouville terms [34, 40],

$$\begin{aligned} V(\Phi ) = 2\Lambda _{0} e^{2\zeta _{0}\Phi } +2 \Lambda e^{2\zeta \Phi }, \end{aligned}$$
(2)

where \(\Lambda _{0}\), \(\Lambda \), \( \zeta _{0}\) and \( \zeta \) are constants that should be determined. In the action (1), \(L(F,\Phi )\) is the Lagrangian of two Born–Infeld-like versions of nonlinear electrodynamics which are coupled to the dilaton field [48, 49],

$$\begin{aligned} L(F,\Phi )=\left\{ \begin{array}{ll} 4\beta ^{2} e^{2\alpha \Phi }\left[ \exp \left( -\frac{e^{- 4\alpha \Phi }F^2}{4\beta ^{2}}\right) -1\right] ,\quad \quad \quad {\mathrm {END}} , &{} \\ &{}\\ -8\beta ^2 e^{2\alpha \Phi } \ln \left( 1+\frac{ e^{-4\alpha \Phi }F^2}{8 \beta ^2}\right) ,\quad ~ \quad \quad \quad {\mathrm {LND}}, \end{array} \right. \end{aligned}$$
(3)

where END and LND stand for an exponential and a logarithmic nonlinear dilaton Lagrangian, respectively. Here \(\alpha \) is a constant which determines the strength of coupling of dilaton and electromagnetic field. The parameter \(\beta \), with dimension of mass, represents the maximal electromagnetic field strength which in string theory can be related to the string tension, \(\beta =\frac{1}{2\pi \alpha '}\)[50]. In fact \(\beta \) determines the strength of the nonlinearity of the electrodynamics. In the limit of large \(\beta \) (\(\beta \rightarrow \infty \)), the system goes to the linear regime and the nonlinearity of the theory disappears and the nonlinear electrodynamic theory reduces to the linear Maxwell electrodynamics. On the other hand, as \(\beta \) decreases (\(\beta \rightarrow 0\)), we go to the strong nonlinear regime of the electromagnetic and thus the behavior of the system will be completely different (see Sect. 5). In Eq. (3) \(F^2=F_{\mu \nu }F^{\mu \nu }\), where \(F_{\mu \nu }\) is the electromagnetic field tensor. By varying the action (1) with respect to the gravitational field \(g_{\mu \nu }\), the dilaton field \(\Phi \) and the electromagnetic field \(A_{\mu }\), we arrive at the following field equations [48, 49]:

$$\begin{aligned} \mathcal{R}_{\mu \nu }= & {} 2 \partial _{\mu }\Phi \partial _{\nu }\Phi +\frac{1}{2}g_{\mu \nu }V(\Phi )\nonumber \\&-\,2e^{-2\alpha \Phi }\partial _{Y}{\mathcal{L}}(Y) F_{\mu \eta } F_{\nu }^{~\eta } \nonumber \\&+\,n\beta ^2 e^{2\alpha \Phi } \left[ 2Y\partial _{Y}{\mathcal{L}}(Y)-{\mathcal{L}}(Y)\right] g_{\mu \nu }, \end{aligned}$$
(4)
$$\begin{aligned}&\nabla ^{2}\Phi =\frac{1}{4}\frac{\partial V}{\partial \Phi }+ n\alpha \beta ^2 e^{2\alpha \Phi }\left[ 2{ Y}\partial _{Y}{\mathcal{L}}(Y)-\mathcal{L}(Y)\right] , \end{aligned}$$
(5)
$$\begin{aligned}&\nabla _{\mu }\left( e^{-2\alpha \Phi } \partial _{Y}{\mathcal{L}}(Y) F^{\mu \nu }\right) =0, \end{aligned}$$
(6)

where \(n=2\) for END and \(n=-\,4\) for LND cases. In the above field equations we have used a shorthand for \(L(F,\Phi )\),

$$\begin{aligned} L(F,\Phi )= & {} 2 n\beta ^2{\mathcal {L}}(Y),~~~~~~~~~{\mathcal {L}}(Y)\nonumber \\= & {} \left\{ \begin{array}{ll} \exp (-Y)-1,\quad \quad \qquad \mathrm{END}, &{} \\ &{}\\ \ln (1+Y),\quad \quad \quad ~\qquad \mathrm{LND}, \end{array} \right. \end{aligned}$$
(7)

and

$$\begin{aligned} Y= \frac{e^{-4\alpha \Phi }F^2}{2 \beta ^2|n|}. \end{aligned}$$
(8)

In the limit case \(\beta \rightarrow \infty \), which is equal to \({\mathcal {L}}(Y)=-Y\) for END and \({\mathcal {L}}(Y)=Y\) for LND cases, the above system of equations recover the corresponding equations for Einstein–Maxwell-dilaton gravity [40].

We would like to find topological solutions of the above field equations. The most general such metric can be written in the form

$$\begin{aligned} \mathrm{d}s^2=-f(r)\mathrm{d}t^2 +{\mathrm{d}r^2\over f(r)}+ r^2R^2(r)\mathrm{d}\Omega _{k}^2 , \end{aligned}$$
(9)

where f(r) and R(r) are functions of r which should be determined, and \(\mathrm{d}\Omega _{k}^2\) is the line element of a two-dimensional hypersurface \(\Sigma \) with constant curvature,

$$\begin{aligned} d\Omega _k^2=\left\{ \begin{array}{ll} \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2,\quad \quad \!\!\mathrm{for}\quad k=1, &{} \\ \mathrm{d}\theta ^2+\theta ^2 \mathrm{d}\phi ^2,\quad \quad \quad \mathrm{for}\quad k=0,&{} \\ \mathrm{d}\theta ^2+\sinh ^2\theta \mathrm{d}\phi ^2, \quad \mathrm{for}\quad k=-1.&{} \end{array} \right. \end{aligned}$$
(10)

For \(k = 1\), the topology of the event horizon is the two-sphere \(S^2\), and the spacetime has the topology \(R^2 \times S^2\). For \(k = 0\), the topology of the event horizon is that of a torus and the spacetime has the topology \(R^2 \times T^2\). For \(k = -1\), the surface \(\Sigma \) is a 2-dimensional hypersurface \(H^2\) with constant negative curvature. In this case the topology of spacetime is \(R^2 \times H^2\).

In the remaining part of this paper, we consider the critical behavior of END and LND black holes.

3 Critical behavior of END black holes

In this section, first of all, we review the solution of dilatonic black holes coupled to EN electrodynamics [48]. Then we construct the Smarr relation and the equation of state of the system to study the critical behavior of the system.

3.1 Review of END black holes

In order to solve the system of Eqs. (4) and (5) for three unknown functions f(r), R(r) and \(\Phi (r)\), we make the ansatz [38]

$$\begin{aligned} R(r)=e^{\alpha \Phi }. \end{aligned}$$
(11)

Inserting this ansatz and metric (9) into the field equations (4)–(6), one can show that these equations have the following solutions [48]:

$$\begin{aligned} \Phi (r)= & {} \frac{\alpha }{\alpha ^{2}+1}\ln \left( \frac{b}{r}\right) , \end{aligned}$$
(12)
$$\begin{aligned} A_{t}^\mathrm{END}= & {} b^{\gamma }\beta (\alpha ^2+1)\left( \frac{\beta b^{\gamma }}{q}\right) ^{\frac{1-\gamma }{\gamma -2}}\left( \frac{1 -\,\alpha ^2}{4}\right) ^{\frac{1}{2\gamma -4}}\nonumber \\&\times \, \Bigg \{-\frac{1}{4}\Gamma \left( \frac{\alpha ^2+1}{4},\frac{1 -\alpha ^2}{4}L_{W}(\eta )\right) \nonumber \\&+\,\frac{1}{\alpha ^2-1}\left[ \Gamma \left( \frac{\alpha ^2+5}{4},\frac{1 -\alpha ^2}{4}L_{W}(\eta )\right) \right. \nonumber \\&\left. -\,\frac{1}{2}\Gamma \left( \frac{\alpha ^2+1}{4}\right) \right] \Bigg \}. \end{aligned}$$
(13)
$$\begin{aligned}&f(r)\mid _\mathrm{END}=-k\frac{ {\alpha }^{2}+1}{ {\alpha }^{2}-1 }{b}^{-\gamma }{r}^{\gamma }\nonumber \\&\quad -\,\frac{m}{r^{1-\gamma }}+\frac{(\Lambda +2\beta ^2) \left( {\alpha }^{2}+1 \right) ^{2}{b}^{\gamma }}{\alpha ^{2}-3 }r^{2-\gamma }\nonumber \\&\quad +\,2 \beta q{\left( \alpha ^2+1\right) ^2} r^{\gamma -1}{\left( \frac{\beta ^2 b^{2\gamma }}{q^2}\right) }^{\frac{1 -\gamma }{2\gamma -4}}{L_W^{\frac{3-2\gamma }{2\gamma -4}}(\eta )}\nonumber \\&\quad \times \,\Bigg \{\frac{L_W^2(\eta )}{\alpha ^2+5}\digamma \left( \frac{\alpha ^2+5}{4}, \frac{\alpha ^2+9}{4},\frac{\alpha ^2-1}{4}L_W(\eta )\right) \nonumber \\&\quad -\,\frac{1}{\alpha ^2\!-\!3}\digamma \left( \frac{\alpha ^2\!-\!3}{4},\frac{\alpha ^2\!+\!1}{4},\frac{\alpha ^2\!-\!1}{4}L_W(\eta )\right) \Bigg \},\nonumber \\ \end{aligned}$$
(14)

where m and q are integration constants which are related to the mass and the charge of the black holes. Also, \(L_W(x)={LambertW(x)}\) is the Lambert function and \( \digamma (a,b,z)\) is the hypergeometric function [51, 52]. Here \(\eta \) and \(\gamma \) are defined by

$$\begin{aligned} \eta \equiv \frac{q^{2}r^{2\gamma -4}}{\beta ^{2}b^{2\gamma }},\qquad \gamma =\frac{2\alpha ^2}{\alpha ^2+1}. \end{aligned}$$
(15)

The above solutions will fully satisfy the system of Eqs. (4) and (5) provided we have

$$\begin{aligned} \zeta _{0}=\frac{1}{\alpha },\qquad \zeta =\alpha ,\qquad \Lambda _0=k\frac{b^{-2}\alpha ^2}{\alpha ^2-1}. \end{aligned}$$
(16)

According to the definition of mass due to Abbott and Deser [53], the mass of the solution (14) is [48]

$$\begin{aligned} {M}=\frac{b^{\gamma }m \omega }{8\pi (\alpha ^2+1)}, \end{aligned}$$
(17)

where \(\omega \) represents the area of the constant hypersurface \(\Sigma \). In Eq. (17), one can find the mass parameter as a function of the horizon radius by considering \(f(r=r_+)=0\) [48]. The charge of the solution is given by [48]

$$\begin{aligned} {Q}=\frac{q\omega }{4\pi }. \end{aligned}$$
(18)

The Hawking temperature of the END black hole can be calculated as [48]

$$\begin{aligned} T_{+}\mid _{\text {END}}= & {} \frac{1}{4\pi }\left( \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) _{r_+}\nonumber \\= & {} -\frac{(\alpha ^2+1)}{4\pi }{r_{+} ^{1-\gamma }}\left\{ k\frac{ b^{-\gamma } r_{+}^{2\gamma -2}}{\alpha ^2-1}\right. \nonumber \\&+\,(\Lambda +2\beta ^2)b^{\gamma }-2\beta qr_{+}^{\gamma -2}\left( \frac{1}{\sqrt{L_{W}(\eta _{+})}}\right. \nonumber \\&\left. \left. -\,\sqrt{L_{W}(\eta _{+})}\right) \right\} , \end{aligned}$$
(19)

where \(\eta _+=\eta ({r=r_+})\). Applying the well-known area law, we can find the entropy of the black hole,

$$\begin{aligned} S=\frac{A}{4}=\frac{b^\gamma r_+^{2-\gamma }\omega }{4}. \end{aligned}$$
(20)

The electric potential of the black hole is obtained [48]:

$$\begin{aligned} U\mid _\mathrm{END}= & {} b^{\gamma }\beta (\alpha ^2+1)\left( \frac{\beta b^{\gamma }}{q}\right) ^{\frac{1-\gamma }{\gamma -2}}\left( \frac{1 -\alpha ^2}{4}\right) ^{\frac{1}{2\gamma -4}}\nonumber \\&\times \,\Bigg \{ -\frac{1}{4}\Gamma \left( \frac{\alpha ^2+1}{4},\frac{1-\alpha ^2}{4} L_{W}(\eta _{+})\right) \nonumber \\&+\,\frac{1}{\alpha ^2-1}\left[ \Gamma \left( \frac{\alpha ^2+5}{4}, \frac{1-\alpha ^2}{4}L_{W}(\eta _{+})\right) \right. \nonumber \\&\left. -\,\frac{1}{2}\Gamma \left( \frac{\alpha ^2+1}{4}\right) \right] \Bigg \}. \end{aligned}$$
(21)

3.2 First law of thermodynamics and phase structure

We start by calculating thermodynamic variables to check the first law of the black hole thermodynamics. We consider the cosmological constant as the black hole pressure and its associated conjugate as the volume of the black hole. As mentioned above, entropy of black hole is related to its horizon area, so we can obtain the thermodynamic volume of the black hole as

$$\begin{aligned} V=\int 4S \mathrm{d}r_+=\frac{(\alpha ^2+1)b^{\gamma }}{(\alpha ^2+3)r_+^{\gamma -3}}\omega \end{aligned}$$
(22)

As we take the cosmological constant as the black hole pressure, the ADM mass should be interpreted as the enthalpy, \(H\equiv M\) rather than the internal energy [54], and it should be a function of extensive quantities: entropy and charge, and intensive quantities: pressure and nonlinear parameter. Indeed, in the extended phase space, another thermodynamic variable is the nonlinear parameter \(\beta \), of which the conjugate is defined as [13]

$$\begin{aligned} B=\left( \frac{\partial M}{\partial \beta }\right) _{S,Q,P}. \end{aligned}$$
(23)

Therefore, the first law takes the form

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+U\mathrm{d}Q+V\mathrm{d}P+B\mathrm{d}\beta . \end{aligned}$$
(24)

The conjugate of \(\beta \) has the dimension of polarization per unit volume and can be interpreted as the vacuum polarization [50]. Throughout this paper, we choose the unit in which, from dimensional analysis, one can find \([\beta ]=[m]=[b]=[q]\), and \(\alpha \) is a dimensionless parameter. We shall also investigate the effects of both the dilaton parameter \(\alpha \) and the nonlinear parameter \(\beta \) on the critical behavior and phase structure of the nonlinear dilaton black holes.

According to the definition (23), the conjugate quantity of the nonlinear parameter for the END black hole is given by

$$\begin{aligned} B\mid _\mathrm{END}= & {} \frac{b^\gamma (\alpha ^2+1)\omega }{8\pi }\Bigg \{\frac{4\beta b^\gamma r_+^{3-2\gamma }}{\alpha ^2-3}\nonumber \\&+\,q(\alpha ^2+1)\left( \frac{\beta b^\gamma }{q}\right) ^{\frac{1-\gamma }{\gamma -2}}L_{W}(\eta _+) ^{\frac{3-2\gamma }{2\gamma -4}}\nonumber \\&\times \,\Bigg [\frac{L_W^2(\eta _+)}{\alpha ^2+5}\digamma \left( \frac{\alpha ^2 +5}{4},\frac{\alpha ^2+9}{4},\frac{\alpha ^2-1}{4}L_W(\eta _+)\right) \nonumber \\&-\,\frac{1}{\alpha ^2-3}\digamma \left( \frac{\alpha ^2-3}{4},\frac{\alpha ^2+1}{4} ,\frac{\alpha ^2-1}{4}L_W(\eta _+)\right) \Bigg ]\Bigg \}.\nonumber \\ \end{aligned}$$
(25)

In the linear regime where \(\beta \rightarrow \infty \), the conjugate of the nonlinear parameter goes to zero. As an example, let us expand B for large \(\beta \) for \(\alpha =0,1\). We find

$$\begin{aligned}&B\mid _\mathrm{END}= \left\{ \begin{array}{ll} \frac{q^4 \omega }{80\pi r^5\beta ^3}-\frac{5 q^6\omega }{432\pi r^9 \beta ^5}+O\left( \frac{1}{\beta ^7}\right) ~~~~~~~\mathrm{for \ \ \alpha =0,} \\ {} &{} \\ \frac{q^4 \omega }{48\pi r^3 b^2\beta ^3}-\frac{q^6\omega }{48\pi r^5 b^4 \beta ^5}+O\left( \frac{1}{\beta ^7}\right) ~~~~\mathrm{for \ \ \alpha =1.} &{} \\ &{} \end{array} \right. \end{aligned}$$
(26)

One can calculate the pressure as

$$\begin{aligned} P=\frac{(\alpha ^2+3) b^\gamma }{(\alpha ^2-3)r_+^\gamma }\frac{\Lambda }{8\pi }, \end{aligned}$$
(27)

which is in accordance with the result of [45, 46]. In the absence of the dilaton field (\(\alpha =0=\gamma \)), the above expression for the pressure reduces to the pressure of RN–AdS black holes in an extended phase spaces [12]. It is easy to show that all conserved and thermodynamic quantities in this theory satisfy the first law of the black hole thermodynamics (24). Using a scaling (dimensional) argument, the corresponding Smarr formula per unit volume \(\omega \) can be written as

$$\begin{aligned} M=\frac{2}{\alpha ^2+1}TS+\frac{\alpha ^2-1}{\alpha ^2+1}(2VP+\beta B)+UQ. \end{aligned}$$
(28)

One can easily check that in the limit case \(\alpha =0\), this relation is exactly the Smarr formula of [15], while in the case of linear Maxwell electrodynamics, it reduces to the Smarr relation of the RN–AdS black hole [12].

3.3 Equation of state

The critical point can be obtained by solving the following equations:

$$\begin{aligned} \frac{\partial P}{\partial v}\Big |_{T_c}=0, \qquad \qquad \frac{\partial ^2 P}{\partial v^2}\Big |_{T_c}=0. \end{aligned}$$
(29)

In order to obtain the critical point, we should introduce the equation of state \(P=P(V,T)\) by Eqs. (19) and (27). It is a matter of calculation to show

$$\begin{aligned} P\mid _\mathrm{END}= & {} \frac{\Gamma T}{r_+}+\frac{\Gamma (\alpha ^2+1)}{2\pi }\Bigg [\frac{kr_+^{\gamma -2}}{2(\alpha ^2-1)b^\gamma }\nonumber \\&+\frac{\beta ^2 b^\gamma }{r_+^\gamma }+\frac{q \beta }{r_+^2}\Big (\sqrt{L_W(\eta _+)}-\frac{1}{\sqrt{L_W(\eta _+)}}\Big )\bigg ],\nonumber \\ \end{aligned}$$
(30)

where we have defined

$$\begin{aligned} \Gamma =\frac{(3+\alpha ^2)}{2(3-\alpha ^2)(\alpha ^2+1)}. \end{aligned}$$
(31)

Note that Eq. (30) does not depend on the volume explicitly. However, if one pays attention to Eq. (22), one sees that the volume is a function of \(r_+\). Thus, we can rewrite Eq. (30) as

$$\begin{aligned} P\mid _\mathrm{END}= & {} \frac{T}{v}-\frac{k(\alpha ^2+3)}{8\pi (\alpha ^2-3)(\alpha ^2-1)} \frac{(v\Gamma )^{\gamma -2}}{b^\gamma }\nonumber \\&-\,\frac{\beta ^2(\alpha ^2+3)}{4\pi (\alpha ^2-3)}\left( \frac{b}{v\Gamma }\right) ^\gamma \nonumber \\&-\,\frac{q\beta (\alpha ^2+3)}{4\pi (\alpha ^2-3)v^2\Gamma ^2}\bigg (\sqrt{L_W(\eta ^\prime )}\nonumber \\&-\,\frac{1}{\sqrt{L_W(\eta ^\prime )}}\bigg ), \end{aligned}$$
(32)

where

$$\begin{aligned} \eta ^\prime =\left( \frac{q~ (v\Gamma )^{\gamma -2}}{\beta ~ b^\gamma }\right) ^2. \end{aligned}$$
(33)

It is interesting to make a dimensional analysis of Eq. (32). Following [12], we can write the physical pressure and temperature as

$$\begin{aligned} {\mathcal {P}}=\frac{\hbar c}{l_{p}^{2}}P,\qquad {\mathcal {T}}=\frac{\hbar c}{\kappa }T, \end{aligned}$$
(34)

where \(l_{p}=\sqrt{\hbar G/c^{3}}\) is the Planck length, \(\kappa \), \(\hbar \) and c are the Boltzmann constant, the reduced Planck constant and the speed of light, respectively. Inserting Eq. (34) in Eq. (30), we can define the specific volume as

$$\begin{aligned} v=\frac{l_p^2 r_+}{\Gamma }. \end{aligned}$$
(35)

Hereafter, we set \(\hbar =c=G=l_p=1\), for simplicity. In order to find the critical volume \(v_c\), the critical temperature \(T_c\) and the critical pressure \(P_c\), we should solve Eq. (29). However, due to the complexity of the equation of state, we consider the large \(\beta \) limit of Eq. (32). It is easy to show that

$$\begin{aligned} P_\mathrm{END}\Big |_{\beta \rightarrow \infty }= & {} \frac{T}{v}-\frac{(\alpha ^2+3)}{8\pi (\alpha ^2-3)b^\gamma }\Bigg \{\frac{k(v\Gamma )^{\gamma -2}}{ (\alpha ^2-1)}\nonumber \\&+\,q^2(v\Gamma )^{\gamma -4}\nonumber \\&-\,\frac{q^4(v\Gamma )^{3\gamma -8}}{4 b^{2\gamma }\beta ^2}\Bigg \}+O\left( \frac{1}{\beta ^4}\right) . \end{aligned}$$
(36)
Fig. 1
figure 1

P–v diagram of END black holes

Full size image

Considering the large \(\beta \) limit, we can obtain the properties of the critical point:

$$\begin{aligned} v_c= & {} \frac{\Pi }{\Gamma }-\frac{q^4(\alpha ^2+4)(\alpha ^2+7)}{8\Gamma k\beta ^2b^{2\gamma }}\Pi ^{(2\gamma -5)}+O\left( \frac{1}{\beta ^4}\right) ,\nonumber \\ P_c= & {} \frac{q^2(\alpha ^2+3)^2}{8\pi (\alpha ^2-3)b^\gamma }\Pi ^{\gamma -4} +\frac{q^4(\alpha ^2+7)}{16\pi \beta ^2b^{3\gamma }}\Gamma \Pi ^{3\gamma -8}\nonumber \\&+\,O\left( \frac{1}{\beta ^4}\right) ,\nonumber \\ T_c= & {} -\frac{k(\alpha ^2+1)}{\pi (\alpha ^2-1)(\alpha ^2+3)b^\gamma }\Pi ^{\gamma -1}\nonumber \\&+\,\frac{q^4(\alpha ^2+4)}{8\pi \beta ^2 b^{3\gamma }}\Pi ^{3\gamma -7}+O\left( \frac{1}{\beta ^4}\right) , \end{aligned}$$
(37)

where

$$\begin{aligned} \Pi =\sqrt{\frac{q^2}{k}\left( \alpha ^2+2\right) (\alpha ^2+3)}. \end{aligned}$$
(38)

Let us note that Eq. (37) is similar to the corresponding one in Born–Infeld-dilaton (BID) black holes [46]. This is an expected result since for large \(\beta \) the equation of state of END and BID is exactly the same. One can find that from Eq. (37) follows the interesting relation

$$\begin{aligned} \rho _{c}= & {} \frac{P_{c}v_{c}}{T_{c}}=-\frac{(\alpha ^2+3)(\alpha ^2-1)}{4(\alpha ^2+2)}\Bigg \{1\nonumber \\&-\frac{q^2}{2(\alpha ^2+2)\beta ^2 b^{2\gamma }} \Pi ^{2\gamma -4}\Bigg \}+O\left( \frac{1}{\beta ^4}\right) . \end{aligned}$$
(39)

In the absence of the dilaton field (\(\alpha =0\)) and considering linear electrodynamics where \(\beta \rightarrow \infty \), we arrive at \(\rho _c={3}/{8}\), which is a universal value for a Van der Waals fluid. This implies that the critical behavior of this type of black holes resembles the Van der Waals gas [12].

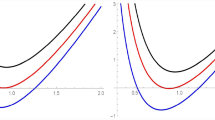
To summarize, our solution can face with a phase transition when temperature is below its critical value. One may predict this behavior by considering an isothermal P–v diagram. It is expected that the P–v diagrams for our solution and the Van der Waals gas have a similar behavior. In Fig. 1 we have plotted the behavior of P in terms of v. From these figures we see that, in the absence/presence of a dilaton field, the nonlinear black hole resemble the Van der Waals fluid behavior.

3.4 Gibbs free energy

In another important approach to determine the critical behavior of a system one refers to its thermodynamic potential. In the canonical ensemble and extended phase space, the thermodynamic potential closely associates with the Gibbs free energy \(G=M-TS\). It is a matter of calculation to show that

$$\begin{aligned} G_\mathrm{END}= & {} \frac{\omega (\alpha ^2+1)b^\gamma }{8\pi }\left\{ \frac{k~r_{+}}{2(\alpha ^2+1)b^\gamma }\right. \nonumber \\&+\frac{(\Lambda +2\beta ^2)(\alpha ^2-1)b^\gamma }{2(\alpha ^2-3)r_{+}^{2\gamma -3}}\nonumber \\&+2q\beta \left( \frac{q}{\beta b^\gamma }\right) ^{\frac{\gamma -1}{\gamma -2}} L_W(\eta _+)^{-\frac{2\gamma -3}{2\gamma -4}}\nonumber \\&\times \left[ \frac{L_W(\eta _+)^2}{\alpha ^2+5}\right. \nonumber \\&\times \left. \digamma \left( \left[ \frac{\alpha ^2+5}{4}\right] , \left[ \frac{\alpha ^2+9}{4}\right] ,\frac{\alpha ^2-1}{4}L_W(\eta _+)\right) \right. \nonumber \\&\left. -\frac{1}{\alpha ^2-3}\digamma \left( \left[ \frac{\alpha ^2-3}{4}\right] ,\left[ \frac{\alpha ^2+1}{4}\right] ,\frac{\alpha ^2-1}{4}\right. \right. \nonumber \\&\times \left. \left. L_W(\eta _+)\right) \right] \nonumber \\&\left. -q\beta r_{+}^{1-\gamma }\left[ \frac{1}{\sqrt{L_W(\eta _+)}}-\sqrt{L_W(\eta _+)}\right] \right\} . \end{aligned}$$
(40)

Expanding for large \(\beta \) in the absence of the dilaton field (\(\alpha =0\)), we arrive at

$$\begin{aligned} G_\mathrm{END}\Big |_{\beta \rightarrow \infty }=\frac{k~r_{+}}{4}-\frac{2\pi r_{+}^3P}{3}+\frac{3 q^2}{4 r_{+}}-\frac{7q^4}{80 r_{+}^5\beta ^2}+O\left( \frac{1}{\beta ^2}\right) . \end{aligned}$$
(41)

This is nothing but the Gibbs free energy of RN–AdS black holes with a nonlinear leading-order correction term [12]. In order to study the Gibbs free energy, we plot Fig. 3a. One can see a swallow-tail behavior in this figure, which indicates a phase transition below a critical value of temperature.

3.5 Critical exponents

Here we would like to study the critical exponents for the END case. For this purpose, we first calculate the specific heat:

$$\begin{aligned} C_V=T\left( \frac{\partial S}{\partial T}\right) \Big |_V. \end{aligned}$$
(42)

We also redefine Eq. (20) as

$$\begin{aligned} S=S(V,T)=\frac{b^{\gamma }\omega }{4}\left[ \frac{(\alpha ^2+3) V}{(\alpha ^2+1)b^\gamma }\right] ^{{(\gamma -2)}/{(\gamma -3)}}. \end{aligned}$$
(43)

It is clear that the entropy does not depend on the temperature in this relation, so \(C_V=0\). This indicates that the relative critical exponent will be zero,

$$\begin{aligned} C_V\propto \left( \frac{T}{T_c}-1\right) ^{\alpha ^\prime }\Rightarrow \alpha ^\prime =0. \end{aligned}$$
(44)

In order to find the other critical exponent we consider the following definition:

$$\begin{aligned} \tau =\frac{T}{T_c}\qquad \qquad p=\frac{P}{P_c}\qquad \qquad \nu =\frac{V}{V_c}. \end{aligned}$$
(45)

Thus, we find

$$\begin{aligned} p\mid _\mathrm{END}= & {} \frac{1}{\rho _c}\frac{\tau }{\nu }-\frac{k(\alpha ^2+3)}{8\pi P_c(\alpha ^2-3)(\alpha ^2-1)}\frac{(v_c\nu \Gamma )^{\gamma -2}}{b^\gamma }\nonumber \\&-\frac{\beta ^2(\alpha ^2+3)}{4\pi P_c(\alpha ^2-3)}\left( \frac{b}{v_c\nu \Gamma }\right) ^\gamma \nonumber \\&-\frac{q\beta (\alpha ^2+3)}{4\pi P_c(\alpha ^2-3)(v_c\nu \Gamma )^2}\bigg (\sqrt{L_W(\eta ^{\prime \prime })}\nonumber \\&-\frac{1}{\sqrt{L_W(\eta ^{\prime \prime })}}\bigg ), \end{aligned}$$
(46)

where

$$\begin{aligned} \eta ^{\prime \prime }=\left( \frac{q~ (v_c\nu \Gamma )^{\gamma -2}}{\beta ~ b^\gamma }\right) ^2. \end{aligned}$$
(47)

Expanding for \(\beta \rightarrow \infty \) yields

$$\begin{aligned} p= & {} \frac{1}{\rho _c}\frac{\tau }{\nu }+\frac{1}{4\pi P_c}\Bigg \{\frac{k (\alpha ^2+1)\Gamma b^{-\gamma }}{(\alpha ^2-1)(\nu \Gamma v_c)^{2-\gamma }}\nonumber \\&-\frac{q^2(\alpha ^2+3)(\nu \Gamma v_c)^{2\gamma -4}}{2(\alpha ^2-3)b^{\gamma }(\nu \Gamma )^\gamma }\Bigg \}. \end{aligned}$$
(48)

Since we would like to find the critical exponent, we should consider the close neighborhood of the critical point, so we expand Eq. (46) near the critical point. Considering \(\tau =t+1\) and \(\nu =(\omega +1)^{1/\epsilon }\) where \(\epsilon =(\alpha ^2+3)/(\alpha ^2+1)\), and taking into account Eq. (46), we get

$$\begin{aligned} p=1+At-Bt\omega -C\omega ^3+O(t\omega ^2,\omega ^4), \end{aligned}$$
(49)

where

$$\begin{aligned}&A=\frac{1}{\rho _c}\qquad B=\frac{1}{\epsilon \rho _c}\nonumber \\&C=\frac{2(\alpha ^2+2)}{3(\alpha ^2+1)^2\epsilon ^3}\nonumber \\&\qquad -\,\frac{(\alpha ^2+7)q^{2\gamma -2}}{3(\alpha ^2+3)^3\beta ^2b^{2\gamma } }\left( \frac{k}{(\alpha ^2+3)(\alpha ^2+2)}\right) ^{2-\gamma }. \end{aligned}$$
(50)

According to the Maxwell equal area law [12], we get

$$\begin{aligned}&p=1+At-Bt\omega _l-C\omega _l^3=1+At-Bt\omega _s-C\omega _s^3\nonumber \\&0= -P_c\int \limits _{\omega _l}^{\omega _s}\omega (Bt+3C\omega ^2)\mathrm{d}\omega , \end{aligned}$$
(51)

where \(\omega _l\) and \(\omega _s\) refer to the volumes of large and small black holes. The only non-trivial solution of Eq. (51) is

$$\begin{aligned} \omega _l=\omega _s=2\sqrt{-\frac{B t}{C}}. \end{aligned}$$
(52)

The behavior of the order parameter near the critical point can be found as

$$\begin{aligned} \Xi =V_c(\omega _l-\omega _s)=2V_c\omega _l=2\sqrt{-\frac{B}{C}}t^{1/2}. \end{aligned}$$
(53)

Therefore, the critical exponent associated with the order parameter should be \(\beta ^\prime =\frac{1}{2}\), which coincides with that in a Van der Waals gas. The isothermal compressibility near the critical point can be obtained:

$$\begin{aligned} \kappa _T=-\frac{1}{V}\frac{\partial V}{\partial P}\Bigg |_T\propto -\frac{V_c}{B P_c}\frac{1}{t}. \end{aligned}$$
(54)

Since \(\kappa _T\propto t^{-\gamma ^\prime }\), we have \(\gamma ^\prime =1\) and as we expect near the critical point it should diverge. The last critical exponent is \(\delta ^\prime \); it describes the relation between the order parameter and the ordering field in the critical point, so we should set \(t=0\) in Eq. (49). We find

$$\begin{aligned} p-1=-C\omega ^3\qquad \Longrightarrow \qquad \delta ^\prime =3. \end{aligned}$$
(55)

It is important to note that all critical exponents in this theory coincide with those of the Van der Waals gas system.

4 Critical behavior of LND black holes

Now, we can repeat all the above steps for LND electrodynamics and consider the effect of this type of nonlinear electrodynamics on the critical behavior of the solutions. First of all, we introduce the metric function and vector potential for this type of the black holes [49],

$$\begin{aligned} A_t^\mathrm{LND}= & {} \frac{q}{r}~{}_3\digamma _2\left( \left[ \frac{1}{2},1, \frac{\alpha ^2+1}{4}\right] ,\Bigg [2,\frac{\alpha ^2+5}{4}\right] ,-\eta \Bigg ), \nonumber \\ \end{aligned}$$
(56)
$$\begin{aligned} f(r)_\mathrm{LND}= & {} -k\frac{ {\alpha }^{2}+1}{ {\alpha }^{2}-1 }{b}^{-\gamma }{r}^{\gamma }-\frac{m}{r^{1-\gamma }}\nonumber \\&+\frac{(\Lambda -4\beta ^2) \left( {\alpha }^{2}+1 \right) ^{2}{b}^{\gamma }}{\alpha ^{2}-3 }r^{2-\gamma }\nonumber \\&+\frac{8 \beta ^2 {(\alpha ^2+1)^2}}{(\alpha ^2-3)^2} b^\gamma r^{2-\gamma }\nonumber \\&\times \Bigg \{1-{}_2\digamma _1\left( \left[ -\frac{1}{2}, \frac{\alpha ^2-3}{4}\right] ,\left[ \frac{\alpha ^2+1}{4}\right] , -\eta \right) \nonumber \\&+\frac{\alpha ^2-3}{2}\left( \sqrt{1+\eta }-\ln \left( \frac{\eta }{2}\right) \right. \nonumber \\&+\left. \ln \left( -1+\sqrt{1+\eta }\right) \right) \Bigg \}, \end{aligned}$$
(57)

where \({}_2\digamma _1\) and \({}_3\digamma _2\) are hypergeometric functions. In order to study the thermodynamical quantities, we first find the temperature as

$$\begin{aligned} T_{+}^\mathrm{LND}= & {} -2k \frac{r_+^{\gamma -1} b^{-\gamma }}{4\pi }-\frac{m(\alpha ^2-3)}{4\pi (\alpha ^2+1)}r_+^{\gamma -2}\nonumber \\&+\frac{8\beta ^2(\alpha ^2+1)}{4\pi (\alpha ^2-3)}b^\gamma r^{1-\gamma }\left( 1-\frac{1}{\sqrt{1+\eta _+}}\right) \nonumber \\&+\frac{8q^2}{4\pi (\alpha ^2-3)}b^{-\gamma }r_+^{\gamma -3}\nonumber \\&\times \Bigg \{2 \times {}_2\digamma _1\left( \left[ \frac{1}{2},\frac{\alpha ^2+1}{4}\right] ,\left[ \frac{\alpha ^2+5}{4}\right] ,-\eta _+\right) \nonumber \\&-\frac{\alpha ^2+1}{\sqrt{1+\eta _+}} \Bigg \}. \end{aligned}$$
(58)

The expression for the entropy is the same as in the END case, because it does not depend on electrodynamics and still obeys the area law. Considering the definition of the electric potential, one may obtain U:

$$\begin{aligned} U_\mathrm{LND}= & {} \frac{q}{r_+}~{}_3\digamma _2\left( \left[ \frac{1}{2},1,\frac{\alpha ^2+1}{4}\right] ,\left[ 2,\frac{\alpha ^2+5}{4}\right] , -\eta _+\right) .\nonumber \\ \end{aligned}$$
(59)

In order to verify the first law of thermodynamics, we should calculate the conjugate of the nonlinear parameter for the LND topological black hole. We obtain

$$\begin{aligned} B_\mathrm{LND}= & {} \frac{(\alpha ^2+1)\beta b^{2\gamma }}{\pi (\alpha ^2-3)r_+^{2\gamma -3}} \Bigg \{\sqrt{1+\eta _+}-\ln \left( \frac{\eta _+}{2}\right) \nonumber \\&+\ln (\sqrt{1+\eta _+}-1)-\frac{\eta _+}{2 \sqrt{1+\eta _+}}\left( 1\right. \nonumber \\&\left. +\frac{1}{\sqrt{1+\eta _+}-1}\right) +\frac{2}{\alpha ^2-3}\nonumber \\&\times \left( 1\!-\!{}_2\digamma _1\left( \left[ -\frac{1}{2},\frac{\alpha ^2\!-\!3}{4}\right] ,\left[ \frac{\alpha ^2+\!1}{4}\right] \!,-\eta _+\right) \right) \nonumber \\&+\frac{\eta _+}{(\alpha ^2+1)}~{}_2\digamma _1\left( \left[ \frac{1}{2}, \frac{\alpha ^2+1}{4}\right] ,\left[ \frac{\alpha ^2+5}{4}\right] ,\right. \nonumber \\&\left. -\eta _+\right) \Bigg \}, \end{aligned}$$
(60)

from which its asymptotic behavior for \(\beta \rightarrow \infty \) and \(\alpha =0,1\) can be obtained:

$$\begin{aligned} B_\mathrm{LND}\Big |_{\beta \rightarrow \infty ,\alpha =0}= & {} \frac{q^4 \omega }{160\pi r^5\beta ^3}-\frac{ q^6\omega }{432\pi r^9 \beta ^5}+O\left( \frac{1}{\beta ^7}\right) ,\nonumber \\ B_\mathrm{LND}\Big |_{\beta \rightarrow \infty ,\alpha =1}= & {} \frac{q^4 \omega }{96\pi r^3 b^2\beta ^3}-\frac{q^6\omega }{240\pi r^5 b^4 \beta ^5}\nonumber \\&+O\left( \frac{1}{\beta ^7}\right) . \end{aligned}$$
(61)

It is clear that these relations are similar to those given in Eq. (26). The definition of the black holes thermodynamic volume is related to the entropy and since the entropy expression does not depend on the type of electrodynamics, the thermodynamical volume is the same as given in Eq. (22). Also, as we mentioned before, the pressure is related to the cosmological constant, so for LND black holes, one can find that the pressure is exactly the same as given in Eq. (27). Finally, it is a matter of calculation to check that all conserved and thermodynamic quantities of LND black holes satisfy the first law of black thermodynamics (24) as well as the Smarr relation (28).

Fig. 2
figure 2

P–v diagram of LND black holes

Full size image

4.1 Equation of state

This section is devoted to the study of the critical behavior of the black hole in the presence of LND electrodynamics. In this regard, we obtain equation of state first,

$$\begin{aligned} P_\mathrm{LND}= & {} \frac{T}{v}+\frac{1}{4\pi v}\frac{k~(\alpha ^2+1)}{b^\gamma (\alpha ^2-1)}(\Gamma v)^{\gamma -1}\nonumber \\&-\,\frac{4}{\pi v}\frac{q^2~(\Gamma v)^{\gamma -3}}{b^\gamma (\alpha ^2-3)}{}_2\digamma _1 \Bigg (\left[ \frac{1}{2},\frac{\alpha ^2+1}{4}\right] , \left[ \frac{\alpha ^2+5}{4}\right] ,-\,\eta ^\prime \Bigg )\nonumber \\&+\frac{1}{\pi v}\frac{\beta ^2 b^\gamma (\alpha ^2+1)}{(\Gamma v)^{\gamma -1}}\nonumber \\&\times \,\Bigg \{-\frac{2}{\alpha ^2-3}{}_2\digamma _1\Bigg (\left[ -\frac{1}{2},\frac{\alpha ^2-3}{4}\right] , \left[ \frac{\alpha ^2+1}{4}\right] ,-\,\eta ^\prime \Bigg )\nonumber \\&+\ln (\sqrt{1+\eta ^\prime }-1)-\ln (\eta ^\prime )+\ln (2)-1\Bigg \}\nonumber \\&+\,\frac{1}{\pi v}\frac{(\alpha ^4-1)b^\gamma }{(\alpha ^2-3)\sqrt{1+\eta ^\prime }}\Big [q^2 b^{-2\gamma }(\Gamma v)^{2\gamma -4}+\,\beta ^2\Big ] (\Gamma v)^{1-\gamma }.\nonumber \\ \end{aligned}$$
(62)

It is a general belief that one can predict a Van der Waals like behavior for a thermodynamic system by studying its P–v diagrams. According to Fig. 2 we can observe that, for specific values of the parameters, a phase transition exists below a critical temperature. It occurs for both large (Fig. 2a) and small (Fig. 2b) values of the nonlinear parameter in the presence of a dilaton field.

One may find the properties of the critical point by using Eq. (62). However, due to the complexity of this equation, it is not easy to investigate the critical point for an arbitrary nonlinear parameter. Therefore, we consider the large \(\beta \) limit of Eq. (62),

$$\begin{aligned}&P_\mathrm{LND}\Big |_{\beta \rightarrow \infty }\nonumber \\&\quad =\frac{T}{v}+\frac{(\alpha ^2+1)}{4\pi v b^\gamma }\Bigg \{-\frac{k}{(\alpha ^2-1)} (v\Gamma )^{\gamma -1}+q^2(v\Gamma )^{\gamma -3}\nonumber \\&\quad -\frac{q^4 }{8 b^{2\gamma }\beta ^2}(v\Gamma )^{3\gamma -7}\Bigg \}. \end{aligned}$$
(63)

In the absence of a dilaton field (\(\alpha =0\)), the equation of state of RN–AdS black holes in an extended phase space [12] is recovered with a leading-order nonlinear correction term,

$$\begin{aligned} P_\mathrm{LND}\Big |_{\beta \rightarrow \infty }=\frac{T}{v}-\frac{k}{2\pi v^2}+\frac{2q^2}{\pi v^4}-\frac{4 q^4}{\pi v^8\beta ^2}. \end{aligned}$$
(64)
Fig. 3
figure 3

Gibbs free energy versus T for \(\beta =q=b=k=1\) and \(\alpha =0.3\)

Full size image

Therefore, for the large \(\beta \) limit, the critical point is obtained, thus

$$\begin{aligned} v_c= & {} \frac{\Pi }{\Gamma }-\frac{5q^4(\alpha ^2+4)(\alpha ^2+7)}{16\Gamma k\beta ^2b^{2\gamma }}\Pi ^{2\gamma -5}\nonumber +O\left( \frac{1}{\beta ^4}\right) ,\\ P_c= & {} \frac{q^2(\alpha ^2+3)^2}{8\pi (\alpha ^2-3)b^\gamma }\Pi ^{\gamma -4}+\frac{5q^4(\alpha ^2+7)}{32\pi \beta ^2 b^{3\gamma }}\Gamma \Pi ^{3\gamma -8}\nonumber \\&+\,O\left( \frac{1}{\beta ^4}\right) ,\nonumber \\ T_c= & {} -\frac{k(\alpha ^2+1)}{\pi (\alpha ^2-1)(\alpha ^2+3)b^\gamma }\Pi ^{\gamma -1} +\frac{5q^4(\alpha ^2+4)}{16\pi \beta ^2 b^{3\gamma }}\Pi ^{3\gamma -7}\nonumber \\&+\,O\left( \frac{1}{\beta ^4}\right) ,\nonumber \\ \rho _c= & {} -\frac{(\alpha ^2+3)(\alpha ^2-1)}{4(\alpha ^2+2)}\Bigg \{1-\frac{5q^2}{4(\alpha ^2+2)\beta ^2 b^{2\gamma }} \Pi ^{2\gamma -4}\Bigg \}\nonumber \\&+\,O\left( \frac{1}{\beta ^4}\right) . \end{aligned}$$
(65)

It is important to note that all the above relations reduce to those of RN–AdS black holes in an extended phase space [12], provided \(\alpha =0\) and \(\beta \rightarrow \infty \). Comparing the results obtained here with Eq. (37), one can find that the critical points in the large \(\beta \) expansion for the two versions of electrodynamics are similar and the same as those of BID given in [46]. This is an expected result since in the large \(\beta \) limit, the Lagrangian of all of these theories have a similar expansion, namely

$$\begin{aligned} L_\mathrm{BID}=L_\mathrm{END}= & {} -F^2 e^{-2\alpha \phi (r)}+\frac{F^4}{8\beta ^2}e^{-6\alpha \phi (r)}\nonumber \\&+O\left( \frac{1}{\beta ^4}\right) ,\nonumber \\ L_\mathrm{END}= & {} -F^2 e^{-2\alpha \phi (r)}+\frac{F^4}{16\beta ^2}e^{-6\alpha \phi (r)}\nonumber \\&+O\left( \frac{1}{\beta ^4}\right) . \end{aligned}$$
(66)

Thus for large \(\beta \) the equation of state and the critical point properties of BID, END and LND electrodynamics are the same.

4.2 Gibbs free energy

Next, we study the Gibbs free energy for LND black holes to characterize a phase transition in the system. It is a matter of calculation to show that the Gibbs free energy of LND black holes is given by

Fig. 4
figure 4

Critical quantities of dilaton black holes. Here we have set \(q=b=k=1\) and \(\alpha =0.2\)

Full size image
Fig. 5
figure 5

\(T_{c}\) versus \(\alpha \) of dilaton black holes with different electrodynamics. Here we have taken \(q=b=k=1\)

Full size image
Fig. 6
figure 6

\(P_{c}\) versus \(\alpha \) of the black holes in different electrodynamics with \(q=b=k=1\)

Full size image
$$\begin{aligned} G_\mathrm{LND}= & {} \frac{k~r_+\omega }{16\pi }\nonumber \\&+\,\frac{(\alpha ^2+1)r^{3-2\gamma }\omega }{4\pi (\alpha ^2-3)}\Bigg \{\frac{2\pi P(\alpha ^2-3)(\alpha ^2-1)(b~r_{+})^\gamma }{(\alpha ^2+3)}\nonumber \\&+\,\frac{2q^2 r_{+}^{2\gamma -4}}{\sqrt{1+\eta _+}} +b^{2\gamma } \beta ^2\Bigg [(\alpha ^2-1)\ln \left( \frac{2\sqrt{1+\eta _+}}{\eta _+}-\frac{2}{\eta _+}\right) \nonumber \\&+\,\frac{(\alpha ^2-1)\eta _++\alpha ^2+1}{\sqrt{1+\eta _+}}-\frac{\alpha ^4-4\alpha ^2-1}{(\alpha ^2-3)}\Bigg ]\nonumber \\&-\frac{2(\alpha ^2-1)\beta ^2 b^{2\gamma }}{(\alpha ^2-3)}\nonumber \\&\times \,{}_2\digamma _1\Bigg (\left[ -\frac{1}{2},\frac{(\alpha ^2-3)}{4}\right] , \left[ \frac{(\alpha ^2+1)}{4}\right] ,-\eta _+\Bigg )\nonumber \\&-\,\frac{4q^2 r_+^{2\gamma -4}}{(\alpha ^2\!+\!1)}{}_2\digamma _1\Bigg (\left[ \frac{1}{2}, \frac{(\alpha ^2\!+\!1)}{4}\right] ,\left[ \frac{(\alpha ^2\!+\!5)}{4}\right] \!,-\eta _+\Bigg )\Bigg \}.\nonumber \\ \end{aligned}$$
(67)

Note that if we expand this relation for large nonlinear parameter \(\beta \), we restore the result of Eq. (41). We have plotted the behavior of Gibbs free energy in terms of the temperature in Fig. 3b one can observe a swallow-tail behavior in this figure when the pressure is smaller that its critical value. This implies that the system experiences a phase transition.

4.3 Critical exponents

Next, we are going to obtain the critical exponent of LND black holes. As we mentioned before, the entropy is equal in the two theories, so \(C_v\) is equal too, and \(\alpha ^\prime =0\) like BID and END theories. In order to calculate the other critical exponent we should follow the approach given in Sect. 3.5. To this end, we compute the equation of state near the critical point for LND theories,

$$\begin{aligned} p=1+At-Bt\omega -C^\prime \omega ^3+O(t\omega ^2,\omega ^4), \end{aligned}$$
(68)

where

$$\begin{aligned} C^\prime= & {} \frac{2(\alpha ^2+2)}{3(\alpha ^2+3)^2\epsilon }\nonumber \\&-\frac{5(\alpha ^2+7)q^{2\gamma -2}}{6(\alpha ^2+3)^3\beta ^2b^{2\gamma } }\left( \frac{k}{(\alpha ^2+3)(\alpha ^2+2)}\right) ^{2-\gamma }. \end{aligned}$$
(69)

It is clear that the form of the above relation is similar to Eq. (49), so as one expects, all remaining critical exponent will be the same as in the case of END theory.

5 Effects of nonlinear gauge field

We have calculated the critical quantities in the limit of large \(\beta \) where the nonlinearity of the theory is small. However, it is clear from the P–v and Gibbs diagrams that there is a similar phase transition in the limit of small \(\beta \) where the nonlinearity of the theory is large. In the limit of small \(\beta \) it is nearly impossible to calculate analytically the critical quantities. Also, in the presence of the dilaton field, it will be very difficult to calculate them even numerically. For some numeric calculations (in the absence of a dilaton field) one may see [15].

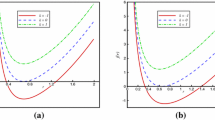
A close look at the critical temperature in both END and LND given in Eqs. (37) and (65) shows that the presence of the nonlinear field makes the critical temperature larger and it will increase with decreasing \(\beta \). One may observe that the increasing in \(T_{c}\) and \(p_{c}\) in LND is stronger than END. In Fig. 4 we have plotted the critical quantities \(T_{c}\) and \(p_{c}\) of LND, END and Maxwell-dilaton (MD) theory in terms of the nonlinear parameter \(\beta \) and we showed that they will go to a same value in the large limit of \(\beta \) where the effects of nonlinearity disappear. Clearly, the linear MD theory is independent of the nonlinear parameter \(\beta \), as can be seen from Fig. 4. It is notable that the critical quantities in LND are the same as those in END for large \(\beta \). However, for small \(\beta \) (nonlinear regime), their behavior is quite different. The behavior of the critical temperature in terms of \(\alpha \) is shown in Fig. 5, for \(0\le \alpha <1\). From these figures, one can see that the behavior of the diagrams differs as the nonlinear parameter \(\beta \) decreases. This implies that in a very strong nonlinear regime, the nonlinearity nature of the theory plays a crucial role. When \(\alpha \rightarrow 1\), the critical temperatures in different types of electrodynamic fields grow toward each other, but it is completely unlike the critical pressure. As one see in Fig. 6, for \(\alpha \rightarrow 1\), the critical pressures become more different.

As we already pointed out, although it is hard to calculate the critical quantities analytically for arbitrary \(\beta \), however, it is quite possible to plot the related diagrams for different \(\beta \). We study Gibbs free energy and P–v behavior in Figs. 7 and 8, to see the difference between the nonlinear theories we have considered. It is clear from these diagrams that the behavior of END, LND and BID black holes is very similar when T or \(\beta \) are large enough. As one expects, for the same T, the differences between the diagrams increase as \(\beta \) decreases (see Fig. 9).

Fig. 7
figure 7

Gibbs free energy versus T of dilaton black holes for \(q=b=k=1\) and \(\alpha =0.2\)

Full size image
Fig. 8
figure 8

P–v diagram of dilaton black holes with different electrodynamics. Here we have taken \(\alpha =0.3\) and \(q=b=k=1\)

Full size image
Fig. 9
figure 9

P–v diagram of dilaton black holes in the same temperature \(T=0.001\) and different \(\beta \). Here we have fixed \(\alpha =0.3\) and \(q=b=k=1\)

Full size image
Fig. 10
figure 10

P–v diagram for BID black holes. Here we have fixed \(\beta =0.45\), \(q=b=1\) and \(k=1\)

Full size image

It was extensively argued in [13] that in the absence of a dilaton field, a black hole with BI nonlinear electrodynamics may have two, one or zero critical points, which depends on the strength of the nonlinear and charge parameters. For BID black holes, only for small values of the dilaton–electromagnetic coupling \(\alpha \) one may see a second critical point. Interestingly enough, as the dilaton parameter \(\alpha \) increases, the second critical point disappears. As an example, we compare P–v diagrams of BID black holes for three values of the dilaton coupling \(\alpha \) in Fig. 10. It is clear from these diagrams that in the absence of a dilaton field (Fig. 10a) or for a weak dilaton field (Fig. 10b), there are two critical points but when the dilaton field increases (Fig. 10c) the second critical point vanishes and we have only one critical point. In the other types of nonlinear electrodynamics such as logarithmic, exponential or power-law Maxwell fields, the second critical point is never seen; neither in the absence nor in the presence of a dilaton field. Also it is worthwhile to mention that for very small value of the nonlinear parameter \(\beta \) there is not any critical point in all types of the above electrodynamics.

6 Zeroth-order phase transition

Let us emphasize that the observed phase transitions in the previous sections, which were similar to the Van der Waals phase transition, are called the first-order phase transition in the literature. It occurs where the Gibbs free energy is continuous, but its first derivative with respect to the temperature and pressure is discontinuous. Now we want to mention that another interesting type of phase transition occurs in a certain range of the metric parameters. This discontinuity in the Gibbs free energy, known as a zeroth-order phase transition, is observed in superfluidity and superconductivity [55]. It is important to note that, due to this transition, the response functions of the black holes thermodynamics diverge, e.g. the isothermal compressibility. Recently, a zeroth-order phase transition was observed in the context of Einstein–Maxwell-dilaton black holes [56]. It was confirmed that the presence of a dilaton field plays a crucial role for such a phase transition [56]. Indeed, a direct relation exists between the zeroth-order portion of the transition curve and the dilaton parameter \(\alpha \) [56]. In other words, we have no zeroth-order phase transition for Einstein–Maxwell (Reissner–Nordstrom) black holes. Moreover, for nonlinear BI electrodynamics, it was shown that a zeroth-order phase transition may occur even in the absence of the dilaton field [57], which means that the nonlinearity of the gauge field can also cause a zeroth-order phase transition in black hole thermodynamics.

Here we would like to explore the possibility of a zeroth-order phase transition in END and LND black holes, where both nonlinearity and the dilaton field are taken into account. In order to see the finite jump in the Gibbs free energy, we plot the diagrams of the Gibbs free energy with respect to the pressure in Figs. 11, 12 and 13 for different values of the metric parameters.

For completeness, we also investigate the phase transition of BID solutions presented in [46]. An interesting case in the BID theory is plotted in Fig. 11. From this figure, we see that, for certain values of the pressure and a special range of dilaton field parameters, both zeroth- and first-order phase transitions may be observed in one diagram. Based on this figure, by increasing the pressure until \(P_1\) a first-order transition occurs. For \(P>P_1\), the Gibbs free energy has two values, and as one can see the acceptable values of the energy are shown with the blue curve, since it includes smaller values of the energy. At point \(P_2\), one can see a discontinuity in the Gibbs free energy, which demonstrates a zeroth-order phase transition.

Also, Fig. 12 shows different critical behaviors of dilatonic black holes in the presence of three nonlinear versions of electrodynamics with respect to the changes in the temperature values when other metric parameters are fixed. In the case of \(T>T_c\), we have no phase transition. When \(T=T_c\), the system experiences a second-order phase transition as we have discussed before. As temperature decreases to \(T_\mathrm{f}<T<T_c\), a zeroth-order phase transition is observed. Finally, at \(T=T_\mathrm{f}\) the first-order phase transition occurs. It is worth mentioning that this behavior is repeated in the Gibbs free energy of all three types of black holes in the presence of nonlinear electrodynamics and non-zero values of the dilaton field.

It is important to note that, looking at Fig. 13, one may wonder that, for fixed values of the parameters, and in the absence of the dilaton field (\(\alpha =0\)), we do not observe a zeroth-order phase transition in END and LND theories. This is in contrast to the BID theory where a zeroth-order phase transition occurred in the small range of nonlinear parameters \(\beta \) even in the absence of a dilaton field (see Fig. 13a). In this figure, the red portion curve shows this behavior as we explained in the close-up of Fig. 11. It is one of the main differences between these three versions of nonlinear electrodynamics, which implies that their behaviors in the case of small values of \(\beta \) completely differ. This indicates that, while the nonlinearity can lead to a zeroth-order phase transition in BI theory, this is not the case for EN and LN theories. In other words, the presence of the dilaton field plays a crucial role for the occurrence of a zeroth-order phase transition in the context of END and LND electrodynamics.

7 Closing remarks

In this paper, we have studied the critical behavior and phase transition of exponential and logarithmic nonlinear electrodynamics in the presence of the dilaton field, which we labeled END and LND, respectively. We extended the phase space by considering the cosmological constant and a nonlinear parameter as thermodynamic variables. We introduced common conditions to find a solution in both theories, such as the potential and metric. We have investigated these two nonlinear theories, separately. As the expansions of the END Lagrangian for a large nonlinear parameter, \(\beta \), and for BID are exactly the same, it is expected that their critical behavior would be the same, in the limit of \(\beta \rightarrow \infty \). We continued our calculation by obtaining the equation of state of END black holes. We observed that P–v diagrams of this theory are similar to those of the Van der Waals gas. By applying the approach of the Van der Waals gas to find the critical point, we concluded that this point is exactly the same as in BID black holes. Besides, the Gibbs free energy diagram confirmed the existence of a phase transition, and finally the critical exponents were obtained, which are exactly the same as the mean field theory.

Fig. 11
figure 11

Gibbs free energy for BID black holes versus pressure for \(T=0.732 T_c\). Here we have fixed \(q=b=1\), \(\alpha =0.025\), \(\beta =0.45\)

Full size image
Fig. 12
figure 12

Gibbs free energy versus pressure for \(\alpha =0.2\), \(\beta =0.45\) and \(q=k=b=1\)

Full size image
Fig. 13
figure 13

Gibbs free energy versus pressure for \(\alpha =0\), \(\beta =0.45\) and \(q=k=b=1\)

Full size image

We also investigated the critical behavior of LND black holes. Again, for \(\beta \rightarrow \infty \), the series expansion of the LND Lagrangian is similar to the END and BID cases, so one expects the critical behavior of this theory to be similar to the BID and END theories in this limit. Our calculations confirmed that the critical behavior of LND theory is exactly the same as those of a Van der Waals gas system.

It is important to note that although the critical behavior of END and LND electrodynamics, in the limit of large nonlinear parameter \(\beta \), is similar to BID black holes explored in Ref. [46]; however, for small values of \(\beta \), the situation quite differs and the behavior of these three types of nonlinear electrodynamics are completely different. For example, it was argued in [13] that BI black holes may have two, one or zero critical points, however, this behavior is not seen for the logarithmic and exponential cases, namely the second critical point is never seen in the absence/presence of the dilaton field.

We also investigated the phase transition of END and LND black holes. In addition to the usual critical (second-order) and first-order phase transitions in END and LND black holes, we observed that a finite jump in the Gibbs free energy is generated by the dilaton–electromagnetic coupling constant, \(\alpha \), for a certain range of pressure. This novel behavior indicates a small/large black hole zeroth-order phase transition in which the response functions of the black holes thermodynamics diverge. It is worthy to note that, for temperature in the range \(T_\mathrm{f}<T<T_c\), a discontinuity occurs in the Gibbs free energy diagram which leads to a zeroth-order phase transition. We find that in the absence of a dilaton field, we do not observe a zeroth-order phase transition in END and LND theories. This is in contrast to the BI theory where a zeroth-order phase transition occurred in a small range of the nonlinear parameters \(\beta \) even in the absence of the dilaton field. We conclude that, while in BI black holes the nonlinearity can lead to a zeroth-order phase transition, this is not the case for EN and LN black holes. In other words, the presence of the dilaton field plays a crucial role for the occurrence of a zeroth-order phase transition in the context of EN and LN electrodynamics.

Finally, we would like to mention that the jump in the Gibbs free energy is observed for three types of dilatonic nonlinear electrodynamics, namely BID, END and LND. However, in the absence of a dilaton field, a zeroth-order phase transition occurs only for BI black holes, which means that the nonlinearity is responsible for this phase transition. However, for LND and END black holes, it seems that the dilaton field is responsible for this type of zeroth-order phase transition. However, for BID theory, both dilaton field and nonlinear electrodynamics can lead to a zeroth-order phase transition. This behavior and the physical reasons behind it need further investigations in future studies.