Abstract
In this paper, we study Joule–Thomson expansion for Kerr–AdS black holes in the extended phase space. A Joule–Thomson expansion formula of Kerr–AdS black holes is derived. We investigate both isenthalpic and numerical inversion curves in the T–P plane and demonstrate the cooling–heating regions for Kerr–AdS black holes. We also calculate the ratio between minimum inversion and critical temperatures for Kerr–AdS black holes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the first studies of Bekenstein and Hawking [1,2,3,4,5,6], black holes as thermodynamic system have been an interesting research field in theoretical physics. The black hole thermodynamics provides fundamental relations between theories such as classical general relativity, thermodynamics and quantum mechanics. Black holes as thermodynamic system have many exciting similarities with general thermodynamic system. These similarities become more obvious and precise for the black holes in AdS space. The properties of AdS black hole thermodynamics have been studied since the seminal paper of Hawking and Page [7]. Furthermore, the charged AdS black holes thermodynamic properties were studied in [8, 9] and it was shown that the charged AdS black holes have a van der Waals like phase transition.
Recently black hole thermodynamics in AdS space has been intensively studied in the extended phase space where the cosmological constant is considered as the thermodynamic pressure. Extended phase space leads to important results: Smarr relation is satisfied for the first law of the black holes thermodynamics in the presence of variable cosmological constant. It also provides the definition of the thermodynamic volume which is more sensible than the geometric volume of the black hole. In addition to similar behaviours with conventional thermodynamic systems, studying the AdS black holes is another important reason for the AdS/CFT correspondence [10]. Considering the cosmological constant as thermodynamic pressure,
and its conjugate quantity as thermodynamic volume,
lead us to investigate thermodynamic properties, rich phase structures and other thermodynamic phenomena for AdS black holes in a similar way to the conventional thermodynamic systems.
Based on this idea, the charged AdS black hole thermodynamic properties and phase transition were studied by Kubiznak and Mann [11]. It was shown in this study that the charged AdS black hole phase transition has the same characteristic behaviors with van der Waals liquid–gas phase transition. They also computed critical exponents and showed that they coincide with exponents of van der Waals fluids. It was shown in [12] that the cosmological constant as pressure requires considering the black hole mass M as the enthalpy H rather than as internal energy U. In recent years, thermodynamic properties and phase transition of AdS black holes have been widely investigated [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54].Footnote 1 The phase transition of AdS black holes in the extended phase space is not restricted to a van der Waals type transition, but also the reentrant phase transition and the triple point for AdS black holes were studied in [31,32,33,34]. The compressibility of rotating AdS black holes in four and higher dimensions was studied in [35, 36]. In [37], a general method was used for computing the critical exponents for AdS black holes which have a van der Waals like phase transition. Furthermore, heat engines behaviours of the AdS black holes have been studied. For example, in [38] two kind of heat engines were proposed by Johnson for charged AdS black holes and heat engines were studied for various black hole solutions in [39,40,41,42,43,44,45,46,47,48,49].Footnote 2 More recently, adiabatic processes [53] and Rankine cycle [54] have been studied for the charged AdS black holes.
In [55], we also studied the well-known Joule–Thomson expansion process for the charged AdS black holes. We obtained inversion temperature to investigate inversion and isenthalpic curves. We also showed heating–cooling regions in T–P plane. However, so far, Joule–Thomson expansion for Kerr–AdS black holes in extended phase space has never been studied. The main purpose of this study is to investigate Joule–Thomson expansion for Kerr–AdS black holes.
The paper is arranged as follows. In Sect. 2, we briefly review some thermodynamic properties of Kerr–AdS black holes which are introduced in [14].Footnote 3 In Sect. 3, we first of all derive a Joule–Thomson expansion formula for Kerr–AdS black hole by using first law and Smarr formula. Then we obtain the equation of inversion pressure \(P_{i}\) and entropy S to investigate the inversion curves. We also show that the ratio between minimum inversion and critical temperatures for Kerr–AdS black holes is the same as the ratio of charged AdS black holes [55]. Finally, we discuss our results in Sect. 4. (Here we use the units \(G_{N}=\hbar =k_{B}=c=1\).)
2 Kerr–AdS black hole
In this section, we briefly review Kerr–AdS black hole thermodynamic properties in the extended phase space. The line element of Kerr–AdS black hole in four dimensional AdS space is given by
where
and l represents AdS curvature radius. The metric parameters m and a are related to the black hole mass M and the angular momentum J by
The mass of a Kerr–AdS black hole in terms of S, J and P [14, 56] is given by
The first law and the corresponding Smarr relation of the Kerr–AdS black hole are given by
respectively, and the Smarr relation can be derived by a scaling argument [12]. From Eq. (7), one can obtain the thermodynamic quantities. The expression for the temperature is
The thermodynamic volume is defined by
Finally, we obtain the angular velocity as follows:
In this section, we obtain some thermodynamic quantities of Kerr–AdS black holes. In the next section, we will use these quantities to investigate Joule–Thomson expansion effects for Kerr–AdS black holes.
3 Joule–Thomson expansion
In this section, we will investigate Joule–Thomson expansion for Kerr–AdS black holes. The expansion is characterized by temperature change with respect to pressure. Enthalpy remains constant during the expansion process. As we know from [12], black hole mass is identified enthalpy in AdS space. Therefore, the black hole mass remains constant during expansion process. Joule–Thomson coefficient \(\mu \), which characterizes the expansion, is given by [57]
Cooling–heating regions can be determined by sign of Eq. (12). Change of pressure is negative since the pressure always decreases during the expansion. The temperature may decrease or increase during process. Therefore temperature determines sign of \(\mu \). If \(\mu \) is positive (negative), cooling (heating) occurs. The inversion curve, which is obtained at \(\mu =0\) for infinitesimal pressure drops, characterizes the expansion process and it determines the cooling–heating regions in the T–P plane.Footnote 4
We begin to derive Joule–Thomson expansion coefficient formula for Kerr–AdS black holes. First, we differentiate Eq. (8) to obtain
Since \(dM=dJ=0\), Eqs. (7) and (13) can be written
respectively. If Eq. (14) can be substituted into Eq. (15), one can obtain
which can be rearranged to give the Joule–Thomson formula as follows:
Here we obtain the Joule–Thomson expansion formula in terms of the Kerr–AdS black hole parameters. At inversion pressure \(P_{i}\), \(\mu \) equals zero and therefore we obtain \(P_{i}\) from Eq. (17),
From Eq. (6), we can obtain the pressure as a function of mass, entropy and angular momentum,
If we combine Eqs. (10), (11) and (19) with Eq. (18), we obtain a relation between inversion pressure and entropy as follows:
The last equation is useful to determine inversion curves, but first we will investigate minimum inversion temperature. Eq. (20) can be given for \(P_{i}=0\)
and we find four roots for this equation. However, one root is physically meaningful. This root is given by
One can substitute Eq. (22) into Eq. (9) and obtain the minimum inversion temperature,
For Kerr–AdS black holes, the critical temperature \(T_{\mathrm{c}}\) is given by [16]
where
The ratio between minimum inversion and critical temperature is given by
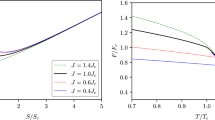
Inversion and isenthalpic (constant mass) curves of Kerr–AdS black holes. Red and black lines present isenthalpic and inversion curves, respectively. From bottom to top, isenthalpic curves correspond to increasing values of M. (Top-left) \(J=1\) and \(M=1.5,2.2.5,3\). (Top-right) \(J=2\) and \(M=2.5,3,3.5,4\). (Bottom-left) \(J=10\) and \(M=10.5,11,11.5,12\). (Bottom-right) \(J=20\) and \(M=20.5,21,21.5,22\)
which is the same as the value of charged AdS black holes [55].
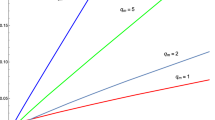
Solving Eq. (20) may not be analytically possible. Therefore, we use numerical solutions to plot inversion curves in the T–P plane. In Fig. 1, we plotted inversion curves for various angular momentum values. In contrast to van der Waals fluids, it can be seen from Fig. 1 that the inversion curves are not closed and there is only one inversion curve. We found similar behaviours for the charged AdS black holes in our previous work [55].
In Fig. 2, we plot isenthalpic (constant mass) and inversion curves for various values of angular momentum in the T–P plane. If the entropy from Eq. (6) can be substituted into Eq. (9), we obtain constant mass curves in the T–P plane. As it can be seen from Fig. 2, the inversion curves divide the plane into two regions. The region above the inversion curves corresponds to cooling region, while the region under the inversion curves corresponds to heating region. Indeed, heating and cooling regions are already determined from the sign of isenthalpic curves slope. The sign of the slope is positive in the cooling region and it changes in the heating region. On the other hand, cooling (heating) does not happen on the inversion curve which plays the role of a boundary between the two regions.
4 Conclusions
In this study, we investigated Joule–Thomson expansion for Kerr–AdS black holes in the extended phase space. The Kerr–AdS black hole Joule–Thomson formula was derived by using the first law of black hole thermodynamics and the Smarr relation. We plotted isenthalpic and inversion curves in the T–P plane. In order to plot the inversion curves, we solved Eq. (20) numerically. Moreover, we obtained the minimum inversion temperature \(T_{i}\) and calculated the ratio between inversion and critical temperatures for Kerr–AdS black holes.
Similar results were reported for the charged AdS black holes in [55] by us. For example, there is only a lower inversion curve for Kerr–AdS and the charged AdS black holes. Therefore, we only consider a minimum inversion temperature \(T_{i}^{\mathrm{min}}\) at \(P_{i}=0\). Cooling regions are not closed for both systems. The ratios between minimum inversion temperatures and critical temperatures are nearly the same for the two black hole solutions. The ratio may deviate from 0.5 for other black hole solutions. The same ratio may be obtained for other black hole solutions in the different limit cases. Furthermore, we restricted the study to a four-dimensional solution. Therefore the ratio may depend on the dimensions of space-time.
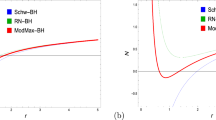
In order to compare the charged AdS/Kerr–AdS black holes with van der Waals fluids, we present schematic inversion curves for van der Waals fluids and the charged AdS/Ker-AdS black holes in Fig. 3. In contrast to the charged AdS and Kerr–AdS black holes, there are upper and lower inversion curves for van der Waals fluids [55]. Therefore the cooling region is closed and we only consider both the minimum inversion temperature \(T_{i}^{\mathrm{min}}\) and the maximum inversion temperature \(T_{i}^{\mathrm{max}}\) for this system. While cooling always occurs above the inversion curves for both black hole solutions, cooling only occurs in the region surrounded by the upper and lower inversions curves for van der Waals fluids.
Notes
See [52] and the references therein.
Indeed, Kerr–Newman–AdS black hole thermodynamics functions are introduced in [14]. But one can easily obtain Kerr–AdS black holes thermodynamic functions, when electric charge Q goes to zero.
There are two approaches for the Joule–Thomson expansion process. The differential and integral versions correspond to infinitesimal and finite pressure drops, respectively. In this paper, we considered differential version of Joule–Thomson expansion for Kerr–AdS black holes. See [57].
References
J.D. Bekenstein, Lett. Nuovo Cimento 4, 737 (1972)
J.D. Bekenstein, Phy. Rev. D 7, 2333 (1973)
J.M. Bardeen, B. Carter, S.W. Hawking, Commun. Math. Phys. 31, 161 (1973)
J.D. Bekenstein, Phys. Rev. D 9, 3292 (1974)
S.W. Hawking, Nature 248, 30 (1974)
S.W. Hawking, Commun. Math. Phys. 43, 199 (1975)
S.W. Hawking, D.N. Page, Commun. Math. Phys. 87, 577 (1983)
A. Chamblin, R. Emparan, C.V. Johnson, R.C. Myers, Phys. Rev. D 60, 064018 (1999)
A. Chamblin, R. Emparan, C.V. Johnson, R.C. Myers, Phys. Rev. D 60, 104026 (1999)
J.M. Maldacena, Int. J. Theor. Phys. 38, 1113 (1999)
D. Kubiznak, R.B. Mann, J. High Energy Phys. 07, 033 (2012)
D. Kastor, S. Ray, J. Traschen, Class. Quantum Gravity 26, 195011 (2009)
B.P. Dolan, Class. Quantum Gravity 28, 235017 (2011)
B.P. Dolan, arXiv:1209.1272 (2012)
J.X. Mo, W.B. Liu, Phys. Lett. B 727, 336 (2013)
S.W. Wei, P. Cheng, Y.X. Liu, Phy. Rev. D 93, 084015 (2016)
S. Gunasekaran, R.B. Mann, D. Kubiznak, J. High Energy Phys. 11, 110 (2012)
E. Spallucci, A. Smailagic, Phys. Lett. B 723, 436 (2013)
A. Belhaj, M. Chabab, H.E. Moumni, L. Medari, M.B. Sedra, Chin. Phys. Lett. 30, 090402 (2013)
R.G. Cai, L.M. Cao, L. Li, R.Q. Yang, J. High Energy Phys. 9, 005 (2013)
R. Zhao, H.H. Zhao, M.S. Ma, L.C. Zhang, Eur. Phys. J. C 73, 2645 (2013)
M.S. Ma, F. Liu, R. Zhao, Class. Quantum Gravity 73, 095001 (2014)
A. Belhaj, M. Chabab, H.E. Moumni, K. Masmar, M.B. Sedra, Int. J. Geom. Methods Mod. Phys. 12, 1550017 (2015)
S. Dutta, A. Jain, R. Soni, J. High Energy Phys. 12, 60 (2013)
G.Q. Li, Phys. Lett. B 735, 256 (2014)
J. Liang, C.B. Sun, H.T. Feng, Europhys. Lett. 113, 30008 (2016)
S.H. Hendi, M.H. Vahidinia, Phys. Rev. D 88, 084045 (2013)
S.H. Hendi, S. Panahiyan, B.E. Panah, J. High Energy Phys. 01, 129 (2016)
J. Sadeghi, H. Farahani, Int. J. Theor. Phys. 53, 3683 (2014)
D. Momeni, M. Faizal, K. Myrzakulov, R. Myrzakulov, Phys. Lett. B 765, 154 (2017)
N. Altamirano, D. Kubiznak, R.B. Mann, Z. Sherkatghanad, Class. Quantum Gravity 31, 042001 (2014)
A.M. Frassino, D. Kubiznak, R.B. Mann, F. Simovic, J. High Energy Phys. 09, 80 (2014)
R.A. Hennigar, R.B. Mann, Entropy 17, 8056 (2015)
S.W. Wei, Y.X. Liu, Phys. Rev. D 90, 044057 (2014)
B.P. Dolan, Phys. Rev. D 84, 127503 (2011)
B.P. Dolan, Class. Quantum Gravity 31, 035022 (2014)
B.R. Majhi, S. Samanta, Phys. Lett. B 773, 203 (2017)
C.V. Johnson, Class. Quantum Gravity 31, 205002 (2014)
C.V. Johnson, Class. Quantum Gravity 33, 135001 (2016)
C.V. Johnson, Class. Quantum Gravity 33, 215009 (2016)
A. Belhaj, M. Chabab, H.E. Moumni, K. Masmar, M.B. Sedra, A. Segui, J. High Energy Phys. 05, 149 (2015)
E. Caceres, P.H. Nguyen, J.F. Pedraza, J. High Energy Phys. 1509, 184 (2015)
K. Jafarzade, J. Sadeghi, Int. J. Theor. Phys. 56, 3387 (2017)
M.R. Setare, H. Adami, Gen. Relativ. Gravity 47, 132 (2015)
C.V. Johnson, Entropy 18, 120 (2016)
C. Bhamidipati, P.K. Yerra, Eur. Phys. J. C 77, 534 (2017)
H. Liu, X.H. Meng, Eur. Phys. J. C 77, 556 (2017)
J.X. Mo, F. Liang, G.Q. Li, J. High Energy Phys. 03, 10 (2017)
M. Zhang, W.B. Liu, Int. J. Theor. Phys. 55, 5136 (2016)
B.P. Dolan, Mod. Phys. Lett. A 30, 1540002 (2015)
N. Altamirano, D. Kubiznak, R.B. Mann, Z. Sherkatghanad, Galaxies 2, 89 (2014)
D. Kubiznak, R.B. Mann, M. Teo, Class. Quantum Gravity 34, 063001 (2017)
S. Lan, W. Liu, arXiv:1701.04662 (2017)
S.W. Wei, Y.X. Liu, arXiv:1708.08176 (2017)
Ö. Ökcü, E. Aydıner, Eur. Phys. J. C 77, 24 (2017)
M.M. Caldarelli, G. Cognola, D. Klemm, Class. Quantum Gravity 17, 399 (2000)
B.Z. Maytal, A. Shavit, Cryogenics 37, 33 (1997)
Acknowledgements
We would like to thank the anonymous referees for their helpful and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Ökcü, Ö., Aydıner, E. Joule–Thomson expansion of Kerr–AdS black holes. Eur. Phys. J. C 78, 123 (2018). https://doi.org/10.1140/epjc/s10052-018-5602-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5602-x