Reconciling EFT and hybrid calculations of the light MSSM Higgs-boson mass

Abstract

Various methods are used in the literature for predicting the lightest CP-even Higgs boson mass in the Minimal Supersymmetric Standard Model (MSSM). Fixed-order diagrammatic calculations capture all effects at a given order and yield accurate results for scales of supersymmetric (SUSY) particles that are not separated too much from the weak scale. Effective field theory calculations allow a resummation of large logarithmic contributions up to all orders and therefore yield accurate results for a high SUSY scale. A hybrid approach, where both methods have been combined, is implemented in the computer code FeynHiggs. So far, however, at large scales sizeable differences have been observed between FeynHiggs and other pure EFT codes. In this work, the various approaches are analytically compared with each other in a simple scenario in which all SUSY mass scales are chosen to be equal to each other. Three main sources are identified that account for the major part of the observed differences. Firstly, it is shown that the scheme conversion of the input parameters that is commonly used for the comparison of fixed-order results is not adequate for the comparison of results containing a series of higher-order logarithms. Secondly, the treatment of higher-order terms arising from the determination of the Higgs propagator pole is addressed. Thirdly, the effect of different parametrizations in particular of the top Yukawa coupling in the non-logarithmic terms is investigated. Taking into account all of these effects, in the considered simple scenario very good agreement is found for scales above 1 TeV between the results obtained using the EFT approach and the hybrid approach of FeynHiggs.

1 Introduction

The properties of the Higgs boson that has been discovered by the ATLAS and CMS collaborations at the CERN Large Hadron Collider [1, 2] are compatible with those predicted for the Higgs boson of the Standard Model (SM) at the present level of accuracy. Despite this apparent success of the SM, there are several open questions that cannot be answered by the SM and ask for extended or alternative theoretical concepts. Supersymmetry is one of best motivated frameworks for physics beyond the Standard Model (BSM), and in particular the Minimal Supersymmetric Standard Model (MSSM) is the most intensively studied scenario providing precise predictions for experimental phenomena in the LHC era.

Apart from associating a superpartner to each SM degree of freedom, the MSSM extends the Higgs sector of the SM by a second complex doublet. Consequently, the MSSM employs two Higgs-boson doublets, denoted by $H_1$ and $H_2$, with hypercharges $-1$ and $+1$, respectively. After minimizing the scalar potential, the neutral components of $H_1$ and $H_2$ acquire vacuum expectation values (vevs), $v_1$ and $v_2$. Without loss of generality, one can assume that the vevs are real and non-negative, yielding

$$\begin{aligned} v^2\equiv v_1^2+v_2^2, \quad \tan \beta \equiv v_2/v_1. \end{aligned}$$

(1)

The two Higgs doublets in the MSSM accommodate five physical Higgs bosons. In lowest order these are the light and heavy $\mathrm CP$-even Higgs bosons, h and H, the $\mathrm CP$-odd Higgs boson, A, and two charged Higgs bosons, $H^\pm$. Two parameters are required to describe the Higgs sector at the tree level (conventionally chosen as $\tan \beta$ and the mass $M_A$ of the $\mathrm CP$-odd Higgs particle); masses and couplings, however, are substantially affected by higher-order contributions.

Until now, experiments have not found direct evidence for supersymmetric (SUSY) particles. On the other hand, precision observables provide an indirect access to the MSSM parameter space from which significant constraints on the allowed parameter regions can be obtained. On top of the classical set of electroweak precision observables, the mass of the detected Higgs boson constitutes an additional important precision observable, $M_h^{\mathrm{exp}}=125.09\pm 0.24\,\, \mathrm {GeV}$ [3]. If the measured value is associated with the mass $M_h$ of the lightest $\mathrm CP$-even Higgs boson within the MSSM (for a recent discussion of the viability of the interpretation in terms of the heavy $\mathrm CP$-even Higgs boson H, see [4]), the comparison of the predicted value with the measurement constitutes an important test of the model with high sensitivity to the SUSY mass scales (see e.g. [5,6,7] for reviews). In order to fully exploit the high precision of the experimental measurement for constraining the SUSY parameter space the accuracy of the theoretical prediction for $M_h$ has to be improved very significantly.

So far, the full one-loop corrections [8,9,10,11], dominant two-loop corrections [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] and partial three-loop results [36,37,38] for the light MSSM Higgs-boson mass have been calculated diagrammatically. Besides fixed-order calculations, effective field theory (EFT) methods have been used to resum large logarithmic contributions in case of a large mass hierarchy between the electroweak and the SUSY scale [39,40,41,42,43]. These EFT calculations, however, are less accurate for relatively low SUSY mass scales owing to terms suppressed by the SUSY scale(s) which correspond to higher-dimensional operators in the EFT framework (see [44] for recent work in this direction).

In order to profit from the advantages of both methods – high accuracy for relatively low SUSY scales in the case of the diagrammatic approach versus high accuracy for a high SUSY scale in the case of the EFT approach – a hybrid method combining both approaches has been developed [45, 46], see also [47, 48] for different implementations. The method introduced in [45, 46] has been implemented into the publicly available code FeynHiggs [11, 17, 49,50,51] such that the fixed-order result is supplemented with higher-order logarithmic contributions.

Comparisons between FeynHiggs and pure EFT codes in the literature [43, 47, 48] have revealed non-negligible differences between the predicted values for $M_h$. In particular, deviations have been observed for large SUSY scales, where terms not captured in the EFT framework are supposed to be negligible. At first glance, such differences appear to be unexpected since the resummation of logarithms included in FeynHiggs is at the same level of accuracy as in pure EFT calculations.

In order to clarify the situation, it is the purpose of this work to perform an in-depth comparison of the various approaches to explain the origin of the observed differences. For simplicity, we choose a single-scale scenario,

$$\begin{aligned} M_{\mathrm{{soft}}} = \mu = M_A\equiv M_{\text {SUSY}}, \end{aligned}$$

(2)

where $M_{\mathrm{{soft}}}$ are the soft SUSY-breaking masses and $\mu$ is the Higgsino mass parameter. Furthermore, all parameters are assumed to be real, i.e. we work in the $\mathrm CP$-conserving MSSM with real parameters.¹ While the chosen single-scale scenario is particularly suitable for the EFT approach, it should be noted that in realistic cases the actual task is to provide the most accurate prediction (together with a reliable estimate of the remaining theoretical uncertainties) for the Higgs-boson masses of the model for a given SUSY mass spectrum which may contain a variety of SUSY scales. We leave an investigation of such multi-scale scenarios for future work.

We shall explain that there are essentially three sources of the observed differences. In a first step, we show that the usual scheme conversion of input parameters is not suitable for the comparison of results containing a series of higher-order logarithms. Such a scheme conversion can lead to large shifts corresponding to formally uncontrolled higher-order terms. Secondly, we analytically identify specific terms arising through the determination of the Higgs propagator pole which cancel with subloop renormalization contributions in the irreducible self-energies of the diagrammatic approach for a large SUSY scale. We develop an improved treatment where unwanted effects from incomplete cancellations are avoided. Thirdly, we show how different parametrizations of non-logarithmic terms can explain remaining differences between the results of FeynHiggs and pure EFT codes for high scales.

The paper is organized as follows. In Sect. 2, we review the different approaches with a particular focus on how the Higgs pole mass is extracted. In Sect. 3, we compare the results of the various approaches for the Higgs pole mass to each other. In Sect. 4, we discuss the issue of using ${\overline{\text {DR}}}$ input parameters as input of an OS calculation. In Sect. 5, we give a brief overview about the levels of accuracy of the $M_h$ evaluation implemented in various codes. In Sect. 6, we present a numerical analysis showing the impact of the effects discussed in the previous sections and numerically compare FeynHiggs to other codes. The conclusions can be found in Sect. 7. Two appendices provide additional details.

2 Calculating the Higgs mass

In this section, we shortly review how the pole mass of the lightest $\mathrm CP$-even Higgs boson of the MSSM is calculated in a pure diagrammatic calculation, in a pure EFT calculation, and in the hybrid approach of FeynHiggs.

2.1 Diagrammatic fixed-order calculation

A well-established way to calculate corrections to the mass of the SM-like Higgs of the MSSM, as well as to the mass of the heavier CP-even neutral Higgs boson and the charged Higgs boson, is a fixed-order Feynman diagrammatic (FD) calculation. The prediction is based on the calculation of Higgs self-energies involving contributions from SM particles, extra Higgs bosons, as well as their corresponding superpartners. In this approach the contributions from all sectors of the model and of all particles in the loop can be incorporated at a given order. The mass effects of all particles in the loop can be taken into account for any pattern of the mass spectrum. If there is however a large splitting between the relevant scales, in particular a large mass hierarchy between the electroweak and the scale of some or all of the SUSY particles, the fixed-order result will contain numerically large logarithms that can spoil the convergence of the perturbative expansion.

In the MSSM with real parameters, after calculating the renormalized Higgs-boson self-energies, the physical masses of the CP-even Higgs bosons h, H can be obtained by finding the poles of their propagator matrix, whose inverse is given by

$$\begin{aligned} \varDelta _{hH}^{-1}=i \begin{pmatrix} p^2 - m_h^2 + \hat{\varSigma }^{\text {MSSM}}_{hh}(p^2) &{} \hat{\varSigma }^{\text {MSSM}}_{hH}(p^2) \\ \hat{\varSigma }^{\text {MSSM}}_{hH}(p^2) &{} p^2 - m_H^2 + \hat{\varSigma }^{\text {MSSM}}_{HH}(p^2) \end{pmatrix},\nonumber \\ \end{aligned}$$

(3)

where $m_h$ ($m_H$) denotes the tree-level mass of the h (H) boson and $\hat{\varSigma }_{hh,hH,HH}$ are the corresponding self-energies. We introduced the label “MSSM” to indicate that the corresponding self-energy contains SM-type contributions as well as non-SM contributions.

Concerning the renormalization, we follow here the approach used in the program FeynHiggs. Accordingly, the circumflex $\hat{ }$ indicates that the self-energies have been renormalized using the mixed on-shell (OS) and ${\overline{\text {DR}}}$-scheme of [11]. In particular, the A-boson mass is renormalized on-shell, whereas the Higgs field renormalization and the renormalization of $\tan \beta$ is performed using the ${\overline{\text {DR}}}$ scheme.

The masses of the weak gauge bosons ($M_Z$, $M_W$) and the electromagnetic charge e are renormalized on-shell, and the tadpole renormalization is carried out such that the tadpole contributions are cancelled by their respective counterterms. The OS vev is a dependent quantity, which is given in terms of the OS values of the observables $M_W$, $s_\mathrm {w}$ and e by

$$\begin{aligned} v_{\text {OS}}^2 = \frac{2 s_\mathrm {w}^2 M_W^2}{e^2}, \end{aligned}$$

(4)

where $s_\mathrm {w}$ denotes the sine of the weak mixing angle. The renormalization of this quantity at the one-loop level is therefore given in terms of the OS counterterms of $M_W$, $s_\mathrm {w}$ and e,

$$\begin{aligned} \frac{2 s_\mathrm {w}^2 M_W^2}{e^2}\rightarrow & {} \frac{2 s_\mathrm {w}^2 M_W^2}{e^2}\cdot \nonumber \\&\cdot \left\{ \frac{\delta M_W^2}{M_W^2}+\frac{c_\mathrm {w}^2}{s_\mathrm {w}^2}\left( \frac{\delta M_Z^2}{M_Z^2}-\frac{\delta M_W^2}{M_W^2}\right) -\frac{\delta e^2}{e^2} \right\} ,\nonumber \\ \end{aligned}$$

(5)

where $\delta M_{W,Z}^2$ are the mass counterterms of the W and Z bosons, respectively, and $\delta e^2$ is the counterterm of the electromagnetic charge ($c_\mathrm {w}^2=1-s_\mathrm {w}^2$). Motivated by the fact that the renormalization of the vev receives a contribution from the field renormalization of the Higgs doublet, we identify the counterterm given in Eq. (5) with $\delta v_{\text {OS}}^2/v_{\text {OS}}^2 + \delta Z_{hh}$, where $\delta Z_{hh}$ is the field renormalization counterterm of the SM-like Higgs field fixed in the ${\overline{\text {DR}}}$ scheme.² Accordingly, the OS counterterm of the vev defined in this way reads

$$\begin{aligned} \frac{\delta v_{\text {OS}}^2}{v_{\text {OS}}^2} = \frac{\delta M_W^2}{M_W^2}+\frac{c_\mathrm {w}^2}{s_\mathrm {w}^2}\left( \frac{\delta M_Z^2}{M_Z^2}-\frac{\delta M_W^2}{M_W^2}\right) -\frac{\delta e^2}{e^2} - \delta Z_{hh}.\nonumber \\ \end{aligned}$$

(6)

The results for the self-energies in FeynHiggs have been reparametrized in terms of the Fermi constant $G_F$ instead of the electric charge e. The corresponding vev $v_{G_F}$ is related to $v_{\text {OS}}$ via

$$\begin{aligned} v_{\text {OS}}^2 = v_{G_F}^2(1+\varDelta r) \quad \text {with }v_{G_F}^2= \frac{1}{2\sqrt{2}G_F}. \end{aligned}$$

(7)

MSSM predictions for the quantity $\varDelta r$ can be found in [52,53,54,55]. The effect of this reparametrization in the one-loop self-energies is formally of two-loop order.

Furthermore (in the default choice), the stop sector is renormalized using the OS scheme, which is defined by applying on-shell conditions for the respective masses: the top-quark mass $M_t$, and the top-squark masses $M_{\tilde{t}_1}$ and $M_{\tilde{t}_2}$. A fourth renormalization condition fixes the mixing of the stops and can be identified with a condition for the top-squark mixing angle.

Employing this scheme, in FeynHiggs the full one-loop corrections to the Higgs self-energies as well as two-loop corrections of $\mathcal{O}(\alpha _t\alpha _s,\alpha _b\alpha _s,\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)$ are implemented [11, 17, 22, 23, 25, 27, 30, 33, 34, 49,50,51]. While those two-loop corrections in the gauge-less limit have been obtained for vanishing external momentum, there is furthermore an option to incorporate the momentum dependence of the corrections at $\mathcal{O}(\alpha _t\alpha _s)$ [56, 57] (see also [58]). Finding the (complex) poles for the case where $\mathrm CP$ conservation is assumed corresponds to solving the equation

$$\begin{aligned}&\left( p^2 - m_h^2 + \hat{\varSigma }_{hh}^{\text {MSSM}}(p^2)\right) \left( p^2 - m_H^2 + \hat{\varSigma }^{\text {MSSM}}_{HH}(p^2)\right) \nonumber \\&\quad -\left( \hat{\varSigma }^{\text {MSSM}}_{hH}(p^2)\right) ^2 = 0. \end{aligned}$$

(8)

In the decoupling limit, $M_A\gg M_Z$, the physical mass of the lightest Higgs boson can approximately be obtained as solution of the simpler equation

$$\begin{aligned} p^2 - m_h^2 + \hat{\varSigma }^{\text {MSSM}}_{hh}(p^2) = 0 \end{aligned}$$

(9)

up to corrections from the hH and HH self-energies, which are suppressed by powers of $M_A$. In the following discussion we will for simplicity use Eq. (9) for determining the pole of the propagator and we will furthermore neglect the imaginary parts of the self-energies. In FeynHiggs the complex poles of the propagator are obtained from the full propagator matrix, taking into account the real and imaginary parts of the Higgs-boson self-energies.

Solving Eq. (9) iteratively for the case where imaginary parts are neglected yields an expression for the Higgs pole mass,

$$\begin{aligned} (M_h^2)_\text {FD}= & {} m_h^2 - \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2) +\hat{\varSigma }_{hh}^{{\text {MSSM}}\prime }(m_h^2) \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2) \nonumber \\&+\cdots , \end{aligned}$$

(10)

where the prime denotes the derivative of the self-energy with respect to the momentum squared. The ellipsis stands for terms involving higher-order derivatives and products of differentiated self-energies. In Appendix B we provide a formula from which these terms can be derived recursively. The Higgs pole mass at a given order is obtained from Eq. (10) via a loop expansion to the appropriate order.

2.2 Effective field theory calculation

Another approach to calculate the mass of the SM-like Higgs boson in the MSSM is using effective field theory (EFT) methods. These allow the resummation of large logarithmic contributions, so that higher-order contributions beyond the order of fixed-order diagrammatic calculations can be incorporated. Without including higher dimensional operators in the effective Lagrangian, contributions suppressed by a heavy scale are however not captured.

In the simplest EFT framework, all SUSY particles are integrated out from the full theory at a common mass scale $M_{\text {SUSY}}$. Below $M_{\text {SUSY}}$ the SM remains as the low-energy EFT. The couplings of the EFT are determined by matching to the MSSM at the scale $M_{\text {SUSY}}$. In the case of the SM as the EFT³ below $M_{\text {SUSY}}$ this concerns only the effective Higgs self-coupling $\lambda$, all the other couplings are fixed by matching them to observables at the low-energy scale. Renormalization group equations (RGEs) are used to correlate the couplings at the high scale $M_{\text {SUSY}}$ and the low scale, typically chosen to be the OS top mass $M_t$ (or $M_Z$).

The effective Higgs self coupling $\lambda (M_t)$ obtained from the matched $\lambda (M_{\text {SUSY}})$ determines the ${\overline{\text {MS}}}$ mass of the SM Higgs boson at the scale $M_t$ via

$$\begin{aligned} \left( m_h^{{\overline{\text {MS}}},\text {SM}}\right) ^2 = 2\, \lambda (M_t)\, v_{\overline{\text {MS}}}^2, \end{aligned}$$

(11)

with the ${\overline{\text {MS}}}$ vev (at the scale $M_t$). The ${\overline{\text {MS}}}$ vev can be related to the on-shell vev via the finite part of $\delta v_{\text {OS}}^2$ defined in Eq. (6),

$$\begin{aligned} v_{\overline{\text {MS}}}^2 = v_{\text {OS}}^2 + \delta v_{\text {OS}}^2 \Big |_\text {fin}. \end{aligned}$$

(12)

It should be noted that since the quantity in Eq. (11) is the SM ${\overline{\text {MS}}}$ vev, in Eq. (12) only SM-type contributions have to be considered in $\delta v_{\text {OS}}^2$.

Getting from the running mass (11) to the physical Higgs mass one has to solve the pole equation for the Higgs-boson propagator,

$$\begin{aligned} p^2 - \left( m_h^{{\overline{\text {MS}}},\text {SM}}\right) ^2 + \tilde{\varSigma }_{hh}^{\text {SM}}(p^2) = 0, \end{aligned}$$

(13)

involving the renormalized SM Higgs boson self-energy (denoted by a tilde)

$$\begin{aligned} \tilde{\varSigma }_{hh}^{\text {SM}}(p^2) = \varSigma _{hh}^{{\text {SM}}}(p^2)\Big |_\text {fin} - \frac{1}{\sqrt{2} v_{\overline{\text {MS}}}}\, T_h^{\text {SM}}\Big |_\text {fin}, \end{aligned}$$

(14)

which is renormalized accordingly in the ${\overline{\text {MS}}}$ scheme at the scale $M_t$ but with the Higgs tadpoles renormalized to zero, i.e. the tadpole counterterm is chosen to cancel the sum of the tadpole diagrams, $T_h^{\text {SM}}$, for the Higgs field,

$$\begin{aligned} \delta T_h^{\text {SM}}= - T_h^{\text {SM}}. \end{aligned}$$

(15)

With all these ingredients, the Higgs pole mass is now obtained as the solution of the equation

$$\begin{aligned} M_h^2 = 2 \lambda (M_t) v_{\overline{\text {MS}}}^2\, -\, \tilde{\varSigma }_{hh}^{\text {SM}}(M_h^2). \end{aligned}$$

(16)

Expanding the Higgs self-energy perturbatively around the tree-level mass $m_h^2$ of the MSSM yields

$$\begin{aligned} (M_h^2)_{\text {EFT}}= & {} 2v_{\overline{\text {MS}}}^2\lambda (M_t) - \tilde{\varSigma }_{hh}^{\text {SM}}(m_h^2) \nonumber \\&-\,\tilde{\varSigma }_{hh}^{{\text {SM}}\prime }(m_h^2)\cdot \left[ 2 v_{\overline{\text {MS}}}^2\lambda (M_t) - \tilde{\varSigma }_{hh}^{\text {SM}}(m_h^2) - m_h^2\right] \,\nonumber \\&+\, \cdots , \end{aligned}$$

(17)

where the ellipsis indicates higher-order terms in the expansion.

We discuss the current status of EFT calculations in Sect. 5.

2.3 Hybrid calculation

In FeynHiggs, the fixed-order approach is combined with the EFT approach in order to supplement the full diagrammatic result with leading higher-order contributions [45, 46]. The logarithmic contributions resummed using the EFT approach are incorporated into Eq. (9),

$$\begin{aligned} p^2-m_h^2+\hat{\varSigma }^{\text {MSSM}}_{hh}(p^2) +\varDelta \hat{\varSigma }_{hh}^2 = 0. \end{aligned}$$

(18)

The quantity $\varDelta \hat{\varSigma }_{hh}$ contains all logarithmic contributions obtained via the EFT approach as well as subtraction terms compensating the logarithmic terms already present in the diagrammatic fixed-order result for $\hat{\varSigma }^{\text {MSSM}}_{hh}$,

$$\begin{aligned} \varDelta \hat{\varSigma }_{hh}^2 = -\big [2 v_{\overline{\text {MS}}}^2\lambda (M_t)\big ]_{\text {log}} - \big [\hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\big ]_{\text {log}}. \end{aligned}$$

(19)

The subscript ‘log’ indicates that we take only logarithmic contributions into account. Note that in $\hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)$ the logarithms appear only explicitly when expanding in $v/M_{\text {SUSY}}$. For more details on the combination of the fixed-order and the EFT result, we refer to [45, 46].

Plugging the expression for $\varDelta \hat{\varSigma }_{hh}$ into Eq. (18), we obtain for the physical Higgs mass

$$\begin{aligned} (M_h^2)_\text {FH}= & {} m_h^2 - \hat{\varSigma }^{\text {MSSM}}_{hh}(M_h^2) + \big [2v_{\overline{\text {MS}}}^2\lambda (M_t)\big ]_{\text {log}} \nonumber \\&+\, \big [\hat{\varSigma }^{\text {MSSM}}_{hh}(m_h^2)\big ]_{\text {log}}\nonumber \\= & {} m_h^2 + \big [2v_{\overline{\text {MS}}}^2\lambda (M_t)\big ]_{\text {log}} - \big [\hat{\varSigma }^{\text {MSSM}}_{hh}(m_h^2)\big ]_{\text {nolog}} \nonumber \\&-\hat{\varSigma }^{{\text {MSSM}}\prime }_{hh}(m_h^2)\left( \big [2v_{\overline{\text {MS}}}^2\lambda (M_t)\big ]_{\text {log}}\right. \nonumber \\&\left. - \big [\hat{\varSigma }^{\text {MSSM}}_{hh}(m_h^2)\big ]_{\text {nolog}}\right) + \ldots . \end{aligned}$$

(20)

We use the label ‘nolog’ to indicate that we take only terms not involving large logarithms into account for the labelled quantity. We again would like to stress that the large logarithms (and thereby the meant non-logarithmic terms) appear only explicitly in $\hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)$ when expanding in $v/M_{\text {SUSY}}$.

Before comparing the various approaches in depth, we also shortly comment on the renormalization scheme conversion needed for the combination of the fixed-order and the EFT calculation. As mentioned before, in FeynHiggs (in the default choice) the stop sector is renormalized using the OS scheme. In contrast, in the EFT calculation, i.e. the calculation of $\lambda (M_t)$, all SUSY parameters enter in ${\overline{\text {DR}}}$-renormalized form. As argued in [46], it is sufficient to convert only the stop mixing parameter $X_t$ using only the one-loop large logarithmic terms,

$$\begin{aligned}&X_t^{{\overline{\text {DR}}},{\text {EFT}}} \nonumber \\&\quad = X_t^{\text {OS}}\cdot \left[ 1 + \left( \frac{\alpha _s}{\pi } -\frac{3 \alpha _t}{16\pi }(1-X_t^2/M_S^2)\right) \ln \frac{M_S^2}{M_t^2}\right] , \end{aligned}$$

(21)

where $M_S^2 = M_{\tilde{t}_1}M_{\tilde{t}_2}$, $\alpha _s= g_3^2/(4\pi )$ (with $g_3$ being the strong gauge coupling) and $\alpha _t= y_t^2/(4\pi )$ (with $y_t$ being the top Yukawa coupling).

3 Comparison of the different approaches

In the following we will discuss the differences between the various approaches. It is obvious from the discussion of the previous section that the diagrammatic fixed-order result and the pure EFT result differ by higher-order logarithmic terms that are contained in the EFT result but not in the diagrammatic fixed-order result as well as by non-logarithmic terms that are contained in the diagrammatic fixed-order result but not in the pure EFT result. In the hybrid approach the diagrammatic fixed-order result is supplemented by the higher-order logarithmic terms obtained by the EFT approach. We focus in the following on the comparison between the hybrid approach and the pure EFT result. In the present section we leave aside issues related to the used renormalization schemes, which will be addressed in Sect. 4.

While the hybrid approach and the pure EFT approach both incorporate the higher-order logarithmic terms obtained by the EFT approach, this does not necessarily imply that all logarithmic terms in the two results are the same. This is due to the fact that the determination of the Higgs-boson mass from the pole of the propagator within the hybrid approach is performed in the full model (in the example considered here the MSSM, incorporating loop contributions from all SUSY particles), while in the EFT approach it is determined in the effective low-scale model (in the considered example the SM). We will demonstrate below that the determination of the propagator pole in the hybrid approach generates logarithmic terms beyond the ones contained in the EFT approach at the two-loop level and beyond which actually cancel in the limit of a heavy SUSY scale with contributions from the subloop renormalization. This cancellation is explicitly demonstrated at the two-loop level. We will furthermore discuss the difference in non-logarithmic terms between the results of the hybrid and the EFT approach.

3.1 Higher-order logarithmic terms from the determination of the pole of the propagator

In the EFT approach where the Higgs boson mass is determined as the pole of the propagator in the SM as the effective low-scale model, while the SUSY particles have been integrated out, the logarithmic terms are given by (see Eq. (17))

$$\begin{aligned} (M_h^2)_{\text {EFT}}^\text {log}= & {} \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {log}} - \tilde{\varSigma }_{hh}^{{\text {SM}}\prime }(m_h^2) \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {log}} \nonumber \\&+\cdots . \end{aligned}$$

(22)

The logarithmic terms contained in the result of the hybrid approach implemented in FeynHiggs are given by (see Eq. (20))

$$\begin{aligned} (M_h^2)_\text {FH}^\text {log}= & {} \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {log}} \nonumber \\&+\left[ \hat{\varSigma }^{{\text {MSSM}}\prime }_{hh}(m_h^2) \right] _{\text {log}}\left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}} \nonumber \\&- \hat{\varSigma }^{{\text {MSSM}}\prime }_{hh}(m_h^2) \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {log}} + \ldots . \end{aligned}$$

(23)

In the decoupling limit ($M_{\text {SUSY}}= M_A \gg M_t$, where in particular the light $\mathrm CP$-even Higgs boson has SM-like couplings), we can split up the MSSM Higgs self-energy into a SM part and a non-SM part,

$$\begin{aligned} \hat{\varSigma }^{{\text {MSSM}}}_{hh}(m_h^2) = \hat{\varSigma }_{hh}^{\text {SM}}(m_h^2) + \hat{\varSigma }_{hh}^{\text {nonSM}}(m_h^2). \end{aligned}$$

(24)

In the mixed OS/${\overline{\text {DR}}}$ scheme of the full diagrammatic calculation, the Higgs field renormalization constants are fixed in the ${\overline{\text {DR}}}$ scheme. For scalar propagators, there is no difference between the ${\overline{\text {DR}}}$ and the ${\overline{\text {MS}}}$ scheme at the one-loop level. Consequently,

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {SM}}\prime }(m_h^2) = \tilde{\varSigma }_{hh}^{{\text {SM}}\prime }(m_h^2) \end{aligned}$$

(25)

holds.

Using this relation, we obtain for the difference between the higher-order logarithmic terms from the determination of the pole of the propagator obtained in the EFT and the hybrid approach

$$\begin{aligned} \varDelta ^\text {log}\equiv & {} (M_h^2)_\text {FH}^\text {log}-(M_h^2)_{\text {EFT}}^\text {log} \nonumber \\= & {} \left[ \hat{\varSigma }^{{\text {nonSM}}\prime }_{hh}(m_h^2)\right] _{\text {log}} \left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}} \nonumber \\&- \hat{\varSigma }^{{\text {nonSM}}\prime }_{hh}(m_h^2) \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {log}} + \ldots \nonumber \\=: & {} \varDelta _{p^2}^\text {log}. \end{aligned}$$

(26)

Since this difference, which is of two-loop order and beyond, results only from the momentum dependence of the non-SM contributions to the Higgs self-energy, we call it $\varDelta _{p^2}^\text {log}$ in the following. We give analytic expressions for $\varDelta _{p^2}^\text {log}$ in Appendix B.

In Sect. 3.3 we will demonstrate at the two-loop level that in the limit of a heavy SUSY scale the quantity $\varDelta _{p^2}^\text {log}$ consisting of “momentum-dependent non-SM contributions” as given in Eq. (26) cancels out with contributions of the Higgs self-energy’s subloop renormalization. Before we address this issue we first compare the non-logarithmic terms in the two approaches.

3.2 Non-logarithmic terms

In the EFT approach, the non-logarithmic terms are given by (see Eq. (17))

$$\begin{aligned} (M_h^2)_{\text {EFT}}^{\text {nolog}}= & {} \left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {nolog}} - \tilde{\varSigma }_{hh}^{\text {SM}}(m_h^2) \nonumber \\&-\,\tilde{\varSigma }_{hh}^{{\text {SM}}\prime }(m_h^2) \Big (\left[ 2v_{\overline{\text {MS}}}^2\lambda (M_t)\right] _{\text {nolog}}\nonumber \\&-\, \tilde{\varSigma }_{hh}^{\text {SM}}(m_h^2) -m_h^2\Big )+ \cdots . \end{aligned}$$

(27)

By construction, all non-logarithmic terms contained in the result of the hybrid approach originate from the fixed-order diagrammatic calculation (see Eq. (20)),

$$\begin{aligned} (M_h^2)_\text {FH}^{\text {nolog}}= & {} m_h^2 - \left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}} \nonumber \\&+\,\left[ \hat{\varSigma }_{hh}^{{\text {MSSM}}\prime }(m_h^2)\right] _{\text {nolog}}\left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}}\nonumber \\&+\,\cdots . \end{aligned}$$

(28)

In this way one- and two-loop terms that are suppressed by the SUSY scale, $\varDelta ^{\text {nolog}}_{v/M_{\text {SUSY}}}$, are included in the result of the hybrid approach. Terms of this kind would result from higher-dimensional operators in the EFT approach. Those terms that are included in the hybrid result as implemented in FeynHiggs but not in the publicly available pure EFT results constitute an important source of difference between the corresponding results, which is expected to be sizeable if some or all SUSY particles are relatively light (see also [44] for a recent discussion of contributions of this kind in the EFT approach). It should be noted that in general terms of $\mathcal{O}(v/M_{\text {SUSY}})$ also originate from solving the full pole mass equation, Eq. (8), rather than the approximated one, Eq. (9).

At zeroth order in $v/M_{\text {SUSY}}$, the non-logarithmic terms of the EFT approach contained in $\lambda (M_t)$ in Eq. (27) agree with the non-SM contributions in Eq. (28). They result from the threshold corrections at the matching scale $M_{\text {SUSY}}$. These threshold corrections are so far only known fully at the one-loop order. At the two-loop order only the $\mathcal{O}(\alpha _s\alpha _t,\alpha _t^2)$ corrections are implemented in publicly available codes so far.⁴ Thus, those terms in $[\hat{\varSigma }_{hh}^{{\text {nonSM}}\prime }(m_h^2)]_{\text {nolog}}[\hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)]_{\text {nolog}}$ being not of $\mathcal{O}(\alpha _t^2)$ are not present in $(M_h^2)_{\text {EFT}}$. At higher orders, all terms involving a derivative of $\hat{\varSigma }_{hh}^{\text {nonSM}}$ are affected. As we will demonstrate in the following section, also the non-logarithmic non-SM contributions arising from the determination of the pole of the propagator cancel out with contributions of the subloop renormalization in the limit of a high SUSY scale.

Apart from these terms and from the non-logarithmic terms of $\mathcal{O}(v/M_{\text {SUSY}})$ discussed above, $\varDelta ^{\text {nolog}}_{v/M_{\text {SUSY}}}$, a further difference between the hybrid approach and the EFT approach is due to the parametrization of the non-logarithmic terms. In the EFT approach all low-scale parameters are ${\overline{\text {MS}}}$ quantities. The results of FeynHiggs, on the other hand, are expressed in terms of physical, i.e. on-shell, parameters. For the top-quark mass both the results expressed in terms of the pole mass, $M_t$, and the running mass at the scale $M_t$, $\overline{m}_t(M_t)$ (see [59] for details on the involved reparametrization) have been implemented (the applied renormalization schemes for SUSY parameters will be discussed below). The Higgs vev is a dependent quantity in FeynHiggs which is expressed in terms of the physical observables $M_W$, $s_\mathrm {w}$ and e according to Eq. (4) (where e is furthermore reparametrized in terms of the Fermi constant, see Eq. (7)). Accordingly, if choosing low-energy SM parameters to express the EFT result, the non-logarithmic terms in this result are parametrized in terms of the ${\overline{\text {MS}}}$ quantities $\overline{m}_t(M_t)$ and $v_{\overline{\text {MS}}}(M_t)$, while depending on the option chosen for the top-quark mass the non-logarithmic terms in FeynHiggs are expressed in terms of either $\overline{m}_t(M_t)$ and $v_{G_F}$ or $M_t$ and $v_{G_F}$. Those parametrizations differ from each other by higher-order terms. The observed differences are therefore related to the remaining uncertainties of unknown higher-order corrections.

It should be noted that also within the EFT approach there is a certain freedom for choosing different parametrizations. For instance, the threshold corrections at the matching scale can be expressed in terms of the SM ${\overline{\text {MS}}}$ top Yukawa coupling or in terms of the MSSM ${\overline{\text {DR}}}$ top Yukawa coupling.

As a result, the deviations $\varDelta ^{\text {nolog}}$ between the non-logarithmic terms in the hybrid approach and the EFT approach arise from the following sources,

$$\begin{aligned} \varDelta ^{\text {nolog}}\equiv & {} (M_h^2)_\text {FH}^{\text {nolog}}-(M_h^2)_{\text {EFT}}^{\text {nolog}} \nonumber \\= & {} \varDelta ^{\text {nolog}}_{v/M_{\text {SUSY}}} + \varDelta ^{\text {nolog}}_\text {para} + \varDelta ^{\text {nolog}}_{p^2}. \end{aligned}$$

(29)

Here $\varDelta ^{\text {nolog}}_{v/M_{\text {SUSY}}}$ are terms present in the hybrid approach that would correspond to higher-dimensional operators in the EFT approach. The term $\varDelta ^{\text {nolog}}_\text {para}$ indicates the differences in the parametrization of the non-logarithmic terms, and

$$\begin{aligned} \varDelta ^{\text {nolog}}_{p^2}:= & {} \left[ \hat{\varSigma }^{{\text {nonSM}}\prime }_{hh}(m_h^2)\right] _{\text {nolog}}\left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}}\nonumber \\&-\left[ \hat{\varSigma }^{{\text {nonSM}}\prime }_{hh}(m_h^2)\right] _{\text {nolog}}^{\mathcal{O}(\alpha _t)}\left[ \hat{\varSigma }_{hh}^{\text {MSSM}}(m_h^2)\right] _{\text {nolog}}^{\mathcal{O}(\alpha _t)} \nonumber \\&+ \Big [\text {higher order terms involving} \nonumber \\&\quad (\partial /\partial p^2)^n \hat{\varSigma }_{hh}^{\text {nonSM}}, n\ge 1\Big ] \end{aligned}$$

(30)

are terms arising from the different determination of the propagator poles, as discussed above.

3.3 Terms arising from the determination of the propagator pole at the two-loop level

We saw in Sects. 3.1 and 3.2 that the different determination of the propagator pole in the hybrid approach and the EFT approach gives rise to both logarithmic and non-logarithmic contributions in which the expressions given for the two approaches in the previous sections differ from each other. We will now explicitly demonstrate at the two-loop level that those differences in fact cancel out in the limit of a heavy SUSY scale if all the relevant terms at this order are taken into account.

As a first step, we write down the correction to $M_h^2$, derived by an explicit diagrammatic calculation. At strict two-loop order, we obtain

$$\begin{aligned} (M_h^2)_\text {FD}= & {} m_h^2 - \hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) - \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2) \nonumber \\&+ \left( \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)+ \hat{\varSigma }_{hh}^{{\text {SM}},(1)\prime }(m_h^2)\right) \cdot \nonumber \\&\cdot \hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2). \end{aligned}$$

(31)

The superscripts indicate the loop-order of the corresponding self-energy.⁵

We obtain the renormalized two-loop self-energy from the unrenormalized one via

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2)= & {} \varSigma _{hh}^{{\text {MSSM}},(2)}(m_h^2) \nonumber \\&+\, (\text {two-loop counterterms}) \nonumber \\&+\, (\text {subloop-ren.}). \end{aligned}$$

(32)

The subloop-renormalization can be derived from the one-loop self-energy via a counterterm-expansion. Expressing all couplings appearing in the one-loop self-energy through masses divided by $v_{G_F}$ (for the remainder of this section we drop the subscript “$G_F$”, i.e. we use the shorthand $v \equiv v_{G_F}$), we can write

$$\begin{aligned}&(\text {subloop-ren.})\nonumber \\&\quad = (\delta v^2)^{\text {MSSM}}\frac{\partial }{\partial v^2}\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&\qquad + \sum _i (\delta m_i)^{\text {MSSM}}\frac{\partial }{\partial m_i}\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&\qquad +\,\text {(field ren.)}.\nonumber \\&\quad = -\frac{(\delta v^2)^{\text {MSSM}}}{v^2} \hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&\qquad +\, \sum _i (\delta m_i)^{\text {MSSM}}\frac{\partial }{\partial m_i}\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&\qquad +\,\text {(field ren.)}, \end{aligned}$$

(33)

where we used in the last line that $\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}\propto 1/v^2$ if all couplings are expressed by the respective mass divided by v.

We are interested in terms involving the finite parts of the derivative of the Higgs self-energy, i.e. terms which could potentially cancel the term proportional to $\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)$ in Eq. (31). At first sight it would seem that terms of this kind could arise from an on-shell field renormalization of the Higgs field. It is well-known, however, that those field renormalization constants drop out of the prediction of the mass parameter order by order in perturbation theory (in FeynHiggs, a ${\overline{\text {DR}}}$ renormalization is employed for the Higgs fields). Also the mass counterterms as well as the genuine two-loop counterterms do not contribute terms that are proportional to $\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)$. The only remaining term is the vev counterterm. According to Eqs. (6) and (7) it is given at the one-loop level by, having the same form in the SM and the MSSM,

$$\begin{aligned} \frac{\delta v^2}{v^2}= & {} \frac{\delta M_W^2}{M_W^2}+\frac{c_\mathrm {w}^2}{s_\mathrm {w}^2}\left( \frac{\delta M_Z^2}{M_Z^2}-\frac{\delta M_W^2}{M_W^2}\right) -\frac{\delta e^2}{e^2} \nonumber \\&+\varDelta r - \delta Z_{hh}. \end{aligned}$$

(34)

The renormalization constant $\delta Z_{hh}$ represents within the MSSM the ${\overline{\text {DR}}}$ field renormalization constant of the SM-like Higgs field, while in the SM it is understood to be the ${\overline{\text {MS}}}$ field renormalization constant of the Higgs field.

We verified by explicit calculation that in the limit of a large SUSY scale the following relation holds

$$\begin{aligned} \frac{(\delta v^2)^{\text {MSSM}}}{v^2}= & {} \frac{(\delta v^2)^{\text {SM}}}{v^2} - \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2) \nonumber \\&+\, \mathcal{O}(v/M_{\text {SUSY}}). \end{aligned}$$

(35)

Using this relation, we can rewrite the two-loop self-energy (omitting terms of $\mathcal{O}(v/M_{\text {SUSY}})$),

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2)= & {} \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2)\Big |_{(\delta v^2)^{\text {MSSM}}\rightarrow (\delta v^2)^{\text {SM}}} \nonumber \\&+\,\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2), \end{aligned}$$

(36)

where the subscript ‘$(\delta v^2)^{\text {MSSM}}\rightarrow (\delta v^2)^{\text {SM}}$’ is used to indicate that the MSSM vev counterterm, appearing in the subloop renormalization, is replaced by its SM counterpart.

Plugging this expression back into Eqs. (33) and (31), we obtain

$$\begin{aligned} (M_h^2)_\text {FD}= & {} m_h^2 - \hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&-\left( \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2)\Big |_{(\delta v^2)^{\text {MSSM}}\rightarrow (\delta v^2)^{\text {SM}}} \right. \nonumber \\&\left. +\,\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2)\right) \nonumber \\&+\left( \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)+ \hat{\varSigma }_{hh}^{{\text {SM}},(1)\prime }(m_h^2)\right) \cdot \nonumber \\&\cdot \,\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2)\nonumber \\= & {} m_h^2 - \hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2) \nonumber \\&-\, \hat{\varSigma }_{hh}^{{\text {MSSM}},(2)}(m_h^2)\Big |_{(\delta v^2)^{\text {MSSM}}\rightarrow (\delta v^2)^{\text {SM}}}\nonumber \\&+\,\hat{\varSigma }_{hh}^{{\text {SM}},(1)\prime }(m_h^2)\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)}(m_h^2). \end{aligned}$$

(37)

We observe that the corresponding subloop renormalization term cancels in Eq. (31) the term $\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)$ involving the non-SM contributions to the Higgs self-energy by which the determination of the propagator pole in the hybrid approach differs from the EFT approach.

The origin of Eq. (35) is the different normalization of the SM-like MSSM Higgs doublet $\varPhi _{\text {MSSM}}$ and the SM Higgs doublet $\varPhi _{\text {SM}}$. Comparing the derivative of the two-point function, appearing in the LSZ factor of amplitudes with external Higgs fields,⁶ we obtain in the limit of a heavy SUSY scale

$$\begin{aligned}&\varPhi _{\text {MSSM}}\left( 1 + \frac{1}{2}\hat{\varSigma }_{hh}^{{\text {MSSM}},(1)\prime }(m_h^2)\right) \nonumber \\&\quad =\varPhi _{\text {SM}}\left( 1 + \frac{1}{2}\hat{\varSigma }_{hh}^{{\text {SM}},(1)\prime }(m_h^2)\right) , \end{aligned}$$

(38)

or equivalently

$$\begin{aligned} \varPhi _{\text {MSSM}}= \varPhi _{\text {SM}}\left( 1 - \frac{1}{2}\hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2)\right) . \end{aligned}$$

(39)

Expressed in terms of a relation between the counterterms of the vevs, this implies Eq. (35).

While as mentioned above the Higgs field renormalization constant drops out in the Higgs mass prediction order by order, it is nevertheless noteworthy that the introduction of an OS field renormalization constant would lead to

$$\begin{aligned} \hat{\varSigma }^{{\text {MSSM}}\prime }_{hh}(m_h^2)\big |_{\delta Z_h^{\text {OS}}} = 0 \end{aligned}$$

(40)

and

$$\begin{aligned} (\delta v^2)^{\text {MSSM}}\big |_{\delta Z_h^{\text {OS}}}&= (\delta v^2)^{\text {SM}}\big |_{\delta Z_h^{\text {OS}}}, \end{aligned}$$

(41)

implying that no terms involving $\hat{\varSigma }_{hh}^{{\text {nonSM}}\prime }$ appear in the subloop renormalization at the two-loop level.

While we have demonstrated this cancellation at the two-loop level, it is to be expected that it would also occur at higher orders. Explicit formulas for higher-order terms of this kind are given in Appendix B. While the described cancellation occurs at the full two-loop level, only partial cancellations occur between the full one-loop self-energy times its derivative and the two-loop self-energy if for the latter certain approximations are made.

In FeynHiggs, the two-loop self-energies are derived in the gaugeless limit (i.e., two-loop corrections of $\mathscr {O}(\alpha _t\alpha _s,$ $\alpha _b\alpha _s,\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)$ are incorporated [22, 23, 25, 27, 33, 34]),⁷ and by default the external momentum of the two-loop graphs is neglected. There is, however, an option to include momentum dependence at $\mathcal{O}(\alpha _t\alpha _s)$ (see [56, 57]). Accordingly, all $\mathcal{O}(\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)$ non-SM terms arising through the determination of the propagator pole at the two-loop level are cancelled in the limit of a large SUSY scale by corresponding subloop renormalization contributions within the diagrammatic calculation (the determination of the propagator pole obviously does not give rise to terms of $\mathcal{O}(\alpha _t\alpha _s,\alpha _b\alpha _s)$). In previous versions of FeynHiggs, we have already taken care when constructing the subtraction terms according to Eq. (19) that we do not subtract logarithmic contributions that are needed for the cancellation with the corresponding terms arising from the determination of the propagator poles. For terms arising through the determination of the propagator pole beyond $\mathcal{O}(\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)$, however, so far the cancellation in the limit of a large SUSY scale did not occur because the corresponding contributions in the irreducible self-energies at the two-loop level and beyond are not incorporated. In order to avoid unwanted effects from an incomplete cancellation, we have removed the uncompensated terms arising from the determination of the propagator pole in FeynHiggs.

4 ${\overline{\text {DR}}}$ parameters as input for an OS calculation

In this section we discuss issues related to the conversion between parameters of OS and ${\overline{\text {DR}}}$ renormalization schemes. While the discussion will focus on the case where ${\overline{\text {DR}}}$ input parameters are converted into OS ones that are then inserted into a result in the OS scheme, it should be stressed that the related problems are not intrinsic to the OS approach. The same problems would occur if a ${\overline{\text {DR}}}$ result were used with OS input parameters. The discussed problems are also not specific to Higgs mass predictions in SUSY models, but would appear whenever there are numerically large higher-order logarithms arising from a large splitting between the relevant scales of the considered quantity. In predictions for the mass of the SM-like Higgs boson within the MSSM, the result is however particularly sensitive to higher-order effects of this kind through the pronounced dependence on the stop mixing parameter $X_t$, which receives large corrections when converting from the ${\overline{\text {DR}}}$ to the OS scheme or vice versa.

In the case where fixed-order results at the n-loop level obtained in two different renormalization schemes are compared with each other, and higher-order logarithms are unknown and not expected to be particularly enhanced, it is well known that the results based on the same type of corrections in two schemes differ by terms that are of $\mathcal{O}(n+1)$. The same is true for different options regarding how to perform the parameter conversion that differ from each other by higher-order contributions. The numerical differences observed in such a comparison can therefore be used as an indication of the possible size of unknown higher-order corrections.

The situation is different, however, in the case that we are considering here, since the comparison is not performed between fixed-order results but between results incorporating a series of (resummed) higher-order logarithms. It is crucial in such a case that the correct form of the higher-order logarithms that can be derived via EFT methods, which in our case arise from the large splitting between the assumed SUSY scale and the weak scale, is maintained in the parameter conversion. We will demonstrate below that the parameter conversion that is usually applied for a comparison of renormalization schemes in fixed-order results does not maintain the correct form of the higher-order logarithms. Since those higher-order logarithms are numerically important, a conversion carried out in the described way leads to very large numerical discrepancies for large values of the SUSY scale.

4.1 Conversion between ${\overline{\text {DR}}}$ and OS parameters applicable to fixed-order results

The most straightforward method used for the conversion of ${\overline{\text {DR}}}$ input parameters to OS parameters in fixed-order results is to derive the shift between a parameter p in the two schemes according to $p^{\text {OS}}= p^{\overline{\text {DR}}}+ \varDelta p$ at the considered loop order, see e.g. [60]. Accordingly, at the full one-loop level, including logarithmic as well as non-logarithmic terms, the conversion from ${\overline{\text {DR}}}$ to OS parameters for the stop mixing parameter and the stop masses, which are particularly relevant in the context of MSSM Higgs mass predictions, reads (for explicit formulas see [22, 23, 25, 59])

$$\begin{aligned} X_t^{\text {OS}}&= X_t^{\overline{\text {DR}}}+ \varDelta X_t, \end{aligned}$$

(42)

$$\begin{aligned} M_{\tilde{t}_1}&= m_{\tilde{t}_1}^{\overline{\text {DR}}}+ \varDelta m_{\tilde{t}_1}, \end{aligned}$$

(43)

$$\begin{aligned} M_{\tilde{t}_2}&= m_{\tilde{t}_2}^{\overline{\text {DR}}}+ \varDelta m_{\tilde{t}_2}. \end{aligned}$$

(44)

Here $\varDelta m_{\tilde{t}_{1,2}}$ is given by the corresponding difference of the ${\overline{\text {DR}}}$ and the OS counterterm. In FeynHiggs, the shift of $X_t$ is obtained by first calculating the OS stop masses and the OS stop mixing angle $\theta _{\tilde{t}}^{\text {OS}}$. These are then used to obtain $X_t^{\text {OS}}$ via

$$\begin{aligned} M_t X_t^{\text {OS}}= (M_{\tilde{t}_1}^2-M_{\tilde{t}_2}^2)\sin \theta _{\tilde{t}}^{\text {OS}}\cos \theta _{\tilde{t}}^{\text {OS}}. \end{aligned}$$

(45)

Relating this prescription for $X_t^{\text {OS}}$ to the ${\overline{\text {DR}}}$ input parameters $X_t^{\overline{\text {DR}}}$, $m_{\tilde{t}_1}^{\overline{\text {DR}}}$, $m_{\tilde{t}_2}^{\overline{\text {DR}}}$, one can see that Eq. (45) contains products of one-loop contributions and therefore involves higher-order terms. Alternatively one could have used an expression for the conversion that is truncated at the one-loop level. The difference between the two prescriptions would be of the order of unknown higher-order corrections in a fixed-order comparison. The on-shell parameters obtained as described above are then used as input of the fixed-order OS renormalized calculation. This means in particular that the knowledge of the initial ${\overline{\text {DR}}}$ parameters is not used any further once the conversion to OS parameters has been carried out. While this procedure is suitable for fixed-order results, it leads to problems if results containing a series of higher-order logarithms are meant to be converted.

Indeed, applying the described parameter conversion to the case of a ${\overline{\text {DR}}}$ result that incorporates higher-order logarithms generates additional higher-order terms causing a deviation in the logarithmic contributions. This can be seen by investigating the Higgs self-energy up to the two-loop level where the parameter $X_t^{\text {OS}}$ obtained from the conversion has been inserted,

$$\begin{aligned} \hat{\varSigma }_{hh}^{\text {OS}}(X_t^{\text {OS}}) =&\hat{\varSigma }_{hh}^{(1),{\text {OS}}}(X_t^{\text {OS}}) + \hat{\varSigma }_{hh}^{(2),{\text {OS}}}(X_t^{\text {OS}}). \end{aligned}$$

(46)

Using instead Eq. (4243) to write $X_t^{\text {OS}}$ in terms of $X_t^{\overline{\text {DR}}}$,

$$\begin{aligned} \hat{\varSigma }_{hh}^{\text {OS}}(X_t^{\text {OS}})= & {} \hat{\varSigma }_{hh}^{(1),{\text {OS}}}(X_t^{\overline{\text {DR}}}+ \varDelta X_t) \nonumber \\&+\, \hat{\varSigma }_{hh}^{(2),{\text {OS}}}(X_t^{\overline{\text {DR}}}+ \varDelta X_t), \end{aligned}$$

(47)

and performing an expansion in $\varDelta X_t$ yields

$$\begin{aligned} \hat{\varSigma }_{hh}^{\text {OS}}(X_t^{\text {OS}})= & {} \hat{\varSigma }_{hh}^{(1),{\text {OS}}}(X_t^{\overline{\text {DR}}}) + \left[ \frac{\partial }{\partial X_t}\hat{\varSigma }_{hh}^{(1),{\text {OS}}}(X_t^{\overline{\text {DR}}})\right] \varDelta X_t\nonumber \\&+\, \hat{\varSigma }_{hh}^{(2),{\text {OS}}}(X_t^{\overline{\text {DR}}}) + \left[ \frac{\partial }{\partial X_t}\hat{\varSigma }_{hh}^{(2),{\text {OS}}}(X_t^{\overline{\text {DR}}})\right] \varDelta X_t\nonumber \\&+\, \mathcal{O}(\varDelta X_t^2) \end{aligned}$$

(48)

$$\begin{aligned}= & {} \hat{\varSigma }_{hh}^{\overline{\text {DR}}}(X_t^{\overline{\text {DR}}}) + \left[ \frac{\partial }{\partial X_t}\hat{\varSigma }_{hh}^{(2),{\text {OS}}}(X_t^{\overline{\text {DR}}})\right] \varDelta X_t\nonumber \\&+\, \mathcal{O}(\varDelta X_t^2). \end{aligned}$$

(49)

Thus, the obtained expression obviously differs from the original ${\overline{\text {DR}}}$ result by terms of 3-loop order and beyond. One would furthermore need to convert also all other parameters entering the self-energy to the ${\overline{\text {DR}}}$ scheme in order to exactly recover the ${\overline{\text {DR}}}$ renormalized self-energy.

4.2 The case of large higher-order logarithms

The higher-order terms in Eq. (49) that are not present in the original ${\overline{\text {DR}}}$ result contain in general logarithmic contributions which for a result containing a series of higher-order logarithms cause a deviation from the logarithmic corrections determined via the RGE. In our numerical discussion in Sect. 6 below we will demonstrate that those higher-order contributions that are induced by the parameter conversion are indeed numerically sizeable.

Another issue that is relevant in a hybrid approach, as pursued in FeynHiggs, where a fixed-order result in the OS scheme is combined with higher-order logarithmic expressions that are expressed in the ${\overline{\text {DR}}}$ scheme concerns the ${\overline{\text {DR}}}$ value of $X_t$ that is used in the EFT part of the calculation. Only logarithmic terms are kept in the relation between $X_t^{{\overline{\text {DR}}},{\text {EFT}}}$ and $X_t^{\text {OS}}$, see Eq. (21). If instead an input value for $X_t^{\overline{\text {DR}}}$ were converted to $X_t^{\text {OS}}$ using the full one-loop contributions according to Eq. (4243), the stop mixing parameter used in the EFT calculation of FeynHiggs, $X_t^{{\overline{\text {DR}}},{\text {EFT}}}$, would differ from the input parameter $X_t^{\overline{\text {DR}}}$.

In order to properly address the case where ${\overline{\text {DR}}}$ parameters associated with a result containing a series of higher-order logarithms are used as input for FeynHiggs, we follow the strategy to perform the parameter conversion in the fixed-order result rather than in the infinite series of higher-order logarithms. For this purpose we have extended FeynHiggs such that the incorporated fixed-order result is given in terms of the ${\overline{\text {DR}}}$ parameters $X_t^{\overline{\text {DR}}}$, $m_{\tilde{t}_1}^{\overline{\text {DR}}}$, $m_{\tilde{t}_2}^{\overline{\text {DR}}}$ (the actual input parameters are the soft-breaking parameters of the stop sector). This new result complements the existing result that is given in terms of the on-shell parameters $X_t^{\text {OS}}$, $M_{\tilde{t}_1}\equiv m_{\tilde{t}_1}^{\text {OS}}$, $M_{\tilde{t}_2}\equiv m_{\tilde{t}_2}^{\text {OS}}$. The reparametrisation on which the new result is based can be viewed as the parameter conversion described in the example of the previous section, but truncated at the two-loop level,

$$\begin{aligned} \hat{\varSigma }_{hh}^{\text {OS}}(X_t^{\text {OS}})\rightarrow & {} \hat{\varSigma }_{hh}^{{\text {OS}}}(X_t^{\overline{\text {DR}}}) + \left[ \frac{\partial }{\partial X_t}\hat{\varSigma }_{hh}^{(1),{\text {OS}}}(X_t^{\overline{\text {DR}}})\right] \varDelta X_t\nonumber \\= & {} \hat{\varSigma }_{hh}^{\overline{\text {DR}}}(X_t^{\overline{\text {DR}}}). \end{aligned}$$

(50)

We have used the same procedure as the one described here for the stop mixing parameter also for the stop masses. The two-loop terms that are induced by the conversion at the one-loop level have been added to the two-loop result derived in the on-shell scheme in order to arrive at the corresponding expression in the ${\overline{\text {DR}}}$ scheme. Compact expressions for these additional terms valid in the case $M_{\text {SUSY}}\gg M_t$ and degenerate $M_L=M_{\tilde{t}_R}=M_{\text {SUSY}}$ can be found in Appendix A. It should be noted that we would have obtained the same result if we had performed the diagrammatic calculation with a ${\overline{\text {DR}}}$ renormalization of the respective parameters instead of reparametrizing the final result. Using the above result given in terms of ${\overline{\text {DR}}}$ parameters, the value of $X_t$ that is used in the EFT part of the calculation equals the ${\overline{\text {DR}}}$ input parameter, $X_t^{{\overline{\text {DR}}},{\text {EFT}}} = X_t^{\overline{\text {DR}}}$. For this setting in FeynHiggs with ${\overline{\text {DR}}}$ input parameters the subtraction terms have been adjusted such that the logarithms already contained in the fixed-order result for the ${\overline{\text {DR}}}$ renormalized self-energy are subtracted (rather than the ones contained in the OS renormalized self-energy, as it is the case for OS input parameters).

Accordingly, depending on the provided input parameters the evaluation of the prediction for the mass of the SM-like Higgs boson in FeynHiggs proceeds in the following ways:

• For on-shell input parameters the on-shell fixed-order result is combined with the higher-order logs obtained in the EFT approach, where $X_t^{{\overline{\text {DR}}},{\text {EFT}}}$ is related to $X_t^{\text {OS}}$ as specified in Eq. (21).

• For ${\overline{\text {DR}}}$ input parameters in the stop sector associated with a result containing a series of higher-order logarithms the ${\overline{\text {DR}}}$ fixed-order result is combined with the higher-order logs obtained in the EFT approach, where $X_t^{{\overline{\text {DR}}},{\text {EFT}}} = X_t^{\overline{\text {DR}}}$.

• For ${\overline{\text {DR}}}$ input parameters in a low-scale SUSY scenario where the impact of higher-order logarithms is expected to be small, both the fixed-order ${\overline{\text {DR}}}$ result and the fixed-order on-shell result can be employed, where for the latter the parameter conversion described in the previous section is used.

5 Comparison of FeynHiggs to other codes

In the previous sections, we investigated methodical differences between the different approaches for predicting the lightest CP-even Higgs boson mass in the MSSM, focusing in particular on the comparison of the hybrid approach implemented in FeynHiggs with a pure EFT calculation. In the following, we compare FeynHiggs numerically to other codes.

Publicly available codes based on diagrammatic fixed-order results or effective potential methods include CPSuperH [61,62,63], SoftSUSY [64], SPheno [65, 66] and SUSPECT [67]. Publicly available pure EFT calculations are SUSYHD [43] and MhEFT [40, 42, 68]. FlexibleSUSY [69], based on SARAH [70,71,72,73], includes both a diagrammatic and an EFT result. Furthermore, it also has the option to use a hybrid method different from the one pursued in FeynHiggs, called FlexibleEFTHiggs [47]. Its basic idea is to include terms suppressed by the SUSY scale into the matching conditions in order to obtain accurate results for both low and high scales. Recently, the same approach has been included into SPheno [48].

The different levels of higher-order corrections implemented in the various diagrammatic codes are listed in [74]. A detailed numerical comparison between various diagrammatic and EFT codes can be found in [47]. In there, it is also discussed in detail how FlexibleEFTHiggs compares to other codes. We therefore focus in this work on a comparison of FeynHiggs to SUSYHD as an exemplary EFT calculation.

Fig. 1

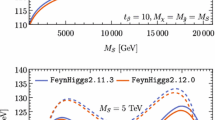
Left: $M_h$ as a function of $M_{\text {SUSY}}$ for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=0$ (solid) and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$ (dashed). The results of FeynHiggs2.13.0 with a ${\overline{\text {DR}}}$ to OS conversion of the input parameters (blue) and a ${\overline{\text {DR}}}$ renormalization of the fixed-order result (red) are compared. Right: Same as left plot, apart that $M_h$ is shown in dependence of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$ for $M_{\text {SUSY}}= 1$ TeV (solid), $M_{\text {SUSY}}= 5$ TeV (dashed) and $M_{\text {SUSY}}= 20$ TeV (dot-dashed). In the bottom panels, the difference between the blue and red curves is shown ($\varDelta M_h = M_h(\text {FH 2.13.0 param conv}) - M_h(\text {FH 2.13.0 } {\overline{\text {DR}}})$)

Before we can investigate the impact of the effects discussed in the previous sections on the comparison of FeynHiggs and SUSYHD, we have to ensure that the RGE results, i.e. the results for $\lambda (M_t)$, of both codes are compatible with each other. Both codes implement full leading and next-to-leading resummation and $\mathcal{O}(\alpha _s\alpha _t,\alpha _t^2)$ next-to-next-to-leading resummation of large logarithms. So the levels of accuracy are basically identical. There are however several differences which are listed below.

• SUSYHD by default uses the top-Yukawa coupling extracted at the NNNLO level. FeynHiggs instead uses the NNLO value by default, which is formally the appropriate setting for the resummation of NNLL contributions. For all numerical results shown in this work, we deactivate the NNNLO corrections to the top-Yukawa coupling in SUSYHD.

• SUSYHD includes the bottom- and tau-Yukawa couplings in the renormalization group running and also includes corresponding one-loop threshold corrections. In FeynHiggs, the bottom and tau Yukawa couplings are set to zero in the EFT calculation. In the fixed-order diagrammatic calculation, however, terms proportional to the bottom Yukawa coupling are included at the one- and two-loop level (at the one-loop level for the case of the tau Yukawa coupling).

• SUSYHD includes the electroweak gauge couplings in the running up to the three-loop level. FeynHiggs takes them into account up to the two-loop level. At the three-loop level, they are set to zero.

• FeynHiggs includes a one-loop running of $\tan \beta$ to relate $\tan \beta (M_t)$, which is used as input of FeynHiggs, to $\tan \beta (M_{\text {SUSY}})$, which enters through the matching at the SUSY scale. In contrast, SUSYHD uses $\tan \beta (M_{\text {SUSY}})$ as input.

• Similarly, FeynHiggs uses a ${\overline{\text {DR}}}$ renormalized Higgsino mass parameter $\mu$ at the scale $M_t$. The running to the scale $M_{\text {SUSY}}$, at which it enters the EFT calculation via the matching conditions at the SUSY scale, is neglected. SUSYHD uses $\mu (M_{\text {SUSY}})$ as input.

More details on the implemented EFT calculations are given in [43, 46].

Despite the listed differences including the different treatment of the renormalization scales of $\tan \beta$ and $\mu$, we find excellent agreement between the results of the RGE running of both codes. The numerical difference of the quantity $v^2\lambda (M_t)$ calculated using the two codes is always $\lesssim 50$ GeV$^2$ for the single scale scenario defined in Eq. (2) and $\tan \beta \sim \mathcal{O}(10)$. This translates into a difference in $M_h$ of $\lesssim 0.1$ GeV.

6 Numerical results

In this section, we present a numerical investigation of the effects discussed in the previous sections and compare the result obtained by FeynHiggs to SUSYHD as an exemplary pure EFT code. We restrict ourselves to the single scale scenario defined in Eq. (2). Apart from the parameters of the stop sector, we neglect all renormalization scheme conversions necessary to relate the parameters of Eq. (2) as defined in FeynHiggs to the parameters as defined in SUSYHD. We furthermore set

$$\begin{aligned} \tan \beta = 10, \end{aligned}$$

(51)

i.e. we use $\tan \beta (M_t)=10$ as input for FeynHiggs and $\tan \beta (M_{\text {SUSY}})=10$ as input for SUSYHD. As mentioned in Sect. 5, the difference in the renormalization scales is negligible for the considered scenario. All soft-breaking trilinear couplings except the one of the scalar top quarks are chosen to be

$$\begin{aligned} A_{e,\mu ,\tau ,u,d,c,s,b} = 0. \end{aligned}$$

(52)

For all soft-breaking parameters (i.e. those of the stop sector), we use the ${\overline{\text {DR}}}$ scheme with the renormalization scale being $M_{\text {SUSY}}$. If not stated otherwise, we use a parametrization of the non-logarithmic contributions in terms of the SM ${\overline{\text {MS}}}$ NNLO top mass and $v_{G_F}$ (see Sect. 3.2), corresponding to choosing runningMT = 1 as FeynHiggs flag.

Fig. 2

Comparison of the $M_h$ predictions of FeynHiggs2.13.0 ${\overline{\text {DR}}}$ with FeynHiggsnew ${\overline{\text {DR}}}$, where in the new version terms arising from the determination of the propagator pole are omitted that go beyond the level of the corrections implemented in the irreducible self-energies. Left: Prediction for $M_h$ as function of $M_{\text {SUSY}}$ for vanishing stop mixing and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 2$. Right: Prediction for $M_h$ as function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$ for $M_{\text {SUSY}}= 1$ TeV (solid), $M_{\text {SUSY}}= 5$ TeV (dashed) and $M_{\text {SUSY}}= 20$ TeV (dot-dashed). In the bottom panels, the difference between the blue and red curves is shown ($\varDelta M_h = M_h(\text {FH 2.13.0 }{\overline{\text {DR}}})-M_h(\text {FH new } {\overline{\text {DR}}})$)

We first look at the numerical difference between employing the type of conversion from ${\overline{\text {DR}}}$ to OS input parameters which is suitable for the comparison of fixed-order results (“FH 2.13.0 param conv”) and using a ${\overline{\text {DR}}}$ renormalized fixed-order result (“FH 2.13.0 ${\overline{\text {DR}}}$”), see the discussion in Sect. 4. The left plot of Fig. 1 shows the corresponding results for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 0\;(2)$ as solid (dashed) lines as a function of $M_{\text {SUSY}}$. One can see that for $M_{\text {SUSY}}\lesssim 5$ TeV the difference between the two methods leads to an approximately constant shift in the prediction for $M_h$. For vanishing mixing the prediction obtained by using a ${\overline{\text {DR}}}$ renormalized fixed-order result is $\sim 0.5$ GeV higher than the one obtained by a naive scheme conversion of the input parameters. For $X_t/M_{\text {SUSY}}= 2$, the shift is larger. The result obtained using a ${\overline{\text {DR}}}$ fixed-order result is $\sim 1{-} 1.5 \,\, \mathrm {GeV}$ smaller than the one obtained by the naive conversion of the input parameters. The shifts occur not only for scales of a few TeV, but also for very low scales ($M_{\text {SUSY}}\simeq 0.3 \,\, \mathrm {TeV}$). Therefore, we conclude that at low scales the observed shifts are mainly caused by non-logarithmic higher-order terms by which the ${\overline{\text {DR}}}$ result and the result involving a parameter conversion differ from each other. As usual, non-logarithmic terms tend to be larger for $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|\sim 2$ than for vanishing stop mixing.

For $M_{\text {SUSY}}\gtrsim 5$ TeV, we observe that the difference be-tween the two results is increasing rapidly to up to $10 \,\, \mathrm {GeV}$ for vanishing mixing and up to $5 \,\, \mathrm {GeV}$ for $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|\sim 2$ in the region up to $M_{\text {SUSY}}\sim 20 \,\, \mathrm {TeV}$. This behavior is mainly due to the fact that the parameter conversion that is used for the comparison of fixed-order results induces higher-order logarithmic contributions that are not compatible with the implemented resummation of logarithms to all orders (see the discussion in Sect. 4.1). For high SUSY scales, where the higher-order logarithmic contributions become numerically large, this mismatch leads to the observed large deviations. To a lesser extent, also the deviation between the input $X_t^{\overline{\text {DR}}}$ and the $X_t^{{\overline{\text {DR}}},{\text {EFT}}}$ used in the EFT calculation plays a role in this context, see Sect. 4.2.

In the right plot of Fig. 1 the two results are compared as a function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$ for $M_{\text {SUSY}}= 1, 5, 20 \,\, \mathrm {TeV}$, shown as solid, dashed and dot-dashed lines, respectively. For $M_{\text {SUSY}}= 1 \,\, \mathrm {TeV}$ and $M_{\text {SUSY}}= 5 \,\, \mathrm {TeV}$ the deviations stay relatively small except for the highest values of $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|$. In contrast, for $M_{\text {SUSY}}= 20 \,\, \mathrm {TeV}$ the uncontrolled higher-order contributions induced by the naive conversion of the input parameters are seen to have a huge effect which even reverts the usual pattern of the dependence on $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|$, giving rise to local minima at $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|\simeq \pm 2.3$. We emphasize again that the same kind of uncontrolled higher-order effects would occur if a naive conversion of OS to ${\overline{\text {DR}}}$ parameters would be used as input for a ${\overline{\text {DR}}}$ result containing a series of numerically large higher-order logarithms. Figure 1 shows that numerical instabilities noticed in comparisons of EFT results with FeynHiggs carried out in the literature are a consequence of an inappropriate application of the conversion of input parameters between the OS and the ${\overline{\text {DR}}}$ schemes. The higher-order contributions implemented in FeynHiggs are seen to be numerically stable up to very high SUSY scales in the considered scenario.

For the further FeynHiggs results shown below we use the ${\overline{\text {DR}}}$ renormalization of the parameters in the stop sector. As a next step we investigate the impact of the terms arising from the determination of the propagator pole. As explained in Sect. 3, there occurs a cancellation in the limit of a large SUSY scale between non-SM terms arising through the determination of the propagator pole and contributions from the subloop renormalization of the irreducible self-energy diagrams. While up to the version FeynHiggs2.13.0 this cancellation was incomplete for terms beyond $\mathcal{O}(\alpha _t^2,\alpha _t\alpha _b,\alpha _b^2)$ (see Eq. (20)), we have modified the determination of the propagator poles in the new version of FeynHiggs such that terms are omitted that would not cancel because their counterpart in the irreducible self-energies is not incorporated at present. In Fig. 2 FeynHiggs2.13.0 ${\overline{\text {DR}}}$ is compared with the new version, which is labelled as FeynHiggsnew ${\overline{\text {DR}}}$. The difference between the two results corresponds essentially to the terms $\varDelta _{p^2}^{\text {logs}}$ and $\varDelta _{p^2}^{\text {nolog}}$ given in Eqs. (26) and (29). In the left plot of Fig. 2, we show the results as a function of $M_{\text {SUSY}}$ for $X_t^{\overline{\text {DR}}}= 0$ and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 2$. One observes that the difference grows nearly logarithmically with $M_{\text {SUSY}}$. This is expected since the largest terms in $\varDelta _{p^2}^{\text {logs}} + \varDelta _{p^2}^{\text {nolog}}$ are in fact logarithms of the SUSY scale over $M_t$. Consequently, for small scales ($M_{\text {SUSY}}\lesssim 1$ TeV), these terms induce only a small upwards shift of $\lesssim 0.5 \,\, \mathrm {GeV}$. For large scales however ($M_{\text {SUSY}}\gtrsim 5 \,\, \mathrm {TeV}$), this shift grows to up to $1.5 \,\, \mathrm {GeV}$ for vanishing stop mixing and $2 \,\, \mathrm {GeV}$ for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 2$. In the right plot of Fig. 2 the difference is depicted as a function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$ for $M_{\text {SUSY}}= 1, 5, 20 \,\, \mathrm {TeV}$, shown as solid, dashed and dot-dashed lines, respectively. One can see that the difference between the two results is approximately quadratically dependent on $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$. This reflects the $X_t^{\overline{\text {DR}}}$ dependence of the derivative of the Higgs-boson self-energy (see Eq. (B.26) below).

Fig. 3

Comparison of the $M_h$ predictions of FeynHiggsnew ${\overline{\text {DR}}}$ with SUSYHD. Left: $M_h$ as function of $M_{\text {SUSY}}$ for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=0$ (solid) and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$ (dashed). Right: $M_h$ as function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}^{\overline{\text {DR}}}$ for $M_{\text {SUSY}}= 1$ TeV (solid), $M_{\text {SUSY}}= 5$ TeV (dashed) and $M_{\text {SUSY}}= 20$ TeV (dot-dashed). In the bottom panels, the difference between the blue and red curves is shown ($\varDelta M_h = M_h(\text {FH new } {\overline{\text {DR}}})-M_h(\text {SUSYHD})$)

Having investigated the numerical impact of the scheme conversion of the input parameters as well as of the terms arising from the determination of the propagator pole, we now turn to a direct comparison of FeynHiggs with SUSYHD.⁸ The FeynHiggs results in this comparison are the ones of the new version, FeynHiggsnew ${\overline{\text {DR}}}$, where the stop sector is renormalized in the ${\overline{\text {DR}}}$ scheme and terms arising from the determination of the propagator pole are omitted that go beyond the level of the corrections implemented in the irreducible self-energies, as described above.

The left plot of Fig. 3 shows $M_h$ as a function of $M_{\text {SUSY}}$ for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 0\;(2)$ as solid (dashed) lines. For vanishing stop mixing and $M_{\text {SUSY}}\gtrsim 1 \,\, \mathrm {TeV}$, we observe an excellent agreement of the FeynHiggs curve with the SUSYHD result. Even for very large scales $M_{\text {SUSY}}\simeq 20 \,\, \mathrm {TeV}$, we find agreement within $\sim 0.5 \,\, \mathrm {GeV}$ in the considered simple numerical scenario, in which all SUSY scales are chosen to be equal to each other. For low scales ($M_{\text {SUSY}}\lesssim 1 \,\, \mathrm {GeV}$), it can be seen that the FeynHiggs result is higher by up to $\sim 1.7 \,\, \mathrm {GeV}$ compared to the SUSYHD result. The origin of this difference are terms suppressed by the SUSY scale, which are included in FeynHiggs but not in SUSYHD, as will be discussed below. For $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$, we basically observe the same behavior as in case of vanishing stop mixing. The overall agreement in the simple numerical scenario is very good (within $\sim 0.7 \,\, \mathrm {GeV}$ for $M_{\text {SUSY}}\gtrsim 0.5 \,\, \mathrm {TeV}$). For low scales ($M_{\text {SUSY}}\lesssim 0.5 \,\, \mathrm {GeV}$), the FeynHiggs result is lower compared to the SUSYHD result by up to $\sim 1 \,\, \mathrm {GeV}$. As in the case of vanishing stop mixing, this can be traced back to terms suppressed by the SUSY scale. We will discuss this and investigate the remaining differences in more detail below.

In the right plot of Fig. 3 the comparison between the $M_h$ prediction of the new FeynHiggs version and SUSYHD is shown as a function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$ for $M_{\text {SUSY}}= 1, 5, 20 \,\, \mathrm {TeV}$, shown as solid, dashed and dot-dashed lines, respectively. Again one can see an overall very good agreement between both codes for $M_{\text {SUSY}}\gtrsim 1\,\, \mathrm {TeV}$ (within $1 \,\, \mathrm {GeV}$) in the considered simple numerical scenario. The agreement is especially good for small $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|$, but the deviations stay below $1 \,\, \mathrm {GeV}$ also for increasing mixing in the stop sector except for the highest values of $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|$ in the case of $M_{\text {SUSY}}= 1\,\, \mathrm {TeV}$. The larger deviations of up to $\sim 2\,\, \mathrm {GeV}$ for $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|\gtrsim 2.5$ in the case of $M_{\text {SUSY}}= 1\,\, \mathrm {TeV}$ are due to terms suppressed by $M_{\text {SUSY}}$ which become large for increasing $|X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}|$.

Fig. 4

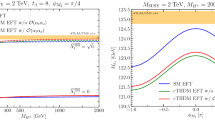
Left: Difference of the $M_h^2$ predictions of FeynHiggsnew ${\overline{\text {DR}}}$ and SUSYHD as a function of $M_{\text {SUSY}}$ for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=0$ (solid) and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$ (dashed). For the parametrization of the diagrammatic result of FeynHiggs the SM NNLO ${\overline{\text {MS}}}$ top-quark mass is chosen. Right: Differences due to the different parametrization of the top-quark mass and the vev in a fixed-order $\mathcal{O}(\alpha _t\alpha _s,\alpha _t^2)$ calculation, taking into account only non-logarithmic terms, as a function of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}$. The difference between the result parametrized in terms of the ${\overline{\text {MS}}}$ NNLO top-quark mass and $v_{G_F}$ and the one parametrized in terms of the ${\overline{\text {MS}}}$ NNLO top-quark mass and $v_{\overline{\text {MS}}}$ is shown

In Fig. 4, we further investigate these remaining differences between FeynHiggs and SUSYHD observed in Fig. 3. In the left plot we show the difference between the results of FeynHiggs and SUSYHD for $M_h^2$ (not for $M_h$). Since in both codes actually $M_h^2$ is calculated, taking the square root of these results can obscure the true dependences of the difference. As an example, if the difference in $M_h^2$ is constant when varying $M_{\text {SUSY}}$, we would not observe a constant difference when comparing the difference in $M_h$. We show in the plot the difference in $M_h^2$ for the case where the fixed-order result of FeynHiggs is parametrized in terms of the SM NNLO ${\overline{\text {MS}}}$ top mass. For $M_{\text {SUSY}}\lesssim 1 \,\, \mathrm {TeV}$ in the case of vanishing mixing and for $M_{\text {SUSY}}\lesssim 3 \,\, \mathrm {TeV}$ in the case of $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$ we observe large gradients. For larger scales ($M_{\text {SUSY}}\gtrsim 3 \,\, \mathrm {TeV}$), the difference is only slowly increasing when raising $M_{\text {SUSY}}$. For vanishing stop mixing, the difference is growing by $\sim 50 \,\, \mathrm {GeV}^2$ when raising $M_{\text {SUSY}}$ from 3 TeV to 20 TeV. For $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$, similarly a growth of $\sim 50 \,\, \mathrm {GeV}^2$ is recognizable. This behavior is mostly due to the differences in the EFT calculations implemented in FeynHiggs and SUSYHD discussed in Sect. 5. In addition, however, we observe an offset relative to the zero axis for $M_{\text {SUSY}}\gtrsim 3$ TeV. For vanishing stop mixing, it is small ($\sim 50 \,\, \mathrm {GeV}^2$), whereas for $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}=2$, the shift is more significant ($\sim 150$ GeV$^2$). The nearly constant offset between the two codes can be traced back to the different parametrization of the non-logarithmic terms discussed in Sect. 3.2.

We further analyse the influence of the different ways to parametrize the non-logarithmic terms in the right plot of Fig. 4. It shows the difference in $M_h^2$ obtained from a diagrammatic calculation of $\mathcal{O}(\alpha _t\alpha _s,\alpha _t^2)$ using different parametrizations of the vev for the non-logarithmic one- and two-loop terms (see Sect. 3.2 for more details). Note that these non-logarithmic terms, apart of $\mathcal{O}(v/M_{\text {SUSY}})$ contributions, stay constant when varying $M_{\text {SUSY}}$. For $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}\sim 2$ the difference between parametrizations in terms of $v_{G_F}$ and $v_{\overline{\text {MS}}}$ (both using the SM NNLO ${\overline{\text {MS}}}$ top-quark mass) amounts to $\sim 170 \,\, \mathrm {GeV}^2$. Such a shift accounts for the main part of the nearly constant offset observed in the left plot of Fig. 4. For $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}\sim 0$ the difference between the parametrizations in terms of $v_{G_F}$ and $v_{\overline{\text {MS}}}$ is seen to become very small. The nearly constant offset for vanishing stop mixing observed in the left plot of Fig. 4 can be explained in a similar way by different parameterization of terms that are not of $\mathcal{O}(\alpha _t\alpha _s,\alpha _t^2)$.

Finally, we briefly comment on the differences between FeynHiggs and other codes that have been reported in the literature. In [43] it was claimed that differences between FeynHiggs and SUSYHD of up to $\sim 9$ GeV would occur for $M_{\text {SUSY}}= 2\,\, \mathrm {TeV}$ and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}\sim \sqrt{6}$. As already noted in [43], this difference was somewhat reduced if the NNLO ${\overline{\text {MS}}}$ top mass was employed in the calculation of FeynHiggs.⁹ While at the time of the comparison carried out in [43] the EFT calculation of FeynHiggs was not yet at the same level of accuracy as the one of SUSYHD, the differences claimed in [43] were in fact primarily caused by an inappropriate application of the conversion of input parameters between the ${\overline{\text {DR}}}$ and the OS scheme. The inappropriate parameter conversion, for which the authors of [43] used their own routine, caused a deviation of 3–$4\,\, \mathrm {GeV}$ for $M_{\text {SUSY}}= 2\,\, \mathrm {TeV}$ and $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}\sim \sqrt{6}$ and was also responsible for the apparent numerical instability at large SUSY scales of the FeynHiggs curve with $X_t^{\overline{\text {DR}}}/M_{\text {SUSY}}= 0$ shown in [43]. The numerical effect of this deviation was larger than the shift caused by employing the NNLO or NNNLO ${\overline{\text {MS}}}$ top-quark mass in FeynHiggs, in contrast to the claim made in [43].

Also the comparison figures shown in [47, 48] are plagued by deficiencies arising from an inappropriate application of the parameter conversion between the ${\overline{\text {DR}}}$ and the OS scheme. We stress again that such a parameter conversion would give rise to the same kind of problems when starting from OS parameters and converting to ${\overline{\text {DR}}}$ ones.

7 Conclusions

We have presented a detailed comparison between various approaches used to predict the mass of the SM-like Higgs boson in the MSSM in a scenario in which all SUSY mass scales are chosen equal to each other. In particular we have compared pure EFT calculations with the hybrid approach, in which an explicit Feynman-diagrammatic fixed-order result is combined with the leading higher-order contributions obtained from EFT methods. In the literature significant deviations between the results obtained via the two approaches have been reported especially at large SUSY scales. In this work, we have identified three sources of the observed differences.

We could show that a large part of the reported discrepancies can be traced back to parameter conversions between different renormalization schemes. In EFT calculations typically the ${\overline{\text {DR}}}$ scheme is used for the renormalization of SUSY breaking parameters, e.g. the stop mixing parameter. In the diagrammatic calculation of FeynHiggs (in the default case) however, the OS scheme is employed in the scalar top sector. We have demonstrated that the usual scheme conversion of input parameters used for the comparison of fixed-order results is not suitable for the comparison of results containing a series of higher-order logarithms. This kind of parameter conversion would induce higher-order logarithmic contributions that are not compatible with the implemented resummation of logarithms to all orders. We have shown that the form of the higher-order logarithms obtained in one scheme can manifestly be maintained if the fixed-order part of the calculation is consistently reparametrized to this scheme. In order to enable this approach for ${\overline{\text {DR}}}$ input parameters, we have extended FeynHiggs such that the results are provided both in terms of the on-shell parameters $X_t^{\text {OS}}$, $M_{\tilde{t}_1}\equiv m_{\tilde{t}_1}^{\text {OS}}$, $M_{\tilde{t}_2}\equiv m_{\tilde{t}_2}^{\text {OS}}$ (as before) and the ${\overline{\text {DR}}}$ parameters $X_t^{\overline{\text {DR}}}$, $m_{\tilde{t}_1}^{\overline{\text {DR}}}$, $m_{\tilde{t}_2}^{\overline{\text {DR}}}$. In practice, this was achieved by reparametrizing the existing OS fixed-order result. We have demonstrated that many of the apparent discrepancies reported in the literature have mainly been caused by an inappropriate application of the conversion of input parameters between the OS and the ${\overline{\text {DR}}}$ schemes. It should be emphasized that this issue is not a problem of the OS renormalization, but analogously appears if OS parameters are used as input for codes employing the ${\overline{\text {DR}}}$ scheme.

Another difference between pure EFT calculations and the hybrid approach arises from the determination of the poles of the Higgs propagator matrix. We have shown explicitly at the two-loop level that there occurs a cancellation in the limit of a large SUSY scale between non-SM terms arising through the determination of the propagator pole and contributions from the subloop renormalization of the irreducible self-energy diagrams. Since we expect that similar cancellations will happen at higher loops, we have modified the determination of the propagator poles in the new version of FeynHiggs such that terms are omitted that would not cancel because their counterpart in the irreducible self-energies is not incorporated at present. Unless otherwise stated, the numerical results presented in this paper have been obtained with this new version of FeynHiggs. Numerically, we found that the terms beyond $\mathcal{O}(\alpha _t^2,\alpha _t\alpha _b)$ for which in previous versions of FeynHiggs the cancellation was incomplete are negligible for low scales ($M_{\text {SUSY}}\lesssim 0.5 \,\, \mathrm {TeV}$). They can be more significant for high scales ($\sim 1.5 \,\, \mathrm {GeV}$ for $M_{\text {SUSY}}\sim 20 \,\, \mathrm {TeV}$).

Furthermore, we investigated the impact of different parametrizations of the non-logarithmic one- and two-loop terms. In this context, we found the top-quark mass and the vev to be especially relevant. Despite the results being formally identical at the strict two-loop level, using e.g. a SM NNLO ${\overline{\text {MS}}}$ top quark mass instead of the OS top quark mass induces changes in the higher-order non-logarithmic contributions.

In our numerical comparison, we focused on a single scale scenario with a moderate $\tan \beta$, which is particularly suited for an EFT calculation. We specifically compared the results of FeynHiggs and the EFT code SUSYHD. Using the NNLO value of the ${\overline{\text {MS}}}$ top Yukawa coupling in SUSYHD (by default the NNNLO value is used in SUSYHD, which leads to a downward shift by $\sim 0.5\,\, \mathrm {GeV}$ in $M_h$), we find very good agreement between the new version of FeynHiggs and SUSYHD for scales $M_{\text {SUSY}}\gtrsim 1 \,\, \mathrm {TeV}$. Such a good agreement is in fact expected for high SUSY scales since the hybrid approach of FeynHiggs incorporates essentially the same logarithmic contributions as pure EFT calculations. For $M_{\text {SUSY}}\lesssim 1 \,\, \mathrm {TeV}$ we observe significant differences between FeynHiggs and SUSYHD due to terms suppressed by the SUSY scale that are not incorporated in the EFT calculation of SUSYHD. The observed differences stay relatively small for the considered simple scenario with a single SUSY scale, reaching $\sim 1 \,\, \mathrm {GeV}$ for $M_{\text {SUSY}}\sim 300 \,\, \mathrm {GeV}$. Larger deviations can be expected in SUSY scenarios with non-negligible mass splittings between the various SUSY particles. Such kind of mass patterns are accounted for in the diagrammatic fixed-order part of the hybrid approach.

The new version of FeynHiggs described in this paper, comprising an improvement in the determination of the propagator poles and an option for using the ${\overline{\text {DR}}}$ scheme for the renormalization of the stop sector, will be made public soon.

The results obtained in this paper provide important input for an improved estimate of the remaining theoretical uncertainties from unknown higher-order corrections. In this context, we would like to stress once more that for the numerical evaluations in this paper we have used a rather simple scenario where all SUSY masses have been set to be equal to each other. Having reconciled the hybrid approach of FeynHiggs with pure EFT calculations for this simple single scale scenario, we are now in a position to assess the accuracy of the theoretical predictions also for more general scenarios with different hierarchies of scales. This will be analysed in a forthcoming publication.

Appendices

Appendix A: Fixed-order conversion: additional two-loop terms

In the limit $M_{\text {SUSY}}\gg M_t$ and degenerate $M_L=M_{\tilde{t}_R}=M_{\text {SUSY}}$, the one-loop contributions from the stop/top sector to the neutral Higgs self-energies at $\mathcal{O}(\alpha _t)$ are given by (for the remainder of this section we drop the subscript “$G_F$”, i.e. we use the shorthand $v \equiv v_{G_F}$)

$$\begin{aligned} \hat{\varSigma }_{11}= & {} \frac{1}{16\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\frac{\mu ^2 X_t^2}{M_S^4}, \end{aligned}$$

(A.1)

$$\begin{aligned} \hat{\varSigma }_{12}= & {} \frac{1}{16\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\frac{\mu X_t}{M_S^2}\left[ 6-\frac{X_t^2}{M_S^2}-\frac{1}{t_\beta }\frac{\mu X_t}{M_S^2}\right] , \end{aligned}$$

(A.2)

$$\begin{aligned} \hat{\varSigma }_{22}= & {} \frac{1}{16\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\left[ -12\ln \frac{M_S^2}{m_t^2}-12\frac{X_t^2}{M_S^2}+\frac{X_t^4}{M_S^4}\right. \end{aligned}$$

(A.3)

$$\begin{aligned}&\left. -\,\frac{2}{t_\beta }\frac{\mu X_t}{M_S^2}\left( 6-\frac{X_t^2}{M_S^2}\right) +\frac{1}{t_\beta ^2}\frac{\mu ^2 X_t^2}{M_S^4}\right] , \end{aligned}$$

(A.4)

where $M_S^2 = M_{\tilde{t}_1}M_{\tilde{t}_2}$, and $m_t$ is either the OS top mass or the ${\overline{\text {MS}}}$ SM top mass. We furthermore introduced the abbreviations

$$\begin{aligned} s_x\equiv \sin x, \quad c_x\equiv \cos x, \quad t_x \equiv \tan x. \end{aligned}$$

(A.5)

If we convert the stop masses and the stop mixing parameter from the OS to the ${\overline{\text {DR}}}$ scheme using the shifts defined in Eqs. (4243)–(44), the following two-loop terms are generated (see Eq. (50)),

$$\begin{aligned} \varDelta \hat{\varSigma }_{11}= & {} \frac{1}{8\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\left[ \frac{\varDelta X_t}{M_S}\frac{\mu ^2 X_t}{M_S^3}-2\frac{\varDelta M_S}{M_S}\frac{\mu ^2 X_t^2}{M_S^4}\right] , \end{aligned}$$

(A.6)

$$\begin{aligned} \varDelta \hat{\varSigma }_{12}= & {} \frac{1}{16\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\left[ \frac{\varDelta X_t}{M_S}\left( -3\frac{\mu X_t^3}{M_S^3}-\frac{2}{t_\beta }\frac{\mu ^2 X_t}{M_S^3}+6\frac{\mu }{M_S}\right) \right. \nonumber \\&\left. +\,\frac{\varDelta M_S}{M_S}\left( 4\frac{\mu X_t^3}{M_S^4}+\frac{4}{t_\beta }\frac{\mu ^2 X_t^2}{M_S^4}-12\frac{\mu X_t}{M_S^2}\right) \right] ,\end{aligned}$$

(A.7)

$$\begin{aligned} \varDelta \hat{\varSigma }_{22}= & {} \frac{1}{8\pi ^2} \frac{1}{s_\beta ^2}\frac{m_t^4}{v^2}\left[ \frac{\varDelta X_t}{M_S}\left( -2\frac{X_t}{M_S} \left( 6-\frac{X_t^2}{M_S^2}\right) \right. \right. \nonumber \\&\left. \left. -\,\frac{3}{t_\beta }\frac{\mu }{M_S}\left( 2-\frac{X_t^2}{M_S^2}\right) +\frac{1}{t_\beta ^2}\frac{\mu ^2 X_t}{M_S^3}\right) \right. \nonumber \\&\left. -\,2\frac{\varDelta M_S}{M_S}\left( 6-6\frac{X_t^2}{M_S^2}+\frac{X_t^4}{M_S^4}\right. \right. \nonumber \\&\left. \left. -\,\frac{2}{t_\beta }\frac{\mu X_t}{M_S^2}\left( 3-\frac{X_t^2}{M_S^2}\right) +\frac{1}{t_\beta ^2}\frac{\mu ^2 X_t^2}{M_S^4}\right) \right] . \end{aligned}$$

(A.8)

The quantity $\varDelta M_S$ is given by

$$\begin{aligned} \varDelta M_S = \frac{1}{2}\left( \frac{\varDelta m_{\tilde{t}_1}}{M_{\tilde{t}_1}}+\frac{\varDelta m_{\tilde{t}_2}}{M_{\tilde{t}_2}}\right) M_S, \end{aligned}$$

(A.9)

where $\varDelta X_t$ and $\varDelta m_{\tilde{t}_{1,2}}$ are defined in Eqs. (4243)–(44).

Note that for all numerical results presented in this work, we used expressions valid also for low $M_{\text {SUSY}}$ ($M_{\text {SUSY}}\sim M_t$) and general SUSY breaking. Note also that the shifts are performed for all self-energies and not only for the hh self-energy as shown exemplary in Sect. 4. Therefore, the procedure remains also valid in non-decoupling scenarios ($M_A \sim M_Z$).

As described in Sect. 4, these two-loop terms are finally added to the respective self-energies, i.e., the $\varDelta \hat{\varSigma }$’s are added to the two-loop self-energies obtained from the diagrammatic calculation. Higher-order terms which would be generated by a scheme conversion of the input parameters are omitted. In this way, the renormalization of the stop sector is changed from the OS to the ${\overline{\text {DR}}}$ scheme. This alternative renormalization scheme will be available as an option in the next FeynHiggs version.

Appendix B: Logarithms arising from the determination of the propagator pole

In this appendix, we give explicit expressions, valid in the decoupling limit, for the logarithms induced by the momentum dependence of the non-SM contributions to the MSSM Higgs self-energy, i.e. for the quantity $\varDelta _{p^2}^{\text {logs}}$ defined in Eq. (26).

In order to derive the $(n+1)$th order iterative solution to the Higgs pole mass equation (see Eq. (9)) in terms of lower order solutions, Fàa di Bruno’s formula (extended chain rule for derivatives) is used,

$$\begin{aligned}&(M_h^2)^{(n+1)}\nonumber \\&\quad =- \sum _{(a_1,...,a_n)\in T_n} \frac{1}{a_1 !\cdot \cdots \cdot a_n !}\cdot \nonumber \\&\qquad \cdot \left[ \left( \frac{\partial }{\partial p^2}\right) ^{(a_1+...+a_n)}\hat{\varSigma }_{hh}^{\text {MSSM}}(p^2)\right] _{p^2=m_h^2}\nonumber \\&\qquad \cdot \prod _{m=1}^n (M_h^2)^{(m)}, \end{aligned}$$

(B.10)

where an n-tuple of non negative integers $(a_1,\ldots ,a_n)$ is an element of $T_n$ if $1\cdot a_1+2\cdot a_2+\cdots +n\cdot a_n = n$.

The zeroth order correction

$$\begin{aligned} (M_h^2)^{(0)} = m_h^2 \end{aligned}$$

(B.11)

serves as starting point of the recursion.

We split $\varDelta _{p^2}^{\text {logs}}$ into a leading, a next-to-leading and a next-to-next-to-leading logarithm piece,

$$\begin{aligned} \varDelta _{p^2}^{\text {logs}} = \varDelta _{p^2}^{\text {LL}} + \varDelta _{p^2}^{\text {NLL}} + \varDelta _{p^2}^{\text {NNLL}} +\cdots . \end{aligned}$$

(B.12)

In FeynHiggs, the full momentum dependence by default is taken into account only at the one-loop level. At the two-loop level, the external momentum is set to zero (see [56, 57] for a discussion of the momentum dependence at the two-loop level). We can therefore split up the non-SM contributions to the Higgs self-energy into a one- and a two-loop piece,

$$\begin{aligned} \hat{\varSigma }_{hh}^{\text {nonSM}}(p^2) = \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)}(p^2) + \hat{\varSigma }_{hh}^{{\text {nonSM}},(2)}(0). \end{aligned}$$

(B.13)

To shorten the expressions for the individual contributions, we first introduce abbreviations. We write the non-SM contributions to the Higgs self-energy as

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)}(m_h^2)= & {} k\left( c_{1,1}^\chi L_\chi + c_{1,1}^A L_A + c_{1,1}^{\tilde{f}} L_S + c_{1,0}\right) , \nonumber \\\end{aligned}$$

(B.14)

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {nonSM}},(2)}(0)= & {} k^2\left( c_{2,2} L_S^2 + c_{2,1} L_S + c_{2,0}\right) , \end{aligned}$$

(B.15)

where $k\equiv (4\pi )^{-2}$ is used to keep track of the loop order and

$$\begin{aligned} L_\chi \equiv \ln \frac{M_\chi ^2}{m_t^2}, \quad L_A\equiv \ln \frac{M_A^2}{m_t^2}, \quad L_S\equiv \ln \frac{M_{\text {SUSY}}^2}{m_t^2}. \end{aligned}$$

(B.16)

Here it should be noted that in this work we set

$$\begin{aligned} M_\chi \equiv M_1 = M_2 = \mu \quad \text{ and } \quad M_\chi = M_A= M_{\text {SUSY}}. \end{aligned}$$

(B.17)

In this appendix, however, we keep them independent to be able to use the expressions also for more general cases.

The subscript of a coefficient $c_{a,b}$ indicates that it is the prefactor of the term $k^a L^b$ ($L=L_\chi ,L_A,L_S$). The corresponding superscript marks the origin of the respective term (from EWinos $\chi$, from heavy Higgses A or from sfermions $\tilde{f}$). These superscripts are used only at the one-loop level to be able to differentiate between the different types of appearing logarithms ($L_\chi$, $L_A$ and $L_S$). In the ${\overline{\text {DR}}}$ scheme, the appearing coefficients up to $\mathcal{O}(v^2/M_{\text {heavy}}^2)$ ($M_{\text {heavy}}=M_\chi ,M_A,M_{\text {SUSY}}$) are given by (for the remainder of this section we drop the subscript “$G_F$”, i.e. we use the shorthand $v \equiv v_{G_F}$)

$$\begin{aligned} c_{1,1}^{\tilde{f}}= & {} -2v^2\left[ 6 y_t^4+\frac{3}{2}y_t^2(g^2+g'^2)c_{2\beta }+\frac{1}{2}g^4+\frac{5}{6}g'^4\right. \nonumber \\&\left. +\frac{1}{6}(3g^4 + 5 g'^4)c_{4\beta }\right] , \end{aligned}$$

(B.18)

$$\begin{aligned} c_{1,1}^{\chi }= & {} -2v^2\left[ \frac{1}{24}g'^4(-11+c_{4\beta })-\frac{3}{8}g^4(5+c_{4\beta })\right. \nonumber \\&\left. -g^2 g'^2 s_{2\beta }^2\right] ,\end{aligned}$$

(B.19)

$$\begin{aligned} c_{1,1}^{A}= & {} -2v^2\left[ \frac{1}{192}g^4(53-28c_{4\beta }-9c_{8\beta })\right. \nonumber \\&\left. +\frac{1}{192}g'^4(29-4c_{4\beta }-9c_{8\beta })\right. \nonumber \\&\left. +\frac{1}{8}g^2 g'^2(5+3c_{4\beta })s_{2\beta }^2\right] , \end{aligned}$$

(B.20)

$$\begin{aligned} c_{1,0}= & {} -2v^2\Bigg \{ 6 y_t^2 \left[ \left( y_t^2+\frac{1}{8}(g^2+g'^2)c_{2\beta }\right) \hat{X}_t^2-\frac{1}{12}y_t^2\hat{X}_t^4\right] \nonumber \\&- \frac{1}{4}y_t^2(g^2+g'^2)\hat{X}_t^2 c_{2\beta }^2 -\frac{3}{16}(g^2+g'^2)^2 s_{4\beta }^2 \nonumber \\&-\left[ \left( \frac{3}{4}-\frac{1}{6}c_{2\beta }^2\right) g^4+\frac{1}{2}g^2g'^2+\frac{1}{4}g'^4\right] \nonumber \\&+\frac{1}{24}(s_\beta +c_\beta )^2\cdot \bigg [-51g^4-24g^2g'^2-13g'^4 \nonumber \\&+\left( (g^2+g'^2)c_{4\beta }+2(g^2-g'^2)s_{2\beta }\right) \nonumber \\&\cdot (3g^2+g'^2)\bigg ]\Bigg \},\end{aligned}$$

(B.21)

$$\begin{aligned} c_{2,2}= & {} - 2 v^2 y_t^4\left( -48g_3^2+9y_t^2\right) , \end{aligned}$$

(B.22)

$$\begin{aligned} c_{2,1}= & {} - 2 v^2 y_t^4\Big [8 g_3^2 \left( 4-12\hat{X}_t^2+\hat{X}_t^4\right) \nonumber \\&-\frac{3}{2}y_t^2\left( 20-12\hat{X}_t^2+\hat{X}_t^4\right) \Big ], \end{aligned}$$

(B.23)

where all appearing couplings are SM ${\overline{\text {MS}}}$ couplings evaluated at $Q=M_t$ (g, $g'$ are the electroweak gauge couplings, and $\hat{X}_t\equiv X_t/M_{\text {SUSY}}$). We write the derivative of the non-SM contributions to the Higgs self-energy as

$$\begin{aligned} \hat{\varSigma }_{hh}^{{\text {nonSM}},(1)\prime }(m_h^2) = k\left( c'_{1,1} L_\chi + c'_{1,0}\right) , \end{aligned}$$

(B.24)

with the primes denoting that the corresponding coefficient appears in the derivative of the self-energy. We again drop contributions of $\mathcal{O}(v^2/M_{\text {heavy}}^2)$. The coefficient multiplying $L_\chi$ originates purely from EWino graphs and reads

$$\begin{aligned} c'_{1,1} = -\frac{1}{2}(3g^2+g'^2). \end{aligned}$$

(B.25)

The non-logarithmic coefficient has contributions from EWinos as well as from stops (neglecting all other Yukawa couplings),

$$\begin{aligned} c'_{1,0} = \underbrace{\frac{1}{2}y_t^2\hat{X}_t^2}_{\text {stop contr.}}\underbrace{-\frac{1}{6}(3g^2+g'^2)(s_\beta +c_\beta )^2}_{\text {EWino contr.}}. \end{aligned}$$

(B.26)

All higher derivatives of $\hat{\varSigma }_{hh}^{\text {nonSM}}(p^2)$ are suppressed, i.e. of $\mathcal{O}(p^2/M_{\text {heavy}}^2)$.

The SM contributions are written in a similar way,

$$\begin{aligned} \left. \left( \frac{\partial }{\partial p^2}\right) ^n\hat{\varSigma }_{hh}^{{\text {SM}},(1)}(p^2)\right| _{p^2=m_h^2} = k\tilde{c}^{n}_1, \end{aligned}$$

(B.27)

where the superscript ’n’ denotes the nth derivative of $\hat{\varSigma }_{hh}^{{\text {SM}},(1)}$. Here, we only give explicit expressions for the pure top Yukawa contributions to the first five derivatives of $\hat{\varSigma }_{hh}^{{\text {SM}},(1)}$,

$$\begin{aligned} \tilde{c}_1^{(1)}= & {} - \frac{1}{2} y_t^2 v^0, \end{aligned}$$

(B.28)

$$\begin{aligned} \tilde{c}_1^{(2)}= & {} \frac{3}{5} y_t^0 v^{-2}, \end{aligned}$$

(B.29)

$$\begin{aligned} \tilde{c}_1^{(3)}= & {} \frac{9}{70} y_t^{-2} v^{-4}, \end{aligned}$$

(B.30)

$$\begin{aligned} \tilde{c}_1^{(4)}= & {} \frac{2}{35} y_t^{-4} v^{-6}, \end{aligned}$$

(B.31)

$$\begin{aligned} \tilde{c}_1^{(5)}= & {} \frac{4}{77} y_t^{-6} v^{-8}. \end{aligned}$$

(B.32)

Equation (B.10) allows now to successively derive all corrections induced by the momentum dependence of the non-SM contributions to the hh self-energy. The generated leading logarithms can be resummed easily, since higher derivatives of $\hat{\varSigma }_{hh}^{\text {nonSM}}$ are always suppressed, as noted before. The resummed expression is given in terms of the c coefficients by

$$\begin{aligned} \varDelta _{p^2}^{\text {LL}}= & {} k^2 \frac{c'_{1,1} L_\chi }{1 + k c'_{1,1} L_\chi } \nonumber \\&\left[ c_{1,1}^\chi L_\chi + c_{1,1}^A L_A + c_{1,1}^{\tilde{f}} L_S + k c_{2,2} L_S^2\right] . \end{aligned}$$

(B.33)

A similar expression can be derived at the NLL level. We obtain

$$\begin{aligned} \varDelta _{p^2}^{\text {NLL}}= & {} k^2 \frac{1}{(1 + k c'_{1,1} L_\chi )^2}\nonumber \\&\cdot \Big [c_{1,1}^\chi c'_{1,0} L_\chi + c_{1,1}^A c'_{1,0} L_A + c_{1,1}^{\tilde{f}} c'_{1,0} L_S + c_{1,0} c'_{1,1} L_\chi \nonumber \\&+\, k\left( c_{1,0} (c'_{1,1})^2 L_\chi ^2 + c_{2,1}c_{1,1}' L_\chi L_S + c_{2,2}c_{1,0}' L_S^2\right) \nonumber \\&+\,k^2 c_{2,1} (c_{1,1}')^2 L_\chi ^2 L_S\Big ]. \end{aligned}$$

(B.34)

At the NLL level however, additional terms proportional to derivatives of the light self-energy exist. Since these derivatives are not suppressed by a heavy mass, it seems not to be possible to resum the corresponding logarithms. Nevertheless, including terms up to the 7-loop order we find a good convergence behavior and an induced shift of $\mathcal{O}(\pm 2 \,\, \mathrm {GeV}^2)$ to $M_h^2$ in the parameter region $M_t < M_{\text {heavy}} \lesssim 20 \,\, \mathrm {TeV}$. The respective shift in $M_h$ is of $\mathcal{O}(50 \,\, \mathrm {MeV})$. We therefore neglect this contribution completely.

At the NNLL level, we take into account only terms proportional to the strong gauge coupling and the top-Yukawa coupling (terms proportional to electroweak gauge couplings are negligible). We find that at this level all terms include derivatives of the SM self-energy. We also find that this contribution to $M_h^2$ is not negligible, $\mathcal{O}(20 \,\, \mathrm {GeV}^2)$. Therefore, we include terms up to the 7-loop order, which are given by

$$\begin{aligned} \varDelta _{p^2}^{\text {NNLL}}= & {} k^3 L_S c'_{1,0}\left[ c_{2,1} - c_{1,1}^{\tilde{f}} \tilde{c}_{1}'\right] \nonumber \\&- k^4 L_S^2 c'_{1,0} \left[ c_{2,2}c'_{1,0}+c_{2,2} \tilde{c}_{1}^{(1)}-\frac{1}{2}\left( c_{1,1}^{\tilde{f}}\right) ^2\tilde{c}_{1}^{(1)}\right] \nonumber \\&+ k^5 L_S^3 c'_{1,0}\left[ c_{1,1}^{\tilde{f}}c_{2,2}\tilde{c}_{1}^{(2)}-\frac{1}{6}\left( c_{1,1}^{\tilde{f}}\right) ^3 \tilde{c}_{1}^{(3)}\right] \nonumber \\&+ \frac{1}{2}k^6 L_S^4 c'_{1,0}\left[ \left( c_{2,2}\right) ^2 \tilde{c}_{1}^{(2)}-c_{2,2}\left( c_{1,1}^{\tilde{f}}\right) ^2 \tilde{c}_{1}^{(3)}\right. \nonumber \\&\left. +\frac{1}{12}\left( c_{1,1}^{\tilde{f}}\right) ^4\tilde{c}_{1}^{(4)}\right] -\frac{1}{2}k^7 L_S^5 c'_{1,0}\left[ \left( c_{2,2}\right) ^2 c_{1,1}^{\tilde{f}} \tilde{c}_{1}^{(3)} \right. \nonumber \\&\left. -\frac{1}{3}c_{2,2}\left( c_{1,1}^{\tilde{f}}\right) ^3 \tilde{c}_{1}^{(4)}+\frac{1}{60}\left( c_{1,1}^{\tilde{f}}\right) ^5\tilde{c}_{1}^{(5)}\right] + \mathcal{O}(k^8),\nonumber \\ \end{aligned}$$

(B.35)

where all terms in the c coefficients proportional to g or $g'$ are set to zero. Correspondingly, the derivatives of the light self-energy only include terms proportional to $y_t$. These are listed in Eqs. (B.28)–(B.32). This loop expansion quickly converges such that we can safely drop higher-order contributions (8-loop and beyond).

We find the electroweak contributions at the NNLL level and even higher-order logarithms (N$^n$L with $n>2$) to be completely negligible. Similar expressions can easily be obtained for the non-logarithmic terms of the same origin (see Eq. (30)).