Non-minimal derivative coupling scalar field and bulk viscous dark energy

Abstract

Inspired by thermodynamical dissipative phenomena, we consider bulk viscosity for dark fluid in a spatially flat two-component Universe. Our viscous dark energy model represents phantom-crossing which avoids big-rip singularity. We propose a non-minimal derivative coupling scalar field with zero potential leading to accelerated expansion of the Universe in the framework of bulk viscous dark energy model. In this approach, the coupling constant, $\kappa$, is related to viscosity coefficient, $\gamma$, and the present dark energy density, $\varOmega _\mathrm{DE}^0$. This coupling is bounded as $\kappa \in [-1/9H_0^2(1-\varOmega _\mathrm{DE}^0), 0]$. We implement recent observational data sets including a joint light-curve analysis (JLA) for SNIa, gamma ray bursts (GRBs) for most luminous astrophysical objects at high redshifts, baryon acoustic oscillations (BAO) from different surveys, Hubble parameter from HST project, Planck CMB power spectrum and lensing to constrain model free parameters. The joint analysis of JLA $+$ GRBs $+$ BAO $+$ HST shows that $\varOmega _\mathrm{DE}^0=0.696\pm 0.010$, $\gamma =0.1404\pm 0.0014$ and $H_0=68.1\pm 1.3$. Planck TT observation provides $\gamma =0.32^{+0.31}_{-0.26}$ in the $68\%$ confidence limit for the viscosity coefficient. The cosmographic distance ratio indicates that current observed data prefer to increase bulk viscosity. The competition between phantom and quintessence behavior of the viscous dark energy model can accommodate cosmological old objects reported as a sign of age crisis in the $\varLambda$CDM model. Finally, tension in the Hubble parameter is alleviated in this model.

1 Introduction

The accelerating expansion of the Universe has been confirmed by many observational data sets [1, 2]. Various observations such as supernova type Ia, cosmic microwave background (CMB) and baryonic acoustic oscillations (BAO) have indicated the break down of general relativity (GR) at cosmic scale [3]. Many scenarios have been proposed to produce a repulsive force in order to elucidate the current accelerating epoch.

There are three approaches for going beyond the model including cosmological constant: the first approach corresponds to dynamical dark energy incorporating field theoretical orientation and phenomenological dark fluids. The second category approach is by modified general relativity including Horndeski’s types such as galileons, chameleons, Brans–Dicke, symmetrons, and other possibilities. In the third strategy, based on a thermodynamics point of view, phenomenological exotic fluids are supposed for an alternative dark energy model [4,5,6,7,8].

Generally, proposing exotic fluids for various applications has historically been highlighted in the first order irreversible processes and also in a second order correction to the dissipative process proposed by Israel [9]. The dissipative process is a generic property of any realistic phenomenon. Accordingly, bulk and shear viscous terms are most relevant parts which should be taken into account for a feasible relativistic fluid [9,10,11,12,13,14,15]. In other words, to recognize the mechanism of heat generation and characteristic of smallest fluctuations one possibility is revealing the presence of dissipative processes. In classical fluid dynamics, the viscosity is a trivial consequence of the internal degree of freedom of the associated particles. The existence of any dissipative process for an isotropic and homogeneous Universe should undoubtedly be scalar, consequently, at the background level, we deal with a bulk viscous model. Some examples to describe the source of the viscosity are as follows: moving cosmic strings through the cosmic magnetic fields and magnetic monopoles in monopole interactions effectively experience various viscous phenomena. Various mechanisms for primordial quantum particle productions and their interactions were also major arguments for viscous fluids [16,17,18,19,20,21,22,23,24].

In the context of exotic fluids, a possible approach to explaining the late time accelerating expansion of the Universe is constructing an exotic fluid including a bulk viscous term. A considerable part of previous studies have been devoted to one component for the dark sector [25,26,27]. A motivation behind the mentioned proposals is avoiding dark degeneracy [28]. The bulk viscosity in cosmological models has also resolved the so-called big-rip problem [29, 30]. Recently, Normann et al., tried to map the viscous radiation or matter to a phantom dark energy model and they showed that phantom dark energy can be misinterpreted due to the existence of non-equilibrium pressure causing viscosity in pressure of either in matter or radiation [25].

An a priori approach for bulk viscous cosmology encouraged some authors to build robust mechanisms to describe a correspondence for the mentioned dissipative term. Indeed without any reasonable model for underlying dissipative processes, one cannot say anything about the presence of such a fluid including exotic properties [31,32,33,34].

In cosmology, inspired by the inflationary paradigm, canonical scalar fields with minimal coupling to gravity have been introduced to explain the origin of extraordinary matters; see [4] and the references therein.

Models with non-canonical scalar fields with minimal coupling or non-minimal coupling are other phenomenological descriptions to construct a dark energy component [35, 36]. An alternative approach is non-minimal derivative coupling, which appears in various approaches such as Jordan–Brans–Dicke theory, quantum field theory and the low-energy limit of the superstrings; see [37] and the references therein. Following a research done by Amendola, many models for non-minimal derivative coupling (NMDC) have been proposed to investigate the inflationary epoch and late time accelerating expansion [38, 39]. Concentrating on cosmological applications of NMDC, Sushkhov et al. showed that, for a specific value of the coupling constant, it is possible to construct a new exact cosmological solution without considering a certain form of scalar field potential [40, 41]. It has been demonstrated that a proper action containing a Lagrangian with NMDC scalar field for dynamical dark energy model enables one to solve phantom-crossing [42, 43]. In a paper by Granda et al., non-minimal kinetic coupling in the framework of Chaplygin cosmology has been considered [44].

In the present paper, we try to propose a modified version for dark energy model inspired by dissipative phenomena in fluids with following advantages and novelties: We will consider a special type of viscosity satisfying the isotropic property of the cosmos at the background level. To make more obvious concerning the knowledge of bulk viscosity, we will rely on modified general relativity to obtain corresponding scalar field giving rise to accelerated expansion of Universe in the context of bulk viscous dark energy scenario. With this mechanism, we will show the correspondence between our viscous dark energy model and the scalar–tensor theories in a two-component dark sectors model in contrast to that of done in [29, 30]. In addition we will demonstrate that our viscous dark energy model without any interaction between dark sectors, has phantom-crossing avoiding big-rip singularity. Considering two components for dark sides of Universe in our approach leads to no bouncing behavior for consistent viscosity coefficient. Generally there is no ambiguity in computation of the cosmos’ age. Observational consequences indicates to resolve tension in the Hubble parameter.

From observational points of view, ongoing and upcoming generation of ground-based and space-based surveys classified in various stages ranging from I to IV, one can refer to background and perturbations of observables [5, 45]. Subsequently, we will rely on the state-of-the-art observational data sets such as supernova type Ia (SNIa), gamma ray bursts (GRBs), baryonic acoustic oscillation (BAO) and CMB evolution based on background dynamics to examine the consistency of our model. Here we have incorporated the contribution of the viscous dark energy in the dynamics of background.

The rest of this paper is organized as follows: in Sect. 2 we introduce our viscous dark energy model as a candidate of dark energy. Background dynamics of the Universe will be explained in this section. We use Lagrangian approach with a non-minimal derivative coupling scalar field in order to provide a theoretical model for clarifying the correspondence of the viscous dark energy, in Sect. 3. Effect of our model on the geometrical parameters of the Universe, namely, comoving distance, Alcock–Paczynski, comoving volume element, the cosmographic parameters will be examined in Sect. 4. To distinguish between viscous dark energy and cosmological constant as a dark energy, we will use Om-diagnostic and Sandage–Loeb tests in the mentioned section. Recent observational data and the posterior analysis will be explored in Sect. 5. Section 6 is devoted to results and discussion concerning the consistency of the viscous dark energy model with the observations, the cosmographic distance ratio, Hubble parameter and cosmic age crisis. Summary and concluding remarks are given in Sect. 7.

2 Bulk viscous cosmology

In this section, we explain a model for dark energy to produce accelerating expansion in the history of the cosmos evolution. To this end, we consider a bulk viscous model, correspondingly, energy-momentum tensor will be modified. We also propose a new solution for mentioned model to construct so-called dynamical dark energy model.

2.1 Background dynamics in the presence of bulk viscosity

Dynamics of the Universe is determined by the Einstein field equations:

$$\begin{aligned} G_{\mu \nu }=8\pi G_{N} T_{\mu \nu }, \end{aligned}$$

(1)

where $G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu }$ is Einstein’s tensor and $G_{N}$ is Newton’s gravitational constant. $T_{\mu \nu }$ is energy-momentum tensor given by

$$\begin{aligned} T_{\mu \nu }=T_{\mu \nu }^\mathrm{{m}}+T_{\mu \nu }^\mathrm{{rad}}+ \overline{T}_{\mu \nu }. \end{aligned}$$

(2)

where $T^\mathrm{{m}}_{\mu \nu }$ and $T_{\mu \nu }^\mathrm{{rad}}$ are the energy-momentum tensor of the matter and radiation, respectively. Generally, tensor $\overline{T}_{\mu \nu }$ includes other sources of gravity, such as scalar fields. For cosmological constant, $\varLambda$, we define the energy-momentum tensor in the form of $\overline{T}_{\mu \nu }=-\frac{\varLambda }{8\pi G_{N}}g_{\mu \nu }$. Here we consider the following form for $T_{\mu \nu }$:

$$\begin{aligned} T_{\mu \nu }= (\rho + p )u_{\mu } u_{\nu }+ pg_{\mu \nu } +2q_{( \mu }u_{\nu )}+\pi _{\mu \nu }, \end{aligned}$$

(3)

in this equation, $\rho$ is energy density and p is the pressure of the fluid, $q_{\mu }=- ( \delta ^{\nu }_{\mu }+u_{\mu } u^{\nu } )T_{\nu \alpha }u^{\alpha }$ is the energy flux vector, and $\pi _{\mu \nu }$ is the symmetric and traceless anisotropic stress tensor [46]. For barotropic fluid, namely $p=p (\rho )$ case, $q_{\mu }$ and $\pi _{\mu \nu }$ are identically zero and one can define equation of state (EoS) in the form of $w (\rho )=p (\rho )/\rho$. Applying the FLRW metric to the Einstein equations with a given $T_{\mu \nu }$, gives Friedmann equations as follows:

$$\begin{aligned} H^{2}+\frac{k}{a^{2}}= & {} \frac{8\pi G_{N}}{3} \rho ,\nonumber \\ \frac{\ddot{a}}{a}= & {} -\frac{4 \pi G_{N}}{3} ( \rho + 3 p ), \end{aligned}$$

(4)

where $\rho =\sum _{i}\rho _{i}$, $p=\sum _{i}p_{i}$ and $H=\frac{\dot{a}}{a}$ are total energy density, total pressure and Hubble parameter, respectively. Also k indicates the geometry of the Universe. The continuity equation for all components reads

$$\begin{aligned} \frac{\mathrm{d}\rho }{\mathrm{d} t}+3 H (\rho + p )=0. \end{aligned}$$

(5)

It turns out that, if there is no interaction between different components of the Universe, consequently, continuity equation for each component becomes

$$\begin{aligned} \frac{\mathrm{d}\rho _{i}}{\mathrm{d}t}+3H (\rho _{i}+p_{i} )=0. \end{aligned}$$

(6)

Now, it is possible to derive EoS in general case, by solving the following equation:

$$\begin{aligned} w_{i}\equiv \frac{p_i}{\rho _i}=-1-\frac{1}{3} \frac{\mathrm{d} \ln {\rho _{i}}}{\mathrm{d} \ln {a}}. \end{aligned}$$

(7)

In the next subsection, we will build a dark energy model, according to viscosity assumption.

2.2 Viscous dark energy model

In this subsection, we consider a bulk viscous fluid as a representative of so-called dark energy which is responsible of late time acceleration. For a typical dissipative fluid, according to Ekart’s theory as a first order limit of the Israel–Stewart model with zero relation time, one can rewrite effective pressure, $p^\mathrm{{eff}}$, in the following form [10]:

$$\begin{aligned} p^\mathrm{{eq}}\rightarrow p^\mathrm{{eff}}= & {} p^\mathrm{{eq}}-\zeta \varTheta (t)\nonumber \\= & {} w (\rho ) \rho -\zeta \varTheta (t), \end{aligned}$$

(8)

where $p^\mathrm{{eq}}$ is pressure at thermodynamical equilibrium. $\zeta$ and $\varTheta \left( t\right)$ are viscosity and expansion scalar, respectively. In general case, $\zeta$ is not constant and there are many approaches to determining the functionality form of viscosity. In general case viscosity is a function for thermodynamical state, i.e., energy density of the fluid, $\zeta (\rho )$ [47, 48]. According to mentioned dissipative approach, we propose the following model for the pressure of the viscous dark energy:

$$\begin{aligned} p^\mathrm{{eff}}_\mathrm{DE}=-\rho _\mathrm{DE}-\zeta \varTheta (t), \end{aligned}$$

(9)

for FLRW cosmology, we have $\varTheta (t)=3H(t)$. In the model that we consider throughout this paper, $\rho _\mathrm{DE}$ is dynamical variable due to its viscosity. In principle, higher order corrections can be implemented in modified energy-momentum tensor, but it was demonstrated that mentioned terms have no considerable influence on the cosmic acceleration [48]. Therefore those relevant terms having dominant contribution for isotropic and homogeneous Universe at large scale are survived. One can expect that the viscosity is affected by individual nature of corresponding energy density and implicitly is generally manipulated by expansion rate of the Universe, accordingly, our ansatz about the dark energy viscosity is:

$$\begin{aligned} \zeta (\rho _\mathrm{DE},H)=\xi \frac{\sqrt{\rho _\mathrm{DE}}}{H}, \end{aligned}$$

(10)

where coefficient $\xi$ is a positive constant and $H=\dot{a}/a$ is Hubble parameter. According to this choice, in the early Universe when the dark matter has dominant contribution, viscosity of dark energy becomes negligible. On the other hand, at late time, this term increases and in dark energy dominated Universe leads to $\xi$.

Inserting Eq. (9) in Eq. (6) and using Eq. (10) in the flat Universe results in the evolution of the bulk viscous model for dark energy in terms of scale factor:

$$\begin{aligned} \rho _\mathrm{DE}\left( a\right) = \rho _\mathrm{DE}^{0} \left( 1 +\frac{9 \xi }{2\sqrt{\rho ^{0}_\mathrm{DE}}}\ln {a} \right) ^{2}. \end{aligned}$$

(11)

Dimensionless dark energy density can be written as

$$\begin{aligned} \varOmega _\mathrm{DE}(a)= & {} \frac{H_{0}^{2}\varOmega ^{0}_\mathrm{DE}}{H^{2}} \left( 1+ \frac{9 \gamma }{2 \sqrt{\varOmega ^{0}_\mathrm{DE}}} \ln {a} \right) ^{2}. \end{aligned}$$

(12)

where $\varOmega ^{0}_\mathrm{DE}=8\pi G_N\rho _\mathrm{DE}^{0}/3H_0^2$ and $\gamma$ is the dimensionless viscosity coefficient defined by

$$\begin{aligned} \gamma \equiv \sqrt{\frac{8\pi G_{N}}{3H_{0}^2}}\xi . \end{aligned}$$

(13)

Therefore the evolution of background in the presense of the viscous dark energy model reads

$$\begin{aligned}&\left( \frac{\dot{a}}{a}\right) ^2=H_0^2 \nonumber \\&\quad \times \left[ \varOmega _\mathrm{r}^0a^{-4}+\varOmega _\mathrm{m}^0 a^{-3}+\varOmega _\mathrm{DE}^0 \left( 1 +\frac{9 \gamma }{2\sqrt{\varOmega ^{0}_\mathrm{DE}}}\ln {a}\right) ^{2}\right] \nonumber \\&\quad +H_0^2(1-\varOmega _\mathrm{tot}^0)a^{-2}, \end{aligned}$$

(14)

here $\varOmega _\mathrm{tot}^0=\varOmega _\mathrm{r}^0+\varOmega _\mathrm{m}^0+\varOmega _\mathrm{DE}^0$ and throughout this paper we consider a flat Universe. We consider two components for the dark sector of the Universe. Also in this case there is no bouncing behavior presenting in one-component phenomenological fluid considered in Ref. [29].

According to Eq. (12), dark energy has a minimum at $\tilde{a}$, where

$$\begin{aligned} \tilde{a}=\exp {\left( \frac{-2 \sqrt{\varOmega ^{0}_\mathrm{DE}}}{9 \gamma }\right) }. \end{aligned}$$

(15)

and this minimum value is equal to zero. The value of $\varOmega _\mathrm{DE}(a)$ for $a\gg \tilde{a}$ and for $a\ll \tilde{a}$ is independent of the present value of dark energy, $\varOmega _\mathrm{DE}^0$, and this value is a pure effect of bulk viscosity. To examine the variation of pressure and energy density of the viscous dark energy, we plot their behavior in Fig. 1. The upper panel of Fig. 1 shows the effective pressure in this model while lower panel corresponds to $\varOmega _\mathrm{DE}(z)$. To make more sense, we compare the behavior of this model with $\varLambda$CDM. This figure demonstrates that at the late time, there is a significant variation in the behavior of the viscous dark energy model, consequently in order to distinguish between cosmological constant and our model we should take into account those indicators which are more sensitive around late time. This kind of behavior probably may affect on the structure formation of the Universe and has unique footprint on large scale structures.

The ratio of the viscous dark energy to energy density of dark matter as a function of scale factor indicates that the modified version of dark energy has late time contribution in the expansion rate of Universe (see Fig. 2). It is worth noting that, for some values of the viscosity, the relative contribution at early epoch is higher than that of in $\varLambda$CDM while for the late time this contribution is less than $\varLambda$CDM demonstrating an almost oscillatory behavior.

Fig. 1

Upper panel pressure of the viscous fluid as a function of scale factor. Lower panel $\varOmega _\mathrm{DE}(z)$ as a function of the redshift. In both cases we changed the value of $\gamma$. The other free parameters have been fixed by SNIa constraint. The $\varLambda$CDM best fit is given by Planck observation

Fig. 2

Ratio of $\varOmega _\mathrm{DE} (a)$ to $\varOmega _m(a)$ as a function of scale factor. The other free parameters have been fixed by SNIa observational constraint. The $\varLambda$CDM best fit is given by Planck observation

Table 1 Various type of singularities in energy density and pressure given from [29, 49]

Interestingly, according to Fig. 1, the viscous DE has non-monotonic evolution. This behavior demonstrates a crossing from quintessence phase to the phantom phase corresponding to a phantom-crossing [50]. According to EoS, one can compute the effective form of equation of state as

$$\begin{aligned} w_\mathrm{eff}(a)\equiv \frac{ \int _1^a w_\mathrm{DE}(a') \mathrm{d}\ln a'}{\int _1^a \mathrm{d}\ln a'}. \end{aligned}$$

(16)

By increasing $\gamma$, we get the so-called phantom-crossing behavior for the viscous dark energy model at late time. For positive (negative) value of the viscosity coefficient, Universe at late time is dominated by phantom (quintessence) component. It has been shown that for $w_\mathrm{DE}<-1$ cosmological models have future singularity. According to previous studies, we summarize future singularities in cosmology in Table 1. In mentioned table $t_s$ and $a_s$ are respectively characteristic time and scale factor, where divergence happens. For $a\rightarrow \infty$, the EoS of the viscous dark energy goes asymptotically to $-1$ and consequently this model belongs to Little-Rip category [29]. In addition, by using Eq. (14), we can write the age of the cosmos at a given scale factor as

$$\begin{aligned} t_0-t(a)=\int _a^1{\frac{\mathrm{d} a}{H_0a \sqrt{\left( 1-\varOmega ^{0}_\mathrm{DE} \right) a^{-3}+ \varOmega ^{0}_\mathrm{DE} \left( 1- \frac{\ln {a}}{\ln {\tilde{a}}}\right) ^{2}}}}.\nonumber \\ \end{aligned}$$

(17)

Solving the scale factor as a function of time for the dark energy dominated era leads to

$$\begin{aligned} \lim _{t\rightarrow \infty }a\left( t\right) \simeq \exp {\left( \mathrm{e}^{\frac{9\gamma H_{0}}{2}\left( t-t_{0}\right) }\right) }. \end{aligned}$$

(18)

Therefore, the energy density reads

$$\begin{aligned} \lim _{t\rightarrow \infty }\rho _\mathrm{DE}\left( t\right) \simeq \rho ^{0}_\mathrm{DE} \mathrm{e}^{9\gamma H_{0}\left( t-t_{0}\right) } . \end{aligned}$$

(19)

According to the above equation, at infinite time, the energy density of the dark energy reaches to infinity when $t\rightarrow \infty$, demonstrating our model has a little-rip singularity. In a one-component Universe, the age of the Universe can be determined via

$$\begin{aligned} \int {\mathrm{d} t}= & {} \int {\frac{\mathrm{d} a}{H_0\varOmega ^{0}_\mathrm{DE} a\left( 1-\frac{\ln {a}}{\ln {\tilde{a}}} \right) } }\nonumber \\= & {} \frac{1}{H_0 \varOmega ^{0}_\mathrm{DE}}\frac{\ln { \frac{\ln {a}}{\ln {\tilde{a}}}}}{\ln {(1/\tilde{a})}}. \end{aligned}$$

(20)

Subsequently, for $a=\tilde{a}$, time is undefined which is a property of a bouncing model [51]. In order to avoid mentioned case, we consider a two-component Universe in spite of the considerations in Ref. [29].

Fig. 3

Scale factor as a function of $(t-t_0)H_0$ for various values of the viscous coefficient. Other free parameters have been fixed by SNIa observational constraint. The $\varLambda$CDM best fit is given by the Planck observation

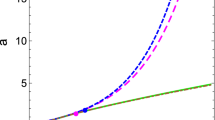
In Fig. 3 we computed the scale factor as a function of $t-t_0$ for various values of the viscosity for the viscous dark energy model. Increasing the value of $\gamma$ increases the age of Universe, but when $\gamma$ is greater than a typical value ($\gamma _{\times }$), the dominant contribution of the viscous dark energy is similar to a quintessence model (see Fig. 3).

In the next section, we propose an action in the scalar–tensor theories which its equation of motions has the same behavior in our viscous dark energy model.

3 Corresponding action of model

As mentioned in introduction, to explain the late time accelerating expansion of the Universe, dynamical dark energy including field theoretical orientation and phenomenological dark fluids, modified general relativity [52, 53] and thermodynamics motivated frameworks have been considered in [8, 54]. There is no consensus on where to draw the line between mentioned categories [5]. According to scalar field point of view, one can assume that the cosmos has been filled by a phenomenological scalar field generating an accelerated phase of expansion without the need of a specific equation of state for an exotic matter. In the previous section, we introduced a bulk viscous fluid model for dynamical dark energy and calculated some cosmological consequences. There are several proposals to describe the bulk viscosity in the Universe. As an example superconducting string can create the viscosity effect for dark fluid [19]. Particle creation in the Universe may cause to an effective viscosity for vacuum [20]. Here based on a theoretical Lagrangian orientation, we will apply a robust method to determine evolution equation of scalar field, to make a possible correspondence between scalar field and viscosity of the dynamical dark energy.

Following the research done by Amendola [38], many models for NMDC have been proposed to investigate the inflationary epoch and late time accelerating expansion of the Universe [38, 39, 55]. Sushkhov showed that, for a specific value of the coupling constants, one can construct new exact cosmological solution without considering a certain form for the scalar field potential [40, 41]. In this section we shall propose a non-minimal derivative coupling scalar field as a correspondence to our dynamical dark energy model. In our viscous dark energy model, it is possible to have phantom-crossing, therefore one of a proper action for describing this dynamical dark energy is an action containing a Lagrangian with NMDC scalar field [42, 43].

3.1 Field equations

We consider the following action containing a Lagrangian with NMDC scalar field [40, 56]:

$$\begin{aligned} \mathscr {S}= & {} \int {\mathrm{d}^{4}x\sqrt{-g}\left( \frac{\mathrm{M}^{2}_{\mathrm{Pl}}}{2} R-\frac{1}{2} (\varepsilon g^{\mu \nu }+\kappa G^{\mu \nu } )\partial _{\mu }\phi \partial _{\nu }\phi \right) }\nonumber \\&+\mathscr {S}_{\mathrm{m}}, \end{aligned}$$

(21)

where R, $\mathrm {M_\mathrm{{Pl}}}$ and $\kappa$ are Ricci scalar, reduced Planck mass and coupling constant between scalar field and Einstein tensor, respectively. In the mentioned action $\varepsilon$ is $+1$ for quintessence and $-1$ for phantom scalar fields and $\mathscr {S}_\mathrm{m}$ is the pressure-less dark matter action. This class of actions with different values for the couplings to the curvature corresponds to the low-energy limit of some higher dimensional theories such as superstring [57,58,59] and quantum gravity [36]. We suppose a zero potential for the scalar field to get rid of any fine-tuned potentials [40]. Varying the action in Eq. (21) with respect to the metric tensor and the scalar field, leads to field equations [40]. The energy-momentum tensor of NMCD field, $T^{\phi }_{\mu \nu }$, is obtained by variation of action (21) with respect to the metric tensor, $g_{\mu \nu }$, and it is:

$$\begin{aligned} T^{\phi }_{\mu \nu }=\varepsilon \varTheta _{\mu \nu }+\kappa \varPi _{\mu \nu }, \end{aligned}$$

(22)

where we defined $\varTheta _{\mu \nu }$ and $\varPi _{\mu \nu }$ according to:

$$\begin{aligned} \varTheta _{\mu \nu }\equiv & {} -\dfrac{1}{2} g_{\mu \nu }(\nabla \phi )^2+ \nabla _{\mu }\phi \nabla _{\nu }\phi , \end{aligned}$$

(23)

and

$$\begin{aligned} \varPi _{\mu \nu }\equiv & {} -\frac{1}{2}R_{\mu \nu }\left( \nabla \phi \right) ^2+\frac{1}{2}g_{\mu \nu }(\Box \phi )^2\nonumber \\&-\frac{1}{2}g_{\mu \nu }G_{\alpha \beta }\nabla ^{\alpha }\phi \nabla ^{\beta }\phi -\frac{1}{2}g_{\mu \nu }R_{\alpha \beta }\nabla ^{\alpha }\phi \nabla ^{\beta }\phi \nonumber \\&+ R_{\mu \alpha \nu \beta }\nabla ^{\alpha }\phi \nabla ^{\beta }\phi -\frac{1}{2}g_{\mu \nu }\nabla _{\beta }\nabla _{\alpha } \phi \nabla ^{\beta }\nabla ^{\alpha }\phi \nonumber \\&+G_{\nu \alpha }\nabla ^{\alpha }\phi \nabla _{\mu }\phi + G_{\mu \alpha }\nabla ^{\alpha }\phi \nabla _{\nu }\phi +\frac{1}{2}R\nabla _{\mu }\phi \nabla _{\nu }\phi \nonumber \\&+ \nabla _{\mu }\nabla ^{\alpha }\phi \nabla _{\nu }\nabla _{\alpha }\phi -\Box \phi \nabla _{\nu }\nabla _{\mu }\phi . \end{aligned}$$

(24)

As mentioned before, by taking the variation of action represented by Eq. (21), general expression for field equation is retrieved. Now we can determine the 00 and 11 components of this equation. The first and second Friedmann equations for mentioned NMDC action with standard model for dark matter read

$$\begin{aligned} H^2=\frac{8\pi G_N}{3} \left[ \rho _m+\frac{\dot{\phi }^2}{2} (\varepsilon -9\kappa H^2 ) \right] \end{aligned}$$

(25)

$$\begin{aligned} -2\dot{H}-3H^2 =4\pi G_N \left[ \varepsilon +\kappa \left( 2\dot{H}+3 H^2+4H\frac{\ddot{\phi }}{\dot{\phi }}\right) \right] \nonumber \\ \end{aligned}$$

(26)

To find differential equation for the scalar field, we should take variation in Eq. (21) with respect to the scalar field considering FRW background metric, namely:

$$\begin{aligned} \varepsilon (\ddot{\phi }+3H\dot{\phi })-3\kappa [ H^2\ddot{\phi }+2H\dot{H}\dot{\phi }+3H^3\dot{\phi } ]=0. \end{aligned}$$

(27)

By combining the Eqs. (27) and (26) one can get Eq. (25).

3.2 Bulk viscous solution

Hereafter, we are looking for finding consistent solutions for coupled differential equations (Eqs. (25), (27)) for a given Hubble parameter. Since we have no scalar potential, it is not necessary to impose additional constraint. The Hubble parameter for the flat bulk viscous dark energy model is

$$\begin{aligned} H^2=H_0^2\left[ \varOmega _\mathrm{m}^0 a^{-3}+\varOmega _\mathrm{DE}^0\left( 1 +\frac{9 \gamma }{2\sqrt{\varOmega ^{0}_\mathrm{DE}}}\ln {a}\right) ^{2}\right] . \end{aligned}$$

(28)

Therefore, we try to find a special solution of Eq. (25) which its Hubble parameter is represented by Eq. (28). It turns out that coupling parameter between Einstein tensor and the kinetic term is related to the viscosity of the dynamical dark energy. In the absence of the viscosity coefficient, the coupling parameter would vanish and the standard minimal action would be retrieved. According to the mentioned explanation, Eq. (25) takes the following form:

$$\begin{aligned}&\left( \frac{\mathrm{d} \tilde{\phi }}{\mathrm{d}a} \right) ^{2} = - \frac{\varOmega ^{0}_\mathrm{{DE}}\left( 1- \frac{\ln {a}}{\ln {\tilde{a}}} \right) ^{2} }{a^{2}\left( \varOmega _\mathrm{{m}}^{0}a^{-3}+\varOmega ^{0}_\mathrm{{DE}}\left( 1- \frac{\ln {a}}{\ln {\tilde{a}}}\right) ^{2}\right) \left\{ \varepsilon - 9\kappa H_0^2 \left[ \varOmega _\mathrm{{m}}^{0}a^{-3}+\varOmega ^{0}_\mathrm{{DE}}\left( 1- \frac{\ln {a}}{\ln {\tilde{a}}}\right) ^{2} \right] \right\} }, \end{aligned}$$

(29)

where we define $\tilde{\phi }\equiv \sqrt{\dfrac{4\pi G_{N} }{3}} \phi$. To avoid possible singularity in the above equation and construct a ghost free action, one can find the following relation between $\varepsilon$ and $\kappa$:

$$\begin{aligned} \kappa =\frac{\varepsilon }{9H_{0}^{2}(1-\varOmega ^{0}_\mathrm{{DE}})}\exp \left( - \frac{2 \sqrt{\varOmega ^{0}_\mathrm{{DE}} }}{3\gamma } \right) . \end{aligned}$$

(30)

In the upper panel of Fig. 4, we plot $\dot{\phi }^2$ as a function of scale factor for $\varepsilon =\pm 1$. Due to the functional form of the dynamical dark energy model and to ensure that the scalar field is a real quantity, therefore, we should take $\varepsilon =-1$, causing the coupling coefficient to become negative. The lower panel of Fig. 4 indicates $\tilde{\phi }$ versus scale factor for best fit values of parameters based on the JLA catalog (see Sect. 5). At the early epoch the contribution of this scalar field as a model of the dynamical dark energy is ignorable; on the contrary at the late time, it affects the background evolution considerably.

Fig. 4

Upper panel evolution of field $\dot{\phi }^{2}$ as a function of scale factor for different value of parameter $\varepsilon$. Lower panel evolution of field $\tilde{\phi }-\tilde{\phi }_0$ as a function of scale factor. Here $\tilde{\phi }_0$ is the initial condition for the scalar field. The other free parameters have been fixed by SNIa observational constraint

In the next section we will use the most recent and precise observational data sets to put constraints on free parameters of our model and to evaluate the consistency of our dynamical dark energy model. Also we will rely on a reliable geometrical diagnostic which is the so-called Om and Sandage–Loeb measures to do possible discrimination between our model and $\varLambda$CDM. A new observable quantity is the so-called cosmographic distance ratio, which is free of the bias effect, and is also considered for this purpose [60,61,62].

4 Effect on the geometrical parameters

In this section, the effect of the viscous dark energy model on the geometrical parameters of the Universe will be examined. We consider comoving distance, apparent angular size (Alcock–Paczynski test), comoving volume element, the age of the Universe, the cosmographic parameters, Om diagnostic and Sandage–Loeb test.

According to the theoretical setup mentioned in Sect. 2, the list of free parameters underlying the theory is as follows:

$$\begin{aligned} \{ {\varTheta _p}\} :\{\gamma , \varOmega _\mathrm{DE}^0,{\varOmega _b}{h^2},{\varOmega _\mathrm{m}}{h^2},{H_0},\tau _\mathrm{opt} ,{\mathscr {A}_s},{n_s}\} \end{aligned}$$

where ${\mathscr {A}_s}$ is the scalar power spectrum amplitude. Also $n_s$ corresponds to an exponent of the mentioned power spectrum. $\varOmega _b{h^2}$ and ${\varOmega _\mathrm{m}}{h^2}$ are dimensionless baryonic and cold dark matter energy density, respectively. The optical depth is indicated by $\tau _\mathrm{opt}$.

4.1 Comoving distance

The radial comoving distance for an object located at redshift z in the FRW metric reads

$$\begin{aligned} r(z;\{ {\varTheta _p}\}) = \int _0^z {\mathrm{d}z'\over H(z';\{ {\varTheta _p}\})}, \end{aligned}$$

(31)

here $H(z';\{ {\varTheta _p}\} )$ is given by Eq. (14). As indicated in Fig. 5, by increasing the value of $\gamma$ when other parameters are fixed, the contribution of the viscous dark energy becomes lower than the cosmological constant. Therefore, the comoving distance is longer than that in the $\varLambda$CDM or quintessence models. For $\gamma >\gamma _{\times }\simeq 0.36$, our result demonstrates a crossover in behavior of comoving distance due to changing the role of the viscous dark energy from phantom to quintessence class (Fig. 5).

Fig. 5

The effect of the viscosity on the radial comoving distance in FRW metric. The other free parameters have been fixed by the SNIa observational constraint. The $\varLambda$CDM best fit is given by the Planck observation

Fig. 6

Upper panel Alcock–Paczynski test compares $\Delta z/{\Delta \theta }$ normalized to the case of $\varLambda$CDM model $(\gamma =0)$ as a function of the redshift for different viscosity coefficients. Lower panel $\mathscr {Y}(z;\{\varTheta _p\})$ for viscous dark energy and $\varLambda$CDM models. In addition three observed points are illustrated for better comparison. The other free parameters have been fixed by SNIa observational constraint. The $\varLambda$CDM best fit is given by Planck observation

4.2 Alcock–Paczynski test

The so-called Alcock–Paczynski test is another interesting probe for dynamics of a background based on anisotropic clustering and it does not depend on the evolution of the galaxies. By measuring the angular size in different redshifts in isotropic rate of expansion case, one can write [63]

$$\begin{aligned} {\Delta z\over \Delta \theta } = H(z;\{ {\varTheta _p}\})r(z;\{ {\varTheta _p}\}) . \end{aligned}$$

(32)

We should point out that one of the advantages of the Alcock–Paczynski test is that it is independent of standard candles as well as evolution of galaxies. Considering the evolution of the cosmological objects’ ratio of radius along the line of sight to the same perpendicular to the line of sight, a complete representation of the mentioned quantity reads

$$\begin{aligned} \mathscr {Y}(z;\{\varTheta _p\})=\frac{z+1}{z} H(z;\{ {\varTheta _p}\})d_A(z;\{ {\varTheta _p}\}), \end{aligned}$$

(33)

here $d_A$ is the angular diameter distance. The observed value for $\mathscr {Y}$ at three redshifts are $\mathscr {Y}(z=0.38)=1.079\pm 0.042$, $\mathscr {Y}(z=0.61)=1.248\pm 0.044$ [64] and $\mathscr {Y}(z=2.34)=1.706\pm 0.083$ [65]. The upper panel of Fig. 6 represents $\Delta z/ \Delta \theta$ as a function of the redshift. We normalized this value to the $\varLambda$CDM model ($H(z;\gamma =0)r(z;\gamma =0)$) constraining by Planck observations. By increasing the contribution of the viscosity when the other parameters are fixed, we find that our model has up and down behavior at low redshift where almost a transition from a dark matter to a dark energy era occurs. The lower panel of Fig. 6 indicates observable values of Alcock–Paczynski for various viscosity coefficients. As illustrated by this figure, increasing the value of the viscosity leads to better agreement with observed data for low redshift, while there is a considerable deviation for high redshift.

4.3 Comoving volume element

Another geometrical parameter is the comoving volume element used in number-count tests such as lensed quasars, galaxies or clusters of galaxies. The mentioned quantity is written in terms of comoving distance and Hubble parameters as follows:

$$\begin{aligned} f(z;\{ {\varTheta _p}\}) \equiv {\mathrm{d}V\over \mathrm{d}z \mathrm{d}\varOmega } =\frac{r^2(z;\{ {\varTheta _p}\})}{H(z;\{ {\varTheta _p}\})}. \end{aligned}$$

(34)

Referring to Fig. 7, one can conclude that the comoving volume element becomes maximum around $z\simeq 2.6$ for $\varLambda$CDM. In the bulk viscous model for $\gamma =0.14$ the maximum occurs at redshift around $z\simeq 2.3$. For larger value of the $\gamma$ exponent, the position of this maximum shifts to the lower redshifts corresponding to the case with lower contribution of viscous dark energy, as indicated in Fig. 2.

Fig. 7

The comoving volume element versus redshift for various values of the $\gamma$ exponent. Increasing $\gamma$ shifts the position of the maximum value of the volume element to lower redshifts. The other free parameters have been fixed by an SNIa observational constraint. The $\varLambda$CDM best fit is given by Planck observation

4.4 Age of the Universe

Another interesting quantity is the age of the Universe computed in a cosmological model. The age of the Universe at given redshift can be computed by integrating from the big bang indicated by infinite redshift up to z:

$$\begin{aligned} t(z; \{\varTheta _p\}) = \int _z^\infty {\mathrm{d}z'\over (1+z')H(z';\{\varTheta _p\})}, \end{aligned}$$

(35)

To compare the age of the Universe we set the lower value of integration to zero and we represent this quantity by $t_0$. We plotted $H_0t_0$ (Hubble parameters times the age of the Universe) as a function of $\gamma$ for values of cosmological parameters constrained by JLA observation in Fig. 8. The age of the Universe has a maximum value for $\gamma _{\times }\simeq 0.36$. This behavior is due to the dynamical nature of our viscous dark energy model. Namely, for lower values of $\gamma <\gamma _{\times }$, viscous dark energy model is almost categorized in phantom class during the wide range of scale factor while underlying dark energy model is devoted to quintessence class by increasing the value of $\gamma >\gamma _{\times }$. The existence of dark energy component is also advocated by “age crises” (for full review of the cosmic age see [66]). In the next section, we will check the consistency of our viscous dark energy model according to comparing the age of the Universe computed in this model and with the age of old high redshift galaxies located in various redshifts.

Fig. 8

The quantity $H_0t_0$ (age of the Universe times the Hubble constant at the present time) as a function of $\gamma$. In our dark energy model, the age of the Universe has a maximum at $\gamma _{\times }\simeq 0.36$ with maximum value equates to $(H_0t_0)_\mathrm{max}=1.052$. We chose other cosmological parameters in a flat Universe with observational constraint using the JLA catalog

4.5 Cosmographic parameters

One of the most intriguing questions concerning the late time accelerating expansion in the Universe is that, the possibility of distinguishing between cosmological constant and dark energy models. There are many attempts in order to answer mentioned question [67,68,69]. High sensitivity as well as model independent properties should be considered for introducing a reliable diagnostic measure. Using cosmography parameters, we are able to study some kinematic properties of the viscous dark energy model. First and second cosmography parameters are Hubble and deceleration parameters. Other kinematical parameters defined by

$$\begin{aligned}&j \equiv \frac{1}{a\, H^{3}} \frac{\mathrm{d}^{3}a}{\mathrm{d}t^{3}},\quad s \equiv \frac{1}{a\, H^{4}} \frac{\mathrm{d}^{4}a}{\mathrm{d}t^{4}},\nonumber \\&l \equiv \frac{1}{a\, H^{5}} \frac{\mathrm{d}^{5}a}{\mathrm{d}t^{5}},\quad m \equiv \frac{1}{a\, H^{6}} \frac{\mathrm{d}^{6}a}{\mathrm{d}t^{6}}. \end{aligned}$$

(36)

these parameters are called jerk, snap, lerk and maxout, respectively. It is worth noting that these parameters are not independent together and they are related to each other by simple equations. If we denote the derivative with respect to the cosmic time by dot, we can write:

$$\begin{aligned}&\dot{H}=-H^{2} (1+q),\nonumber \\&\ddot{H}=H^{3} ( j+3 q+2 ),\nonumber \\&\dddot{H}=H^{4} [ s-4 j-3 q ( q+4 )-6],\nonumber \\&\ddddot{H}=H^{5} [l-5 s+10 (q+2 )j+30 (q+2 )q+24 ], \nonumber \\&H^{(5)}=H^{6}\{ m-10j^{2}-120 j ( q+1)\nonumber \\&\quad -3 [2l+5 (24 q+18q^{2}+2q^{3}-2s-qs+8)]\}. \nonumber \\ \end{aligned}$$

(37)

In Fig. 9 we show $\dot{a}$, q(z), lerk, snap, lerk and maxout the cosmographic parameters of our model in comparison to $\varLambda \mathrm {CDM}$ model. As indicated in the mentioned figures at low redshift there is a meaningful difference between the bulk viscous model and $\varLambda \mathrm {CDM}$ model [69]. Comparison between our plots with that of computed for $\varLambda$CDM reveals the consistent results for low viscous coefficient [69].

Fig. 9

Upper panel the $\frac{H(z)}{(1+z)}$ as a function of the redshift. Middle panel deceleration probe diagnostic. Lower panel jerk, snap, lerk and maxout parameters for the bulk viscous model with respect to $\varLambda {\mathrm{CDM}}$ model. Solid lines represents corresponding quantity for $\varLambda {\mathrm{CDM}}$. Other lines are associated with different values for viscosity. The rest of free parameters have been fixed according to JLA observation at 1$\sigma$ confidence level

4.6 $Om$ diagnostic

The Om diagnostic method is indeed a geometrical diagnostic which combines Hubble parameter and redshift. It can differentiate dark energy model from $\varLambda \mathrm {CDM}$. Sahni and his collaborators demonstrated that, irrespective to matter density content of Universe, acceleration probe can discriminate various dark energy models [67]. $Om (z)$ diagnostic for our spatially flat Universe reads

$$\begin{aligned} Om(z;\{\varTheta _P\}) \equiv \frac{{\mathscr {H}}^2(z;\{\varTheta _P\}) -1}{(1+z)^3-1}. \end{aligned}$$

(38)

where ${\mathscr {H}}\equiv \frac{H}{H_0}$ and H is given by Eq. (14). For $\varLambda {\mathrm{CDM}}$ model $Om(z)=\varOmega _m^0$ while for other dark energy models, Om(z) depends on redshift [68]. Phantom like dark energy corresponds to the positive slope of $Om (z)$ whereas the negative slope means dark energy behaves like quintessence [70]. In addition, Om(z) depends upon no higher derivative of the luminosity distance in comparison for w(z) and the deceleration parameter q(z), therefore, it is less sensitive to observational errors [67]. Another feature of $Om (z)$ is that the growth of $Om (z)$ at late time favors the decaying dark energy models [71].

Figure 10 indicates acceleration probe measure for the cosmological constant with different values of equation of states and the viscous dark energy model. The viscous dark energy model with $\gamma <\gamma _{\times }$ belongs to phantom like dark energy. In mentioned figure, solid lines represents Om(z) for cosmological constant. Dashed and dashed-dot lines represents Om(z) for $\varLambda$CDM with $w=-0.90$ and $w=-1.20$, respectively. Think solid line with corresponding 1$\sigma$ confidence interval determined by JLA observation represents Om(z) for the viscous dark energy model for $\gamma =0.14$. A long-dashed line corresponds to $\gamma =0.60$ demonstrating that dynamical dark energy model has almost quintessence behavior during the evolution of the Universe.

4.7 Sandage–Loeb test

Another interesting measure is Sandage–Loeb test [72]. This criterion assesses the redshift drift of the Lyman-$\alpha$ spectra forest observed for distant quasars in the range of $2\le z \le 5$ [73,74,75]. This quantity is defined by

$$\begin{aligned} \Delta v \equiv \frac{c \Delta z}{1+z}=cH_0 \Delta t_0 \left( 1-\frac{\mathscr {H}(z)}{1+z} \right) , \end{aligned}$$

(39)

where c is the speed of light. Expansion history of our cosmos can be examined by Sandage–Loeb test corresponding to its direct geometric measurement. $\Delta t_0$ is observation time interval in Eq. (39). Figure 11 indicates dimensionless quantity, $\Delta v/c H_0\Delta t_0$, versus redshift. Higher value of the viscosity leads to more deviation from $\varLambda$CDM model.

5 Consistency with recent observations

In this section, we consider most recent observational data sets to constrain free parameters of our model. Accordingly, we are able to check the consistency of the viscous dark energy model. In principle one can refer to the following observables to examine the nature of dark energy:

• (I) Expansion rate of the Universe.

• (II) Variation of gravitational potential, producing ISW effect.

• (III) Cross-correlation of CMB and large scale structures.

• (IV) Growth of structures.

• (V) Weak lensing.

Throughout this paper, we concentrate on almost evolution expansion such as distance modulus of supernova type Ia and the gamma ray bursts (GRBs), baryon acoustic oscillations (BAO) and Hubble space telescope (HST). The CMB power spectrum which is mainly affected by background evolution is also considered. The new cosmographic data sets, namely the cosmographic distance ratio and age test, will be used for further consistency considerations. We assume a flat background, so $\varOmega ^0_\mathrm{tot} = \varOmega ^0_\mathrm{m}+\varOmega ^0_b+\varOmega ^0_r+\varOmega ^0_\mathrm{DE}=1$. We fixed energy density of radiation by other relevant observations [76]. The priors considered for the parameter space have been reported in Table 2.

Fig. 10

Om(z) diagnostic: solid lines represents Om(z) for the cosmological constant. Dashed and dot-dashed lines represents Om(z) for $\varLambda$CDM with $w=-0.90$ and $w=-1.20$, respectively. Thick solid line with corresponding 1$\sigma$ confidence interval determined by JLA observation represents Om(z) for the viscous dark energy model for $\gamma =0.14$. A long-dashed line corresponds to $\gamma =0.60$ demonstrating that dynamical dark energy model has almost quintessence behavior during the evolution of the Universe

Fig. 11

The dimensionless redshift drift for various values of the viscosity of the viscous dark energy model. At the early time, the value of this parameter is more than the standard model due to contribution of the viscosity. In this plot we assume that $c=1$

Table 2 Priors on parameter space, used in the posterior analysis in this paper

5.1 Luminosity distance implication

The supernova type Ia (SNIa) is supposed to be a standard candle in cosmology, therefore we are able to use observed SNIa to determine the cosmological distance. SNIa is the main evidence for late time accelerating expansion [1, 2]. Direct observations of SNIa do not provide a standard ruler but rather gives a distance modulus defined by

$$\begin{aligned} \mu (z;\{\varTheta _p\})\equiv & {} m - M \nonumber \\= & {} 5\log _{10} \left( {\frac{{{d_L}(z;\{\varTheta _p\})}}{{Mpc}}} \right) + 25 , \end{aligned}$$

(40)

where m and M are apparent and absolute magnitudes, respectively. For a spatially flat Universe, the luminosity distance defined in the above equation reads

$$\begin{aligned} d_L(z;\{\varTheta _p\}) = \frac{c}{{{H_0}}}(1 + z) \int _0^z \frac{dz'}{\mathscr {H}(z';\{\varTheta _p\})}. \end{aligned}$$

(41)

In order to compare the observational data set with that of predicted by our model, we utilize likelihood function with the following $\chi ^2$:

$$\begin{aligned} \chi ^2_\mathrm{SNIa}\equiv \Delta \mu ^{\dag }\cdot \mathscr {C}^{-1}_\mathrm{SNIa}\cdot \Delta \mu , \end{aligned}$$

(42)

where $\Delta \mu \equiv \mu _\mathrm{obs}(z)-\mu (z;\{\varTheta _p\})$ and $\mathscr {C}_\mathrm{SNIa}$ is the covariance matrix of SNIa data sets. $\mu _\mathrm{obs}(z)$ is observed distance modulus for a SNIa located at redshift z (relevant data sets and corresponding covariance is available on website [77]). Marginalizing over $H_0$ as a nuisance parameter yields [76]

$$\begin{aligned} \chi ^2_\mathrm{SNIa}=\mathscr {M}^{\dag }\cdot \mathscr {C}_\mathrm{SNIa}^{-1}\cdot \mathscr {M}+\mathscr {A}_\mathrm{SNIa}+\mathscr {B}_\mathrm{SNIa}, \end{aligned}$$

(43)

where $\mathscr {M}\equiv \mu _\mathrm{obs}(z)-25-5\log _{10}[H_0d_L(z;\{\varTheta _p\})/c]$, and

$$\begin{aligned}&\mathscr {A}\equiv -\frac{\left[ \sum _{i,j}\mathscr {M}(z_i;\{\varTheta _p\})\mathscr {C}^{-1}_\mathrm{SNIa}(z_i,z_j)-\ln 10/5\right] ^2}{\sum _{i,j}\mathscr {C}^{-1}_\mathrm{SNIa}(z_i,z_j)} ,\nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned}&\mathscr {B}\equiv -2\ln \left( \frac{\ln 10}{5}\sqrt{\frac{2\pi }{\sum _{i,j}\mathscr {C}^{-1}_\mathrm{SNIa}(z_i,z_j)}}\right) . \end{aligned}$$

(45)

We also take into account gamma ray bursts (GRBs) proposed as most luminous astrophysical objects at high redshift as the complementary standard candles. For GRBs, the $\chi ^2_\mathrm{GRBs}$ is given by

$$\begin{aligned} \chi ^2_\mathrm{GRBs}=\sum _{i}\frac{\mathscr {M}^2(z_i;\{\varTheta _p\})}{\sigma _i^2}+\mathscr {A}_\mathrm{GRBs}+\mathscr {B}_\mathrm{GRBs}, \end{aligned}$$

(46)

where

$$\begin{aligned} \mathscr {A}_\mathrm{GRBs}\equiv & {} -\frac{\left[ \sum _{i}\frac{\mathscr {M}(z_i;\{\varTheta _p\})}{\sigma _i^2}-\ln 10/5\right] ^2}{\sum _{i}\frac{1}{\sigma _i^2}}, \end{aligned}$$

(47)

$$\begin{aligned} \mathscr {B}_\mathrm{GRBs}\equiv & {} -2\ln \left( \frac{\ln 10}{5}\sqrt{\frac{2\pi }{\sum _{i}\frac{1}{\sigma _i^2}}}\right) . \end{aligned}$$

(48)

Finally for SNIa and GRBs observations, we construct $\chi ^2_{SG}\equiv \chi ^2_\mathrm{SNIa}+\chi ^2_\mathrm{GRBs}$. In this paper we used recent joint light-curve analysis (JLA) sample constructed from the SNLS and SDSS SNIa data, together with several samples of low redshift SNIa [76]. We also utilize the “Hymnium” sample including 59 samples for GRBs data set. These data sets have been extracted out of 109 long GRBs [78].

5.2 Baryon acoustic oscillations

Baryon acoustic oscillations or in brief BAO at recombination era are the footprint of oscillations in the baryon-photon plasma on the matter power spectrum. It can be utilized as a typical standard ruler, calibrated to the sound horizon at the end of the drag epoch. Since the acoustic scale is so large, BAO are largely unaffected by nonlinear evolution. The BAO data can be applied to measure both the angular diameter distance, $D_A(z;\{\varTheta _p\})$, and the expansion rate of the Universe $H(z;\{\varTheta _p\})$ either separately or through their combination as [76]:

$$\begin{aligned} D_V(z;\{\varTheta _p\}) = \left[ (1+z)^2 D_A^2 (z;\{\varTheta _p\}) \frac{cz}{H(z;\{\varTheta _p\})} \right] ^{1/3}, \end{aligned}$$

(49)

where $D_V (z;\{\varTheta _p\})$ is volume-distance. The distance ratio used as BAO criterion is defined by

$$\begin{aligned} d_\mathrm{BAO}(z;\{\varTheta _p\})\equiv \frac{r_{s}(z;\{\varTheta _p\})}{D_V(z;\{\varTheta _p\})}, \end{aligned}$$

(50)

here $r_{s}(z;\{\varTheta _p\})$ is the comoving sound horizon. In this paper to take into account different aspects of BAO observations and improving our constraints, we use 6 reliable measurements of BAO indicators including Sloan Digital Sky Survey (SDSS) data release 7 (DR7) [80], SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS) [81], WiggleZ survey [82] and 6dFGS survey [79]. BAO observations contain 6 measurements from redshift interval, $z\in [0.1,0.7]$ (for observed values at higher redshift one can refer to [84]). The observed values for mentioned redshift interval have been reported in Table 3. Also the inverse of covariance matrix is given by

$$\begin{aligned}&{\mathscr {C}}^{-1}_\mathrm{BAO} = \left( \begin{array}{r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r} 4444.4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 34.602 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 20.661157 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 24532.1 &{} -25137.7 &{} 12099.1 \\ 0 &{} 0 &{} 0 &{} -25137.7 &{} 134598.4 &{} -64783.9 \\ 0 &{} 0 &{} 0 &{} 12099.1 &{} -64783.9 &{} 128837.6 \\ \end{array} \right) . \end{aligned}$$

(51)

Therefore $\chi ^2_\mathrm{BAO}$ is written by

$$\begin{aligned} \chi ^2_\mathrm{BAO}\equiv \Delta d^{\dag }\cdot {\mathscr {C}}^{-1}_\mathrm{BAO}\cdot \Delta d. \end{aligned}$$

(52)

In the above equation $\Delta d(z;\{\varTheta _p\})\equiv d_\mathrm{obs}(z)-d_\mathrm{BAO}(z;\{\varTheta _p\})$ and ${\mathscr {C}}^{-1}_\mathrm{BAO}$ is given by Eq. (51). The $d_\mathrm{obs}(z)$ is reported in Table 3.

Table 3 Observed data for BAO [83]

5.3 CMB observations

Another part of data to put observational constraints on free parameter of the viscous dark energy model is devoted to CMB observations. Here we use the following likelihood function for CMB power spectrum observations:

$$\begin{aligned} \chi ^2_\mathrm{CMB-power}=\Delta C^{\dag }\cdot \mathscr {M}_\mathrm{CMB}^{-1}\cdot \Delta C, \end{aligned}$$

(53)

where $\Delta C_{\ell }\equiv C_{\ell }^\mathrm{obs}-C_{\ell }(\{\varTheta _p\})$ and $\mathscr {M}_\mathrm{CMB}$ is the covariance matrix for the CMB power spectrum. As a complementary part for the CMB observational constraints, we also used CMB lensing from SMICA pipeline of Planck 2015. To compute CMB power spectrum for our model, we used Boltzmann code CAMB [85]. Here, we do not consider dark energy clustering, consequently, at the first step, perturbations in radiation, baryonic and cold dark matters are mainly affected by background evolution which is modified due to presence of the viscous dark energy. However, the precise computation of perturbations should be taken into account perturbation in the viscous dark energy, but since DE in our model at the early Universe is almost similar to cosmological constant, consequently mentioned terms at this level of perturbation can be negligible. This case is out of the scope of the current paper and we postpone such accurate considerations for another study. We made a careful modification to the CAMB code and combined with publicly available cosmological Markov Chain Monte Carlo code CosmoMC [86].

5.4 HST-key project

In order to adjust better constraint on the local expansion rate of Universe, we use the Hubble constant measurement from Hubble space telescope (HST). Therefore additional observational point for analysis is [87]:

$$\begin{aligned} H_0=73.8 \pm 2.4\,\text {km s}^{-1} \ \text {Mpc}^{-1}. \end{aligned}$$

In the next section, we will show the results of our analysis for best fit values for the free parameters and their confidence intervals for one and two dimensions.

6 Results and discussion

As discussed in previous section, to examine the consistency of our viscous dark energy model with most recent observations, we use the following tests:

• 1. SNIa luminosity distance from joint light-curve analysis (JLA) which made from SNLS and SDSS SNIa compilation.

• 2. GRBs data sets for large interval of redshift as a complementary part for luminosity distance constraints.

• 3. BAO data from galaxy surveys SDSS DR11, SDSS DR11 CMASS, 6dF.

• 4. CMB temperature fluctuations angular power spectrum from Planck 2015 results.

• 5. CMB lensing from SMICA pipeline of Planck 2015.

• 6. Hubble constant measurement from Hubble space telescope (HST) ($H_0=73.8 \pm 2.4 \text {km s}^{-1} \ \text {Mpc}^{-1}$) with a flat prior.

• 7. Cosmographic distance ratio test.

• 8. Hubble parameter for different redshifts.

• 9. Cosmic age test.

Fig. 12

Upper panel distance modulus of bulk viscous model compared with JLA and GRBs data. Lower panel BAO observables for the viscous dark energy and $\varLambda$CDM models. The observed data sets are reported in Table 3

Fig. 13

Marginalized posterior function for various free parameters of the dynamical dark energy model. The dashed line represents observational constraint by joint analysis JLA $+$ GRBs. The solid line corresponds to BAO analysis while long-dashed line indicates observational consistency for HST project

In the upper panel of Fig. 12, we plot the luminosity distance for the $\varLambda$CDM best fit (solid line) and the viscous dark energy model for different values of $\gamma$. In our viscous dark energy model, the EoS at late time belongs to phantom type, therefore by increasing the value of $\gamma$ when the other parameters are fixed, the contribution of the viscous dark energy becomes lower than the cosmological constant. Subsequently, the distance modulus is longer than that for the cosmological constant. For complementary analysis, we also added GRBs results for the observational constraint. The lower panel indicates the BAO observable quantity. The higher value of viscosity for the dark energy model causes good agreement between model and observations. In such a case, the consistency with early observations decreases, therefore, there is a trade off in determining $\gamma$ with respect to late and early time

Table 4 Best fit values for the viscous dark energy using JLA and combination with GRBs at $68 \%$ confidence interval

Table 5 Bayesian $68 \%$ confidence limits for a model based on JLA, BAO, HST and JLA + GRBs + BAO + HST

observational data sets. A marginalized posterior probability function for various free parameters of the viscous dark energy model have been indicated in Fig. 13. In this figure we find that different observations to confine $\gamma$, $\varOmega ^0_\mathrm{{DE}}$ and $H_0$ are almost consistent. The results of a Bayesian analysis to find best fit values for the free parameters of viscous dark energy model (Table 2) at $1\sigma$ confidence interval have been reported in Table 4. In Table 5 the best fit values for the parameters using BAO, HST and the combination of observations, JLA $+$ GRBs $+$ BAO $+$ HST (JGBH), have been reported at $68\%$ confidence interval.

Fig. 14

Marginalized confidence regions at 68 and $95\%$ confidence levels

The contour plots for various pairs of free parameters are indicated in Fig. 14. Our results demonstrate that there exists acceptable consistency between different observations in determining best fit values for the free parameters of the viscous dark energy model. Figure 15 illustrates the contour plot in the $\varOmega _\mathrm{DE}^0$–$\gamma$ plane. The effect of changing the Hubble constant at the present time on the degeneracy of the mentioned parameters represents that by increasing the value of $H_0$, the best fit value for the viscous dark energy density at present time increases while the viscosity parameter is almost not sensitive.

It turns out that at the early Universe the cosmological constant has no role in evolution of the Universe; on the contrary, it is an opportunity for a dynamical dark energy to contribute effectively on that epoch. However, according to Fig. 2 the viscous dark energy to cold dark matter ratio at early epoch asymptotically goes to zero, nevertheless, we use CMB observation to examine the consistency of our viscous model. In Fig. 16, we indicate the behavior of our dynamical dark energy model on the power spectrum of CMB. The higher the value of $\gamma$, the lower contribution of the dynamical dark energy model at the late time (see Fig. 2), resulting in lower value of ISW effect. Consequently, the value of $\ell (\ell +1)C_{\ell }$ for small $\ell$ decreases. For $\gamma >\gamma _{\times }$ due to changing the nature of the dark energy model, the mentioned behavior is no longer valid and the Sachs–Wolfe plateau becomes larger (see the lower panel of Fig. 16). Considering Planck TT data, the best fit values are $\gamma =0.32^{+0.31}_{-0.26}$ and $\varOmega _\mathrm{DE}^0=0.684^{+0.026}_{-0.028}$ at $68\%$ confidence interval in a flat Universe. Planck TT observation does not provide a strong constraint on viscous parameter, $\gamma$. CMB lensing observational data put a strict constraint on the $\gamma$ coefficient as reported in Table 6.

Combining JLA $+$ GRBs $+$ BAO $+$ HST with Planck TT data leads to a tight constraint on both $\gamma$ and $\varOmega _\mathrm{{DE}}^0$. On the other hand, if we combine JLA, GRBs, BAO and HST (JGBH), our results demonstrate that $\gamma =0.1404\pm 0.0014$ and $\varOmega _\mathrm{DE}^0=0.696\pm 0.010$ consequently as regards accuracy improves remarkably.

The tension in the value of $H_0$ in this model disappears if we compare the best fit value for $H_0$ using local observations and that of determined by CMB. This result is due to the early behavior of our viscous dark energy model.

Fig. 15

The effect of varying $H_0$ on the degeneracy between $\varOmega _\mathrm{DE}^0$–$\gamma$ in the contour enclosing 68 and $95\%$ confidence intervals

Fig. 16

Upper panel CMB power spectrum for bulk viscous and $\varLambda$CDM model. Lower panel the viscous coefficient leads to ups and downs in power spectrum for higher $\ell$ while for small $\ell$ due to ISW contribution the plateau of power varies depending on value of $\gamma$

Table 6 Bayesian $68 \%$ confidence limits for a model based on Planck TT, CMB Lensing and Planck TT + JGBH

In what follows we deal with the cosmographic distance ratio, the Hubble parameter and cosmic age to examine an additional aspect of the viscous dark energy model. Recently Miyatake et al. used the cross-correlation optical weak lensing and CMB lensing and introduced a purely geometric quantity. This quantity is the so-called cosmographic distance ratio defined by [60,61,62]

$$\begin{aligned} r\equiv \frac{D_A(a_\mathrm{L},a_\mathrm{g})D_A(a_\mathrm{c})}{D_A(a_\mathrm{L},a_\mathrm{c})D_A(a_\mathrm{g})}, \end{aligned}$$

(54)

where $D_A$ is the angular diameter distance. $a_\mathrm{L}$, $a_\mathrm{g}$ and $a_\mathrm{c}$ are scale factors for lensing structure, the background galaxy source plane and CMB, respectively. Here we used three observational values reported in [88] based on CMB and Galaxy lensing. Figure 17 represents r as a function of the redshift for the best values constrained by various observations in the viscous dark energy model. A higher value of the viscosity leads to better coincidence with current observations. Since in our model the maximum best value for viscosity is given by the Planck TT observation, which is $\gamma =0.32^{+0.31}_{-0.26}$ at $1\sigma$ confidence interval, one can conclude that current observational data for r have been mostly affected by CMB when we consider the viscous dark energy model as a dynamical dark energy.

Fig. 17

Cosmographic distance ratio for the viscous dark energy model. The solid line corresponds to $\gamma =0.14$ according to best fit by JLA observation, a dotted line indicates the case $\gamma =0.40$ and a dash-dot line is for $\gamma =0.80$. Observed data are given from [88]

Table 7 H(z) measurements (in unit [$\mathrm {km\,s^{-1}\,Mpc^{-1}}$]) and their errors [89]

We inspect the Hubble parameter in our model. To this end, by using Eq. (14) one can compute the rate of expansion as a function if redshift and compare it with the observed Hubble parameter listed in Table 7 for various redshift [89].

Figure 18 shows Hubble expansion rate for viscous dark energy model. There is good agreement between this model and observed values for small $\gamma$. In Table 7 we summarize all H(z) measurements used in upper panel of Fig. 18.

One can rewrite $\mathscr {H}(z;\{\varTheta _p\})\equiv H(z;\{\varTheta _p\})/H_0$ and we introduce the relative difference $\Delta \mathscr {H}(z;\{\varTheta _p\})$ as follows:

$$\begin{aligned} \Delta \mathscr {H}(z;\{\varTheta _p\})=100 \times \left[ \frac{\mathscr {H}(z;\{\varTheta _p\})}{\mathscr {H}_{\varLambda CDM}(z)} -1 \right] . \end{aligned}$$

(55)

The above quantity has been illustrated in the lower panel of Fig. 18 as a function of the redshift. For higher value of $\gamma$ at small redshift, we get a pronounced difference between viscous dark energy and cosmological constant.

Fig. 18

Upper panel Hubble parameter in comparison with various observational values for H(z). Lower panel relative difference of dimensionless Hubble parameter as a function of the redshift for various values of the viscosity

The cosmic age crisis is long standing subject in the cosmology and is a proper litmus test to examine dynamical dark energy model. Due to many objects observed at intermediate and high redshifts, there exist some challenges to accommodate some of old high redshift galaxies (OHRG) in $\varLambda$CDM model [90]. There are many suggestion to resolve mentioned cosmic age crisis [91,92,93], however, this discrepancy has not completely removed yet and it becomes as smoking gun of evidence for the advocating dark energy component. As an illustration, Simon et al. demonstrated the lookback time redshift data by computing the age of some old passive galaxies at the redshift interval $0.11\le z\le 1.84$ with 2 high redshift radio galaxies at $z=1.55$, which is named LBDS 53W091 with age equates to 3.5-Gyr [94, 95] and the LBDS 53W069 a 4.0-Gyr at $z=1.43$ [96], totally they used 32 objects [97]. In addition, nine extremely old globular clusters older than the present cosmic age based on 7-year WMAP observations have been found in [98]. Beside the mentioned objects to check the smoking gun of dark energy models, a quasar APM $08279+5255$ at $z=3.91$, with an age equal to $t=2.1_{-0.1}^{+0.9}$ Gyr, is considered [99]. To check the age-consistency, we introduce the quantity

$$\begin{aligned} \tau (z_i;\{\varTheta _p\})= & {} \frac{t(z_i;\{\varTheta _p\})}{t_\mathrm{obs}(z_i)}, \quad i=1\cdots 42, \end{aligned}$$

(56)

where $t(z_i;\{\varTheta _p\})$ is the age of the Universe computed by Eq. (35) and $t_\mathrm{obs}(z_i)$ is an estimation for the age of the ith old cosmological object. In the above equation $\tau \ge 1$ corresponds to compatibility of the model based on the observed objects. Nine extremely old globular clusters are located in M31 and we report their $\tau$ values in Table 8. As indicated in the mentioned table, only B050 is in tension over $4\sigma$ with current observations. In addition in Fig. 19, we illustrate the value of $\tau$ for the rest of the data for various observational constraints. At $2\sigma$ confidence interval, there is no tension with cosmic age in the viscous dark energy model even for a very old high redshift quasar, $08279+5255$, at $z=3.91$. Therefore, all old objects used in the age crisis analysis can be accommodated by considering the viscous dark energy model.

Finally, considering the bulk viscous model and by combining different observations, one can improve the age crisis in the framework of very old globular clusters and high redshift objects.

Table 8 The $\tau$ value for nine old globular cluster located in the M31 galaxy [98]

Fig. 19

$\tau$ as a function of the redshift for 32 old objects. Data have been given from [96, 97, 99]

7 Summary and conclusions

In this paper, we examined a modified version for dark energy model inspired by dissipative phenomena in fluids according to Eckart theory as the zero-order level for the thermodynamical dissipative process. In order to satisfy the statistical isotropy, we assumed a special form for he dark energy bulk viscosity. In this model, we have two components for the energy contents without any interaction between them. Our viscous dark energy model showed phantom-crossing which avoids the big-rip singularity. Our results, however, indicated that the energy density of the viscous dark energy becomes zero at a typical scale factor, $\tilde{a}$ (Eq. (15)), depending on the viscous coefficient, interestingly there is no ambiguity for the time definition in the mentioned model (see Eq. (20) for the one-component case).

We have also proposed a non-minimal derivative coupling scalar field with zero potential to describe viscous dark energy model for a two-component Universe. In this approach, the coupling parameter is related to the viscous coefficient and the present dark energy density. For zero value of $\gamma$, the standard action for canonical scalar field to be retrieved. To achieve real value for scalar field, $\varepsilon$ should be negative. According to Eq. (30), the coupling parameter is bounded according to $\kappa \in [-1/9H_0^2(1-\varOmega _\mathrm{DE}^0), 0]$. Evolution of $\tilde{\phi }$ indicated that the scalar field has no monotonic behavior as the scale factor increases. Subsequently, at $\tilde{a}$ the value of $\rho _{\phi }$ becomes zero corresponding to the phantom-crossing era.

From observational consistency points of view, we examined the effect of the viscous dark energy model on the geometrical parameters, namely, comoving distance, Alcock–Paczynski test, comoving volume element and age of the Universe. The comoving radius of the Universe for $\gamma <\gamma _{\times }$ shows growing behavior, indicating the phantom type of the viscous dark energy. The Alcock–Paczynski test showed that there is a sharp variation in the relative behavior of the viscous dark energy model with respect to the cosmological constant at low redshift. The redshift interval for the occurring mentioned variation is almost independent from the viscous coefficient. The comoving volume element increased by increasing the viscous coefficient for $\gamma <\gamma _{\times }$, which results in growing number-count of cosmological objects.

To discriminate between different candidates for dark energy, there are some useful criteria. In this paper, the cosmographic parameters have been examined and relevant results showed that at the late time it is possible to distinguish viscous dark energy from cosmological constant. As indicated in Fig. 9 at low redshift there is a meaningful differences between the bulk viscous model and $\varLambda \mathrm {CDM}$ model. For completeness, we also used the Om-diagnostic method and Sandage–Loeb test to evaluate the behavior of the viscous dark energy model. Mentioned measures are very sensitive to classifying our model depending on the $\gamma$ parameter. For small $\gamma$, Om(z) represents the phantom type and it is possible to distinguish this model from $\varLambda$CDM.

To perform a systematic analysis and to put observational constraints on model free parameters reported in Table 2, we considered supernovae, gamma ray bursts, baryonic acoustic oscillation, Hubble Space Telescope, Planck data for CMB observations. To compare theoretical distance modulus with observations, we used recent SNIa catalogs and gamma ray bursts including higher redshift objects. The best fit parameters according to SNIa by the JLA catalog are $\varOmega _b h^2=0.0232^{+0.0019}_{-0.0027}$, $\varOmega _\mathrm{DE}^0=0.701\pm 0.025$, $\gamma =0.1386^{+0.0034}_{-0.0024}$ and $H_0=68.8^{+2.1}_{-2.8}$ in the $68\%$ confidence limit. Including GRBs data increased the viscous dark energy content at the present time. The best fit values from the joint analysis of JLA $+$ GRBs $+$ BAO $+$ HST results in $\varOmega _\mathrm{DE}^0=0.696\pm 0.010$, $\gamma =0.1404\pm 0.0014$ and $H_0=68.1\pm 1.3$ at $1\sigma$ confidence interval (see Tables 4, 5). According to Planck TT observation, the value of the viscosity coefficient increases considerably and grows to $\gamma =0.32^{+0.31}_{-0.26}$. The tension in the Hubble parameter is almost resolved in the presence of the viscous dark energy component. A joint analysis of JGBH $+$ Planck TT causes $H_0=67.9\pm 1.1$ at 68% level of confidence. It is worth noting that using the late time observations confirmed that the viscous dark energy model is at a reliable level (see Fig. 13), while according to our results reported in Table 6, taking into account early observations such as the CMB power spectrum removes the mentioned tight constraint. Marginalized contours have been illustrated in Fig. 14. The power spectrum of TT represented that the viscous dark energy model has small amplitude ups and downs for large $\ell$, which describes observational data better than $\varLambda$CDM.

As a complementary approach in our investigation, we have also examined the cosmographic distance ratio and age crisis revisited by very old cosmological objects at different redshifts. According to the cosmographic distance ratio we found that a higher value of the viscosity leads to better agreement with current observational data. Therefore, the viscous dark energy model constrained by Planck TT observation ($\gamma =0.32^{+0.31}_{-0.26}$) is more compatible with data given in [88]. In the context of the viscous dark energy model, current data for r are mostly affected by CMB used in determining gravitational lensing shear (see Fig. 17).

Since there is competition between phantom and quintessence behavior of the viscous dark energy model, it is believed that the challenge of accommodation of a cosmological old object can be revisited. We used 32 objects located in $0.11\le z\le 1.84$ accompanying nine extremely old globular clusters hosted by M31 galaxy. As reported in Table 8, almost all tensions in the age of all old globular clusters in our model have been resolved at $2\sigma$ confidence interval. However, the value of $\tau$ for quasar APM $08279+5255$ at $z=3.91$, with $t=2.1_{-0.1}^{+0.9}$ Gyr is less than unity, but in the $68\%$ confidence limit it is accommodated by the viscous dark energy model for all observational catalogs (see Fig. 19).

As a concluding remark we must point out that theoretical and phenomenological modeling of dark energy in order to diminish the ambiguity about this kind of energy content have been considerably of particular interest. In principle, to give a robust approach to examining dark energy models beyond cosmological constant, background dynamics and perturbations should be considered. The main part of the present study was devoted to background evolution. Taking into account higher order perturbations to constitute a robust approach in the context of large scale structure resulting in more clear view about the nature of dark energy. The contribution of coupling between dark sectors in the presence of the viscosity for dark energy according to our approach is another useful aspect. Indeed considering the dynamical nature for dark energy constituent of our Universe potentially enables us to resolve tensions in observations [100]. These parts of our research are in progress and we will be addressing them later.