Cosmological dynamics of spatially flat Einstein–Gauss–Bonnet models in various dimensions: high-dimensional $\Lambda$-term case

Abstract

In this paper we perform a systematic study of spatially flat $[(3+D)+1]$-dimensional Einstein–Gauss–Bonnet cosmological models with $\Lambda$-term. We consider models that topologically are the product of two flat isotropic subspaces with different scale factors. One of these subspaces is three-dimensional and represents our space and the other is D-dimensional and represents extra dimensions. We consider no ansatz of the scale factors, which makes our results quite general. With both Einstein–Hilbert and Gauss–Bonnet contributions in play, $D=3$ and the general $D\ge 4$ cases have slightly different dynamics due to the different structure of the equations of motion. We analytically study the equations of motion in both cases and describe all possible regimes with special interest on the realistic regimes. Our analysis suggests that the only realistic regime is the transition from high-energy (Gauss–Bonnet) Kasner regime, which is the standard cosmological singularity in that case, to the anisotropic exponential regime with expanding three and contracting extra dimensions. Availability of this regime allows us to put a constraint on the value of Gauss–Bonnet coupling $\alpha$ and the $\Lambda$-term – this regime appears in two regions on the $(\alpha , \Lambda )$ plane: $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \le -3/2$ and $\alpha > 0$, $\alpha \Lambda \le (3D^2 - 7D + 6)/(4D(D-1))$, including the entire $\Lambda < 0$ region. The obtained bounds are confronted with the restrictions on $\alpha$ and $\Lambda$ from other considerations, like causality, entropy-to-viscosity ratio in AdS/CFT and others. Joint analysis constrains ($\alpha$, $\Lambda$) even further: $\alpha > 0$, $D \ge 2$ with $(3D^2 - 7D + 6)/(4D(D-1)) \ge \alpha \Lambda \ge - (D+2)(D+3)(D^2 + 5D + 12)/(8(D^2 + 3D + 6)^2)$.

1 Introduction

It already has been more then a hundred years since the formulation of the General Relativity (GR) by Albert Einstein, but apparently the idea of extra dimensions is even older than that. Indeed, it was Nordström who constructed the first ever extra-dimensional model [1] in 1914, and this model unified Nordström’s second gravity theory [2] with Maxwell’s electromagnetism. Later in 1915 Einstein introduced General Relativity [3], but still it took almost four years to prove that Nordström’s theory and others were wrong. During the solar eclipse of 1919, the bending of light near the Sun was measured and the deflection angle was in perfect agreement with GR, while Nordström’s theory, being scalar gravity, predicted a zeroth deflection angle.

Unlike Nordström’s scalar gravity, his idea about extra dimensions survived, and in 1919 Kaluza proposed [4] a similar model but based on GR: in his model five-dimensional Einstein equations could be decomposed into four-dimensional Einstein equations plus Maxwell’s electromagnetism. To perform such a decomposition, the extra dimensions should be “curled” or compactified into a circle and “cylindrical conditions” should be imposed. Later in 1926, Klein proposed [5, 6] a nice quantum mechanical interpretation of this extra dimension and so the theory called Kaluza–Klein was formally formulated. Remarkably, their theory unified all known interactions at that time. With time, more interactions became known and it became clear that to unify them all, more extra dimensions are needed. Nowadays, one of the promising theories to unify all interactions is M/string theory.

The presence of the curvature-squared corrections in the Lagrangian of the gravitational counterpart of string theories is one of their distinguishing features. Scherk and Schwarz [7] were the first to demonstrate the presence of the $R^2$ and $R_{\mu \nu } R^{\mu \nu }$ terms in the Lagrangian of the Virasoro–Shapiro model [8, 9]. The presence of a curvature-squared term of the $R^{\mu \nu \lambda \rho } R_{\mu \nu \lambda \rho }$ type was found [10] in the low-energy limit of the $E_8 \times E_8$ heterotic superstring theory [11] to match the kinetic term for the Yang–Mills field. Later it was demonstrated [12] that the only combination of quadratic terms that leads to a ghost-free nontrivial gravitation interaction is the Gauss–Bonnet (GB) term:

$$\begin{aligned} L_{GB} = L_2 = R_{\mu \nu \lambda \rho } R^{\mu \nu \lambda \rho } - 4 R_{\mu \nu } R^{\mu \nu } + R^2. \end{aligned}$$

This term, first found by Lanczos [13, 14] (therefore it is sometimes referred to as the Lanczos term) is an Euler topological invariant in (3+1)-dimensional space-time, but not in (4+1) and higher dimensions. Zumino [15] extended Zwiebach’s result on higher-than-squared curvature terms, supporting the idea that the low-energy limit of the unified theory might have a Lagrangian density as a sum of contributions of different powers of curvature. In this regard the Einstein–Gauss–Bonnet (EGB) gravity could be seen as a subcase of more general Lovelock gravity [16], but in the current paper we restrict ourselves to only quadratic corrections and so to the EGB case.

All extra-dimensional theories have one thing in common – one needs to explain where additional dimensions are “hiding”, since we do not sense them, at least with the current level of experiments. One of the ways to hide extra dimensions, and to recover four-dimensional physics, is to build a so-called “spontaneous compactification” solution. Exact static solutions with the metric chosen as a cross product of a (3+1)-dimensional manifold and a constant curvature “inner space”, were found for the first time in [17], but the (3+1)-dimensional manifold being Minkowski (the generalization for a constant curvature Lorentzian manifold was done in [18]). In the context of cosmology, it is more useful to consider a spontaneous compactification in the case with the four-dimensional part given by a Friedmann–Robertson–Walker metric. In this case it is also natural to consider the size of the extra dimensions being time dependent and not than static. Indeed, in [19] it was exactly demonstrated that in order to have a more realistic model one needs to consider the dynamical evolution of the extra-dimensional scale factor. In [18], the equations of motion with time-dependent scale factors were written for arbitrary Lovelock order in the special case of a spatially flat metric (the results were further proven in [20]). The results of [18] were further analyzed for the special case of 10 space-time dimensions in [21]. In [22], the dynamical compactification solutions were studied with the use of Hamiltonian formalism. More recently, searches for spontaneous compactifications were made in [23], where the dynamical compactification of the (5+1)-dimensional Einstein–Gauss–Bonnet model was considered; in [24, 25] with different metric Ansätze for scale factors corresponding to (3+1)- and extra-dimensional parts; and in [26,27,28], where general (e.g., without any Ansatz) scale factors and curved manifolds were considered. Also, apart from cosmology, the recent analysis has focused on properties of black holes in Gauss–Bonnet [29,30,31,32,33,34,35,36,37] and Lovelock [38,39,40,41,42] gravities, features of gravitational collapse in these theories [43,44,45], general features of spherical-symmetric solutions [46], and many others.

If we want to find exact solutions, the most common Ansatz used for the scale factor is an exponential or a power law. Exact solutions with exponents for both the (3+1)- and extra-dimensional scale factors were studied for the first time in [47], where an exponentially increasing (3+1)-dimensional scale factor and an exponentially shrinking extra-dimensional scale factor were described. Power-law solutions have been analyzed in [18, 48] and more recently in [20, 49,50,51,52], so that by now there is an almost complete description of the solutions of this kind (see also [53] for comments regarding physical branches of the power-law solutions). Solutions with exponential scale factors [54] have also been studied in detail, namely, the models with both variable [55] and constant [56] volume; the general scheme for constructing solutions in EGB was developed and generalized for general Lovelock gravity of any order and in any dimensions [57]. Also, the stability of the solutions was addressed in [58] (see also [59] for stability of general exponential solutions in EGB gravity), and it was demonstrated that only a handful of the solutions could be called “stable”, while the most of them are either unstable or have neutral/marginal stability, and so additional investigation is required.

In order to find all possible regimes of Einstein–Gauss–Bonnet cosmology, one needs to go beyond an exponential or power-law Ansatz and keep the scale factor generic. We are particularly interested in models that allow dynamical compactification, so that we consider the metric as the product of a spatially three-dimensional and extra-dimensional parts. In that case the three-dimensional part is “our Universe” and we expect for this part to expand while the extra-dimensional part should be suppressed in size with respect to the three-dimensional one. In [26] we demonstrated that the existence of phenomenologically sensible regime when the curvature of the extra dimensions is negative and the Einstein–Gauss–Bonnet theory does not admit a maximally symmetric solution. In this case both the three-dimensional Hubble parameter and the extra-dimensional scale factor asymptotically tend to the constant values. In [27] we performed a detailed analysis of the cosmological dynamics in this model with generic couplings. Recently we studied this model in [28] and demonstrated that, with an additional constraint on the couplings, Friedmann-type late-time behavior could be restored.

The current paper is a spiritual successor of [60, 61], where we investigated cosmological dynamics of the vacuum and low-dimensional $\Lambda$-term Einstein–Gauss–Bonnet model. In both papers the spatial section is a product of two spatially flat manifolds with one of them three-dimensional, which represents our Universe and the other is extra dimensional. In [60] we considered a vacuum model, while in [61] and in the current paper one finds the model with the cosmological term. In [60] we demonstrated that the vacuum model has two physically viable regimes – the first of them is the smooth transition from high-energy GB Kasner to low-energy GR Kasner. This regime appears for $\alpha > 0$ at $D=1,\,2$ (the number of extra dimensions) and for $\alpha < 0$ at $D \ge 2$ (so that at $D=2$ it appears for both signs of $\alpha$). The other viable regime is a smooth transition from high-energy GB Kasner to anisotropic exponential regime with expanding three-dimensional section (“our Universe”) and contracting extra dimensions; this regime occurs only for $\alpha > 0$ and at $D \ge 2$. In [61] we considered low-dimensional $\Lambda$-term case and it appears that only one of the realistic regimes from the vacuum case is present in the low-dimensional $\Lambda$-term case, namely, the transition from high-energy GB Kasner to anisotropic exponential regime with expanding three-dimensional section (“our Universe”) and contracting extra dimensions; the low-energy GR Kasner is forbidden in the presence of the $\Lambda$-term so the corresponding transition do not occur. But this is not the only difference – in the $D=1$ $\Lambda$-term case there are no viable regimes at all, making it pathological (in contrast, the vacuum $D=1$ case has a GB Kasner to GR Kasner viable transition). In $D=2$ we have a realistic regime – GB Kasner to anisotropic exponential solution, but it appears only for $\Lambda > 0$, so that we do not have viable AdS cosmologies in $D=\{1, 2\}$. Thus in this paper we continue the investigation of the $\Lambda$-term case for $D=3$ and general $D \ge 4$ cases. Let us also note that in [26,27,28] we considered a similar model but with both manifolds a constant (generally non-zero) curvature; the realistic regime in that model has exponential expansion of the three-dimensional subspace and constant-size extra dimensions.

Both in [61] and in the present paper we consider the cosmological dynamics in the presence of a $\Lambda$-term. In both papers we consider both signs for the value of the cosmological constant. For a cosmologist, especially a physical cosmologist, it could sound as a blasphemy, but in the high-energy and gravitation theory it is a usual pre-requisite. For instance, $\Lambda < 0$ is needed for a black hole to reach thermal equilibrium with a heat bath [62], or to derive a correct definition of some of the Noether charges [63, 64] (see also [65]). Thus we conclude that there are enough reasons to consider both signs of the $\Lambda$-term.

The structure of the manuscript is as follows: first we write down general equations of motion for Einstein–Gauss–Bonnet gravity, then we rewrite them for our Ansatz. In the following sections we analyze them for $D=3$ and the general $D\ge 4$ cases, considering the $\Lambda$-term case in this paper only. Each case is followed by a brief discussion of the results and properties of this particular case; after considering all cases we discuss their properties, generalities, and differences, compare the limits on $\alpha$ and $\Lambda$ with those from other sources, and draw conclusions.

2 Equations of motion

As mentioned above, we consider the spatially flat anisotropic cosmological model in Einstein–Gauss–Bonnet gravity with $\Lambda$-term as a matter source (the vacuum model was considered previously in [60]). The equations of motion for such model include both first and second Lovelock contributions and could easily be derived from the general case (see, e.g., [20]). We consider the flat anisotropic metric

$$\begin{aligned} g_{\mu \nu } = \mathop {\mathrm{diag}}\nolimits \{ -1, a_1^2(t), a_2^2(t),\ldots , a_n^2(t)\}; \end{aligned}$$

(1)

the Lagrangian of this theory has the form

$$\begin{aligned} \mathcal{L} = R + \alpha \mathcal{L}_2 - 2\Lambda , \end{aligned}$$

(2)

where R is the Ricci scalar and $\mathcal{L}_2$,

$$\begin{aligned} \mathcal{L}_2 = R_{\mu \nu \alpha \beta } R^{\mu \nu \alpha \beta } - 4 R_{\mu \nu } R^{\mu \nu } + R^2 \end{aligned}$$

(3)

is the Gauss–Bonnet Lagrangian. Then substituting (1) into the Riemann $R_{\mu \nu \alpha \beta }$ and Ricci $R_{\mu \nu }$ tensors and the scalar in (2) and (3), and varying (2) with respect to the metric, we obtain the equations of motion,

$$\begin{aligned}&2 \left[ \sum \limits _{j\ne i} (\dot{H}_j + H_j^2) + \sum \limits _{\begin{array}{c} \{ k> l\} \\ \ne i \end{array}} H_k H_l \right] \nonumber \\&\quad + 8\alpha \left[ \sum \limits _{j\ne i} (\dot{H}_j + H_j^2) \sum \limits _{\begin{array}{c} \{k>l\} \\ \ne \{i, j\} \end{array}} H_k H_l + 3 \sum \limits _{\begin{array}{c} \{ k> l> \\ m > n\} \ne i \end{array}} H_k H_l H_m H_n \right] - \Lambda = 0\nonumber \\ \end{aligned}$$

(4)

as the ith dynamical equation. The first Lovelock term – the Einstein–Hilbert contribution – is in the first set of brackets and the second term – Gauss–Bonnet – is in the second set; $\alpha$ is the coupling constant for the Gauss–Bonnet contribution and we put the corresponding constant for Einstein–Hilbert contribution to unity. Also, since we consider spatially flat cosmological model, scale factors do not hold much in the physical sense and the equations are rewritten in terms of the Hubble parameters $H_i = \dot{a}_i(t)/a_i(t)$. Apart from the dynamical equations, we write down a constraint equation,

$$\begin{aligned} 2 \sum \limits _{i> j} H_i H_j + 24\alpha \sum \limits _{i> j> k > l} H_i H_j H_k H_l = \Lambda . \end{aligned}$$

(5)

As mentioned in the Introduction, we want to investigate the particular case with the scale factors split into two parts – separately three dimensions (three-dimensional isotropic subspace), which are supposed to represent our world, and the remaining represent the extra dimensions (D-dimensional isotropic subspace). So we put $H_1 = H_2 = H_3 = H$ and $H_4 = \cdots = H_{D+3} = h$ (D denotes the number of additional dimensions) and the equations take the following form: the dynamical equation that corresponds to H,

$$\begin{aligned}&2 \left[ 2 \dot{H} + 3H^2 + D\dot{h} + \displaystyle \frac{D(D+1)}{2} h^2 + 2DHh\right] \nonumber \\&\quad + 8\alpha \left[ 2\dot{H} \left( DHh + \displaystyle \frac{D(D-1)}{2}h^2 \right) \right. \nonumber \\&\quad \left. + D\dot{h} \left( H^2 + 2(D-1)Hh + \displaystyle \frac{(D-1)(D-2)}{2}h^2 \right) \right. \nonumber \\&\quad \left. + 2DH^3h + \displaystyle \frac{D(5D-3)}{2} H^2h^2 \right. \nonumber \\&\quad \left. + D^2(D-1) Hh^3 + \displaystyle \frac{(D+1)D(D-1)(D-2)}{8} h^4 \right] \nonumber \\&\quad -\Lambda =0, \end{aligned}$$

(6)

the dynamical equation that corresponds to h,

$$\begin{aligned}&2 \left[ 3 \dot{H} {+} 6H^2 {+} (D-1)\dot{h} {+} \displaystyle \frac{D(D-1)}{2} h^2 + 3(D{-}1)Hh\right] \nonumber \\&\quad + 8\alpha \Bigg [ 3\dot{H} \left( H^2 + 2(D-1)Hh \right. \nonumber \\&\quad \left. + \displaystyle \frac{(D-1)(D-2)}{2}h^2 \right) + (D-1){\dot{h}}\nonumber \\&\quad \times \left. \left( 3H^2 + 3(D-2)Hh + \displaystyle \frac{(D-2)(D-3)}{2}h^2 \right) + 3H^4 \right. \nonumber \\&\quad \left. + 9(D-1)H^3h + 3(D-1)(2D-3) H^2h^2\right. \nonumber \\&\quad \left. + \displaystyle \frac{3(D-1)^2 (D-2)}{2} Hh^3 \right. \nonumber \\&\quad + \displaystyle \frac{D(D-1)(D-2)(D-3)}{8} h^4\Bigg ] - \Lambda =0, \end{aligned}$$

(7)

and the constraint equation,

$$\begin{aligned}&2 \left[ 3H^2 + 3DHh + \displaystyle \frac{D(D-1)}{2} h^2 \right] \nonumber \\&\quad + 24\alpha \left[ DH^3h + \displaystyle \frac{3D(D-1)}{2}H^2h^2\right. \nonumber \\&\quad \left. + \displaystyle \frac{D(D-1)(D-2)}{2}Hh^3 \right. \nonumber \\&\left. \quad + \displaystyle \frac{D(D-1)(D-2)(D-3)}{24}h^4\right] = \Lambda . \end{aligned}$$

(8)

Looking at (6) and (7) one can see that for $D\ge 4$ the equations of motion contain the same terms, while for $D=\{1, 2, 3\}$ the terms are different (say, for $D=3$ terms with the $(D-3)$ multiplier are absent and so on) and the dynamics should be different also. As mentioned above, in this paper we are going to consider only the $\Lambda$-term case; the vacuum case we considered in the previous paper [60], while the general case with a perfect fluid with an arbitrary equation of state as well as the effect of curvature, is going to be considered in the papers to follow. As noted before, in this particular paper we consider the $D=3$ and general $D\ge 4$ cases – the low-dimensional $D=\{1, 2\}$ cases were considered in the previous paper [61].

3 $D=3$ case

In this case the equations of motion take the form (H-equation, h-equation, and constraint equation, respectively)

$$\begin{aligned}&4\dot{H} + 6H^2 + 6\dot{h} + 12h^2 + 12Hh + 8\alpha \nonumber \\&\times (6\dot{H}h (H + h) + 3\dot{h} (H^2 + h^2 + 4Hh) +18H^2h^2 \nonumber \\&+18Hh^3 + 3h^4 + 6H^3h) -\Lambda = 0, \end{aligned}$$

(9)

$$\begin{aligned}&6\dot{H} + 12H^2 + 4\dot{h} + 6h^2 + 12Hh + 8\alpha \nonumber \\&\quad \times ( 3\dot{H} (H^2 + 4Hh + h^2) + 6\dot{h} H (H+h) + 6Hh^3 \nonumber \\&\quad + 18H^2h^2 + 18H^3h + 3H^4 ) -\Lambda = 0, \end{aligned}$$

(10)

$$\begin{aligned} 6 H^2 + 18Hh + 6h^2 + 24\alpha (3H^3h {+} 9H^2h^2 {+} 3Hh^3 ) = \Lambda .\nonumber \\ \end{aligned}$$

(11)

From (8) one can clearly see that the constraint equation is always cubic with respect to H, but it could be linear, quadratic, cubic or quartic with respect to h in the cases $D=1$, $D=2$, $D=3$ and $D \ge 4$, respectively. In the previous paper, dedicated to the low-D case [61], we solved the constraint equation with respect to h. Since the current paper is dedicated to study $D=3$ and $D\ge 4$ cases, we solve the constraint with respect to H – by the way, in the paper dedicated to the vacuum case [60], we did exactly the same. Obviously, both choices – to solve the constraint with respect to h or H – give the same results but with different levels of complexity.

Fig. 1

H(h) graphs for the $D=3$ case: $\alpha < 0$, $\Lambda < 0$ on a; $\alpha < 0$, $\Lambda > 0$ with $\alpha \Lambda \ge -5/8$ on b and with $\alpha \Lambda < -5/8$ on c; $\alpha > 0$, $\Lambda < 0$ with $\alpha \Lambda > -1/8$ on d and with $\alpha \Lambda < -1/8$ on e; $\alpha > 0$, $\Lambda > 0$ on f. Different branches are presented by different linestyle/color combinations: $H_1$ by solid black line, $H_2$ by solid gray and $H_3$ by dashed gray (see the text for more details)

Solving (11) with respect to H gives us three roots, $H_1$, $H_2$, and $H_3$, whose expressions are too long to write them down here. Consideration of the discriminant of (11) (with respect to H) gives us two values for $\alpha \Lambda$ where the behavior qualitatively changes: $\alpha \Lambda = \{-5/8, -1/8\}$. We presented H(h) graphs in Fig. 1. On panels (a)–(c) we presented the results for $\alpha < 0$ and on (d)–(f) for the $\alpha > 0$ cases. In particular, panel (a) represents $\alpha < 0$, $\Lambda < 0$ case, panel (b) $\alpha < 0$, $\Lambda > 0$ with $\alpha \Lambda \ge -5/8$, and panel (c) $\alpha < 0$, $\Lambda > 0$ with $\alpha \Lambda < -5/8$. On the $\alpha > 0$ domain, panel (d) corresponds to $\Lambda < 0$ with $\alpha \Lambda > -1/8$, while panel (e) corresponds to $\alpha \Lambda < -1/8$. Finally, on panel (f) we presented H(h) for $\alpha > 0$, $\Lambda > 0$ case. Let us comment on these cases a bit.

From Fig. 1a we can see that, for $\alpha < 0$, $\Lambda < 0$ neither $H_1$ nor $H_2$ have $h\rightarrow 0$ asymptotes – only $H_3$ has. Thus both $H_1$ and $H_2$ have a limited domain of definition, while $H_3$ is defined everywhere except $h=0$, and it has a removable discontinuity at some $h > 0$. At this point the solution does not follow the branch, but “jumps” to another branch – from $H_3$ to $H_2$. Similarly the solution smoothly jumps from $H_1$ to $H_2$ at $h<0$, $H>0$ and from $H_3$ to $H_1$ at $h>0$, $H<0$. The case $\alpha < 0$, $\Lambda > 0$ with $\alpha \Lambda > -5/8$, presented in Fig. 1b, has all branches with finite or infinite limits at $h\rightarrow 0$, but all of them are directional: $\lim _{h\rightarrow 0+0} H \ne \lim _{h\rightarrow 0-0} H$. Also in this case all three branches are defined everywhere. Similarly to the previous case, we have solutions which change branches, while evolving – $H_1$ branch shifts to $H_3$ at $h=0$ and $H_2$ shifts to $H_1$ at the same point – we describe it further while discussing the regimes and their abundances. For $\alpha < 0$, $\Lambda > 0$ with the $\alpha \Lambda < -5/8$ case presented in Fig. 1c we again have finite or infinite limits at $h\rightarrow 0$; they also are directional and in this case the domain of definition is not entire $h \in \mathbb {R}$ for all branches; also we have more abundant changes between the branches.

In Fig. 1d–f we presented $\alpha > 0$ cases. Panel (d) corresponds to $\Lambda < 0$ with $\alpha \Lambda > -1/8$ while (e) – the same but with $\alpha \Lambda < -1/8$. One can see that the difference between these two is the existence of additional isolated regions of definition for the $H_1$ and $H_2$ branches. They give some additional regimes (and “redistributing” evolution between $H_2$ and $H_3$ for $h<0$) but since they are isolated, they cannot give rise to viable regimes – we will check this when describing regimes. Finally, in Fig. 1f we presented H(h) curves for $\alpha > 0$, $\Lambda > 0$ case. All these three cases also have their share of branch changing and while describing the actual regimes we pay close attention to these changes.

Looking at Fig. 1 we can make predictions for the existence of isotropic solutions – indeed, as isotropy requires $H=h$, we can tell from Fig. 1 that we have one isotropic solution for panels (a) and (f), two for panel (b) and no solutions for the rest of the panels.

Our analysis of the previous cases [60, 61] revealed that we may expect to encounter exponential solutions – isotropic and anisotropic. Below we find the condition for both kinds of exponential solutions to exist. Isotropic solutions are governed by the equation

$$\begin{aligned} 360\alpha H^4 + 30 H^2 - \Lambda = 0, \end{aligned}$$

(12)

and one can see that it is a biquadratic equation with respect to H. Thus for solutions to exist we need not only positivity of the discriminant, but also positivity of the roots. Then, skipping the derivation, we can see that for $\alpha > 0$, $\Lambda < 0$ there are no isotropic solutions, for $\alpha > 0$, $\Lambda > 0$ as well as for $\alpha < 0$, $\Lambda < 0$ there is one, and for $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda < -5/8$ there are no solutions, while for $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda > -5/8$ there are two.

The existence of anisotropic exponential solutions is governed by the following equation:

$$\begin{aligned}&20736 \xi ^4 - 17280 \xi ^3 + (4032\zeta + 2736)\xi ^2 \nonumber \\&\quad - (528\zeta + 216)\xi + (4\zeta ^2 + 12\zeta + 9) = 0, \end{aligned}$$

(13)

where $\xi = \alpha h^2$ and $\zeta = \alpha \Lambda$. Its discriminant $\Delta = 328683126924509184 (8\zeta + 5) (8\zeta - 3) (2\zeta - 1)^4$ clearly gives us values for $\zeta$ which separate regions with different root numbers. Thus for $\zeta < \zeta _1 = -5/8$ we have four roots – two for $\xi < 0$ (and so $\alpha < 0$ since $\xi = \alpha h^2$) and two for $\xi > 0$. At $\zeta = \zeta _1$ negative roots coincide and for $0> \zeta > \zeta _1$ they disappear, while positive roots remain. For positive $0< \zeta < \zeta _2 = 3/8$ we have two positive roots, for $\zeta = \zeta _2$ its number increases to three and for $\zeta _2< \zeta < \zeta _3 = 1/2$ it further increases to four. At $\zeta = \zeta _3$ it reduces to two and finally for $\zeta > \zeta _3$ they disappear – so that for $\zeta > \zeta _3 = 1/2$ there are no anisotropic exponential solutions; the same situation we have in the case of the $D=2$ $\Lambda$-term [61].

Fig. 2

$\dot{h}(h)$ (black) and $\dot{H}(h)$ (gray) curves for $\alpha < 0$ $D=3$ $\Lambda$-term cases: $\Lambda < 0$ on a–c – $H_1$ branch on a, $H_2$ branch on b and $H_3$ branch on c; $\Lambda > 0$ with $\alpha \Lambda \ge -5/8$ on d–f – $H_1$ branch on d, $H_2$ branch on e and $H_3$ branch on f; $\Lambda > 0$ with $\alpha \Lambda < -5/8$ on g–i – $H_2$ on all three panels – large scale on g and detailed features for $h<0$ on h and for $h>0$ on i (see the text for more details)

Fig. 3

$\dot{h}(h)$ (black) and $\dot{H}(h)$ (gray) curves for $\alpha > 0$, $\Lambda < 0$ $D=3$ $\Lambda$-term cases: $\zeta \le \zeta _{cr}$ on a–c and $\zeta > \zeta _{cr}$ on d–f. On a and d we presented the $H_1$ branch, on b and e – $H_2$ and on c and f – $H_3$ (see the text for more details)

Fig. 4

$\dot{h}(h)$ (black) and $\dot{H}(h)$ (gray) curves for $\alpha > 0$, $\Lambda > 0$ $D=3$ $\Lambda$-term cases: $H_1$ on a and $H_2$ on the remaining: $\alpha \Lambda < 3/8$ on b, detail of $\alpha \Lambda = 3/8$ on c, the same detail for $1/2> \alpha \Lambda > 3/8$ on d, $\alpha \Lambda = 1/2$ on e and $\alpha \Lambda > 1/2$ on f (see the text for more details)

Before describing the resulting $\dot{h}(h)$ and $\dot{H}(h)$ graphs and the regimes, let us make a note on definitions. They are similar to those we used in previous papers [60, 61]: we denote power-law regimes with $K_i$ and the index i corresponds to the sum of Kasner exponents $\sum p$: $\sum p=1$ for GR ($K_1$) and $\sum p=3$ for GB ($K_3$). In this study we do not have $K_1$ for reasons discussed in [61]; formally we should not have $K_3$ either but in the GB regime $H_i \ggg \Lambda$, so we can treat the $\Lambda$-term regime as asymptotically flat (see [61] for details). Apart from the power-law solutions we could have exponential solutions – we denote them as E with indices indicating their features – say, $E_\mathrm{iso}$ is an isotropic exponential solution; if there are two different isotropic exponential solutions, we denote them as $E_\mathrm{iso}^1$ and $E_\mathrm{iso}^2$. Anisotropic exponential solutions are denoted just as E and the indices enumerate the solutions (e.g., $E_1$, $E_2$ etc.).

For the further analysis we solve (9)–(10) with respect to $\dot{h}$ and $\dot{H}$ and substitute the $H_i(h)$ branches into them; as a result we have three $\dot{h}_i(h)$ and $\dot{H}_i(h)$ curves which correspond to three branches. The expressions for $\dot{h}_i(h)$ and $\dot{H}_i(h)$ are too lengthy so we do not write them down but present them in Figs. 2, 3 and 4 for different cases.

In Fig. 2 we presented $\dot{h}(h)$ (in black) and $\dot{H}(h)$ (in gray) curves for $\alpha < 0$ $D=3$ $\Lambda$-term cases: $\Lambda < 0$ on panels (a)–(c) – $H_1$ branch on (a), $H_2$ branch on (b) and $H_3$ branch on (c); $\Lambda > 0$ with $\alpha \Lambda \ge -5/8$ on panels (d)–(f) – $H_1$ branch on (d), $H_2$ branch on (e) and $H_3$ branch on (f); $\Lambda > 0$ with $\alpha \Lambda < -5/8$ on panels (g)–(i) – $H_2$ on all three panels – large scale on panel (g) and detailed features for $h<0$ and for $h>0$ on panels (h) and (i).

But before investigating individual regimes, let us note on how to read the H(h) and $\dot{h}(h)$, $\dot{H}(h)$ graphs together. As we will see further, all the regimes are divided into two groups – those existing within the same branch and those with “jumps” between the branches. The former of them are quite easy to describe – let us consider, for instance, the $h < 0$ regime at the $H_3$ branch in $\alpha < 0$, $\Lambda < 0$ case. In this case H(h) is presented as a gray dashed line in the third quadrant of Fig. 1a – one can check that it is valid for $h\in (-\infty , 0)$. The corresponding $\dot{h}(h)$ and $\dot{H}(h)$ graphs are presented in Fig. 2c (again, $h<0$ region). With use of a Kasner exponents analysis (as in [60, 61]) we can prove that the asymptote behavior is $K_3$ at $h\rightarrow -\infty$ and $K_3$ at $h\rightarrow 0-0$, but these $K_3$ are a bit different (see below) and an exponential solution (isotropic, since the H(h) curve crosses $H=h$ in that point), which gives us $E_\mathrm{iso} \rightarrow K_3$ as a sole regime ¹. As a good example of the latter group – with evolutionary curves experiencing “jumps” from one branch to another, we can consider the $h > 0$ regime at $H_3$ and $H_2$ branches in $\alpha < 0$, $\Lambda < 0$ case. In this case the H(h) is presented as gray dashed and solid gray lines in the first quadrant of Fig. 1a. One can see that at some $h = h_\mathrm{div}> 0$ the $H_3$ branch “jumps” from $H > 0$ to $H < 0$. Physically there are no jumps, it is just the description of the evolutionary curve switching from $H_3$ to $H_2$ (the connection between dashed gray and solid gray lines in the first quadrant of Fig. 1a). Thus the physical evolution in this case is governed by the $H_3$ branch for $0 < h \le h_\mathrm{div}$ and by $H_2$ for $h \ge h_\mathrm{div}$. Then the $\dot{h}(h)$ and $\dot{H}(h)$ curves should be taken from $h>0$ part of Fig. 2b for $h \ge h_\mathrm{div}$, which corresponds to the $H_2$ branch and from the $h>0$ part of Fig. 2c for $0 < h \le h_\mathrm{div}$, which corresponds to the $H_3$ branch, and “glue” them together. The resulting $\dot{h}(h)$ and $\dot{H}(h)$ are similar (with mirror symmetry) to the previous case and so the regime is $K_3 \rightarrow E_\mathrm{iso}$ (again, different $K_3$ for $h\rightarrow 0+0$ and for $h\rightarrow +\infty$) – the regimes also have mirror symmetry (time reversal) with respect to those in the previous case. The described above scheme is used in all cases with “regime jumps”, considered below.

First let us describe $\alpha < 0$, $\Lambda < 0$ regimes – $H_1$ branch (see Fig. 2a) for $h < 0$ has $K_3$ as past asymptote and switch to $H_2$ in future with another $K_3$ asymptote (see Fig. 1a). A similar situation is with $h>0$ – there the $H_1$ branch describes a future $K_3$ asymptote and the past is $K_3$ from the $H_3$ branch. Another branch, $H_2$, is presented in Fig. 2b, and for $h<0$ it is complementary for the $H_1$ branch – they form $K_3 \rightarrow K_3$ transition. For $h>0$ this branch has an isotropic exponential solution as a future attractor and $K_3$ as a past attractor; the additional past attractor is another $K_3$ from $H_3$. Finally the $H_3$ branch, presented in Fig. 2c, is smooth in ($h<0$, $H<0$) and has two parts in $h>0$ – one part with $H>0$ and another with $H<0$ (see Fig. 1a). So for $h<0$ we have two regimes $E_\mathrm{iso} \rightarrow K_3$ but with two different $K_3$ – one at $h\rightarrow 0$ and another at $h\rightarrow -\infty$. For $h>0$, the part with $H<0$ serves as a past $K_3$ asymptote for the $K_3\rightarrow K_3$ transition from $H_3$ to $H_1$, while the $H>0$ part is one of the past $K_3$ asymptotes for an isotropic exponential solution from $H_2$. To summarize, in the $\alpha < 0$, $\Lambda < 0$ case there are no viable regimes – we have only $K_3\rightarrow K_3$ and $K_3 \leftrightarrow E_\mathrm{iso}$.

The second case, $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \ge -5/8$, is presented in Figs. 2d–f and 1b. The first branch, $H_1$, is presented in Fig. 2d. One can see that both parts – $h<0$ and $h>0$ – have $K_3$ at $h\rightarrow \pm \infty$ and shift to other branches at $h=0$. One also cannot miss that $H_2$ (Fig. 2e) and $H_3$ (Fig. 2f) branches have “mirror symmetry” with respect to $h=0$. One can see that there are two exponential solutions, both of them are isotropic, we denote the solution at smaller |h| as $E_\mathrm{iso}^1$ and at larger |h| as $E_\mathrm{iso}^2$. Thus $H_2$ in $h<0$ domain has $E_\mathrm{iso}^1$ as a past asymptote and $K_3$ as a future (another future $K_3$ asymptote is on the $H_1$ branch). In the $h>0$ domain the $H_2$ branch has $E_\mathrm{iso}^2$ as a future asymptote and two different $K_3$ – for $h\rightarrow 0$ and $h\rightarrow +\infty$. The description for $H_3$ is similar to the description of $H_2$ with the above-mentioned “mirror symmetry” kept in mind – $E_\mathrm{iso}^1$ is replaced with $E_\mathrm{iso}^2$ and vice versa, the past asymptote with the future one and vice versa and so on. To summarize, in this case of $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \ge -5/8$ we also do not have viable regimes – we have two different isotropic exponential solutions and different $K_3$ as both past and future asymptotes. Let us note that as $\alpha \Lambda$ decreases, the separation between $E_\mathrm{iso}^1$ and $E_\mathrm{iso}^2$ reduces as well, so for $\alpha \Lambda = -5/8$ the two isotropic exponential solutions coincide.

With further decrease of $\alpha \Lambda$ – for $\alpha \Lambda < -5/8$ – the situation changes and the corresponding H(h) curves are presented in Fig. 1c. The $H_1$ branch looks exactly the same as in the previous case, Fig. 2d, and so do the regimes – $K_3$ as a past asymptote for $h<0$ and future asymptote for $h>0$ and a transition to another branch at $h=0$. Another branch, $H_2$, is presented in Fig. 2g–i – large scale on panel (g) and two detailed exponential solutions – for $h<0$ on (h) and for $h>0$ on (i). So for $h<0$ on the “outer” part we have $K_3$ as a past asymptote after branch changing, $h<0$, the “inner” part has an anisotropic exponential solution $E_1$ as a past asymptote and branch changing at $h=0$ and at some $h_1< 0$. The regimes for $h>0$ include $K_3$ as a past asymptote and regime changing at some $h_1>0$, and an anisotropic exponential solution $E_2$ as a future asymptote with $K_3$ and branch switching at some $h_0 > 0$. The final branch, $H_3$, has the same “mirror symmetry” as described above so all the regimes could be obtained from the description of $H_2$ with appropriate replacements, similar to the procedure for $H_2$ ($h\rightarrow -h$, $H\rightarrow -H$, past $\rightarrow$ future etc.). Combined analysis shows that in this case there are no isotropic exponential solutions but there are anisotropic ones. But all of them have $H>0$, $h>0$ (so both three- and extra-dimensional spaces are expanding), and for that reason we cannot call them viable.

Our analysis continues with the $\alpha > 0$ cases and we start with $\Lambda < 0$ presented in Fig. 3. On the upper row we presented $\zeta \le \zeta _{cr}$ ($\alpha \Lambda \le -1/8$), while on the bottom row we have $\zeta > \zeta _{cr}$. On panels (a) and (d) we presented $H_1$ branch, on (b) and (e) – $H_2$ and on (c) and (f) – $H_3$. Comparing with panels (e) and (f) from Fig. 1, we can see the difference between these two cases – for $\zeta > \zeta _{cr}$ we have two additional singular regimes. So for $H_1$ we have $K_3$ as a future (for $h<0$) or past (for $h>0$) asymptote of another regime and for $\zeta > \zeta _{cr}$ we additionally have an $nS\rightarrow nS$ transition with part of this transition happening on the $H_3$ (for $h<0$) and $H_2$ (for $h>0$) branches. For $H_2$ we have $K_3$ as a past asymptote for $h<0$ and anisotropic exponential solution $E_2$ as a future asymptote for $h>0$. In addition for $\zeta > \zeta _{cr}$ we have a part of the $nS\rightarrow nS$ transition for $h>0$ and another anisotropic exponential solution $E_1$ (future asymptote) is shifted from $H_3$ to $H_2$ for $h<0$. Finally for $H_3$ we have an anisotropic exponential solution $E_2$ as a past asymptote and anisotropic exponential solution $E_1$ as a future asymptote for $h<0$ and an anisotropic exponential solution $E_1$ as a past asymptote for $h>0$. For $\zeta > \zeta _{cr}$ the anisotropic exponential solution $E_1$ is shifted to $H_2$ and an additional part of the $nS\rightarrow nS$ transition is introduced. In this case of $\alpha > 0$, $\Lambda < 0$ we have viable $K_3 \rightarrow E_{1, 2}$ regimes (transition from Gauss–Bonnet Kasner regime to anisotropic exponential expansion) and they occur regardless of $\alpha \Lambda \le -1/8$ or $\alpha \Lambda > -1/8$.

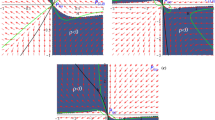
The final case to consider is $\alpha > 0$, $\Lambda > 0$, which is presented in Fig. 4. On panel (a) we presented the behavior of $H_1$ and it remains the same for all values of $\alpha \Lambda$ for this case. We can see that there is an isotropic exponential solution as a past asymptote and $K_3$ as a future asymptote for $h<0$ and opposite behavior – future asymptote for isotropic solution and past for $K_3$ – for $h>0$. Both halves change the branch at $h=0$. On the remaining panels of Fig. 4 we presented the behavior for $H_2$. On panel (b) we presented the behavior for $\alpha \Lambda < 3/8$: on the outermost part of $h<0$ one can see an anisotropic exponential solution $E_1$ as a future asymptote and $K_3$ and nS as past asymptotes on $h\rightarrow -\infty$ and the boundary of the region, respectively. On the innermost part of $h<0$ we can see $K_3$ as a past asymptote and branch change on the boundary. The innermost part of $h>0$ have branch changes on both $h=0$ and on the boundary. This way for $H_2$ we have $K_3$ for $h\rightarrow 0-0$ but no regime for $h\rightarrow 0+0$ (since it is a branch change), so $K_3$ is reached directionally. Finally, the outermost part of $h>0$ demonstrates the $nS\rightarrow nS$ transition and then $nS\rightarrow E_2$ and $K_3 \rightarrow E_2$, with growth of h. With increase of $\alpha \Lambda$ the area between two nonstandard singularities begins to change – both $\dot{h}(h)$ and $\dot{H}(h)$ increase and at $\alpha \Lambda = 3/8$ they “touch” zero, as depicted in Fig. 4c. This creates an anisotropic exponential solution $E_{3, 4}$ which is a past asymptote for one of nonstandard singularities and the future asymptote – for another. With further increase of $1/2> \alpha \Lambda > 3/8$ the $\dot{h}(h)$ and $\dot{H}(h)$ curves further increase and form two anisotropic exponential solutions $E_3$ and $E_4$, adding an exotic $E_3 \rightarrow E_4$ transition to the described above picture (see Fig. 4d). Finally at $\alpha \Lambda = 1/2$, which is presented in Fig. 4e, drastic changes occur – an anisotropic exponential solution $E_1$ from $h<0$ and nonstandard singularities from $h>0$ disappear, leaving us with the $E_3 \rightarrow E_4$ and $K_3 \rightarrow E_4$ regimes. At $\alpha \Lambda > 1/2$ both singularities are back, while anisotropic exponential solutions disappear, leaving us with $nS\rightarrow nS$ and $K_3 \rightarrow nS$. Thus in the case of $\alpha > 0$, $\Lambda > 0$ we have two viable regimes for $\alpha \Lambda < 1/2$ ($K_3 \rightarrow E_1$ at $h<0$ and $K_3 \rightarrow E_2$ at $h>0$ ²), one viable regime for $\alpha \Lambda = 1/2$ ($K_3 \rightarrow E_2$) and no viable regimes for $\alpha \Lambda > 1/2$. Let us note that this is quite similar to what we saw in the $D=2$ case [61].

The $H_3$ branch is symmetric (in the above sense) to $H_2$ – past and future asymptotes are interchanged as well as the signs for H and h and so on, so we are not giving a separate description of $H_3$ regimes. Also due to this symmetry, all anisotropic exponential solutions of $H_3$ are past asymptotes so it does not give rise to any viable regimes.

It is also useful to provide an analysis in $\{p_\mathrm{H}, p_\mathrm{h}\}$ coordinates – in Kasner exponents space. They are defined by $p_\mathrm{H} = - H^2/\dot{H}$ and $p_\mathrm{h} = - h^2/\dot{h}$, so we substitute the expressions for $\dot{H}(h)$ and $\dot{h}(h)$ as well as H(h) for the individual branch and obtain the expression for the Kasner exponents. Again, they are very large so we do not write them down but perform an analysis of all regimes in $\{p_\mathrm{H}, p_\mathrm{h}\}$ coordinates – the same as what we have done in [60, 61]. The analysis proved that we properly described all the regimes and that at $h\rightarrow \pm \infty$ (and some of $h\rightarrow 0$ – which we claimed during the description) are really Gauss–Bonnet Kasner regimes. We provide the limiting values for $p_\mathrm{h}$ and $p_\mathrm{H}$ in Table 1. There we use the following notations for two particular values of Kasner exponents: $p_1 = (34\sqrt{5} - 76)/(123 - 55\sqrt{5}) \approx 1.618$ and $p_2 = -(34\sqrt{5} + 76)/(123 + 55\sqrt{5}) \approx -0.618$.

We already mentioned the “mirror symmetry” between the $H_2$ and $H_3$ branches – we often detected it while describing $\dot{h}(h)$ and $\dot{H}(h)$ and the regimes. One can see from Fig. 1 that H(h) curves also have a certain symmetry – with just $h>0$ or $H>0$ half the entire picture could be recovered. For this reason, when collecting regimes for the $\alpha < 0$ cases, we limit ourselves just to the $H>0$ regimes. This way we discard contracting isotropic regimes and only the expanding regimes remain; discarded regimes are “time-reversed” compared with the remaining ones. For $\alpha > 0$ we keep only regimes which involve stable (future asymptote) exponential solutions, as their unstable counterparts (past asymptotes) could be retrieved just by “time-reversal”.

Table 1 Summary of $D=3$ power-law $\Lambda$-term regimes

Table 2 Summary of nontrivial $D=3$ $\alpha < 0$ $\Lambda$-term regimes

Table 3 Summary of nontrivial $D=3$ $\alpha > 0$ $\Lambda$-term regimes

So we summarize the regimes in Tables 2 and 3. Apart from what we just mentioned about the regimes presented and regimes skipped, we also skip all ranges for h which lies outside the domain of definition for H(h) curves in Fig. 1. In Table 2 we present the regimes for $\alpha < 0$. One can see that, for both $\Lambda < 0$ and $\Lambda >0$, $\alpha \Lambda \ge -5/8$, there are only two regimes – $K_3 \rightarrow K_3$, and $K_3 \rightarrow E_\mathrm{iso}$, and none of them is viable. For $\alpha \Lambda < -5/8$ we have two anisotropic exponential regimes, but both of them at large $\alpha \Lambda$ have $H>0$ and $h>0$, so both three-dimensional and extra-dimensional parts are expanding, which could violate the observations, so we cannot call them viable (at least, they are definitely less viable than those with contracting extra dimensions). But at $\alpha \Lambda = -3/2$ the situation changes – for $E_1$ we have $h=0$ with $H>0$, while for $E_2$ we have $H=0$ with $h>0$. With further decrease of $\alpha \Lambda < -3/2$ we have $h<0$ with $H>0$ for $E_1$ and $h>0$ with $H<0$ for $E_2$. Since in the $D=3$ case both spaces are three-dimensional, it is unimportant which one is expanding while the other is contracting – we call the expanding one “our Universe” and the contracting one has the extra dimensions, so for $\alpha \Lambda < -3/2$ we have two viable regimes. Let us finally note that this case is similar to $D=2$ [61].

For $\alpha > 0$ (see Table 3) we also report viable regimes. There we two of them: $K_3 \rightarrow E_1$ and $K_3 \rightarrow E_2$ for $\Lambda < 0$, the same two regimes for $\alpha > 0$, $\alpha \Lambda < 1/2$ and only one $K_3 \rightarrow E_2$ for $\alpha \Lambda = 1/2$. For $\alpha \Lambda > 1/2$ there are no viable regimes anymore.

4 General $D\ge 4$ case

In this case we use the general equations (6)–(8). The procedure is exactly the same as in the previous section – we solve the constraint equation (8) with respect to H and obtain three branches $H_1$, $H_2$, and $H_3$, then solve the dynamical equations (6)–(7) with respect to $\dot{h}$ and $\dot{H}$ and substitute the individual branches to get $\dot{h}_i$ and $\dot{H}_i$ for each branch.

The expressions for $H_i(h)$ are lengthy so we do not write them down, but we provide the results for the analysis. If we analyze the discriminant of (8) with respect to H and then the discriminant of the resulting equation with respect to $h^2$ (exactly as in the previous section), we obtain the critical values for $\zeta = \alpha \Lambda$:

$$\begin{aligned} \zeta _1= & {} - \displaystyle \frac{(D+2)(D+3)}{4D(D+1)},\nonumber \\ \zeta _2= & {} \displaystyle \frac{\root 3 \of {\mathcal {D}_2 (D-1)^2}}{12(D-2)(D-1)D(D+1)} \nonumber \\&+ \displaystyle \frac{(D^6 - 6D^5 {+} 10D^4 - 20D^2 + 24D {+} 36)(D{-}1)}{3D(D-2)(D{+}1)\root 3 \of {\mathcal {D}_2 (D-1)^2}}\nonumber \\&+ \displaystyle \frac{D^3 - 9D^2 + 8D + 24}{12D(D-2)(D+1)},~\text{ where } \nonumber \\ \mathcal {D}_2= & {} 10D^{10} + 6D^9 \mathcal {D}_1 - 100D^9 - 30D^8 \mathcal {D}_1\nonumber \\&+ 330 D^8 + 30D^7 \mathcal {D}_1 - 240 D^7 + 54D^6 \mathcal {D}_1 \nonumber \\&- 600D^6 - 84D^5 \mathcal {D}_1 + 240D^5 - 24D^4 \mathcal {D}_1\nonumber \\&+ 1520D^4 + 48D^3 \mathcal {D}_1 + 640 D^3 \nonumber \\&- 2880D^2 + 1728~\text{ and }~\nonumber \\ \mathcal {D}_1= & {} \displaystyle \frac{(D-4)(D-3)(D+2)}{(D-1)(D+1)}\sqrt{\displaystyle \frac{(D-4)(D+2)}{D(D-2)}}. \end{aligned}$$

(14)

Additionally, for $\alpha < 0$, $\Lambda > 0$ there are two domains – in one of them the resulting curves intersect $H=0$, while in the other they do not and these domains are separated by

$$\begin{aligned} \zeta _3 = - \displaystyle \frac{D(D-1)}{4(D-2)(D-3)}. \end{aligned}$$

(15)

The resulting $H_i(h)$ curves in most of the cases resemble those from $D=3$ case. This happening for entire $\alpha < 0$ domain with different $\zeta _1$ for $D=3$ (where $\zeta _1 = -5/8$) and $D\ge 4$ cases, so the actual $H_i(h)$ curves for this case are presented in Fig. 1a–c. The only difference between the $D=3$ and $D\ge 4$ cases is that for the latter there is an additional regime presented in Fig. 5a for $\alpha \Lambda < \zeta _3$. One can see that in the $D=3$ case the $H_i(h)$ curves always cross the $H=0$ axis, while in the general $D\ge 4$ case it is no longer the case (compare Fig. 1c with Fig. 5a). But, as we will state later, this does not affect the actual regimes – the difference is that the corresponding exponential solution “moves” from ($H>0$, $h>0$) to ($H<0$, $h>0$), but since both of them are non-realistic, this additional case with $\alpha \Lambda < \zeta _3$ does not affect the results.

For $\alpha > 0$ there are differences between these two cases – the value for $\zeta _2$, which separates the regimes, is negative for $D=3$ and positive for $D\ge 4$, so the differences also “moved” from $\Lambda < 0$ in $D=3$ to $\Lambda > 0$ in $D\ge 4$. So the general $D\ge 4$ case with $\alpha > 0$, $\Lambda < 0$ looks exactly like $D=3$ $\alpha > 0$, $\Lambda < 0$ with $\alpha \Lambda > -1/8$, presented in Fig. 1d; the situation presented in Fig. 1e does not appear in the general $D\ge 4$ case. Finally, due to the above mentioned shift of $\zeta _2$ into the positive $\Lambda$ domain, we additionally have a regime for $\alpha > 0$, $\Lambda > 0$, $\alpha \Lambda < \zeta _2$, presented in Fig. 5b; for $\alpha \Lambda \ge \zeta _2$ the situation looks exactly like in Fig. 1f.

Let us also note that $\zeta _2$ is a growing function of D and

$$\begin{aligned} \lim \limits _{D\rightarrow \infty } \zeta _2 = \displaystyle \frac{\root 3 \of {16}}{12} + \displaystyle \frac{\root 3 \of {256}}{48} + \displaystyle \frac{1}{12} \approx 0.4256. \end{aligned}$$

(16)

Fig. 5

Additional H(h) graphs for the $D\ge 4$ case: $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda < \zeta _3$ in a and $\alpha > 0$, $\Lambda > 0$, $\alpha \Lambda < \zeta _2$ in b. Different branches presented by different linestyle/color combinations: $H_1$ by solid black line, $H_2$ by solid gray and $H_3$ by dashed gray (see the text for more details)

One can see that on the (a), (e), and (f) panels of Fig. 1 we have one isotropic solution ($H=h$), on (c) two and on (b) and (d) no isotropic solutions. There is a theoretical explanation: isotropic exponential solutions are governed by the equation

$$\begin{aligned}&D(D+1)(D+2)(D+3)\alpha H^4 \nonumber \\&\quad + (D+2)(D+3) H^2 - \Lambda = 0, \end{aligned}$$

(17)

and one can see that it is a biquadratic equation with respect to H. Thus for solutions to exist we need not only positivity of the discriminant, but positivity of the roots. Then, skipping the derivation, we can see that for $\alpha > 0$, $\Lambda < 0$ there are no isotropic solutions, for $\alpha > 0$, $\Lambda > 0$ as well as for $\alpha < 0$, $\Lambda < 0$ there is one, and for $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda < \zeta _1$ there are no solutions, while for $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda > \zeta _1$ there are two. In this regard, the scheme is quite the same as in the $D=3$ case.

The existence of anisotropic exponential solutions is governed by the following equation:

$$\begin{aligned}&D^2 (D+1) (D-1)^2 (D-2) (4D^2 + 60D - 72)\xi ^4\nonumber \\&\quad - D (D-1)^2 (40D^3 + 40D^2 + 96D - 288) \xi ^3 \nonumber \\&\quad + [ D(D-1)(136 D^2 - 200D + 48)\zeta + (D-1)\nonumber \\&\quad \times (16D^3 + 128D^2 - 24D - 144)] \xi ^2 \nonumber \\&\quad - [ (104 D^2 - 152D + 48)\zeta + 12(D-2)(D-3)]\xi \nonumber \\&\quad + (4\zeta ^2 + 12\zeta + 9) = 0, \end{aligned}$$

(18)

where, as usual, $\xi = \alpha h^2$ and $\zeta = \alpha \Lambda$. If we consider and solve the discriminant of (18) (we are not writing it down for it is a 19th order polynomial in D), the solutions are

$$\begin{aligned} \zeta _4= & {} \displaystyle \frac{1}{2} \displaystyle \frac{D^2 - 4D + 6}{D(D-2)},\quad \zeta _1,~\zeta _5 = \displaystyle \frac{3}{4} \displaystyle \frac{D(D+3)}{D^2 + 15D - 18},\nonumber \\ \zeta _6= & {} \displaystyle \frac{1}{4} \displaystyle \frac{3D^2 - 7D + 6}{D(D-1)}, \end{aligned}$$

(19)

where $\zeta _6$ is triple root and $\zeta _1$ is the same as in (14). One can note that for $D<6$ $\zeta _4 > \zeta _5$ while for $D>6$ $\zeta _4 < \zeta _5$ and for $D=6$ they coincide. So that $D=6$ is special case and its dynamics could be a bit different – we comment on it further. Finally let us find $D\rightarrow \infty$ limits: $\lim \limits _{D\rightarrow \infty } \zeta _4 = 1/2$, $\lim \limits _{D\rightarrow \infty } \zeta _1 = -1/4$, $\lim \limits _{D\rightarrow \infty } \zeta _5 = 3/4$, $\lim \limits _{D\rightarrow \infty } \zeta _6 = 3/4$, but always $\zeta _6 > \zeta _5$.

The expressions for $\dot{h}(h)$ and $\dot{H}(h)$ are also lengthy so we will not write them down. When describing $H_i$ curves we mentioned that most of the cases coincide with those in $D=3$ case; the same is true for the regimes. The $\alpha < 0$, $\Lambda < 0$ regimes are exactly the same as in the $D=3$ case. The next regimes, $\alpha < 0$, $\Lambda > 0$ at $\zeta \equiv \alpha \Lambda \ge \zeta _1$, are the same as in the case $D=3$ $\alpha \Lambda \ge -5/8$, and at $\zeta _1 < \zeta$ the regimes are the same as in the case $D=3$, $\alpha \Lambda < -5/8$. One can see that the H(h) curves differ starting from $\zeta < \zeta _3$, but this does not change the regimes – indeed, for both subcases we have the same anisotropic exponential solution $E_2$, but for $\zeta > \zeta _3$ it has $H > 0$, while for $\zeta < \zeta _3$ it has $H < 0$. But since this solution has $h > H$, it is not viable for both these cases. Thus, despite the differences in the H(h) curves, the regimes for $\alpha < 0$ are the same as in the $D=3$ case and the only viable one is the $K_3 \rightarrow E_1$ transition if $\alpha \Lambda \le -3/2$ is fulfilled.

Now let us turn our attention to $\alpha > 0$ regimes. For $\Lambda < 0$ the H(h) curves and the regimes are the same as in $D=3$ case with $\alpha \Lambda < -1/8$. The $\alpha \Lambda > -1/8$ counterpart from $D=3$ does not exist in the general $D \ge 4$ case, as the separation $\zeta \equiv \alpha \Lambda$ value “moved” from negative values ($-1/8$ for $D=3$) to positive $\zeta _2$ from (14). Since the regimes are the same, the viable regime $K_3 \rightarrow E_1$ is also present in the $D \ge 4$ case for the entire $\Lambda < 0$ range. Finally, the case $\alpha > 0$, $\Lambda > 0$ exhibits the most interesting dynamics, similar to the $D=3$ case. First of all, due to the differences in the H(h) structure, for $\zeta < \zeta _2$ (see Fig. 5a) the $E_1$ anisotropic exponential solution has two $K_3$ regimes which lead to it, making the entire $h < 0$ range leading to viable compactification in $E_1$. For $\zeta \ge \zeta _2$ the situation is the same as in $D=3$ case – only $h < h_{e1}$ leads to a $K_3 \rightarrow E_1$ transition. The second difference is in the “fine structure” of the additional exponential solutions. First it was described in $D=2$ and they appear in the $15/32 \le \zeta \le 1/2$ range [61], for $D=3$ they appear in the $3/8 \le \zeta \le 1/2$ range and for the $D \ge 4$ case they appear for $\min \{\zeta _4, \zeta _5\} \le \zeta \le \zeta _6$. By now we skip the description of the fine structure of these solutions and address it in the Discussions section. The realistic regimes in the general case are the same as in $D=3$ – it is $K_3 \rightarrow E_1$ from $H_2$ branch in the $H>0$, $h<0$ quadrant, and it is manifest if $\alpha \Lambda \le \zeta _6$.

Thus the dynamics of the general $D \ge 4$ case is very similar to the $D=3$ one and the regimes are the same. The only differences are in the details of the solutions (like in $\alpha < 0$, $\Lambda > 0$ case) and the ranges, with the former affecting only non-realistic regimes. We can say that the regimes are the same as in the $D=3$ case and these can be seen in Tables 2 and 3. The realistic compactification regimes exist for $\alpha < 0$, $\Lambda > 0$ with $\alpha \Lambda \le -3/2$ and $\alpha > 0$ with $\alpha \Lambda \le \zeta _6$, including entirely the range $\Lambda < 0$.

5 Discussions

In this paper we investigated the existence and abundance of different regimes in the $D=3$ and general $D \ge 4$ cases with $\Lambda$-term. Particular attention is paid to the solution which allows for dynamical compactification. Similar to the previously considered low-dimensional ($D=1, 2$) $\Lambda$-term cases [61], the only viable dynamics is the transition from high-energy Kasner regime to anisotropic exponential regime with expanding three-dimensional space (“our Universe”) and contracting extra-dimensional space. The majority of the non-viable regimes have a nonstandard singularity as either future or past asymptote, and it is defined as follows. As we can see from the equations of motion (4), they are nonlinear with respect to the highest derivative,³ so formally we can solve them with respect to it. Then the highest derivative is expressed as a ratio of two polynomials, both depending on H. And there could be a situation when the denominator of this expression is equal to zero, while the numerator is not. In this case $\dot{H}$ diverges while H is (generally) non-zero and regular. In our study we saw nonstandard singularities with divergent $\dot{h}$ or both $\dot{h}$ and $\dot{H}$ at non-zero or sometimes zeroth H. This kind of singularity is “weak” by Tipler’s classification [69], and “type II” in the classification by Kitaura and Wheeler [70, 71]. Recent studies of the singularities of this kind in the cosmological context in Lovelock and Einstein–Gauss–Bonnet gravity demonstrate [27, 49, 50, 52, 54] that their presence is not suppressed and they are abundant for a wide range of initial conditions and parameters and sometimes [50] they are the only option for future behavior.

Below we summarize our findings for $D=3$ and general $D \ge 4$ $\Lambda$-term cases and discuss the general results for the $\Lambda$-term case (with [61] taken into account).

The first case to consider, $D=3$, demonstrates two viable regimes $K_3 \rightarrow E_{1, 2}$ for $\alpha < 0$, $\Lambda > 0$ and $\alpha \Lambda \le -3/2$ (see Table 2) and two more regimes $K_3 \rightarrow E_{1, 2}$ for $\alpha > 0$, $\alpha \Lambda \le 1/2$, including $\Lambda < 0$ (see Table 3). The former of them in the $\alpha \Lambda = -3/2$ limiting case have either $h=0$ (for $E_1$) or $H=0$ (for $E_2$); the latter in the limiting case $\alpha \Lambda = 1/2$ have only the $K_3 \rightarrow E_2$ transition.

The second, general $D \ge 4$ case, has dynamics very similar to the $D=3$ case and so the regimes – for $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \le -3/2$ we have the $K_3 \rightarrow E_1$ transition and again, similar to the $D=2, 3$ cases, we have $h=0$ for $\alpha \Lambda = -3/2$. Another viable regime for the general case occurs at $\alpha > 0$, $\alpha \Lambda \le \zeta _6$ from (19) (including $\Lambda < 0$). So the regimes are exactly the same, but the coverage of the second regime – with $\alpha > 0$ – is different. In the case of $D=3$ we have this regime if $\alpha \Lambda \le 1/2$, while in the general D cases it is $\alpha \Lambda \le \zeta _6$, with greater area on $(\alpha , \Lambda )$ space than in the $D=3$ case.

To summarize all $\Lambda$-term cases, the only pathological one is $D=1$ – all the remaining ones have viable $K_3 \rightarrow E_{3+D}$ ($E_{3+D}$, anisotropic exponential regime with different expansion rates in 3 and D dimensions) transition over an open range of parameters: for $D=2$ we have viable solutions in two domains – $\alpha > 0$, $\alpha \Lambda \le 1/2$ and $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \le -3/2$. In $D=3$ we have a “doubled” number of regimes in the same two domains. We used the term “doubled” because in $D=3$ both spaces are three-dimensional and so it is irrelevant which one is expanding and which one is contracting – the expanding one is “our Universe” and the contracting one is extra dimensional. Finally, in the general $D \ge 4$ case we have the same regimes but with greater coverage over the $(\alpha , \Lambda )$ plane. Thus we can conclude that with increase of the number of extra dimensions, the occurrence of the transition from high-energy Kasner to anisotropic exponential solution $K_3 \rightarrow E_{3+D}$ (realistic compactification) is increasing.

This way the viable compactification regimes are the same in all $D \ge 2$ cases (but with different coverage), but the fine structure of the other exponential solutions in $\alpha > 0$, $\Lambda > 0$ domain is different. We described it in detail in the $D=2$ case (see [61]), in less detail in $D=3$ and we skipped it for the general $D \ge 4$ case, so now let us briefly summarize this structure for all different cases. Of additional interest is the above-mentioned $D=6$ case – with $\zeta _4 = \zeta _5$ it demonstrates a bit different behavior. So we summarized the regimes for the $H_2$–$H_3$ branches for viable values for H and h ($h<0$, $H>0$) in Table 4.

Table 4 Fine structure of $\alpha > 0$ $\Lambda > 0$ exponential solutions

From Table 4 one can clearly see realistic compactification regimes and restrictions on $\alpha \Lambda$ when they occur. In $D=2$ it is $K_3 \rightarrow E_1$ at the beginning of the regimes string and one can clearly see that it occurs only for $\alpha \Lambda \le 1/2$ (the arrow indicate the regime transition with respect to the “standard” time direction – from past asymptote to future asymptote). In $D=3$ it is also $K_3 \rightarrow E_1$ but now it is in the end of regimes string and it also occurs only for $\alpha \Lambda \le 1/2$. Similarly, for general $D \ge 4$ (including $D=6$) it is $K_3 \rightarrow E_1$ in the end of regimes string and it occurs for $\alpha \Lambda \le \zeta _6$. Thus one can see that the fine structure of the regimes is different in different D but it does not affect the realistic regimes. One last note, as we mentioned above, for $D<6$ $\zeta _4 > \zeta _5$ while for $D>6$ $\zeta _4 < \zeta _5$, so that for $D > 6$ $\zeta _4$ and $\zeta _5$ should be exchanged (in Table 4 they input as $\zeta _4 > \zeta _5$).

At this point it is appropriate to address another point – in [61] we mentioned that some of the exponential solutions have directional stability. It is also could be clearly seen from Table 4 – the solutions ($\rightarrow E \leftarrow$) are stable, the solutions ($\leftarrow E \rightarrow$) are unstable and finally the solutions ($\rightarrow E \rightarrow$) have directional stability. The stability of exponential solutions in EGB and Lovelock gravity was addressed in [58] and for general EGB case in [59]. The results of these studies could be summarized as follows – the exponential solution with non-zero total expansion rate ($\sum H_i$) is stable if $\sum H_i > 0$ and unstable if $\sum H_i < 0$. All solutions – both stable and unstable – follow this rule, but in this scheme there is no place for directional stability, it could seem. But in reality there is – indeed, the solutions with directional stability have $\sum H_i = 0$ – constant volume solutions (see [56] for more detail). Thus in the direction which give $\sum H_i > 0$ they are stable while in the opposite direction – with $\sum H_i < 0$ – unstable. This situations is very well illustrated in Fig. 4c, d – on panel (c) we have $nS \rightarrow E \rightarrow nS$ and it demonstrate directional stability – indeed, for $H > H_E$ we have $\sum H_i > 0$, while for $H < H_E$ we have $\sum H_i < 0$. On panel (d) the regimes are $nS \rightarrow E_1 \leftarrow E_2 \rightarrow nS$ and $E_1$ is stable (we have $\sum H_i > 0$), while $E_2$ is unstable (we have $\sum H_i < 0$).

Fig. 6

Summary of the bounds on ($\alpha , \Lambda$) from this paper alone on a; from other considerations found in the literature on b and the intersection between them on c (see the text for more details)

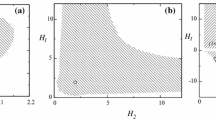
As we have found the domains on ($\alpha$, $\Lambda$) plane which give us realistic regimes, it is interesting to compare these bounds with those coming from other considerations. The results of this comparison are presented in Fig. 6. In Fig. 6a we presented the summary of the results from the current paper – $\alpha < 0$, $\Lambda > 0$, $\alpha \Lambda \le -3/2$ in the second quadrant and $\alpha > 0$, $\alpha \Lambda \le \eta _0 \equiv \zeta _6$ from (19) on $\alpha > 0$ half-plane. In Fig. 6b we collected all available constraints on $\alpha \Lambda$ from other considerations. Among them a significant part is based on the different aspects of Gauss–Bonnet gravity in AdS spaces – from consideration of shear viscosity to entropy ratio as well as causality violations and CFTs in dual gravity description there were obtained limits on $\alpha \Lambda$ [72,73,74,75,76,77,78,79]:

$$\begin{aligned}&- \displaystyle \frac{(D+2)(D+3)(D^2 + 5D + 12)}{8(D^2 + 3D + 6)^2} \equiv \eta _2 \le \alpha \Lambda \le \eta _1 \nonumber \\&\equiv \displaystyle \frac{(D+2)(D+3)(3D + 11)}{8D(D+5)^2}. \end{aligned}$$

(20)

The limits for dS ($\Lambda > 0$) are less numerous and are based on different aspects (causality violations, perturbation propagation and so on) of black hole physics in dS spaces. The most stringent constraint coming from these considerations is [35, 39, 80]

$$\begin{aligned} \alpha \Lambda \ge \eta _3 \equiv - \displaystyle \frac{D^2 + 7D + 4}{8(D-1)(D+2)}. \end{aligned}$$

(21)

At this point, two clarifications are required. First, this limit is true for both $\alpha \lessgtr 0$ and $\Lambda \lessgtr 0$, so that in the $\alpha > 0$, $\Lambda < 0$ quadrant two limits are applied: $\alpha \Lambda \ge \eta _2$ from (20) and $\alpha \Lambda \ge \eta _3$ from (21). One can easily check that $\eta _2 > \eta _3$ for $D \ge 2$ so that the constraint from (20) is the most stringent in this quadrant. Secondly, one can see that the limit in (21) is not defined for $D=1$. Indeed, in this case the limit is special (see [29]), but for $D=1$ there are no viable cosmological regimes (see [61]); thus we consider $D \ge 2$ only.

One can see that the bounds on ($\alpha , \Lambda$) cover three quadrants and our analysis allows one to constrain the remaining sector: $\alpha > 0$, $\Lambda > 0$. But if we consider joint constraints from both Fig. 6a, b, the resulting area is presented in Fig. 6c. There one can see that the regimes in the $\alpha < 0$ sector disappear due to the fact that always $\eta _3 > -3/2$ – the ($\alpha , \Lambda$) which have viable cosmological dynamics in the $\alpha < 0$ sector disagree with (21). To conclude, if we consider our bounds on ($\alpha$, $\Lambda$) together with those previously obtained (see (20)–(21)), the resulting bounds are

$$\begin{aligned}&\alpha > 0, \quad D \ge 2, \quad \displaystyle \frac{3D^2 - 7D + 6}{4D(D-1)} \equiv \eta _0 \ge \alpha \Lambda \ge \eta _2\nonumber \\&\quad \equiv - \displaystyle \frac{(D+2)(D+3)(D^2 + 5D + 12)}{8(D^2 + 3D + 6)^2}. \end{aligned}$$

(22)

The result that the joint analysis suggests that only $\alpha > 0$ is interesting and important – indeed, the constraints on ($\alpha , \Lambda$) considered so far do not distinguish between $\alpha \lessgtr 0$, and there are several considerations which favor $\alpha > 0$. The most important of them is the positivity of $\alpha$ coming from the heterotic string setup, where $\alpha$ is associated with the inverse string tension [29], but there are several others like the holographic entanglement entropy being ill defined [81]. Thus our joint analysis supports $\alpha > 0$ as well.

6 Conclusions

In this paper we finalized the study of different regimes in EGB cosmologies with $\Lambda$-term. We compared the regimes of existence and abundance of different D within $\Lambda$-term cases, and now it is time to compare the $\Lambda$-term and vacuum cases.

The main difference between the $\Lambda$-term and vacuum cases is the absence of a “Kasner transition” [transitions from high-energy (Gauss–Bonnet) Kasner to low-energy (GR) one] in the $\Lambda$-term case and its presence in the vacuum. The reason for this difference is simple – as we demonstrated in [61], in the presence of a $\Lambda$-term power-law solutions do not exist. Some sort of unstable $K_1$ we reported in [61] for the $D=1$ $\Lambda$-term case, but it is singular and is never reached so it is unphysical. Formally, the high-energy Kasner regime of $K_3$ also should not exist, but in the high-energy limit $H_i \ggg \Lambda$ and so $\Lambda /H_i \lll 1$, and we can treat the high-energy $\Lambda$-term regime as the vacuum. Thus for the vacuum cases we have as viable cases both “Kasner transitions” and transitions from GB Kasner to anisotropic exponential solutions, while for the $\Lambda$-term cases we have only the latter. But for the vacuum cases we have only one viable exponential regime, while for the $\Lambda$-term we have two. Also, for the vacuum cases, viable exponential regimes exist only for $\alpha > 0$, while for $\Lambda$-term one of them exists for $\alpha > 0$ while another exists for $\alpha < 0$.

This is another difference between vacuum and $\Lambda$-term solutions – the abundance of the exponential solutions. This topic for the anisotropic case was investigated in [57] and one can clearly see that the number of solutions substantially decreases in the vacuum case. The case of isotropic solutions is easier to address – indeed, in the isotropic case, (6)–(8) reduce to a single equation:

$$\begin{aligned} \alpha D (D{+}1)(D+2)(D+3) H^4 {+} (D+2)(D+3)H^2 = \Lambda .\nonumber \\ \end{aligned}$$

(23)

In the vacuum case $\Lambda \equiv 0$ (23) has only one root, $H^2 = - 1/(\alpha D(D+1))$, while in the $\Lambda$-term case we could have up to two roots. And this is exactly what we observe – in the vacuum case [60] we always have only one isotropic solution, while in the $\Lambda$-term cases ([61] and the present paper) we have up to two. Similarly, if we consider higher (say, nth order) Lovelock orders, we shall have up to n isotropic solutions in the $\Lambda$-term case and up to $(n-1)$ solutions in the vacuum case.

The results of our paper entail a list of all regimes and the bounds on ($\alpha$, $\Lambda$) where the viable cosmologies exist within. The latter could be compared with similar bounds but from other considerations, and this comparison is presented in Fig. 6; the joint analysis (Fig. 6c) suggests that only $\alpha > 0$, $D \ge 2$ is allowed.

This finalizes our paper and the discussion of its results. We claim that we thoroughly investigated the case under consideration and analytically obtained the bounds on ($\alpha$, $\Lambda$) which allow for the existence of the cosmologically viable regimes. The investigation of the viable Gauss–Bonnet cosmologies does not end here – there are other interesting effects like curvature and other matter sources which could affect the viability, and we shall consider these effects in the near future.