A chiral covariant approach to $\varvec{\rho \rho }$ scattering

Abstract

We analyze vector meson–vector meson scattering in a unitarized chiral theory based on a chiral covariant framework restricted to $\rho \rho$ intermediate states. We show that a pole assigned to the scalar meson $f_0(1370)$ can be dynamically generated from the $\rho \rho$ interaction, while this is not the case for the tensor meson $f_2(1270)$ as found in earlier work. We show that the generation of the tensor state is untenable due to the extreme non-relativistic kinematics used before. We further consider the effects arising from the coupling of channels with different orbital angular momenta which are also important. We suggest to use the formalism outlined here to obtain more reliable results for the dynamical generation of resonances in the vector–vector interaction.

1 Introduction

It is now commonly accepted that some hadron resonances are generated by strong non-perturbative hadron–hadron interactions. Arguably the most famous example is the $\Lambda (1405)$, which arises from the coupled-channel dynamics of the strangeness $S=-1$ ground -state octet meson–baryon channels in the vicinity of the $\pi \Sigma$ and $K^-p$ thresholds [1]. This resonance also has the outstanding feature of being actually the combination of two near poles, the so-called two-pole nature of the $\Lambda (1405)$. In a field-theoretic sense, one should consider this state as two particles. This fact was predicted theoretically [2, 3] and later unveiled experimentally [4] (see also the discussion in Ref. [5]). Another example is the scalar meson $f_0(980)$ close to the $\bar{K}K$ threshold, which is often considered to arise due to the strong S-wave interactions in the $\pi \pi$–$\bar{K}K$ system with isospin zero [6,7,8]. A new twist was given to this field in Ref. [9] where the S-wave vector–vector ($\rho \rho$) interactions were investigated and it was found that due to the strong binding in certain channels, the $f_2(1270)$ and the $f_0(1370)$ mesons could be explained as $\rho \rho$ bound states. This approach offered also an explanation why the tensor state $f_2$ is lighter than the scalar one $f_0$, as the leading order attraction in the corresponding $\rho \rho$ channel is stronger. This work was followed up by extensions to SU(3) [10], to account for radiative decays [11, 12], and much other work; see e.g. the short review in Ref. [13].

These findings concerning the $f_2(1270)$ are certainly surprising and at odds with well-known features of the strong interactions. It is a text-book result that the $f_2(1270)$ fits very well within a nearly ideally mixed P-wave $q\bar{q}$ nonet comprising as well the $a_2(1320)$, $f'_2(1525)$ and $K_s^*(1430)$ resonances [14,15,16,17]. Values for this mixing angle can be obtained from either the linear or quadratic mass relations as in Ref. [17]. Non-relativistic quark model calculations [18], as well as with relativistic corrections [19], predict that the coupling of the tensor mesons to $\gamma \gamma$ should be predominantly through helicity two by an E1 transition. This simple $q\bar{q}$ picture for the tensor $f_2(1270)$ resonance has been recently validated by the analyses performed in Ref. [20] of the high-statistics Belle data [21,22,23,24,25] on $\gamma \gamma \rightarrow \pi \pi$ in both the neutral and the charged pion channels. Another point of importance in support of the $q\bar{q}$ nature of the $f_2(1270)$ is Regge theory, since this resonance lies in a parallel linear exchange-degenerate Regge trajectory with a “universal” slope parameter of around 1 GeV [26,27,28,29,30]. Masses and widths of the first resonances with increasing spin lying on this Regge trajectory ($\rho$, $f_2$, $\rho _3$, $f_4$) are nicely predicted [31] by the dual-hadronic model of Lovelace–Shapiro–Veneziano [32,33,34].

One should stress that the results of Ref. [9] were obtained based on extreme non-relativistic kinematics, ${\mathbf {p}}_i^2/m_\rho ^2\simeq 0$, with ${\mathbf {p}}$ the rho-meson three-momentum and $m_\rho$ the vector-meson mass. This approximation, however, leads to some severe simplifications:

• Due to the assumed threshold kinematics, the full $\rho$ propagator was reduced to its scalar form, thus enabling the use of techniques already familiar from the pion–pion interaction [8]. This was applied when considering the iteration of the interactions in the Bethe–Salpeter equation.

• Based on the same argument, the algebra involving the spin and the isospin projectors of the two vector-meson states could considerably be simplified.

However, as $\sqrt{s_\mathrm{th}} = 2m_\rho = 1540$ MeV, the lighter of the bound states obtained in Ref. [9] is already quite far away from the $2\rho$ threshold, with a nominal three-momentum of modulus larger than a 60% of the $\rho$ mass. It is therefore legitimate to question the assumptions there involved. In this work, we will reanalyze the same reactions using a fully covariant approach. This is technically much more involved than the formalism of the earlier work. However, as our aim is to scrutinize the approximations made there, we stay as much as possible close to their choice of parameters. Besides, we also consider $\rho \rho$ higher partial waves since the authors of Ref. [9] only considered scattering in S-wave because of the same type of near-threshold arguments. The inclusion of these higher partial waves is also important when moving away from threshold. As it will be shown, the near-threshold approximation is only reliable very close to threshold.

There is one further issue not considered in Ref. [9] concerning the multiple coupled-channel nature in the energy region where these resonances (for the $f_0(1370)$ and $f_2(1272)$) appear. Regarding this point, a set of 13 coupled channels were taken into account in the study of Ref. [35] of the $J^{PC}=0^{++}$ meson scattering. Of special significance in their analysis among the channels considered are the two-pseudoscalar ones of $\pi \pi$, $K\bar{K}$, $\eta \eta$, $\eta \eta '$ and the two-resonance modes (mimicking multi-meson states) of $\sigma \sigma$, $\rho \rho$ and $\omega \omega$. A main conclusion of this reference is that the coupled-channel dynamics is crucial to fully understand the meson spectrum in the energy region around 1.5 GeV, which spans the $\rho \rho$ threshold region, as also concluded in Ref. [36]. In particular Ref. [35] found that the $f_0(1370)$ was mostly a bare state stemming from the SU(3) octet of bare $0^{++}$ scalar resonances with mass around 1.4 GeV. This conclusions was reached by the almost coincidence of the couplings of this resonance to the two-pseudoscalar channels calculated both from the tree-level Lagrangian and from the residue of the meson–meson amplitudes at the resonance pole. Furthermore, the mass from the pole position of the $f_0(1370)$ is also very close to the bare mass of this octet of scalar resonances. Reference [35] derived the couplings of the vector–vector states to the pseudoscalar–pseudoscalar states and to $\sigma \sigma$ by invoking minimal coupling [37], although the direct transitions between the vector–vector channels were not included. We fill partially this gap here by considering the direct scattering between the $\rho \rho$ states but at the same time we keep the strong assumption of Ref. [9] of neglecting any other channels. In this sense it would be very valuable to improve the work of Ref. [35] by incorporating this new formalism to treat vector–vector scattering. This, however, goes beyond the scope of this research, as our main emphasis here lies on extending and critically reviewing the model of Ref. [9] by taking into account the relativistic corrections and higher partial waves.

Our work is organized as follows: in Sect. 2 we outline the formalism to analyze $\rho \rho$ scattering in a covariant fashion. In particular, we retain the full propagator structure of the $\rho$, which leads to a very different analytic structure of the scattering amplitude compared to the extreme non-relativistic framework. We also perform a partial-wave projection technique, which allows us to perform the unitarization of the tree-level scattering amplitudes using methods well established in the literature. An elaborate presentation of our results is given in Sect. 3, where we also give a detailed comparison to the earlier work based on the non-relativistic framework. Next, we consider the effect of the coupling between channels with different orbital angular momentum. We also improve the unitarization procedure by considering the first-iterated solution of the N / D method in Sect. 4, reinforcing our results obtained with the simpler unitarization method. We conclude with a summary and a discussion in Sect. 5. A detailed account of the underlying projection formalism is given in Appendix A.

Fig. 1

Feynman diagrams for the tree-level amplitude $\rho ^+\rho ^-\rightarrow \rho ^+\rho ^-$

2 Formalism

The inclusion of vector mesons in a chiral effective Lagrangian can be done in a variety of different ways, such as treating them as heavy gauge bosons, using a tensor field formulation or generating them as hidden gauge particles of the non-linear $\sigma$-model. All these approaches are equivalent, as shown e.g. in the review [37]. While in principle the tensor field formulation is preferable in the construction of chiral-invariant building blocks, we stick here to the hidden symmetry approach as this was also used in Ref. [9].

To be specific, the Lagrangian for the interactions among vector mesons is taken from the pure gauge-boson part of the non-linear chiral Lagrangian with hidden local symmetry [38, 39],

$$\begin{aligned} \mathcal{L}'=&-\frac{1}{4}\langle F_{\mu \nu }F^{\mu \nu }\rangle . \end{aligned}$$

(1)

Here, the symbol $\langle \ldots \rangle$ denotes the trace in SU(2) flavor space and the field strength tensor $F_{\mu \nu }$ is

$$\begin{aligned} F_{\mu \nu }&=\partial _\mu V_\nu -\partial _\nu V_\mu -ig[V_\mu ,V_\nu ], \end{aligned}$$

(2)

with the coupling constant $g=M_V/2 f_\pi$ and $f_\pi \approx 92$ MeV [5] the weak pion decay constant. The vector field $V_\mu$ is

$$\begin{aligned} V_\mu =&\left( \begin{array}{lll} \frac{1}{\sqrt{2}}\rho ^0 &{} \quad \rho ^+ \\ \rho ^- &{} \quad - \frac{1}{\sqrt{2}}\rho ^0 \end{array} \right) . \end{aligned}$$

(3)

From the Lagrangian in Eq. (1) one can straightforwardly derive the interaction between three and four vector mesons, with the corresponding Lagrangians denoted as $\mathcal{L}'_3$ and $\mathcal{L}'_4$, respectively. The former one gives rise to $\rho \rho$ interactions through the exchange of a $\rho$ meson and the latter corresponds to purely contact interactions. We did not include the $\omega$ resonance in Eq. (3), since it does not contribute to the interaction part (in the isospin limit).

Consider first the contact vertices for the 4$\rho$ interaction. These can be derived from Eq. (2) by keeping the terms proportional to $g^2$, leading to

$$\begin{aligned} \mathcal{L}'_4=&\frac{g^2}{2}\langle V_\mu V_\nu V^\mu V^\nu - V_\mu V^\mu V_\nu V^\nu \rangle . \end{aligned}$$

(4)

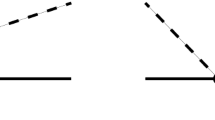
The three different isospin (I) amplitudes for $\rho \rho$ scattering ($I=0$, 1 and 2) can be worked out from the knowledge of the transitions $\rho ^+(p_1)\rho ^-(p_2)\rightarrow \rho ^+(p_3)\rho ^-(p_4)$ and $\rho ^+(p_1)\rho ^-(p_2)\rightarrow \rho ^0(p_3)\rho ^0(p_4)$ by invoking crossing as well. We have indicated the different four-momenta by $p_i$, $i=1,\ldots ,4$. The scattering amplitude for the former transition is denoted by $A(p_1,p_2,p_3,p_4)$ and the latter one by $B(p_1,p_2,p_3,p_4)$, which are shown in Figs. 1 and 2, respectively.

Fig. 2

Feynman diagrams for the tree-level amplitude $\rho ^+\rho ^-\rightarrow \rho ^0\rho ^0$

The contributions to those amplitudes from $\mathcal{L}'_4$, cf. Eq. (4), are indicated by the subscript c and are given by

$$\begin{aligned} A_c(k_1,k_2,k_3,k_4)&= -2 g^2(2\epsilon (1)_\mu \epsilon (2)_\nu \epsilon (3)^\nu \epsilon (4)^\mu \nonumber \\&\quad -\epsilon (1)_\mu \epsilon (2)^\mu \epsilon (3)_\nu \epsilon (4)^\nu \nonumber \\&\quad -\epsilon (1)_\mu \epsilon (2)_\nu \epsilon (3)^\mu \epsilon (4)^\nu ),\nonumber \\ B_c(k_1,k_2,k_3,k_4)&= 2g^2(2\epsilon (1)_\mu \epsilon (2)^\mu \epsilon (3)_\nu \epsilon (4)^\nu \nonumber \\&\quad - \epsilon (1)_\mu \epsilon (2)_\nu \epsilon (3)^\mu \epsilon (4)^\nu \nonumber \\&\quad - \epsilon (1)_\mu \epsilon (2)_\nu \epsilon (3)^\nu \epsilon (4)^\mu ). \end{aligned}$$

(5)

In this equation, the $\epsilon (i)_\mu$ corresponds to the polarization vector of the $i\mathrm{th}$ $\rho$. Each polarization vector is characterized by its three-momentum ${\mathbf {p}}_i$ and third component of the spin $\sigma _i$ in its rest frame, so that $\epsilon (i)_\mu \equiv \epsilon ({\mathbf {p}}_i,\sigma _i)_\mu$. Explicit expressions of these polarization vectors are given in Eqs. (A.9) and (A.10) of Appendix A. In the following, so as to simplify the presentation, the tree-level scattering amplitudes are written for real polarization vectors. The same expressions are valid for complex ones by taking the complex conjugate of the polarization vectors attached to the final particles.¹

Fig. 3

Three-$\rho$ vertex from $\mathcal{L}'_3$

Considering the one-vector exchange terms, we need the three-vector interaction Lagrangian $\mathcal{L}'_3$. It reads

$$\begin{aligned} \mathcal{L}'_3=&ig\langle (\partial _\mu V_\nu -\partial _\nu V_\mu )V^\mu V^\nu \rangle . \end{aligned}$$

(6)

The basic vertex is depicted in Fig. 3 which after a simple calculation can be written as

$$\begin{aligned} V_3&=-\sqrt{2}g\Big [(q_\mu \epsilon (1)_\nu -q_\nu \epsilon (1)_\mu )\epsilon (3)^\mu \epsilon (2)^\nu \nonumber \\&\quad -\;(k_\mu \epsilon (2)_\nu -k_\nu \epsilon (2)_\mu ) \epsilon (1)^{\mu } \epsilon (3)^\nu \nonumber \\&\quad -\;(p_\mu \epsilon (3)_\nu -p_\nu \epsilon (3)_\mu )\epsilon (2)^\mu \epsilon (1)^\nu \Big ]. \end{aligned}$$

(7)

In terms of this vertex, one can straightforwardly calculate the vector exchange diagrams in Figs. 1 and 2. The expression for the t-channel $\rho$-exchange amplitude, the middle diagram in Fig. 1, and denoted by $A_t(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4)$, is

$$\begin{aligned}&A_t(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4) \nonumber \\&\quad =\frac{2g^2}{(p_1-p_3)^2-m_\rho ^2+i 0^+} \nonumber \\&\qquad \times \;\big [(p_1( p_2+ p_4) +p_3 ( p_2 + p_4)) \epsilon _1\cdot \epsilon _3 \epsilon _2\cdot \epsilon _4\nonumber \\&\qquad +4(\epsilon _1\cdot k_3 \epsilon _4\cdot k_2 \epsilon _2\cdot \epsilon _3 +\epsilon _1\cdot k_3 \epsilon _2\cdot k_4 \epsilon _3\cdot \epsilon _4 \nonumber \\&\qquad +\epsilon _3\cdot k_1 \epsilon _4\cdot k_2 \epsilon _1\cdot \epsilon _2 +\epsilon _2\cdot k_4 \epsilon _3 \cdot k_1 \epsilon _1\cdot \epsilon _4 )\nonumber \\&\qquad -2(\epsilon _1\cdot k_3 (\epsilon _3 \cdot k_2 + \epsilon _3 \cdot k_4) \epsilon _2\cdot \epsilon _4 \nonumber \\&\qquad +\epsilon _3\cdot k_1 (\epsilon _1\cdot k_2+\epsilon _1\cdot k_4)\epsilon _2\cdot \epsilon _4 \nonumber \\&\qquad +\epsilon _2\cdot k_4 (\epsilon _4\cdot k_1+\epsilon _4\cdot k_3)\epsilon _1\cdot \epsilon _3\nonumber \\&\qquad +\epsilon _4\cdot k_2 (\epsilon _2\cdot k_1+\epsilon _2\cdot k_3)\epsilon _1\cdot \epsilon _3 ) \big ], \end{aligned}$$

(8)

where for brevity, we have rewritten $\epsilon (i)\rightarrow \epsilon _i$, and the scalar products involving polarization vectors are indicated with a dot. The u-channel $\rho$-exchange amplitude $A_u(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4)$ can be obtained from the expression of $A_t$ by exchanging $p_3\leftrightarrow p_4$ and $\epsilon _3\leftrightarrow \epsilon _4$. In the exchange for the polarization vectors they always refer to the same arguments of three-momentum and spin, that is, $\epsilon ({\mathbf {p}}_3,\sigma _3)\leftrightarrow \epsilon ({\mathbf {p}}_4,\sigma _4)$. In this way,

$$\begin{aligned}&A_u(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4) \nonumber \\&\quad = A_t(p_1,p_2,p_4,p_3;\epsilon _1,\epsilon _2,\epsilon _4,\epsilon _3). \end{aligned}$$

(9)

Notice that the second diagram in Fig. 2 is a sum of the t-channel and u-channel $\rho$-exchange diagrams.

The s-channel exchange amplitude (the last diagram in Fig. 1) can also be obtained from $A_t$ by performing the exchange $p_2\leftrightarrow -p_3$ and $\epsilon _2\leftrightarrow \epsilon _3$, with the same remark as above for the exchange of polarization vectors. We then have

$$\begin{aligned}&A_s(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4) \nonumber \\&\quad =A_t(p_1,-p_3,-p_2,p_4;\epsilon _1,\epsilon _3,\epsilon _2,\epsilon _4). \end{aligned}$$

(10)

The total amplitudes for $\rho ^+\rho ^-\rightarrow \rho ^+\rho ^-$ and $\rho ^+\rho ^-\rightarrow \rho ^0\rho ^0$ are

$$\begin{aligned} A&=A_c+A_t+A_s,\nonumber \\ B&=B_c+A_t+A_u, \end{aligned}$$

(11)

with the usual arguments $(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4)$. By crossing we also obtain the amplitude for $\rho ^+\rho ^+\rightarrow \rho ^+\rho ^+$ [that we denote $C(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4)$] from the one for $\rho ^+\rho ^-\rightarrow \rho ^+\rho ^-$ by exchanging $p_2\leftrightarrow -p_4$ and $\epsilon _2\leftrightarrow \epsilon _4$, that is,

$$\begin{aligned}&C(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4)\nonumber \\&\quad = A(p_1,-p_4,p_3,-p_2;\epsilon _1,\epsilon _4,\epsilon _3,\epsilon _2). \end{aligned}$$

(12)

The amplitude C is purely $I=2$, which we denote $T^{(2)}$. The amplitude B is an admixture of the $I=0$, $T^{(0)}$, and $I=2$ amplitudes,

$$\begin{aligned} B&=\frac{1}{3}(T^{(0)}-T^{(2)}), \end{aligned}$$

(13)

from which we find that

$$\begin{aligned} T^{(0)}&=3B+C. \end{aligned}$$

(14)

To isolate the $I=1$ amplitude, $T^{(1)}$, we take the $\rho ^+\rho ^-$ elastic amplitude A, which obeys the following isospin decomposition:

$$\begin{aligned} A&=\frac{1}{6}T^{(2)}+\frac{1}{2}T^{(1)}+\frac{1}{3}T^{(0)}. \end{aligned}$$

(15)

Taking into account Eqs. (14) we conclude that

$$\begin{aligned} T^{(1)}=2A-2B-C. \end{aligned}$$

(16)

In terms of these amplitudes with well-defined isospin, the expression in Eq. (A.48) for calculating the partial-wave amplitudes in the $\ell S J I$ basis (states with well-defined total angular momentum J, total spin S, orbital angular momentum $\ell$ and isospin I), denoted as $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}(s)$ for the transition $(\bar{\ell }\bar{S}JI)\rightarrow (\ell S JI)$, simplifies to

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}(s)=&\,\frac{Y_{\bar{\ell }}^{0}(\hat{\mathbf {z}})}{2(2J+1)} \sum _{\begin{array}{c} \sigma _1,\sigma _2,\bar{\sigma }_1\\ \bar{\sigma }_2,m \end{array}} \int \mathrm{d}\hat{{\mathbf {p}}}'' \, Y_\ell ^m({\mathbf {p}}'')^* (\sigma _1\sigma _2M|s_1s_2S) \nonumber \\&\times (m M \bar{M}|\ell S J)(\bar{\sigma }_1\bar{\sigma }_2\bar{M}| \bar{s}_1\bar{s}_2\bar{S}) (0\bar{M}\bar{M}|\bar{\ell }\bar{S}J)\nonumber \\&\times T^{(I)}(p_1,p_2,p_3,p_4;\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4), \end{aligned}$$

(17)

with s the usual Mandelstam variable, ${\mathbf {p}}_1=|{\mathbf {p}}|\hat{\mathbf {z}}$, ${\mathbf {p}}_2=-|{\mathbf {p}}|\hat{\mathbf {z}}$, ${\mathbf {p}}_3={\mathbf {p}}''$ and ${\mathbf {p}}_4=-{\mathbf {p}}''$, $M=\sigma _1+ \sigma _2$ and $\bar{M}=\bar{\sigma }_1+\bar{\sigma }_2$

The Mandelstam variables t and u for $\rho \rho$ scattering in the isospin limit are given by $t=-2{\mathbf {p}}^2(1-\cos \theta )$ and $u=-2{\mathbf {p}}^2(1+\cos \theta )$, with $\theta$ the polar angle of the final momentum. The denominator in $A_t$ due to the $\rho$ propagator, cf. Eq. (8), vanishes for $t=m_\rho ^2$ and similarly the denominator in $A_u$ for $u=m_\rho ^2$. When performing the angular projection in Eq. (17) these poles give rise to a left-hand cut starting at the branch point $s=3m_\rho ^2$. This can easily be seen by considering the integration on $\cos \theta$ of the fraction $1/(t-m_\rho ^2+i\varepsilon )$, which gives the same result both for the t and the u channel exchange,

$$\begin{aligned}&\frac{1}{2}\int _{-1}^{+1}d\cos \theta \frac{1}{-2{\mathbf {p}}^2(1-\cos \theta )-m_\rho ^2+i\varepsilon }\nonumber \\&\quad =-\frac{1}{4{\mathbf {p}}^2}\log \left( \frac{4{\mathbf {p}}^2+m_\rho ^2}{m_\rho ^2}+\frac{4{\mathbf {p}}^2}{m_\rho ^4}i\varepsilon \right) , \end{aligned}$$

(18)

with $\varepsilon \rightarrow 0^+$. The argument of the $\log$ becomes negative for $4{\mathbf {p}}^2<-m_\rho ^2$, which is equivalent to $s<3m_\rho ^2$. Because of the factor ${\mathbf {p}}^2\varepsilon$ the imaginary part of the argument of the $\log$ below the threshold is negative which implies that the proper value of the partial-wave amplitude on the physical axis below the branch point at $s=3m_\rho ^2$ is reached in the limit of vanishing negative imaginary part of s. The presence of this branch point and left-hand cut was not noticed in Ref. [9], where only the extreme non-relativistic reduction was considered, so that the $\rho$ propagators in the $\rho$-exchange amplitudes collapsed to just a constant.

Once we have calculated the partial-wave projected tree-level amplitude we proceed to its unitarization making use of standard techniques within unitary chiral perturbation theory [2, 8, 40]. This is a resummation technique that restores unitarity and also allows one to study the resonance region. It has been applied to many systems and resonances by now, e.g. in meson–meson, meson–baryon, nucleon–nucleon and WW systems. Among many others we list some pioneering work for these systems [2, 3, 8, 41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]. In the last years this approach has been applied also to systems containing mesons and baryons made from heavy quarks, some references on this topic are [57,58,59,60,61].

The basic equation to obtain the final unitarized T matrix in the subspace of coupled channels $\ell S J I$, with the same JI, is²

$$\begin{aligned} T^{(JI)}(s)=&\left[ I-V^{(JI)}(s)\cdot G(s)\right] ^{-1}\cdot V^{(JI)}(s). \end{aligned}$$

(19)

Here, G(s) is a diagonal matrix made up by the two-point loop function g(s) with $\rho \rho$ as intermediate states,

$$\begin{aligned} g(s)\rightarrow&~~i\int \frac{d^4 q}{(2\pi )^4}\frac{1}{(q^2-m_\rho ^2)((P-q)^2-m_\rho ^2)}, \end{aligned}$$

(20)

where $P^2=s$ and within our normalization, cf. Eq. (A.53), $\mathrm{Im}~g(s)=-|{\mathbf {p}}|/8\pi \sqrt{s}$. The loop function is logarithmically divergent and it can be calculated once its value at a given reference point is subtracted. In this way, one can write down a once-subtracted dispersion relation for g(s) whose result is³

$$\begin{aligned} g(s)=&\frac{1}{(4\pi )^2}\left( a(\mu )+\log \frac{m^2_\rho }{\mu ^2}+\sigma \left[ \log (\sigma +1)-\log (\sigma -1)\right] \right) , \end{aligned}$$

(21)

with

$$\begin{aligned} \sigma =&\sqrt{1-\frac{4m_\rho ^2}{s}}, \end{aligned}$$

(22)

and $\mu$ is a renormalization scale typically taken around $m_\rho$, such the sum $a(\mu )+\log m_\rho ^2/\mu ^2$ is independent of $\mu$. The subtraction constant in Eq. (21) could depend on the quantum numbers $\ell$, S and J, but not on I due to the isospin symmetry [3].

To compare with the results of Ref. [9], we also evaluate the function g(s) introducing a three-momentum cutoff $q_\mathrm{max}$, the resulting g(s) function is denoted by $g_c(s)$,

$$\begin{aligned} g_c(s)&=\frac{1}{2\pi ^2}\int _0^{q_\mathrm{max}}\mathrm{d}q \frac{q^2}{w(s-4w^2+i\varepsilon )}, \end{aligned}$$

(23)

with $w=\sqrt{q^2+m_\rho ^2}$. This integral can be done algebraically [62]

$$\begin{aligned} g_c(s)&=\frac{1}{(4\pi )^2} \left( \sigma \left[ \log \left( \sigma \sqrt{1+\frac{m_\rho ^2}{q_\mathrm{max}^2} }+1\right) \right. \right. \nonumber \\&\quad \left. \left. - \log \left( \sigma \sqrt{1+\frac{m_\rho ^2}{q_\mathrm{max}^2} }-1\right) \right] \right. \nonumber \\&\quad \left. +2\log \left\{ \frac{m_\rho }{q_\mathrm{max}} \left( 1+\sqrt{1+\frac{m_\rho ^2}{q_\mathrm{max}^2}}\right) \right\} \right) . \end{aligned}$$

(24)

Typical values of the cutoff are around 1 GeV. The unitarity loop function g(s) has a branch point at the $\rho \rho$ threshold ($s=4m_\rho ^2$) and a unitarity cut above it ($s>4m_\rho ^2$). The physical values of the T-matrix $T^{(JI)}(s)$, with $s>4m_\rho ^2$, are reached in the limit of vanishing positive imaginary part of s. Notice that the left-hand cut present in $V^{(JI)}(s)$ for $s<3m_\rho ^2$ does not overlap with the unitarity cut, so that $V^{(JI)}(s)$ is analytic in the complex s-plane around the physical s-axis for physical energies. In this way, the sign of the vanishing imaginary part of s for $V^{(JI)}(s)$ is of no relevance in the prescription stated above for reaching its value on the real axis with $s<3m_\rho ^2$ according to the Feynman rules.

We can also get a natural value [2] for the subtraction constant a in Eq. (21) by matching g(s) and $g_c(s)$ at threshold where $\sigma =0$. For $\mu =m_\rho$, a usual choice, the final expression simplifies to

$$\begin{aligned} a=-2\log \frac{q_\mathrm{max}}{m_\rho }\left( 1+\sqrt{1+\frac{m_\rho ^2}{q_\mathrm{max}^2}}\right) . \end{aligned}$$

(25)

By varying $q_{max}$ in this equation in the range of typical values around 1 GeV (avoiding the explicit resolution of hadrons into its quark–gluon constituents for shorter wave lengths) one studies the generation of states within the asymptotic hadronic degrees of freedom. In this way one circumvents the fine tuning of subtraction constants, a process that is associated with pre-existing (quark–gluon) states [63].

It is also worth noticing that Eq. (19) gives rise to a T-matrix $T^{(IJ)}(s)$ that is gauge invariant in the hidden local symmetry theory because this equation just stems from the partial-wave projection of a complete on-shell tree-level calculation within that theory, which certainly is gauge invariant.

3 Results

One of our aims is to check the stability of the results of Ref. [9] under relativistic corrections, particularly regarding the generation of the poles that could be associated with the $f_0(1370)$ and $f_2(1270)$ resonances as obtained in that paper. The main source of difference between our calculated $V^{(JI)}(s)$ and those in Ref. [9] arises from the different treatment of the $\rho$-meson propagator. The point is that the authors of Ref. [9] take the non-relativistic limit of this propagator so that from the expression $1/(t-m_\rho ^2)$, cf. Eq. (8), or $1/(u-m_\rho ^2)$, only $-1/m_\rho ^2$ is kept. This is the reason that the tree-level amplitudes calculated in Ref. [9] do not have the branch-point singularity at $s=3m_\rho ^2$ nor the corresponding left-hand cut for $s<3m_\rho ^2$. It turns out that, for the isoscalar tensor case, the resonance $f_2(1270)$ is below this branch point, so that its influence cannot be neglected when considering the generation of this pole within this approach.

Fig. 4

S-wave potentials $V^{(JI)}(s)$ (in MeV) for our calculation (real part: red solid line, imaginary part: black dotted line) and for the calculation of Ref. [9] (blue dashed lines)

3.1 Uncoupled S-wave scattering

The issue on the relevance of this branch-point singularity in the $\rho$-exchange amplitudes was not addressed in Ref. [9] and it is indeed very important. This is illustrated in Fig. 4 where we plot the potentials $V^{(JI)}(s)$ in S-wave ($\ell =0$) (only S-wave scattering is considered in Ref. [9]).⁴ From top to bottom and left to right we show in the figure the potentials for the quantum numbers (J, I) equal to (0, 0), (2, 0), (0, 2), (2, 2) and (1, 1). The red solid and black dotted lines correspond to the real and imaginary parts of our full covariant calculation of the $V^{(JI)}(s)$, respectively, while the blue dashed ones are the results of Ref. [9]. The imaginary part in our results for $V^{(JI)}(s)$ appears below $s<3m_\rho ^2$ due to the left-hand cut that arises from the t- and u-channel $\rho$-exchanges.

It can be seen that our results and those of Ref. [9] are typically similar near threshold ($s=4m_\rho ^2$) but for lower values of s they typically depart quickly due to the onset of the branch-point singularity at $s=3m_\rho ^2$. The strength of this singularity depends on the channel, being particularly noticeable in the $(J,I)=(2,0)$ channel, while for the (0, 0) channel it is comparatively weaker.

The strongest attractive potentials in the near-threshold region occur for $(J,I)=(0,0)$ and (2, 0) and in every of these channels Ref. [9] found a bound-state pole that the authors associated with the $f_0(1370)$ and $f_2(1272)$ resonances, respectively. For the (0, 0) quantum numbers the pole position is relatively close to the $\rho \rho$ threshold, while for (2, 0) it is much further away. Two typical values of the cutoff $q_\mathrm{max}$ were used in Ref. [9], $q_\mathrm{max}=875$ and 1000 MeV. We employ these values here, too, together with $q_\mathrm{max}=m_\rho$ (so that we consider three values of $q_\mathrm{max}$ separated by around 100 MeV), and study the pole positions for our $T^{(JI)}(s)$ amplitudes in S wave. We only find a bound state for the isoscalar scalar case, while for the tensor case no bound state is found. In Table 1 we give the values of the pole positions for our full calculation for $q_\mathrm{max}=m_\rho$ (first), 875 (second) and 1000 MeV (third row). For comparison we also give in round brackets the bound-state masses obtained in Ref. [9], when appropriate. As indicated above, the strong differences for $V^{(20)}(s)$ between our full covariant calculation and the one in Ref. [9] in the extreme non-relativistic limit, cf. Fig. 4b, imply the final disappearance of the deep bound state for the isoscalar tensor case. The nominal three-momentum of a $\rho$ around the mass of the $f_2(1270)$ has a modulus of about $0.6m_\rho \simeq 460$ MeV and for such high values of three-momentum relativistic corrections are of importance, as explicitly calculated here. On the contrary, the (0, 0) pole is located closer to the $\rho \rho$ threshold and the results are more stable against relativistic corrections, though one still finds differences of around 20 MeV in the bound-state mass.

Table 1 Pole position for the partial wave $T^{(00)}(s)$ (second column), residue (third column) and compositeness (fourth column) as a function of the three-momentum cutoff $q_{max}$ (1st column). In the last three rows we take into account the finite width of the $\rho$ in the evaluation of the g(s) function, as indicated between parentheses by (conv). For details, see the text

In addition we also show in the third column of Table 1 the residue of $T^{(00)}(s)$ at the pole position $s_P$. For a generic partial wave $T^{(JI)}_{\ell S;\bar{\ell }S}(s)$, its residue at a pole is denoted by $\gamma ^{(JI)}_{\ell S}\gamma ^{(JI)}_{\bar{\ell }\bar{S}}$ and is defined as

$$\begin{aligned} \gamma ^{(JI)}_{\ell S} \gamma ^{(JI)}_{\bar{\ell }\bar{S}}&= -\lim _{s\rightarrow s_P} (s-s_P) T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}(s). \end{aligned}$$

(26)

In terms of these couplings one can also calculate the compositeness $X^{(JI)}_{\ell S}$ associated with this bound state [64,65,66],

$$\begin{aligned} X_{\ell S}^{(JI)}&=-{\gamma ^{(JI)}_{\ell S;\ell S}}^2 \left. \frac{\partial g(s)}{\partial s}\right| _{s_P}, \end{aligned}$$

(27)

which in our case determines the $\rho \rho$ component in such bound state. Notice that the derivative of g(s) from Eq. (21) (which is negative below threshold) does not depend on the subtraction constant; the dependence on the latter enters implicitly by the actual value of the pole position $s_P$. Of course, if one uses a three-momentum cutoff then $g_c(s)$ must be employed in the evaluation of $X^{(JI)}_{\ell S}$. The compositeness obtained for the pole positions in Table 1 is given in the fourth column of the same table. As expected the $\rho \rho$ component is dominant, with $X_{00}^{(00)}>0.5$, and increases as the pole moves closer to threshold, so that it is 73% for $q_\mathrm{max}=m_\rho$ and $\sqrt{s_P}=1516$ MeV.

We can also determine the pole positions when g(s) is calculated with exact analytical properties, Eq. (21), and taking for a the values from Eq. (25) as a function of $q_\mathrm{max}$. The results are given Table 2, where we also give the residue at the pole position and the calculated compositeness, in the same order as in Table. 1. The results obtained are quite close to those in this table so that we refrain of further commenting on them. Nonetheless, we should stress again that we do not find any pole for the isoscalar tensor case.

We could try to enforce the generation of an isoscalar tensor pole by varying $q_\mathrm{max}$, when using $g_c(s)$, or by varying a, if Eq. (21) is used. In the former case a much lower value of $q_\mathrm{max}$ is required than the chiral expansion scale around 1 GeV ($q_{\text {max}}\lesssim 400$ MeV), while for the latter a qualitatively similar situation arises when taking into account the relationship between a and $q_\mathrm{max}$ of Eq. (25). Even more serious are two facts that happen in relation with this isoscalar tensor pole. First, one should stress that such pole appears associated to the evolution with $q_\mathrm{max}$ or a of a pole in the first Riemann sheet, which violates analyticity. This is shown in Fig. 5 where we exhibit the evolution of this pole as a function of $q_\mathrm{max}$. We start the series at a low value of $q_\mathrm{max}=300$ MeV, where we have two poles on the real axis, and increase the cutoff in steps of $\delta q_\mathrm{max}=50$ MeV. These two poles get closer and merge for $q_\mathrm{max}=403.1$ MeV. For larger values of the cutoff the resulting pole moves deeper into the complex plane of the physical or first Riemann sheet. Second, we find that $X^{(20)}_{02}$ is larger than 1. For example, for $q_{\text {max}}=400$ MeV, there are two poles at 1422.4 and 1463.4 MeV with $X^{(20)}_{02}=2.7$ and 3.8, in order, which of course makes no sense as compositeness factors have to be less or equal to one.

Table 2 Pole positions for the partial wave $T^{(00)}(s)$ (second column), residue (third column) and compositeness (fourth column) as a function of the subtraction constant a (1st column). In the last three rows we take into account the finite width of the $\rho$ in the evaluation of the g(s) function, this is indicated between parentheses by (conv)

Fig. 5

Evolution of the poles in the physical Riemann sheet for the isoscalar tensor channel as a function of $q_\mathrm{max}$. Two poles are present on the real axis for our starting value of $q_{\text {max}}=300$ MeV, and along the trajectory we increase $q_\mathrm{max}$ in steps of $\delta q_{\text {max}}=50$ MeV. The two poles merge at $q_{\text {max}}=403.1$ MeV and for larger values of the cutoff there is one pole that moves deeper into the complex plane

Next, we take into account the finite width of the $\rho$ meson in the evaluation of the unitarity two-point loop function g(s). As a result the peak in the modulus squared of the isoscalar scalar amplitude now acquires some width due to the width itself of the $\rho$ meson. To take that into account this effect we convolute the g(s) function with a Lorentzian mass squared distribution for each of the two $\rho$ mesons in the intermediate state [9, 45, 46]. The resulting unitarity loop function is denoted by $\mathfrak {g}(s)$ and is given by

$$\begin{aligned} \mathfrak {g}(s)&=\frac{1}{N^2}\int _{(m_\rho -2\Gamma _\rho )^2}^{(m_\rho +2\Gamma _\rho )^2}\mathrm{d}m_1^2\frac{\Gamma m_1/\pi }{(m_1^2-m_\rho ^2)^2+m_1^2\Gamma ^2}\nonumber \\&\quad \times \int _{(m_\rho -2\Gamma _\rho )^2}^{(m_\rho +2\Gamma _\rho )^2}\mathrm{d}m_2^2\frac{\Gamma m_2/\pi }{(m_2^2\!-\!m_\rho ^2)^2\!+\!m_2^2\Gamma ^2} g(s,m_1^2,m_2^2). \end{aligned}$$

(28)

The normalization factor N is

$$\begin{aligned} N=\int _{(m_\rho -2\Gamma _\rho )^2}^{(m_\rho +2\Gamma _\rho )^2}\mathrm{d}m^2\frac{\Gamma m/\pi }{(m^2-m_\rho ^2)^2+m^2\Gamma ^2}, \end{aligned}$$

(29)

with $\Gamma (m)$ the width of the $\rho$ meson with mass m. Due to the P-wave nature of this decay to $\pi \pi$, we take into account its strong cubic dependence on the decaying pion three-momentum and use the approximation

$$\begin{aligned} \Gamma (m)&=\Gamma _\rho \left( \frac{m^2-4m_\pi ^2}{m_\rho ^2-4m_\pi ^2}\right) ^3 \theta (m-2m_\pi ) \end{aligned}$$

(30)

with $m_\pi$ the pion mass and $\Gamma _\rho \cong 148$ MeV [5]. The function $g(s,m_1^2,m_2^2)$ is the two-point loop function with different masses, while in Eq. (21) we give its expression for the equal mass case. When evaluated in terms of a dispersion relation it reads

$$\begin{aligned} g(s,m_1^2,m_2^2)&=\frac{1}{16\pi ^2}\bigg \{{a}(\mu )+\log \frac{m_1^2}{\mu ^2} \nonumber \\&\quad +\frac{s-m_1^2+m_2^2}{2s}\log \frac{m_2^2}{m_1^2} \nonumber \\&\quad +\frac{\lambda ^{1/2}(s)}{2s}\bigg [\log \big (\lambda ^{1/2}(s)+s-m_2^2+m_1^2\big ) \nonumber \\&\quad -\log \big (\lambda ^{1/2}(s)-s+m_2^2-m_1^2\big ) \nonumber \\&\quad +\log \big (\lambda ^{1/2}(s)+s+m_2^2-m_1^2\big ) \nonumber \\&\quad -\log \big (\lambda ^{1/2}(s)-s-m_2^2+m_1^2\big )\bigg ]\bigg \}, \end{aligned}$$

(31)

with $\lambda ^{1/2}(s)=\sqrt{s^2 + m_1^4 + m_2^4 -2 s m_1^2 -2 s m_2^2 -2 m_1^2 m_2^2}$. The algebraic expression of this function when calculated with a three-momentum cutoff for different masses can be found in Ref. [62], to which we refer the interested reader.

Fig. 6

The amplitude squared $|T^{00}|^2$ when using the convoluted g(s) function with a cutoff $q_\mathrm{max}$. The blue dashed line corresponds to $q_\mathrm{max}=775$ MeV, the red solid one to 875 MeV and the black dotted one to 1000 MeV

When using the convoluted g(s) function we find similar masses for the peak of $|T^{(00)}|^2$ in the (0, 0) channel compared to the case without convolution. The resulting peak positions are given in the last three rows of Tables 1 and 2. The effects of the non-zero $\rho$ width are clearly seen in Fig. 6, where we plot $|T^{(00)}(s)|^2$ for the different values of $q_{\max }$ shown in Table 1. The shape of the peaks follows quite closely a Breit–Wigner form, though it is slightly wider to the right side of the peak. We find that the width decreases with the increasing value of $q_{\max }$, being around 45, 65 and 95 MeV for $q_{\max }=1000$, 875 and 775 MeV, respectively, of similar size as those found in Ref. [9]. When using a subtraction constant instead of $q_\mathrm{max}$, relating them through Eq. (25), the picture is quite similar. The peak positions are given in the last three columns of Table 2 while the widths obtained are around 105, 70 and 50 MeV for $a=-1.70$, $-1.94$ and $-2.14$, in order. These widths are significantly smaller than the PDG values assigned to the $f_0(1370)$ resonance of 200–500 MeV [5].

Fig. 7

$|T^{(00)}(s)|^2$ with the $\pi \pi$ box diagram contribution included for different values of $\Lambda$ in F(q), cf. Eq. (33). Specifically, $\Lambda =1200$ (black solid line), 1300 (red dashed line) and 1400 MeV (blue dotted line), for $q_\mathrm{max}=875$ (left panel) and $q_\mathrm{max}=1000$ MeV (right panel)

Due to the coupling of the $\rho \rho$ and $\pi \pi$, this pole could develop a larger width. This is approximated in Ref. [9] by considering the imaginary part of the $\pi \pi$ box diagram, with a $\rho \rightarrow \pi \pi$ vertex at each of the vertices of the box. These vertices are also worked out from the non-linear chiral Lagrangian with hidden gauge symmetry [38, 39]. We refer to Ref. [9] for details on the calculation of this contribution. According to this reference one has to add to $V^{(00)}_{00;00}$ and to $V^{(20)}_{02;02}$ the contribution $V_{2\pi }^{(JI)}$, given by

$$\begin{aligned} V_{2\pi }^{(00)}&=20i\,\mathrm{Im}\widetilde{V}_{\pi \pi },\nonumber \\ V_{2\pi }^{(20)}&=8i\,\mathrm{Im}\widetilde{V}_{\pi \pi }. \end{aligned}$$

(32)

In the calculation of the function $\widetilde{V}_{\pi \pi }$, Ref. [9] introduces a monopole form factor F(q) for each of the four $\rho \rightarrow \pi \pi$ vertices in the pion box calculation,

$$\begin{aligned} F(q)=\frac{\Lambda ^2-m_\pi ^2}{\Lambda ^2-(k-q)^2} \end{aligned}$$

(33)

with $k^0=\sqrt{s}/2$, ${\mathbf {k}}=0$, $q^0=\sqrt{s}/2$ and ${\mathbf {q}}$ the integration variables. This introduces a sizable dependence of the results on the value of $\Lambda$. Nonetheless, in order to compare with Ref. [9] we follow the very same scheme of calculation and take the same values for $\Lambda$, that is, 1200, 1300 and 1400 MeV.⁵

The inclusion of the $\pi \pi$ box diagram, on top of the convolution with the $\rho$ mass squared distribution for calculating the g(s) function, does not alter the previous conclusion on the absence of a pole in the isoscalar tensor channel. However, the isoscalar scalar pole develops a larger width around 200–300 MeV, which increases with $\Lambda$, as can be inferred from Fig. 7, where we plot $|T^{(00)}(s)|^2$. On the other hand, the position of the peak barely changes compared to the one given in the last two rows of Table 1. Tentatively this pole could be associated to the $f_0(1370)$ resonance, which according to Refs. [35, 67] decays mostly to $\pi \pi$ with a width around 200 MeV. In the PDG [5] the total width of the $f_0(1370)$ is given with a large uncertainty, within the range 200–500 MeV and the $\pi \pi$ decay mode is qualified as dominant. The nearby $f_0(1500)$ resonance has a much smaller width, around 100 MeV, and its coupling and decay to $\pi \pi$ is suppressed. These properties of the $f_0(1500)$ are discussed in detail in Ref. [35].

3.2 Coupled-channel scattering

We now consider the impact on our results when allowing for the coupling between $\rho \rho$ channels with different orbital angular momenta, an issue not considered in Ref. [9]. In Table 3 we show the different channels that couple for given JI quantum numbers and pay special attention to the $(J,I)=(0,0)$ and (2, 0) channels. Apart from the conservation of J and I, one also has to impose invariance under parity, which avoids the mixing between odd and even $\ell$’s.

Table 3 Coupled channels with different orbital angular momentum

Table 4 Bound-state poles in the partial-wave amplitudes of quantum numbers $(J,I)=(0,0)$ with varying cutoff $q_\mathrm{max}$, which is indicated in the first column. The masses (second column), the residues to $(\ell , S)=(0,0)$ and (2, 2) (third and fourth columns) and the compositeness coefficients $X^{00)}_{00}$ and $X^{00)}_{22}$ (sixth and seventh columns) are also given. For the lighter poles the compositeness coefficients are small and negative, so that they cannot be interpreted as physical states contrary to common wisdom [64,65,66]

Table 5 Bound-state poles in the partial-wave amplitudes of quantum numbers $(J,I)=(2,0)$ with different cutoffs $q_\mathrm{max}$, indicated in the first column. The masses (second column) and the residues to $(\ell , S)=(0,2)$, (2, 0) and (2, 2) (third, fourth and fifth columns) are shown. Here, “$-0.0$” denotes a small but negative number

When including coupled-channel effects, one finds two poles in the channels with $(J,I)=(0,0)$, which are reported in Table 4 for various values of $q_\mathrm{max}$ (shown in the first column). We give from left to right the pole mass (second column), the residues (third and fourth ones) and compositeness coefficients (fifth and sixth ones) of the different channels, $(\ell , S)=(0,0)$ and (2, 2), respectively. One of the poles is heavier and closer to the $\rho \rho$ threshold with similar properties as the pole in the uncoupled case, compare with Table 1, particularly for $q_\mathrm{max}=775$ MeV. Nonetheless, as $q_\mathrm{max}$ increases the difference of the properties of this pole between the coupled and uncoupled cases is more pronounced. In particular let us remark that now $X_{00}^{(00)}$ is always ${\gtrsim }0.7$ and for $q_\mathrm{max}=1$ GeV the residue to the channel $(\ell , S) =(0,0)$ is much larger than in the uncoupled case. Additionally, we find now a lighter pole which lies above the branch-point singularity at $\sqrt{3}\,m_\rho \simeq 1343$ MeV. For lower values of the cutoff $q_\mathrm{max}$ this pole couples more strongly to the $(\ell , S)=(2,2)$ channel, but as the cutoff increases its residue for the channel $(\ell , S)=(0,0)$ also increases in absolute value and it is the largest for $q_\mathrm{max}=1$ GeV. It is then clear that both channels $(\ell , S)=(0,0)$ and (2, 2) are relevant for the origin of this pole. Note that the residues for this lighter pole are negative, which is at odds with the standard interpretation of the residue $(\gamma ^{(00)}_{\ell S})^2$ of a bound state as the coupling squared. This implies that the compositeness coefficients $X^{(00)}_{\ell S}$ are all negative, which is at odds with a probabilistic interpretation as suggested in Refs. [64,65,66] for bound states. The moduli of the $|X^{(00)}_{\ell S}|$ are all small because this lighter pole lies quite far from the $\rho \rho$ threshold. The fact that its mass is not far from the strong branch-point singularity at $\sqrt{3}\,m_\rho$ implies that this pole is very much affected by the left-hand cut discontinuity. In this respect, it might well be that the presence of this pole with anomalous properties is just an artifact of the unitarization formula of Eq. (19), which treats the left-hand cut discontinuity of the potential perturbatively. One can answer this question by solving exactly the N / D method [68,69,70,71,72], so that the left-hand cut discontinuity of the potential is properly treated and the resulting amplitude has the right analytical properties. Let us recall that Eq. (19) is an approximate algebraic solution of the N / D method by treating perturbatively the left-hand cut discontinuities of the coupled partial waves [40, 49, 52, 53]. For the uncoupled scattering such effects are further studied in detail in the next section.

For the $(J,I)=(2,0)$ partial waves we have three coupled channels, $(\ell , S)=(0,2)$, (2, 0) and (2, 2) and, contrary to the uncoupled case, we now find a pole that lies above the branch-point singularity. We give its mass and residues for different $q_\mathrm{max}$ in Table 5, with the same notation as in Table 4. Notice that these pole properties are very stable under the variation of $q_\mathrm{max}$. This pole couples by far much more strongly to the channel with $(\ell , S)=(2,2)$ than to any other channel. This indicates that it is mainly due to the dynamics associated with the $(\ell , S)=(2,2)$ channel. But the same comments are in order here as given above for the lighter isoscalar scalar pole, because its residues shown in Table 5 are negative and so are the corresponding compositeness coefficients. Hence, the lighter pole for $(J,I)=(0,0)$ and the one found for (2, 2) cannot be considered as robust results of our analysis. This has to be contrasted to the case of the heavier isoscalar scalar pole that is stable under relativistic corrections, coupled-channel effects and has quite standard properties regarding its couplings and compositeness coefficients.

4 First-iterated solution of the N / D method

In this section for definiteness we only consider uncoupled scattering. We have in mind the $(J,I)=(0,0)$ and $(J,I)=(2,0)$ quantum numbers to which special attention has been paid in the literature concerning the generation of poles that could be associated with the $f_0(1370)$ and $f_2(1270)$ resonances, as discussed above. Further applications of the improved unitarization formalism presented in this section are left for future work.

According to the N / D method [73] a partial-wave amplitude can be written as

$$\begin{aligned} T&=\frac{N(s)}{D(s)}, \end{aligned}$$

(34)

where the function D(s) has only the unitarity or right-hand cut (RHC) while N(s) only has the left-hand cut (LHC). The secular equation for obtaining resonances and bound states corresponds to look for the zeros of D(s),

$$\begin{aligned} D(s_i)=0. \end{aligned}$$

(35)

Below threshold along the real s axis this equation is purely real because D(s) has a non-vanishing imaginary part only for $s>s_\mathrm{th}$.

However, with our unitarization procedure from leading-order unitary chiral perturbation theory (UChPT)⁶ we have obtained the approximation

$$\begin{aligned} T^{(JI)}(s)&=\frac{V^{(JI)}(s)}{1-V^{(JI)}(s)g_c(s)}, \end{aligned}$$

(36)

and the resulting equation to look for the bound states is

$$\begin{aligned} D_U(s)&=1-V(s)g_c(s)=0. \end{aligned}$$

(37)

Notice that Eq. (36), contrary to the general Eq. (35), has an imaginary part below the branch-point singularity at $s=3m^2$. Nonetheless, if the LHC were perturbative this imaginary part would not have prevented having a strong peak in the amplitude if there were already a bound state below the branch-point singularity when the LHC is neglected. However, this is by far not the case for the pole associated with the $f_2(1270)$ in Ref. [9], which clearly indicates the instability of this approach under the inclusion of relativistic corrections.

We can go beyond this situation by considering the first-iterated solution to the N / D method. This is indeed similar to Eq. (36) but improving upon it because it allows us to go beyond the on-shell factorization employed in this equation. In the first-iterated N / D solution one identifies the numerator function N(s) to the tree-level calculation $V^{(JI)}(s)$ and employs the exact dispersive expression for D(s). Namely, it reads⁷

$$\begin{aligned} N(s)&=V^{(JI)}(s),\nonumber \\ D(s)&=\gamma _0+\gamma _1(s-s_{th})+\frac{1}{2}\gamma _2(s-s_{s_\mathrm{th}})^2\nonumber \\&\quad +\frac{(s-s_\mathrm{th})s^2}{\pi }\int _{s_\mathrm{th}}^\infty \mathrm{d}s'\frac{\rho (s')V^{(JI)}(s')}{(s'-s_\mathrm{th})(s'-s)(s')^2},\nonumber \\ T_{ND}(s)&=\frac{N(s)}{D(s)}, \end{aligned}$$

(38)

with the phase space factor $\rho (s)$ given by $\rho (s)=\sigma (s)/16\pi$. We have taken three subtractions in the dispersion relation for D(s) because $V^{(JI)}(s)$ diverges as $s^2$ for $s\rightarrow \infty$.

From our present study we have concluded that $T^{(JI)}(s)$ is stable in the threshold region under relativistic corrections as well as under the addition of coupled $\rho \rho$ higher partial waves. Because of the stability of the results in this region under relativistic corrections and by visual inspection of the potentials in Fig. 4 one concludes that the near-threshold region is quite safe of the problem related to the branch-point singularity of the LHC associated with one-$\rho$ crossed-channel exchanges. We then determine the subtractions constants, $\gamma _0$, $\gamma _1$ and $\gamma _2$ in D(s) by matching $T_{ND}(s)$, Eq. (38), and $T^{(JI)}(s)$, Eq. (36), around threshold ($s_\mathrm{th}$). At the practical level it is more convenient to match 1 / T(s), so that in the threshold region up to $\mathcal{O}(s^3)$ one has

$$\begin{aligned}&\gamma _0+\gamma _1 (s-s_{th})+\frac{1}{2}\gamma _2(s-s_{s_\mathrm{th}})^2 \nonumber \\&\quad =1-V(s)g_c(s)-\frac{(s-s_\mathrm{th})s^2}{\pi }\nonumber \\&\qquad \times \int _{s_\mathrm{th}}^\infty \mathrm{d}s'\frac{\rho (s')V(s')}{(s'-s_\mathrm{th})(s'-s)(s')^2} \nonumber \\&\quad \equiv \omega (s). \end{aligned}$$

(39)

In this way,

$$\begin{aligned} \gamma _0&=1-V(s_\mathrm{th})g_c(s_\mathrm{th}),\nonumber \\ \gamma _1&=\omega '(s_\mathrm{th}),\nonumber \\ \gamma _2&=\omega ''(s_\mathrm{th}). \end{aligned}$$

(40)

The dependence of our present results on the cutoff used in $T^{(JI)}(s)$ stems from the matching conditions of Eq. (40). However, let us stress that the analytical properties of D(s) and N(s) are correct, they have the RHC and LHC with the appropriate extent and branch-point singularities, respectively, and the resulting amplitude is unitarized.

Fig. 8

D(s) function, Eq. (38), for $(J,I)=(0,0)$. Above threshold only the real part is shown

Fig. 9

$(J,I)=(0,0)$. Real (left) and imaginary (right panel) parts of D(s) compared also with $D_U(s)=1-V^{(00)}(s)g_c(s)$ from leading-order UChPT

4.1 Results $J=0$, $I=0$

We plot D(s) for $(J,I)=(0,0)$ in Fig. 8 for $q_\mathrm{{max}}=0.7$, 1 and 1.3 GeV by the red solid, green dashed and blue dash-dotted lines, in order. The crossing with the zero line (dotted one) indicates the mass of the bound state. This mass decreases with increasing $q_\mathrm{max}$, being around 1.4 GeV for the largest cutoff and very close to threshold for the smallest. In Fig. 9 we compare the real (left) and imaginary parts (right panel) of D(s) and $D_U(s)=1-V(s)g_c(s)$ for a cutoff of 1 GeV. We do not show more values of the cutoff because the same behavior results. The function D(s) and $D_U(s)$ match up to around the branch-point singularity at $\sqrt{s}=3m_\rho ^2$. Below it $D_U(s)$ becomes imaginary, cf. Eq. (37), while D(s) remains real and has this right property by construction, cf. Eq. (38). Above threshold the imaginary parts of both functions coincide as demanded by unitarity. We see that for these quantum numbers our new improved unitarization formalism and the one used to derive Eq. (19) agree very well. The bound-state mass remains the same as given in Table 1 because the functions D(s) and $D_U(s)$ match perfectly well in the region where these poles occur, as is clear from Fig. 9. This should be expected because for $(J,I)=(0,0)$ the branch-point singularity is much weaker than for other cases, e.g. $(J,I)=(2,0)$, as discussed above.

Fig. 10

D(s) function, Eq. (38), for $(J,I)=(2,0)$. Above threshold only the real part is shown

4.2 Results $J=2$, $I=0$

We plot D(s) for $(J,I)=(2,0)$ in Fig. 10 for $q_\mathrm{{max}}=0.7$, 1 and 1.3 GeV by the red solid, green dashed and blue dash-dotted lines, respectively. One can see that in this region the function D(s) is large and negative so that there is by far no pole in the $f_2(1270)$ region. In order to show the curves more clearly we use only $q_\mathrm{max}=1$ GeV in Fig. 11, for other values of $q_{\mathrm{max}}$ the behavior is the same. In the left panel we compare the real parts of $T_{ND}(s)$ (black solid) and $T^{(20)}(s)$ (red dashed) while in the right panel we proceed similarly for the real parts of D(s) and $D_U(s)=1-V^{(20)}(s) g_c(s)$, with the same type of lines in order. All the functions match near the threshold region and above it, but they strongly depart once we approach the LHC branch-point singularity at $s=3m_\rho ^2$ and beyond (for smaller values of s). Notice that D(s), which has no such branch-point singularity, follows then the smooth decreasing trend already originating for $3m^2<s<4m^2$. For $(J,I)=(0,0)$ the corresponding smooth trend is that of a decreasing function; cf. Fig. 8. The branch-point singularity is clearly seen in $T^{(20)}(s)$ because it is proportional to $V^{(20)}(s)$.

Fig. 11

$(J,I)=(2,0)$. Left panel real part of $T_{ND}(s)$ (black solid) compared with that of $T^{(20)}(s)$ (red dashed). Right panel comparison between the real parts of D(s) (black solid) and $D_U(s)=1-V^{(20)}(s)g_c(s)$ (red dashed)

In summary, the conclusions obtained in Sect. 3.1 regarding the generation of the pole that could be associated with the $f_0(1370)$ and the absence of that associated with the $f_2(1270)$ as claimed in Ref. [9] fully hold. As a matter of fact, they get reinforced after considering the more elaborated unitarization process that is obtained here by taking the first-iterated N / D solution.

5 Summary and conclusions

In this paper, we have revisited the issue of resonance generation in unitarized $\rho \rho$ scattering using a chiral covariant formalism. The main results of our study can be summarized as follows:

• (i) We have developed a partial-wave projection formalism that is applicable to the covariant treatment of $\rho \rho$ scattering. In particular, we point out that accounting for the full $\rho$-meson propagator leads to a branch point in the partial-wave projected amplitudes at $s = 3m_\rho ^2 \simeq 1.8\,$GeV$^2$, about 208 MeV below the $2\rho$ threshold. This branch point does not appear in the extreme non-relativistic treatment of the propagator.

• (ii) Evaluating the T-matrix using the standard form, see Eq. (19), which treats the left-cut perturbatively, we find a pole in the scalar isoscalar channel close to the $\rho \rho$ threshold that can be associated with the $f_0(1370)$ resonance, in agreement with the findings of Ref. [9], though there are relatively small quantitative differences.

• (iii) In contrast to Ref. [9], we do not find a tensor state below the scalar one. This can be traced back to the influence of the aforementioned branch point. We therefore conclude that the state that is identified in Ref. [9] with the $f_2(1270)$ is an artifact of the non-relativistic approximation and its generation does not hold from the arguments given in that reference.

• (iv) We have also worked out the effects of the coupling between $\rho \rho$ channels with higher orbital angular momenta, which soon become strong when one departs from threshold and lead to additional states. These, however, have negative composite coefficients and are thus not amenable to a simple bound-state interpretation. As these states are close to the branch point at $s= 3m_\rho ^2$, the perturbative treatment of the left-hand cut, as employed in Sect. 3.2, is certainly not sufficient to decide as regards their relevance.

• (v) We have improved the treatment of the left-hand cut by employing the first-iterated N / D method, in particular this method avoids the factorization approach of leading order UChPT. We worked the solutions that follow for uncoupled scattering in the $(J,I)=(0,0)$ and (2, 0) channels. The outcome fully agrees with the conclusions already obtained from UChPT and, notably, the absence of a pole that could be associated with the $f_2(1270)$ is firmly reinforced.

A lesson from points (iii) and (v) is clear. A strongly attractive interaction around the threshold of a given channel is by far not sufficient condition to generate a multi-hadron bound state. This argument, as used in Ref. [9], is in general terms too naive because it does not take into account the possible rise of a singularity in the true potential between the range of validity of the approximation used and the predicted bound-state mass from the latter. It could be rephrased as trying to deduce the values of the function $1/(1+x)$ for $x<-1$ by knowing its values for x around 0.

We conclude that the approach presented here should be used to investigate the possible generation of meson resonances from the interaction of vector mesons. In the next steps, we will investigate how the relativistic effects affect the conclusions of the SU(3) calculation of Ref. [10] and will further sharpen the framework along the lines mentioned, in particular by solving exactly the N / D equations [70,71,72]. On top of this, a realistic treatment of the meson spectroscopy in the region above 1 GeV definitely requires the inclusion of more channels than just $\rho \rho$ (or more generally vector–vector ones). However, the formalism developed here could be very valuable to accomplish this aim phenomenologically if implemented in multi-channel studies, e.g. by extending the work of Ref. [35].

Partial-wave projection formalism

In this appendix we detail the projection formalism used in this work to calculate the different $\rho \rho$ partial waves. First, we give the expression for the polarization vectors for a massive spin-one particle with a three-momentum ${\mathbf {p}}$ and third component of spin $\sigma$ in the z axis of its rest frame, which we denote by $\varepsilon ({\mathbf {p}},\sigma )$. In the rest frame they are given by

$$\begin{aligned} \varepsilon (\mathbf {0},\sigma )=&\left( \begin{array}{c} 0\\ \varvec{\varepsilon }_\sigma \end{array} \right) , \end{aligned}$$

(A.1)

with

$$\begin{aligned} \varvec{\varepsilon }_0=\left( \begin{array}{c} 0\\ 0\\ 1 \end{array}\right) , \quad \varvec{\varepsilon }_{\pm 1}=\frac{\mp 1}{\sqrt{2}} \left( \begin{array}{c} 1\\ \pm i\\ 0 \end{array}\right) . \end{aligned}$$

(A.2)

Next, we take a Lorentz transformation $U({\mathbf {p}})$ along the vector ${\mathbf {p}}$ that takes the particle four-momentum at rest to its final value,

$$\begin{aligned} U( {\mathbf {p}})\left( \begin{array}{c} m\\ \mathbf {0} \end{array} \right) =&\left( \begin{array}{c} E_p\\ {\mathbf {p}}\end{array} \right) , \end{aligned}$$

(A.3)

with $E_p=\sqrt{m^2+{\mathbf {p}}^2}$. We also introduce the rotation $R({\hat{\mathbf {p}}})$ that takes $\hat{\mathbf {z}}$ to ${\hat{\mathbf {p}}}$,

$$\begin{aligned} R({\hat{\mathbf {p}}})\hat{\mathbf {z}}&={\hat{\mathbf {p}}}. \end{aligned}$$

(A.4)

In terms of the polar ($\theta$) and azimuthal ($\phi$) angles of ${\hat{\mathbf {p}}}$, this rotation is defined as

$$\begin{aligned} R({\hat{\mathbf {p}}})&=R_z(\phi )R_y(\theta ), \end{aligned}$$

(A.5)

with the subscripts z and y indicating the axis of rotation. For later convenience we write the Lorentz transformation $U({\mathbf {p}})$ as

$$\begin{aligned} U({\mathbf {p}})&=R(\hat{{\mathbf {p}}})B_z(|{\mathbf {p}}|)R({\hat{\mathbf {p}}})^{-1}, \end{aligned}$$

(A.6)

where $B_z(|{\mathbf {p}}|)$ is a boost along the $\hat{\mathbf {z}}$ axis with velocity $v=-\beta$ and $\beta =|{\mathbf {p}}|/E_p$. Namely,

$$\begin{aligned} B_z(|{\mathbf {p}}|)= \left( \begin{array}{cccc} \gamma &{} \quad 0 &{} \quad 0 &{} \quad \gamma \beta \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ \gamma \beta &{} \quad 0 &{} \quad 0 &{} \quad \gamma \end{array} \right) \end{aligned}$$

(A.7)

and

$$\begin{aligned} \gamma =\frac{1}{\sqrt{1-\beta ^2}}. \end{aligned}$$

(A.8)

Notice that one could also include any arbitrary rotation around the $\hat{\mathbf {z}}$ axis to the right end of Eq. (A.5). Of course, this does not have any affect on either Eqs. (A.4) and (A.6) (for the latter one let us note that $B_z(|{\mathbf {p}}|)$ commutes with a rotation around the $\hat{\mathbf {z}}$ axis).

The action of $U({\mathbf {p}})$ on $\epsilon (\mathbf {0},\sigma _i)$ gives us the polarization vectors with definite three-momentum ${\mathbf {p}}$, whose expressions are

$$\begin{aligned} \varepsilon (\mathbf {p},0)&=\left( \begin{array}{c} \gamma \beta \cos \theta \\ \frac{1}{2}(\gamma -1)\sin 2\theta \cos \phi \\ \frac{1}{2}(\gamma -1)\sin 2\theta \sin \phi \\ \frac{1}{2}\left( 1+\gamma +(\gamma -1)\cos 2\theta \right) \end{array}\right) ,\nonumber \\ \varepsilon (\mathbf {p},\pm 1)&=\mp \frac{1}{\sqrt{2}}\left( \begin{array}{c} \gamma \beta e^{\pm i\phi }\sin \theta \\ 1+(\gamma -1)e^{\pm i\phi }\sin ^2\theta \cos \phi \\ \pm i+(\gamma -1)e^{\pm i \phi }\sin ^2\theta \sin \phi \\ \frac{1}{2}(\gamma -1)e^{\pm i\phi }\sin 2\theta \end{array}\right) . \end{aligned}$$

(A.9)

The previous equation can be written in more compact form as

$$\begin{aligned} \varepsilon ({\mathbf {p}},\sigma )=\left( \begin{array}{c} \gamma \beta \hat{{\mathbf {p}}}\cdot \varvec{\varepsilon }_\sigma \\ \varvec{\varepsilon }_\sigma + \hat{{\mathbf {p}}}\,(\gamma -1) \hat{{\mathbf {p}}} \cdot \varvec{\varepsilon }_\sigma \end{array} \right) . \end{aligned}$$

(A.10)

In terms of the polarization vectors in Eq. (A.10) we can write the vector field for the neutral $\rho ^0$ particle, $\rho ^0_\mu (x)$, as

$$\begin{aligned} \rho ^0_\mu (x)&=\sum _\sigma \int \frac{d^3p}{(2\pi )^32E_p} \nonumber \\&\quad \times \left\{ \varepsilon ({\mathbf {p}},\sigma )_\mu e^{-ip \,x} a({\mathbf {p}},\sigma ) + \varepsilon ({\mathbf {p}},\sigma )^*_\mu e^{ip \,x} a({\mathbf {p}},\sigma )^\dagger \right\} , \end{aligned}$$

(A.11)

with the corresponding similar expressions for the $\rho ^\pm (x)$ fields. Here $a({\mathbf {p}},\sigma )$ and $a({\mathbf {p}},\sigma )^\dagger$ refer to the annihilation and creation operators, with the canonical commutation relation

$$\begin{aligned}{}[a({\mathbf {p}}',\sigma '),a({\mathbf {p}},\sigma )^\dagger ]=\delta _{\sigma \sigma '} (2\pi )^3 2E_p \delta ({\mathbf {p}}-{\mathbf {p}}'). \end{aligned}$$

(A.12)

In order to check the time-reversal and parity-invariance properties of the vector–vector scattering amplitudes worked out from the chiral Lagrangians in Eq. (1) we notice that the polarization vectors in Eq. (A.9) satisfy the following transformation properties:

$$\begin{aligned} \varepsilon (-{\mathbf {p}},\sigma )^*&=(-1)^\sigma (-\varepsilon ({\mathbf {p}},\sigma )_0,\varvec{\varepsilon }({\mathbf {p}},\sigma )),\nonumber \\ \varepsilon (-{\mathbf {p}},\sigma )&= (-\varepsilon ({\mathbf {p}},\sigma )_0,\varvec{\varepsilon }({\mathbf {p}},\sigma )). \end{aligned}$$

(A.13)

A one-particle state $|{\mathbf {p}},\sigma \rangle$ is obtained by the action of the creation operators on the vacuum state,

$$\begin{aligned} |{\mathbf {p}},\sigma \rangle =&a({\mathbf {p}},\sigma )^\dagger | \mathbf {0},\sigma \rangle . \end{aligned}$$

(A.14)

From Eq. (A.12) it follows the following normalization for such states:

$$\begin{aligned} \langle {\mathbf {p}}',\sigma '|{\mathbf {p}},\sigma \rangle&= \delta _{\sigma '\sigma } (2\pi )^3 2E_p \delta ({\mathbf {p}}'-{\mathbf {p}}). \end{aligned}$$

(A.15)

Next, we consider a two-body state characterized by the CM three-momentum ${\mathbf {p}}$ and the third components of spin $\sigma _1$ and $\sigma _2$ in their respective rest frames. This state is denoted by $|{\mathbf {p}},\sigma _1\sigma _2\rangle$. Associated to this, we can define the two-body state with orbital angular momentum $\ell$ with its third component of orbital angular momentum m, denoted by $|\ell m,\sigma _1\sigma _2\rangle$ as

$$\begin{aligned} |\ell m,\sigma _1\sigma _2\rangle&=\frac{1}{\sqrt{4\pi }}\int \mathrm{d}{\hat{\mathbf {p}}}\,Y_\ell ^m(\hat{{\mathbf {p}}})|{\mathbf {p}},\sigma _1\sigma _2\rangle . \end{aligned}$$

(A.16)

Let us show first that this definition is meaningful because the state $|\ell m,\sigma _1\sigma _2\rangle$ transforms under the rotation group as the direct product of the irreducible representations associated to the orbital angular momentum $\ell$ and the spins $s_1$ and $s_2$ of the two particles.

Every single-particle state $|{\mathbf {p}},\sigma \rangle$ under the action of a rotation R transforms as

$$\begin{aligned} R|{\mathbf {p}},\sigma \rangle&=R U({\mathbf {p}})|\varvec{0},\sigma \rangle =U({\mathbf {p}}')U({\mathbf {p}}')^{-1}R U({\mathbf {p}})|\varvec{0},\sigma \rangle , \end{aligned}$$

(A.17)

and ${\mathbf {p}}'=R{\mathbf {p}}$.⁸ It is straightforward to show that

$$\begin{aligned} R=U({\mathbf {p}}')^{-1}R U({\mathbf {p}}). \end{aligned}$$

(A.18)

For that we explicitly write the Lorentz transformations $U({\mathbf {p}}')$ and $U({\mathbf {p}})$ as in Eq. (A.6) so that

$$\begin{aligned} U({\mathbf {p}}')^{-1}R U({\mathbf {p}})&=R(\hat{{\mathbf {p}}}')B_z(|{\mathbf {p}}|)^{-1}R(\hat{{\mathbf {p}}}')^{-1} R R(\hat{{\mathbf {p}}})\nonumber \\&\quad \times \; B_z(|{\mathbf {p}}|)R(\hat{{\mathbf {p}}})^{-1}. \end{aligned}$$

(A.19)

Next, the product of rotations $R(\hat{{\mathbf {p}}}')^{-1} R R(\hat{{\mathbf {p}}})$ is a rotation around the z axis, $R_z(\gamma )$, since it leaves invariant $\hat{\mathbf {z}}$. Thus,

$$\begin{aligned} R(\hat{{\mathbf {p}}}')^{-1} R R(\hat{{\mathbf {p}}})=R_z(\gamma ), \end{aligned}$$

(A.20)

or, in other terms,

$$\begin{aligned} R(\hat{{\mathbf {p}}}')&= R R(\hat{{\mathbf {p}}}) R_z(\gamma )^{-1}, \end{aligned}$$

(A.21)

Taking into account Eqs. (A.20) and (A.21) in Eq. (A.19) it follows the result in Eq. (A.18) because $B_z(|{\mathbf {p}}|)$ and $R_z(\gamma )$ commute. Then Eq. (A.17) implies that

$$\begin{aligned} R|{\mathbf {p}},\sigma \rangle&=U({\mathbf {p}}')R|\varvec{0},\sigma \rangle =\sum _{\sigma '}D^{(s)}(R)_{\sigma '\sigma }|{\mathbf {p}}',\sigma '\rangle , \end{aligned}$$

(A.22)

with $D^{(s)}(R)$ the rotation matrix in the irreducible representation of the rotation group with spin s.

Now, we can use this result to find the action of the rotation R on the state $|{\mathbf {p}},\sigma _1\sigma _2\rangle$, which is the direct product of the states $|{\mathbf {p}},\sigma _1\rangle$ and $|-{\mathbf {p}},\sigma _2\rangle$ (once the trivial CM movement is factorized out [76]). In this way,

$$\begin{aligned} R|{\mathbf {p}},\sigma _1\sigma _2\rangle&=\sum _{\sigma _1',\sigma _2'}D^{(s_1)}(R)_{\sigma _1'\sigma _1} D^{(s_2)}(R)_{\sigma _2'\sigma _2} |{\mathbf {p}}',\sigma _1'\sigma _2'\rangle . \end{aligned}$$

(A.23)

We are now ready to derive the action R on $|\ell m,\sigma _1\sigma _2\rangle$,

$$\begin{aligned} R|\ell m,\sigma _1\sigma _2\rangle&=\sum _{\sigma _1',\sigma _2'}D^{(s_1)}(R)_{\sigma _1'\sigma _1} D^{(s_2)}(R)_{\sigma _2'\sigma _2} \nonumber \\&\quad \times \frac{1}{\sqrt{4\pi }}\int \mathrm{d}{\hat{\mathbf {p}}}'\,Y_\ell ^m(R^{-1}\hat{{\mathbf {p}}}')|{\mathbf {p}}',\sigma _1'\sigma _2'\rangle \nonumber \\&=\sum _{\sigma _1',\sigma _2',m'} D^{(\ell )}(R)_{m'm} D^{(s_1)}(R)_{\sigma _1'\sigma _1} \nonumber \\&\quad \times D^{(s_2)}(R)_{\sigma _2'\sigma _2} |\ell m',\sigma _1'\sigma _2'\rangle . \end{aligned}$$

(A.24)

In this equation we have made use of the property of the spherical harmonics

$$\begin{aligned} Y_\ell ^m(R^{-1}{\hat{\mathbf {p}}}')&=\sum _{m'} D^{(\ell )}(R)_{m'm} Y_\ell ^{m'}({\hat{\mathbf {p}}}'). \end{aligned}$$

(A.25)

Equation (A.24) shows that under rotation the states defined in Eq. (A.16) have the right transformation under the action of a rotation R, and our proposition above is shown to hold.

Now, because of the transformation in Eq. (A.24), corresponding to the direct product of spins $s_1$, $s_2$ and $\ell$, we can combine these angular momentum indices and end with the LSJ basis. In the latter every state is labeled by the total angular momentum J, the third component of the total angular momentum $\mu$, orbital angular momentum $\ell$ and total spin S (resulting from the composition of spins $s_1$ and $s_2$). Namely, we use the notation $|J\mu ,\ell S\rangle$ for these states which are then given by

$$\begin{aligned} |J\mu ,\ell S \rangle&=\sum _{\sigma _1,\sigma _2,m,M} (\sigma _1\sigma _2 M|s_1s_2S)(m M \mu |\ell S J) |\ell m,\sigma _1\sigma _2\rangle , \end{aligned}$$

(A.26)

where we have introduced the standard Clebsch–Gordan coefficients for the composition of two angular momenta.⁹ Next we introduce the isospin indices $\alpha _1$ and $\alpha _2$ corresponding to the third components of the isospins $\tau _1$ and $\tau _2$. This does not modify any of our previous considerations since isospin does not transform under the action of spatial rotations. Within the isospin formalism the $\rho \rho$ states obey Bose–Einstein statistics and these symmetric states are defined by

$$\begin{aligned}&|{\mathbf {p}},\sigma _1\sigma _2, \alpha _1\alpha _2\rangle _S \nonumber \\&\quad =\frac{1}{\sqrt{2}}\left( |{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle +|-{\mathbf {p}},\sigma _2\sigma _1,\alpha _2\alpha _1\rangle \right) , \end{aligned}$$

(A.27)

with the subscript S indicating the symmetrized nature of the state under the exchange of the two particles. One can invert Eq. (A.16) and give the momentum-defined states in terms of those with well-defined orbital angular momentum,

$$\begin{aligned} |{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle&=\sqrt{4\pi } \sum _{\ell ,m} Y_\ell ^m(\hat{{\mathbf {p}}})^* |\ell m,\sigma _1\sigma _2,\alpha _1\alpha _2\rangle \nonumber \\&=\sqrt{4\pi } \sum _{\begin{array}{c} J,\mu ,\ell ,m\\ S,M,I,t_3 \end{array}} Y_\ell ^m(\hat{{\mathbf {p}}})^* \nonumber \\&\quad \times (\sigma _1\sigma _2 M|s_1s_2S) (m M \mu |\ell S J) \nonumber \\&\quad \times (\alpha _1 \alpha _2 t_3|\tau _1\tau _2 I) |J\mu ,\ell S,I t_3\rangle , \end{aligned}$$

(A.28)

with I the total isospin of the particle pair and $t_3$ is the third component. Taking into account this result we can write the symmetrized states as

$$\begin{aligned} |{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle _S&=\sqrt{4\pi } \sum _{\begin{array}{c} J,\mu ,\ell ,m\\ S,M,I,t_3 \end{array}} \frac{1+(-1)^{\ell +S+I}}{\sqrt{2}}\nonumber \\&\quad \times (\sigma _1\sigma _2 M|s_1 s_2 S) (m M \mu |\ell S J) \nonumber \\&\quad \times (\alpha _1 \alpha _2 t_3|\tau _1\tau _2 I) Y_\ell ^m(\hat{{\mathbf {p}}})^* |J\mu , \ell S, I t_3 \rangle . \end{aligned}$$

(A.29)

In deducing this expression we have taken into account the following symmetric properties of the Clebsch–Gordan coefficients:

$$\begin{aligned} (\sigma _2\sigma _1 M|s_2 s_1 S)&= (-1)^{S-s_1-s_2}(\sigma _1\sigma _2 M|s_1 s_2 S),\nonumber \\ (\alpha _2\alpha _1 t_3|t_2 t_1 I)&=(-1)^{I-t_1-t_2}(\alpha _1\alpha _2 t_3|\tau _1\tau _2 I),\nonumber \\ Y_\ell ^m(-\hat{{\mathbf {p}}})&=(-1)^\ell Y_\ell ^m(\hat{{\mathbf {p}}}). \end{aligned}$$

(A.30)

Of course, due to the fact that we are dealing with indistinguishable bosons within the isospin formalism it follows that $s_1=s_2$, $\tau _1=\tau _2$ as well as that $2\tau _1$ and $2s_1$ are even numbers. The combination $(1+(-1)^{\ell +S+I})/\sqrt{2}$ in Eq. (A.29) is denoted in the following as $\chi (\ell S T)$ and takes into account the Bose–Einstein symmetric character of the two particles, so that only states with even $\ell +S+I$ are allowed.

The inversion of Eq. (A.29) gives (we assume in the following that $\ell +S+I=$even, so that $\chi (\ell S T)=\sqrt{2}$)

$$\begin{aligned}&|J\mu ,\ell S, I t_3\rangle = \frac{1}{\sqrt{8\pi }} \sum _{\begin{array}{c} \sigma _1,\sigma _2\\ M,m\\ \alpha _1,\alpha _2 \end{array} } \int \mathrm{d}\hat{{\mathbf {p}}} Y_\ell ^m(\hat{{\mathbf {p}}}) (\sigma _1\sigma _2 M|s_1s_2S)\nonumber \\&\quad \times (m M \mu |\ell S J) (\alpha _1 \alpha _2 t_3|\tau _1\tau _2 I) |{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle _S. \end{aligned}$$

(A.31)

We can also express the state $|J\mu ,\ell S,I t_3\rangle$ in terms of the states $|{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle$ without symmetrization by inverting Eq. (A.28). We would obtain the same expression as Eq. (A.31), but with a factor $1/\sqrt{4\pi }$ instead of $1/\sqrt{8\pi }$, namely

$$\begin{aligned}&|J\mu ,\ell S, I t_3\rangle = \frac{1}{\sqrt{4\pi }} \sum _{\begin{array}{c} \sigma _1,\sigma _2\\ M,m\\ \alpha _1,\alpha _2 \end{array} } \int \mathrm{d}\hat{{\mathbf {p}}} Y_\ell ^m(\hat{{\mathbf {p}}}) (\sigma _1\sigma _2 M|s_1s_2S) \nonumber \\&\quad \times (m M \mu |\ell S J) (\alpha _1 \alpha _2 t_3|\tau _1\tau _2 I) |{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle . \end{aligned}$$

(A.32)

The extra factor of $1/\sqrt{2}$ in Eq. (A.31) is a symmetrization factor because of the Bose–Einstein symmetry properties of the two-particle state in the symmetrized states $|{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle _S$, which disappears when employing the nonsymmetrized states. In order to obtain the normalization of the states $|J\mu ,\ell S,I t_3 \rangle$ it is indeed simpler to use Eq. (A.32) though, of course, the same result is obtained if starting from Eq. (A.31). The two-body particle states with definite three-momentum satisfy the normalization

$$\begin{aligned} \langle {\mathbf {p}}',\sigma '_1\sigma '_2,\alpha '_1\alpha '_2|{\mathbf {p}},\sigma _1\sigma _2,\alpha _1\alpha _2\rangle&=\frac{16 \pi ^2 \sqrt{s}}{|{\mathbf {p}}|} \delta ({\hat{\mathbf {p}}}'-{\hat{\mathbf {p}}}), \end{aligned}$$

(A.33)

The total energy conservation guarantees that the modulus of the final and initial three-momentum in Eq. (A.34) is the same, which we denote by $|{\mathbf {p}}|$. In terms of this result and Eq. (A.32) it follows straightforwardly by taking into account the orthogonal properties of Clebsch–Gordan coefficients and spherical harmonics that

$$\begin{aligned}&\langle J' \mu ' , \ell ' S' , I' t_3' | J \mu , \ell S , I t_3 \rangle \nonumber \\&\quad = \frac{ 4 \pi \sqrt{s} }{|{\mathbf {p}}|} \delta _{J'J}\delta _{\mu '\mu }\delta _{\ell '\ell }\delta _{S'S}\delta _{I'I}\delta _{t'_3t_3} \end{aligned}$$

(A.34)

We are interested in the partial-wave amplitude corresponding to the transition between states with quantum numbers $J\bar{\ell } \bar{S} I$ to states $J \ell S I$, which corresponds to the matrix element

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&= \langle J\mu ,\ell S,I t_3|\hat{T}|J\mu ,\bar{\ell } \bar{S}, I t_3\rangle , \end{aligned}$$

(A.35)

with $\hat{T}$ the T-matrix scattering operator. Here we take the convention that the quantum numbers referring to the initial state are barred. Of course, the matrix element in Eq. (A.35) is independent of $\mu$ and $t_3$ because of invariance under rotations in ordinary and isospin spaces, respectively. We can calculate this scattering matrix element in terms of those in the basis with definite three-momentum by replacing in Eq. (A.35) the states in the $J\ell S$ basis as given in Eq. (A.31). We then obtain in a first step

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&= \frac{1}{8\pi }\sum \int \mathrm{d}\hat{{\mathbf {p}}}\int \mathrm{d}\hat{{\mathbf {p}}}' \,Y_\ell ^m(\hat{{\mathbf {p}}}')^* Y_{\bar{\ell }}^{\bar{m}}(\hat{{\mathbf {p}}}) \nonumber \\&\quad \times (\sigma _1\sigma _2 M|s_1s_2 S)(m M \mu |\ell S J)(\alpha _1\alpha _2 t_3|\tau _1\tau _2I)\nonumber \\&\quad \times (\bar{\sigma }_1\bar{\sigma }_2 \bar{M}|\bar{s}_1\bar{s}_2 S)(\bar{m} \bar{M} \mu |\bar{\ell } \bar{S} J) (\bar{\alpha }_1\bar{\alpha }_2 t_3|\bar{\tau }_1\bar{\tau }_2I)\nonumber \\&\quad \times {}_S\langle {\mathbf {p}}',\sigma _1\sigma _2,\alpha _1\alpha _2|\hat{T}|{\mathbf {p}},\bar{\sigma }_1\bar{\sigma }_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S, \end{aligned}$$

(A.36)

Here we have not shown the explicit indices over which the sum is done in order not to overload the notation.¹⁰ We use next the rotation invariance of the T-matrix operator $\hat{T}$ to simplify the previous integral so that, at the end, we have just the integration over the final three-momentum angular solid. There are several steps involved that we give in quite detail. The referred rotational invariance of $\hat{T}$ implies that it remains invariant under the transformation $\hat{T}\rightarrow R(\hat{{\mathbf {p}}})\hat{T}R(\hat{{\mathbf {p}}})^\dagger$, which implies at the level of the matrix elements that

$$\begin{aligned}&_S\langle {\mathbf {p}}',\sigma _1\sigma _2,\alpha _1\alpha _2|\hat{T}| {\mathbf {p}},\bar{\sigma }_1\bar{\sigma }_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S\nonumber \\&\quad ={}_S\langle {\mathbf {p}}',\sigma _1\sigma _2,\alpha _1\alpha _2|R({\hat{\mathbf {p}}})\hat{T}R({\hat{\mathbf {p}}})^\dagger | {\mathbf {p}},\bar{\sigma }_1\bar{\sigma }_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S. \end{aligned}$$

(A.37)

Under the action of the rotation $R(\hat{{\mathbf {p}}})^\dagger$ ($R(\hat{{\mathbf {p}}})^\dagger \hat{{\mathbf {p}}}=\hat{\mathbf {z}}$ and $R(\hat{{\mathbf {p}}})^\dagger \hat{{\mathbf {p}}}'=\hat{{\mathbf {p}}}''$) the final and initial states transform as, cf. Eq. (A.23),

$$\begin{aligned}&R(\hat{{\mathbf {p}}})^\dagger |{\mathbf {p}},\bar{\sigma }_1\bar{\sigma }_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S\nonumber \\&\quad =\sum _{\bar{\sigma }'_1,\bar{\sigma }'_2} D^{(\bar{s}_1)}_{\bar{\sigma }_1'\bar{\sigma }_1}(R^\dagger ) D^{(\bar{s}_2)}_{\bar{\sigma }_2'\bar{\sigma }_2}(R^\dagger ) |\hat{\mathbf {z}},\bar{\sigma }'_1\bar{\sigma }'_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S,\nonumber \\&R(\hat{{\mathbf {p}}})^\dagger |{\mathbf {p}}',\sigma _1\sigma _2,\alpha _1\alpha _2\rangle _S\nonumber \\&\quad =\sum _{\sigma '_1,\sigma '_2} D^{(s_1)}_{\sigma _1'\sigma _1}(R^\dagger ) D^{(s_2)}_{\sigma _2'\sigma _2}(R^\dagger )|\hat{{\mathbf {p}}}'',\sigma '_1\sigma '_2,\alpha _1\alpha _2\rangle _S, \end{aligned}$$

(A.38)

with the convention that R inside the argument of the rotation matrices refers to $R(\hat{{\mathbf {p}}})$. We insert Eqs. (A.37) and (A.38) into Eq. (A.36), and next transform $\hat{{\mathbf {p}}}'\rightarrow \hat{{\mathbf {p}}}''$ as integrations variables, take into account the invariance of the solid angle measure under such rotation and use Eq. (A.25) for

$$\begin{aligned} Y_{\bar{\ell }}^{\bar{m}}({\hat{\mathbf {p}}})&=Y_{\bar{\ell }}^{\bar{m}}(R(\hat{{\mathbf {p}}})\hat{\mathbf {z}})= \sum _{\bar{m}'} D^{(\bar{\ell })}_{\bar{m}'\bar{m}}(R^\dagger )Y_{\bar{\ell }}^{\bar{m}'}(\hat{\mathbf {z}}),\nonumber \\ Y_{\ell }^m({\hat{\mathbf {p}}}')&=Y_{\ell }^m(R(\hat{{\mathbf {p}}})\hat{{\mathbf {p}}}'')=\sum _{m'}D^{(\ell )}_{m'm}(R^\dagger )Y_\ell ^{m'}(\hat{{\mathbf {p}}}''). \end{aligned}$$

(A.39)

Then Eq. (A.36) for $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}$ can be rewritten as

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=\frac{1}{8\pi }\sum \int \mathrm{d}\hat{{\mathbf {p}}} \int \mathrm{d}\hat{{\mathbf {p}}}'' (\sigma _1\sigma _2 M|s_1s_2 S)(m M \mu |\ell S J) \nonumber \\&\quad \times (\alpha _1\alpha _2 t_3|\tau _1\tau _2 I) D_{\sigma '_1\sigma _1}^{(s_1)}(R^\dagger )^* D_{\sigma '_2\sigma _2}^{(s_2)}(R^\dagger )^* \nonumber \\&\quad \times D_{m'm}^{(\ell )}(R^\dagger )^* Y_\ell ^{m'}(\hat{{\mathbf {p}}}'')^* (\bar{\sigma }_1\bar{\sigma }_2\bar{M}|\bar{s}_1\bar{s}_2 \bar{S}) \nonumber \\&\quad \times (\bar{m}\bar{M}\mu |\bar{\ell }\bar{S}J) (\bar{\alpha }_1\bar{\alpha }_2t_3|\bar{\tau }_1\bar{\tau }_2I)\nonumber \\&\quad \times D^{(\bar{s}_1)}_{\bar{\sigma }_1'\bar{\sigma }_1}(R^\dagger ) D^{(\bar{s}_2)}_{\bar{\sigma }_2'\bar{\sigma }_2}(R^\dagger ) D^{(\bar{\ell })}_{\bar{m}'\bar{m}}(R^\dagger ) Y_{\bar{\ell }}^{\bar{m}'}(\hat{\mathbf {z}}) \nonumber \\&\quad \times {}_S\langle {\mathbf {p}}'',\sigma _1'\sigma _2',\alpha _1\alpha _2|\hat{T}|\, |{\mathbf {p}}|\hat{\mathbf {z}},\bar{\sigma }_1'\bar{\sigma }_2',\bar{\alpha }_1\bar{\alpha }_2\rangle _S. \end{aligned}$$

(A.40)

Let us recall that from the composition of two rotation matrices one has [76, 77]

$$\begin{aligned}&\sum _{m_1,m_2}(m_1m_2M|\ell _1\ell _2L)D^{(\ell _1)}_{m'_1m_1}(R) D^{(\ell _2)}_{m'_2m_2}(R)\nonumber \\&\quad =\sum _{M'}(m'_1m'_2M'|\ell _1\ell _2L)D_{M'M}^{(L)}(R). \end{aligned}$$

(A.41)

We apply this result first to two combinations in Eq. (A.40):

$$\begin{aligned}&\sum _{\sigma _1,\sigma _2}(\sigma _1\sigma _2M|s_1s_2S)D_{\sigma '_1\sigma _1}^{(s_1)}(R^\dagger ) D_{\sigma '_2\sigma _2}^{(s_2)}(R^\dagger )\nonumber \\&\quad =\sum _{M'}(\sigma '_1\sigma '_2 M'|s_1s_2S)D_{M'M}^{(S)}(R^\dagger )\nonumber \\&\sum _{\bar{\sigma }_1,\bar{\sigma }_2}(\bar{\sigma }_1\bar{\sigma }_2\bar{M}|\bar{s}_1\bar{s}_2\bar{S}) D^{(\bar{s}_1)}_{\bar{\sigma }'_1\bar{\sigma }_1}(R^\dagger )D^{(\bar{s}_2)}_{\bar{\sigma }'_2\bar{\sigma }_2}(R^\dagger )\nonumber \\&\quad =\sum _{\bar{M}'}(\bar{\sigma }'_1\bar{\sigma }'_2\bar{M}'|\bar{s}_1\bar{s}_2\bar{S}) D_{\bar{M}'\bar{M}}^{(\bar{S})}(R^\dagger ), \end{aligned}$$

(A.42)

so that Eq. (A.40) becomes

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=\frac{1}{8\pi }\sum \int \mathrm{d}\hat{{\mathbf {p}}}\int \mathrm{d}\hat{{\mathbf {p}}}'' (\sigma _1' \sigma _2' M' |s_1 s_2 S ) D_{M'M}^{(S)}(R^\dagger )^* \nonumber \\&\quad \times D_{m'm}^{(\ell )}(R^\dagger )^*(m M \mu |\ell S J) (\alpha _1\alpha _2 t_3|\tau _1\tau _2 I) Y_\ell ^{m'}(\hat{{\mathbf {p}}}'')^*\nonumber \\&\quad \times (\bar{\sigma }_1'\bar{\sigma }_2' \bar{M}'|\bar{s}_1\bar{s}_2\bar{S}) D_{\bar{M}'\bar{M}}^{(\bar{S})}(R^\dagger ) D_{\bar{m}'\bar{m}}^{(\bar{\ell })}(R^\dagger ) \nonumber \\&\quad \times (\bar{m}\bar{M}\mu |\bar{\ell }\bar{S}J) (\bar{\alpha }_1\bar{\alpha }_2t_3|\bar{\tau }_1\bar{\tau }_2I) Y_{\bar{\ell }}^{\bar{m}'}(\hat{\mathbf {z}})\nonumber \\&\quad \times {}_S\langle {\mathbf {p}}'',\sigma _1'\sigma _2',\alpha _1\alpha _2|\hat{T}|\, |{\mathbf {p}}|\hat{\mathbf {z}},\bar{\sigma }_1'\bar{\sigma }_2',\bar{\alpha }_1\bar{\alpha }_2\rangle _S. \end{aligned}$$

(A.43)

The same relation in Eq. (A.41) is applied once more to the following combinations in Eq. (A.43):

$$\begin{aligned}&\sum _{m,M} (m M \mu |\ell S J) D_{M'M}^{(S)}(R^\dagger ) D_{m'm}^{(\ell )}(R^\dagger ) \nonumber \\&\quad = \sum _{\mu '}(m' M' \mu '|\ell S J) D_{\mu '\mu }^{(J)}(R^\dagger ),\nonumber \\&\sum _{\bar{m},\bar{M}} (\bar{m}\bar{M}\mu |\bar{\ell } \bar{S} J) D_{\bar{M}'\bar{M}}^{(\bar{S})}(R^\dagger ) D_{\bar{m}'\bar{m}}^{(\bar{\ell })}(R^\dagger ) \nonumber \\&\quad = \sum _{\bar{\mu }'} (\bar{m}'\bar{M}'\bar{\mu }'|\bar{\ell }\bar{S}J)D_{\bar{\mu }'\mu }^{(J)}(R^\dagger ). \end{aligned}$$

(A.44)

We take Eq. (A.44) into Eq. (A.43) which now reads

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=\frac{1}{8\pi }\sum \int \mathrm{d}\hat{{\mathbf {p}}}\int \mathrm{d}\hat{{\mathbf {p}}}'' (\sigma _1' \sigma _2' M' |s_1 s_2 S )\nonumber \\&\quad \times (m'M'\mu '|\ell S J) (\alpha _1\alpha _2 t_3|\tau _1\tau _2 I) Y_\ell ^{m'}(\hat{{\mathbf {p}}}'')^*\nonumber \\&\quad \times (\bar{\sigma }_1'\bar{\sigma }_2' \bar{M}'|\bar{s}_1\bar{s}_2\bar{S}) (\bar{m}'\bar{M}'\bar{\mu }'|\bar{\ell }\bar{S}J) (\bar{\alpha }_1\bar{\alpha }_2t_3|\bar{\tau }_1\bar{\tau }_2I)\nonumber \\&\quad \times Y_{\bar{\ell }}^{\bar{m}'}(\hat{\mathbf {z}})D_{\mu '\mu }^{(J)}(R^\dagger )^*D_{\bar{\mu }'\mu }^{(J)}(R^\dagger ) \nonumber \\&\quad \times {}_S\langle {\mathbf {p}}'',\sigma _1'\sigma _2',\alpha _1\alpha _2|\hat{T}|\, |{\mathbf {p}}|\hat{\mathbf {z}},\bar{\sigma }_1'\bar{\sigma }_2',\bar{\alpha }_1\bar{\alpha }_2\rangle _S \end{aligned}$$

(A.45)

Now, the partial-wave amplitude $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}$ is independent of $\mu$ so that we have

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=\frac{1}{2J+1}\sum _{\mu =-J}^J T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}. \end{aligned}$$

(A.46)

The same result in Eq. (A.45) is obtained with the product $D_{\mu '\mu }^{(J)}(R^\dagger )^*D_{\bar{\mu }'\mu }^{(J)}(R^\dagger )$ replaced by

$$\begin{aligned} \frac{1}{2J+1}\sum _{\mu =-J}^J D_{\mu '\mu }^{(J)}(R^\dagger )^*D_{\bar{\mu }'\mu }^{(J)}(R^\dagger )=\frac{\delta _{\bar{\mu }'\mu '}}{2J+1}, \end{aligned}$$

(A.47)

as follows from the unitarity character of the rotation matrices. As a consequence any dependence in $\hat{{\mathbf {p}}}$ present in the integrand of Eq. (A.45) disappears in the average of Eq. (A.46), the integration in the solid angle $\hat{{\mathbf {p}}}$ is trivial and it gives a factor $4\pi$. Taking into account the Kronecker delta from Eq. (A.47) in the third component of the total angular momentum and a new one that arises because $Y_{\bar{\ell }}^{\bar{m}'}(\hat{\mathbf {z}})$ is not zero only for $\bar{m}'=0$, we then end with the following expression for $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}$:

$$\begin{aligned} T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=\frac{Y_{\bar{\ell }}^{0}(\hat{\mathbf {z}})}{2(2J+1)} \sum _{\begin{array}{c} \sigma _1,\sigma _2,\bar{\sigma }_1 \\ \bar{\sigma }_2,\alpha _1,\alpha _2\\ \bar{\alpha }_1,\bar{\alpha }_2,m \end{array}} \int \mathrm{d}\hat{{\mathbf {p}}}'' \, Y_\ell ^{m}(\hat{{\mathbf {p}}}'')^* (\sigma _1\sigma _2M|s_1s_2S) \nonumber \\&\quad \times (m M \bar{M}|\ell S J)(\bar{\sigma }_1\bar{\sigma }_2\bar{M}| \bar{s}_1\bar{s}_2\bar{S}) (0\bar{M}\bar{M}|\bar{\ell }\bar{S}J) \nonumber \\&\quad \times (\alpha _1\alpha _2t_3|\tau _1\tau _2I)(\bar{\alpha }_1\bar{\alpha }_2t_3|\bar{\tau }_1\bar{\tau }_2I) \nonumber \\&\quad \times {}_S\langle {\mathbf {p}}'',\sigma _1\sigma _2,\alpha _1\alpha _2|\hat{T}|\, |{\mathbf {p}}|\hat{\mathbf {z}},\bar{\sigma }_1\bar{\sigma }_2,\bar{\alpha }_1\bar{\alpha }_2\rangle _S, \end{aligned}$$

(A.48)

where we have removed the primes on top of the spin and orbital angular momentum third-component symbols and in the previous sum $M=\sigma _1+ \sigma _2$ and $\bar{M}=\bar{\sigma }_1+\bar{\sigma }_2$.

Next, we derive the unitarity relation corresponding to our normalization for the partial-wave projected amplitudes $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}$. We write the $\hat{S}$ matrix as

$$\begin{aligned} \hat{S}&=I-i \hat{T} \end{aligned}$$

(A.49)

which satisfies the standard unitarity relation

$$\begin{aligned} \hat{S} \cdot \hat{S}^\dagger&=\mathbb {I}, \end{aligned}$$

(A.50)

with $\mathbb {I}$ the identity matrix. In terms of the T-matrix, cf. (A.49), this implies that

$$\begin{aligned} \hat{T}-\hat{T}^\dagger&=-i \hat{T}\hat{T}^\dagger . \end{aligned}$$

(A.51)

Expressed with the matrix elements in the basis $\ell S J$ this relation becomes

$$\begin{aligned} 2 \mathrm{Im}\hat{T}^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=- \langle J\mu ,\ell S,T t_3|\hat{T}\hat{T}^\dagger |J\mu ,\bar{\ell }\bar{S},T t_3\rangle . \end{aligned}$$

(A.52)

In deriving the left-hand side of this equation we have taken into account that because of time-reversal symmetry $T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}=T^{(JI)}_{\bar{\ell }\bar{S};\ell S}$. On the right-hand side we introduce now a two-body resolution of the identity of states $|J\mu ,\ell S,I t_3\rangle$ (we have restricted our vector space to the one generated by these states) such that, taking into account their normalization in Eq. (A.34), one ends with

$$\begin{aligned} \mathrm{Im}T^{(JI)}_{\ell S;\bar{\ell }\bar{S}}&=-\sum _{\ell '',S''} \frac{|{\mathbf {p}}''|}{8\pi \sqrt{s}}T^{(JI)}_{\ell ,S;\ell '',S''}{T^{(JI)}}^*_{\ell '',S'';\bar{\ell }\bar{S}}. \end{aligned}$$

(A.53)

The phase space factor is included in the diagonal matrix

$$\begin{aligned} \rho _{ij}&=\frac{|{\mathbf {p}}|_i}{8\pi \sqrt{s}}\delta _{ij}. \end{aligned}$$

(A.54)

A more standard definition of the S-matrix implies the definition

$$\begin{aligned} \hat{S}\rightarrow S=2\rho ^{\frac{1}{2}} \hat{S} \rho ^{\frac{1}{2}}&=I-2i\rho ^{\frac{1}{2}}\hat{T}\rho ^{\frac{1}{2}}, \end{aligned}$$

(A.55)

such that now the diagonal matrix elements of the identity operator I and S are just 1 and $\eta _ie^{2i\delta _i}$, in order, where $\eta _i$ is the inelasticity for channel i and $\delta _i$ its phase shift.

Finally, let us mention that a partial-wave expansion of the helicity amplitudes (not $\ell SJ$ partial waves as here) for vector–vector scattering was developed in Ref. [78]. The main point in this reference is to provide partial-wave amplitudes in the helicity basis which are free of kinematical singularities, while here we are interested in deriving non-perturbative $\rho \rho$ scattering amplitudes from the hidden local gauge Lagrangian.