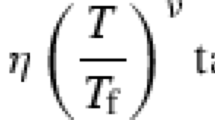1 Introduction

Imperfect fluids in cosmology are characterized by the fact that the different components of cosmic fluids are coupled and, having different internal equation of states, their cooling rates turn out to be different as the Universe expands. As a consequence, a deviation of the system from equilibrium occurs. The different cooling rates of the components are responsible for the presence of a bulk viscous pressure of the cosmic medium as a whole. The latter is the only possible dissipative phenomenon for an homogeneous and isotropic UniverseFootnote 1 (see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] and references therein). In particular, in the Friedman–Robertson–Walker (FRW) Universe, the dissipation is described by a scalar quantity (the bulk viscosity as referred to the thermodynamical approach [42]). Bulk viscosity enters Einstein’s field equations, altering the thermal histories of (relic) particles, compared with cosmology with perfect fluids, and therefore their abundance.Footnote 2

The aim of this paper is to explore the implications of cosmology with bulk viscosity in relation to the gravitino problem (see for example [47,48,49]). Since gravitinos couple to ordinary matter only through the gravitational interaction, it follows that their couplings are Planck suppressed, which implies a (quite) long lifetime,

$$\begin{aligned} \tau _{3/2}\sim \frac{M_\mathrm{Pl}^2}{m^3_{3/2}}\simeq 10^5\left( \frac{1\text { TeV}}{m_{3/2}}\right) ^3\text{ s }. \end{aligned}$$

Here \(m_{3/2}\) is the mass of the particle \(\sim \) \(10^2\) GeV. Particles with such a long lifetime generate some issues in cosmology since if they decay after the nucleosynthesis, their decay products (which can be gauge bosons and their gaugino partners) would destroy light elements, destroying the successful predictions of Big Bang Nucleosynthesis (BBN). This problem can be avoided putting an upper bound on the reheating temperature. In the framework of GR and from the Boltzmann equation it turns out that the gravitino abundance \(Y_{3/2}=n_{3/2}/s\) (here \(s=\displaystyle {\frac{2\pi ^2}{45}}\, g_* T^3\)) is proportional to the reheating temperature \(T_R\) [50,51,52,53],

$$\begin{aligned} Y_{3/2} \simeq 10^{-11}\frac{T_R}{10^{10}\text { GeV}}. \end{aligned}$$
(1.1)

Then by requiring that the abundance (1.1) remains small for a successful prediction of BBN one gets the constraint on the reheating temperature [54, 55]

$$\begin{aligned} T_R \lesssim (10^6 -10^7) \text { GeV} \quad \text {for } \ m_{3/2} \sim {\mathscr {O}}(10^2\text {GeV}). \end{aligned}$$
(1.2)

In turn this bound opens a serious question for the inflationary models (and for some models of leptogenesis) due to the fact that these models tend to predict a reheating temperature larger than the upper bound (1.2) [56, 57] (see also [58,59,60,61]).

The paper is organized as follows. In Sect. 2 we derive the field equations of the cosmological background in presence of imperfect fluids. The analysis of the gravitino problem in the framework of bulk viscosity cosmology is studied in Sect. 3. Conclusions are briefly drawn in Sect. 4.

2 Imperfect fluid

The energy-momentum tensor of imperfect fluids is given by [62]

$$\begin{aligned} T_{\alpha \beta }=\rho u_\alpha u_\beta +(p+\varPi )h_{\alpha \beta }+q_\alpha u_\beta +q_\beta u_\alpha +\pi _{\alpha \beta }.\nonumber \\ \end{aligned}$$
(2.1)

Here \(\varPi \) is the scalar pressure (or the bulk viscous pressure), \(h_{\alpha \beta }=g_{\alpha \beta }+u_\alpha u_\beta \) is the projector tensor, \(q^\alpha \) is a quantity connected to the flux of the energy, and finally \(\pi _{\alpha \beta }\) is the so called anisotropic stress tensor. The quantities \(q^\alpha \) and \(\pi _{\alpha \beta }\) satisfy the relations \(q^\alpha u_\alpha =0, \ \pi _{\alpha \beta }u^\beta = 0 = \pi ^\alpha _{\alpha }\). By making use of symmetries imposed by the fact that the Universe is isotropic and homogeneous, one gets \(q_\alpha =0=\pi _{\alpha \beta }\). The only term allowed is the scalar dissipation \(\varPi \) [42]. Moreover, one finds that the energy-momentum conservation law \(T^{\alpha \beta }_{;\beta }=0\) reads \({\dot{\rho }}+\varTheta (\rho +p+\varPi )=0\). where the dot stands for the derivative with respect to the cosmic time and \(\varTheta = u^\alpha _{;\alpha }\). In an homogeneous and isotropic (spatially flat) Universe, the Einstein equations read [62]

$$\begin{aligned} H^2 = \frac{\kappa \rho }{3}, \quad {\dot{H}}=-\frac{\kappa }{2}(\rho +p+\varPi ), \end{aligned}$$
(2.2)

where \(H={\dot{a}}/{a}\) is the Hubble parameter and \(\kappa = 8\pi G= 8\pi M_\mathrm{Pl}^{-2}\) (\(M_\mathrm{Pl} \simeq 1.22 \times 10^{19}\) GeV is the Planck mass).

In the radiation dominated era, where the energy density is \(\rho =\displaystyle {\frac{\pi ^2 g_*}{30}T^4}\) and the pressure is \(p=\displaystyle {\frac{\rho }{3}}\) (\(g_*\sim 10^2\) counts the relativistic degrees of freedom), one finds that the Hubble parameter evolves according to the equation [62]

$$\begin{aligned} \frac{\ddot{H}}{H}-2 \frac{{\dot{H}}^2}{H^2}-6 H^2 c_b^2+\frac{1}{\tau }\left( \frac{\dot{H}}{H}+2H\right) =0, \end{aligned}$$
(2.3)

where \(\tau (=\tau (t))\) is the relaxation time (physically it is interpreted as the mean free time of the relativistic particle), which in general is time dependent, while \(c_b^2\equiv \frac{\zeta }{(\rho +p)\tau }\) is the propagation velocity of a viscous pulse (\(\zeta \) s the bulk viscosity coefficient), which may assume valuesFootnote 3 \(0\leqslant c_b^2\leqslant 2/3\) [3,4,5, 42, 66]. These results refer to the case in which the number of particles is conserved. Taking into account the particle production, i.e. \(\nabla _\mu N^\mu =n\varGamma \ne 0\), it follows that the viscous pressure assumes the form \(\varPi =-(\rho +p)\varGamma /\varTheta \), with \(\varTheta =3H\) (obtained for isentropic particle production \({\dot{s}}=0\)), which is entirely determined by the particle production rate. For a radiation dominated era \(p=\rho /3\) and \(ns=(\rho +p)/T\), so that the evolution of the Hubble parameter is given by

$$\begin{aligned} \frac{\ddot{H}}{H}-\frac{5}{4}\frac{{\dot{H}}^2}{H^2}+3{\dot{H}} - 6H^2\left( c_b^2-\frac{1}{2}\right) +\frac{1}{\tau }\left( \frac{\dot{H}}{H}+2H\right) =0. \end{aligned}$$
(2.4)

In what follows we shall refer to (2.3), the results being very similar to the case (2.4).

To solve Eq. (2.3) we look at solutions for H(t) of the form

$$\begin{aligned} H(t) = H_L \left( \frac{t}{t_L}\right) ^\varUpsilon , \end{aligned}$$
(2.5)

where \(H_L\), \(t_L\) and \(\varUpsilon \) are undetermined constants. To have a hot early Universe we confine ourselves to the case \(\varUpsilon <0\). From (2.2) one infers the relation between the cosmic time and the temperature T,

$$\begin{aligned} t= & {} t_L C \left( \frac{T}{M_\mathrm{Pl}}\right) ^{\frac{2}{\varUpsilon }}, \nonumber \\ C\equiv & {} \left( \frac{8 \pi ^3 g_*}{90}\right) ^{\frac{1}{2\varUpsilon }}\left( \frac{M_\mathrm{Pl}}{H_L}\right) ^{\frac{1}{\varUpsilon }}, \end{aligned}$$
(2.6)

which allows one to cast the expansion rate in the following formFootnote 4:

$$\begin{aligned} H = A(T) H_\mathrm{GR}, \quad H_\mathrm{GR}= \frac{1}{2t}, \end{aligned}$$
(2.7)

where

$$\begin{aligned} A(T)=\eta \left( \frac{T}{T_\mathrm{ref}}\right) ^\nu , \quad \nu \equiv \frac{2(\varUpsilon +1)}{\varUpsilon }, \end{aligned}$$
(2.8)
$$\begin{aligned} \eta \equiv 2H_L t_L \left[ \left( \frac{4\pi ^3 g_*}{45}\right) ^{1/2}\frac{T_\mathrm{ref}^2}{M_\mathrm{Pl} H_L}\right] ^{\frac{\varUpsilon +1}{\varUpsilon }}. \end{aligned}$$

Here \(T_\mathrm{ref}\) is a reference temperature, which can be fixed for example as the BBN temperature \(T_\mathrm{BBN}\) (\(T_\mathrm{BBN}\simeq (10^{-2}\)–\(10^{-4})\) GeV). Inserting (2.5) into (2.3) one derives the expression for the characteristic relaxation time,

$$\begin{aligned} \tau H = \frac{1+\frac{\varUpsilon }{2Ht}}{3c_b^2+\frac{\varUpsilon (1+\varUpsilon )}{2H^2t^2}}. \end{aligned}$$
(2.9)

Before we investigate the gravitino problem, we focus on some aspects related to the cosmological model under consideration:

  • Due to the successful predictions of the BBN, we shall refer to the pre-BBN epoch since it is not directly constrained by cosmological observations. We require that at the instant \(t_*\) the Universe starts to evolve according to standard cosmological model, i.e. although the bulk viscosity effects are small during the radiation dominated era, we assume that at \(t>t_*\) the adiabatic index is exactly 1/3, so that they vanish. To determine \(t_*\), we set \(H(t_*)=H_\mathrm{GR}(t_*)\), which implies

    $$\begin{aligned} t_*=t_L\left( \frac{1}{2t_LH_L}\right) ^{\frac{1}{1+\varUpsilon }}, \quad \varUpsilon \ne -1. \end{aligned}$$
    (2.10)

    To preserve the BBN predictions, we then require \(t_* \lesssim t_\mathrm{BBN}\), where

    $$\begin{aligned} t_\mathrm{BBN}\simeq (10^{-2}\text {--}10^3) \text{ s }\sim (10^{22}-10^{27}) \text{ GeV }^{-1}. \end{aligned}$$

  • To get a first insight of the model (that considerably simplify the Boltzmann equation) we work in the regime \(|{\dot{T}}/T| > H\), where

    $$\begin{aligned} \frac{\dot{T}}{T}=\frac{\varUpsilon }{2t}=\frac{\varUpsilon }{2C t_L} \left( \frac{T}{M_\mathrm{Pl}}\right) ^{-\frac{2}{\varUpsilon }}. \end{aligned}$$
    (2.11)

    The condition \(|{\dot{T}}/T| > H\) occurs for

    $$\begin{aligned} t< {\tilde{t}}, \quad {\tilde{t}}\equiv t_L\left( \frac{|\varUpsilon |}{2t_LH_L}\right) ^{\frac{1}{1+\varUpsilon }}=|\varUpsilon |^{\frac{1}{1+\varUpsilon }}t_*. \end{aligned}$$
    (2.12)

3 Gravitino problem in cosmology with bulk viscosity

As pointed out in the Introduction, gravitino is generated by means of thermal scattering in the primordial plasma. This occurs during the reheating era after Inflation. To describe the gravitino production one makes use of the Boltzmann equation for the number density of species in a thermal bath. The relevant equation for gravitino production is

$$\begin{aligned} \frac{\mathrm{d} n_{3/2}}{\mathrm{d}t}+3Hn_{3/2}=\langle \sigma v \rangle n_{\text {rad}}^2. \end{aligned}$$
(3.1)

Here \(n_{3/2, \text {rad}}\) refers to gravitino and relativistic species, while \(\langle \ldots \rangle \) stands for the thermal average of the gravitino cross section \(\sigma \) times the relative velocity of scattering radiation (\(v \sim 1\)), \(\sigma v\sim M_\mathrm{Pl}^{-2}\). In (3.1) the term \(\displaystyle {\frac{m_{3/2}}{\langle E_{3/2}\rangle } \frac{n_{3/2}}{\tau _{3/2}}}\) has been neglected. Here \(\displaystyle {\frac{m_{3/2}}{\langle E_{3/2}\rangle }}\) is the average Lorentz factor. Introducing the abundances of the gravitino and of the relativistic particles, \(Y_{3/2}=n_{3/2}/s\) and \(Y_{\text {rad}}=n_{\text {rad}}/s\), respectively, the Boltzmann equation (3.1) assumes the form

$$\begin{aligned} \frac{\mathrm{d}Y_{3/2}}{\mathrm{d}T}+\frac{3}{{\dot{T}}}\left( \frac{{\dot{T}}}{T}+H\right) Y_{3/2}=\frac{ s \langle \sigma v \rangle }{{\dot{T}}} Y_{\text {rad}}^2. \end{aligned}$$
(3.2)

In the regime \(|{\dot{T}/T}|> H\) the Boltzmann equation (3.2) reduces to the form

$$\begin{aligned} \frac{\mathrm{d}Y_{3/2}}{\mathrm{d}T}+\frac{3}{T} Y_{3/2}=\frac{ s \langle \sigma v \rangle }{{\dot{T}}} Y_{\text {rad}}^2. \end{aligned}$$
(3.3)

The \(Y_{3/2}\)-term in (3.2) survives because the adiabatic condition is lost in the cosmological model under consideration, contrarily to the standard cosmology. By integrating from \(T_R\) (\(\gg \) \({\tilde{T}}\)) to the temperature \({\tilde{T}}\), where \({\tilde{T}} \gtrsim T_\mathrm{BBN}\) is the temperature corresponding to the instant \({\tilde{t}}\) defined in (2.12), we find that the general solution to (3.3) (with the initial condition \(Y_{3/2}(T_R)=0\)) is

$$\begin{aligned} Y_{3/2}(T={\tilde{T}}) = {\mathscr {B}} \, \varTheta _{\varUpsilon }(T_R, {\tilde{T}}), \end{aligned}$$
(3.4)

where

$$\begin{aligned}&\varTheta _{\varUpsilon } \equiv \left( \frac{{\tilde{T}}}{M_\mathrm{Pl}}\right) ^\varDelta - \left( \frac{T_{R}}{{\tilde{T}}}\right) ^3 \left( \frac{T_{R}}{M_\mathrm{Pl}}\right) ^\varDelta \end{aligned}$$
(3.5)
$$\begin{aligned}&\varDelta = 3+\frac{2}{\varUpsilon }, \end{aligned}$$
(3.6)
$$\begin{aligned}&{\mathscr {B}} \equiv \alpha _0 \alpha _L, \end{aligned}$$
(3.7)
$$\begin{aligned}&\alpha _0 \equiv \frac{2\pi ^2g_*}{45(1+3\varUpsilon )}\left( \frac{4\pi ^3g_*}{45}\right) ^{\frac{1}{2\varUpsilon }} \left[ M_\mathrm{Pl}^2 \langle \sigma v\rangle Y_{\text {rad}}^2\right] , \end{aligned}$$
(3.8)
$$\begin{aligned}&\alpha _L \equiv (M_\mathrm{Pl}t_L)\left( \frac{M_\mathrm{Pl}}{H_L}\right) ^{\frac{1}{\varUpsilon }}, \end{aligned}$$
(3.9)

with \(\alpha _0 \sim {\mathscr {O}}(0-1)\) for values of \(\varUpsilon \) here considered (the above relations hold for \(\varUpsilon \ne -1/3\)). From Eq. (2.10) one obtains an expression for \(t_L\) given by

$$\begin{aligned} t_L = t_* (2H_L t_*)^{\frac{1}{\varUpsilon }}, \end{aligned}$$
(3.10)

which inserted into (3.9) yields

$$\begin{aligned} \alpha _L=2^{\frac{1}{\varUpsilon }}(M_\mathrm{Pl} t_*)^{\frac{1+\varUpsilon }{\varUpsilon }}, \quad M_\mathrm{Pl} t_* \sim 10^{41} \quad \text {for } \ t_*=t_\mathrm{BBN}. \end{aligned}$$
(3.11)

Interestingly, \(\alpha _L\) is independent on free parameter \(t_L\) and \(H_L\).

Let us now determine the values of the gravitino abundance \(Y_{3/2}\) for different values of \(\varUpsilon \). First of all, it is simple to show that values of \(\varUpsilon >0\) yield \(Y_{3/2}<0\), which is physically not acceptable. Moreover, Eqs. (3.4)–(3.9) and (3.11) imply that \(\alpha _L \ll 1\) for \(\varUpsilon \) varying in the range \(-1< \varUpsilon < 0\). Consistently with the cosmological model with bulk viscosity here considered, we have also to analyze the behavior of the relaxation time \(\tau H\) during the evolution of the Universe. From (2.9) it turns out to be given by (\(t<{\tilde{t}}\) in the pre-BBN era)

$$\begin{aligned} \tau H = \frac{1+ \frac{\varUpsilon }{|\varUpsilon |}\frac{1}{x^{1+\varUpsilon }}}{3c_b^2 + \frac{2 \varUpsilon (1+\varUpsilon )}{|\varUpsilon |^2}\frac{1}{x^{2(1+\varUpsilon )}}}, \quad x = \left( \frac{t}{{\tilde{t}}}\right) <1. \end{aligned}$$
(3.12)

This function is plotted in Fig. 1, with \(c^2_b = 2/3\) and \(c^2_b = 10^{-5}\) (see Sect. 2). The parameters \(\{\varUpsilon , x\}\) have to assume values such thatFootnote 5 \(0\lesssim \tau H < 1\).

Fig. 1
figure 1

\(\tau H\) vs. \(\{\varUpsilon , x=t/{\tilde{t}}\}\) (see Eq. (3.12)), with \(-1< \varUpsilon <0\), \(0\lesssim x < 1\), and \(c_b^2=2/3\) (upper panel) and \(c_b^2=10^{-5}\) (lower panel)

Full size image

As it is clear from (3.4)–(3.9), the gravitino abundance is weakly depending on the reheating temperature \(T_R\) for a range of values of the parameter \(\varUpsilon \). Let us set \({\tilde{T}}=10^{\omega }\) GeV. In the case \(|\varUpsilon |\ll 1\), the gravitino abundance reads

$$\begin{aligned} Y_{3/2}\simeq \alpha _L \left( \frac{M_\mathrm{Pl}}{{\tilde{T}}}\right) ^\frac{2}{|\varUpsilon |}\simeq \left[ 2 \times 10^{-2(2+\omega )}\right] ^{\frac{1}{|\varUpsilon |}}, \end{aligned}$$

which implies \(\omega > -2\) in order that \(Y_{3/2}\ll 1\) and we solve the late abundance gravitino problem. Taking, for example, \(\omega =-1\) and \(|\varUpsilon |\sim 10^{-2}\) one gets \({\tilde{T}}\simeq 10^2\) MeV and the gravitino abundance \(Y_{3/2}({\tilde{T}})\) is completely negligible. Moreover, in the regime \(|\varUpsilon |\ll 1\) it follows that the relaxation time is \(\tau H\sim \frac{|\varUpsilon |x}{2}\ll 1\). As a specific example, consider \(\varUpsilon = -1/6\). In such a case the gravitino abundance \(Y_{3/2}\) is again weakly depending on the reheating temperature \(T_R\). Moreover, one has \(t_*=t_L(2t_L H_L)^{-6/5}\), \({\tilde{t}}\simeq t_*/10\), and the late gravitino abundance turns out to be \(Y_{3/2} \sim 10^{-18}\ll 1\). From Eqs. (2.5) and (2.10) one obtains

$$\begin{aligned} \tau H=\frac{1-\frac{1}{x^{5/6}}}{3c_b^2-\frac{10}{x^{5/3}}}, \quad x= \left( \frac{t}{{\tilde{t}}}\right) <1 . \end{aligned}$$
(3.13)

The function \(\tau H\) vs. x is plotted in Fig. 2 for different values of \(c_b^2\). As we can see, the relaxation time is, for all epochs before BBN \(t<{\tilde{t}}< t_*\), smaller than the Hubble time, i.e. \(\tau < H^{-1}\), as expected for a fluid description.

Fig. 2
figure 2

\(\tau H\) vs. \(x=t/{\tilde{t}}\) (see Eq. (3.13)), with \(0\lesssim x < 1\)

Full size image

As seen till now, particular values of \(\varUpsilon \) imply that the late gravitino abundance \(Y_{3/2}\) is independent (or weakly depending) on the reheating temperature \(T_R\). The latter, however, influences the evolution of \(Y_{3/2}\) for increasing values of \(\varUpsilon \). Consider, for example, the value \(\varUpsilon =-1/2\). From Eq. (3.4) it follows

$$\begin{aligned} Y_{3/2}\simeq 2.5\times 10^{-23}\frac{{\text {GeV}}}{\tilde{T}}\left( \frac{T_R}{\tilde{T}}\right) ^2, \end{aligned}$$
(3.14)

while \({\tilde{t}}\simeq t_*/4\). Notice that \(\varTheta _{\varUpsilon =-1/2}<0\) and \(\alpha _0 <0\), so that the two negative signs compensate to give a positive \(Y_{3/2}\) (see (3.5) and (3.8)). The behaviors of \(Y_{3/2}\) and \(\tau H\) are plotted in Fig. 3.

The above analysis refers to \(-2/3< \varUpsilon <0\), (\(\varDelta <0\)). Let us analyze now the regime \(-1 < \varUpsilon \leqslant -2/3\) (\(\varDelta \geqslant 0\)). For \(\varUpsilon =-2/3\) one obtains \({\tilde{t}}\simeq 0.3 t_*\), and

$$\begin{aligned} Y_{3/2}\simeq 1.1\times 10^{-21}\left( \frac{T_R}{\tilde{T}}\right) ^3. \end{aligned}$$

Requiring \(Y_{3/2}\lesssim 10^{-10}\) one infers \(T_R/{\tilde{T}}\lesssim 4.6\times 10^{3}\), i.e. to solve the late gravitino overproduction the temperature \({\tilde{T}}\) must be closer and closer to the reheating temperature \(T_R\), which does not seem a favorable scenario. Moreover, the relaxation time turns out to be \(\tau H\gtrsim {\mathscr {O}}(1)\), as arises from Fig. 1, making the model not suitable for the solution of the gravitino abundance, at least in the approximation \(|{\dot{T}}/T|>H\). A similar unfavorable scenario follows also for the cases \(-1< \varUpsilon <-2/3\) and \(\varUpsilon < -1\).

Fig. 3
figure 3

Upper panel \(Y_{3/2}\) vs. \(T_R/{\tilde{T}}\) (see Eq. (3.14)), for different values of \({\tilde{T}}\) such that \(T_R\gg {\tilde{T}}\). Lower panel \(\tau H\) vs. \(x=t/{\tilde{t}}\) (see Eq. (3.12)), with \(0\lesssim x < 1\)

Full size image

To summarize, the cosmological model with bulk viscosity provides favorable scenarios for solving the late overproduction of gravitinos in the case the parameter \(\varUpsilon \) falls down in the range \(-2/3 < \varUpsilon \lesssim 0\). In this case, in fact, the cosmological evolution of the Universe deviates considerably from the one based on the standard cosmological model (without bulk viscosity effects), as discussed in the previous section. The range of values \(-1 < \varUpsilon \leqslant -2/3\), \(\varUpsilon >0\) and \(\varUpsilon < -1\), instead, is excluded or partially acceptable, at least in the approximation here considered.

4 Conclusions

In this paper, we have reviewed the gravitino problem in a cosmological model in which bulk viscosity effects are taken into account. To avoid the late overproduction of the gravitinos by thermal scattering in the primordial plasma, we have exploited the fact that if the cosmic fluid is imperfect then the cosmic evolution of the Universe gets modified as compared with the case of perfect fluids (the expansion rate of the Universe can be written in the form \(H=A(T)H_\mathrm{GR}\), where the factor A(T) accounts for bulk viscosity effects). This affects the Boltzmann equation, which describes the time evolution of the gravitino abundance. Moreover, for some choice of the parameters, the late gravitino abundance is weakly depending on the reheating temperature. Cosmology with bulk viscosity provides therefore scenarios able to avoid the late overproduction of gravitinos. It will certainly be interesting to extend this analysis to the case of non-thermal perturbative gravitino production (see for example [84, 85]). This analysis will be addressed elsewhere.