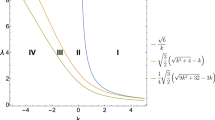
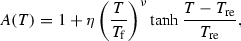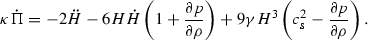Abstract
In this paper we discuss some consequences of cosmological models in which the primordial cosmic matter is described by a relativistic imperfect fluid. The latter takes into account the dissipative effects (bulk viscosity) arising from different cooling rates of the fluid components in the expanding Universe. We discuss, in particular, the effects of the bulk viscosity on Big Bang Nucleosynthesis and on the thermal relic abundance of particles, looking at recent results of PAMELA experiment. The latter has determined an anomalous excess of positron events, which cannot be explained by conventional cosmology and particle physics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Bulk viscous pressure in cosmic media arises as a consequence of the coupling among the different components of the cosmic substratum. Since these components have different internal equation of state, their cooling is different as the Universe expands, giving rise to a deviation of the system from equilibrium. The different cooling rates of the components generate a bulk viscous pressure of the cosmic medium as a whole, which for a homogeneous and isotropic Universe is the only possible dissipative phenomenon.Footnote 1 These dissipative processes are described in terms of an imperfect fluid (see [1–42] and references therein). In a FRW Universe, the dissipation is a scalar and can be therefore described as a bulk viscosity as referred to the thermodynamical approach [42].
Since bulk viscosity enters into the Einstein field equations, it is natural to expect that it may affects the evolution of the primordial Universe. Such a modification of the standard cosmology alters the thermal histories of (relic) particles, hence their abundance. This scenario can be realized before the Big Bang Nucleosynthesis (BBN) epoch, a period of the evolution of the Universe not directly constrained by cosmological observations. When the expansion rate of the Universe is enhanced (as compared to the one derived for a perfect fluid), thermal relics decouple with larger relic abundance. The change in the Hubble rate may therefore have its imprint on the relic abundance of dark matter, such as WIMPs, axions, heavy neutrinos, and so on. These studies are strongly motivated by recent astrophysical results which involve cosmic ray electrons and positrons [43–47], antiprotons [48], and \(\gamma \)-rays [49–51]. Particular attention is devoted to the presence of the peak in the cosmic positron spectrum at energies above 100 GeV observed in PAMELA experiment [43] (see also [52–60]). Moreover, in this paper the effects of the viscous Universe are also investigated in the framework of the Big Bang Nucleosynthesis (BBN), i.e. the primordial light element abundance such as \({}^3 He\), \({}^4 He\), \(D\), \({}^7 Li\), and in the framework of matter–antimatter asymmetry in the Universe referring in particular to the so called gravitational baryogenesis, a mechanism that gives rise to the origin of matter–antimatter asymmetry through a coupling between the baryon/lepton currents and the scalar curvature of the Universe.
The paper is organized as follows. In Sect. 2 we recall the main features of the bulk viscosity. In Sect. 3 we derive the constraints provided by Big Bang Nucleosynthesis. Section 4 is devoted to the analysis of relic thermal abundance, and we derive the order of magnitude of the mass of the dark matter particles required to explain the PAMELA experiment. In Sect. 5 we discuss an interesting aspect of bulk viscosity in connection with the origin of matter–antimatter asymmetry in the early Universe. Our conclusions are discussed in Sect. 6.
2 Imperfect fluid
The general form of the energy-momentum tensor is [61]
where \(\Pi \) is the scalar pressure (the bulk viscous pressure), \(h_{\alpha \beta }=g_{\alpha \beta }+u_\alpha u_\beta \) is the projector tensor, \(q^\alpha \) is related to the energy flux, \(\pi _{\alpha \beta }\) is the anisotropic stress. \(q^\alpha \) and \(\pi _{\alpha \beta }\) satisfy the relations
Symmetries related to an isotropic and homogeneous Universe impose \(q_\alpha =0=\pi _{\alpha \beta }\), and only the scalar dissipation \(\Pi \) is possible [42]. The energy-momentum conservation law \(T^{\alpha \beta }_{\,\,\,\,\,;\, \beta }=0\) reads
where the dot stands for the derivative with respect to the cosmic time and \(\Theta = u^\alpha _{\,\,\,\, ;\, \alpha }\).
In a homogeneous and isotropic (spatially flat) Universe, the Einstein equations read [61]
where \(H={\dot{a}}/{a}\) is the Hubble parameter and \(\kappa = 8\pi G= 8\pi m_\mathrm{P}^{-2}\) (\(m_\mathrm{P} \simeq 1.22 \times 10^{19}\) GeV is the Planck mass).
The general equation for the evolution of the Hubble parameter is given by [61]
where \(\tau \) is the relaxation time (the mean free time of the relativistic particle), which in general is time dependent, \(\tau =\tau (t)\),
\(c_\mathrm{b}^2\equiv \frac{\zeta }{(\rho +p)\tau }\) is the propagation velocity of a viscous pulse [62], and \(\zeta \) is the coefficient of the bulk viscosity. In a viscous medium the sound velocity is \(v^2 = c_\mathrm{s}^2+c_\mathrm{b}^2 \leqslant 1\), i.e. the sound propagates with a subluminal velocity. We also used \(\Theta =3H\).
In the ultra-relativistic regime (radiation dominated era) one has
where \(g_*\simeq 106.7\) are the relativistic degrees of freedom, the field equation (4) reads [61]
2.1 The universe with particle production
In this section we study the case of isentropic (or adiabatic) particle production, i.e. the number of particle is not conserved. Although the isentropic condition implies a constant entropy for particle, entropy production is still present because of the enlargement of the phase space of the system due to the increasing number of perfect fluid particles.
If the number of particles is not conserved, one has to use [61]
where \(\Gamma ={\dot{N}}/N\) and \(N=na^3\) (\(N\) is number of particles in the comoving volume \(a^3\)). \(\Gamma > 0\) (\(<\)0) means particle creation (annihilation). It is important to stress that a nonvanishing particle production rate gives rise to an effective bulk pressure of the cosmic fluid. Moreover, in a phenomenological description, \(\Gamma \) is an input quantity whose expression is calculated from the microphysics underlying the physical phenomena.Footnote 2
Using the Gibbs equation \(T\mathrm{d}s=\mathrm{d}\displaystyle {\frac{\rho }{n}}-p\, \mathrm{d}\displaystyle {\frac{1}{n}}\) and Eqs. (2) and (6) one gets
The condition \({\dot{s}}=0\) (isentropic particle production) implies that the viscous pressure is entirely determined by the particle production rate
It then follows [61]
In this description the cosmic substratum is a perfect fluid with varying particle number (and not a conventional dissipative fluid).
The combination of Eqs. (3) and (8) yields
The time evolution of the Hubble expansion rate \(H\) is given by [61]
This is the counterpart of (5) for \(\Gamma \ne 0\). In the particular case \(p=\rho /3\) and \(ns=(\rho +p)/T\), Eq. (12) reduces to the following expression:
3 Bulk viscosity and big bang nucleosynthesis constraints
Since pre BBN epoch is a period of the evolution of the Universe not directly constrained by cosmological observations, one has to require that the effects of bulk viscosity could be well manifested before the BBN starts, hence for times \(t_*\) (or temperatures \(T_*\)) smaller than those characterizing BBN: \(t_* \ll t_{\text {BBN}}\sim (10^{-2}\)–\(10^{2})\) s (or \(T_* \gg T_{\text {BBN}}\sim (10\)–\(0.1)\) MeV). However, it is worth to investigate what constraints the BBN provides once bulk viscosity effects are taken into account in the evolution of the Universe (this analysis is performed for a power law evolution of the scale factor \(a(t) \propto t^{\varsigma }\)).
During the BBN, the relevant weak interactions are governed by the processes
The weak interaction rate of particles in thermal equilibrium is given by [63, 64]
where
with \(m_{\mathrm{n,p}}\) the neutron and proton masses. Here
is the sum of the weak interaction rates.
To estimate the primordial mass fraction of \({}^4 He\), one usually defines [63, 64]
where \(\lambda =e^{-(t_\mathrm{n}-t_\mathrm{f})/\tau }\), \(t_\mathrm{f}\) and \(t_\mathrm{n}\) are the time of the freeze-out of the weak interactions and of the nucleosynthesis, respectively, \(\tau _\mathrm{n}\simeq 887\) s is the neutron mean life, and \(x(t_\mathrm{f})=e^{-\mathcal{Q}/T(t_\mathrm{f})}\) is the neutron to proton equilibrium ratio. The function \(\lambda (t)\) represents the fraction of neutrons that decay into protons in the time \(t\in [t_\mathrm{f}, t_\mathrm{n}]\). Deviations from \(Y_\mathrm{p}\) (generated by the variation of the freezing temperature \(T_\mathrm{f}\)) are given by
In the above equation we have set \(\delta T(t_\mathrm{n})=0\) because \(T_\mathrm{n}\) is fixed by the deuterium binding energy [65, 66]. By making use of the current estimation on \(Y_\mathrm{p}\) [67]
one obtains
Exact solutions of Eq. (4) are, in general, extremely difficult to determine. We make therefore the ansatz \(\omega \approx p/\rho \approx \partial p/\partial \rho \approx 1/3\) (the Universe evolves isotropically) and that the scale factor evolves, due to bulk viscosity, as \(a(t) \propto t^{\varsigma }\), where \(\varsigma =1/2+\delta \) with \(\delta \ll 1\). Therefore, the expansion rate of the Universe can be written in the form
where \( H_{\mathrm{GR}}=\frac{1}{2t}\) is the expansion rate obtained in General Relativity with perfect fluids. Imposing that the expansion rate of the Universe is equal of the interaction rate, \(\Lambda \simeq H\), one derives the freeze-out temperature \(T=T_\mathrm{f}(1+\frac{\delta T_\mathrm{f}}{T_\mathrm{f}})\), with \(T_\mathrm{f}\sim 0.6\) MeV and
i.e.
Hence, in the case \(\Gamma =0\), from Eq. (5) it follows that the relaxation time is given by \(\tau H = C \varsigma (1-2\varsigma )\), with \(C=\left[ \frac{17}{16}-\frac{3}{2}c_\mathrm{b}^2\right] ^{-1}\sim \mathcal{O}(1)\). For \(\Gamma \ne 0\), Eq. (13) implies \(\tau H = \frac{1}{3}\left( 1-\frac{1}{2\varsigma }\right) \left[ c_\mathrm{b}^2-\frac{1}{2}\left( 1-\frac{1}{2\varsigma }\right) \right] ^{-1}\) (this relation shows \(\tau H> 0\) provided \(c_\mathrm{b}> \frac{1}{2}\sqrt{\frac{2\varsigma -1}{\varsigma }}\) and \(\varsigma >1/2\), i.e. the internal fluid dynamics limits the amplitude of the effective viscous pressure [61]).
The trace of the energy-momentum tensor (Eq. 1) reads
which implies (\(R=-\kappa \mathcal{T}\))
Using the definition of the scalar curvature \(R=-6({\ddot{a}}/a+{\dot{a}}^2/a^2)\) and \(a\sim t^\varsigma \), one infers
hence
Both \(\tau \) and \(\Pi \) vanish in the limit \(\varsigma =1/2\) (\(\delta =0\)). Since
the dissipative \(\Pi \) term in (3) represents indeed a tiny perturbation to the energy density.
4 Dark matter relic abundance
As we have seen in the previous sections, scalar pressure can give rise to a different evolution of the early universe, which may deviate from the standard cosmology provided by general relativity. In this section we wish to discuss how these modifications of the standard cosmology affect the thermal relic abundance.
It is nowadays a very consolidate fact that our Universe is dominated by dark matter (as well as by dark energy, responsible of the accelerated expansion of the Universe), whose ratio with the critical density satisfies the bounds [68] \(0.092 \le \Omega _\mathrm{CDM} h^2 \le 0.124\), where \(h=100\) km s\(^{-1}\) Mpc\(^{-1}\) is the reduced Hubble constant. Favorite candidates for non-baryonic cold dark matter seem to be the weakly interacting massive particles (WIMPs), which decoupled from the thermal plasma in the early Universe. The interest in these particles as dark matter follows from the fact that the abundance of WIMPs in chemical equilibrium in the early Universe agrees with the expected one in the context of cold dark matter.
According to standard cosmology and particle physics, the calculation of the relic densities of particles is based on the assumption that the period of the Universe dominated by radiation began before the main production of relics and that the entropy of matter is conserved during this epoch and the subsequent one. Once these assumptions are relaxed, a different relic density of particles is expected. In this scenario, therefore, any contribution to the energy density modifies the Hubble expansion rate, which is reflected in a modification of the relic density values [69–78].
To account for the enhancement of the expansion rates, it is usual to write [77, 78]
Here \(H\) refers to the expansion rate of the cosmological model modified by bulk viscosity effects discussed in the previous sections, while \(H_\mathrm{GR}\) refers to the expansion rate of standard cosmology with perfect fluids.
The function \(A(T)\) assumes values greater than 1 (\(A(T) > 1\)) at large temperatures, and \(A(T)\rightarrow 1\) before BBN set up. The latter value is imposed by successful predictions of BBN on the abundance of primordial light elements. The function \(A(T)\) can be conveniently parameterized as [77, 78] (see also [79, 80])
where \(\eta \) and \(\nu \) are free parameters that characterize the specific cosmological model, and \(T_\mathrm{f}\simeq 17.3\) GeV is the normalization temperature: \(A(T_\mathrm{f})=1+\eta \). The factor \(1+\eta \) is hence the enhancement factor of the Hubble rate at the time of the WIMPs’ freeze-out.Footnote 3
To explain the PAMELA data, together with \(\Omega _\chi h^2 =\Omega h^2\big |^{\text {WMAP}}_{\text {CDM}}=0.1131\pm 0.0034\) [81] for dark matter annihilation into \(e^+ e^-\) (here \(\Omega \equiv \rho /\rho _\mathrm{c}\), where \(\rho _\mathrm{c} \simeq 8.1 \times 10^{-47}\) GeV\(^4\) is the critical energy density, and \(\chi \) refers to dark matter particles), the values of the parameter \(\eta \) must be [77, 78]
In this range, the values of the WIMPs dark matter masses are
In particular, one has
Let us now apply these results to an expanding Universe in presence of bulk viscosity, considering the cases of both \(\Gamma =0\) and \(\Gamma \ne 0\).
4.1 The case \(\Gamma =0\)
Owing to the presence of a scalar pressure, a tiny deviation from standard cosmological evolution is expected. Let us therefore assume that the evolution of the Universe during the radiation dominated era is governed by the scale factor \(a\sim t^\varsigma \). The Hubble expansion rate can be written as
i.e. it corresponds to an overall boost of the Hubble expansion rate. Equations (24) and (25) imply \(2\varsigma = 1+\eta \) and \(\nu =0\).
In particular, if one takes into account BBN constraints, Eq. (21), then it follows that \(\eta =2\delta \simeq 10^{-3}\), hence, according to (29), the dark matter mass satisfying this condition is of the order \(m_\chi \sim 10^2\) GeV.
4.2 The case \(\Gamma \ne 0\)
The ansatz for the scale factor \(a\sim t^\varsigma \) implies that during the radiation dominated era, the rates \(H\) and \(\Gamma \), related by Eq. (11), can be written in the form
Moreover, it also follows that
These relations imply \(\rho \sim T^4\).
The exponent \(\varsigma \) in the scalar factor \(a\) cannot be therefore arbitrary, but it is determined by Eq. (31). For simplicity we consider the case \(\Gamma = \alpha H\), with \(\alpha \ne 3\). One gets \(\varsigma =\frac{3}{2(3-\alpha )}\). For \(0 \leqslant \alpha < 3\), the Universe hence evolves more rapidly (\(a\sim t^{\frac{3}{2(3-\alpha )}}\)) with respect to the standard case (\(a\sim t^{1/2}\)), leading to an enhancement of the Hubble expansion rate. The latter is related to the standard one, \(H_\mathrm{GR}\), by the relation (30). Comparing with (24) and (25), one hence obtains
According to (28), the dark matter mass is the order of \(m_\chi \sim (10^2\)–\(10^3)\) GeV for \(\alpha \approx 3\), i.e. \(\eta \gg 1\), while \(\alpha \ll 1\), i.e. \(\eta <1\), yields \(m_\chi \sim 10^2\) GeV, as follows from (29).
4.3 A general solution for \(\Gamma =0\) and \(\Gamma \ne 0\)
In this section we discuss a more general solution to Eq. (5). During the pre-BBN, the expansion rate of the Universe can be parameterized as
where \(H_L\), \(t_L\), and \(\Upsilon \) are constants. The relation between the cosmic time and the temperature \(T\) follows from the field equation (3). One infers
It is straightforward to determine the enhancement factor \(A(T)\). Writing \(H = A(T) H_\mathrm{GR} = A(T)/ (2t) \), one immediately obtains
By fixing parameters entering into (36) one can obtain the conditions for which Eqs. (27), (28), and (29) are fulfilled. Therefore, dark matter particles with mass of the order of \((10^2\)–\(10^3)\) GeV can be accommodated in this model.
The characteristic time \(\tau (t)\) can be obtained by substituting (34) into Eq. (5),
To give an estimation of \(\tau H\), we consider some special cases:
(a) Taking \(\Upsilon \gg 1\), one gets \(\nu \sim 2\), \(t_L\sim \eta \displaystyle {\sqrt{\frac{45}{4\pi ^3 g_*}}\frac{m_\mathrm{P}}{T_\mathrm{f}}}\), from which it follows that \(\tau \sim t_L/\Upsilon \).
(b) In the opposite limit \(\Upsilon \ll 1\), and for \(H_L \lesssim H\), one infers \(\tau H\sim 1/3c_\mathrm{b}^2\).
Mutatis mutandis, similar results follow for \(\Gamma \ne 0\) by using (13), i.e. in the case of particle production.
5 Gravitational baryogenesis
In this section we would like discuss an interesting effect of the bulk viscosity related to the generation of baryon asymmetry. The origin of the baryon number asymmetry in the Universe is still an unsolved problem [64, 82–89]. The success of the big bang nucleosynthesis [90, 91] and the observations of Cosmic Microwave Background anisotropies (combined with the large structure of the Universe [92, 93]) show that the parameter characterizing such an asymmetry is of the order
where \(n_B\) (\(n_{\bar{B}}\)) is the baryon (antibaryon) number density and \(s\) the entropy of the Universe (\(s=2\pi ^2g_{*}T^3/45\)).
In this paper we refer to the model proposed in [94]. Here the baryon number asymmetry is due to a dynamical breaking of CPT (and CP) symmetry that is generated by the coupling of the derivative of the Ricci scalar curvature \(R\) with the baryon current \(J^\mu \) [94],
where \(M_*\) is the cutoff scale characterizing the effective theory. If there exist interactions that violate the baryon number \(B\) in thermal equilibrium, then a net baryon asymmetry can be generated and gets frozen in below the decoupling temperature \(T_\mathrm{D}\). Here the thermal equilibrium of interaction that violate \(B\) does not refer to those interactions that generate the bulk viscosity, as discussed in the Sect. 1. From (38) it follows that
where \({\dot{R}}=\mathrm{d}R/\mathrm{d}t\). The effective chemical potential for baryons and antibaryons is \(\mu _B={\dot{R}}/M_*^2 =-\mu _{\bar{B}}\), and the net baryon number density at the equilibrium turns out to be (as \(T\gg m_B\), where \(m_B\) is the baryon mass) \(n_B=g_\mathrm{b}\mu _B T^2/6\). \(g_\mathrm{b}\sim \mathcal{O}(1)\) is the number of intrinsic degrees of freedom of baryons. The baryon number to entropy ratio, which defines the baryon asymmetry, is therefore [94]
where \(g_*\sim 106.7\). The trace of the field equations gives
Deviations from the standard cosmology provide a non-vanishing \({\dot{R}}\), so that a net baryon asymmetry can be generated also during the radiation dominated era (\(\omega =1/3\)). Notice that casual effects are not relevant in this context. To compute \({\dot{\Pi }}\) we confine ourselves to the caseFootnote 4 \(\Gamma \ne 0\).
Using Eqs. (8) and (10), and taking \(\Gamma \sim H\) and \(M_* = m_\mathrm{P}/\sqrt{8\pi }\), it follows that
so that the baryon number asymmetry (39) is
The net baryon asymmetry (37) follows for a decoupling temperature of the order \(T_\mathrm{D}\sim 10^{-3}m_\mathrm{P}\), i.e. at GUT scales. An interesting model of baryogenesis related to bulk viscosity and noise has been discussed in [95–97].
6 Conclusion
In this paper we have analyzed some cosmological consequences of imperfect fluids, which are characterized by an energy-momentum tensor that contains, in general, the bulk viscosity pressure, the energy flux and the anisotropic stress. The bulk viscosity term, which we were mainly interested in, arises in mixture of matter (either of different species as in a radiative fluid or of the same species but with different energies as in a Maxwell–Boltzmann gas) or particle production.
Deviation from the standard cosmological evolution, induced in our case by scalar pressure, have important impact on the problem of dark matter in the Universe. The recent results of PAMELA experiment may be interpreted as identifying relic particles as the main constituents of dark matter. The scalar pressure generates in the early Universe an enhancement of the Hubble expansion rate, giving rise to thermal relics with a larger abundance. We have estimated that the mass of the WIMPs dark matter, required to explain the excess of positron events found in PAMELA experiment, must be \(\sim \)10\(^2\) GeV. Moreover, the consequences of the bulk viscosity on the big bang nucleosynthesis have been discussed for a Universe whose scale factor evolves as a power law, \(a(t)\sim t^\zeta \), yielding \(|\zeta -1/2| < 10^{-4}\), and, finally, we have shown that bulk viscosity effects could play a non-trivial role for the generation of the matter–antimatter asymmetry, at least in those models in which such an asymmetry is generated by means of a coupling of the curvature scalar derivative to the baryon current.
Notes
More specifically, bulk viscosity effects account for the rapid expansion or compression of a fluid ceasing to be in thermal equilibrium. As a consequence, the bulk viscosity gives a measure of the pressure that is necessary for restoring the equilibrium to a compressed or expanding system. This condition arises in a natural way in a cosmological expanding background, such as the early Universe.
A more realistic scenario requires one to consider a Universe with two or more fluids. For the case of two fluids, the continuity equations read
$$\begin{aligned} {\dot{\rho }}_i+\Theta (\rho _i+p_i)=\sum _i \varepsilon _i\Gamma _i \rho _i, \end{aligned}$$with \(i=1, 2\) and \(\varepsilon _1= 1=-\varepsilon _2\). Although these fluids do not separately satisfy the energy-momentum conservation, the total energy density does \({\dot{\rho }}+\Theta (\rho +p)=0\), with \(\rho \simeq \rho _1+\rho _2\) and \(p\simeq p_1+p_2\). In our case we are assuming for simplicity \(\rho \simeq \rho _1 \gg \rho _2\).
To be more precise, the function \(A(T)\) is parameterized such that for temperatures \(T>T_\mathrm{re}\) it assumes the form
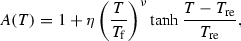
while for \(T\le T_{\mathrm{re}}\) it approaches 1. The temperature \(T_{\mathrm{re}}\) denotes the temperature at which the Hubble rate reenters the standard rate of general relativity, while \(T_\mathrm{f}\) is a reference temperature, assumed in [77, 78] as the temperature at which the WIMPs dark matter freezes out in the standard cosmology (\(T_\mathrm{f} \simeq 17.3\) GeV). In general, \(T_\mathrm{f}\) varies by varying the dark matter mass, \(m_\chi \). To avoid contradictions with big bang nucleosynthesis, it is required that \(T_{\mathrm{re}}\gtrsim 1\) MeV. Estimations carried out in [77, 78] have been obtained by setting \(T_{\mathrm{re}}=1\) MeV. In the regime \(T\gg T_{\mathrm{re}}\), the function (26) behaves as (25).
In the case \(\Gamma =0\) the expression of \(\Pi \) is [61] \(\kappa \Pi = -3\gamma H^2 -2 {\dot{H}}\), and its time derivative turns out to be
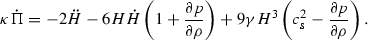
Assuming that during the pre-BBN the Universe evolves according to (34), direct calculations show that a net baryon asymmetry can be generated, and that the observed value (37) can be obtained for appropriate fine tuning of free parameters \(\{\Upsilon , H_L, t_L\}\). Instead, in the case in which the scale factor evolves as \(\sim t^\varsigma \), and BBN constraints are taking into account, a net baryon asymmetry is still generated, but it is too small with respect to the observed value (37).
References
W. Zimdahl, D.J. Schwarz, A.B. Balakin, D. Pavon, Phys. Rev. D 64, 063501 (2001)
R. Colistete, J.C. Fabris, J. Tossa, W. Zimdahl, Phys. Rev. D 76, 103516 (2007)
W. Zimdahl, A.B. Balakin, Phys. Rev. D 58, 063503 (1998)
W. Zimdahl, Phys. Rev. D 57, 2245 (1998)
D. Pavon, J. Triginer, W. Zimdahl, Phys. Rev. D 574, 6101 (1996)
P. Ilg, HCh. Ottinger, Phys. Rev. D 61, 023510 (1999)
R.F. Sawyer, Phys. Rev. D 74, 043527 (2006)
F.P. Wolvaardt, R. Marteens, arXiv:gr-qc/9611041
S. Nojiri, S.D. Odintsov, Phys. Rev. D 72, 023003 (2005)
S. Capozziello, V.F. Cardone, E. Elizalde, S. Nojiri, S.D. Odintsov, Phys. Rev. D 73, 043512 (2006)
I. Brevik, E. Elizalde, S. Nojiri, S.D. Odintsov, Phys. Rev. D 84, 103508 (2011)
S. Nojiri, S.D. Odintsov, Phys. Lett. B 639, 144 (2006)
S. Nojiri, S.D. Odintsov, Prog. Theor. Phys. Suppl. 190, 155 (2011)
K. Subramanian, J.D. Barrow, Phys. Rev. D 58, 083502 (1998)
J.R. Wilson, G.J. Mathews, G.M. Fuller, Phys. Rev. D 75, 043521 (2007)
S. Hofmann, D.J. Schwaarz, H. Stoker, Phys. Rev. D 64, 083507 (2001)
X. Chen, E.A. Spiegel, Mon. Not. R. Astron. Soc. 323, 865 (2001)
A. Avelino, U. Nucamendi, JCAP 04, 006 (2009)
A. Avelino, R. Garcia-Salcedo, T. Gonzalez, U. Nucamendi, I. Quiros, JCAP 1308, 012 (2013)
I. Brevik, Ø. Grøn, Relativistic Viscous Universe Models. arXiv:1409.8561 [gr-qc] (e-print)
I. Brevik, Ø. Grøn, Astrophys. Space Sci. 347, 399 (2013)
I.H. Brevik, S.V. Pettersen, Phys. Rev. D 61, 127305 (2000)
I.S. Kohli, M.C. Haslam, Phys. Rev. D 89, 043518 (2014)
R. Myrzakulov, L. Sebastiani, S. Zerbini, Galaxies 1, 93 (2013)
M.R. Setare, V. Kamali, Phys. Lett. B 736, 86 (2014)
M.R. Setare, V. Kamali, JHEP 1303, 066 (2013)
M.R. Setare, V. Kamali, Gen. Relat. Grav. 46, 1698 (2014)
M.R. Setare, V. Kamali, Warm-viscous inflation model on the brane in the light of BICEP2. arXiv:1312.2832 [physics.gen-ph] (e-print)
A. Tawfik, T. Harko, Phys. Rev. D 85, 084032 (2012)
T. Harko, M.K. Mak, Class. Quant. Grav. 20, 407 (2003)
H. Velten, Th.R.P. Carames, J.C. Fabris, L. Casarini, R.C. Batista, Structure formation in a \(\Lambda \) viscous CDM universe. arXiv:1410.3066 [astro-ph.CO] (e-print)
W.S. Hipolito-Ricaldi, H.E.S. Velten, W. Zimdahl, Phys. Rev. D 82, 063507 (2010)
C.P. Singh, S. Kumar, A. Pradhan, Class. Quant. Grav. 24, 455 (2007)
G.M. Kremer, F.P. Devecchi, Phys. Rev. D 67, 047301 (2003)
E. Elizalde, V.V. Obukhov, A.V. Timoshkin, Mod. Phys. Lett. A 29, 1450132 (2014)
V. Romano, D. Pavon, Phys. Rev. D 47, 1396 (1993)
V. Romano, D. Pavon, Phys. Rev. D 50, 2572 (1994)
J.C. Fabris, S.V.B. GonÃğalves, R. de Sa Ribeiro, Gen. Relat. Grav. 38, 495 (2006)
H. Okumara, F. Yonezawa, Phys. A 321, 207 (2003)
M. Giovannini, Phys. Lett. B 622, 349 (2005)
M. Bastero-Gil, A. Berera, I.G. Moss, R.O. Ramos, arXiv:1401.1149 [astro-ph.CO]
R. Marteens, Casual Thermodynamics in Relativity. arXiv:astro-ph/9609119
O. Adriani et al., arXiv:0810.4995 [astro-ph]
J. Chang et al., Nature 456, 362 (2008)
A.A. Abdo et al., The Fermi LAT Collaboration, Phys. Rev. Lett. 102, 181101 (2009)
F. Aharonian et al., H.E.S.S. Collaboration, Phys. Rev. Lett. 101, 261104 (2008)
F. Aharonian et al., H.E.S.S. Collaboration, Astron. Astrophys. 508, 561 (2009)
O. Adriani et al., Phys. Rev. Lett. 102, 051101 (2009)
F. Aharonian et al., Phys. Rev. Lett. 97, 221102 (2006)
T.A. Porter, F.T.F. Collaboration, arXiv:0907.0294 [astro-ph]
A.A. Abdo, Astrophys. J. 703, 1249 (2009)
N. Arkani-Hamed, D.P. Finkbeiner, T.R. Slatyer, N. Weiner, Phys. Rev. D 79, 015014 (2009)
B.E. Robertson, A.R. Zentner, Phys. Rev. D 79, 083525 (2009)
M. Cirelli, M. Kadastik, M. Raidal, A. Strumia, Nucl. Phys. B 813, 1 (2009)
I. Cholis, L. Goodenough, D. Hooper, M. Simet, N. Weiner, arXiv:0809.1683
F. Donato, D. Maurin, P. Braun, T. Delahaye, P. Salati, Phys. Rev. Lett. 102, 071301 (2009)
K. Ishiwata, S. Matsumoto, T. Moroi, arXiv:0811.0250
D. Hooper, P. Blasi, P.D. Serpico, arXiv:0810.1527
P. Blasi, Phys. Rev. Lett. 103, 051104 (2009)
P. Blasi, P.D. Serpico, Phys. Rev. Lett. 103, 081103 (2009)
W. Zimdahl, Phys. Rev. D 61, 083511 (2000)
W.A. Hiscock, L. Lindblom, Ann. Phys. (N.Y.) 151, 466 (1983)
J. Bernstein, L.S. Brown, G. Feinberg, Rev. Mod. Phys. 61, 25 (1989)
E.W Kolb, M.S. Turner, The Early Universe. (Addison-Wesley, New York, 1989)
D.F. Torres, H. Vucetich, A. Plastino, Phys. Rev. Lett. 79, 1588 (1997)
G. Lambiase, Phys. Rev. D 72, 087702 (2005)
A. Coc et al., Astrophys. J. 600, 544 (2004)
D.N. Spergel et al., WMAP Collaboration, arXiv:astro-ph/0603449
M. Kamionkowski, M.S. Turner, Phys. Rev. D 42, 3310 (1990)
D.I. Santiago, D. Kalligas, R.V. Wagoner, Phys. Rev. D 58, 124005 (1998)
S. Profumo, P. Ullio, JCAP 0311, 006 (2003)
P. Salati, Phys. Lett. B 571, 121 (2003)
R. Catena, N. Fornengo, A. Masiero, M. Pieroni, F. Rosati, Phys. Rev. D 70, 063519 (2004)
R. Catena, N. Fornengo, A. Masiero, M. Pietroni, M. Schelke, JHEP 10, 003 (2008)
G. Lambiase, JCAP 10, 028 (2012)
S. Capozziello, M. de Laurentis, G. Lambiase, Phys. Lett. B 715, 1 (2012)
R. Catena, N. Fornengo, M. Pato, L. Pieri, A. Masiero, Phys. Rev. D 81, 123522 (2010)
M. Schelke, R. Catena, N. Fornengo, A. Masiero, M. Pietroni, Phys. Rev. D 74, 083505 (2006)
G. Gelmini, P. Gondolo, arXiv:1009.3690 [astro-ph.CO]
G. D’Amico, M. Kamionkowski, K. Sigurdson, arXiv:0907.1912 [astro-ph.CO]
E. Komatsu et al., WMAP Collaboration, Astrophys. J. Suppl. 180, 330 (2009)
S. Davidson, E. Nardi, Y. Nir, Phys. Rep. 466, 105 (2008)
C.S. Fong, E. Nardi, A. Riotto, Adv. High Energy Phys. 2012, 158303 (2012)
W. Buchmuller, P. Di Bari, M. Plumacher, New J. Phys. 6, 105 (2004)
W. Buchmuller, P. Di Bari, M. Plumacher, Ann. Phys. 315, 305 (2005)
G. Lambiase, S. Mohanty, A.R. Prasanna, Int. J. Mod. Phys. D 22, 1330030 (2013)
J.M. Cline, arXiv:hep-ph/0609154
A.D. Dolgov, arXiv:hep-ph/0511213
A. Riotto, arXiv:hep-ph/9807454
C.J. Copi, D.N. Schramm, M.S. Turner, Science 267, 192 (1995). arXiv:astro-ph/9407006
S. Burles, K.M. Nollet, M.S. Turner, Phys. Rev. D 63, 063512 (2001)
D. N. Spergel et al., arXiv:astro-ph/0603449
C.L. Bennet et al., Astrophys. J. Suppl. Ser. 148, 15 (2003)
H. Davoudiasl, R. Kitano, G.D. Kribis, H. Murayama, P. Steinhardt, Phys. Rev. Lett. 93, 201301 (2004)
M. Bastero-Gil, A. Berera, R.O. Ramos, J.G. Rosa, JCAP 1410, 053 (2014)
M. Bastero-Gil, A. Berera, R.O. Ramos, J.G. Rosa, Phys. Lett. B 712, 425 (2012)
S. Bartrum, A. Berera, J.G. Rosa, arXiv:1412.5489 [hep-ph]
Acknowledgments
A.I. acknowledges the Czech Science Foundation (GAČR), Contract No. 14-07983S, for partial support. G.L. thanks the Agenzia Spaziale Italiana (ASI) for partial support through the contract ASI number I/034/12/0. The authors thank the referee for comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Iorio, A., Lambiase, G. Thermal relics in cosmology with bulk viscosity. Eur. Phys. J. C 75, 115 (2015). https://doi.org/10.1140/epjc/s10052-015-3337-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-015-3337-5