1 Introduction

In the early twentieth century, it was found that some principal questions could not be resolved by Newton’s theory. One of the most notable problems was the prediction of Mercury orbit’s orientation. Addressing these deficits, in 1915 Einstein published a tensorial theory of gravitation which is known as general relativity (GR). GR theory has been accepted as a principal method to define geometrical characteristics of space-time. Black holes and the existence of gravitational waves are the most considerable anticipations of GR theory. Recent observations of gravitational waves from a binary black hole merger by the LIGO and Virgo collaboration provided a firmly evidence of Einstein’s theory [1]. In order to have an effective GR theory, one needs the language of geometry. Hence, the approach one prefers is to concentrate on the technique of geometry without taking into account the complicated algebraic significances.

On the other hand, the coupling of the nonlinear sources and GR attracted much attention because of their specific properties. Interesting properties of various nonlinear electrodynamics have been studied before by many authors [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. One of the special classes of the nonlinear electrodynamic sources is the power-law Maxwell invariant (PMI), of which the Lagrangian is an arbitrary power of the Maxwell Lagrangian [26,27,28,29,30]. It is notable that this Lagrangian is invariant under the conformal transformation \(g_{\mu \nu }\longrightarrow \Omega ^{2}g_{\mu \nu }\) and \(A_{\mu }\longrightarrow A_{\mu }\), where \(g_{\mu \nu } \) and \(A_{\mu }\) are the metric tensor and the electromagnetic potential, respectively. This model is considerably richer than Maxwell theory, and in a special case (unit power), it reduces to a linear Maxwell field (see Refs. [26,27,28,29,30], for more details). The studies on the black object solutions coupled to the PMI field have got a lot of attention in the past decade [31,32,33,34,35,36].

Another attractive feature of the PMI theory is its conformal invariance, when the power of the Maxwell invariant is a quarter of space-time dimensions (\( (n+1)/4\), where \((n+1)\) is related to the dimensions of space-time). In other words, for the special choice of \(power = dimensions/4\) (\(s=(n+1)/4\), where s is the power of PMI), one obtains a traceless energy-momentum tensor which leads to conformal invariance. It is notable that the idea is to take advantage of the conformal symmetry to construct the analogs of 4-dimensional Reissner–Nordström solutions with an inverse square electric field in arbitrary dimensions (see Refs. [30, 37,38,39,40] for more details).

In recent years, increasing attention was given to black hole physics, specially its critical behavior and phase transition. Besides, interesting consequences of the AdS/CFT correspondence can motivate one to investigate the anti de Sitter space-time. The thermodynamical behavior of the black holes in asymptotically anti de Sitter space-time was studied first by Hawking and Page [41,42,43,44]. Generally, at the critical point where the phase transition occurs, discontinuity/divergency of a state space variable such as heat capacity is observed [45].

Recently, the consideration of the cosmological constant as a thermodynamical variable, pressure, opened up new avenues in studying black holes. It was possible to obtain a van der Waals like behavior and the second order phase transition in the thermodynamical phase structure of the black holes. In addition, it was shown that for specific black holes, reentrant of the phase transition and existence of triple point could be observed [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. The consideration of the cosmological constant as a thermodynamical variable has been supported by studies that are conducted in the context of the classical thermodynamics of the black holes and gauge/gravity duality [70,71,72,73,74]. One of the methods for obtaining van der Waals like critical points is through the use of the heat capacity with a relation between the cosmological constant and pressure [75]. This method has been employed in several papers and it was shown that its results are consistent with those obtained through regular methods.

On the other hand, geometrical thermodynamics (GT), which was first employed by Gibbs and Caratheodory, is another interesting way for investigation of the black hole phase transition. Regarding this method, one could build a phase space by employing the thermodynamical potential and its corresponding extensive parameters. Meanwhile, divergence points of the thermodynamical Ricci scalar provide information related to thermodynamic phase transition points. Historically speaking, first, Weinhold introduced a metric on the equilibrium thermodynamical phase space [76, 77] and after that, it was redefined by Ruppeiner from a different point of view [78, 79]. It is worthwhile to mention that there is a conformally relationship between Ruppeiner/Weinhold metric. One can see that the conformal factor is the inverse of the temperature [80]. None of Weinhold and Ruppeiner metrics were invariant under the Legendre transformation. The first Legendre invariance metric was introduced by Quevedo [81, 82], which can remove some problems of Weinhold/Ruppeiner methods. Although the Quevedo metric can solve some issues of the previous methods, it is confronted with other problems in specific systems. Therefore, in order to remove these problems, a new method was proposed in Refs. [83,84,85,86] which is known as the HPEM (Hendi–Panahiyan–Eslam Panah–Momennia) metric. In this paper, we want to study the thermal stability and phase transition in the context of the methods of GT and extended phase space for black holes in Einstein gravity with the PMI source in higher dimensions. It is notable that, in recent years, phase transition, curvatures, Hessian matrix, and Nambu brackets have been studied via a new GT method [87,88,89,90] which, here, we are not interested in.

The structure of this paper is as follows. First, we introduce the field equations and black hole solutions in Einstein–PMI gravity. Next, the temperature and heat capacity for the black hole solution obtained will be investigated and the stability will be studied. The Weinhold, Ruppeiner, and Quevedo metrics for studying geometrical thermodynamics of these black holes are employed. It will be seen that these metrics fail to provide fruitful results. So, we employ the HPEM metric and study the phase transition of these black holes in the context of GT. Next, the critical points are extracted through the use of the proportionality between the cosmological constant and pressure. Finally, we finish our paper with some closing remarks.

2 Field equations and solutions

The action of \((n+1)\)-dimensional Einstein gravity in the presence of a power-law Maxwell field with the negative cosmological constant can be written as

$$\begin{aligned} I=-\frac{1}{16\pi }\int \limits _{M}\mathrm{d}^{n+1}x\sqrt{-g}\left[ R-2\Lambda +(-F)^{s}\right] , \end{aligned}$$
(1)

where R is the Ricci scalar and s is a constant determining the nonlinearity power of the electromagnetic field. The Maxwell invariant is \(F=F_{\mu \nu }F^{\mu \nu }\), where \(F_{\mu \nu }\) is the electromagnetic tensor, which is equal to \(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\), and \(A_{\mu } \) is the gauge potential one-form. One can obtain the field equations by varying action (1) with respect to the gravitational and gauge fields, \(g_{\mu \nu }\) and \(A_{\mu }\), respectively,

$$\begin{aligned}&G_{\mu \nu }+\Lambda g_{\mu \nu } =T_{\mu \nu }, \end{aligned}$$
(2)
$$\begin{aligned}&\partial _{\mu }\left[ \sqrt{-g}(-F)^{s-1}F^{\mu \nu }\right] =0. \end{aligned}$$
(3)

In the presence of the nonlinear power-law Maxwell invariant field, one can show that the energy-momentum tensor becomes

$$\begin{aligned} T_{\mu \nu }=\left[ \frac{1}{2}g_{\mu \nu }(-F)^{s}+2sF_{\mu \sigma }F_{\nu }^{\sigma }(-F)^{s-1}\right] , \end{aligned}$$
(4)

and for the case of \(s=1\), Eqs. (2)–(4) reduce to well-known Einstein–Maxwell theory [91]. We apply the following static metric of \((n+1)\)-dimensional space-time:

$$\begin{aligned} \mathrm{d}s^{2}=-W(r)dt^{2}+ \frac{\mathrm{d}r^{2}}{W(r)}+{r^{2}}\mathrm{d}\Omega _{n-1}^{2} , \end{aligned}$$
(5)

where W(r) is an arbitrary function of the radial coordinate, which should be determined, and \(\mathrm{d}\Omega _{n-1}^{2}\) is the line element of the \((n-1)\)-dimensional hypersurface with volume \(\omega _{n-1}\) which has constant curvature \((n-1)(n-2)k\),

$$\begin{aligned} \mathrm{d}\Omega _{n-1}^{2}= & {} \left\{ \begin{array}{l@{\quad }l} \mathrm{d}\theta _{1}^{2}+\sum \nolimits _{i=2}^{n-1}\prod \nolimits _{j=1}^{i-1}\sin ^{2}\theta _{j}\mathrm{d}\theta _{i}^{2} &{} k=1 ,\\ \mathrm{d}\theta _{1}^{2}+\sinh ^{2}\theta _{1}\left[ \mathrm{d}\theta _{2}^{2}+\sum \nolimits _{i=3}^{n-1}\prod \nolimits _{j=2}^{i-1}\sin ^{2}\theta _{j}d\theta _{i}^{2}\right] &{} k=-1 ,\\ \sum \nolimits _{i=1}^{n-1}\mathrm{d}\phi _{i}^{2} &{} k=0. \end{array} \right. \nonumber \\ \end{aligned}$$
(6)

Regarding the constant k, one finds that the boundary of \(t=constant\) and \(r=constant\) can be a positive (spherical), negative (hyperbolic), and zero (flat) constant curvature hypersurface. Since we are going to obtain the electrically charged solutions, we consider the consistent gauge potential one-form as \(A=h(r)dt\). By considering this radial gauge potential, we find that the Maxwell invariant will be \(F=-\left( \frac{\mathrm{d}h(r)}{\mathrm{d}r}\right) ^{2}\), and therefore, regardless of the values of the nonlinearity parameter (s), the solutions are well defined. Now, taking into account the mentioned gauge potential with Eqs. (2) and (3), one can obtain the metric function as well as the electromagnetic field in the following forms [56]:

$$\begin{aligned} W(r)= & {} k-\frac{2\Lambda r^{2}}{n(n-1)}-\frac{m}{r^{n-2}}\nonumber \\&+\left\{ \begin{array}{ll} -\frac{2^{n/2}q^{n}}{r^{n-2}}\ln \left( \frac{r}{l}\right) &{} s=\frac{n}{2} ,\\ \frac{(2s-1)^{2}\left( \frac{(n-1)(2s-n)^{2}q^{2}}{(n-2)(2s-1)^{2}}\right) ^{s}}{r^{2(ns-3s+1)/(2s-1)}(n-1)(n-2s)} &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(7)
$$\begin{aligned} F_{tr}=\frac{\mathrm{d}h(r)}{\mathrm{d}r}=\left\{ \begin{array}{ll} -\frac{q}{r} &{} s=\frac{n}{2} ,\\ -q\left( \frac{2s-n}{2s-1}\right) \sqrt{\frac{\left( n-1\right) }{2(n-2)}} r^{-\left( \frac{n-1}{2s-1}\right) } &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(8)

where q and m are integration constants which are related to the electric charge (Q) and the ADM mass (M) of the black hole in the following manner:

$$\begin{aligned} M=\frac{(n-1)}{16\pi }m, \end{aligned}$$
(9)
$$\begin{aligned} Q=\left\{ \begin{array}{ll} \frac{n}{2\pi }2^{\frac{n-6}{2}}q^{n-1} &{} s=\frac{n}{2} ,\\ \frac{\sqrt{2}(2s-1)s}{8\pi }\left( \frac{n-1}{n-2}\right) ^{s-1/2}\left( \frac{(n-2s)q}{2s-1}\right) ^{2s-1} &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(10)

By using the area law, the black hole entropy could be determined as

$$\begin{aligned} S=\frac{r_{+}^{n-1}}{4}, \end{aligned}$$
(11)

where \(r_{+}\) is the radius of horizon (event horizon). We can also obtain the Hawking temperature of the black hole on the outer (event) horizon by using surface gravity interpretation

$$\begin{aligned} T= & {} \frac{1}{2\pi }\sqrt{-\frac{1}{2}\left( \nabla _{\mu }\chi _{\nu }\right) \left( \nabla ^{\mu }\chi ^{\nu }\right) }=\frac{W^{\prime }(r_{+}) }{4\pi } \nonumber \\= & {} \frac{\left( n-2\right) k}{4\pi r_{+}}-\frac{r_{+}\Lambda }{2\pi (n-1)}\nonumber \\&-\left\{ \begin{array}{l@{\quad }l} \frac{2^{\frac{n-4}{2}}q^{n}}{\pi r_{+}^{n-1}} \\ &{} s=\frac{n}{2}, \\ \frac{\left( 2s-1\right) }{4\pi (n-1)}\frac{\left( \frac{(n-1)(2s-n)^{2}q^{2} }{(n-2)(2s-1)^{2}}\right) ^{s}}{r_{+}^{(2s\left( n-2\right) +1)/(2s-1)}} &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(12)

where \(\chi =\partial _{t} \) is the Killing vector of the event horizon. Also, the black hole electric potential (U) could be measured at infinity with respect to the event horizon \(r_{+}\),

$$\begin{aligned} U=\left\{ \begin{array}{l@{\quad }l} -q\ln \left( \frac{r_{+}}{l}\right) &{} s=\frac{n}{2} ,\\ \sqrt{\frac{\left( n-1\right) }{2(n-2)}}\frac{q}{r_{+}^{(n-2s)/(2s-1)}} &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(13)

It is straightforward to show that these quantities satisfy the first law of thermodynamics,

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+U\mathrm{d}Q. \end{aligned}$$
(14)

The case where \(s=\frac{n}{2}\) is known as conformally invariant Maxwell (CIM). Throughout the paper, we will divide the solutions to the cases of CIM (where \(s=\frac{n}{2}\)) and PMI (\(s\ne \frac{n}{2}\)) solutions. In the following, by using the geometrical thermodynamics approach, we want to study the phase transitions of the black hole.

3 The thermodynamical structure

3.1 Temperature

3.1.1 PMI case

In the case of PMI, it is evident that the signature of the temperature depends on the choices of the different parameters. Here, for the AdS spherical case, the topological (\(\kappa \)) and the cosmological constant (\(\Lambda \)) terms are contributing to positivity of the temperature. Interestingly, for the charge term, depending on the choices of nonlinearity parameter, s, this term may contribute to the negativity or positivity of temperature. For \(s>1/2\), the charge term will always have a negative effect on the temperature, while, for violation of this condition, it will have a positive contribution. It is crucial to mention that this dual behavior is due to the contribution of the generalization to the nonlinear electromagnetic field. In other words, by setting \(s=1\), the charge term will only have a negative effect on the temperature (contribution to positivity does not exist). This highlights the effects of the nonlinear electromagnetic field on the thermodynamical structure of black holes. That being said, one can point out that, for violation of the mentioned condition, for spherically symmetric AdS black holes, the temperature will be positive without any root.

For small values of the horizon radius, the dominant term is the charge term, while, for large values of the horizon radius, the \(\Lambda \) term will be dominant. For spherically symmetric AdS space-time, \(\Lambda \) term is positive. Therefore, for large values of the horizon radius, the temperature will be positive. Therefore, there exists a root for the temperature, \(r_{0}\), in which for \(r_{+}<r_{0}\), the temperature is negative and solutions are not physical.

On the contrary, due to the negative contribution of the \(\Lambda \) in spherical dS space-time, the temperature will be negative for large values of the horizon radius. The effective term here is the topological term. In other words, by suitable choices of the different parameters, for a region of the horizon radius, the topological term would be dominant, which results into the formation of an extremum (maximum) and the existence of two roots. Between these two roots, the temperature is positive and solutions are physical (otherwise, the temperature is negative). It is worthwhile to mention that, for the hyperbolic horizon, the temperature will always be negative in this case. Therefore, there is no physical solution at all in this case.

Now, we focus on the effects of each parameter on negativity/positivity of the temperature. Evidently, by increasing dimensions, the effect of the topological and charge terms increase while the opposite takes place for \(\Lambda \). As for the nonlinearity parameter, for \(r_{+}>1\), if \(0.5<s<1\), then the effects of the charge term is an increasing function of s, while if \(1<s\), the effects of the charge term will be a decreasing function of s. It is worthwhile to mention that, for \(r_{+}<1,\) for both cases of \(0.5<s<1\) and \(1<s\), the charge term is a decreasing function of the nonlinearity parameter. We should point it out that we have excluded \(s=1\), since it is the Maxwell case. In addition, the effect of the charge term is an increasing function of the electric charge. Now, by considering the mentioned effects, one is able to determine the thermodynamical behavior of these black holes in the context of temperature and study different limits which these black holes have.

Fig. 1
figure 1

HPEM metric \(\mathcal {R}\) (dashed line), T (dotted line), \(\alpha \) (dashed-dotted line), and \(C_{Q}\) (continuous line) versus \( r_{+}\) for \(\Lambda =-1\), \(s=1.2\) and \(n=4\); left and middle panels \(q=0.1\), right panel \(q=1\) (for different scales)

Full size image

3.1.2 CIM case

In the CIM case, the contribution of the charged term is always toward negativity of the temperature. The dominant term for small values of the horizon radius is the charge term, which is negative. For medium and large values of the horizon radius, the dominant terms, respectively, are the topological and \(\Lambda \) terms. Considering the dominance of different terms, depending on the choices of topology and type of space-time, the temperature could be one of the following cases:

  1. (I)

    For dS space-time and \(k=0\), \(-1\), all the terms in temperature are negative. Therefore, the temperature will be negative and the solutions are not physical.

  2. (II)

    For dS space-time and \(k=1\), only the topological term is positive whereas the charge and \(\Lambda \) are negative. Remembering that, for small and large black holes, the dominant terms are q and \(\Lambda \) terms, it is possible to find two roots for the temperature and one maximum which is located at the positive values of temperature. This leads to presence of physical solutions only for medium black holes while, for large and small black holes, physical black holes are absent.

  3. (III)

    For AdS space-time, the \(\Lambda \) term has positive contribution. Remembering that, for small and large black holes, dominant terms are q and \(\Lambda \) terms, respectively, irrespective of the topological structure of the black holes, there exists a root for the temperature. For black holes smaller than this root, the temperature is negative and solutions are non-physical. For \(k=0\), \(-1\), the temperature is only an increasing function of the horizon radius. Whereas, by suitable choices of different parameters, in the case of \(k=1\), the temperature may acquire one or two extrema. The behavior of temperature in this case is similar to \(T-r_{+}\) diagrams in extended phase space (similar ones in van der Waals like black holes), which indicates that a second order phase transition takes place for these black holes. It is worthwhile to mention that extrema in temperature are matched with divergencies in the heat capacity which results into the existence of second order phase transition in the thermodynamical structure of the black holes.

3.2 Heat capacity and stability

Next, we study the stability conditions of these black holes. To do so, we employ the canonical ensemble which is based on the heat capacity. The stability conditions are determined by the behavior of heat capacity. In other words, the sign of the heat capacity represents thermal stability/instability of the system. The positivity indicates that system under consideration is in thermally stable state. In addition, there are two types of points which could be extracted by using the heat capacity: bound and phase transition points. The bound point is where the heat capacity (temperature) acquires a root. The reason for calling it bound point comes from the fact that it is where the sign of temperature is changed. Since the negative temperature is representing a non-physical solution, this point marks a bound point. On the other hand, phase transition point is where a discontinuity exists for the heat capacity.

The heat capacity is given by

$$\begin{aligned} C_{Q}=\frac{\left( \frac{\partial M}{\partial S}\right) _{Q}}{\left( \frac{ \partial ^{2}M}{\partial S^{2}}\right) _{Q}}=T\left( \frac{\partial S}{ \partial T}\right) _{Q}, \end{aligned}$$
(15)

where by employing Eqs. (11) and (12), one can find

$$\begin{aligned} C_{Q}=\left\{ \begin{array}{ll} -\frac{(n-1)(n-2)kr_{+}^{2n-3}-2\Lambda r_{+}^{2n-1}-2^{\frac{n}{2}}\left( n-1\right) q^{n}r_{+}^{n-1}}{4\left[ (n-2)kr_{+}^{n-2}+\frac{2\Lambda }{(n-1) }r_{+}^{n}-2^{\frac{n}{2}}\left( n-1\right) q^{n}\right] } &{} s=\frac{n}{2}, \\ -\frac{\left( n-1\right) (n-2)kr_{+}^{\frac{4ns-n+2}{2s-1}}-2\Lambda r_{+}^{ \frac{4s\left( n+1\right) -n}{2s-1}}-(2s-1)\left( \frac{(n-1)(n-2s)^{2}q^{2} }{(n-2)(2s-1)^{2}}\right) ^{s}r_{+}^{\frac{6s+n\left( 2s-1\right) }{2s-1}}}{4 \left[ (n-2)kr_{+}^{\frac{2(ns+1)}{2s-1}}+\frac{2\Lambda }{(n-1)}r_{+}^{ \frac{2s(n+2)}{2s-1}}-\frac{(2s\left( n-2\right) +1)}{(n-1)}\left( \frac{ (n-1)(n-2s)^{2}q^{2}}{(n-2)(2s-1)^{2}}\right) ^{s}r_{+}^{\frac{6s}{2s-1}} \right] r_{+}} &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(16)

3.2.1 PMI case

The positivity of the heat capacity is determined by the signature of denominator and numerator of it. Here, in order to have a positive heat capacity, two different cases could be considered; whether the numerator (A) and the denominator (B) are positive or both of them are negative (\(A\times B>0 \));

$$\begin{aligned} A= & {} 2\Lambda r_{+}^{\frac{4s\left( n+1\right) -n}{2s-1}}+(2s-1)\left( \frac{ (n-1)(n-2s)^{2}q^{2}}{(n-2)(2s-1)^{2}}\right) ^{s}\nonumber \\&\times r_{+}^{\frac{6s+n\left( 2s-1\right) }{2s-1}}-(n-1)(n-2)kr_{+}^{\frac{n\left( 4s-1\right) +2}{2s-1}}, \\ B= & {} (n-2)kr_{+}^{\frac{2(ns+1)}{2s-1}}+\frac{2\Lambda }{(n-1)}r_{+}^{\frac{ 2s(n+2)}{2s-1}}\nonumber \\&-\frac{(2s\left( n-2\right) +1)}{(n-1)}\left( \frac{ (n-1)(n-2s)^{2}q^{2}}{(n-2)(2s-1)^{2}}\right) ^{s}r_{+}^{\frac{6s}{2s-1}}. \end{aligned}$$

Therefore, two set of conditions should be satisfied to have a positive heat capacity, hence, thermally stable solutions. Due to complexity of the heat capacity obtained for the PMI case, it is not possible to extract bound and phase transition points analytically. Therefore, we employ numerical approach to study stability and obtain bound and phase transition points of these black holes. The results of numerical evaluation is presented in the diagrams of Figs. 1, 2, and 3.

Fig. 2
figure 2

HPEM metric \(\mathcal {R}\) (dashed line), T (dotted line), \(\alpha \) (dashed-dotted line), and \(C_{Q}\) (continuous line) versus \( r_{+}\) for \(\Lambda =-1\), \(q=1.1\) and \(n=4\); left panel \(s=0.9\), middle and right panels \(s=1.4\) (for different scales)

Full size image
Fig. 3
figure 3

HPEM metric \(\mathcal {R}\) (dashed line), T (dotted line), \(\alpha \) (dashed-dotted line), and \(C_{Q}\) (continuous line) versus \( r_{+}\) for \(\Lambda =-1\), \(q=1.1\) and \(s=1.2\); left panel \(n=4\), middle and right panels \(n=5\) (for different scales)

Full size image

Depending on the choices of the different parameters, for AdS space-time, the temperature could be only an increasing function of the horizon radius with one root (right panel of Fig. 1 and left panels of Figs. 2 and 3) or it may acquire extrema with one root (left and middle panels of Fig. 1; middle and right panels of Figs. 2 and 3). The temperature and heat capacity have the same root. This is the bound point. For \(r_{+}<r_{0}\) (\(r_{0}\) is the root), solutions have negative temperature and heat capacity. Therefore, in this region, solutions are non-physical ones.

For small values of q, the temperature will have two extrema. In places of these extrema, the heat capacity is divergent (left and middle panels of Fig. 1). In other words, in places of these extrema, the system has second order phase transitions. By increasing the electric charge, these extrema vanish and only a bound point will remain (right panel of Fig. 1). As for the nonlinearity parameter, its effects are opposite of those of the electric charge. In other words, by increasing the nonlinearity parameter, the extrema for the temperature and divergencies for the heat capacity are formed (middle and right panels of Fig. 2), while, for small values of this parameter, only the bound point is observed (left panel of Fig. 2). The effects of the dimensionality are similar to those observed for the nonlinearity parameter. This means that, by increasing dimensionality, two extrema are formed and the system will have second order phase transitions in its phase space in higher dimensions (Fig. 3).

Fig. 4
figure 4

HPEM metric \(\mathcal {R}\) (dashed line), T (dotted line), \(\alpha \) (dashed-dotted line), and \(C_{Q}\) (continuous line) versus \( r_{+}\) for \(\Lambda =-1\), \(l=1\), and \(n=4\); left and middle panels \(q=0.1\), right panel \(q=1\) (for different scales)

Full size image
Fig. 5
figure 5

HPEM metric \(\mathcal {R}\) (dashed line), T (dotted line), \(\alpha \) (dashed-dotted line) ,and \(C_{Q}\) (continuous line) versus \( r_{+}\) for \(\Lambda =-1\), \(q=1.1\) and \(l=1\); left panel \(n=4\), middle and right panels \(n=7\) (for different scales)

Full size image

As for stability, if only a bound point is observed, physical stable solutions are observed only for \(r_{0}<r_{+}\). The formation of extrema modifies the stability conditions of these black holes. In this case, bound point and two divergencies of the heat capacity determine the stable regions and phase transitions. Between the bound point and the smaller divergence point, both temperature and heat capacity are positive. Therefore, the solutions are physical and stable in this region. On the other hand, between two divergencies, the temperature is positive, while the heat capacity is negative, which leads to solutions being physical and unstable. Finally after the larger divergency, both heat capacity and temperature are positive and solutions are stable. The thermodynamical concepts indicate that the system in an unstable state has a phase transition and acquires stability. By taking this matter into account, in the case of a smaller divergency a phase transition of larger to smaller takes place, while the reverse happens in a larger divergency.

3.2.2 CIM case

First, let us study the conditions for the positivity/negativity of the solutions. In order to have positive heat capacity, one needs to satisfy \( A^{\prime }\times B^{\prime }>0\), in which

$$\begin{aligned} A^{\prime }= & {} 2\Lambda r_{+}^{2n-1}+2^{\frac{n}{2}}\left( n-1\right) q^{n}r_{+}^{n-1}-(n-1)(n-2)kr_{+}^{2n-3}, \\ B^{\prime }= & {} (n-2)kr_{+}^{n-2}+\frac{2\Lambda }{(n-1)}r_{+}^{n}-2^{\frac{n }{2}}\left( n-1\right) q^{n}, \end{aligned}$$

where \(A^{\prime }\) and \(B^{\prime }\) are, respectively, the numerator and the denominator of the heat capacity.

It is not possible to obtain roots and divergencies of the heat capacity for this case, analytically. Therefore, we employ numerical methods and plot diagrams for studying the effects of different parameters in Figs. 4 and 5.

It is evident that, for small q, the temperature has one root with two extrema. The roots of temperature and heat capacity coincide, while the extrema of the temperature are matched with the divergencies of the heat capacity. These divergencies are phase transition points. Increasing the electric charge leads to elimination of the phase transition points, while there exists a root for the temperature and heat capacity (see Fig. 4 for more details). The opposite behavior is observed for the effects of dimensionality. This means that, by increasing dimensionality, the system with one bound point acquires one root and two divergencies. In other words, by increasing dimensions, the thermodynamical structure of the black holes is modified and black holes will have a second order phase transition in their phase diagrams (Fig. 5).

3.3 Geometrical thermodynamics

Regarding ordinary laboratory systems (short-range interaction property; entropy proportional to volume), it is expected that one may obtain the same thermodynamic properties for all ensembles. However, taking into account the holography conception, one finds that black holes are not ordinary systems (long-range interaction property; entropy proportional to area) [94,95,96,97,98,99,100]. Therefore, one may obtain different results in the context of various ensembles of the black hole thermodynamics [101]. Regardless of tracing ensemble dependency, it was shown that there are some extra poles (or mismatch with other methods) in the Ricci scalar of Weinhold, Ruppeiner, and Quevedo metrics. The existence of these anomalies/mismatches motivate one to build another Legendre invariant thermodynamic metric, which can be conformally related to the Quevedo metric. The HPEM metric is the same as the Quevedo metric up to a conformal factor. Since the differences in the conformal factor come from the mass and its derivatives, it is expected that HPEM enjoys Legendre invariance, but with a different Legendre multiplier. It is also worthwhile to mention that the Legendre invariance alone is not sufficient to guarantee a unique picture of thermodynamical metrics in terms of their curvatures [102]. In other words, in addition to Legendre invariance, we need to require curvature invariance under a change of representation. As a result, it will be worthwhile to consider the investigation of both Legendre and curvature invariances.

Here, we will employ the geometrical thermodynamics to study both bound and phase transition points of these black holes. The geometrical thermodynamics is based on constructing phase space by using one of the thermodynamical quantities as the thermodynamical potential. The information regarding bound and phase transition points are stored in the Ricci scalar of this phase space. In other words, the divergencies of this Ricci scalar present bound and phase transition points. (For more details regarding the meaning of the curvature scalar in geometrical thermodynamics, we refer the reader to Ref. [92]). Depending on the choice of the thermodynamical potential, the components of the phase space differ (this is due to the fact that each thermodynamical quantity has its specific extensive parameters). There are several well-known methods for constructing a phase space; see Weinhold [76, 77], Ruppeiner [78, 79], Quevedo [81, 82], and HPEM [83,84,85,86]. In order to investigate the thermodynamical properties of the system, the successful method has divergencies which exactly are matched with bound and phase transition points. The mentioned well-known thermodynamical metrics in the context of geometrical thermodynamics are given by

$$\begin{aligned} \mathrm{d}s^{2}=\left\{ \begin{array}{l@{\quad }l} Mg_{ab}^{W}\mathrm{d}X^{a}\mathrm{d}X^{b} &{} \mathrm{Weinhold} ,\\ -T^{-1}Mg_{ab}^{R}\mathrm{d}X^{a}\mathrm{d}X^{b} &{} \mathrm{Ruppeiner}, \\ \left( SM_{S}+QM_{Q}\right) \left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) &{} \mathrm{Quevedo} \\ S\frac{M_{S}}{M_{QQ}^{3}}\left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) , &{} \mathrm{HPEM} \end{array} \right. \end{aligned}$$
(17)

in which \(M_{X}=\partial M/\partial X\) and \(M_{XX}=\partial ^{2}M/\partial X^{2}\). The denominators of their Ricci scalars will be [83]

$$\begin{aligned} denom(\mathcal {R})=\left\{ \begin{array}{l@{\quad }l} M^{2}\left( M_{SS}M_{QQ}-M_{SQ}^{2}\right) ^{2} &{} \mathrm{Weinhold} ,\\ M^{2}T\left( M_{SS}M_{QQ}-M_{SQ}^{2}\right) ^{2} &{} \mathrm{Ruppeiner} ,\\ M_{SS}^{2}M_{QQ}^{2}\left( SM_{S}+QM_{Q}\right) ^{3} &{} \mathrm{Quevedo}, \\ 2S^{3}M_{SS}^{2}M_{S}^{3} &{} \mathrm{HPEM}. \end{array} \right. \end{aligned}$$
(18)
Fig. 6
figure 6

\(\mathcal {R}\) (dashed line), T (dotted line), and \(C_{Q}\) (continuous line) versus \(r_{+}\) for \(\Lambda =-1\), \(s=1.2\), \(q=0.5\) and \(n=4\); left Weinhold metric, right panel Quevedo metric (for different scales)

Full size image

It is worthwhile to mention that Weinhold and Ruppeiner metrics were formally introduced as the Hessian of the internal energy (mass) and entropy, respectively,

$$\begin{aligned} \mathrm{d}s^{2}=\left\{ \begin{array}{l@{\quad }l} \frac{\partial ^{2} M}{\partial X^{a} \partial X^{b}}\mathrm{d}X^{a}\mathrm{d}X^{b} &{} \mathrm{Weinhold} ,\\ -\frac{\partial ^{2} S}{\partial X^{a} \partial X^{b}}\mathrm{d}X^{a}\mathrm{d}X^{b} &{}\mathrm{Ruppeiner}.\\ \end{array} \right. \end{aligned}$$
(19)

Later, it was shown that these two methods are conformally related by adding terms which could be seen in Eq. (17). In this paper, we employ the forms which are given in Eq. (17) for the Weinhold and Ruppeiner methods.

Before we continue our study, it is worthwhile to make a few remarks regarding HPEM metric. The HPEM and Quevedo metrics have similar structures up to a conformal factor with the same signature, which is (\(-+++\cdots \)). In Ref. [93], it was shown that it is possible to obtain an infinite number of Legendre invariant metrics. The simplest way to construct Legendre invariant metrics is to apply a conformal transformation. Considering the similar structure of the HPEM and Quevedo metrics with the same signature, it is expected that, with a different Legendre multiplier, HPEM also enjoys Legendre invariance. The studies conducted in the context of HPEM metric showed that signature of the curvature scalar of this metric around divergencies provides the possibility of recognizing the type of phase transition (smaller to larger or vice versa). In addition, by studying signature, it is possible to differ bound and phase transition points from one another. These differences in signature around divergencies also enables one to have a picture regarding stability/instability of the black holes. One of the main properties of this metric is to include bound points in its divergencies. This results into having a better and more complete picture regarding thermodynamical structure of the black holes comparing to previous metrics. In addition, it was shown that the results of this metric is in agreement with other methods of studying thermodynamical structure of the black holes such as the heat capacity, van der Waals like diagrams, etc. [75, 103, 104].

The existence of \(M_{S}\) and \(M_{SS}\) in the denominator of the HPEM metric ensures that bound and phase transition points are matched with divergencies of the Ricci scalar without any extra divergency. As for Quevedo metric, since \( M_{SS}\) is present in the denominator of the this metric, phase transition points are matched with divergencies of the Ricci scalar. On the other hand, the bound points are matched only when

$$\begin{aligned} M_{S}=-\frac{QM_{Q}}{S}, \end{aligned}$$
(20)

which in general is not satisfied. In addition, the presence of \( M_{QQ}\) may lead to existence of extra divergencies which are not matched with bound and phase transition points. Such a case has been reported for several black holes before [83,84,85,86]. Analytical evaluation shows that \(M_{QQ}\) for these black holes will not lead to any extra divergency, but \(M_{S}=-\frac{QM_{Q}}{S}\) is not satisfied.

Recently, in Ref. [105], it was pointed out that Quevedo metric should have the following form instead of the one pointed out in Eq. (17):

$$\begin{aligned} \mathrm{d}s^{2}=M\left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) , \end{aligned}$$
(21)

where the denominator of its Ricci scalar will be

$$\begin{aligned} denom(\mathcal {R})=M^{3}M_{SS}^{2}M_{QQ}^{2}. \end{aligned}$$
(22)

Here, the condition which was observed for the previous case (20) is eliminated for the Ricci scalar. The divergencies of the heat capacity are included through the presence of the \(M_{SS}^{2}\) term. Meanwhile, the existence of \(M_{QQ}\) results in the presence of divergencies for the Ricci scalar, which are not consistent with any phase transition point. Recently, by several studies it was shown that it is possible for the mass of the black holes to have root(s) [106, 107]. This indicates that, for this form of the Quevedo metric, the existence of M and its roots may provide the possibility of the existence of divergencies in its Ricci scalar which are not matched with any phase transition point. Therefore, cases of mismatch between the divergencies of the Ricci scalar of this Quevedo metric and phase transition points are possible. It is worthwhile to mention that this case of the Quevedo metric does not include bound points in the divergencies of its Ricci scalar.

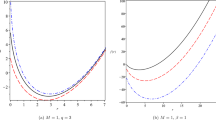
In the cases of Weinhold and Ruppeiner, it was not analytically possible to see whether divergencies of the Ricci scalars of these methods coincide completely with bound and phase transition points. Therefore, we employed numerical methods and plotted some diagrams (see Fig. 6).

Evidently, employing the Weinhold and Quevedo metrics will lead to inconsistent results regarding bound and phase transition points. In other words, by taking a closer look at the plotted diagrams (see Fig. 6), it is obvious that there is a mismatch between the divergencies of the Ricci scalar of the Weinhold metric and bound and phase transition points. In addition, the Quevedo metrics fail to produce a divergency in its Ricci scalar, which is in coincidence with the bound point. On the contrary, divergencies of the Ricci scalar of the HPEM metric coincide with the bound and phase transition points completely (see Figs. 1, 2, 3, 4, and 5).

One of the interesting properties of the HPEM metric is the behavior of its Ricci scalar around bound and phase transition points. If the divergency is related to the phase transition of larger to smaller black holes, the signature of the Ricci scalar around it is positive. On the contrary, for a phase transition of smaller to larger black holes, the sign of the Ricci scalar around this divergence point is negative. As for the bound point, interestingly, the signature of the Ricci scalar changes around this divergence point. These changes in the signature of the Ricci scalar enable one to recognize the type of points without prior knowledge regarding the heat capacity. As for Ruppeiner, since it has a conformal relation with the Weinhold metric, the same results are applicable for the phase transition points. But, due to the existence of the temperature in the denominator of the Ricci scalar of Ruppeiner, the bound points are matched with some of the divergencies.

To summarize, we saw that employing the Weinhold, Ruppeiner, and Quevedo metrics leads to the existence of divergencies in the Ricci scalar which are not matched with the obtained bound and phase transitions of the heat capacity, while the HPEM metric provides a consistent number of divergencies in the places of bound and phase transition points. Furthermore, the characteristic behavior of the Ricci scalar of the HPEM metric enables one to recognize the type of point and phase transition.

3.4 Critical behavior in extended phase space

In this section, we will conduct a study regarding the possible existence of critical and van der Waals like behavior for the solutions. Recently, there has been a novel interpretation for the cosmological constant in AdS black holes. Instead of considering this parameter as a fixed one, it was proposed to consider it as a thermodynamical variable. By doing so, the thermodynamical structure of the black holes is enriched and it is possible to introduce new phenomenologies, such as van der Waals like behavior and a phase transition for black holes. The van der Waals like behavior of these black holes through the usual method was investigated in Ref. [56]. Here, we would like to study critical values through a new method which was introduced in Ref. [75]. In this method, the cosmological constant is replaced by its proportional pressure in the heat capacity. Then, by using the denominator of the heat capacity and solving it with respect to the pressure, a relation for the pressure is obtained which is different from the usual equation of state. The maximum of this relation marks a place in which phase transition takes place. In other words, the maximum of this relation in the P–\(r_{+}\) diagram corresponds to the critical pressure. This method was employed in several papers and it was shown to have results consistent with those extracted through the usual methods [75, 103, 104].

The proportionality between the cosmological constant and the pressure is given by

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }. \end{aligned}$$
(23)

By replacing the cosmological constant with its corresponding thermodynamical pressure, the mass of the black holes will play the role of enthalpy instead of internal energy. Using this new concept for the mass of the black holes, it is a matter of calculation to obtain the volume of the black holes, conjugate to the thermodynamical pressure, in the following form:

$$\begin{aligned} V=\left( \frac{\partial H}{\partial P} \right) =\left( \frac{\partial M}{\partial P} \right) =\frac{r_{+}^{n-2}}{n-2}. \end{aligned}$$
(24)

Evidently, the volume is a smooth function of the horizon radius and it is only horizon radius and dimension dependent. This relation between the horizon radius and volume provides the possibility of employing the horizon radius instead of the volume to study phase diagrams of the black holes. In other words, the horizon radii in which the system has a phase transition could be used to obtain the critical volume of our thermodynamical systems.

Now, by using the heat capacity (16) with (23) and solving the denominator of the heat capacity with respect to thermodynamical pressure, one obtains the following relation for the pressure:

$$\begin{aligned}&P=\left\{ \begin{array}{l@{\quad }l} \frac{\left( n-1\right) }{16\pi r_{+}^{n}}\left[ \left( n-2\right) kr_{+}^{n-2}-2^{\frac{n}{2}}\left( n-1\right) q^{n}\right] &{} s=\frac{n}{2} ,\\ \frac{\left( 2\left( 2-n\right) s-1\right) \left[ \frac{(n-1)(n-2s)^{2}q^{2} }{(n-2)(2s-1)^{2}}\right] ^{s}r_{+}^{\frac{6s}{2s-1}}+k(n-1)(n-2)r_{+}^{ \frac{2\left( ns+1\right) }{2s-1}}}{16\pi r_{+}^{\frac{2s(n+2)}{2s-1}}} &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(25)
Fig. 7
figure 7

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(n=3\), and \(s=1.2\); \(q=0.9\) (continuous line), \(q=1\) (dashed line), and \(q=1.1\) (dotted line)

Full size image

Using this relation, we are in a position to study the possible existence of phase transition for these black holes. The relation for the pressure obtained consists two terms: a charge term and a topological term. The charge term has always negative contribution to pressure. Therefore, the existence of critical behavior is determined by the topological term. That being said, one can automatically conclude that, for \(k=0,-1\), no critical behavior exists. In other words, for these two cases, the pressure will be negative, which indicates that no critical behavior is observed. Regarding the fact that maximum of the pressure (25) is where a second order phase transition takes place, one can, analytically, show that the maximum of this pressure is located at the following horizon radius:

$$\begin{aligned}&r_\mathrm{critical/\max }=\left\{ \begin{array}{l@{\quad }l} \left( \frac{2^{\frac{\left( n-2\right) }{2}}n\left( n-1\right) q^{n}}{k(n-2) }\right) ^{\frac{1}{n-2}} &{} s=\frac{n}{2} ,\\ \left( \frac{2s^{2}(n-2)+s}{k(n-2)(2s-1)}\right) ^{\frac{2s-1}{s(n-3)+1} }\left( \frac{(n-1)(n-2s)^{2}}{(n-2)(2s-1)^{2}}q^{2}\right) ^{\frac{s(2s-1)}{ s(n-3)+1}} &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(26)

where by replacing the horizon radius, one finds

$$\begin{aligned} P_\mathrm{critical/\max }= & {} \left\{ \begin{array}{l@{\quad }l} \frac{k\left( n-1\right) (n-2)^{2}}{16n\pi }\left( \frac{2^{\frac{\left( n-2\right) }{2}}n\left( n-1\right) q^{n}}{k(n-2)}\right) ^{\frac{2}{2-n}} &{} s=\frac{n}{2} ,\\ \frac{{k}^{{\frac{s(n+1)-1}{s(n-3)+1}}}{\Upsilon }}{16\pi (2s-1)^{{\frac{ 2-8s^{2}}{1+(n-3)s}}}}\left( 1-\frac{2k\left[ \frac{(n-2)(2s-1)^{2}}{(n-1)} \right] ^{{\frac{(n-3)s^{2}+(n-2)s+1}{s(n-3)+1}}}}{s^{2}\left[ 2s(n-2)+1 \right] \left[ q^{2}(n-2s)^{2}\right] ^{s}}\right) &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(27)

in which

$$\begin{aligned} {\Upsilon }=\frac{(n-2)^{{\frac{4s^{2}+s(n-1)-1}{1+(n-3)s}}}(n-1)^{{\frac{ 1-4s^{2}+s(n-1)}{1+(n-3)s}}}}{\left\{ q^{2s}(n-2s)^{2s}\left[ 1+2s(n-2) \right] s\right\} ^{{\frac{2(2s-1)}{1+\left( n-3\right) s}}}}. \end{aligned}$$

The relation obtained for the critical pressure indicates that the positivity of critical pressure is subject to variation of different parameters. It is evident that, for a Ricci-flat horizon (\(k=0\)), there is no positive critical pressure, whereas, for \(k=-1\), one can obtain a real positive critical pressure when \(\frac{s(n+1)-1}{s(n-3)+1}\in \mathbb {N}\). In the case of a spherical horizon (\(k=1\)), the sign of \(P_\mathrm{critical/\max }\) depends on the values of the nonlinearity, dimensionality, and electric charge. One may find that, for sufficiently large values of q, s, and n, the second term will be less than one and one can obtain a positive critical pressure, while, for the usual values of the parameter mentioned, \(P_\mathrm{critical/\max }\) can be negative and one concludes there is no critical behavior. In order to show the effects of different parameters on the critical behavior of the system, we plot various P–\(r_{+}\) and P–T diagrams (Figs. 7, 8, 9, and 10).

Fig. 8
figure 8

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(s=1.2\), and \(q=1.1\); \(n=3\) (continuous line), \(n=4\) (dashed line), and \(n=5\) (dotted line)

Full size image
Fig. 9
figure 9

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(n=3\), and \(q=1.1\); \(s=0.7\) (continuous line), \(s=0.8\) (dashed line), and \(s=0.9\) (dotted line)

Full size image
Fig. 10
figure 10

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(n=3\), and \(q=1.1\); \(s=1.1\) (continuous line), \(s=1.2\) (dashed line), and \(s=1.25\) (dotted line)

Full size image
Fig. 11
figure 11

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(n=3\), and \(l=1\); \(q=0.9\) (continuous line), \(q=1\) (dashed line), and \(q=1.1\) (dotted line)

Full size image
Fig. 12
figure 12

Left panel P versus \(r_{+}\) diagrams; right panel P versus T diagrams. For \(k=1\), \(l=1\), and \(q=1.1\); \(n=4\) (continuous line), \(n=5\) (dashed line), and \(n=6\) (dotted line)

Full size image

Evidently, critical pressure is a decreasing function of the electric charge while its corresponding critical horizon radius is an increasing function of this parameter (left panel of Fig. 7). As for the effects of dimensionality, one can see that both critical horizon radius and pressure are increasing functions of this parameter (left panel of Fig. 8). The effects of the nonlinearity parameter should be separated into two branches; for \(0.5<s<1,\) the critical pressure is a decreasing function of s,  while the corresponding critical horizon is an increasing function of it (left panel of Fig. 9). On the contrary, for \(1<s\), the critical pressure is an increasing function of the nonlinearity parameter whereas its critical horizon radius is a decreasing function of it (left panel of Fig. 10). These opposite behaviors for these two branches highlight the differences between this nonlinear electromagnetic field and the Born–Infeld like case in which the effects of the nonlinearity parameter are fixed.

As for the CIM case, evidently, critical temperature and pressure are decreasing functions of the electric charge, while the critical horizon radius is an increasing function of it (Fig. 11). The effects of dimensionality is opposite of the variation of electric charge. This means that the critical pressure and temperature are increasing functions of the dimensionality, while the critical horizon radius is a decreasing function of this parameter (Fig. 12).

3.5 van der Waals properties

In this subsection, we will investigate some van der Waals like properties of the solutions in the extended phase space. By the presence of pressure in the thermodynamical quantities and having equation of state at hand, one is able to extract the volume expansion coefficient, speed of sound, and isothermal compressibility coefficient of these black holes.

The volume expansion coefficient is calculated at constant pressure and it represents changes in volume of the black holes which take place due to heat transfer. The volume expansion coefficients for the two cases of this paper are given by [108]

$$\begin{aligned}&\alpha =\frac{1}{V}\left( \frac{\partial V}{\partial T}\right) _{P}=\left\{ \begin{array}{l@{\quad }l} \,{\frac{4\pi n\left( n-1\right) \,{r}_{+}^{n+1}}{16\,\pi \,P{r} _{+}^{n+2}-k\left( n-1\right) \left( n-2\right) {r}_{+}^{n}+{q}^{n}{2} ^{n/2}\left( n\left( n-2\right) +{1}\right) {r}_{+}^{2}},} &{} s=\frac{n}{2} ,\\ \frac{4\pi \,n\,\left( n-1\right) {r}_{+}^{{\frac{2\,s\left( n-2\right) +1}{ 2\,s-1}}}}{16\pi P\,{r}_{+}^{\,{\frac{2s\left( n-1\right) }{2\,s-1}} }-k\left( n-1\right) \left( n-2\right) {r}_{+}^{{\frac{2\left( s\left( n-3\right) +1\right) }{2\,s-1}}}+\frac{\left( {q}^{2}\left( n-1\right) \left( n-2\,s\right) ^{2\,}\right) ^{s}\left( 2\,s\left( n-2\right) +1\right) }{\left( n-2\right) ^{s}\left( 2\,s-1\right) ^{2\,s}}}, &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(28)

The isothermal compressibility coefficient is calculated at constant temperature and it represents the corresponding effects of the variation in volume with respect to change in pressure. Here, one can obtain this coefficient as [108]

$$\begin{aligned} \kappa _{T}=-\frac{1}{V}\left( \frac{\partial V}{\partial P}\right) _{T}=\left\{ \begin{array}{l@{\quad }l} {\frac{16\pi n{r}_{+}^{n+2}}{16\,\pi \,P{r}_{+}^{n+2}-k\left( n-1\right) \left( n-2\right) {r}_{+}^{n}+{2}^{n/2}{q}^{n}\left( n\left( n-2\right) +{1} \right) {r}_{+}^{2}}}, &{} s=\frac{n}{2} ,\\ \frac{16\pi n\,{r}_{+}^{{\frac{2s\left( n-1\right) }{2\,s-1}}}}{16\pi \,P{r} _{+}^{{\frac{2s\left( n-1\right) }{2\,s-1}}}-k\left( n-1\right) \left( n-2\right) {r}_{+}^{{\frac{2\left( s\left( n-3\right) +1\right) }{2\,s-1}}}+ \frac{\left( {q}^{2}\left( n-1\right) \left( n-2\,s\right) ^{2}\right) ^{s}\left( 2\,s\left( n-2\right) +1\right) }{\left( n-2\right) ^{s}\left( 2\,s-1\right) ^{2\,s}}}, &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$
(29)

where we have employed

$$\begin{aligned} \left( \frac{\partial V}{\partial P}\right) _{T}\left( \frac{\partial P}{ \partial T}\right) _{V}\left( \frac{\partial T}{\partial V}\right) _{P}=-1. \end{aligned}$$
(30)

The speed of sound in black holes does not have the usual meaning. Here, while the area of the black holes is fixed, the speed of sound indicates a breathing mode for variation of the volume with pressure. For obtaining the speed of sound, one should first calculate the homogeneous density, which, for the two cases here, can be written as [109, 110]

$$\begin{aligned} \rho =\frac{M}{V}=\left\{ \begin{array}{l@{\quad }l} P+{\frac{kn\left( n-1\right) }{16\pi \,{r}_{+}^{2}}}-{\frac{{2}^{n/2\,}{q} ^{n}n\,\left( n-1\right) \ln \left( \frac{r_{+}}{l}\right) }{16\pi \,{r} _{+}^{n}},} &{} s=\frac{n}{2}, \\ P+{\frac{n\left( n-1\right) \,k}{16\pi \,{r}_{+}^{2}}}+\frac{n\,\left( {q} ^{2}\left( n-1\right) \left( n-2\,s\right) ^{2\,}\right) ^{s}\left( 2\,s-1\right) ^{2}}{16{\pi }\left( n-2\right) ^{s}\left( 2\,s-1\right) ^{2\,s}\left( n-2\,s\right) {r}_{+}^{{\frac{2\,s\left( n-1\right) +1}{2\,s-1} }}}, &{} \mathrm{otherwise}.\\ \end{array} \right. \end{aligned}$$
(31)

Now, by employing the method of Refs. [109, 110], we obtain

$$\begin{aligned} c_{s}^{-2}=\frac{\partial \rho }{\partial P }=1+\rho \kappa , \end{aligned}$$
(32)

which confirms that the speed of sound for these black holes is in the valid region of \(0\le c_{s}^{2}\le 1\).

The volume expansion and isothermal compressibility coefficients obtained have identical denominators. Therefore, their divergencies are matched. Here, we focus only on the volume expansion coefficient. In order to have a better picture regarding the meaning of divergencies and the sign of this quantity, we have plotted its diagrams with the heat capacity and the Ricci scalar of HPEM metric in Figs. 1, 2, 3, 4, and 5 (dashed-dotted lines).

First of all, as one can see, the divergencies of volume expansion coefficient and heat capacity match. This shows that phase transition points that are observed in the heat capacity could be detected by studying the divergencies of the volume expansion coefficient as well. In other words, the divergencies of the volume expansion coefficient mark points in which black holes have a second order phase transition. In the absence of a divergency for the volume expansion coefficient, this quantity is positive valued. On the contrary, when this quantity acquires divergences, its sign changes at the divergence points. By taking a closer look at the phase diagrams, one can see that the regions in which black holes are stable, the volume expansion coefficient is positive valued. On the contrary, in the unstable regions (negative heat capacity), the sign of the volume expansion coefficient is negative. Here, we see that the sign of the heat capacity and the volume expansion coefficient are identical in the physical regions (positive), while in the non-physical region (negative temperature), there is a difference between the signs of these two quantities. It is worthwhile to mention that, for the negative volume expansion coefficient, the speed of sound will exceed the speed of light which is not physically acceptable. This indicates that between the two divergencies, no physical black hole solutions exist.

Evidently, different approaches toward studying the critical behavior of black holes yield consistent results regarding the number and places of phase transition points. But, as one can see, each one of the phase diagrams carries specific information regarding the thermodynamical structure and properties of the black holes which could not be acquired by other phase diagrams. Therefore, for having a better and more complete picture regarding thermodynamical behavior/structure/properties of the black holes, studying different phase diagrams is necessary and crucial.

4 Conclusion

In this paper, we have investigated the thermodynamical structure of Einstein black holes in the presence of the PMI nonlinear electromagnetic field through new techniques.

It was shown that the behavior of the temperature and stability conditions for these black holes were functions of different parameters describing the phase structure of these black holes. Interestingly, it was shown that the nonlinearity of the system and the electric charge are two opposing factors in phase structure of these black holes. This behavior precisely highlights the differences between this theory of the nonlinear electromagnetic field and Born–Infeld like theories. In Born–Infeld theories, the effects of nonlinearity parameter and electric charge are similar. Here, we see that in PMI theory, these effects are mutually opposite.

Next, geometrical thermodynamics was employed to investigate the thermodynamical behavior of these black holes. It was pointed out that employing the Ruppeiner, Weinhold, and Quevedo metrics will lead to anomaly while using HPEM metric, one obtains consistent results. The properties of the HPEM metric around bound and phase transition points were highlighted as well. It was shown that (un)changing the sign of the thermodynamical Ricci scalar around divergence points helps one to distinguish a bound point from phase transition ones.

In addition, the proportionality between the cosmological constant and the thermodynamical pressure in the denominator of the heat capacity was employed to extract a relation for thermodynamical pressure (independent of equation of state). Using the new pressure relation, it was possible to study the critical behavior of the black hole system. Besides, the effects of the different parameters on the critical pressure and horizon radius were investigated and it was shown that positivity of critical pressure and horizon radius were subjects to the choices of the different parameters. In other words, it was possible to eliminate the existence of the second order phase transition in the phase space of these black holes by specific choices of different parameters.

Finally, we have conducted a study regarding the thermodynamical properties of these black holes including the volume expansion coefficient, speed of sound, and isothermal compressibility coefficient. We have pointed out that divergencies of the volume expansion coefficient were matched with phase transition points in the heat capacity. This leads to a coincidence between divergencies of the Ricci scalar of the HPEM and volume expansion coefficient. Furthermore, we showed that the signs of the volume expansion coefficient were the same as that of the heat capacity in physical regions (\(T>0\)), while in the non-physical region (\(T<0\)), these two signs were opposite.

The thermodynamical behavior that we observed here highly depends on the choices of the nonlinearity parameter. In specific regions of the nonlinearity parameter we observed a series of the effects which were modified in other regions for the nonlinearity parameter. This characteristic behavior is not observed in a Born–Infeld like family of the nonlinear electromagnetic fields. This means that the PMI theory not only differs from Born–Infeld like theories in form, but the characteristic behavior is different and is only observed in this theory of the nonlinear electromagnetic field. These modifications in the thermodynamical behavior of the black holes signal the fact that the evolution of black holes in this theory is different from other charged black holes. Therefore, the trace of these differences may be observable in properties such as quasi-normal modes, gravitational waves, and Hawking radiation and provide interesting case studies in other aspects of physics such as gauge/gravity duality.