1 Introduction

The study of relativistic quantum systems under the influence of magnetic field and scalar potentials has attracted attention of researchers in various branches of physics. It is well known that these potentials can be inserted into the Dirac equation,

$$\begin{aligned}{}[\beta \varvec{\gamma }\cdot \mathbf {p}+\beta M] \psi ( \mathbf {r}) =E\psi ( \mathbf {r}), \end{aligned}$$
(1)

through the three usual substitutions, known as minimal, vector, and scalar couplings, whose representation is denoted, respectively, by

$$\begin{aligned}&\mathbf {p} \rightarrow \mathbf {p}-e\mathbf {A},\end{aligned}$$
(2)
$$\begin{aligned}&E \rightarrow E-V(r), \end{aligned}$$
(3)
$$\begin{aligned}&M \rightarrow M+S(r). \end{aligned}$$
(4)

With this representation, a variety of relativistic and nonrelativistic effects can be studied. Moreover, these couplings differ in the manner how they are inserted into the Dirac equation [1]. The minimal coupling (2) is useful for studying the dynamics of a spin-1/2 charged particle in a magnetic field. For example, using this model, we can study Landau levels [2], the Aharonov–Bohm effect [3], the quantum Hall effect [4], and other effects associated with a magnetic field.

It is well known that the prescription (3) acts differently on electron and positron states, respectively, and the eigenvalue spectrum of the particle is not symmetric. In this case, bound states exist for only one of the two kinds of particles. In other words, we can say that, for vector coupling, the potential couples to the charge. In the context of the Dirac equation, this coupling has been used, for example, to study the influence of a harmonic oscillator on the Aharonov–Casher problem [5], the Aharonov–Bohm effect for a spin-1/2 particle in the case that a 1 / r potential is present [6], the effects of nongauge potentials on the spin-1/2 Aharonov–Bohm problem [7], quasiclassical theory of the Dirac equation with applications in the physics of heavy-light mesons [8], and confining potentials with a pure vector coupling [9]. In the Schrödinger theory, it also has important applications, such as: the dynamics of an electron in a two-dimensional quantum ring [10, 11], quantum particles constrained to move on a conical surface [12], and the effect of singular potentials on the harmonic oscillator [13].

In the case of the scalar coupling (4), it is added to the mass term of the Dirac equation and, therefore, it can be interpreted as an effective, position-dependent mass and, furthermore, it also acts equally on particles and antiparticles. This coupling has been used, for example, to obtain an exact solution of the Dirac equation for a charged particle with position-dependent mass in the Coulomb field [14], to study the relativistic quantum dynamics of a charged particle in cosmic string spacetime [15, 16], scattering of a fermion in the background of a smooth step potential with a general mixing of vector and scalar Lorentz structures with the scalar coupling stronger than or equal to the vector coupling [17], inclusion of the generalized Hulthén potential in the case of the smooth step mass distribution [18], and the extension of PT-symmetric quantum mechanics [19]. The coupling (4) also has important applications in nonrelativistic quantum mechanics. The Schrödinger equation with a position-dependent mass has attracted a lot of attention due to the wide range of applications in various areas of material science and condensed matter physics. For example, it was used to study the dynamics of an one-dimensional harmonic oscillator [20], the derivation of the Shannon entropy for a particle with a nonuniform solitonic mass density [21], the displacement operator for quantum systems [22, 23], the use of instantaneous Galilean invariance to derive the expression for the Hamiltonian of an electron [24], the determination of some potential functions for exactly solvable nonrelativistic problems [25], and the Hermitian, rotationally invariant one-band Schrödinger Hamiltonian [26].

The cases in which the couplings are composed by a vector (3) and a scalar (4) potential, with \(S=V (S=-V)\), are usually pointed out as necessary condition for the occurrence of exact spin (pseudospin) symmetry. It is well known that the spin and pseudospin symmetries are SU(2) symmetries of a Dirac Hamiltonian with vector and scalar potentials. The pseudospin symmetry was introduced in nuclear physics many years ago [27, 28] to account for the degeneracies of orbitals in single-particle spectra. Also, it is known that the spin symmetry occurs in the spectrum of a meson with one heavy quark [29] and an anti-nucleon bound in a nucleus [30], and the pseudospin symmetry occurs in the spectrum of nuclei [31].

In this work, we study the quantum dynamics of a spin-1/2 charged particle in the presence of a magnetic field with scalar and vector couplings. This system has been considered in Ref. [32]. The difference between our approach and that one is that, here, we solve the problem in a rigorous way taking into account other questions which have not been analyzed by the authors. For example, we address the absence of the term which depends explicitly on the spin in the equation of motion. Since we are considering the dynamics of a particle with spin, such a term cannot be neglected in the equation of motion [33]. Moreover, as the authors make a connection with the Aharonov–Bohm problem, the presence of this term has important implications on the physical quantities of interest, such as energy eigenvalues, the scattering matrix, and the phase shift (see Ref. [34] for more details). By taking into account the term that depends explicitly on the spin in the Pauli equation, we address the system in connection with the spin-1/2 Aharonov–Bohm problem [35] and analyze the questions of (a) the existence of isolated solutions to the first order equation Dirac, and (b) the general dynamics in all space, including the \(r=0\) region. We use the self-adjoint extension method to determine the most relevant physical quantities, such as the energy spectrum and wave functions by applying boundary conditions allowed by the system. The self-adjoint extension method is very useful to address physical systems whose Hamiltonian involves some singular term, such as, for example, in monopole fields [36, 37], fermions in an Aharonov–Bohm field [38, 39], and in fermion–soliton systems with position-dependent mass [40, 41].

The paper is organized as follows. In Sect. 2, we consider the Dirac equation in \((2+1)\) dimensions with minimal, scalar, and vector couplings, and we derive the set of first order differential equations. These equations are useful to investigate possible isolated solutions to the problem. In Sect. 3, we solve the first order Dirac equation in connection with the Aharonov–Bohm problem and scalar and vector couplings. We found that, for certain values assumed by the physical parameters of the system, isolated solutions exist, and we discuss the limits of validity of them. In Sect. 4, we derive the Pauli equation and study the dynamics of the system taking into account exact symmetry spin and pseudospin limits. In Sect. 5, we briefly discuss some concepts of the self-adjoint extension method and specify the boundary conditions at the origin which will be used. In Sect. 6, the expressions for the energy eigenvalues and wave functions are determined for both symmetry limits, and we compare them with the results of Ref. [32]. We verify that the presence of the spin element in the equation of motion introduces a correction in the expressions for the bound state energy eigenvalues. In Sect. 7, we present our concluding remarks.

2 Equation of motion

We begin with the Dirac equation (1) in \((2+1)\) dimensions in polar coordinates (\(\hbar =c=1\)),

$$\begin{aligned} \left\{ \beta \varvec{\gamma }\cdot {\varvec{\pi }}+\beta \left[ M+S(r) \right] \right\} \psi (\mathbf {r}) =\left[ E-V(r) \right] \psi (\mathbf {r}) , \end{aligned}$$
(5)

where \({\varvec{\pi }}=\left( {{\pi }} _{r}, {{\pi }}_{\varphi }\right) =(-i\partial _{r},-i\partial _{\varphi }/r-eA_{\varphi })\), \(\mathbf {r}=(r,\varphi )\), and \(\psi \) is a two-component spinor. The \(\varvec{\gamma }\) matrices in Eq. (5) are given in terms of the Pauli matrices as [42]

$$\begin{aligned}&\beta \gamma ^{r}=\sigma _{1}\cos \varphi +s\sigma _{2}\sin \varphi =\left( \begin{array}{c@{\quad }c} 0 &{} e^{-is\varphi }\\ e^{+is\varphi } &{} 0 \end{array} \right) , \end{aligned}$$
(6)
$$\begin{aligned}&\beta \gamma ^{\varphi } =-\sigma _{1}\cos \varphi +s\sigma _{2}\sin \varphi =\left( \begin{array}{c@{\quad }c} 0 &{} -ise^{-is\varphi }\\ ise^{+is\varphi } &{} 0 \end{array} \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\beta =\sigma _{3}=\left( \begin{array}{c@{\quad }c} 1 &{} 0\\ 0 &{} -1 \end{array} \right) , \end{aligned}$$
(8)

where s is twice the spin value, with \(s=+1\) for spin “up” and \(s=-1\) for spin “down”. Equation (5) can be written more explicitly as

$$\begin{aligned} e^{-is\varphi }[ \pi _{r}-is\pi _{\varphi }] \psi _{2}= & {} \left[ E-M-\varSigma (r) \right] \psi _{1}, \end{aligned}$$
(9)
$$\begin{aligned} e^{+is\varphi }[ \pi _{r}+is\pi _{\varphi }] \psi _{1}= & {} \left[ E+M-\varDelta (r) \right] \psi _{2}, \end{aligned}$$
(10)

where \(\varSigma (r) =V(r) +S(r) \) and \( \varDelta (r) =V(r) -S(r) \).

If one adopts the following decomposition:

$$\begin{aligned} \left( \begin{array}{c} \psi _{1} \\ \psi _{2} \end{array} \right) =\left( \begin{array}{c} \textstyle \sum \limits _{m}f_{m}(r)\;e^{im\varphi } \\ \textstyle i\sum \limits _{m}g_{m}(r)\;e^{i(m+s)\varphi } \end{array} \right) , \end{aligned}$$
(11)

with \(m+1/2=\pm 1/2,\pm 3/2,\ldots \), with \(m\in \mathbb {Z}\), and inserts this into Eqs. (9) and (10), one obtains

$$\begin{aligned}&\left[ \frac{\mathrm{d}}{\mathrm{d}r}+\frac{s\left( m+s\right) }{r}-esA_{\varphi }\right] g(r)=\left[ E-M-\varSigma (r) \right] f(r),\end{aligned}$$
(12)
$$\begin{aligned}&\left[ -\frac{\mathrm{d}}{\mathrm{d}r}+\frac{sm}{r}-esA_{\varphi }\right] f(r)=\left[ E+M-\varDelta (r) \right] g(r). \end{aligned}$$
(13)

Note that the above equations are coupled. However, if \(\varSigma (r) \) or \(\varDelta (r) \) is made zero in any of the equations, we can uncouple them easily. We will see below that this results in important physical consequences for the physical system in question.

3 Isolated solutions for the Dirac equation of motion

In this section, we investigate the existence of isolated solutions in the quantum motion of a fermionic massive charged particle in \((2+1)\) dimensions. This is accomplished by considering the particle at rest, i.e., \( E=\pm M\), directly in the first order equations in Eqs. (12) and (13). Such a solution is well known to be excluded from the Sturm–Liouville problem, and this has been investigated under diverse perspectives in the last years [43–50]. We are seeking for bound-state solutions subject to the normalization condition

$$\begin{aligned} \int _{0}^{\infty }\big ( |f_{m}(r)|^{2}+|g_{m}(r)|^{2}\big ) r\,\mathrm{d}r=1. \end{aligned}$$
(14)

In order to determine the isolated bound-state solutions, we consider \( \varSigma (r) =0\) in Eq. (12), so that, for \(E=M\), we can write

$$\begin{aligned}&\left[ \frac{\mathrm{d}}{\mathrm{d}r}+\frac{s(m+s)}{r}-seA_{\varphi }\right] g_{m}(r)=0,\end{aligned}$$
(15)
$$\begin{aligned}&\left[ -\frac{\mathrm{d}}{\mathrm{d}r}+\frac{sm}{r}-seA_{\varphi }\right] f_{m}(r)=2(M-V(r)) g_{m}(r), \end{aligned}$$
(16)

whose general solutions are

$$\begin{aligned} g_{m}(r)= & {} a_{+}r^{-s\left( m+s\right) }e^{se\int A_{\varphi }\mathrm{d}r},\end{aligned}$$
(17)
$$\begin{aligned} f_{m}(r)= & {} \left[ b_{+}-a_{+}I(r)\right] r^{sm}e^{-se\int A_{\varphi }\mathrm{d}r}, \end{aligned}$$
(18)

where \(a_{+}\) and \(b_{+}\) are constants, and I(r) is given by

$$\begin{aligned} I(r)=\int \mathrm{d}r[ 2M-2V(r)] e^{2se\int A_{\varphi }(r) \mathrm{d}r}, \end{aligned}$$
(19)

which, for a given V(r) and \(A_{\varphi }(r) \), can be expressed in terms of the upper incomplete Gamma function [51],

$$\begin{aligned} \varGamma (a,x)=\int _{x}^{\infty }t^{a-1}e^{-t}\mathrm{d}t,\quad \mathfrak {R}(a)>0. \end{aligned}$$
(20)

Let us now analyze the solutions for \(E=-M\) and consider \(\varDelta (r) =0\) in Eq. (13). For this case, we write

$$\begin{aligned}&\left[ \frac{\mathrm{d}}{\mathrm{d}r} +\frac{s\left( m+s\right) }{r} -esA_{\varphi }(r) \right] g(r)=-2\left[ M+V(r) \right] f(r), \end{aligned}$$
(21)
$$\begin{aligned}&\left[ -\frac{\mathrm{d}}{\mathrm{d}r}+\frac{sm}{r}-esA_{\varphi }(r) \right] f(r) =0, \end{aligned}$$
(22)

whose general solution is

$$\begin{aligned} f_{m}(r)= & {} a_{-}r^{sm}e^{-se\int A_{\varphi }\mathrm{d}r},\end{aligned}$$
(23)
$$\begin{aligned} g_{m}(r)= & {} [ b_{-}-a_{-}H(r)] r^{-s\left( m+s\right) }e^{se\int A_{\varphi }\mathrm{d}r}, \end{aligned}$$
(24)

where

$$\begin{aligned} H(r)=\int \mathrm{d}r\left[ 2M-2V(r) \right] e^{-2se\int A_{\varphi }\mathrm{d}r}. \end{aligned}$$
(25)

Now, let us consider the particular case where the particle moves in a constant magnetic field and in the presence of the Aharonov–Bohm effect. The vector potential in the Coulomb gauge is

$$\begin{aligned} \mathbf {A}=\mathbf {A}_{1}+\mathbf {A}_{2}, \end{aligned}$$
(26)

with

$$\begin{aligned} \mathbf {A}_{1}=\frac{B_{0}r}{2}\hat{\varvec{\varphi }},\quad \mathbf {A}_{2}= \frac{\phi }{r}\hat{\varvec{\varphi }}, \end{aligned}$$
(27)

where \(B_{0}\) is the magnetic field magnitude and \(\phi \) is the flux parameter. The potentials in Eq. (26) both provide one magnetic field perpendicular to the plane \((r,\varphi ) \), namely

$$\begin{aligned} \mathbf {B}=\mathbf {B}_{1}+\mathbf {B}_{2}, \end{aligned}$$
(28)

with

$$\begin{aligned} \mathbf {B}_{1}= & {} \mathbf {\nabla }\times \mathbf {A}_{1}=B_{0}{\hat{\mathbf {z}}},\end{aligned}$$
(29)
$$\begin{aligned} \mathbf {B}_{2}= & {} \mathbf {\nabla }\times \mathbf {A}_{2}=\phi \frac{\delta (r)}{r}{\hat{\mathbf {z}}}, \end{aligned}$$
(30)

where \(\mathbf {B}_{1}\) is an external magnetic field and \(\mathbf {B}_{2}\) is the magnetic field due to a solenoid. If the solenoid is extremely long, the field inside is uniform, and the field outside is zero. However, in a general dynamics, the particle is allowed to access the \(r=0\) region. In this region, the magnetic field is non-null. If the radius of the solenoid is \(r_{0}\approx 0\), then the relevant magnetic field is \(\mathbf {B}_{2}\sim \delta (r)\) as in Eq. (30). This situation has not been accomplished in Ref. [32], which is crucial to give meaning to the term that explicitly depends on the spin, namely, the Pauli term appearing in the second order differential equation. This issue will be considered later when we treat solutions for the case \(E\ne \pm M\). Using Eqs. (29) and (30), we have

$$\begin{aligned} \int A_{\varphi }\mathrm{d}r=\frac{B_{0}r^{2}}{4}+\phi \ln r. \end{aligned}$$
(31)

If \(\phi >0\) and \(B_{0}>0\), for \(E=M\), we have bound-state solutions only in the following cases:

$$\begin{aligned}&\left( \begin{array}{c} f_{m}(r) \\ g_{m}(r) \end{array} \right) =\left( \begin{array}{c} 1 \\ 0 \end{array} \right) b_{+}r^{m-\lambda }e^{-\delta r^{2}},\quad \Bigg \{ \begin{array}{l} s=+1, \\ a_{+}=0, \end{array},\end{aligned}$$
(32)
$$\begin{aligned}&\left( \begin{array}{c} f_{m}(r) \\ g_{m}(r) \end{array} \right) =\left( \begin{array}{c} 0 \\ 1 \end{array} \right) a_{+}r^{m-\lambda -1}e^{-\delta r^{2}},\quad \Bigg \{ \begin{array}{l} s=-1, \\ b_{+}=M=V=0, \end{array} \end{aligned}$$
(33)

and for \(E=-M\),

$$\begin{aligned}&\left( \begin{array}{c} f_{m}(r) \\ g_{m}(r) \end{array} \right) =\left( \begin{array}{c} 0 \\ 1 \end{array} \right) b_{-}r^{m-\lambda -1}e^{-\delta r^{2}},\quad \Bigg \{ \begin{array}{l} s=-1, \\ a_{-}=0, \end{array} \end{aligned}$$
(34)
$$\begin{aligned}&\left( \begin{array}{c} f_{m}(r) \\ g_{m}(r) \end{array} \right) =\left( \begin{array}{c} 1 \\ 0 \end{array} \right) a_{-}r^{m-\lambda }e^{-\delta r^{2}},\quad \Bigg \{ \begin{array}{l} s=+1, \\ b_{+}=M=V=0, \end{array} \end{aligned}$$
(35)

where \(\delta =eB_{0}/4\) and \(\lambda =e\phi \). Note that the above results are independent of the values of s, m, and \(\lambda \) to ensure a bound state. This is because the function \(e^{-\delta r^{2}}\) predominates over the polynomials \(r^{m-\lambda }\) and \(r^{m-\lambda -1}\). If we consider \(B_{0}=V(r) =0\), which leads to the usual Aharonov–Bohm effect, the solution for \(E=M\) reads

$$\begin{aligned} g_{m}(r)= & {} a_{+}r^{s\left[ \lambda -\left( m+s\right) \right] },\text { } \end{aligned}$$
(36)
$$\begin{aligned} f_{m}(r)= & {} \left[ b_{+}-a_{+}\tilde{I}(r)\right] r^{s\left( m-\lambda \right) }, \end{aligned}$$
(37)

where

$$\begin{aligned} \tilde{I}(r)=\frac{2M}{2s\lambda +1}r^{2s\lambda +1}. \end{aligned}$$
(38)

For \(E=-M\), we get

$$\begin{aligned} f_{m}(r)= & {} a_{-}r^{s(m-\lambda ) },\end{aligned}$$
(39)
$$\begin{aligned} g_{m}(r)= & {} [ b_{-}-a_{-}\tilde{H}(r)] r^{s[ \lambda -(m+s)]}, \end{aligned}$$
(40)

where

$$\begin{aligned} \tilde{H}(r)=\frac{2M}{-2s\lambda +1}r^{-2s\lambda +1}. \end{aligned}$$
(41)

Unlike the cases of Eqs. (32)–(35), if we impose the requirement that \(B_{0}\) and V(r) are zero, there exist no bound-state solutions of square-integrable type. In other words, for any values of s, m, and \(\lambda \) in Eqs. (36)–(41), the integral (14) diverges.

4 Equation of motion and analysis of symmetries

In this section, we investigate the dynamics for \(E\ne \pm M\). To this aim, we choose to work with Eq. (5) in its quadratic form. After application of the operator

$$\begin{aligned} \beta [ ( M+S(r) ) +\beta ( E-V(r)) +\varvec{\gamma }\cdot \varvec{\pi }] , \end{aligned}$$
(42)

we get

$$\begin{aligned}&\big \{\mathbf {p}^{2}-2e[ ( \mathbf {A}_{1}+\mathbf {A} _{2}) \cdot \mathbf {p}] +e^{2}( \mathbf {A}_{1}+\mathbf {A} _{2}) ^{2}\big \} \psi (\mathbf {r}) \nonumber \\&\quad +\,\big \{ [M+S(r)] ^{2}-[ E-V(r)]^{2}-es\varvec{\sigma }\cdot ( \mathbf {B}_{1}+\mathbf {B} _{2})\big \} \psi ( \mathbf {r}) \nonumber \\&\quad -\left( \frac{\partial S(r) }{\partial r}\sigma _{2}+i\frac{ \partial V(r) }{\partial r}\sigma _{1}\right) \psi (\mathbf {r}) =0. \end{aligned}$$
(43)

In this stage, it is worthwhile to mention that Eq. (43) is the correct quadratic form of the Dirac equation with minimal, vector, and scalar couplings, because the Pauli term is considered.

4.1 Exact spin symmetry limit: \(S=V\)

The condition for establishing the exact symmetry boundary implies that the solution is of the form

$$\begin{aligned} \psi _{1}=\sum _{m}f_{m}(r)\;e^{im\varphi }. \end{aligned}$$
(44)

So, by making \(S=V\) (or equivalently \(\varDelta (r) =0\) [52, 53]) in Eq. (10) and using the solution (44) in Eq. (43), the equation for \(f_{m}(r) \) is found to be

$$\begin{aligned}&\left[ -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}} -\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}+\frac{m^{2}}{r^{2}} -2e\left( \frac{B_{0}r}{2}+\frac{\phi }{r}\right) \frac{m}{r}+\frac{ e^{2}B_{0}^{2}r^{2}}{4}\right] f_{m}(r) \nonumber \\&\quad +\left[ \frac{e^{2}\phi ^{2}}{r^{2}}+e^{2}B_{0}\phi -es\left( B_{0}+\phi \frac{\delta (r)}{r}\right) \right] f_{m}(r) \nonumber \\&\quad +\left[ M^{2}-E^{2}+2( E+M) V\right] f_{m}(r) =0. \end{aligned}$$
(45)

Assuming V(r) as in Ref. [32], i.e., of the form

$$\begin{aligned} V(r) =a\,r^{2}+\frac{b}{r^{2}}, \end{aligned}$$
(46)

Equation (45) becomes

$$\begin{aligned} Hf_{m}(r) =k^{2}f_{m}(r), \end{aligned}$$
(47)

with

$$\begin{aligned}&H=H_{0}-es\phi \frac{\delta (r)}{r},\end{aligned}$$
(48)
$$\begin{aligned}&H_{0}=-\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}-\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}+\frac{\nu ^{2}}{r^{2}} +\eta ^{2}\,r^{2}, \end{aligned}$$
(49)

where

$$\begin{aligned}&\nu ^{2} =( m-e\phi ) ^{2}+2b( E+M) , \end{aligned}$$
(50)
$$\begin{aligned}&\eta ^{2} =\frac{e^{2}B_{0}^{2}}{4}+2a( E+M), \end{aligned}$$
(51)
$$\begin{aligned}&k^{2} =meB_{0}-e^{2}B_{0}\phi +esB_{0}+( E^{2}-M^{2}). \end{aligned}$$
(52)

As pointed out in Ref. [32], the potential V(r) in Eq. (46) describes an anharmonic oscillator. This model is a particular case of a class proposed in Ref. [10] to study the Landau quantization and the Aharonov–Bohm effect in a two-dimensional ring as an exactly soluble model. The model considered in Ref. [10] has an advantage because, besides the model considered here, it also describes other physical systems, such as a one-dimensional ring, a straight 2D wire, a single quantum dot and an isolated antidot.

4.2 Exact pseudospin symmetry limit: \(S=-V\)

In this case, the condition for establishing the exact pseudospin symmetry limit implies that the resolution is related to the down component of the spinor in Eq. (11), namely

$$\begin{aligned} \psi _{2}=i\sum _{m}g_{m}(r)\;e^{i(m+s)\varphi }. \end{aligned}$$
(53)

By making \(S=-V\) (or equivalently \(\varSigma (r) =0\) in Eq. (9) and again using Eq. (53) in Eq. (43), the equation for \(g_{m}(r) \) can be found:

$$\begin{aligned} \tilde{H}g_{m}(r) =\tilde{k}^{2}g_{m}(r) , \end{aligned}$$
(54)

with

$$\begin{aligned}&\tilde{H}=\tilde{H}_{0}-es\phi \frac{\delta (r)}{r},\end{aligned}$$
(55)
$$\begin{aligned}&\tilde{H}_{0}=-\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}-\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}+\frac{\tilde{\nu }^{2}}{ r^{2}}+\tilde{\eta }^{2}\,r^{2}, \end{aligned}$$
(56)

where

$$\begin{aligned}&\tilde{\nu }^{2} =( m+s-e\phi ) ^{2}+2b( E-M) ,\end{aligned}$$
(57)
$$\begin{aligned}&\tilde{\eta }^{2} =\frac{e^{2}B_{0}^{2}}{4}+2a( E-M) , \end{aligned}$$
(58)
$$\begin{aligned}&{\tilde{k}}^{2} =( m+s) eB_{0}-e^{2}B_{0}\phi +esB_{0}-(M^{2}-E^{2}) . \end{aligned}$$
(59)

5 Self-adjoint extension analysis

In this section, we review some concepts as regards the self-adjoint extension approach. An operator \(\mathscr {O}\), with domain \(\mathscr {D}({\mathscr {O}})\), is said to be self-adjoint if and only if \(\mathscr {O}=\mathscr {O} ^{\dagger }\) and \(\mathscr {D}(\mathscr {O})=\mathscr {D}(\mathscr {O}^{\dagger })\), \(\mathscr {O}^{\dagger }\) being the adjoint of the operator \(\mathscr {O}\). For smooth functions \(\xi \in C_{0}^{\infty }(\mathbb {R}^{2})\) with \(\xi (0)=0\), we should have \(H\xi =H_{0}\xi \), and it is possible to interpret the Hamiltonian \(H_{0}\) (49) as a self-adjoint extension of \( H_{0}|_{C_{0}^{\infty }(\mathbb {R}^{2}/\{0\})}\) [54–56]. The self-adjoint extension approach consists, essentially, in extending the domain of \(\mathscr {D}( \mathscr {O})\) in order to match \(\mathscr {D}(\mathscr {O}^{\dagger })\). From the theory of symmetric operators, it is a well-known fact that the symmetric radial operator \(H_{0}\) is essentially self-adjoint for \(\nu \ge 1 \), while, for \(\nu <1\), it admits a one-parameter family of self-adjoint extensions [57], \(H_{0,\lambda _{m}}\), where \(\lambda _{m}\) is the self-adjoint extension parameter. To characterize this family, we will use the approach in [58, 59], which is based on the boundary conditions at the origin. All the self-adjoint extensions \(H_{0,\lambda _{m}}\) of \(H_{0}\) are parameterized by the boundary condition at the origin,

$$\begin{aligned} \varPsi _{0}=\lambda _{m}\varPsi _{1}, \end{aligned}$$
(60)

with

$$\begin{aligned}&\varPsi _{0}= \lim _{r\rightarrow 0^{+}}r^{\nu }f_{m}(r), \end{aligned}$$
(61)
$$\begin{aligned}&\varPsi _{1}= \lim _{r\rightarrow 0^{+}}\frac{1}{r^{\nu }}\left[ f_{m}(r)-\varPsi _{0}\frac{1}{r^{\nu }}\right] , \end{aligned}$$
(62)

where \(\lambda _{m}\in \mathbb {R}\). For \(\lambda _{m}=0\), we have the free Hamiltonian (without the \(\delta \) function) with regular wave functions at the origin, and for \(\lambda _{m}\ne 0\) the boundary condition in Eq. (60) permits an \(r^{-\nu }\) singularity in the wave functions at the origin.

6 The bound state energy and wave function

In this section, we determine the energy spectrum by solving Eq. (47). For \(r\ne 0\), the equation for the component \(f_{m}(r)\) can be transformed by the variable change \(\rho =\eta r^{2}\), resulting in

$$\begin{aligned} \rho f_{m}^{\prime \prime }(\rho )+f_{m}^{\prime }(\rho )-\left( \frac{{\nu } ^{2}}{4\rho }+\frac{\rho }{4}-\frac{k^{2}}{4\eta }\right) f_{m}(\rho )=0. \end{aligned}$$
(63)

Due to the boundary condition in Eq. (60), we seek regular and irregular solutions for Eq. (63). Studying the asymptotic limits of Eq. (63) leads to the following regular (\(+\)) (irregular (\(-\))) solution:

$$\begin{aligned} f_{m}(\rho )=\rho ^{\pm \frac{\nu }{2}}e^{-\frac{\rho }{2}}F(\rho ). \end{aligned}$$
(64)

With this, Eq. (63) is rewritten as

$$\begin{aligned} \rho F^{\prime \prime }(\rho )+( 1\pm \nu -\rho ) F^{\prime }(\rho )-\left( \frac{1\pm \nu }{2}-\frac{k^{2}}{4\gamma }\right) F(\rho )=0. \end{aligned}$$
(65)

Equation (63) is of the confluent hypergeometric equation type,

$$\begin{aligned} zF^{\prime \prime }(z)+(b-z)F^{\prime }(z)-aF(z)=0. \end{aligned}$$
(66)

In this manner, the general solution for Eq. (63) is

$$\begin{aligned} f_{m}(r)= & {} a_{m}\rho ^{\frac{\nu }{2}}e^{-\frac{\rho }{2} }\;F( d_{+},1+\nu ,\rho ) \nonumber \\&+\,b_{m}\rho ^{-\frac{\nu }{2}}e^{-\frac{\rho }{2}}\;F(d_{-},1-\nu ,\rho ) , \end{aligned}$$
(67)

with

$$\begin{aligned} d_{\pm }=\frac{1\pm \nu }{2}-\frac{k^{2}}{4\eta }. \end{aligned}$$
(68)

In Eq. (67), F(a, b, z) is the confluent hypergeometric function of the first kind [51] and \(a_{m}\) and \( b_{m} \) are, respectively, the coefficients of the regular and irregular solutions.

In this point, we apply the boundary condition in Eq. (60). Doing this, one finds the following relation between the coefficients \(a_{m}\) and \( b_{m}\):

$$\begin{aligned} \lambda _{m}\eta ^{\nu }=\frac{b_{m}}{a_{m}}\left[ 1+\frac{\lambda _{m}k^{2} }{4(1-\nu )}\lim _{r\rightarrow 0^{+}}r^{2-2\nu }\right] . \end{aligned}$$
(69)

We note that \(\lim _{r\rightarrow 0^{+}}r^{2-2\nu }\) diverges if \(\nu \ge 1\). This condition implies that \(b_{m}\) must be zero if \(\nu \ge 1\) and only the regular solution contributes to \(f_{m}(r)\). For \(\nu <1\), when the operator \(H_{0}\) is not self-adjoint, there arises a contribution of the irregular solution to \(f_{m}(r)\) [34, 60–63]. In this manner, the contribution of the irregular solution for the system’s wave function stems from the fact that the operator \(H_{0}\) is not self-adjoint.

For \(f_{m}(r)\) to be a bound state wave function, it must vanish at large values of r, i.e., it must be normalizable. So, from the asymptotic representation of the confluent hypergeometric function, the normalizability condition is translated into

$$\begin{aligned} \frac{b_{m}}{a_{m}}=-\frac{\varGamma (1+\nu )}{\varGamma (1-\nu )}\frac{\varGamma (d_{-})}{\varGamma (d_{+})}. \end{aligned}$$
(70)

From Eq. (69), for \(\nu <1\), we have

$$\begin{aligned} \frac{{b_{m}}}{{a_{m}}}=\lambda _{m}\eta ^{\nu }. \end{aligned}$$
(71)

By combining Eqs. (70) and (71), one finds

$$\begin{aligned} \frac{\varGamma (d_{+})}{\varGamma (d_{-})}=-\frac{1}{\lambda _{m}\gamma ^{\nu }} \frac{\varGamma (1+\nu )}{\varGamma (1-\nu )}. \end{aligned}$$
(72)

Equation (72) implicitly determines the bound state energy for the system for different values of the self-adjoint extension parameter. Two limiting values for the self-adjoint extension parameter deserve some attention. For \(\lambda _{m}=0\), when the \(\delta \) interaction is absent, only the regular solution contributes for the bound state wave function. On the other side, for \(\lambda _{m}=\infty \), only the irregular solution contributes for the bound state wave function. For all other values of the self-adjoint extension parameter, both regular and irregular solutions contribute to the bound state wave function. The energies for the limiting values are obtained from the poles of the gamma function, namely,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} d_{+}=-n \quad \text{ for } \lambda _{m}=0, &{} \text{(regular } \text{ solution) }, \\ d_{-}=-n \quad \text{ for } \lambda _{m}=\infty , &{} \text{(irregular } \text{ solution) }, \end{array} \right. \end{aligned}$$
(73)

with n a nonnegative integer, \(n=0,1,2,\ldots \). By manipulation of Eq. (73), we obtain

$$\begin{aligned} E^{2}-M^{2}= & {} 2\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a( E+M) }\nonumber \\&\times \left[ 2n+1\pm \sqrt{( m-e\phi ) ^{2}+2b(E+M)}\right] \nonumber \\&+\,e^{2}B_{0}\phi -meB_{0}-esB_{0},\quad S=V, \end{aligned}$$
(74)
$$\begin{aligned} E^{2}-M^{2}= & {} 2\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a( E-M)} \nonumber \\&\times \left[ 2n+1\pm \sqrt{( m+s-e\phi ) ^{2}+2b(E-M)}\right] \nonumber \\&+\,e^{2}B_{0}\phi -( m+s) eB_{0}-esB_{0},\quad S=-V. \end{aligned}$$
(75)

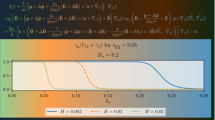
As an illustration the profiles of the energy under the exact spin symmetry limit (\(S=V\)) as a function of the magnetic field \(B_{0}\) and with spin projection parameter values \(s=1\) and \(s=-1\) are shown in Figs. 1 and 2, respectively. From Figs. 1 and 2 we can note that the ground state \(n=0\) corresponds to the lowest energies, as it should for particle energy levels.

Fig. 1
figure 1

Plots of the energy (\(\varDelta (r)=0\)) as a function of the magnetic field \(B_{0}\) for \(s=1\) and different values of n and m: \(n=0\) (solid line), \(n=1\) (dashed line), and \(n=2\) (dotted line)

Full size image
Fig. 2
figure 2

Plots of the energy (\(\varDelta (r)=0\)) as a function of the magnetic field \(B_{0}\) for \(s=-1\) and different values of n and m: \(n=0\) (solid line), \(n=1\) (dashed line), and \(n=2\) (dotted line)

Full size image

In particular, it should be noted that for the case when \(\nu \ge 1\) or when the \(\delta \) interaction is absent, only the regular solution contributes for the bound state wave function (\(b_{m}=0\)), and the energy is given by Eq. (74) using the plus sign. The unnormalized bound state wave functions for our problem are

$$\begin{aligned} f_{m}(r)= & {} \left[ \frac{e^{2}B_{0}^{2}}{4}+2a( E+M) \right] ^{\pm \frac{1}{4}\sqrt{( m-e\phi ) ^{2}+2b(E+M) } }\nonumber \\&\times \, r^{\pm \sqrt{( m-e\phi ) ^{2}+2b( E+M) }}e^{-\frac{1}{ 2}\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a( E+M) }r^{2}} \nonumber \\&\times \, F\bigg ( -n,1\pm \sqrt{( m-e\phi ) ^{2}+2b(E+M)},\nonumber \\&\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a\left( E+M\right) } r^{2}\bigg ),\quad S=V,\end{aligned}$$
(76)
$$\begin{aligned} g_{m}(r)= & {} \left[ \frac{e^{2}B_{0}^{2}}{4}+2a( E-M) \right] ^{\pm \frac{1}{4}\sqrt{( m+s-e\phi ) ^{2}+2b( E-M)}}\nonumber \\&\times \, r^{\pm \sqrt{( m+s-e\phi ) ^{2}+2b( E-M)}}e^{-\frac{1 }{2}\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a( E-M)}r^{2}} \nonumber \\&\times \, F\bigg ( -n,1\pm \sqrt{( m+s-e\phi ) ^{2}+2b(E-M)},\nonumber \\&\sqrt{\frac{e^{2}B_{0}^{2}}{4}+2a( E-M)} r^{2}\bigg ),\quad S=-V. \end{aligned}$$
(77)

The self-adjoint extension is related with the presence of the \(\delta \) interaction. In this manner, the self-adjoint extension parameter must be related with the \(\delta \) interaction coupling constant \(\phi s\). In fact, as shown in Refs. [34, 64] (see also Refs. [60, 65]), from the regularization of the \(\delta \) interaction, it is possible to find such a relationship. Using the regularization method, one obtains the following equation for the bound state energy:

$$\begin{aligned} \frac{\varGamma (d_{+})}{\varGamma (d_{-})}=-\frac{1}{r_{0}^{2\nu }}\left( \frac{ \phi s+\alpha \nu }{\phi s-\alpha \nu }\right) \frac{1}{\gamma ^{\nu }}\frac{ \varGamma ( 1+\nu ) }{\varGamma ( 1-\nu ) }. \end{aligned}$$
(78)

By comparing Eqs. (72) and (78), this relation is found to be

$$\begin{aligned} \frac{1}{\lambda _{m}}=\frac{1}{r_{0}^{2\nu }}\left( \frac{\phi s+\alpha \nu }{\phi s-\alpha \nu }\right) \end{aligned}$$
(79)

where \(r_{0}\) is a very small radius which comes from the \(\delta \) regularization [34, 64]. The result of Eq. (79) provides an explicit formula for the self-adjoint extension parameter \(\lambda _{m}\). We have, therefore, derived the most important quantities for the system without any arbitrary parameter coming from the self-adjoint extension method.

7 Nonrelativisitic limit

Let us now examine the nonrelativistic limit of Eq. (43) by setting \(E=M+\mathscr {E}\), with \(M\gg \mathscr {E}\), for the two cases \(S=V\) and \(S=-V\). After applying this limit, we find

$$\begin{aligned} H\psi =2M\mathscr {E}\psi , \end{aligned}$$
(80)

where

$$\begin{aligned} H=\left( \mathbf {p}-e\mathbf {A}\right) ^{2}-es\varvec{\sigma }\cdot \mathbf {B}+2M[ S(r) +V(r)] . \end{aligned}$$
(81)

Using the ansatz of Eq. (11) in Eq. (80), again, we get the equation for \(f_{m}(r) \) (for \(S=V\)),

$$\begin{aligned}&\left[ -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}-\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}+\frac{\bar{\nu }^{2}}{ r^{2}}+\bar{\eta }^{2}\text { }r^{2}-es\phi \frac{\delta (r)}{r}\right] f_{m}(r) \nonumber \\&\quad -\,\mathscr {E}f_{m}(r) =0, \end{aligned}$$
(82)

where

$$\begin{aligned}&\bar{\nu }^{2} =\left( m-e\phi \right) ^{2}+4Mb, \end{aligned}$$
(83)
$$\begin{aligned}&\bar{\eta }^{2} =\frac{e^{2}B_{0}^{2}}{4}+4Ma, \end{aligned}$$
(84)
$$\begin{aligned}&\bar{k}^{2} =meB_{0}-e^{2}B_{0}\phi +esB_{0}+2M\mathscr {E}. \end{aligned}$$
(85)

On the other hand, for \(S=-V\), the term involving the potential is now identically zero. The resulting equation is given by

$$\begin{aligned}&\left[ -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}-\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}+\frac{\breve{\nu }^{2}}{ r^{2}}+\breve{\eta }^{2}\text { }r^{2}-es\phi \frac{\delta (r)}{r}\right] g_{m}(r) \\&\quad -\,\mathscr {E}g_{m}(r) =0, \end{aligned}$$

where

$$\begin{aligned}&\breve{\nu }^{2} =( m+s-e\phi ) ^{2}, \end{aligned}$$
(86)
$$\begin{aligned}&\breve{\eta }^{2} =\frac{e^{2}B_{0}^{2}}{4}, \end{aligned}$$
(87)
$$\begin{aligned}&\breve{k}^{2} =eB_{0}( m+s) -e^{2}B_{0}\phi +esB_{0}+2M\mathscr {E}. \end{aligned}$$
(88)

In order to determine the energy spectrum, we use the same technique as above. Performing the same steps as for the relativistic case, one obtains the energy levels,

$$\begin{aligned} \mathscr {E}= & {} \frac{1}{M}\sqrt{\frac{e^{2}B_{0}^{2}}{4}+4Ma}\left[ 2n+1\pm \sqrt{( m-e\phi ) ^{2}+4Mb}\right] \nonumber \\&+\frac{1}{2M}\left[ e^{2}B_{0}\phi -( m+s) eB_{0}-esB_{0}\right] ,\quad S=V,\end{aligned}$$
(89)
$$\begin{aligned} \mathscr {E}= & {} \frac{1}{2M}eB_{0}( 2n+1\pm \vert m-e\phi \vert )\nonumber \\&+\frac{1}{2M}\left[ e^{2}B_{0}\phi -( m+s) eB_{0}-esB_{0}\right] ,\quad S=-V. \end{aligned}$$
(90)

The corresponding wave functions are given by

$$\begin{aligned} f_{m}(r)= & {} \left( \frac{e^{2}B_{0}^{2}}{4}+4Ma\right) ^{\pm \frac{1}{4} \sqrt{( m-e\phi ) ^{2}+4Mb}}\nonumber \\&\times \, r^{\pm \sqrt{( m-e\phi ) ^{2}+4Mb}}e^{-\frac{1}{2}\sqrt{\frac{e^{2}B_{0}^{2}}{4}+4Ma}r^{2}} \nonumber \\&\times \, F\Biggl ( -n,1\pm \sqrt{( m-e\phi ) ^{2}+4Mb},\nonumber \\&\sqrt{ \frac{e^{2}B_{0}^{2}}{4}+4Ma}r^{2}\Biggr ),\quad S=V,\end{aligned}$$
(91)
$$\begin{aligned} f_{m}(r)= & {} \left[ \frac{e^{2}B_{0}^{2}}{4}\right] ^{\pm \frac{1}{4}\vert m-e\phi \vert }r^{\pm \vert m-e\phi \vert }e^{-\frac{1}{4} eB_{0}r^{2}}\nonumber \\&\times \, F\left( -n,1\pm \vert m-e\phi \vert ,\frac{1}{2} eB_{0}r^{2}\right) ,\quad S=-V. \end{aligned}$$
(92)

8 Conclusions

In this paper, we have studied the relativistic quantum dynamics of a spin-1/2 charged particle with minimal, vector, and scalar couplings. The minimal coupling was chosen so as to lead to the spin-1/2 Aharonov–Bohm effect. In a first attempt, we have solved the first order Dirac equation. We verified that there are isolated solutions for the system for some special cases. These solutions depend on the values assumed by the spin projection parameter s, as well as on the choice of the scalar and vector potential functions, S(r) and V(r).

In contrast to the literature, we have considered the correct quadratic form of the Dirac equation with minimal, vector, and scalar couplings. As we have mentioned before, in the approach of Ref. [32] the authors have not taken into account the term that depends explicitly on the spin in the Pauli equation of motion. We have revisited the dynamics of the system in detail and shown that the correct approach should involve the spin element. Thus, we have derived the Pauli equation and studied the dynamics of the system taking into account the exact symmetry spin and pseudospin limits. Because the equation of motion includes a \(\delta \) function, we have used the self-adjoint extension method to specify the proper boundary conditions at the origin. The analytical solutions of the model allow a calculation of the expressions for the energy eigenvalues and wave functions for both symmetry limits. We verify that the presence of the spin element in the equation of motion introduces a correction in the expressions for the bound state energy and wave functions, a fact that does not occur in Ref. [32].