1 Introduction

Dense plasmas, where quantum effects are important, can, for example, be found in different types of solid-state plasmas [1, 2], various astrophysical environments [3, 4], and certain forms of laser–plasma interactions [5, 6]. Such plasmas have been modelled using hydrodynamic [7] and kinetic equations [8], where, in the present paper, the focus is on the latter class of theories. Quantum kinetic equations can be derived, for example, from the Green’s function formalism [9, 10] or from the density matrix approach [11, 12]. Recently, several quantum kinetic models for plasmas have been put forward, within the Hartree approximation [12,13,14,15] or the Hartree–Fock approximation [16,17,18]. In the latter case, exchange effects are also included, which might be important in various applications [1, 2, 8]. Depending on the scope of the theory, the density matrix can be based on the Schrödinger equation [8], the Pauli equation [13], or the Dirac equation, where the latter equation can be applied in the weakly [19] or fully [12] relativistic approximation.

In order to produce a quantum kinetic theory of electrons from the Dirac equation, certain restrictions need to be applied. Firstly, pair-production must be negligible, such that a Foldy–Wouthuysen transformation [20, 21] can be applied to separate electron states from positron states. This puts restrictions on the maximal electric field strength, which should be well below the critical field \(E_\text {cr} = m^2 c^3/|q|\hbar \), and the characteristic spatial scales of the fields, which should be much longer than the Compton length \( L_c = \hbar /m\,c\). Here m and q are the electron mass and charge, respectively, c is the speed of light in vacuum, and \(\hbar \) is the reduced Planck’s constant. Given these restrictions, there are two different regimes that can be studied. Firstly, there is the fully relativistic regime, where the relativistic factor \(\gamma \) fulfills \(\gamma -1\sim 1\), in which case the de Broglie length \(\lambda _\text {dB} = \hbar /p_{\mathrm {ch}}\) is of the same order as \(L_{c}\). Here \(p_{\mathrm {ch}}\) is the characteristic momentum of the electrons—determined by the Fermi temperature \(T_{F}\) or the thermodynamic temperature T whichever is larger. Since, according to the applicability conditions, this means that the spatial scales must be longer than the de Broglie length, particle dispersive effects cannot be included in the fully relativistic regime [12]. However, for the second case, the weakly relativistic regime with \(\gamma -1\ll {1}\), we have \(\lambda _{dB}\gg L_{c}\), and as a consequence, a theory including particle dispersive effects based on the Dirac equation can be formulated. This is the main goal of the present paper. We thus generalize the work presented in Ref. [13] based on the Pauli equation, by including several new effects, such as spin–orbit interaction, Thomas precession and the polarization currents associated with the spin. We also generalize the results of Ref. [19], by also covering the short scale physics down to spatial scales of the order of the de Broglie length.

Our approach is as follows. We start from the Pauli Hamiltonian including the spin-o-rbit interaction. In Sect. 2, we apply a combined Wigner- and Q-transform (for the spin) using the gauge-independent approach of Stratonovich [22, 23], to formulate our scalar kinetic theory. Our main result is the kinetic equation, Eq. (58) in Sect. 2.5.

In Sect. 3, in order to demonstrate the usefulness of the present theory, we have calculated two examples from linearized theory: electromagnetic waves in a non-magnetized plasma and electrostatic waves propagating parallel to an external magnetic field. Classically, an external magnetic field does not affect parallel propagating electrostatic waves. By contrast, the present model predicts a condition, depending on the magnetic field, for resonant wave–particle interaction, generalizing those of previous works. We use this result to calculate the magnetic field dependence of the damping rate.

Finally, in Sect. 4, we compare our model with some theories from the recent research literature.

2 The gauge invariant Wigner function and the spin transformation

We will consider the semi-relativistic Pauli Hamiltonian

$$\begin{aligned} {\hat{H}} = \frac{{\hat{\varvec{\pi }}}^2}{2m} + q{\hat{\phi }} - \mu _e \varvec{\sigma }\cdot {\hat{\mathbf {B}}} + \frac{\mu _e}{2mc^2}\left( {\hat{\varvec{\pi }}} \times {\hat{\mathbf {E}}} - {\hat{\mathbf {E}}} \times {\hat{\varvec{\pi }}} \right) \cdot \varvec{\sigma }, \end{aligned}$$
(1)

including the spin–orbit interaction, applying the mean field approximation. This means we are dropping interactions due to exchange effects and due to correlations (see e.g. [16,17,18, 24]) associated with the two-particle correlation function, and possibly also higher order correlations in the BBGKY-hierarchy [25], limiting ourselves to the Hartree approximation. Here \({\hat{\varvec{\pi }}} = {\hat{\mathbf {p}}} - q\hat{\mathbf{A}}\) is the gauge invariant momentum operator, \({\hat{\phi }}, \hat{{\mathbf {A}}}\) are the scalar and vector potentials and \(\mu _e\) is the electron magnetic moment. Note that the spin–orbit interaction is written in a symmetric form so as to make the Hamiltonian Hermitian, which is necessary to have unitary time evolution.

Our goal is to formulate a scalar quantum kinetic theory based on the gauge invariant Wigner function [22, 23], that is,

$$\begin{aligned} W(\mathbf {x}, \mathbf {p}, t)_{\alpha \beta } = {\text {tr}} \left[ {\hat{W}}(\mathbf {x}, \mathbf {p}, t) \rho _{\alpha \beta }\right] = \int d^3 {\mathbf {r}} \, \langle {\mathbf {r}} | {\hat{W}} {\hat{\rho }}_{\alpha \beta } | {\mathbf {r}} \rangle , \end{aligned}$$
(2)

where \(\alpha ,\beta \) are the Pauli spin indices, and this trace is only over the spatial degrees of freedom. We work in the Heisenberg picture so that the operator \({\hat{W}}(\mathbf {x}, \mathbf {p}, t)\) is time-dependent, but the density matrix \(\rho \) is not. The operator \({\hat{W}}(\mathbf {p}, \mathbf {x}, t)\) can be expressed as a Fourier transform

$$\begin{aligned} {\hat{W}}(\mathbf {x}, \mathbf {p}, t)&= \left( {\mathcal {F}}(\hat{T})\right) (\mathbf {x}, \mathbf {p}) \nonumber \\&= \int \frac{d^3 u}{(2\pi \hbar )^3}\frac{d^3 v}{(2\pi \hbar )^3} e^{-\frac{i}{\hbar }({\mathbf {u}} \cdot \mathbf {p}+ {\mathbf {v}} \cdot \mathbf {x})} \, \hat{T}({\mathbf {u}}, {\mathbf {v}}), \end{aligned}$$
(3)

where the operator \({\hat{T}}({\mathbf {u}}, {\mathbf {v}}, t)\) is given by

$$\begin{aligned} \hat{T}({\mathbf {u}}, {\mathbf {v}}, t) = \exp \left[ \frac{i}{\hbar }({\mathbf {u}} \cdot {\hat{\varvec{\pi }}} + {\mathbf {v}} \cdot {\hat{\mathbf {x}}}) \right] . \end{aligned}$$
(4)

To obtain a scalar function from the matrix-valued \({\hat{W}}_{\alpha \beta }\), one can use the spin transform

$$\begin{aligned} f(\mathbf {x}, \mathbf {p}, {\mathbf {s}})&= \frac{1}{4\pi } {\text {tr}}[ (1 + {\mathbf {s}}\cdot \varvec{\sigma }) W ] \nonumber \\&= \frac{1}{4\pi } \sum _{\alpha ,\beta } [\delta _{\alpha \beta } + \mathbf {s}\cdot \varvec{\sigma }_{\alpha \beta }] W_{\beta \alpha }, \end{aligned}$$
(5)

which is a Husimi Q-function for the spin [26]. This transform was used in Ref. [13] for a theory including only the magnetic dipole interaction.

If we let

$$\begin{aligned} {\hat{S}} = \frac{1}{4\pi } (1 + {\mathbf {s}} \cdot \varvec{\sigma }) , \end{aligned}$$
(6)

then

$$\begin{aligned} f = {{\,\mathrm{Tr}\,}}[ {\hat{S}} {\hat{W}} \rho ], \end{aligned}$$
(7)

i.e. f is the expectation value of \({\hat{S}} {\hat{W}}\). Note that \({\hat{S}}\) and \({\hat{W}}\) are both Hermitian and commute, which implies that f is real. The Heisenberg equation of motion then gives

$$\begin{aligned} \partial _t f = {{\,\mathrm{Tr}\,}}\left[ \left( {\hat{S}} \partial _t {\hat{W}} - \frac{i}{\hbar }{\hat{S}} [{\hat{W}}, {\hat{H}}] - \frac{i}{\hbar }[{\hat{S}}, {\hat{H}}] {\hat{W}} \right) \rho \right] , \end{aligned}$$
(8)

where in this and the previous equation, the trace is over both the spin indices and the spatial degrees of freedom. The only effect of \(\partial _t {\hat{W}}\) is to give the \(\partial _t {\mathbf {A}}\) contribution to the electric field in the Lorentz force.

The remainder of this section presents the calculations involved in expressing the right-hand side of this equation in terms of f, with the conclusion presented in Sect. 2.5. The steps are similar to those in Ref. [23], where the spin-independent terms in the kinetic equation are found.

2.1 Gross structure of the calculation

Throughout, quantities with hats are operators and quantities without hats are c-numbers, except the Pauli spin operator \(\varvec{\sigma }\) which is always an operator (a finite dimensional one, i.e., a matrix). We will also use the summation convention for repeated indices, and use commas to denote derivatives, e.g., \(E_{i,j} = \partial E_i / \partial x_j\).

The main thrust of the calculation is to take the matrix elements \(\langle x' | \cdots | x \rangle \) between position eigenstates of the operators on the right-hand side of (8) then to move as much as possible outside the inner product using commutation relations and the Baker–Campbell–Haussdorff formulas for \({\hat{T}}\), Eq. (4), below, to put everything in terms of phase-space differential operators on f. For a simplest-cases demonstration, we recommend the treatment in Ref. [23] of the scalar potential.

Baker–Campbell–Haussdorff formulas for \({\hat{T}}\) can be found [23] and will be useful in the following, as we shall often want to put \({\hat{\pi }}\):s or \({\hat{x}}\):s on the left or the right, as needed. They are:

$$\begin{aligned} \hat{T}(u,v)&= \exp \left[ \frac{i}{2\hbar } u\cdot v \right] \\&\quad \times \exp \left[ \ \frac{i}{\hbar }v\cdot \big (\hat{x}- q u \cdot \textstyle \int _0^1 d\tau \, {\hat{A}}(\hat{x}+ \tau u)\big ) \right] \\&\quad \times \exp \left[ \frac{i}{\hbar }u\cdot {{\hat{p}}}\right] \\&= \exp \left[ -\frac{i}{2\hbar } u\cdot v \right] \exp \left[ \frac{i}{\hbar }u\cdot {{\hat{p}}}\right] \\&\quad \times \exp \left[ \ \frac{i}{\hbar }v\cdot \big (\hat{x}- q u \cdot \textstyle \int _0^1 d\tau \, {\hat{A}}(\hat{x}+ \tau u)\big ) \right] \\&= \exp \left[ \frac{i}{2\hbar } u\cdot v \right] \exp \left[ \ \frac{i}{\hbar }v\cdot \hat{x}\right] \exp \left[ \frac{i}{\hbar }u\cdot {{\hat{\pi }}}\right] \\&= \exp \left[ -\frac{i}{2\hbar } u\cdot v \right] \exp \left[ \ \frac{i}{\hbar }u\cdot {\hat{\pi }} \right] \exp \left[ \frac{i}{\hbar }v\cdot {{\hat{x}}}\right] . \end{aligned}$$

One can note that these occur in pairs related by operator orderings.

The commutator is linear in \({\hat{H}}\), and the terms in the evolution equation for \({\hat{W}}\) corresponding to the lowest order (“non-relativistic”) part of the Hamiltonian have already been computed in [13]. Therefore we will here be concerned only with the spin–orbit contribution

$$\begin{aligned} {\hat{H}}_{\text {SO}} = \frac{\mu _e }{2 m c^2} ({\hat{\varvec{\pi }}} \times {\hat{\mathbf {E}}} - {\hat{\mathbf {E}}} \times {\hat{\varvec{\pi }}} ) \cdot \varvec{\sigma }. \end{aligned}$$
(9)

We will denote the contribution from this Hamiltonian by \( \left( \partial _t f \right) _{\text {SO}} \).

The spin–orbit interaction Hamiltonian has the form \(\varvec{\sigma }\cdot \hat{{\mathbf {V}}}\), and hence we find

$$\begin{aligned} {[}{\hat{W}}, {\hat{H}}_\text {SO}]&= \sigma _i [{\hat{W}} , {\hat{V}}_i], \end{aligned}$$
(10)
$$\begin{aligned} {[}{\hat{S}}, {\hat{H}}_\text {SO}]&= 2i \, s_i \epsilon _{ijk} {\hat{V}}_j \sigma _k. \end{aligned}$$
(11)

Then using \(\sigma _i\sigma _j = \delta _{ij} + i \epsilon _{ijk} \sigma _k\), we get

$$\begin{aligned} {\hat{S}} [{\hat{W}}, {\hat{H}}_{\text {SO}}] = (\sigma _j + s_j + i\epsilon _{ijk} s_i \sigma _k) [{\hat{W}} , {\hat{V}}_j]. \end{aligned}$$
(12)

For the second commutator, we write \(\hat{{\mathbf {V}}}{\hat{W}}\) as the sum of its symmetric and anti-symmetric parts

$$\begin{aligned}&2i\epsilon _{ijk} s_i {\hat{V}}_j \sigma _k {\hat{W}} \nonumber \\&\quad = i\epsilon _{ijk} s_i \sigma _k \left( \big ({\hat{V}}_j{\hat{W}} + {\hat{W}}{\hat{V}}_j \big ) + [\hat{V_j}, {\hat{W}}] \right) \end{aligned}$$
(13)

and clearly, the second part cancels with cross product part of \({\hat{S}} [{\hat{W}}, {\hat{H}}_{\text {SO}}]\) in Eq. (12). Now we just need to use

$$\begin{aligned} \partial _{s_i} {\hat{S}} = \frac{1}{4\pi } \left( \sigma _i - s_i s_j \sigma _j \right) , \end{aligned}$$
(14)

(see footnoteFootnote 1) which implies

$$\begin{aligned} (\partial _{s_i} + s_i) {\hat{S}}&= \frac{1}{4\pi } \left( \sigma _i + s_i \right) , \end{aligned}$$
(15)
$$\begin{aligned} \epsilon _{ijk} \partial _{s_i} ( s_j {\hat{S}} )&= \frac{1}{4\pi } \epsilon _{ijk} \sigma _i s_j, \end{aligned}$$
(16)

and thus

$$\begin{aligned} \left( \partial _t f \right) _\text {SO}= & {} - \frac{i}{\hbar }{{\,\mathrm{Tr}\,}}\Big \{ \big [ (\partial _{s_i} + s_i) {\hat{S}} [{\hat{W}}, \hat{V_i} ] \nonumber \\&\quad + \epsilon _{ijk} \partial _{s_i} s_j {\hat{S}}[{\hat{W}}, \hat{V_k}]_+ \big ] \rho \Big \} . \end{aligned}$$
(17)

The remaining, laborious, task is to evaluate and take the Fourier transform of \(\hat{T}({\hat{\varvec{\pi }}}\times {\hat{\mathbf {E}}}) \pm ({\hat{\varvec{\pi }}}\times {\hat{\mathbf {E}}}) \hat{T}\), then express the result in terms of differential operators—functions of \(\partial _p\) and \(\partial _x\)—acting on \({\hat{W}}\). These operators can be taken outside the trace, so that they act on f, and this will give the kinetic equation. Since

$$\begin{aligned}{}[{{\hat{T}}}, {\hat{\varvec{\pi }}} \times {\hat{\mathbf {E}}}]&= [{{\hat{T}}}, {\hat{\varvec{\pi }}}] \times {\hat{\mathbf {E}}} + {\hat{\varvec{\pi }}} \times [{{\hat{T}}}, {\hat{\mathbf {E}}}], \end{aligned}$$
(18)

we need to evaluate the commutators with \({\hat{\varvec{\pi }}}\) and \({\hat{\mathbf {E}}}\). This is sufficient, because for any operator \( {\hat{O}} \)

$$\begin{aligned}{}[{\hat{W}}, {\hat{O}}^\dagger ] = - [{\hat{W}}, {\hat{O}}]^\dagger , \end{aligned}$$
(19)

since \({\hat{W}}\) is Hermitian, and we get the commutator with the Hermitian ordering [which appears in Eq. (9)] by reading off the “imaginary part” of \([{\hat{W}}, {\hat{\varvec{\pi }}}\times {\hat{\mathbf {E}}}]\). Sections 2.2 to 2.4 present the details.

2.2 The commutator \([{\hat{W}}, {\hat{\mathbf {E}}}]\)

In Sects. 2.2 to 2.4, we will typically omit boldface for vector quantities; the type of each quantity should be apparent from context.

Using Eq. (4), we can write the operator \({{\hat{T}}}\) with \({\hat{\Theta }}(u) = \exp (\frac{i}{\hbar }u\cdot \hat{p})\) on the right. Since \({{\hat{p}}}\) is the generator of translations, the operator \(\Theta (u)\) acts like

$$\begin{aligned} {\hat{\Theta }}(u) |x\rangle&= |x-u\rangle \end{aligned}$$
(20)
$$\begin{aligned} {\hat{\Theta }}(u) f({{\hat{x}}})&= f(\hat{x}+ u){\hat{\Theta }}(u) \end{aligned}$$
(21)

and thus, using Eq. (4) to put the translation operator on the left, with the other factors commuting with \(\hat{E}\),

$$\begin{aligned}{}[{{\hat{T}}}, {{\hat{E}}}_i] = \hat{T}(u,v) \left( \hat{E}_i({{\hat{x}}}) - \hat{E}_i({{\hat{x}}} - u) \right) \end{aligned}$$
(22)

Now we need an expression for the product \({\hat{\varvec{\pi }}}\times [{{\hat{T}}}, {\hat{\mathbf {E}}}]\) in terms of \({{\hat{T}}}\). By putting the commutator in the form Eq. (22), we can use any expression for \({{\hat{T}}}\) as is most appropriate. The one that is most appropriate here is Eq. (4) since we can lift the result from Ref. [23] their (4.30b), and its Hermitian conjugate:

$$\begin{aligned} {\hat{\pi }}_i \exp \left( \frac{i}{\hbar }u\cdot {\hat{\pi }} \right)&= \left( \frac{\hbar }{i} \frac{\partial }{\partial u_i} - q \int _0^1 d\tau \, (1-\tau )\right. \nonumber \\&\left. \quad \times [u\times \hat{B}({\hat{r}} + \tau u)]_i \right) \exp \left( \frac{i}{\hbar }u\cdot {\hat{\pi }} \right) , \end{aligned}$$
(23)
$$\begin{aligned}&\quad \times \exp \left( -\frac{i}{\hbar }u\cdot {\hat{\pi }} \right) {\hat{\pi }}_i\nonumber \\&\quad = \exp \left( -\frac{i}{\hbar }u\cdot {\hat{\pi }} \right) \left( -\frac{\hbar }{i} \overset{\leftarrow }{ \frac{\partial }{\partial u_i} }\right. \nonumber \\&\qquad \left. -q\!\int _0^1\!\! d\tau \, (1{-}\tau ) [u\times \hat{B}({\hat{r}}{+}\tau u)]_i\!\!\right) . \end{aligned}$$
(24)

We thus have that the operator \(\pi _i [{{\hat{T}}}, E_j]\) can be expressed as \(\pi _i [{{\hat{T}}}, E_j] = \hat{O}^B_{ij} + \hat{O}^D_{ij}\) where

$$\begin{aligned} \hat{O}^B_{ij}&= -q \int _0^1 d\tau \, (1-\tau ) [u\times \hat{B}(\hat{x}+ \tau u)]_i \hat{T}(u,v) \nonumber \\&\quad \times \left( \hat{E}_j({{\hat{x}}}) - \hat{E}_j({{\hat{x}}} - u) \right) , \end{aligned}$$
(25)
$$\begin{aligned} \hat{O}^D_{ij}&= e^{-\frac{i}{2\hbar } u\cdot v}\left[ \frac{\hbar }{i} \frac{\partial }{\partial u_i} \exp \left( \frac{i}{\hbar }u\cdot \hat{\pi }\right) \right] \nonumber \\&\quad \times \exp \left( \frac{i}{\hbar }v\cdot \hat{x}\right) \left( \hat{E}_j(\hat{x}) - \hat{E}_j(\hat{x}- u)\right) . \end{aligned}$$
(26)

Now let \(|x'\rangle , |x''\rangle \) be eigenstates of \({{\hat{x}}}\) (at the appropriate time). Use Eq. (4) so that the \(\hat{x}\) operators are on the left in \({{\hat{T}}}\).

Let \({\hat{Q}}^B_{ij}\) be the Fourier transform in u, v of \(\hat{O}^B_{ij}\). Then, letting \(e^{i{\hat{\Phi }}} = \exp \left[ \ -\frac{iq}{\hbar } u \cdot \int _0^1 d\tau \, \hat{A}(\hat{x}+ \tau u) \right] \) its matrix elements are

$$\begin{aligned}&\langle x' | {\hat{Q}}^B_{ij} | x'' \rangle = {\mathcal {F}}\left[ \langle x'| \hat{O}^B_{ij} | x''\rangle \right] \nonumber \\&\quad = -q{\mathcal {F}} \bigg [ e^{\frac{i}{\hbar }v\cdot (x' + u/2)} \int _0^1 d\tau \, (1-\tau ) \nonumber \\&\qquad \times [u\times B(x' + \tau u)]_i \langle x'| e^{i\Phi } e^{\frac{i}{\hbar }u \cdot \hat{p}}\nonumber \\&\qquad \left( \hat{E}_j({{\hat{x}}}) - \hat{E}_j({{\hat{x}}} - u) \right) |x''\rangle \bigg ]\nonumber \\&\quad = -q{\mathcal {F}}\left[ e^{\frac{i}{\hbar }v\cdot (x' + u/2)} \int _0^1 d\tau \, (1-\tau )\right. \nonumber \\&\left. \qquad \times [u\times B(x' + \tau u)]_i \langle x'| e^{i\Phi } \left( \hat{E}_j({{\hat{x}}} \!+\! u) - \hat{E}_j({{\hat{x}}}) \right) |x''\!-\! u\rangle \right] \nonumber \\&\quad = -q{\mathcal {F}}\left[ e^{\frac{i}{\hbar }v\cdot (x' + u/2)} \int _0^1 d\tau \, (1-\tau )\right. \nonumber \\&\left. \qquad \times [u\times B(x' \!+\! \tau u)]_i \big ( E_j(x' \!+\! u) \!-\! E_j(x')\big ) \langle x'| e^{i\Phi } |x''\!-\! u\rangle \right] .\nonumber \\ \end{aligned}$$
(27)

At this point we see that the Fourier transform in v can be carried out and will give an expression proportional to \(\delta ( x'-x + u/2 )\). Hence the matrix elements of \({\hat{Q}}^B_{ij}(x,p)\) remain unchanged if we change \(x'\) to \(x -u/2\) in the arguments of the fields. In the integral over \(\tau \), we also change variables to \(\tau -1/2\) for a somewhat simpler expression.

We can then restore the operators making up \({{\hat{T}}}\), resulting in

$$\begin{aligned} \langle x' | {\hat{Q}}^B_{ij} | x'' \rangle= & {} -q{\mathcal {F}} \int _{-1/2}^{1/2} d\tau \, \left( \frac{1}{2}-\tau \right) [u\times B(x + \tau u)]_i \nonumber \\&\times \big ( E_j(x + u/2) - E_j(x - u/2)\big )\nonumber \\&\times \langle x'| e^{\frac{i}{2\hbar }u\cdot v} e^{\frac{i}{\hbar }v \cdot x} e^{i{\hat{\Phi }}} |x''\rangle \nonumber \\= & {} -q{\mathcal {F}} \left[ \int _{-1/2}^{1/2} d\tau \, \left( \frac{1}{2}\!-\!\tau \right) [u\times B(x \!+\! \tau u)]_i \big ( E_j(x \nonumber \right. \\&\left. + u/2) \!-\! E_j(x \!-\! u/2)\big ) \langle x' | \hat{T}(u,v) |x'' \rangle \right] \end{aligned}$$
(28)

Since the Fourier transform sends \(u \mapsto i \hbar \partial _p\), we can now express this operator in terms of \({\hat{W}}\) and its derivatives. First, use that

$$\begin{aligned} E_j(x + u/2) - E_j(x - u/2) = u_k \int _{-1/2}^{1/2} d\tau E_{j,k} (x + \tau u) , \end{aligned}$$
(29)

and note that this quantity is real. In the integral with B, 1/2 is even and \(-\tau \) is odd, so even and odd powers of \(i\tau \hbar \partial _p\) in the expansion of B survive the integration, respectively. Since we want the imaginary part, it is the term with \(-\tau \) that we should keep, and in conclusion

$$\begin{aligned} {\text {Im}} \left( {\hat{Q}}^B_{ij}\right)= & {} -q\hbar ^2 \int _{-1/2}^{1/2} d\tau \, \tau [\partial _p \times B(x + i\tau \hbar \partial _p )]_i\nonumber \\&\quad \times \int _{-1/2}^{1/2} d\sigma \, E_{j,k}(x + i\sigma \hbar \partial _p) \partial _{p_k} {\hat{W}}.\nonumber \\ \end{aligned}$$
(30)

We now turn to \({\hat{O}}^D_{ij}\). Note that from the expression for \(\hat{T}\) in Eq. (4) we have

$$\begin{aligned} \frac{\partial }{\partial u_i} \hat{T}= -\frac{i}{2\hbar } v_i \hat{T}+ e^{-\frac{i}{2\hbar } u\cdot v} \frac{\partial }{\partial u_i} e^{\frac{i}{\hbar }u\cdot {{\hat{\pi }}}} e^{\frac{i}{\hbar }v\cdot {\hat{x}} } \end{aligned}$$
(31)

and hence

$$\begin{aligned} {\hat{O}}^D_{ij} = \hat{T}\left[ \frac{v_i}{2} + \frac{\hbar }{i} \overset{\leftarrow }{\frac{\partial }{\partial u_i}} \right] \big ({\hat{E}}_j({\hat{x}}) - {\hat{E}}_j({\hat{x}} - u)\big ). \end{aligned}$$
(32)

The first term can be handled using the argument above, except that the Fourier transform in v will send \(v_i\) to \(i\hbar \partial _{x_i} \delta (x) \). The result is that

$$\begin{aligned}&{\mathcal {F}} \left[ \langle x' | \hat{T}\frac{v_i}{2} \big ({\hat{E}}_j({\hat{x}}) - {\hat{E}}_j({\hat{x}} - u)\big ) |x'' \rangle \right] \nonumber \\&\quad = -\frac{\hbar }{2i} \partial _{x_i} \left[ \big ( E_j(x + i \hbar \partial _p/2)\right. \nonumber \\&\left. \qquad - E_j(x - i\hbar \partial _p/2) \big ) \langle x' | {\hat{W}} |x'' \rangle \right] \end{aligned}$$
(33)

but this quantity is real, and so makes no contribution to the evolution equation. For the term with the u-derivative, we integrate by parts in the Fourier transform, i.e.,

$$\begin{aligned}&{\mathcal {F}}\left[ \left( \frac{\partial }{\partial u_i} {\hat{T}} \right) \big ({\hat{E}}_j({\hat{x}}) - {\hat{E}}_j({\hat{x}} - u)\big ) \right] \nonumber \\&\quad = {\mathcal {F}} \left[ p_i \hat{T}\big ({\hat{E}}_j({\hat{x}}) - {\hat{E}}_j({\hat{x}} - u)\big ) - \frac{\hbar }{i}{\hat{T}} {\hat{E}}_{j,i}({\hat{x}} - u) \right] . \nonumber \\ \end{aligned}$$
(34)

In the first term, \(p_i\) can be taken outside the Fourier transform, and the remaining operator is treated like above resulting in

$$\begin{aligned}&{\mathcal {F}}\left[ \langle x' | {\hat{O}}_{ij}^D | x'' \rangle \right] = \left[ p_i \big (E_j(x + i\hbar \partial _p/2) \right. \nonumber \\&\left. \quad - E_j(x - i\hbar \partial _p/2) \big ) - \frac{\hbar }{i}E_{j,i}(x-i\hbar \partial _p/2) \right] \langle x' | {\hat{W}} |x''\rangle . \nonumber \\ \end{aligned}$$
(35)

We can write this in a somewhat simpler form as

$$\begin{aligned} E_j(x + i\hbar \partial _p/2) - E_j(x - i\hbar \partial _p/2) = i\hbar (\partial _{x_k} {\tilde{E}}_j) \partial _{p_k} \end{aligned}$$
(36)

where we have introduced the notation

$$\begin{aligned} {\tilde{E}}_j = \int _{-1/2}^{1/2} E_j(x + i\hbar \tau \partial _p) \, d\tau . \end{aligned}$$
(37)

To summarize, we obtain

$$\begin{aligned} {\text {Im}}({\hat{\varvec{\pi }}} \times [{\hat{W}}, {\hat{\mathbf {E}}} ]) = (\mathbf {p}+ \Delta {\tilde{\mathbf {p}}}) \times {\tilde{\mathbf {E}}} ( \hbar \overset{\leftarrow }{\partial _x} \cdot \overset{\rightarrow }{\partial _p}) {\hat{W}} \end{aligned}$$
(38)

where

$$\begin{aligned} \Delta {\tilde{\mathbf {p}}} = -\frac{q\hbar }{i}\partial _p \times \int _{-1/2}^{1/2} \, d\tau \tau \mathbf {B}(\mathbf {x}+ i\hbar \tau \partial _p). \end{aligned}$$
(39)

The quantities \({\tilde{\mathbf {E}}}\) and \(\Delta {\tilde{\mathbf {p}}}\) are the same as in Refs. [13, 23]. Since Eq. (38) is to be contracted with the Pauli matrices, in the kinetic equation it represents the spin-orbit force.

2.3 The commutator \([{\hat{W}}, {\hat{\varvec{\pi }}}]\)

We use Eq. (4) for \({\hat{T}}\), so that

$$\begin{aligned}{}[\hat{T}, {\hat{\pi }}_i] E_j&= [-{\hat{\pi }}_i, \hat{T}] E_j = -e^{-\frac{i}{2\hbar } u\cdot v} \left[ \hat{\pi _i}, \exp \left( \frac{i}{\hbar }u\cdot {\hat{\pi }}\right) \right. \nonumber \\&\left. \quad \times \exp \left( \frac{i}{\hbar }v\cdot {\hat{x}} \right) \right] E_j \nonumber \\&= e^{-\frac{i}{2\hbar } u\cdot v}\left( -v_i + q \int _0^1 d\tau \, [u\times {\hat{B}}({\hat{x}} + \tau u)]_i \right) \nonumber \\&\quad \times \exp \left( \frac{i}{\hbar }u\cdot {\hat{\pi }}\right) \exp \left( \frac{i}{\hbar }v\cdot {\hat{x}}\right) E_j \nonumber \\&= -v_i {\hat{T}}(u,v) E_j \nonumber \\&\quad + q\int _0^1 d\tau [u\times {\hat{B}}({\hat{x}} + \tau u)]_i \hat{T}(u,v) E_j \nonumber \\&= {\hat{O}}^A_{ij} + {\hat{O}}^C_{ij} , \end{aligned}$$
(40)

also using (4.25) from Ref. [23]. We can now look at the matrix elements of \( {\mathcal {F}} \left[ {\hat{O}}^A_{ij} \right] \), but it is of the form in Eq. (33) except we have only one \({\hat{E}}\) operator, \({\hat{E}}({\hat{x}})\). Therefore,

$$\begin{aligned} {\mathcal {F}} \left[ \langle x' | {\hat{O}}^A_{ij} |x''\rangle \right]= & {} \langle x' | \frac{\hbar }{i} \partial _{x_i} \left[ E_j(x+ i \hbar \partial _p/2) {\hat{W}} \right] | x'' \rangle \nonumber \\= & {} \langle x' | \frac{\hbar }{i}\left[ E_{j,i}(x + i\hbar \partial _p/2) {\hat{W}} \right. \nonumber \\&\left. + E_j(x + i\hbar \partial _p/2) \partial _{x_i} {\hat{W}} \right] | x'' \rangle . \end{aligned}$$
(41)

We see that the imaginary part of \(E_{i,j}\) term cancels the imaginary part of the corresponding term in Eq. (35), since when dividing by i, even powers of \(i\hbar \partial _p\) should be kept. For the second term, we can integrate by parts to show that

$$\begin{aligned}&\int _{-1/2}^{1/2} E_j(x + \tau u) \, d\tau + u_k \int _{-1/2}^{1/2} \tau E_{j,k}(x + \tau u) \, d\tau \nonumber \\&\quad = \frac{1}{2} \big (E_j(x + u/2) + E_j(x - u/2)\big ) \end{aligned}$$
(42)

Again keeping even powers of \(i\hbar \partial _p\) since we are dividing by i,

$$\begin{aligned}&{\text {Im}} \frac{\hbar }{i} E_j(x + i\hbar \partial _p)\nonumber \\&\quad = -\frac{\hbar }{2} \big ( E_j(x + i\hbar \partial _p/2) + E_j(x - i\hbar \partial _p/2) \big )\nonumber \\&\quad = - \hbar {\tilde{E}}_j - i\hbar ^2 \partial _{p_k} \int _{-1/2}^{1/2} \tau E_{j,k}(x + i\hbar \tau \partial _p) \, d\tau . \end{aligned}$$
(43)

This is the “hidden momentum” velocity correction term \(\propto \mathbf {E}\times \mathbf {s}\) [27] (to be discussed more below), but with \(\mathbf {E}= {\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}\) where \(\Delta {\tilde{\mathbf {E}}}\) is higher order in \(\hbar \).

Following steps like those above, and using Eq. (42) again, one readily expresses the matrix elements of \({\hat{O}}^C_{ij}\) in terms of those of \({\hat{W}}\). The result is that

$$\begin{aligned} \langle x' | {\hat{O}}^C_{ij} | x''\rangle = \epsilon _{inm} {\tilde{B}}_m ( {\tilde{E}}_j + \Delta {\tilde{E}}_j ) \partial _{p_n} \langle x' | {\hat{W}} | x'' \rangle \end{aligned}$$
(44)

which, in the kinetic equation, will give

$$\begin{aligned}&\epsilon _{ijk} \epsilon _{inm} \tilde{B_m} ( {\tilde{E}}_j + \Delta {\tilde{E}}_j ) \partial _{p_n} \sigma _k {\hat{W}} \nonumber \\&\quad \propto \big [ \big ( ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}) \times \varvec{\sigma }\big ) \times {\tilde{\mathbf {B}}} \big ] \cdot \partial _p {\hat{W}}, \end{aligned}$$
(45)

i.e., it is the correction to the magnetic force due to the relation between momentum and velocity. Here \({\tilde{\mathbf {B}}}\) is defined in the same way as \({\tilde{\mathbf {E}}}\), Eq. (37).

2.4 The spin transform

It remains to evaluate the terms in the kinetic equation arising from the spin transform, proportional to

$$\begin{aligned} \epsilon _{ijk} s_i \sigma _k \big ( ({\hat{\varvec{\pi }}} \times {\hat{\mathbf {E}}} - {\hat{\mathbf {E}}} \times {\hat{\varvec{\pi }}})_j{\hat{W}} + {\text {H.c.}} \big ) \end{aligned}$$

where \({\text {H.c.}}\) denotes the Hermitian conjugate. Using Eq. (23) again we establish that

$$\begin{aligned} {\hat{\pi }}_k {\hat{E}}_l({\hat{x}}) {\hat{T}}&= ({\mathcal {D}}_k{\hat{T}}) E_l({\hat{x}} - u), \end{aligned}$$
(46)
$$\begin{aligned} {\hat{E}}_l({\hat{x}}) {\hat{\pi }}_k {\hat{T}}&= {\hat{E}}_l({\hat{x}}) {\mathcal {D}}_k{\hat{T}}, \end{aligned}$$
(47)

where \({\mathcal {D}}_k\) is the operator

$$\begin{aligned} {\mathcal {D}}_k = \frac{\hbar }{i} \frac{\partial }{\partial u_k} + \frac{v_k}{2} - q \int _0^1 d\tau \, (1- \tau ) [u\times {\hat{B}}({{\hat{x}}} + u\tau )]_k. \end{aligned}$$
(48)

Hence the product \(({\hat{\varvec{\pi }}} \times {\hat{\mathbf {E}}} - {\hat{\mathbf {E}}} \times {\hat{\varvec{\pi }}})_j {\hat{T}}\) is given by

$$\begin{aligned}&\epsilon _{jkl}(\hat{\pi }_k \hat{E}_l - \hat{E}_j \hat{\pi }_k) {\hat{T}} = \epsilon _{jkl}(\hat{\pi }_k \hat{E}_l + \hat{E}_k \hat{\pi }_l) {\hat{T}}\nonumber \\&\quad = \epsilon _{jkl} \left[ \frac{\hbar }{i} \left( \frac{\partial {\hat{T}} }{\partial u_k} {\hat{E}}_l({\hat{x}} - u) + {\hat{E}}_l({\hat{x}}) \frac{\partial {\hat{T}}}{\partial u_k} \right) \right. \nonumber \\&\left. \qquad + v_k {\hat{E}}_l ({\hat{x}}){\hat{T}} - 2 I_k E_l({\hat{x}}){\hat{T}} \right] , \end{aligned}$$
(49)

where

$$\begin{aligned} I_k = \int _0^1 d\tau \, (1- \tau ) [u\times {\hat{B}}({{\hat{x}}} + u\tau )]_k. \end{aligned}$$
(50)

Differentiating \({\hat{E}}_l(\hat{x}) \hat{T}= \hat{T}{\hat{E}}_l(\hat{x}- u)\) with respect to \(u_k\) we obtain

$$\begin{aligned} {\hat{E}}_l({\hat{x}}) \frac{\partial }{\partial u_k} {\hat{T}} = \frac{\partial {\hat{T}}}{\partial u_k} {\hat{E}}_l({\hat{x}} - u) - {\hat{T}} {\hat{E}}_{l,k} ({\hat{x}} - u). \end{aligned}$$
(51)

so that

$$\begin{aligned}&\frac{\partial {\hat{T}} }{\partial u_k} {\hat{E}}_l({\hat{x}} - u) + {\hat{E}}_l({\hat{x}}) \frac{\partial {\hat{T}}}{\partial u_k}\nonumber \\&\quad = 2{\hat{E}}_l({\hat{x}}) \frac{\partial {\hat{T}}}{\partial u_k} + {\hat{T}} {\hat{E}}_{l,k}({\hat{x}} - u) \nonumber \\&\quad = 2{\hat{E}}_l({\hat{x}}) \frac{\partial {\hat{T}}}{\partial u_k} + {\hat{E}}_{l,k}({\hat{x}}) {\hat{T}}. \end{aligned}$$
(52)

Putting this into Eq. (49), all terms are similar to ones already seen, and we will provide only an outline of the remaining calculations. The operator of the type \({\hat{E}}_l({\hat{x}}) \frac{\partial {\hat{T}}}{\partial u_k}\) we can handle as in Eq. (34), resulting in

$$\begin{aligned} \sim p_k {\tilde{E}}_j (x-i\hbar \partial _p/2) W , \end{aligned}$$

and following the argument leading to Eq. (43), when taking the real part, we will get

$$\begin{aligned} \sim p_k ({\tilde{E}}_l + \Delta {\tilde{E}}_l) W. \end{aligned}$$
(53)

For the term proportional to \(v_k\) in Eq. (49), we use that \({\mathcal {F}} : v_k \mapsto i\hbar \partial _{x_k} \delta (x)\) as leading up to Eq. (33). When taking the real part, the term where the derivative acts on E cancels with the derivative term from Eq. (52) and what remains is

$$\begin{aligned} \sim i \hbar \left( E_l(x + i\hbar \partial _p/2 ) - E_l(x - i\hbar \partial _p /2 ) \right) \partial _{x_k} W, \end{aligned}$$
(54)

which can be simplified using Eq. (36).

Following steps like those for \({\hat{O}}^B\) (Eq. (25) and following), the final term in Eq. (49), proportional to \(I_k\), will give us a contribution of the form

$$\begin{aligned} -\int _{-1/2}^{1/2} d\tau \, \left( \frac{1}{2}-\tau \right) [u\times B(x + \tau u)]_k E_l(x - u/2) {\hat{T}}. \end{aligned}$$
(55)

When taking the real part of the Fourier transform of this, there will be two terms,

$$\begin{aligned}&\sim \int _{-1/2}^{1/2} \tau [ i\hbar \partial _p\times B(x + i\hbar \tau \partial _p )]_k \, d\tau \left( E_l(x + i \hbar \partial _p/2 )\right. \nonumber \\&\left. \quad + E_l(x - i \hbar \partial _p/2 ) \right) \nonumber \\&\quad W \propto \Delta {\tilde{\mathbf {p}}} \times ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}) W, \end{aligned}$$
(56)

which is in line with previous generalisations, and

$$\begin{aligned}&\sim \int _{-1/2}^{1/2} [ i\hbar \partial _p\times B(x + i\hbar \tau \partial _p )]_k \, d\tau \, \left( E_l(x - i \hbar \partial _p/2 ) \right. \nonumber \\&\left. \quad - E_l(x + i \hbar \partial _p/2 ) \right) \nonumber \\&\quad W \propto ({\tilde{\mathbf {B}}} \times \hbar \partial _p ) \times ({\tilde{\mathbf {E}}} \hbar \overset{\leftarrow }{\partial _x} \cdot \overset{\rightarrow }{\partial _p}) W, \end{aligned}$$
(57)

which is of a new type. However, both are order \(\hbar ^2\), so their limits could not have been found in previous works that were either \(\hbar \) or didn’t include the spin–orbit interaction.

Thus, the spin torque is modified to add a term proportional to \(({\tilde{\mathbf {p}}} + \Delta {\tilde{\mathbf {p}}} ) \times ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}) + \frac{q}{2}({\tilde{\mathbf {B}}} \times \hbar \partial _p ) \times \cdot ({\tilde{\mathbf {E}}} \hbar \overset{\leftarrow }{\partial _x} \cdot \overset{\rightarrow }{\partial _p})\). The overall sign and coefficient of this term is found by matching its long-scale limit to the model in Ref. [19]

2.5 Conclusion

The evolution equation for f follows directly by taking the expectation value of the evolution equation for \({\hat{W}}\). It is

$$\begin{aligned}&\partial _t f + \frac{1}{m} \left( \mathbf {p}+ \Delta {\tilde{\mathbf {p}}} + \frac{\mu _e}{2mc^2} ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}) \times (\mathbf {s}+ \nabla _s) \right) \cdot \nabla _x f \nonumber \\&\quad + q \left[ ({\tilde{\mathbf {E}}} \!+\! \left( \mathbf {p}\!+\! \Delta {\tilde{\mathbf {p}}} \!+\! \frac{\mu _e}{2mc^2} ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}}) \times (\mathbf {s}+ \nabla _s) \right) \times {\tilde{\mathbf {B}}} \right] \nonumber \\&\quad \times \nabla _p f + \mu _e \left( {\tilde{\mathbf {B}}} - \frac{\mathbf {p}+ \Delta {\tilde{\mathbf {p}}}}{2mc^2} \times {\tilde{\mathbf {E}}} \right) \cdot (\mathbf {s}+ \nabla _s) (\overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) f \nonumber \\&\quad + \frac{2\mu _e}{\hbar } \left[ \mathbf {s}\times \left( {\tilde{\mathbf {B}}} + \Delta {\tilde{\mathbf {B}}} - \frac{1}{2mc^2} \left( {\tilde{\mathbf {p}}} + \Delta {\tilde{\mathbf {p}}} \right) \times ({\tilde{\mathbf {E}}} + \Delta {\tilde{\mathbf {E}}})\nonumber \right. \right. \\&\left. \left. \quad - \frac{q}{4mc^2}({\tilde{\mathbf {B}}} \times \hbar \partial _p ) \times \cdot ({\tilde{\mathbf {E}}} \hbar \overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) \right) \right] \cdot \nabla _s f = 0. \end{aligned}$$
(58)

For reference, the notation used is

$$\begin{aligned} {\tilde{\mathbf {E}}}(\mathbf {x})&= \int _{-1/2}^{1/2} \mathbf {E}(\mathbf {x}+ i\hbar \tau \nabla _p /2) \, d\tau \nonumber \\&= \Big [\mathbf {E}\int _{-1/2}^{1/2} \cos ( \hbar \tau \overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) \, d\tau \Big ](\mathbf {x}), \end{aligned}$$
(59)
$$\begin{aligned} \Delta {\tilde{\mathbf {E}}}(\mathbf {x})&= i\hbar \int _{-1/2}^{1/2} \tau \mathbf {E}(\mathbf {x}+ i\hbar \tau \nabla _p) \, d\tau (\overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) \nonumber \\&= -\hbar \Big [ \mathbf {E}\int _{-1/2}^{1/2} \sin ( \hbar \tau \overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) \, d\tau \, \overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} \Big ](\mathbf {x}), \end{aligned}$$
(60)
$$\begin{aligned} \Delta {\tilde{\mathbf {p}}}&= -iq\hbar \int _{-1/2}^{1/2} \tau \mathbf {B}(\mathbf {x}+ i\hbar \tau \nabla _p) \, d\tau \times \nabla _p\nonumber \\&= q\hbar \Big [\mathbf {B}\int _{-1/2}^{1/2} \sin (\hbar \tau \overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} ) \, d\tau \Big ](\mathbf {x}) \times \nabla _p, \end{aligned}$$
(61)

with \({\tilde{\mathbf {B}}}\), \(\Delta {\tilde{\mathbf {B}}}\) defined in the same way as \({\tilde{\mathbf {E}}}\), \(\Delta {\tilde{\mathbf {E}}}\). Functions of operators are defined in terms of their Taylor series.

There are five new terms in Eq. (58) as compared to Ref. [13]. In order, they represent: the “hidden momentum” (see below) correction to the velocity in the diffusion and magnetic force terms, respectively; the spin–orbit force; the spin torque due to spin–orbit interaction, including the Thomas precession; and the last term, which is non-linear in the fields and higher-order in \(\hbar \). This term lacks an analog in Ref. [19]; the others are short-scale generalizations of terms found in Ref. [19] similar to how Ref. [23] generalizes the Vlasov equation.

We have denoted the electron magnetic moment by \(\mu _e\) to allow for an anomalous magnetic moment, i.e., \(\mu _e = \frac{g}{2} \mu _B\) where \(\mu _B\) is the Bohr magneton and \(g = 2 + \frac{\alpha }{\pi } + \ldots \). That \(g \ne 2\) leads to a mismatch between the cyclotron frequency and Larmor frequency, resulting in non-classical resonances [28], as will be seen below.

The system is closed with Maxwell’s equations with polarization and magnetization,

$$\begin{aligned} \nabla \cdot \mathbf {E}&= \frac{1}{\epsilon _0}( \rho _f - \nabla \cdot {\mathbf {P}} ), \end{aligned}$$
(62)
$$\begin{aligned} \nabla \times \mathbf {B}&= \mu _0 {\mathbf {J}}_f + \mu _0 \nabla \times {\mathbf {M}} + \frac{1}{c^2} \frac{\partial \mathbf {E}}{\partial t} + \mu _0 \frac{\partial {\mathbf {P}}}{\partial t}. \end{aligned}$$
(63)

The free charge \(\rho _f\) is given by

$$\begin{aligned} \rho _f = q \int f \, d\Omega , \end{aligned}$$
(64)

introducing \(d\Omega = d^3p \, d^2 s\). Finding the continuity equation for \(\rho _f\) using Eq. (58), the free current \({\mathbf {J}}_f\) is given by

$$\begin{aligned} {\mathbf {j}}_f = q\int {\mathbf {v}} f \, d\Omega = q\int \left( \frac{\mathbf {p}}{m} + \frac{3\mu _e \mathbf {E}\times \mathbf {s}}{2m^2c^2} \right) f \, d\Omega , \end{aligned}$$
(65)

and while it may appear strange that we do not have \(\mathbf {p}\parallel {\mathbf {v}}\), this is the function on phase space in Weyl correspondence with \(\hat{{\mathbf {v}}} = \frac{i}{\hbar } [{\hat{H}}, {\hat{\mathbf {x}}} ]\). This is an example of “hidden momentum”, common to systems with magnetic moments [27, 29,30,31], and is found already in the long-scale length limit [19], and also in Ref. [12].

Finally, the polarization and magnetization densities are given by

$$\begin{aligned} {\mathbf {P}}&= -3\mu _e \int \frac{\mathbf {s}\times \mathbf {p}}{2mc^2} f \, d\Omega , \end{aligned}$$
(66)
$$\begin{aligned} {\mathbf {M}}&= 3\mu _e \int {\mathbf {s}} f \, d\Omega . \end{aligned}$$
(67)

Here, a factor 3 appears due to the normalization of the spin transform; the magnetization is proportional to the expectation value of \(\varvec{\sigma }\).

It should be noted that a model very similar to Eq. (58) was recently presented by Hurst et al. [32], starting from the same Hamiltonian. Their model, however, is formulated in terms of a scalar quantity \(f_0\) and a vector quantity \({\mathbf {f}}\), the mass and spin densities, respectively. Mathematically, this is writing the Hermitian matrix-valued Wigner function in the basis \(\{ I, \varvec{\sigma }\}\), and the correspondence between models is that \(f_0 = \int f \, d^2s\) and \({\mathbf {f}} = 3\int \mathbf {s}f \, d^2s\). Hurst et al. find the same charge and current densities as we doFootnote 2 including the same “hidden momentum” in the free current or velocity. They also find the new non-linear term in the spin torque.

Hurst et al. [32] derived their model using a completely different method, based on a gauge invariant expression for the Moyal bracket [33]. While our results are equivalent to those of Ref. [32], apart from some details to be discussed in the next section, we note that the derivation made here has a value in itself. In case generalizations of the governing equations are sought for, aiming to extend the regime of validity, having more than one route to follow increases the possibility for success. We will return to related issues in Sects. 3 and 4.

Finally, we note that several models somewhat similar to Eq. (58), but allowing for fully relativistic motion have been published in the literature, see e.g. [34,35,36]. While these models allow for \(\mathbf{p}\sim mc\), they are subject to other limitations and/or drawbacks. Specifically, this includes not separating between electron and positron states and using a perturbative quantum mechanical treatment [36].

3 Linear waves

To illustrate the usefulness of Eq. (58) we study linear waves in a homogeneous plasma. We consider two cases: first electrostatic waves in a magnetized plasma, then electromagnetic waves in an unmagnetized plasma. From now on, we will let \(c = 1\) to simplify the notation.

The momentum is expressed in cylindrical coordinates \(\mathbf {p}= (p_{\perp },\varphi _p,p_z)\) and the spin in spherical coordinates \({\mathbf {s}} = \sin {\theta _s}\cos {\varphi _s}\hat{{\mathbf {z}}} + \sin {\theta _s}\sin {\varphi _s}\hat{{\mathbf {y}}} + \cos {\theta _s}\hat{{\mathbf {z}} }\). In the linearization of Eq. (58) variables are separated according to \(f = f_0(p_\perp , p_z, \theta _s) + f_1(x,p,s,t)\), \(\mathbf {E}= \mathbf {E}_1\) and \(\mathbf {B}= B_0 \hat{\mathbf{z }} + \mathbf {B}_1\), where the subscripts 0 and 1 denote unperturbed and perturbed quantities respectively. Eq. (58) then becomes

$$\begin{aligned}&\frac{\partial f_1}{\partial t} + \frac{\mathbf {p}}{m} \cdot \nabla _x f_1+ \Big (\frac{\mathbf {p}}{m}\times \mathbf {B}_0\Big ) \cdot \nabla _pf_1 + \frac{2\mu _e}{h}(\mathbf {s}\times \mathbf {B}_0)\cdot \nabla _s f_1 \nonumber \\&\quad = -q\left[ \tilde{\mathbf {E}}+ \left( \frac{\mathbf {p}+ \Delta {\tilde{\mathbf {p}}}}{m} + \frac{\mu _e}{m}(\tilde{\mathbf {E}}+ \Delta \tilde{\mathbf {E}})\times (\mathbf {s}+ \nabla _s) \right) \nonumber \right. \\&\left. \qquad \times {\mathbf {B}}_0 + \frac{\mathbf {p}}{m}\times \tilde{\mathbf {B}}_1 \right] \cdot \nabla _pf_0\nonumber \\&\qquad +\mu _e\nabla _x \Bigg [ \Big (\tilde{\mathbf {B}}_1 -\frac{\mathbf {p}\times \tilde{\mathbf {E}}}{2m} \Big )\cdot (\mathbf {s}+ \nabla _s) \Bigg ]\cdot \nabla _pf_0 \nonumber \\&\qquad - \frac{2\mu _e}{\hbar } \mathbf {s}\times \Bigg [\tilde{\mathbf {B}}+\Delta \tilde{\mathbf {B}}-\frac{q\hbar ^2}{4m} \big ( {\mathbf {B}}_0 \times \nabla _p \big )\times \big (\tilde{\mathbf {E}}\overset{\leftarrow }{\nabla _x} \cdot \overset{\rightarrow }{\nabla _p} \big ) \nonumber \\&\qquad - \frac{(\mathbf {p}+ \Delta \tilde{\mathbf {p}}) \times (\tilde{\mathbf {E}}+ \Delta \tilde{\mathbf {E}}) }{2m}\Bigg ] \cdot \nabla _sf_0. \end{aligned}$$
(68)

In general the background distribution can be divided into its spin-up and spin-down components [37]

$$\begin{aligned} f_0(p_\perp , p_z, \theta _s) = \frac{1}{4\pi } \sum _{\nu = \pm 1} F_{0\nu }(p_\perp , p_z) (1 + \nu \cos \theta _s). \end{aligned}$$
(69)

In the sums below it will be implicit that \(\nu \) takes the values \(\pm 1\).

3.1 Electrostatic waves

In this geometry we consider: \({\mathbf {B}}_0 = B_0\hat{{\mathbf {z}}}\), \({\mathbf {k}} = k\hat{{\mathbf {z}}}\) and \({\mathbf {E}} = E\hat{{\mathbf {z}}}\). The perturbed parameters follow the plane-wave ansatz according to \(f_1= \tilde{f}e^{i\mathbf{k} \cdot \mathbf{x} -\omega t}\). The left hand side of Eq. (68) can then be written

$$\begin{aligned} \Big [ i\omega -i\frac{kp_z}{m}+ \omega _{ce}\frac{\partial }{\partial \varphi _p}+ \omega _{cg}\frac{\partial }{\partial \varphi _s} \Big ]f_1=RHS, \end{aligned}$$
(70)

where \(\omega _{ce}\) is the cyclotron frequency, \(\omega _{cg} = \frac{g}{2}\omega _{ce}\) and RHS is the right hand side of Eq. (68). Making an expansion of \({\tilde{f}}_1\) in eigenfunctions of the operators of the right hand side of Eq. (68) [37] we write

$$\begin{aligned} {\tilde{f}}_1(\mathbf {p}, \mathbf {s}) = \sum _{\alpha , \beta }\frac{1}{2\pi }g_{\alpha , \beta }(p_{\perp }, p_z, \theta _s) e^{-i(\alpha \varphi _s+\beta \varphi _p)}. \end{aligned}$$
(71)

Substituting Eq. (71) in Eq. (70), we can now express \(f_1\) in terms of \(f_0\)

$$\begin{aligned} f_1= & {} \frac{A}{\omega - kp_z/m} + \frac{B_{+} e^{i(\varphi _s - \varphi _p)} }{\omega - kp_z/m + \Delta \omega _{ce}} \nonumber \\&+ \frac{B_{-} e^{-i(\varphi _s - \varphi _p)}}{\omega - kp_z/m - \Delta \omega _{ce}}, \end{aligned}$$
(72)

where

$$\begin{aligned} A&= \sum _\nu -iq{\tilde{E}}\frac{\partial F_{0\nu }}{\partial p_z}, \end{aligned}$$
(73)
$$\begin{aligned} B_{\pm }&= i\mu _e \sum _\nu \sin {\theta _s} \left( -\frac{q B_0}{4m}({\tilde{E}} + \Delta {\tilde{E}}) \frac{\partial F_{0\nu }}{\partial p_{\perp }}\right. \nonumber \\&\quad \left. - \frac{\nu p_{\perp }}{2m\hbar }({\tilde{E}} + \Delta {\tilde{E}}) F_{0\nu } \pm \frac{ kp_{\perp }{\tilde{E}}}{4m} \frac{\partial F_{0\nu }}{\partial p_z} \nonumber \right. \\&\left. \quad {\mp } \frac{ \nu k \hbar qB_0 {\tilde{E}}}{4m} \frac{\partial ^2 F_{0\nu }}{\partial p_{\perp }p_z } \right) , \end{aligned}$$
(74)

and \(\Delta \omega _{ce}=\omega _{cg}-\omega _{ce}\). Next, noting that the magnetization current \({\mathbf {J}}_m = \nabla \times {\mathbf {M}} = 0\), we calculate the total current \(\mathbf{J} =\mathbf{J} _f + \mathbf{J} _p\), where \(\mathbf{J} _f\) and \(\mathbf{J} _p\) are the free and polarization current respectively, in order to obtain the dispersion relation. Note that the operators contained in \(\tilde{\mathbf {E}}\) and \(\Delta \tilde{\mathbf {E}}\) act on \(F_0\) as translation of the kinetic momentum, see “Appendix A” for more details. Introducing the notation

$$\begin{aligned} p_q&= \frac{\hbar k}{2},\\ p_{\text {res}}^\pm&= \frac{m \omega }{k} \pm p_q, \end{aligned}$$

the dispersion relation is then

$$\begin{aligned} \epsilon (k, \omega ) = 1 + \chi _{fL} + \chi _{pL} = 0, \end{aligned}$$
(75)

where

$$\begin{aligned} \chi _{fL}&= \frac{4\pi ^2q^2}{p_q k^2 m} \int d^2p \, \left( \frac{1}{p_{\text {res}}^+ - p_z} - \frac{1}{p_{\text {res}}^- - p_z} \right) F_{0\nu }, \end{aligned}$$
(76)
$$\begin{aligned} \chi _{pL}&= - \frac{\pi ^2\mu _e^2 }{km^2} \sum _{\pm ,\nu }\nonumber \\&\int d^2p \bigg [ \frac{p_{\perp }^2}{m\hbar }(\nu {\mp } 1) - \omega _{ce} (1{\mp } 2\nu ) \bigg ] \nonumber \\&\bigg ( \frac{1}{p_{\text {res}}^{\mp } \!-\! p_z \!+\! m\Delta \omega _{ce}/k } \!-\! \frac{1}{p_{\text {res}}^\pm - p_z - m\Delta \omega _{ce}/k } \bigg ) F_{0\nu }. \end{aligned}$$
(77)

Here \(\chi _{fL}\) and \(\chi _{pL}\) are the contributions due to the free and polarization currents, respectively. We stress that in the first factor in \(\chi _{pL}\), the sum over ± and \(\nu \) corresponds to four terms in total. Below we will use the indices f and p with the same meaning also for other quantities. We note that \(\chi _{fL}\) is the same susceptibility as for spinless quantum plasmas [38]. However, \(\chi _{pL}\) generalizes previous results [19] to cover also the short-scale physics. Specifically, this means that the denominators of Eq. (77), responsible for the resonant wave-particle interaction to be studied below, are a new property of the present theory. To obtain such denominators we need to keep all extra features of the present theory; spin–orbit interaction, the polarization current associated with the spin, particle dispersive effects, and also use the QED-corrected expressions for the spin-precession frequency.

Next, in order to examine how the spin affects the dynamic of the plasma, the Landau damping will be calculated and the contributions of \(\chi _{fL}\) and \(\chi _{pL}\) will be compared. Starting from Eq. (75), we Taylor expand \(\epsilon (k,\omega _r + i\gamma \)) around \(\omega _r\) [39], which leads to

$$\begin{aligned} \gamma = - \frac{{\text {Im}}\epsilon (k, \omega _r)}{\partial ({\text {Re}}\epsilon )/\partial \omega |_{\omega =\omega _r} } \quad \text {for} \quad |\gamma | \ll |\omega _r|. \end{aligned}$$
(78)

Analogously to Eq. (75), \({\text {Im}}\epsilon \) can be divided into \({\text {Im}}\epsilon = {\text {Im}}(\chi _{fL}) + {\text {Im}}(\chi _{pL})\). Using the Plemelj formula, we get

$$\begin{aligned} {\text {Im}}\chi _{fL }&= \frac{8\pi ^3 q^2 m }{\hbar k^3} \nonumber \\&\quad \int dp_{\perp }p_{\perp } \Big [ F_{0\nu }(p_z = p_{\text {res}}^+) - F_{0\nu }(p_z = p_{\text {res}}^-) \Big ], \end{aligned}$$
(79)
$$\begin{aligned} {\text {Im}}\chi _{pL}&= \frac{\pi ^3\mu _e^2 }{k} \sum _{\pm ,\nu }\nonumber \\&\quad \int dp_{\perp }p_{\bot } \Big [ \frac{p_{\bot }^2}{m\hbar }(\nu \pm 1) -\omega _{ce}(1 {\mp } 2\nu ) \Big ]\nonumber \\&\quad \Big [ F_{0\nu }(p_z = p_{\text {res}}^{\mp } + m\Delta \omega _{ce}/k)\nonumber \\&\quad - F_{0\nu }(p_z = p_{\text {res}}^\pm - m\Delta \omega _{ce}/k) \Big ]. \end{aligned}$$
(80)

To see how \({\text {Im}}\chi _{pL}\) contributes to \(\gamma \) compared to \({\text {Im}}\chi _{fL}\), we define

$$\begin{aligned} \Gamma = \frac{\gamma _{p}}{\gamma _{p} + \gamma _{f}} = \frac{{\text {Im}}\chi _{pL}}{{\text {Im}}(\chi _{fL} + \chi _{pL})}. \end{aligned}$$
(81)

The next step is to specify \(F_{0\nu }\). For simplicity, we will consider a Maxwell–Boltzmann distribution \(F_{0\nu } = C_\nu e^{-p^2/p_{\text {th}}^2}e^{-\nu \mu _e B_0/k_{B}T}\) where \(C_\nu \) is the normalization constant according to \(\int d^3p d^2 s \, F_{0\nu } = N_{0\nu }\), where \( N_{0\nu } \) are the densities of spin-up (\( \nu =+1 \)) and spin-down particles (\( \nu =-1 \)). This condition implies the textbook result that the magnetization is proportional to \(\tanh \frac{\mu _e B}{k_B T}\). Note, however, that the above is just a special case, as the theory presented here is applicable for arbitrary ratios of \(T/T_F\). For the case of completely or partially degenerate electrons, we just need to adopt the thermodynamic background distribution function given by Eq. (60) of Ref. [13]. We then have

$$\begin{aligned} {\text {Im}}\chi _{fL}&= \frac{\sqrt{\pi } m^2\omega _p^2}{\hbar k^3p_{\text {th}}} \left[ e^{-(p_{\text {res}}^-/p_{\text {th}})^2} - e^{-(p_{\text {res}}^+/p_{\text {th}})^2} \right] , \end{aligned}$$
(82)
$$\begin{aligned} {\text {Im}}\chi _{pL}&= \frac{\hbar ^2 \omega _p^2\sqrt{\pi }}{32m^2kp_{\text {th}}} \sum _{\pm } \Bigg [ \frac{-p_{\text {th}}^2}{m\hbar } \left( \tanh \frac{\mu _BB_0}{k_BT} \pm 1 \right) \nonumber \\&\quad - \omega _{ce} \bigg ( 1 \pm 2 \tanh \frac{\mu _BB_0}{k_BT} \bigg ) \Bigg ] \nonumber \\&\quad \times \Big [ e^{-\big (p_{\text {res}}^{\mp } + m\Delta \omega _{ce}/k \big )^2/p_{\text {th}}^2} - e^{-\big (p_{\text {res}}^\pm - m\Delta \omega _{ce}/k \big )^2/p_{\text {th}}^2} \Big ]. \end{aligned}$$
(83)

Finally, the real part of the dispersion relation \(\omega _r(k)\) has to be specified explicitly in order to obtain \(\Gamma \). Assuming that \(\chi _{pL}\) in Eq. (75) is small compared to \(\chi _{fL}\) (see footnoteFootnote 3) we neglect it for the purposes of computing \(\omega _r\). This gives us

$$\begin{aligned}&\epsilon _r \approx 1- \frac{m\omega _p^2}{k\omega \sqrt{\pi }p_{\text {th}}}\nonumber \\&\quad \int dp_z\left[ \frac{p_z/\hbar k- 1/2}{p_{res}^{+}-p_z } - \frac{p_z/\hbar k+ 1/2}{p_{res}^{-} -p_z } \right] e^{-p_z^2/p_{\text {th}}^2}.\nonumber \\ \end{aligned}$$
(84)

Assuming \(\omega \gg kv_{th}/m \pm \hbar k^2/2m \), we can make a Taylor expansion of the denominators up to first non-vanishing order. The real part of the dispersion relation \(\omega _r(k)\) is then

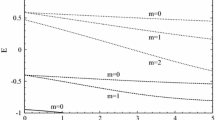
$$\begin{aligned} \omega _r(k)= \pm \sqrt{\omega _p^2 + k^2v_{th}^2 + \frac{\hbar ^2k^4}{4m^2}}. \end{aligned}$$
(85)

Using this expression of \(\omega \) in Eqs. (82) and (83), we can plot \(\Gamma \), see Fig. 1. In general the spin contribution to the damping dominates (i.e., \(\Gamma \rightarrow 1\)) for long wavelengths, whereas the free current contribution dominates (i.e., \(\Gamma \rightarrow 0\)) for shorter wavelengths. The transition between these regimes is dependent on the normalized magnetic field \(B_n = \mu _B B / m\) and the quantum parameter \(H = \hbar \omega _p / m v_\text {th}^2\). We have performed the computation in Fig. 1 for various other values of \(v_\text {th}\), however, this reveals that the location of the transition region, expressed in \(k_n = kv_\text {th}/\omega _p\), is almost independent of \(v_\text {th}\).

From a general point of view, quantum extensions of classical plasma models are of most interest for high density plasmas. Particularly when the temperatures are not too high. This has been discussed in detail by for example Refs. [1, 8]. However, in addition to quantum phenomena induced by a high density, spin polarization due to a strong magnetic field also favors quantum modifications of classical behavior. Specifically, we note that the spin induced damping displayed in Fig. 1 requires a very strong magnetic field, as already the smallest value presented here \(B_n=0.05\) represents an external magnetic field of the order \(5\times 10^8 \text { T}\), corresponding to a value common in pulsar atmospheres. The even larger values given in the panels below correspond to the magnetar regime.

Fig. 1
figure 1

The fraction \(\Gamma \) is plotted versus the normalized wave number \(k_n=kv_{th}/\omega _p\) for different values of \(B_n=\mu _BB_0/m\) and \(H = \hbar \omega _p/m v_\text {th}^2\) with thermal speed \(v_{th}=0.05c\)

Full size image

3.2 Electromagnetic waves

In this geometry we look at electromagnetic waves in unmagnetized plasmas with \(\mathbf{k} = k\hat{{\mathbf {z}}}\), \({\mathbf {E}} = E\hat{{\mathbf {x}}}\) and \({\mathbf {B}} = B\hat{{\mathbf {y}}}\). We will allow for a background distribution depending on both \(p_\perp \) and \(p_z\), but assume it to be spin-independent, as there is no background magnetic field. Dividing f, E and B into perturbed and unperturbed quantities, Eq. (68) becomes

$$\begin{aligned}&\left[ \frac{\partial }{\partial t} + \mathbf {p}\cdot \nabla _x \right] f_1 = -q \Big (\tilde{\mathbf {E}}+ \frac{\mathbf {p}}{m}\times \mathbf {B}\Big )\cdot \nabla _p f_0 \nonumber \\&\quad - \mu _e\nabla _x\Big [ \left( \mathbf {s}+ \nabla _s\right) \cdot \Big (\mathbf {B}- \frac{\mathbf {p}\times \tilde{\mathbf {E}}}{2m}\Big ) \Big ] \cdot \nabla _pf_0. \end{aligned}$$
(86)

Using an expansion of \(f_1\) like that in Eq. (71) \(f_1\) is computed as,

$$\begin{aligned} f_1 = \frac{-1}{\omega - kp_z/m} \left[ A\cos {\varphi _p} - B\sin {\varphi _p} - C\sin {\varphi _s} \right] , \end{aligned}$$
(87)

where

$$\begin{aligned} A&= iq{\tilde{E}} \frac{\partial f_0}{\partial p_{\perp }} + i\frac{q{\tilde{B}}}{m} \Big ( p_{\bot } \frac{\partial f_0}{\partial p_{z}} - p_{z} \frac{\partial f_0}{\partial p_{\perp }} \Big ), \end{aligned}$$
(88)
$$\begin{aligned} B&= -\frac{k\mu _Bp_{\perp } }{2m} {\tilde{E}} \cos {\theta _s}\frac{\partial f_0}{\partial p_z}, \end{aligned}$$
(89)

and

$$\begin{aligned} C&= k\mu _e\Big ( {\tilde{B}} + \frac{p_z}{2m}{\tilde{E}} \Big ) \sin {\theta _s}\frac{\partial f_0}{\partial p_z}. \end{aligned}$$
(90)

Next we calculate the total current \({\mathbf {J}}_{T} = {\mathbf {J}}_{f} + {\mathbf {J}}_{p} + {\mathbf {J}}_{m}\), which together with Maxwell’s equations gives us the dispersion relation

$$\begin{aligned} 1 - \frac{k^2}{\omega ^2} + \chi _{fT} + \chi _{pT} + \chi _{mT} = 0, \end{aligned}$$
(91)

where

$$\begin{aligned} \chi _{fT}&=- \frac{\omega _p^2}{\omega ^2}- \frac{4\pi ^2 q^2k^2}{m^3 \omega ^2}\nonumber \\&\int d^2p\, p_{\perp }^2 \frac{f_0}{(\omega ^2-kp_z/m)^2 - \hbar ^2k^4/4m^2}, \end{aligned}$$
(92)
$$\begin{aligned} \chi _{mT}&= \frac{-8\pi ^2k^2\mu _e^2}{m\omega ^2}\nonumber \\&\int d^2p \frac{k^2- \omega ^2/2}{(\omega -kp_z/m)^2 - \hbar ^2k^4/4m^2}f_0, \end{aligned}$$
(93)
$$\begin{aligned} \chi _{pT}&= \frac{4\pi ^2k^2\mu _e^2}{m}\nonumber \\&\int d^2p \frac{f_0 }{(\omega -kp_z/m)^2 - \hbar ^2k^4/4m^2} \nonumber \\&\Big [1+ \frac{p_{\perp }^2}{4m^2}- \frac{\hbar ^2 k^2}{8}-\frac{\omega p_z}{km} +\frac{p_z^2}{2m^2} \Big ]. \end{aligned}$$
(94)

Here the indices f, m, p stand for the contributions to the susceptibility due to the free, magnetization, and polarization currents, respectively.

To shed some further light on the dispersion relation Eq. (91), we consider the limit of the vanishing background pressure. We then immediately obtain

$$\begin{aligned} \omega ^2 = k^2 + \omega _p^2 \bigg [1 + \frac{\hbar ^2k^2}{4m^2} \frac{\big ( \omega ^2-k^2-\hbar ^2k^4/16m^2 \big )}{\omega ^2-\hbar ^2k^4/4m^2} \bigg ].\nonumber \\ \end{aligned}$$
(95)

This example is given for pedagogical purposes, to illustrate how different quantum contributions of the model tend to enter the picture: In the quantum correction to the classical dispersion relation, the term in the numerator proportional to \(\omega ^2\) comes from the spin orbit interaction, the term proportional to \(k^2\) comes from the magnetic dipole force, and the terms proportional to \(\hbar ^2 k^4\) (both the term in the denominator and in the numerator) are due to the particle dispersive effects. The quantum correction of the classical theory appears since the both the magnetic dipole force and the spin–orbit term couples the transverse and longitudinal degrees of freedom. As a direct result, the pressureless limit displayed in Eq. (95) ends up with the free-particle dispersion relation in the denominator of the second term.

While Eq. (95) highlights the physics in a simple manner we need to stress that the quantum modification of the classical dispersion relation Eq. (91) is of most interest for high density plasmas, in which case the Fermi pressure is important even if the thermal pressure is small. Thus, for realistic applications, we typically must use the full expressions Eqs. (93)–(94) for the susceptibilies, rather than Eq. (95).

4 Discussion

The model derived here, Eqs. (58)–(67), is a generalization of the governing equations of Asenjo et al. [19] allowing for short macroscopic scale lengths, i.e. of the order of the de Broglie length. Alternatively, we can view the model as a generalization of Zamanian et al. [13] into the weakly relativistic regime. A kinetic theory based on the same Hamiltonian has previously been constructed by Hurst et al. [32]. Their approach leads to two coupled equations for a scalar \(f_{0}\) and a vector \({\mathbf {f}}\), see Sect. 2.5.

From a practical point of view, we note that a theory with only a single scalar variable representing the particles, as ours, is better suited for analytical calculations. The theory of Hurst et al. [32], on the other hand, is better suited for numerical calculations. While their basic equations are considerably different from those of the present paper, nevertheless the evolution equations of Ref. [32] generalize Hurst et al. [15] in the same way as our results generalize those of Zamanian et al. [13]. However, as Ref. [15] concluded, their model is equivalent to that of Ref. [13], we can similarly conclude that the model presented here is equivalent to that of Ref. [32], apart from the small but significant detail that we include the contribution from the anomalous magnetic moment.

To demonstrate the usefulness of our model we have calculated the linear dispersion relation for two simple cases: Electrostatic waves propagating parallel to an external magnetic field and electromagnetic waves in an un-magnetized plasma. The electrostatic dispersion relation possesses two roots. The usual Langmuir root and a root induced by the spin resonances with \(\omega \simeq \Delta \omega _{c}\) [19]. Here we have focused on the Langmuir root, showing that even when the real part of the frequency is almost unaffected by the spin dynamics, the wave-particle damping can still be significantly modified.

For the electromagnetic wave mode we note that all the new terms can be expressed in terms of the longitudinal susceptibility. Physically it means that the spin-terms couples the longitudinal and the transverse degrees of freedom. However, for scale lengths much longer than the Compton length (\(k\ll mc/\hbar \)) this coupling is relatively weak.

A new feature of the present theory as compared to previous works is seen already for linear wave propagation, and comes from the denominators \((\omega -kp_{z}/m\pm \Delta \omega _{c}\pm \hbar k^{2}/2m)^{-1}\) seen in Eq. (76). We note the importance of not letting \(\mu _e=\mu _B\) here, as otherwise we would get \(\Delta \omega _{c}=0\). The physical origin of the resonances corresponding to \((\omega -kp_{z}/m\pm \Delta \omega _{c}\pm \hbar k^{2}/2m)=0\) comes from energy momentum conservation written in the form

$$\begin{aligned} \hbar \omega _{2}&= \hbar \omega _{1} \pm \hbar \Delta \omega _{c} \pm \hbar \omega , \end{aligned}$$
(96)
$$\begin{aligned} \hbar k_{2}&= \hbar k_{1}\pm \hbar k. \end{aligned}$$
(97)

Here \((k_{1},\omega _{1})\) and \((k_{2},\omega _{2})\) are the wavenumbers and frequencies of free particles before and after the interaction with the wave field, fulfilling the free particle dispersion relation \(\omega _{1,2}=\hbar k_{1,2}^{2}/2m\). The generalization from previous results (e.g., Refs. [38, 40]) comes from the term \(\pm \hbar \Delta \omega _{c}\) in (96), corresponding to resonant particles gaining an amount \(\hbar \omega _{c}\) of perpendicular kinetic energy, at the same time as the magnetic dipole energy drops by \(\hbar \omega _{cg}\), or vice versa. For our particular case of electrostatic waves propagating parallel to \({\mathbf {B}}_{0}\), the kinetic energy and magnetic dipole energy always change in opposite directions, as reflected by the appearance of \(\Delta \omega _{c}\) in (96). However, in a more general setting, the energy relation will be of the form

$$\begin{aligned} \hbar \omega _{2}=\hbar \omega _{1}\pm \hbar n\omega _{c}\pm \hbar \omega _{cg}\pm \hbar \omega , \end{aligned}$$
(98)

whereas Eq. (97) will be unaffected. Here n is an integer and all sign combinations for the last three terms in (98) are possible.

Finally we point out a problem of future interest; to compute the ponderomotive force starting from Eqs. (58) to (67). Previous results [41] indicates that the spin-orbit interaction can give a substantial contribution. Hence it would be of interest to see to what extent the short-scale physics of the present model modify the results of Ref. [41].