1 Introduction

The polarized muon decay at rest (PMDaR) is a suitable process to probe the space-time structure and to search for the effects coming from the right-handed chirality of Dirac neutrinos as well as CP violation (CPV) [in terms of the CPT invariant theorem, the time reversal violation (TRV) implies CPV and vice versa] in the purely leptonic charged weak interactions [1–3]. This reaction may also be used to study the question of lepton number violation and of the nature of the neutrino [4]. In order to make these tests feasible, the outgoing neutrinos have to be observed. So far all the tests concerning the muon decay base on the precise measurements of the electron (positron) observables and of the (anti)neutrino energy spectrum. It is worthwhile remarking the high-precision measurements of the angle–energy spectrum of positrons and of the parity violation made recently by TWIST Collaboration [5]. The KARMEN experiment [6] has measured the energy distribution of electron neutrinos emitted in positive muon decay. The possibility of measuring the neutrino energy spectrum has first been proposed by Fetscher [7, 8]. The obtained results indicate the dominant vector-axial (\(V-A\)) [9, 10] structure of the charged current weak interaction according to the standard model (SM) prediction [11–13]. This means that only left-chiral massless Dirac neutrinos may take part in a charged weak interaction, while parity violation is maximal. As is well known, the neutrino oscillation experiments indicate the nonzero neutrino mass and provide first evidence for physics beyond the minimal SM.

One should clearly stress that mentioned above observables include mainly the contributions from the squares of coupling constants of the right-chirality neutrinos and at most from the interferences within exotic couplings, which are both very tiny. The transverse components of electron (positron) spin polarization contain only the interference terms between the standard vector and nonstandard scalar (and tensor) couplings of left-chirality (anti)neutrinos. All the eventual interference terms between the standard left-chirality neutrino and exotic right-chirality neutrino couplings are strongly suppressed by a tiny neutrino mass.

In spite of agreement with all the data within errors, the SM can not be viewed as a ultimate theory. One of the fundamental aspects, which are not explained in the SM, is an origin of parity violation at current energies. The another crucial problem is impossibility to explain the observed baryon asymmetry of Universe [14] through a single CP-violating phase of the Cabibbo–Kobayashi–Maskawa quark-mixing matrix [15]. Presently the CP violation is observed only in the decays of neutral K- and B-mesons [16–18]. Till now there is no direct evidence of the CP violation in the leptonic and semileptonic processes. However, the future superbeam and neutrino factory experiments aim at the measurement of the CP-violating effects in the lepton sector, where both neutrino and antineutrino oscillation might be observed [19, 20]. Moreover, the flavor violation in the neutrino experiments as well as the composition and origin of the observed dark matter cannot be understood in the framework of SM. It is noteworthy that there are also some hints in experimental data such as the anomalies observed in short baseline and reactor neutrino experiments and the possibility of existence dark radiation. The above phenomena may be related to the right-handed chirality of neutrinos with different masses [21]. The numerous nonstandard schemes including exotic \(V+A\), scalar (\(S\)), tensor (\(T\)), pseudoscalar (\(P\)) couplings of interacting right-chirality neutrinos, and new sources of CP-breaking phases have appeared.

As the present precise tests do not detect the right-chirality neutrinos, it seems meaningful and natural to search for new tools with the linear terms from the exotic couplings obtained in a model-independent way. It would allow one to compare the predictions of various nonstandard gauge models with the experiments. Furthermore, the existence of interferences would enable us to look for the TRV effects. The relevant tools could be the neutrino observables carrying information on the components of (anti)neutrino spin polarization. Presently such tests are still extremely difficult, because they require the observation of final neutrinos, intensive neutrino beam coming from the polarized source and efficient neutrino polarimeters. However, many experimental groups working with the neutrino beams, polarized muon decay, and artificial (anti)neutrino sources could try to realize the neutrino polarimetry experiments. In this paper, we analyze a scenario with the right-chirality neutrinos produced in the PMDaR by \(V+A\) interaction at low energies. Such an interaction may occur in the various versions of left–right symmetric models (LRSM) with \(SU(2)_{\mathrm{L}}\times SU(2)_{\mathrm{R}}\times U(1)\) as the gauge group [22–29]. The LRSM emerged first in the framework of grand unified theories. They restore the parity symmetry at high energies and give its violation at low energies as a result of gauge symmetry breaking. There are many theoretical and experimental papers devoted to the \(V+A\) weak interaction effects, lepton flavor, and CPV in the various leptonic and semileptonic processes, e.g. [30–36].

The main goal is to show how the angle–energy distribution of the Dirac \(\nu _{\mu }\)’s produced in the PMDaR depends on the interference terms between the standard vector coupling of the left-chirality neutrinos and exotic vector couplings of the right-chirality ones in the limit of vanishing \(\nu _{\mu }\) mass. It allows to estimate the flux of \(\nu _{\mu }\)’s for a detector in the shape of flat circular ring with a low threshold, both for the SM prediction and the case of neutrino left–right mixture. We show that the angle–energy neutrino distribution may also be used to probe the CP-violating phases. In addition, we analyze the effects of neutrino mass and mixing. Our study is not made in the framework of a concrete version of the left–right symmetric model.

This paper is organized as follows: Sect. 2 contains the basic assumptions as to the production process of \(\nu _{\mu }\) beam. In the Sect. 3, the results for the energy–angle distribution of \(\nu _{\mu }\)’s coming from the PMDaR are presented. In Sect. 4, we present the numerical results concerning the \(\nu _{\mu }\) flux both for the SM and the case of left–right-chirality \(\nu _{\mu }\) mixture, when \(\nu _{\mu }\) beam may be transversely polarized. Finally, we summarize our considerations.

The results are presented in the limit of infinitesimally small mass for all the particles produced in the PMDaR. The density operators [37] for the polarized initial muon and for the polarized outgoing \(\nu _{\mu }\) are used. We use the system of natural units with \(\hbar =c=1\), Dirac–Pauli representation of the \(\gamma \)-matrices and the \((+, -, -, -)\) metric [38].

2 Polarized muon decay at rest: muon neutrino beam

We assume that the PMDaR \((\mu ^{-} \rightarrow e^- + \overline{\nu }_{e} + \nu _{\mu })\) is a source of the Dirac \(\nu _{\mu }\) beam. This process is described at a level of lepton-number-conserving four-fermion point interaction. We admit the presence of the exotic vector \(g_{\mathrm{LR}, \mathrm{RL}, \mathrm{RR}}^\mathrm{V}\) couplings in addition to the standard vector \(g_{\mathrm{LL}}^\mathrm{V}\) coupling. The indices (L, R) describe the chirality of the final electron and initial stopped muon, respectively. It means that the outgoing \(\nu _{\mu }\) flux is a mixture of the left-chirality and right-chirality \(\nu _{\mu }\)’s. The amplitude for the above process is of the form

$$\begin{aligned} M_{\mu ^{-}}&= \frac{G_{\mathrm{F}}}{\sqrt{2}}\left\{ g_{\mathrm{LL}}^{\mathrm{V}}\left( \overline{u}_{e}\gamma _{\alpha }(1-\gamma _5)v_{\nu _{e}}\right) \left( \overline{u}_{\nu _{\mu }} \gamma ^{\alpha }(1 - \gamma _{5})u_{\mu }\right) \right. \nonumber \\&\quad + g_{\mathrm{RR}}^{\mathrm{V}}\left( \overline{u}_{e}\gamma _{\alpha }(1+\gamma _5)v_{\nu _{e}}\right) \left( \overline{u}_{\nu _{\mu }} \gamma ^{\alpha }(1 + \gamma _{5})u_{\mu }\right) \nonumber \\&\quad + g_{\mathrm{LR}}^{\mathrm{V}}\left( \overline{u}_{e}\gamma _{\alpha }(1-\gamma _5)v_{\nu _{e}}\right) \left( \overline{u}_{\nu _{\mu }} \gamma ^{\alpha }(1 + \gamma _{5})u_{\mu }\right) \nonumber \\&\quad \left. + g_{\mathrm{RL}}^{\mathrm{V}}\left( \overline{u}_{e}\gamma _{\alpha }(1+\gamma _5)v_{\nu _{e}}\right) \left( \overline{u}_{\nu _{\mu }} \gamma ^{\alpha }(1 - \gamma _{5})u_{\mu }\right) \right\} ,\nonumber \\ \end{aligned}$$
(1)

where \( v_{\nu _{e}}\) and \(\overline{u}_{e}\) \((u_{\mu }\;\) and \(\; \overline{u}_{\nu _{\mu }})\) are the Dirac bispinors of the outgoing electron antineutrino and electron (initial muon and final \(\nu _{\mu }\)), respectively.

\(G_{\mathrm{F}} = 1.1663788(7)\times 10^{-5}\,\text{ GeV }^{-2} (0.6\,\mathrm{ppm})\) (MuLan Collab.) [39] is the Fermi constant. Our analysis is carried out in the limit of massless neutrino, then the left-chirality \(\nu _{\mu }\) possesses negative helicity, while the right-chirality one has positive helicity; see [32]. In the SM, only \(g_{\mathrm{LL}}^{\mathrm{V}}\) is nonzero value. Table 1 displays the current limits for the \(g^{\mathrm{V}}_{\mathrm{LL}}\), \(g_{\mathrm{LR}, \mathrm{RL}, \mathrm{RR}}^\mathrm{V}\) couplings [40]. Because we allow for the nonconservation of the combined symmetry CP, all the coupling constants \(g_{\mathrm{LL}}^\mathrm{V}, g_{\mathrm{LR}, \mathrm{RL}, \mathrm{RR}}^\mathrm{V}\) are complex.

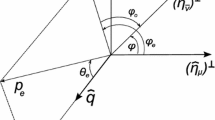
Table 1 Current limits on the nonstandard couplings
Full size table

The initial muon is at rest and polarized. Its polarization is denoted by the unit vector \({\varvec{\hat{\eta }_{\mu }}}\). The production plane is spanned by \({\varvec{\hat{\eta }_{\mu }}}\) and the outgoing \(\nu _{\mu }\) LAB momentum unit vector \({\hat{\mathbf {q}}}\); see Fig. 1.

Fig. 1
figure 1

Production plane for \(\nu _{\mu }\) produced in PMDaR

Full size image

As is well known, in this plane, the polarization vector \({\varvec{\hat{\eta }_{\mu }}}\) can be expressed, with respect to the \(\hat{\mathbf{q}}\), as a sum of the longitudinal component of the muon polarization \(({\varvec{\hat{\eta }_{\mu }}}\cdot \hat{\mathbf{q}}){\hat{\mathbf {q}}} \) and transverse component of the muon polarization \({\varvec{\eta _{\mu } ^{\perp }}} \), which is defined as \( {\varvec{\eta _{\mu }^{\perp }}} = {\varvec{\hat{\eta }_{\mu }}}- ({\varvec{\hat{\eta }_{\mu }}}\cdot \hat{\mathbf{q}}) {\hat{\mathbf {q}}}\).

Calculations are carried out with use of the covariant density matrices for the polarized initial muon and the polarized outgoing \(\nu _{\mu }\) [37]. The formula for the Lorentz boosted spin polarization 4-vector of massive \(\nu _{\mu }\) \(S^\prime \) (in the laboratory frame) is as follows:

$$\begin{aligned} S^\prime&= (S^{\prime 0}, \mathbf{S^\prime }),\end{aligned}$$
(2)
$$\begin{aligned} S^{\prime 0}&= \frac{{|\mathbf q|}}{m_{\nu }}({ \varvec{\hat{\eta }_{\nu }}}\cdot {\hat{\mathbf {q}}}), \end{aligned}$$
(3)
$$\begin{aligned} \mathbf{S^\prime }&= \left( \frac{E_{\nu }}{m_{\nu }}({ \varvec{\hat{\eta }_{\nu }}}\cdot {\hat{\mathbf {q}}}){\hat{\mathbf {q}}} + {\varvec{\hat{\eta }_{\nu }}} - ({ \varvec{\hat{\eta }_{\nu }}}\cdot {\hat{\mathbf {q}}}){\hat{\mathbf {q}}}\right) , \end{aligned}$$
(4)

where \({\varvec{\hat{\eta }_{\nu }}}\) is the unit 3-vector of the \(\nu _{\mu }\) polarization in its rest frame; \(({\varvec{\hat{\eta }_{\overline{\nu }}}}\cdot \hat{\mathbf{q}}){\hat{\mathbf {q}}}\) is the longitudinal component of \(\nu _{\mu }\) polarization; \({\varvec{\hat{\eta }_{\nu }}} - ({ \varvec{\hat{\eta }_{\nu }}}\cdot {\hat{\mathbf {q}}}){\hat{\mathbf {q}}} = {\varvec{\eta _{\nu }^{\perp }}} \) is the transverse component of \(\nu _{\mu }\) polarization. The formula for the covariant density matrix of the polarized \(\nu _{\mu }\) in the massless limit is given by

$$\begin{aligned}&\lim _{m_{\nu }\rightarrow 0}\bigg \{\Lambda _{\nu }^{(s)}\equiv u(\mathbf{q}, {\varvec{\hat{\eta }_{\nu }}})\overline{u}(\mathbf{q}, {\varvec{\hat{\eta }_{\nu }}})\bigg \} \nonumber \\&\quad =\lim _{m_{\nu }\rightarrow 0} \frac{1}{2}\bigg \{\left[ (q^{\mu }\gamma _{\mu }) + m_{\nu }\right] \left[ 1 + \gamma _{5}(S^{\prime \mu }\gamma _{\mu })\right] \bigg \}\nonumber \\&\quad = \frac{1}{2}\bigg \{(q^{\mu }\gamma _{\mu }) \left[ 1 + \gamma _{5}({\varvec{\hat{\eta }_{\nu }}}\cdot {\hat{\mathbf {q}}}) + \gamma _{5} S^{\prime \perp }\cdot \gamma \right] \bigg \}, \end{aligned}$$
(5)

where \(u(\mathbf{q}, {\varvec{\hat{\eta }_{\nu }}})\) is the positive energy plane wave massive spinor solution to Dirac’s equation of spin polarization vector \({\varvec{\hat{\eta }_{\nu }}}\); \(S^{\prime \perp } = (0, {\varvec{\eta _{\nu }^{\perp }}})\). We see that in spite of the singularity \(m_{\nu }^{-1}\) in \(S^\prime \), the density matrix \(\Lambda _{\nu }^{(s)}\) including \({ \varvec{\eta _{\nu }^{\perp }}}\) remains finite. It is worthwhile to point out that the last term in the projector has a different \(\gamma \)-matrix structure from that of the longitudinal polarization contribution. This term will be responsible for the non-vanishing interference between the standard coupling of left-chirality \(\nu _{\mu }\)’s and exotic coupling of right-chirality ones in the angle–energy distribution of \(\nu _{\mu }\)’s from the PMDaR in the massless limit.

3 Energy–angle distribution of muon neutrinos

In this section, we show how the energy–angle distribution of \(\nu _{\mu }\)’s depends on the interference terms between the standard and exotic couplings in the limit of vanishing \(\nu _{\mu }\) mass.

The proper formula, obtained after the integration over all the momentum directions of the outgoing electron and electron antineutrino, is of the form

$$\begin{aligned} \frac{\mathrm{d}^2 \Gamma }{ \mathrm{d}y \mathrm{d}\Omega _\nu } = \left( \frac{\mathrm{d}^2 \Gamma }{\mathrm{d}y \mathrm{d}\Omega _\nu }\right) _{(\mathrm{LL} + \mathrm{LR} + \mathrm{RL} + \mathrm{RR})} + \left( \frac{\mathrm{d}^2 \Gamma }{\mathrm{d}y \mathrm{d}\Omega _\nu }\right) _{(I)} \end{aligned}$$
(6)
$$\begin{aligned}&\left( \frac{\mathrm{d}^2 \Gamma }{ \mathrm{d}y \mathrm{d}\Omega _\nu }\right) _{(\mathrm{LL} + \mathrm{LR} + \mathrm{RL} + \mathrm{RR})} \nonumber \\&\quad = \frac{G_{\mathrm{F}}^2 m_{\mu }^5 }{768\pi ^4} \bigg [ (1-{ \varvec{\hat{\eta }_{\nu }}}\cdot \hat{\mathbf{q}}) \left( |g_{\mathrm{LL}}^{\mathrm{V}}|^2+|g_{\mathrm{RL}}^{\mathrm{V}}|^2\right) \nonumber \\&\quad \quad \cdot y^2( -2y+3 -(2y-1){\varvec{\hat{\eta }_{\mu }}}\cdot \hat{\mathbf{q}}) \nonumber \\&\quad \quad + (1+{ \varvec{\hat{\eta }_{\nu }}}\cdot \hat{\mathbf{q}})\left( |g_{\mathrm{LR}}^{\mathrm{V}}|^2 +|g_{\mathrm{RR}}^{\mathrm{V}}|^2\right) \nonumber \\&\quad \quad \cdot y^2( -2y+3 + (2y-1){ \varvec{\hat{\eta }_{\mu }}}\cdot \hat{\mathbf{q}}) \bigg ], \end{aligned}$$
(7)
$$\begin{aligned}&\left( \frac{\mathrm{d}^2 \Gamma }{\mathrm{d}y \mathrm{d}\Omega _\nu }\right) _{(I)}\nonumber \\&\quad = \frac{G_{\mathrm{F}}^2 m_{\mu }^5}{384\pi ^4} y^2 \bigg [\left( \mathrm{Re}\left( g_{\mathrm{LL}}^\mathrm{V} g_{\mathrm{LR}}^{V*}\right) + \mathrm{Re}\left( g_{\mathrm{RL}}^\mathrm{V} g_{\mathrm{RR}}^{V*}\right) \right) ({ \varvec{\eta _{\nu }^{\perp }}}\cdot { \varvec{\hat{\eta }_{\mu }}}) \nonumber \\&\quad \quad - \left( \mathrm{Im}\left( g_{\mathrm{LL}}^\mathrm{V} g_{\mathrm{LR}}^{V*}\right) + \mathrm{Im}\left( g_{\mathrm{RL}}^\mathrm{V} g_{\mathrm{RR}}^{V*}\right) \right) {\varvec{\eta _{\nu }^{\perp }}}\cdot ({\hat{\mathbf {q}}} \times {\varvec{\hat{\eta }_{\mu }}}) \bigg ]. \end{aligned}$$
(8)

Here, \(y=2E_\nu /m_{\mu }\) is the reduced \(\nu _\mu \) energy for the muon mass \(m_\mu \); it varies from \(0 \) to \(1\). \(\mathrm{d}\Omega _\nu \) is the solid angle differential for \(\nu _\mu \) momentum \(\hat{\mathbf{q}}\).

Equation (8) includes the interference term between the \(g_{\mathrm{LL}}^{\mathrm{V}}\) (left-chirality \(\nu _\mu \)) and exotic \(g_{\mathrm{LR}}^\mathrm{V}\) (right-chirality \(\nu _\mu \)) couplings, so it is linear in the exotic coupling contrary to Eq. (7) and the interference between the exotic \(g_{\mathrm{RL}}^\mathrm{V}\) and \(g_{\mathrm{RR}}^\mathrm{V}\) couplings. We see that the interference terms do not vanish in the massless \(\nu _\mu \) limit. It is necessary to stress that there is a different dependence on the \(y\) between quadratic terms and interferences. For \({\varvec{\hat{\eta }_{\mu }}} \cdot {\hat{\mathbf { q}}}= 0\), the interference part can be rewritten in the following way:

$$\begin{aligned}&\left( \frac{\mathrm{d}^2 \Gamma }{\mathrm{d}y \mathrm{d}\Omega _\nu }\right) _{(I)}\nonumber \\&\quad = \frac{G_{\mathrm{F}}^2 m_{\mu }^5 }{384\pi ^4} \left| { \varvec{\eta _{\nu }^{\perp }}}\right| \left| {\varvec{\eta _{\mu } ^{\perp }}}\right| \nonumber \\&\quad \quad \times \bigg \{ \left| g_{\mathrm{LL}}^\mathrm{V}\right| \left| g_{\mathrm{LR}}^{\mathrm{V}}\right| \cos (\phi + \alpha ) + \left| g_{\mathrm{RL}}^{\mathrm{V}}\right| \left| g_{\mathrm{RR}}^{\mathrm{V}}\right| \cos (\phi + \beta )\bigg \}y^2, \end{aligned}$$
(9)

where \(\phi \) is the angle between \({ \varvec{\eta _{\nu }^{\perp }}}\) and \({\varvec{\eta _{\mu } ^{\perp }}}\) only, Fig. 1; \(\alpha \equiv \alpha _{\mathrm{V}}^{\mathrm{LL}} - \alpha _{\mathrm{V}}^{\mathrm{LR}}\), \(\beta \equiv \alpha _{\mathrm{V}}^{\mathrm{RL}} - \alpha _{\mathrm{V}}^{\mathrm{RR}} \) are the relative phases between the \(g^{\mathrm{V}}_{\mathrm{LL}}\), \(g^{\mathrm{V}}_{\mathrm{LR}}\), and \( g^{\mathrm{V}}_{\mathrm{RL}}, g^{\mathrm{V}}_{\mathrm{RR}}\) couplings, respectively.

It can be noticed that the relative phases \(\alpha , \beta \) different from \(0, \pi \) would indicate the CP violation in the CC weak interaction. We see that even in the massless limit the helicity structure of interaction vertices may allow for a helicity flip provided the quantity \({\varvec{\eta _{\nu }^{\perp }}}\), which is left invariant under Lorentz boost. The interference part, Eq. (9), includes only the contributions from the transverse component of the initial muon polarization \({\varvec{\eta _{\mu } ^{\perp }}} \) and the transverse component of the outgoing neutrino polarization \({\varvec{\eta _{\nu }^{\perp }}}\). Both transverse components are perpendicular with respect to the \(\hat{\mathbf{q}}\).

Using the current data [40], we calculate the upper limit on the magnitude of \({\varvec{\eta _{\nu }^{\perp }}} \) and lower bound for the \(({\varvec{\hat{\eta }_{\nu }}}\cdot \hat{\mathbf{q}})\) [32]:

$$\begin{aligned} \left| {\varvec{\eta _{\nu }^{\perp }}}\right|&= 2\sqrt{Q_{L}^{\nu }(1-Q_{L}^{\nu })} \le 0.082, \end{aligned}$$
(10)
$$\begin{aligned} \left| {\varvec{\hat{\eta }_{\nu }}}\cdot \hat{\mathbf{q}}\right|&= \left| 1- 2 Q_{L}^{\nu }\right| \ge 0.997, \end{aligned}$$
(11)
$$\begin{aligned} Q_{L}^{\nu }&= 1 -\left| g_{\mathrm{RR}}^\mathrm{V}\right| ^{2} - \left| g_{\mathrm{LR}}^\mathrm{V}\right| ^{2}\ge 0.998, \end{aligned}$$
(12)

where \(Q_{L}^{\nu }\) is the probability of finding the left-chirality \(\nu _{\mu }\).

If the neutrino beam comes from the unpolarized muon decay at rest, there are no interference terms in the \(\nu _\mu \) spectral function.

It is noteworthy that the effects coming from the neutrino mass and mixing are very tiny and they may be neglected. In order to show this, we use the final density matrix for the mass eigenstates \(m_1, m_2\) of \(\nu _{\mu }\) to avoid breaking the fundamental principles of quantum field theory. We assume that at the neutrino detector (target) \(\nu _\mu = \cos \theta \nu _1 + \sin \theta \nu _2\). In this way, the differential \(\nu _{\mu }\) spectrum is of the form

$$\begin{aligned} \frac{\mathrm{d}^2 \Gamma }{ \mathrm{d}y \mathrm{d}\Omega _\nu }&= \cos ^2 \theta \frac{\mathrm{d}^2 \Gamma }{ \mathrm{d}y_1 \mathrm{d}\Omega _\nu } + \sin ^2 \theta \frac{\mathrm{d}^2 \Gamma }{\mathrm{d}y_2 \mathrm{d}\Omega _\nu }\nonumber \\&=\gamma _{(V)}^{(\phi )}\left[ y_{1}^2 + \sin ^{2} \theta \frac{\delta m_{\nu }^{2}}{m_{\mu }^2} + O\left( \frac{\delta m_{\nu }^{2}}{m_{\mu }^2}\right) \right] , \end{aligned}$$
(13)

where \(\gamma _{\mathrm{V}}^{(\phi )}= \frac{G_{\mathrm{F}}^2 m_{\mu }^5 }{384\pi ^4} |{\varvec{\eta _{\nu }^{\perp }}}| |{\varvec{\eta _{\mu } ^{\perp }}}| \Big \{ |g_{\mathrm{LL}}^\mathrm{V} ||g_{\mathrm{LR}}^{\mathrm{V}}|cos(\phi + \alpha ) +|g_{\mathrm{RL}}^{\mathrm{V}}||g_{\mathrm{RR}}^{\mathrm{V}}|cos(\phi + \beta )\Big \}\). Taking into account the available data, the linear contribution from the mass mixing \(\frac{\delta m_{\nu }^{2}}{m_{\mu }^2}\) is viewed as extremely small \(({\sim }10 ^{-19})\).

It is worthwhile remarking that if one admits the production of \(\nu _\mu \)’s with right-handed chirality by the exotic scalar and tensor interactions, there is no interferences between the standard vector and exotic couplings in the limit of vanishing \(\nu _\mu \) mass. When one computes the angle–energy distribution of electron antineutrinos, the mentioned interference terms appear and do not vanish in the massless limit (analysis made in [41]).

4 Neutrino flux

In order to find the \(\nu _{\mu }\) flux, we assume that the hypothetical detector has the shape of flat circular ring with a low threshold \(T_{\mathrm{e}}^{\mathrm{th}}=10 \,\mathrm{eV}\) \((y_{\mathrm{e}}^{\mathrm{th}}=0.0062)\) corresponding to \(E_{\nu }^{\mathrm{min}}=1603.44 \, \mathrm{eV}\). In addition, one assumes that neutrino source is located in the center of the ring detector and polarized perpendicularly to the ring. It means that we must integrate the angle–energy distribution of \(\nu _\mu \)’s over the neutrino energy in the range \([1603.44 \, \mathrm{eV}, m_{\mu }/2]\), and over \(\mathrm{d}\Omega _\nu \) in the proper range, i.e. \(\phi _{\nu } \in [0,2\pi ]; \theta _{\nu } \in [\pi /2 -\delta , \pi /2 + \delta ]\). Then it is multiplied by \(N_{\mu }/S_{\mathrm{D}}\) yet, where \(N_{\mu }=10^{21}\) is the number of polarized muons decaying per 1 year. \(S_{\mathrm{D}}=4 \pi R^2 \sin \delta \), where \(R=L=2205 \,\mathrm{cm}\) is the inner radius of the detector that is equal to the distance \(L\) between the muon neutrino source and detector, \(\delta = 0.01\). In this way one gets the information on the number of \(\nu _\mu \)’s passing through \(S_{\mathrm{D}}\) in the direction perpendicular to \({ \varvec{\hat{\eta }_{\mu }}}\). Figure 2 displays the dependence of neutrino flux \(N_{\nu }^{\perp }\) on the \(\phi \) angle for the case of CP conservation (short-dashed line) and of CP violation (long-dashed line) in the presence of \(V+A\) interaction, when \(\hat{\mathbf{q }}\perp {\varvec{\hat{\eta }_{\mu }}}\). The solid line describes only the contribution from the left-chiral \(\nu _{\mu }\), i.e. from \(g_{\mathrm{LL}}^{\mathrm{V}}, g_{\mathrm{RL}}^{\mathrm{V}}\) couplings.

Using the available data [40], we get the flux of \(\nu _{\mu }\) beam for the SM (per 1 year): \( \Phi _{\overline{\nu }}^{\perp (\mathrm{SM})}=7.48 \cdot 10^{18}\,\mathrm{cm}^{-2}\,\mathrm{year}^{-1}\), when \({ \varvec{\hat{\eta }_{\nu }}}\cdot \hat{\mathbf{q}} =-1, g_{\mathrm{LL}}^{\mathrm{V}}=1\). The lower limit on the flux of left-chirality \(\nu _{\mu }\)’s in the presence of exotic couplings is \( \Phi _{\overline{\nu }}^{\perp (g_{\mathrm{LL}}^{\mathrm{V}},g_{\mathrm{RL}}^{\mathrm{V}})}=7.457 \cdot 10^{18}\,\mathrm{cm}^{-2}\,\mathrm{year}^{-1}\). The upper bound on the magnitude of neutrino flux connected with the interferences \(g_{\mathrm{LL}}^{\mathrm{V}}g_{\mathrm{LR}}^{\mathrm{V}}\), \(g_{\mathrm{RL}}^{\mathrm{V}}g_{\mathrm{RR}}^{\mathrm{V}}\) is \(\Phi _{\overline{\nu }}^{\perp ,\mathrm{inter}}= 1.2\cdot 10^{16}\,\mathrm{cm}^{-2}\,\mathrm{year}^{-1}\), when CP symmetry is violated, i.e. \(\phi =\pi /2, \alpha =\beta =3\pi /2\). The same value can be obtained for CP conservation assuming for example \(\phi =\pi , \alpha =\beta =\pi \). We see that the estimated interference effect is two orders smaller compared to value for the left-chiral \(\nu _{\mu }\)’s. The numerics are made with the normalized couplings.

Fig. 2
figure 2

Plot of \(N_{\nu }^{\perp } \) as a function of \(\phi \): CP violation, \(\alpha =\beta =3\pi /2\) (long-dashed line); CP conservation \(\alpha =\beta =\pi \) (short-dashed line); solid line concerns contribution from \(g_{\mathrm{LL}}^{\mathrm{V}}, g_{\mathrm{RL}}^{\mathrm{V}}\) couplings (left-chirality \(\nu _{\mu }\))

Full size image

5 Conclusions

In this paper, we have investigated the PMDaR in the presence of the exotic \(V+A\) interaction, when the (anti)neutrinos have Dirac nature and may have right-chirality.

We have shown that the angle–energy distribution of \(\nu _{\mu }\)’s produced in the PMDaR includes the terms with interference between the standard \(g_{\mathrm{LL}}^{\mathrm{V}}\) (left-handed chirality of \(\nu _\mu \)) and exotic \(g_{\mathrm{LR}}^\mathrm{V}\) (right-handed chirality of \(\nu _\mu \)) couplings, which are independent of the \(\nu _{\mu }\) mass. These interferences are exclusively proportional to the \(T\)-even and \(T\)-odd transverse components of \(\nu _{\mu }\) polarization \({\varvec{\eta _{\mu } ^{\perp }}}\). It is necessary to point out that if the interacting left- and right-chirality \(\nu _{\mu }\) are produced in the PMDaR, the \(\nu _{\mu }\) polarization vector may acquire the transversal component.

Next, we have computed the flux of the \(\nu _{\mu }\) beam for the assumed configuration of detector in the case of the SM prediction, and the upper limits on the \(\nu _{\mu }\) flux in the case of left–right \(\nu _{\mu }\) mixture.

We have also displayed that the eventual effects connected with the neutrino mass and mixing in the angle–energy distribution of \(\nu _{\mu }\)’s are inessential \(({\sim }10^{-19})\), when the distance between the \(\nu _{\mu }\) source and detector is relatively small \(L\sim 22\,m\).

The measurements of neutrino observables seem to be a real challenge for experimental groups, but could shed some more light on the existence of right-chiral interacting (anti)neutrinos and of the nonstandard CP-violating phases in the leptonic processes than the current experiments with the electron (positron) observables. Let us recall that in the electron observables, the eventual interference terms between the standard and exotic \(V+A\) couplings are strongly suppressed by the tiny (anti)neutrino mass. One should remark that the appearance of non-vanishing interference term in the massless neutrino limit between the non-standard scalar \(g_{\mathrm{RR}}^{\mathrm{S}}\) and standard \(g_{\mathrm{LL}}^{\mathrm{V}}\) couplings in the transversal electron polarization is possible. However, in this case the neutrinos have only the left-handed chirality.

It is worthwhile emphasizing that there is a well known technique of producing the polarized muons at rest (TWIST, PSI, KARMEN, BooNE Collaborations). A great experience of mentioned laboratories should be used in studies on the efficient neutrino polarimeter. The PMDaR is not a unique weak process, where the right-chiral interacting neutrinos can be generated, so it is meaningful to look for the other polarized (anti)neutrino sources.

Finally, one ought to point out that even in the massless \(\nu _{\mu }\) limit, there are physical and in principle observable effects coming from the mixture between the left- and right-handed helicity components in the spin \(1/2\) quantum state, when the exotic \(V+A\) interaction is admitted.