1 Introduction

One of the fundamental problems in the neutrino physics is whether the neutrinos \((\nu )\)’s are the Dirac or Majorana fermions. The question of the \(\nu \) nature can be probed in the context of non-vanishing \(\nu \) mass and of standard vector-axial \((V-A)\) weak interaction with only the left chiral (LCh) \(\nu \)’s [1–5], using purely leptonic processes such as the polarized muon decay at rest (PMDaR) or the neutrino–electron elastic scattering (NEES). There is an alternative way within the relativistic limit, when one admits the existence of exotic scalar (S), tensor (T), pseudoscalar (P) and \(V+A\) weak interactions of the right chiral (RCh) \(\nu \)’s (right-handed helicity when \(m_{\nu } \rightarrow 0\)) in addition to the \(V-A\) interaction of the LCh ones in the above processes. The appropriate tests involving the mass dependence have been proposed by Kayser [6] and Langacker [7]. It is also worthwhile noting the other interesting ideas regarding the \(\nu \) nature problem [8–14]. One ought to emphasize that at present the neutrinoless double beta decay (NDBD) seems to be the best tool to investigate the \(\nu \) nature [15–17], however, the processes mentioned above may also shed some light on this problem.

First tests concerning the problem of distinguishing between the Dirac and Majorana \(\nu \)’s in the relativistic limit, when one departs from the \({V}-{A}\) interaction and one allows for the exotic S, T, P weak interactions in the NEES, have been reported by Rosen [18] and Dass [19]. The leptonic processes are also suitable to probe the time reversal violation (TRV) effects.

It is relevant to point out that the existing data still leaves a small space for the exotic couplings of the interacting RCh \(\nu \)’s. It is noteworthy that the effects coming from the interacting \(\nu \)’s with right-handed chirality are also important for interpreting of results on the NDBD [20]. Unfortunately, the proposed quantities in [18, 19] are composed of the squares of exotic couplings of the RCh \(\nu \)’s and at most of the interferences within exotic couplings, which are both very tiny. Furthermore, both transverse components of electron (positron) spin polarization and neutrino energy spectrum in the PMDaR contain only the interference terms between the standard V and non-standard S, T couplings of LCh \(\nu \)’s. All the eventual interferences between the standard couplings of LCh and exotic couplings of RCh \(\nu \)’s vanish, because are proportional to a tiny \(\nu \) mass and do not produce the effect. As the current experiments do not detect the RCh \(\nu \)’s, it seems meaningful to search for new tools including the linear terms from the exotic couplings that are independent of the \(\nu \) mass, and obtained in model-independent way. It would enable one to compare the predictions of various non-standard schemes with the experimental data, and look for the TRV effects. The suitable observables could be the \(\nu \) quantities carrying information on the transversal components of (anti)neutrino spin polarization, both T-odd and T-even. Presently, such tests are still not available, because they require the observation of final \(\nu \)’s, the strong \(\nu \) beam coming from the polarized source and the efficient \(\nu \) polarimeters. However, it is worthy of indicating the potential possibilities of experiments of the \(\nu \) polarimetry in the connection with the \(\nu \) nature problem, the existence of interacting RCh \(\nu \)’s and the non-standard TRV phases predicted by many extensions of the SM. Let us recall that the SM cannot be viewed as a ultimate theory, because it does not clarify the origin of parity violation (PV) at current energies,Footnote 1 the observed baryon asymmetry of universe [21] through a single CP-violating phase of the Cabibbo–Kobayashi–Maskawa quark-mixing matrix (CKM) [22], the large hierarchy fermion masses, and other fundamental aspects. This situation led to the appearance of various non-standard gauge models including the Majorana (and Dirac) \(\nu \)’s, exotic TRV interactions, mechanisms explaining the origin of fermion generations, masses, mixing and smallness of \(\nu \) mass. It is worthwhile to note the concept of non-standard interactions (NSI) of \(\nu \)’s [23–26], which may be generated by the mechanisms of massive neutrino models [27–31]. The constraints (or evidence) on the NSI can help to interpret the sub-leading contributions in the high-precision neutrino oscillation experiments, and to understand the supernova explosion. The phenomenology of NSI have been widely explored [32–46]. However, from the perspective of the main goal of this paper, it is suitable to mention the non-standard models including the interacting RCh \(\nu \)’s. We mean, e.g., the left–right symmetric models (LRSM) [47–53], composite models (CM, where tensor and scalar interactions are generated by the exchange of constituents) [54–56], models with extra dimensions (MED) [57], the unparticle models (UP) [58–70]. In the MED all the particles of the SM are trapped on the three-brane, while the RCh \(\nu \)’s can move in the extra dimensions. This mechanism explains why the interactions of RCh \(\nu \)’s with the SM particles are extremely small and have never been observed so far. Concerning the UP scenario, it is worthy of stressing that in this scheme the leptons with the different chiralities can couple with the spin-0 scalar, spin-1 vector, spin-2 tensor unparticle sectors. Consequently, the amplitudes for low energy processes have the form of the unparticle four-fermion contact interaction, and they contain the non-standard components of other structures than the \({V}-{A}\) interactions. But what is essential is that currently there is no conclusive response to the choice of new non-standard model, because the experimental possibilities are still limited. There is a constant need of increment of the precision of present tests at low energies, and on the other hand, it is sensible to consider new observables allowing for the interference effects between the standard and exotic couplings, because such quantities are much more sensitive to the new physics.

In this paper, we focus on the elastic scattering of \(\nu \) beams (Dirac \(\overline{\nu }_e\)’s and \(\nu _\mu \)’s; Majorana \(\nu _e\)’s and \(\nu _\mu \)’s) off the unpolarized electron target. We show in model-independent way how the participation of the exotic S, T,  \({V}+{A}\) couplings of RCh \(\nu \)’s (\(\overline{\nu }\)’s) in addition to the standard couplings of LCh ones can be utilized to distinguish the Dirac from Majorana \(\nu \)’s, and to test the TRV in the relativistic limit. It should be clearly pointed out that we consider the flavour-eigenstate (current) neutrinos in the PMDaR and NEES. Even if the amplitudes for the PMDaR in the case of flavour Dirac and Majorana \(\nu \)’s are the same, the NEES as the detection process allows one to discriminate between the both types of current \(\nu \)’s. If the flavour \(\nu \)’s are assumed to be the superpositions of the mass-eigenstate \(\nu \)’s, then the amplitude for the production of Dirac \(\nu \)’s in the PMDaR is distinct from the one for the Majorana case. This scenario will be analyzed in the next study.

Fig. 1
figure 1

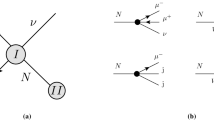
Production plane of the \(\overline{\nu }_{e}\) beam is spanned by the vectors \(\hat{\eta }_{\mu }\) and \({\hat{\mathbf {q}}}\) for \(\mu ^{-} \rightarrow e^- + \overline{\nu }_{e} + \nu _{\mu }\). Reaction plane is spanned by the vectors \(\hat{\mathbf p}_{e}\) and \(\hat{\mathbf q}\) for \(\overline{\nu }_{e} + e^{-}\rightarrow \overline{\nu }_{e} +e^{-}\). \(\hat{\eta }_{\overline{\nu }}\) is expressed, with respect to \(\hat{\mathbf q}\), as a sum of \((\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q}){\hat{\mathbf {q}}}\) and \((\hat{\eta }_{\overline{\nu }})^{\perp }\equiv \eta _{\overline{\nu }}^\perp \)

Full size image

2 Elastic scattering of Dirac electron antineutrinos and of muon neutrinos off unpolarized electrons

We assume that the incoming Dirac \(\overline{\nu }_{e}\) and \(\nu _\mu \) beams come from the decay of polarized negative muons at rest \((\mu ^{-} \rightarrow e^- + \overline{\nu }_{e} + \nu _{\mu })\) and are the superpositions of left–right chiral states with a fixed direction of the transversal spin polarization with respect to the production plane. LCh \(\overline{\nu }_{e}\)’s (\(\nu _\mu \)’s) are mainly detected by the standard \(V-A\) interaction and RCh ones are detected only by the exotic scalar, tensor, \(V+A\) interactions in the elastic scattering on the unpolarized electron target; \(\overline{\nu }_{e} + e^{-}\rightarrow \overline{\nu }_{e} +e^{-}\) \((\nu _{\mu } + e^{-}\rightarrow \nu _{\mu } +e^{-})\). Our scenario admits also the detection of \(\overline{\nu }_{e}\)’s (\(\nu _\mu \)’s) with left-handed chirality by the non-standard S and T interactions. Below we present a detailed analysis in the case of \(\overline{\nu }_{e}\)’s, but a similar study must be carried out for \(\nu _\mu \)’s. Both \(\overline{\nu }_{e}\)’s and \(\nu _\mu \)’s may produce the azimuthal asymmetry in the angular distribution of scattered electrons. The production plane for the \(\overline{\nu }_{e}\) beam, shown in Fig. 1, is spanned by the unit vector \(\hat{\eta }_{\mu }\) of the muon polarization and the \(\overline{\nu }_{e}\) LAB momentum unit vector \({\hat{\mathbf {q}}}\). In this plane, the vector \(\hat{\eta }_{\mu }\) can be expressed, with respect to \(\hat{\mathbf {q}}\), as a sum of \(({\hat{\eta }_{\mu }}\cdot {\hat{\mathbf {q}}}){\hat{\mathbf {q}}} \) and \((\hat{\eta }_{\mu })^{\perp }\equiv \eta _{\mu }^{\perp } = \hat{\eta }_{\mu }- (\hat{\eta }_{\mu }\cdot \hat{\mathbf {q}}) {\hat{\mathbf {q}}}\). The reaction (detection) plane is spanned by the direction of the outgoing electron momentum \( \hat{\mathbf {p}}_{e}\) and \(\hat{\mathbf {q}}\), Fig. 1. The amplitude for the \(\overline{\nu }_{e} e^{-}\) scattering at low energies is as follows:

$$\begin{aligned} M^{D}_{\overline{\nu }_{e} e^{-}}= & {} -\frac{G_{F}}{\sqrt{2}}\{(\overline{u}_{e'}\gamma ^{\alpha }(c_{V}^{L} - c_{A}^{L}\gamma _{5})u_{e}) (\overline{v}_{\nu _{e}} \gamma _{\alpha }(1 - \gamma _{5})v_{\nu _{e'}})\nonumber \\&+ (\overline{u}_{e'}\gamma ^{\alpha }(c_{V}^{R} + c_{A}^{R}\gamma _{5})u_{e}) (\overline{v}_{\nu _{e}} \gamma _{\alpha }(1 + \gamma _{5})v_{\nu _{e'}}) \nonumber \\&+ c_{S}^{R}(\overline{u}_{e'}u_{e})(\overline{v}_{\nu _{e}} (1 - \gamma _{5})v_{\nu _{e'}}) \nonumber \\&+ \frac{1}{2}c_{T}^{R}(\overline{u}_{e'}\sigma ^{\alpha \beta }u_{e})(\overline{v}_{\nu _{e}} \sigma _{\alpha \beta }(1 - \gamma _{5})v_{\nu _{e'}})\nonumber \\&+ c_{S}^{L}(\overline{u}_{e'}u_{e})(\overline{v}_{\nu _{e}} (1 + \gamma _{5})v_{\nu _{e'}}) \nonumber \\&+ \frac{1}{2}c_{T}^{L}(\overline{u}_{e'}\sigma ^{\alpha \beta }u_{e})(\overline{v}_{\nu _{e}} \sigma _{\alpha \beta }(1 + \gamma _{5})v_{\nu _{e'}}) \}, \end{aligned}$$
(1)

where \(G_{F} = 1.1663788(7)\times 10^{-5}\,\text{ GeV }^{-2} (0.6 \, \mathrm{ppm})\) [71] is the Fermi constant. The coupling constants are denoted with the superscripts L and R as \(c_{V}^{L, R} \), \(c_{A}^{L, R}\), \(c_{S}^{R, L}\), \(c_{T}^{R, L}\), respectively, to the incoming \(\overline{\nu }_{e}\) of left- and right-handed chirality. Because we take into account the TRV, all the coupling constants are complex. Calculations are carried out with use of the covariant density matrix for the polarized initial \(\overline{\nu }_{e}\) and \(\nu _\mu \), respectively. The formula for the projector \(\varLambda _{\overline{\nu }}^{(s)}\) in the relativistic limit is given by

$$\begin{aligned} \lim _{E_{\overline{\nu }}\rightarrow \infty }\varLambda _{\overline{\nu }}^{(s)}= & {} \frac{1}{2}\{(q^{\mu }\gamma _{\mu }) [1 - \gamma _{5}(\hat{\eta }_{\overline{\nu }}\cdot {\hat{\mathbf {q}}}) - \gamma _{5} S^{\prime \perp }\cdot \gamma ]\}, \end{aligned}$$
(2)

where \(\hat{\eta }_{\overline{\nu }}\) is the unit 3-vector of \(\overline{\nu }_{e}\) spin polarization in its rest frame; \((\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q}){\hat{\mathbf q}}\) is the longitudinal component of \(\overline{\nu }_{e}\) spin polarization; \((\hat{\eta }_{\overline{\nu }})^{\perp }\equiv \eta _{\overline{\nu }}^{\perp } = \hat{\eta }_{\overline{\nu }} - (\hat{\eta }_{\overline{\nu }}\cdot {\hat{\mathbf q}}){\hat{\mathbf q}} \) is the transversal component of \(\overline{\nu }_{e}\) spin polarization; \(S^{\prime \perp } = (0, \eta _{\overline{\nu }}^{\perp })\).

We see that in spite of the singularities \(m_{\overline{\nu }}^{-1}\) in the Lorentz boosted spin polarization 4-vector of massive \(\overline{\nu }_{e}\) \(S^\prime \) (in the laboratory frame), the projector \(\varLambda _{\overline{\nu }}^{(s)}\) including \(\eta _{\overline{\nu }}^{\perp }\) remains finite [72]. One should notice that the last term in \(\varLambda _{\overline{\nu }}^{(s)}\) has a different \(\gamma \)-matrix structure from that of the longitudinal polarization contribution. This term is generating the non-vanishing interferences between the standard and exotic couplings in the differential cross section for the \(\overline{\nu }_{e} e^{-}\) \((\nu _\mu e^{-})\) scattering.

Using the current data for the muon decay at rest [73], we calculate the upper limit on the magnitude of \(\eta _{\overline{\nu }}^{\perp }\) and the lower bound for \((\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q})\) for \(\overline{\nu }_{e}\)’s [74–76]:

$$\begin{aligned}&|\eta _{\overline{\nu } }^{\perp }| = 2\sqrt{Q_{L}^{\overline{\nu }}(1-Q_{L}^{\overline{\nu }})} \le 0.552, \end{aligned}$$
(3)
$$\begin{aligned}&\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q} = 2 Q_{L}^{\overline{\nu }} -1 \ge 0.834, \end{aligned}$$
(4)
$$\begin{aligned} Q_{L}^{\overline{\nu }}= & {} 1 - \frac{1}{4}(|g_{LR}^S|^{2} + |g_{LL}^S|^{2}) - 3 |g_{LR}^T|^{2}\nonumber \\&- |g_{RL}^V|^{2}-|g_{RR}^V|^{2}\ge 0.917. \end{aligned}$$
(5)

The limits for \(\nu _\mu \)’s can also be obtained:

$$\begin{aligned}&|\eta _{\nu }^{\perp }| = 2\sqrt{Q_{L}^{\nu }(1-Q_{L}^{\nu })} \le 0.693, \end{aligned}$$
(6)
$$\begin{aligned}&|\hat{\eta }_{\nu }\cdot \hat{\mathbf q}| = |1- 2 Q_{L}^{\nu }| \ge 0.721, \end{aligned}$$
(7)
$$\begin{aligned} Q_{L}^{\nu }= & {} 1 - \frac{1}{4}(|g_{RL}^S|^{2} + |g_{LL}^S|^{2})- 3|g_{RL}^T|^{2}\nonumber \\&-|g_{LR}^V|^{2}-|g_{RR}^V|^{2} \ge 0.861. \end{aligned}$$
(8)

The coupling constants \(g_{\varepsilon \mu }^\gamma \) with the indices \(\varepsilon \) and \(\mu \) indicate the chirality (left or right) of the electron and muon for the given interaction \(\gamma =V, S, T\), respectively. It means that the chirality of neutrino is equal to the one of its associate lepton, while it is opposite for the S, T interactions.

2.1 Azimuthal distribution of recoil electrons in the case of Dirac electron antineutrinos and muon neutrinos

In order to get the correct estimates for the azimuthal asymmetry of recoil electrons, the contributions from the \(\overline{\nu }_{e}\)’s and \(\nu _\mu \)’s have to be added, because the final state electrons are experimentally indistinguishable. We assume the detector to have the shape of a flat circular ring, while the neutrino source is located in the centre of the ring detector and polarized perpendicular to the ring. We also assume that the measurement of the scattering angle and of the azimuthal angle of recoil electron with a good precision is possible. The basic parameters of the hypothetical detector, running for 1 year, are as follows: the detector threshold \(T_{e}^{\mathrm{th}} \simeq 10 \,eV\), the minimal value of initial \(\nu \) energy \(E_{\nu }^{\min } \simeq 1600 \, eV\), the number of target electrons \(N_e = 2.097 \cdot 10^{34} \) (75 kton of Fe), the number of muons decaying per 1 year \(N_\mu = 10^{21}\), the detector efficiency \(\varepsilon =1 \) (for simplicity, one takes the efficiency as unity for energies above the threshold), the inner radius of the detector R that is equal to a distance between the \(\nu \) source and the detector \(R=L\simeq 22 \, \mathrm{m}\), \(\delta = 0.01\), \(S_{D}=4 \pi R^2 \sin \delta \).

We are interested in the azimuthal distribution of event number:

$$\begin{aligned}&\frac{\mathrm{d} N}{\mathrm{d}\phi _{e}} = N_e \sum _{i}^{\overline{\nu }_{e}, \nu _{\mu }} \int _{y_{i}^{min}}^{y_{i}^{\max }=1} \frac{\mathrm{d} \varPhi _{i}^{\perp }}{\mathrm{d}y_{i}} \left( \int _{y_{e}^{\mathrm{th}}}^{y_{e}^{\max }(y_{i})} \frac{\mathrm{d}^{2} \sigma _{i}}{\mathrm{d} y_{e} \mathrm{d} \phi _{e}} \mathrm{d} y_{e} \right) \mathrm{d}y_{i}, \nonumber \\&\frac{\mathrm{d} \varPhi _{i}^{\perp }}{\mathrm{d}y_{i}} = \frac{ N_\mu }{S_D} \int _{0}^{2\pi } \left( \int _{\pi /2-\delta }^{\pi /2 +\delta }\frac{\mathrm{d}^2\varGamma }{ \mathrm{d} y_{i} \mathrm{d} \Omega _{i}} \sin \theta _{i} \mathrm{d} \theta _{i} \right) \mathrm{d}\phi _{i}. \end{aligned}$$
(9)

The angle-energy distributions of \(\overline{\nu }_{e}\)’s and of \(\nu _\mu \)’s from the PMDaR are in [77] and in the appendix, respectively. The differential cross section for the scattering of Dirac \(\overline{\nu }_{e}\)’s off the unpolarized electrons, in the relativistic limit, is of the form (the formula in [77] does not contain the contributions from the \(c_{S,T}^{L} \) couplings because they do not interfere with the \(c_{V,A}^{L}\))

$$\begin{aligned}&\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} = \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V- A)} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V+A)} \\&\quad + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(S, T)} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V S)} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(A T)},\nonumber \end{aligned}$$
(10)
$$\begin{aligned}&\bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V- A)} = B \bigg \{ (1+\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q} ) \bigg [|c_{V}^{L} - c_{A}^{L}|^{2}\\&\quad + |c_{V}^{L}+ c_{A}^{L}|^{2}(1-y_{e})^{2} - \frac{m_{e}y_{e}}{E_{\overline{\nu }}}(|c_{V}^{L}|^{2} - |c_{A}^{L}|^{2}) \bigg ] \bigg \}, \nonumber \end{aligned}$$
(11)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V+A)} = B \bigg \{ (1-\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q} ) \bigg [|c_{V}^{R} - c_{A}^{R}|^{2} }\\&\quad + |c_{V}^{R} + c_{A}^{R}|^{2}(1-y_{e})^{2} - \frac{m_{e}y_{e}}{E_{\overline{\nu }}}(|c_{V}^{R}|^{2} - |c_{A}^{R}|^{2}) \bigg ] \bigg \},\nonumber \end{aligned}$$
(12)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(S, T)} = B\Bigg \{ (1-\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q})\bigg [ \frac{1}{2}y_{e}\left( y_{e}+2\frac{m_{e}}{E_{\overline{\nu }}}\right) |c_{S}^{R}|^{2} } \nonumber \\&\quad + \left( (2-y_{e})^2 -\frac{m_{e}}{E_{\overline{\nu }}}y_{e}\right) |{c_{T}^{R}}|^{2} - y_{e}(y_{e}-2)\mathrm{Re}(c_{S}^{R}c_{T}^{*R}) \bigg ] \nonumber \\&\quad + (1+ \hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q})\bigg [ \frac{1}{2}y_{e}\left( y_{e}+2\frac{m_{e}}{E_{\overline{\nu }}}\right) |c_{S}^{L}|^{2} \\&\quad + \left( (2-y_{e})^2 -\frac{m_{e}}{E_{\overline{\nu }}}y_{e}\right) |{c_{T}^{L}}|^{2} - y_{e}(y_{e}-2)\mathrm{Re}(c_{S}^{L}c_{T}^{*L}) \bigg ] \Bigg \}, \nonumber \end{aligned}$$
(13)
$$\begin{aligned}&{\Bigg (\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V S)} = B \bigg \{ - 2 \sqrt{y_{e}\left( y_{e}+2\frac{m_{e}}{E_{\overline{\nu }}}\right) }}\\&\quad \cdot [(\eta _{\overline{\nu }}^{ \perp }\cdot { \hat{\mathbf p}_{\mathbf e}}) \mathrm{Re}(c_{V}^{L}c_{S}^{R*}) + \eta _{\overline{\nu }}^{ \perp }\cdot ({\hat{{\mathbf {p}}}_{e} \times {\hat{\mathbf{q}}}})\mathrm{Im}(c_{V}^{L}c_{S}^{R*})] \Bigg \}, \nonumber \end{aligned}$$
(14)
$$\begin{aligned}&{\bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(A T)} = B \bigg \{ - 2 \sqrt{y_{e}\left( y_{e}+2\frac{m_{e}}{E_{\overline{\nu }}}\right) }}\nonumber \\&\quad \cdot [\eta _{\overline{\nu }}^{ \perp }\cdot ({\hat{\mathbf {p}}_{{\mathbf {e}}} \times {\hat{\mathbf{q}}}})\mathrm{Im}(c_{A}^{L}c_{T}^{R*}) + (\eta _{\overline{\nu }}^{ \perp }\cdot {\hat{\mathbf {p}}_{{\mathbf {e}}}}) \mathrm{Re}(c_{A}^{L}c_{T}^{R*})] \bigg \};\nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned} y_{e}\equiv & {} \frac{T_{e}}{E_{\overline{\nu }}}=\frac{m_{e}}{E_{\overline{\nu }}}\frac{2 \cos ^{2}\theta _{e}}{(1+\frac{m_{e}}{E_{\nu }})^{2}-\cos ^{2}\theta _{e}} \end{aligned}$$
(16)

is the ratio of the kinetic energy of the recoil electron \(T_{e}\) to the incoming antineutrino energy \(E_{\overline{\nu }}\); \(\theta _{e}\) is the angle between \( \hat{\mathbf p}_{e}\) and \(\hat{\mathbf q}\) (recoil electron scattering angle); \(m_{e}\) is the electron mass; \(\phi _{e}\) is the angle between the production plane and the reaction plane (azimuthal angle of outgoing electron momentum); \(B\equiv \left( E_{\overline{\nu }_e} m_{e}/4\pi ^2\right) \left( G_{F}^{2}/2\right) \). It is important to note that the differential cross section for \(\nu _\mu \)’s has a similar form with the following changes: \(c_{V}^{L, R}, c_{A}^{L, R}, c_{S}^{L, R}, c_{T}^{L, R}\rightarrow g_{V}^{L, R}, - g_{A}^{L, R}, g_{S}^{L, R}, - g_{T}^{L, R}\); \(\hat{\mathbf q} \rightarrow - \hat{\mathbf q}\); \(\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q} \rightarrow - \hat{\eta }_{\nu } \cdot \hat{\mathbf q}\); \(\eta _{\overline{\nu }}^{ \perp }\rightarrow - \eta _{\nu }^{ \perp }\). We see that the interference terms, Eqs. (14) and (15), between the standard \(c_{V, A}^{L}\) and exotic \(c_{S, T}^{R}\) couplings survive in the relativistic limit. The interferences between the exotic \(c_{V, A}^{R}\) and \(c_{S, T}^{L} \) couplings are also possible, but give a very tiny contribution and are omitted. There are no interferences between \(c_{V, A}^{L}\) and \(c_{S, T}^{L} \) couplings of the LCh \(\overline{\nu }_{e}\)’s for \(m_{\overline{\nu }}\rightarrow 0\). In addition, the interference terms between \(c_{V, A}^{L}\) and \(c_{V, A}^{R}\) couplings also vanish in the relativistic limit. It can be noticed that the interferences include only the contributions from the transverse components of the \(\overline{\nu }_{e}\) spin polarization, both T-even and T-odd:

$$\begin{aligned}&{\left( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\right) _{(VS)} + \left( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\right) _{(AT)} = - 2 B |\eta _{\overline{\nu }}^{ \perp }|} \nonumber \\&\quad \cdot \sqrt{\frac{m_{e}}{E_{\overline{\nu }}}y_{e}\left[ 2-\left( 2+\frac{m_{e}}{E_{\overline{\nu }}}\right) y_{e}\right] }\cdot \{ |c_{V}^{L}||c_{S}^{R}| \nonumber \\&\quad \cos (\phi +\beta _{VS}-\phi _e)+ |c_{A}^{L}||c_{T}^{R}|\cos (\phi +\beta _{AT}-\phi _e) \},\nonumber \\ \end{aligned}$$
(17)

where \(\phi \) is the angle between \(\eta _{\overline{\nu }}^{\perp }\) and \(\eta _{\mu }^{\perp }\) only (this angle is a CP-violating phase); \(\phi _0 = \phi - \phi _e\) is the angle between \({\mathbf p}_{e}^{\perp }\) and \(\eta _{\overline{\nu }}^{\perp }\), Fig. 1; \(\beta _{VS} \equiv \beta _{V}^{L} - \beta _{S}^{R}, \beta _{AT} \equiv \beta _{A}^{L} - \beta _{T}^{R} \) are the relative phases between the \(c_{V}^{L}, c_{S}^{R}\) and \( c_{A}^{L}, c_{T}^{R}\) couplings, respectively. The relative phases \(\beta _{VS}, \beta _{AT}\) different from \(0, \pi \) would indicate the CPV in the NEES. We see that in the relativistic limit the helicity structure of interaction vertices may allow for a helicity flip provided the quantity \(\eta _{\overline{\nu }}^{ \perp }\), which is left invariant under Lorentz boost. For the standard \({V}-{A}\) interaction, there is no dependence on the \(\phi _{e}\), it means that the azimuthal distribution is symmetric. In the case of the superposition of LCh and RCh \(\overline{\nu }_{e}\)’s, the interference terms are proportional to \(|\eta _{\nu }^{\perp }|\) and depend on \(\phi _e\). It generates the azimuthal asymmetry in the angular distribution of scattered electrons.

Using the experimental values of standard couplings: \(c_{V}^{L}= 1+ (-0.04 \pm 0.015), c_{A}^{L}= 1+ (-0.507 \pm 0.014)\) [73], we find the upper limits on the exotic couplings in the NEES: \(|c_{S}^{L}|\le 0.02, |c_{S}^{R}|\le 0.437, |c_{T}^{L}|\le 0.01, |c_{T}^{R}|\le 0.431, |c_{V}^{R}|\le 0.015, |c_{A}^{R}|\le 0.005\), simultaneously shifting the standard values to new ones \(c_{V'}^{L}=0.975, c_{A'}^{L}=0.507\), which still lie within the experimental bars. The similar analysis for the \(\nu _{\mu }\)’s provides the upper limits on the exotic couplings \(g_{k}^{L,R}, k=S, T, V, A\). If one uses the above limits, one gets the same magnitude of total cross section as in the standard case. Equation (9) allows one to compute the event number and neutrino flux (from \(\overline{\nu }_{e}\)’s and \(\nu _{\mu }\)’s) predicted by the SM, respectively:

$$\begin{aligned} \left( \frac{\mathrm{d} N}{\mathrm{d}\phi _{e}}\right) _{\mathrm{SM}}\simeq & {} 4.536 \times 10^{9} \text{ per } \text{1 } \text{ year }, \\ \varPhi _{\mathrm{SM}}^{\perp }\simeq & {} 1.497 \times 10^{19}\, \mathrm{cm}^{-2}\, \mathrm{year}^{-1}.\nonumber \end{aligned}$$
(18)

Now, we calculate the upper limits on the azimuthal asymmetry of event number between the \((0,\pi )\) and \((\pi , 2\pi )\) angles (up–down asymmetry) using the upper limits on \(|\eta _{\overline{\nu }}^{\perp }|, |\eta _{\nu }^{\perp }|\) and lower bound on \(|(\hat{\eta }_{\overline{\nu }}\cdot \hat{\mathbf q})|, |(\hat{\eta }_{\nu }\cdot \hat{\mathbf q})|\):

$$\begin{aligned} A(\phi _{e'})= & {} \frac{\int _{\phi _{e'}}^{\phi _{e'} + \pi } \frac{\mathrm{d} N}{\mathrm{d}\phi _{e}} \mathrm{d}\phi _{e} - \int _{\phi _{e'} + \pi }^{\phi _{e'} + 2\pi } \frac{\mathrm{d} N}{\mathrm{d}\phi _{e}} \mathrm{d}\phi _{e}}{\int _{\phi _{e'}}^{\phi _{e'} + \pi } \frac{\mathrm{d} N}{\mathrm{d}\phi _{e}} \mathrm{d}\phi _{e} + \int _{\phi _{e'} + \pi }^{\phi _{e'} + 2\pi } \frac{\mathrm{d} N}{\mathrm{d}\phi _{e}} \mathrm{d}\phi _{e}}. \end{aligned}$$
(19)

We get for the case of TRV \((\phi +\beta _{VS}=\frac{\pi }{2}, \phi + \beta _{AT}=\frac{\pi }{2})\) and time reversal conservation (TRC; \(\phi +\beta _{VS}=0, \phi + \beta _{AT}=0\)), respectively:

$$\begin{aligned} A_{D}(\phi _{e'})^{T\hbox {-}\mathrm{viol}}\le & {} - 2 \times 10^{-3} \,\cos ( \phi _{e'}),\\ A_{D}(\phi _{e'})^{T\hbox {-}\mathrm{cons}}\le & {} 2 \times 10^{-3} \,\sin ( \phi _{e'})\nonumber . \end{aligned}$$
(20)

It is worthy of emphasizing that the integrations of function, present in the interferences, over \(y_{e}\) and then over y affect significantly on the small value of the azimuthal asymmetry.

3 Elastic scattering of Majorana electron and muon neutrinos off unpolarized electrons

It is important to point out that the considered scenario concerns the flavour (current) \(\nu \) eigenstates similarly as for the Dirac case. The amplitude for the elastic scattering of the Majorana electron neutrinos (\(\nu _{e}\)’s) on the unpolarized electrons at low energies has the form (a similar amplitude is for \(\nu _\mu \)’s with the appropriate change of couplings \(c_V, c_A, c_V^{'}, c_A^{'}, c_{S, T}^{L,R} \rightarrow g_V, g_A, g_V^{'}, g_A^{'}, g_{S, T}^{L,R}\))

$$\begin{aligned}&{ M^{M}_{\nu _{e} e^{-}} = \frac{2G_{F}}{\sqrt{2}}\{-(\overline{u}_{e'}\gamma ^{\alpha }(c_{V} - c_{A}\gamma _{5})u_{e}) (\overline{u}_{\nu _{e'}}\gamma _{\alpha }\gamma _{5} u_{\nu _{e}}) }\nonumber \\&\quad + (\overline{u}_{e'}\gamma ^{\alpha }(c_{V}^{'} + c_{A}^{'}\gamma _{5})u_{e}) (\overline{u}_{\nu _{e'}}\gamma _{\alpha }\gamma _{5} u_{\nu _{e}}) \nonumber \\&\quad + c_{S}^{L}(\overline{u}_{e'}u_{e})(\overline{u}_{\nu _{e'}} (1 - \gamma _{5})u_{\nu _{e}})\nonumber \\&\quad + c_{S}^{R}(\overline{u}_{e'}u_{e})(\overline{u}_{\nu _{e'}}(1 + \gamma _{5})u_{\nu _{e}})\}. \end{aligned}$$
(21)

We see that the above matrix element in the neutrino part does not contain the contribution from the V and T interactions in contrast to the Dirac case, where both terms partake. The contribution from the \(V+A\) interaction is also admitted. In addition, the A and S contributions are multiplied by a factor 2. This arises from the fact that the Majorana neutrino is described by the self-conjugate field. The absence of the index L (R) for \(c_V, c_A\) (\(c_V^{'}, c_A^{'}\)) couplings means that both LCh and RCh \(\nu _{e}\)’s may participate in the standard A (non-standard \(A^{'}\)) interaction of Majorana \(\nu _{e}\)’s. Consequently, the new term with the interference between \(c_V\) and \(c_{S}^{L}\) couplings in the differential cross section appears. Such interference vanishes in the Dirac case. Similar interferences occur between \(c_V^{'}\) and \(c_{S}^{L,R}\), but give negligible contributions. All the couplings are assumed to be complex as for the Dirac case. The other assumptions concerning the production of \(\nu _{e}\) beam and the detection of \(\nu _{e}\)’s by the interaction with the unpolarized electron target are the same as in the Dirac scenario.

3.1 Azimuthal distribution of recoil electrons in the case of Majorana neutrinos

The differential cross section for the scattering of Majorana current \( \nu _{e}\)’s on the unpolarized electrons in the relativistic limit has the form (the formula for \( \nu _{\mu }\)’s can be obtained by the above mentioned change of couplings)

$$\begin{aligned} \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}= & {} \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V- A)} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{( V^{'}+ A^{'})} \nonumber \\&+ \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V-A)(V^{'}+ A^{'})} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(S_{L}, S_{R})} \nonumber \\&+ \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V S_{R})} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V S_{L})} \nonumber \\&+ \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V^{'} S_{L})} + \bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V^{'} S_{R})}, \end{aligned}$$
(22)
$$\begin{aligned}&{\bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V- A)} = B \bigg \{ - \frac{2 m_{e}y_{e}}{E_{\nu }}(|c_{V}|^{2} - |c_{A}|^{2})} \nonumber \\&\quad + |c_{V} + c_{A}|^{2} (2+ (1+\hat{\eta }_{\nu }\cdot \hat{\mathbf q})(y_{e}-2)y_{e})\nonumber \\&\quad + |c_{V} - c_{A}|^{2} (2 + (1-\hat{\eta }_{\nu }\cdot \hat{\mathbf q})(y_{e}-2)y_{e}) \bigg \}, \end{aligned}$$
(23)
$$\begin{aligned}&{\bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}} \bigg )_{(V^{'}+ A^{'})} = B \bigg \{ - \frac{2 m_{e}y_{e}}{E_{\nu }}(|c_{V}^{'}|^{2} - |c_{A}^{'}|^{2}) }\nonumber \\&\quad + |c_{V}^{'} - c_{A}^{'}|^{2} (2+ (1+\hat{\eta }_{\nu }\cdot \hat{\mathbf q})(y_{e}-2)y_{e})\nonumber \\&\quad + |c_{V}^{'} + c_{A}^{'}|^{2} (2+ (1-\hat{\eta }_{\nu }\cdot \hat{\mathbf q})(y_{e}-2)y_{e})\bigg \}, \end{aligned}$$
(24)
$$\begin{aligned}&{\bigg ( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V-A)(V^{'}+ A^{'})} }\nonumber \\&\quad = 4 B \bigg \{ \mathrm{Re}(c_{A}c_{A}^{'*})\bigg (2+ (y_{e}-2)y_{e} + \frac{ m_{e}y_{e}}{E_{\nu }}\bigg ) \\&\quad \quad + (\mathrm{Re}(c_{V}c_{A}^{'*})- \mathrm{Re}(c_{A}c_{V}^{'*})) (y_{e}-2)y_{e} \hat{\eta }_{\nu }\cdot \hat{\mathbf q} \nonumber \\&\quad \quad + \mathrm{Re}(c_{V}c_{V}^{'*})\bigg (-2 - (y_{e}-2)y_{e} + \frac{ m_{e}y_{e}}{E_{\nu }}\bigg ) \bigg \}, \nonumber \end{aligned}$$
(25)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(S_L,S_R)} = B\bigg \{ 2 y_{e}\left( y_{e}+2\frac{m_{e}}{E_{\nu }}\right) }\\&\quad \cdot [ (1+\hat{\eta }_{\nu }\cdot \hat{\mathbf q})|c_{S}^{R}|^{2} + (1-\hat{\eta }_{\nu }\cdot \hat{\mathbf q})|c_{S}^{L}|^{2}]\bigg \},\nonumber \end{aligned}$$
(26)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V S_R)} = B \bigg \{ 4 \sqrt{y_{e}(y_{e}+2\frac{m_{e}}{E_{\nu }})}}\\&\quad \cdot [ (\eta _{\nu }^{ \perp }\cdot {\hat{\mathbf p}_{\mathbf e}}) \mathrm{Re}(c_{V}c_{S}^{R*}) - \eta _{\nu }^{\perp }\cdot ({\hat{\mathbf {p}}_{\mathbf {e}} \times \hat{{\mathbf {q}}}})\mathrm{Im}(c_{V}c_{S}^{R*}) ] \bigg \}, \nonumber \end{aligned}$$
(27)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V S_L)} = B \bigg \{ 4 \sqrt{y_{e}(y_{e}+2\frac{m_{e}}{E_{\nu }})}} \\&\quad \cdot [ (\eta _{\nu }^{ \perp }\cdot {\hat{\mathbf p}_{\mathbf e}}) \mathrm{Re}(c_{V}c_{S}^{L*}) + \eta _{\nu }^{ \perp }\cdot ({\hat{\mathbf {p}}_{\mathbf {e}} \times \hat{{\mathbf {q}}}})\mathrm{Im}(c_{V}c_{S}^{L*}) ] \bigg \},\nonumber \end{aligned}$$
(28)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V^{'} S_L)} = B \bigg \{ 4 \,\sqrt{y_{e}(y_{e}+2\frac{m_{e}}{E_{\nu }})}}\\&\quad \cdot [ - (\eta _{\nu }^{ \perp }\cdot {\hat{\mathbf p}_{\mathbf e}}) \mathrm{Re}(c_{V}^{'}c_{S}^{L*}) - \eta _{\nu }^{ \perp }\cdot ({\hat{\mathbf {p}}_{\mathbf {e}} \times \hat{{\mathbf {q}}}})\mathrm{Im}(c_{V}^{'}c_{S}^{L*})] \bigg \}, \nonumber \end{aligned}$$
(29)
$$\begin{aligned}&{\bigg (\frac{\mathrm{d}^{2}\sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\bigg )_{(V^{'} S_R)} = B \bigg \{ 4 \sqrt{y_{e}(y_{e}+2\frac{m_{e}}{E_{\nu }})}}\\&\quad \cdot [ - (\eta _{\nu }^{ \perp }\cdot {\hat{\mathbf p}_{\mathbf e}}) \mathrm{Re}(c_{V}^{'}c_{S}^{R*}) + \eta _{\nu }^{ \perp }\cdot ({\hat{\mathbf {p}}_{\mathbf {e}} \times \hat{{\mathbf {q}}}})\mathrm{Im}(c_{V}^{'}c_{S}^{R*}) ] \bigg \}\nonumber . \end{aligned}$$
(30)

The significant contribution from the interference between the \(c_V\) and \(c_{S}^{L,R}\) couplings can be written down as follows:

$$\begin{aligned}&{\left( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\right) _{(V S_R)} + \left( \frac{\mathrm{d}^{2} \sigma }{\mathrm{d}y_{e} \mathrm{d}\phi _{e}}\right) _{(V S_L)}}\nonumber \\&\quad = 4 B |\eta _{\nu }^{ \perp }| \sqrt{\frac{m_{e}}{E_{\nu }}y_{e}\left[ 2-\left( 2+\frac{m_{e}}{E_{\nu }}\right) y_{e}\right] }\nonumber \\&\quad \quad \cdot |c_{V}|\{ |c_{S}^{R}|\cos (\phi - \alpha _{VS_R}-\phi _e)\nonumber \\&\quad \quad + |c_{S}^{L}|\cos (\phi +\alpha _{VS_L}-\phi _e) \}, \end{aligned}$$
(31)

where \(\alpha _{VS_R} \equiv \alpha _{V} - \alpha _{S}^{R}, \alpha _{VS_L} \equiv \alpha _{V} - \alpha _{S}^{L} \) are the relative phases between the \(c_{V}, c_{S}^{R}\) and \( c_{V}, c_{S}^{L}\) couplings, respectively. Now, we calculate the upper limits on the azimuthal asymmetry between \((0,\pi )\) and \((\pi , 2\pi )\) angles for the TRV \((\phi +\alpha _{VS_R}=\frac{\pi }{2}, \phi + \alpha _{VS_L}=\frac{\pi }{2})\) and TRC \((\phi +\alpha _{VS_R}=0, \phi + \alpha _{VS_L}=0)\), using the same limits as for the Dirac case:

$$\begin{aligned} A_{M}(\phi _{e'}^{T\hbox {-}\mathrm{viol}})\le & {} 6 \times 10^{-3}\, \cos (\phi _{e'}), \\ A_{M}(\phi _{e'}^{T\hbox {-}\mathrm{cons}})\le & {} - 6 \times 10^{-3} \, \sin (\phi _{e'})\nonumber . \end{aligned}$$
(32)

We see that the possible effect of up–down azimuthal asymmetry for the Majorana flavour \(\nu _{e}\)’s and \(\nu _\mu \)’s is larger than in the Dirac case. Moreover, there is a different dependence on the angle \(\phi _{e'}\) in the case of the TRV and TRC, similarly to the Dirac neutrinos, so the precise measurement of maximal azimuthal asymmetry would answer the question of whether the TRV takes place.

4 Conclusions

We have shown that there is the distinction between the Dirac and Majorana flavour \(\nu \)’s in the relativistic limit, when the incoming \(\nu \) beam is the superposition of LCh and RCh states, and has the fixed direction of transversal component of the (anti)neutrino spin polarization with respect to the production plane. If the \(\nu \) beam comes from the polarized source (e.g. PMDaR), where the exotic \(S, T, V+A\) interactions produce the current \(\nu \)’s with the right-handed chirality, while the \(V-A\) interaction generates the LCh flavour \(\nu \)’s, the (anti)neutrino polarization vector may acquire the transversal component (both T-even and T-odd), which is left invariant under Lorentz boost. Next, this left–right chiral superposition is scattered off the unpolarized electrons in the presence of both standard and exotic interactions. The precise measurement of the azimuthal asymmetry of recoil electrons, generated by the interference terms between the standard and exotic couplings, proportional to \(\eta _{\nu }^{ \perp }\), could allow one to distinguish between the Dirac and Majorana flavour \(\nu \)’s, and test the TRV. Both the flavour \(\overline{\nu }_e\)’s (\(\nu _e\)’s) and the \(\nu _\mu \)’s may generate the azimuthal asymmetry. It is worthwhile pointing out that there is a well-known technique of producing the polarized muons at rest [54] (e.g. TRIUMF and other laboratories). However, in practice the discrimination of two scenarios is extremely difficult, because the interference terms depend on unknown \(\eta _{\nu }^{\perp }\). For the Majorana \(\nu \)’s, the upper limit on the expected magnitude of up–down azimuthal asymmetry is larger than for the Dirac case. The potential experiment should verify if the angular distribution of recoil electrons is azimuthally symmetric in the relativistic limit according to the SM. If the departure from the symmetry was visible and too large to be caused by the Dirac \(\nu \)’s, it would leave some place for the Majorana \(\nu \)’s. However, it would require the correct subtraction of background events and, moreover, the asymmetry values would have to be measured with the error bars small enough to eliminate the Dirac case. The basic difference between the both cases follows from the absence of interference terms between the standard and exotic tensor interactions in the differential cross section for the Majorana \(\nu \)’s. The additional distinction arises from the occurrence of interference between the standard and S couplings of the LCh Majorana \(\nu \)’s. This type of interference annihilates for the Dirac \(\nu \)’s.

It is also important to note that the eventual effects connected with the neutrino mass and mixing for the tests with a near detector are inessential; see e.g. [77]. The admittance of \(\nu \) mass eigenstates in the PMDaR and in the ENES, when the exotic interactions are present, seems to be important for the long-range \(\nu \) oscillation experiments.

It is relevant to stress that the azimuthal asymmetry measurements require the very intense polarized (anti)neutrino sources and large unpolarized (polarized) target of electrons (or nucleons), and also long duration of experiment. It is worthy of searching for the other polarized (anti)neutrino sources than the considered the PMDaR, which produce only single \(\nu \) flavour. To make the above tests feasible, the low-threshold, real-time detectors should measure with a high resolution both the polar angle and the azimuthal angle of outgoing electron momentum (event number in \(\phi _e\)-bins). Our analysis has been carried out for the detector (running for 1 year) in the shape of flat circular ring with the \(\nu \) source located in the centre of this ring and polarized perpendicularly to it, and the basic parameters presented in Sect. 2.1. In the next study, we are going to carry out the detailed analysis for the \(\nu \) mass eigenstates in the production process and in the ENES. We will show whether the proposed number of polarized muons and of the target electrons are the required choice for the physical goals. Both the statistical and the systematic errors have to be taken into account to verify that there is the choice of angular bins leading to the statistical errors that are small enough to detect the non-zero azimuthal asymmetry.

It is necessary to point out that there is a real interest in the development of low-threshold technology in the context of dark matter searches and the study of neutrino interactions. The silicon cryogenic detectors, the high purity germanium detectors (Neganov et al. arXiv:hep-ex/0105083), the semiconductor detectors [78] and the bolometers [79] are worth mentioning. The two experiments aiming at the measurement of recoil electron scattering angle and of azimuthal angle, i.e. Hellaz [80, 81] and Heron [82], have also been proposed. Recently, the interesting proposal for particle detection based on the infrared quantum counter concept has emerged (Borghesani et al. arXiv:1506.07987 [physics.ins-det]). Finally, our studies are reported in hope that it may encourage the neutrino collaborations working with the polarized muon decay, other artificial polarized \(\nu \) sources and neutrino beams to revive the discussion of the measurements of the azimuthal asymmetry of recoil electrons. It seems to be a real challenge, but new tests using the neutrino polarimeters could shed a light on the \(\nu \) nature, detect the existence of the exotic couplings of interacting RCh \(\nu \)’s, the non-standard phases of TRV and complete the present measurements based on the electron (positron) observables [83] and the energy spectrum of \(\nu \)’s [84].