1 Introduction

Gravity in higher dimensions has attained considerable attention with the development of string theory. Concerning the effect of string theory on gravitational physics, one may construct a low energy effective action which includes both the Einstein–Hilbert Lagrangian (as the first order term) and the higher curvature terms. However, this approach may lead to field equations of fourth order and ghosts as well. This problem has been solved by a particular higher curvature gravity theory called Lovelock gravity [1]. The field equation in this gravity theory is only second order and the quantization of Lovelock gravity theory is free of ghosts [2]. In this context, it is of interest to investigate both the black hole solutions and their thermodynamics in Lovelock gravity [3–29]. Moreover, it is natural to consider the nonlinear terms in the matter side of the action while accepting the nonlinear terms on the gravity side [3]. Motivated by this, Ref. [3] presented topological black hole solutions in Lovelock–Born–Infeld gravity. Both the thermodynamics of asymptotically flat black holes for \(k=1\) and the thermodynamics of asymptotically AdS rotating black branes with a flat horizon were investigated there in detail. However, concerning the charged topological AdS black holes in Lovelock–Born–Infeld gravity, only the temperature was given in Ref. [3]. Reference [18] further studied their entropy and specific heat at constant charge. However, the expression of the entropy seems incomplete, for \(k\) is missing. The thermodynamics in the extended space needs to be further explored. Probing this issue is important because it is believed that the physics of black holes in higher dimensions is essential to understand the full theory of quantum gravity.

As is well known, the phase transition is a fascinating phenomenon in classical thermodynamics. Over the past decades, phase transitions of black holes have aroused more and more attention. The pioneering phase transition research of AdS black holes can be traced back to the discovery of the famous Hawking–Page phase transition between the Schwarzschild AdS black hole and thermal AdS space [30]. Recently, a revolution in this field has been led by \(P\)–\(V\) criticality research [31–44] in the extended phase space. Kubizňák et al. [31] perfectly completed the analogy between charged AdS black holes and the liquid–gas system first observed by Chamblin et al. [45, 46]. The approach of treating the cosmological constant as thermodynamic pressure and its conjugate quantity as thermodynamic volume is essential with the increasing attention of considering the variation of the cosmological constant in the first law of black hole thermodynamics recently [47–53].

Here, we would like to investigate the thermodynamics and phase transition of charged topological AdS black holes in Lovelock–Born–Infeld gravity in the extended phase space. Some related efforts have been made recently. \(P\)–\(V\) criticality of both four-dimensional [32] and higher-dimensional [44] Born–Infeld AdS black holes has been investigated. A new parameter, called the Born–Infeld vacuum polarization, was defined to be conjugate to the Born–Infeld parameter [32]. It was argued that this quantity is required for the consistency of both the first law of thermodynamics and the Smarr relation. Moreover, Cai et al. [40] studied \(P\)–\(V\) criticality of Gauss–Bonnet AdS black holes. It was found that no \(P\)–\(V\) criticality can be observed for Ricci flat and hyperbolic Gauss–Bonnet black holes. However, for the spherical case, \(P\)–\(V\) criticality can be observed even when the charge is absent, implying that the charge may not be an indispensable factor for the existence of \(P\)–\(V\) criticality. Such an interesting result motivates us to probe further third order Lovelock gravity to explore whether it is a peculiar property due to the higher derivative terms of the curvature. So we will mainly investigate their effects on \(P\)–\(V\) criticality. Moreover, we will probe the combined effects of higher derivative terms of curvature and the nonlinear electrodynamics.

In Sect. 2, the solutions of charged topological AdS black holes in Lovelock–Born–Infeld gravity will be briefly reviewed and their thermodynamics will be further investigated. In Sect. 3, a detailed study will be carried out in the extended phase space for the limit case \(\beta \rightarrow \infty \) so that we can concentrate on the effects of third order Lovelock gravity. In Sect. 4, the effects of nonlinear electrodynamics will also be included. In the end, a brief conclusion will be drawn in Sect. 5.

2 Thermodynamics of charged topological black holes in Lovelock–Born–Infeld gravity

The action of third order Lovelock gravity with nonlinear Born–Infeld electromagnetic field is [3]

$$\begin{aligned}&I_{G}=\frac{1}{16\pi }\int \hbox {d}^{n+1}x\sqrt{-g}\nonumber \\&\quad \times \big (-2\Lambda +{\mathcal L}_1+\alpha _2{\mathcal L}_2+ \alpha _3{\mathcal L}_3+L(F)\big ), \end{aligned}$$
(1)

where

$$\begin{aligned}&{\mathcal L}_1=R,\end{aligned}$$
(2)
$$\begin{aligned}&{\mathcal L}_2=R_{\mu \nu \gamma \delta }R^{\mu \nu \gamma \delta } -4R_{\mu \nu }R^{\mu \nu }+R^2, \end{aligned}$$
(3)
$$\begin{aligned}&{\mathcal L}_3=2R^{\mu \nu \sigma \kappa }R_{\sigma \kappa \rho \tau }R^{\rho \tau }_{\;\;\;\;\mu \nu }+8R^{\mu \nu }_{\;\;\;\; \sigma \rho }R^{\sigma \kappa }_{\;\;\;\;\nu \tau }R^{\rho \tau }_{\;\;\;\;\mu \kappa }\nonumber \\&\qquad \quad +24R^{\mu \nu \sigma \kappa }R_{\sigma \kappa \nu \rho }R^{\rho }_{\;\;\mu } \nonumber \\&\qquad \quad +3RR^{\mu \nu \sigma \kappa }R_{\sigma \kappa \mu \nu } +24R^{\mu \nu \sigma \kappa } R_{\sigma \mu }R_{\kappa \nu }\nonumber \\&\qquad \quad +16R^{\mu \nu }R_{\nu \sigma } R^{\sigma }_{\;\;\mu }-12RR^{\mu \nu }R_{\mu \nu }+R^3,\end{aligned}$$
(4)
$$\begin{aligned}&L(F)=4\beta ^2\left( 1-\sqrt{1+\frac{F^2}{2\beta ^2}}\right) . \end{aligned}$$
(5)

In the above action, \(\beta , \alpha _2\) and \(\alpha _3\) are Born–Infeld parameter, the second and third order Lovelock coefficients, respectively, while \({\mathcal L}_1\), \({\mathcal L}_2\), \({\mathcal L}_3\) and \(L(F)\) are Einstein–Hilbert, Gauss–Bonnet, third order Lovelock, and Born–Infeld Lagrangians, respectively. Considering the case

$$\begin{aligned} \alpha _2&= \frac{\alpha }{(n-2)(n-3)}, \end{aligned}$$
(6)
$$\begin{aligned} \alpha _3&= \frac{\alpha ^2}{72{\left( \begin{array}{c}n-2\\ 4\end{array}\right) }}, \end{aligned}$$
(7)

Reference [3] derived the \((n+1)\)-dimensional static solution as

$$\begin{aligned} \hbox {d}s^2=-f(r)\hbox {d}t^2+\frac{\mathrm{d}r^2}{f(r)}+r^2\hbox {d}\Omega ^2, \end{aligned}$$
(8)

where

$$\begin{aligned} f(r)&= k+\frac{r^2}{\alpha }(1-g(r)^{1/3}),\end{aligned}$$
(9)
$$\begin{aligned} g(r)&= 1+\frac{3\alpha m}{r^n}-\frac{12\alpha \beta ^2}{n(n-1)}\nonumber \\&\times \Big [1-\sqrt{1+\eta }-\frac{\Lambda }{2\beta ^2}+ \frac{(n-1)\eta }{(n-2)}\digamma (\eta )\Big ],\end{aligned}$$
(10)
$$\begin{aligned} \hbox {d}\Omega ^2&= \left\{ \begin{array}{l@{\quad }l} \hbox {d}\theta _1^2+\sum _{i=2}^{n-1} \prod _{j=1}^{i-1}\sin ^2\theta _j\hbox {d}\theta ^2_i &{}\quad k=1\\ \hbox {d}\theta _1^2+\sinh ^2\theta _1\hbox {d}\theta _2^2\\ \quad + \sinh ^2\theta _1\sum _{n-1}^{i=3} \prod _{j=2}^{i-1} \sin ^2\theta _j\hbox {d}\theta ^2_i &{}\quad k=-1\\ \sum _{i-1}^{n-1}\hbox {d}\phi ^2_i &{}\quad k=0 \end{array} \right. .\nonumber \\ \end{aligned}$$
(11)

\(\hbox {d}\Omega ^2\) denotes the line element of \((n-1)\)-dimensional hypersurface with constant curvature \((n-1)(n-2)k\) and \(\digamma (\eta )\) denotes the hypergeometric function as follows:

$$\begin{aligned} \digamma (\eta )=\,_2F_1\Big (\Big [\frac{1}{2}, \frac{n-2}{2n-2}\Big ],\Big [\frac{3n-4}{2n-2}\Big ],-\eta \Big ), \end{aligned}$$
(12)

where

$$\begin{aligned} \eta =\frac{(n-1)(n-2)q^2}{2\beta ^2r^{2n-2}}. \end{aligned}$$
(13)

The Hawking temperature has been derived in Ref. [3] as

$$\begin{aligned} T=\frac{(n-1)k[3(n-2)r_+^4+3(n-4)k\alpha r_+^2+(n-6)k^2\alpha ^2]+12r_+^6\beta ^2(1-\sqrt{1+\eta _+}\,)-6\Lambda r_+^6}{12\pi (n-1)r_+(r_+^2+k\alpha )^2}. \end{aligned}$$
(14)

However, only the Hawking temperature is not enough to discuss \(P\)–\(V\) criticality in the extended phase space. So we would like to calculate other relevant quantities.

Solving the equation \(f(r)=0\), one can obtain the parameter \(m\) in terms of the horizon radius \(r_+\) as

$$\begin{aligned} m&= \frac{r_+^n}{3\alpha }\left\{ -1+\frac{(r_+^2+k\alpha )^3}{r_+^6}\right. \nonumber \\&+\left. \frac{12\alpha \beta ^2\left[ 1-\frac{\Lambda }{2\beta ^2}- \sqrt{1+\eta }+\frac{(n-1)\digamma (\eta )\eta }{n-2}\right] }{n(n-1)}\right\} . \end{aligned}$$
(15)

Then the mass of \((n+1)\)-dimensional topological AdS black holes can be derived as

$$\begin{aligned} M&= \frac{(n-1)\Sigma _k}{16\pi }m=\frac{(n-1)\Sigma _k r_+^n}{48\pi \alpha }\left\{ -1+\frac{(r_+^2+k\alpha )^3}{r_+^6}\right. \nonumber \\&\left. +\frac{12\alpha \beta ^2\left[ 1-\frac{\Lambda }{2\beta ^2}-\sqrt{1+\eta }+\frac{(n-1)\digamma (\eta ) \eta }{n-2}\right] }{n(n-1)}\right\} , \end{aligned}$$
(16)

where \(\Sigma _k\) denotes the volume of the \((n-1)\)-dimensional hypersurface mentioned above.

The entropy can be calculated as

$$\begin{aligned}&S=\int \limits _{0}^{r_+}\frac{1}{T}\left( \frac{\partial M}{\partial r_+}\right) \hbox {d}r\nonumber \\&\quad =\frac{\Sigma _k(n-1)r_+^{n-5}}{4}\left( \frac{r_+^4}{n-1}+\frac{2kr_+^2\alpha }{n-3}+ \frac{k^2\alpha ^2}{n-5}\right) . \end{aligned}$$
(17)

Note that the above integration is accomplished under the condition of \(n>5\). For \(n\leqslant 5\) the integration is divergent. So in this paper, we would mainly investigate the case of \(n=6\), which corresponds to the seven-dimensional black holes. The third term of the entropy in Eq. (17) does not appear in the expression of the entropy of Gauss–Bonnet black holes [40]. Our result also extends the expression in Ref. [18] where \(k\) was missing.

In the extended phase space, one may identify the pressure of the black hole as [31]

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }. \end{aligned}$$
(18)

The mass of black holes should be interpreted as enthalpy rather than the internal energy. In this context, the Gibbs free energy can be derived through

$$\begin{aligned} G=H-TS=M-TS. \end{aligned}$$
(19)

After a tedious calculation, we can obtain

$$\begin{aligned} G&= \frac{\Sigma _kr_+^{n-6}}{48\pi \alpha (r_+^2+k\alpha )^2} \left\{ (n-1)r_+^6(r_+^2+k\alpha )^2\right. \nonumber \\&\times \left[ -1+\frac{(r_+^2+k\alpha )^3}{r_+^6}\right. \nonumber \\&\left. +\frac{12\alpha \beta ^2 \left( 1-\frac{\Lambda }{2\beta ^2}-\sqrt{1+\eta }+\frac{(n-1) \digamma (\eta )\eta }{n-2}\right) }{n(n-1)}\right] \nonumber \\&-\alpha \left( \frac{r_+^4}{n-1}+\frac{2kr_+^2\alpha }{n-3}+ \frac{k^2\alpha ^2}{n-5}\right) \nonumber \\&\times \Big [(n-1)k \Big (3(n-2)r_+^4+3(n-4)k\alpha r_+^2\nonumber \\&\left. +\,(n-6)k^2 \alpha ^2\Big )-6\Lambda r_+^6+12r_+^6\beta ^2(1-\sqrt{1+\eta _+}\,)\Big ]\!\right\} \nonumber \\ \end{aligned}$$
(20)

Imitating the approach of Refs. [32, 40], the first law of thermodynamics in the extended phase space can be rewritten as

$$\begin{aligned} \hbox {d}M=T\hbox {d}S+\Phi \hbox {d}Q+V\hbox {d}P+{\mathcal A}\hbox {d}\alpha +{\mathcal B}\hbox {d}\beta , \end{aligned}$$
(21)

where \({\mathcal A}\) and \({\mathcal B}\) denote the quantities conjugated to the Lovelock coefficient and the Born–Infeld parameter, respectively. They can be obtained as

$$\begin{aligned} {\mathcal A}&= \Big (\frac{\partial M}{\partial \alpha }\Big )_{S,Q,P,\beta }=\frac{k^2(n-1)r_+^{n-6} (3r_+^2+2k\alpha )\Sigma _k}{48\pi }\nonumber \\&-\frac{1}{2}k(n-1)r_+^{n-5}T\Big (\frac{r_+^2}{n-3}+\frac{k\alpha }{n-5}\Big )\Sigma _k,\end{aligned}$$
(22)
$$\begin{aligned} {\mathcal B}&= \Big (\frac{\partial M}{\partial \beta }\Big )_{S,Q,P,\alpha }=\frac{\Sigma _kr_+^{-n}}{8n\pi \beta }\nonumber \\&\times \left\{ 2r_+^{2n}\beta ^2\left( 2-\sqrt{4+\frac{2(n-1)(n-2)q^2r_+^{2-2n}}{\beta ^2}}\;\right) \right. \nonumber \\&+ (n-2)(n-1)q^2r_+^2\;_2F_1\Big (\Big [\frac{1}{2}, \frac{n-2}{2n-2}\Big ],\Big [\frac{3n-4}{2n-2}\Big ],\nonumber \\&-\left. \frac{(n-1)(n-2)q^2}{2\beta ^2r^{2n-2}}\Big )\right\} \end{aligned}$$
(23)

Comparing Eq. (22) with the Gauss–Bonnet black holes in Ref. [40], one may find extra terms due to third order Lovelock gravity. Note that Eq. (21) is limited to the case of charged topological black holes in Lovelock Born–Infeld gravity in which the second and the third order Lovelock coefficients are related via the Lovelock coefficient \(\alpha \). For the general case and a nice physical interpretation of the quantity conjugate to the Lovelock coefficient; see Ref. [15], where the Smarr relation and the first law of thermodynamics in Lovelock gravity were thoroughly investigated and it was shown that the conjugate quantity \(\Psi ^{(k)}\) to the Lovelock coefficient \(b_k\) consists of three terms related to mass, entropy, and the anti-symmetric Killing–Lovelock potential, respectively.

3 \(P\)–\(V\) criticality of a limit case

To concentrate on the effects of third order Lovelock gravity, we would like to investigate an interesting limit case in this section and leave the issue of nonlinear electrodynamics to be further investigated in Sect. 4.

When \(\beta \rightarrow \infty \), the Born–Infeld Lagrangian reduces to the Maxwell form and \(\digamma (\eta )\rightarrow 1\). So one can have

$$\begin{aligned} g(r)\rightarrow 1+\frac{3\alpha m}{r^n}+\frac{6\alpha \Lambda }{n(n-1)}-\frac{3\alpha q^2}{r^{2n-2}}. \end{aligned}$$
(24)

The temperature for this limit case can be simplified as

$$\begin{aligned} T=\frac{(n-1)k[3(n-2)r_+^4+3(n-4)k\alpha r_+^2+(n-6)k^2\alpha ^2]-6\Lambda r_+^6-3(n-2)(n-1)q^2r_+^{8-2n}}{12\pi (n-1)r_+(r_+^2+k\alpha )^2}. \end{aligned}$$
(25)

Substituting Eq. (18) into Eq. (25), one can find the expression for \(P\) as

$$\begin{aligned} P&= \frac{n-1}{48\pi }\left[ \frac{12\pi T}{r_+}+\frac{24k\pi \alpha T}{r_+^3}+\frac{12k^2\pi \alpha ^2T}{r_+^5}+\frac{3k(2-n)}{r_+^2}\right. \nonumber \\&+\left. \frac{3k^2\alpha (4-n)}{r_+^4}-\frac{k^3(n-6)\alpha ^2}{r_+^6}+3(n-2)q^2r_+^{2-2n}\right] .\nonumber \\ \end{aligned}$$
(26)

We can identify the specific volume \(v\) as

$$\begin{aligned} v=\frac{4r_+}{n-1}. \end{aligned}$$
(27)

Then Eq. (26) can be transformed into

$$\begin{aligned}&P=\frac{T}{v}+\frac{32kT\alpha }{(n-1)^2v^3}+ \frac{256k^2T\alpha ^2}{(n-1)^4v^5}-\frac{k(n-2)}{(n-1)\pi v^2}\nonumber \\&\quad -\frac{16k^2(n-4)\alpha }{(n-1)^3\pi v^4}-\frac{256k^3(n-6)\alpha ^2}{3(n-1)^5\pi v^6}+\frac{16^{n-2}(n-2)q^2}{\pi (n-1)^{2n-3}v^{2n-2}}.\nonumber \\ \end{aligned}$$
(28)

The possible critical point should satisfy the following conditions:

$$\begin{aligned}&\frac{\partial P}{\partial v}=0,\end{aligned}$$
(29)
$$\begin{aligned}&\frac{\partial ^2 P}{\partial v^2}=0. \end{aligned}$$
(30)

Firstly, we would focus on the spherical case corresponding to \(k=1\). The equation of state reads

$$\begin{aligned} P&= \frac{T}{v}\!+\!\frac{32T\alpha }{(n-1)^2v^3}\!+\! \frac{256T\alpha ^2}{(n-1)^4v^5}\!-\!\frac{(n-2)}{(n-1)\pi v^2}\nonumber \\&-\frac{16(n\!-\!4)\alpha }{(n\!-\!1)^3\pi v^4}\!-\!\frac{256(n\!-\!6)\alpha ^2}{3(n\!-\!1)^5\pi v^6} \!+\!\frac{16^{n-2}(n-2)q^2}{\pi (n-1)^{2n-3}v^{2n-2}}.\nonumber \\ \end{aligned}$$
(31)

When \(q=0,n=6\), Eqs. (29) and (30) can be analytically solved and the corresponding physical quantities can be obtained as

$$\begin{aligned} T_c=\frac{1}{\pi \sqrt{5\alpha }},\;v_c=\frac{4\sqrt{\alpha }}{\sqrt{5}},\;P_c=\frac{17}{200\pi \alpha },\;\frac{P_cv_c}{T_c}=\frac{17}{50}.\nonumber \\ \end{aligned}$$
(32)

We can see clearly that the critical temperature is inversely proportional to \(\sqrt{\alpha }\), while the critical specific volume is proportional to it. The critical pressure is inversely proportional to \(\alpha \). However, the ratio \(\frac{P_cv_c}{T_c}\) is independent of the parameter \(\alpha \). Our results demonstrate again that \(P\)–\(V\) criticality may exist even in the uncharged case. That may be attributed to the effect of higher derivative terms of curvature.

When \(q\ne 0,n=6\), one can obtain the corresponding physical quantities at the critical point as listed in Table 1 by solving Eqs. (29) and (30) numerically. From Table 1, one can find that there exists only one critical point for all the cases studied. The physical quantities at the critical point \(T_c, v_c,P_c\) depend on both the charge and the parameter \(\alpha \), which is related to the second and the third order Lovelock coefficients. With the increasing of \(\alpha \) or \(q\), both \(T_c\) and \(P_c\) decrease, while \(v_c\) increases. However, the ratio \(\frac{P_cv_c}{T_c}\) decreases with \(\alpha \) but increases with \(q\).

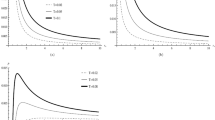
Table 1 Critical values for \(k=1,n=6,\beta \rightarrow \infty \)
Full size table

To learn about \(P\)–\(V\) criticality behavior more intuitively, we plot the \(P\)–\(v\) diagram in Fig. 1. When the temperature is less than the critical temperature \(T_c\), the isotherm can be divided into three branches. Both the large radius branch and the small radius branch are stable, corresponding to a positive compression coefficient, while the medium radius branch is unstable, corresponding to a negative compression coefficient. The phase transition between the small black hole and the large black hole is analogous to the van der Waals liquid–gas phase transition. Figure 1a–c, and d show the impact of the charge on \(P\)–\(V\) criticality, while Fig. 1c, e, and f show the effect of \(\alpha \). The comparisons are in accord with the analytical results in Table 1. We also plot both the two-dimensional and the three-dimensional Gibbs free energy graph for \(q=0,n=6\) in Fig. 2 and for the case \(q=1,n=6\) in Fig. 3. Below the critical temperature, the Gibbs free energy graphs display the classical swallow tail behavior implying the occurrence of the first order phase transition. Above the critical temperature, there is no swallow tail behavior.

Fig. 1
figure 1

\(P\) vs. \(v\) for a \(n=6,\alpha =1,q=0\), b \(n=6,\alpha =1,q=0.5\), c \(n=6,\alpha =1,q=1\), d \(n=6,\alpha =1,q=2\), e \(n=6,\alpha =0.5,q=1\) and f \(n=6,\alpha =2,q=1\)

Full size image
Fig. 2
figure 2

a \(G\) vs. \(T\) for \(k=1, n=6,\alpha =1,q=0\), “\(P=0.015<P_c\), blue curve”, “\(P=0.02<P_c\), black curve”, “\(P=P_c=0.02706\), red curve”, “\(P=0.04>P_c\), purple curve” b \(G\) vs. \(P\) and \(T\) for \(k=1, n=6,\alpha =1,q=0\)

Full size image
Fig. 3
figure 3

a \(G\) vs. \(T\) for \(k=1, n=6,\alpha =1,q=1\), “\(P=0.015<P_c\), blue curve”, “\(P=0.02<P_c\), black curve”, “\(P=P_c=0.02653\), red curve”, “\(P=0.04>P_c\), purple curve” and b \(G\) vs. \(P\) and \(T\) for \(k=1, n=6,\alpha =1,q=1\)

Full size image

Secondly, we would discuss the \(k=0\) case corresponding to Ricci flat topology. The equation of state reads

$$\begin{aligned} P=\frac{T}{v}+\frac{16^{n-2}(n-2)q^2}{\pi (n-1)^{2n-3}v^{2n-2}}. \end{aligned}$$
(33)

For \(n=6\), utilizing Eq. (33), one can obtain

$$\begin{aligned} \frac{\partial P}{\partial v}=-\frac{T}{v^2}-\frac{524288q^2}{390625\pi v^{11}}, \end{aligned}$$
(34)

which is always negative for nontrivial temperature. So there would be no \(P\)–\(V\) criticality for \(k=0\).

Thirdly, we would investigate the \(k=-1\) case corresponding to hyperbolic topology. The equation of state reads

$$\begin{aligned}&P=\frac{T}{v}-\frac{32T\alpha }{(n-1)^2v^3}+\frac{256T\alpha ^2}{(n-1)^4v^5}+\frac{(n-2)}{(n-1)\pi v^2}\nonumber \\&\quad -\frac{16(n-4)\alpha }{(n-1)^3\pi v^4}+\frac{256(n-6)\alpha ^2}{3(n-1)^5\pi v^6} +\frac{16^{n-2}(n-2)q^2}{\pi (n-1)^{2n-3}v^{2n-2}}.\nonumber \\ \end{aligned}$$
(35)

Similarly, when \(q=0,n=6\), Eqs. (29) and (30) can be analytically solved and the corresponding physical quantities can be obtained as

$$\begin{aligned} T_c=\frac{1}{2\pi \sqrt{\alpha }},\;v_c=\frac{4\sqrt{\alpha }}{5},\;P_c=\frac{5}{8\pi \alpha },\;\frac{P_cv_c}{T_c}=1. \end{aligned}$$
(36)

When \(q\ne 0,n=6\), one can obtain the numerical solutions of Eqs. (29) and (30) as listed in Table 2. These results are quite different from those in previous literature which demonstrated that \(P\)–\(V\) criticality only exists in the \(k=1\) case for topological black holes in both Einstein gravity and Gauss–Bonnet gravity [31, 40].

Table 2 Critical values for \(k=-1,n=6,\beta \rightarrow \infty \)
Full size table

To gain an intuitive picture, we plot the \(P\)–\(v\) diagram in Fig. 4, which shows strange behaviors different from van der Waals liquid–gas phase transition. The isotherm at the critical temperature is quite similar to the van der Waals liquid–gas system. However, for the uncharged case in Fig. 4a, the isotherms below or above the critical temperature both behave as the coexistence phase which is similar to the behaviors of van der Waals liquid–gas system below the critical temperature. For the charged case in Fig. 4b, the “phase transition” picture is quite the reverse of van der Waals liquid–gas phase transition. Above the critical temperature the behavior is “van der Waals like” while the behavior is “ideal gas like” below the critical temperature. This process is achieved by lowering the temperature rather than increasing the temperature. We also plot the Gibbs free energy in Fig. 5 and “swallow tail” behavior can be observed.

Fig. 4
figure 4

\(P\) vs. \(v\) for a \(k=-1, n=6,\alpha =1,q=0\), b \(k=-1, n=6,\alpha =1,q=1\)

Full size image
Fig. 5
figure 5

\(G\) vs. \(T\) for a \(k=-1, n=6,\alpha =1,q=0\), “\(P=0.15<P_c\), blue curve”, “\(P=P_c=0.19894\), red curve”, “\(P=0.24>P_c\), black curve” and b \(k=-1, n=6,\alpha =1,q=1\), “\(P=0.25<P_c\), blue curve”, “\(P=P_c=0.26507\), red curve”, “\(P=0.29>P_c\), black curve”, “\(P=0.32>P_c\), purple curve”

Full size image

The results above are so strange that motivates us to check whether they are physical. The non-negative definiteness of the entropy demands that

$$\begin{aligned} \frac{r_+^4}{n-1}+\frac{2kr_+^2\alpha }{n-3}+ \frac{k^2\alpha ^2}{n-5}\ge 0. \end{aligned}$$
(37)

In fact, when \(n=6\), the L.H.S. of the above inequality can be obtained by utilizing Eq. (27) as

$$\begin{aligned} \frac{125v^4}{256}-\frac{25v^2\alpha }{24}+\alpha ^2. \end{aligned}$$
(38)

Denoting \(v^2\) as \(x\), one can consider the equation

$$\begin{aligned} \frac{125x^2}{256}-\frac{25\alpha x}{24}+\alpha ^2=0, \end{aligned}$$
(39)

with the discriminant

$$\begin{aligned} \Delta =\left( \frac{25\alpha }{24}\right) ^2-4\times \alpha ^2\times \frac{125}{256}=-\frac{125\alpha ^2}{144}. \end{aligned}$$
(40)

Note that, for any nontrivial value of \(\alpha \), the discriminant of Eq. (39) is always negative, implying that the values of entropy are always positive for any specific volume \(v\).

4 Inclusion of the nonlinear electrodynamics

In this section, we would like to take into account the effect of nonlinear electrodynamics to complete the analysis of topological AdS black holes in Lovelock–Born–Infeld gravity.

Utilizing Eqs. (13) and (18), Eq. (14) can be rewritten as

$$\begin{aligned} P&= \frac{T}{v}+\frac{32kT\alpha }{(n-1)^2v^3}+ \frac{256k^2T\alpha ^2}{(n-1)^4v^5}-\frac{k(n-2)}{(n-1)\pi v^2}\nonumber \\&-\frac{16k^2(n-4)\alpha }{(n-1)^3\pi v^4}-\frac{256k^3(n-6)\alpha ^2}{3(n-1)^5\pi v^6} \nonumber \\&-\frac{\beta ^2}{4\pi }\left\{ 1-\sqrt{1+\frac{2^{4n-5}(n-2)(n-1)q^2 [(n-1)v]^{2-2n}}{\beta ^2}}\right\} .\nonumber \\ \end{aligned}$$
(41)

Similarly, we would discuss the \(k=1\) case corresponding to spherical topology first. The equation of state reads

$$\begin{aligned} P&= \frac{T}{v}+\frac{32T\alpha }{(n-1)^2v^3}+\frac{256T\alpha ^2}{(n-1)^4v^5}-\frac{(n-2)}{(n-1)\pi v^2}\nonumber \\&-\frac{16(n-4)\alpha }{(n-1)^3\pi v^4}-\frac{256(n-6)\alpha ^2}{3(n-1)^5\pi v^6} \nonumber \\&-\frac{\beta ^2}{4\pi }\left\{ 1-\sqrt{1+\frac{2^{4n-5}(n-2)(n-1)q^2[(n-1)v]^{2-2n}}{\beta ^2}}\right\} .\nonumber \\ \end{aligned}$$
(42)

One can obtain the corresponding physical quantities at the critical point as listed in Table 3 by numerically solving Eqs. (29) and (30) for the case \(n=6\). As is shown, the physical quantities at the critical point \(T_c, v_c,P_c\) depend on the charge, the Lovelock coefficient \(\alpha \), and the Born–Infeld parameter \(\beta \). With the increasing of \(\alpha \) or \(q\), both \(T_c\) and \(P_c\) decrease while \(v_c\) increases. However, the ratio \(\frac{P_cv_c}{T_c}\) decreases with \(\alpha \) but increases with \(q\). These observations are similar to the limit case \(\beta \rightarrow \infty \). With the increasing of \(\beta \), \(T_c\), \(P_c\) decrease while \(v_c\) and the ratio \(\frac{P_cv_c}{T_c}\) increase. However, only slight differences can be observed concerning the impact of nonlinear electrodynamics. That may be attributed to the parameter region we choose. Readers who are interested in the “Schwarzschild like” behavior of Born–Infeld black holes can read the interesting paper Ref. [32]. For an intuitive understanding, we plot the \(P\)–\(v\) diagram in Fig. 6a and show the effect of the parameter \(q\) and \(\alpha \) in Fig. 7.

Table 3 Critical values for different dimensions for \(k=1,n=6\)
Full size table
Fig. 6
figure 6

\(P\) vs. \(v\) for a \(k=1,n=6,\alpha =1,\beta =1,q=1\) and b \(k=-1,n=6,\alpha =1,\beta =1,q=1\)

Full size image
Fig. 7
figure 7

Isotherm at the critical temperature for a \(k=1,n=6,\beta =1,q=1\) and b \(k=1,n=6,\beta =1,\alpha =1\)

Full size image

Secondly, we would discuss the \(k=0\) case corresponding to Ricci flat topology. The equation of state reads

$$\begin{aligned}&P=\frac{T}{v} -\frac{\beta ^2}{4\pi }\nonumber \\&\quad \times \left\{ 1-\sqrt{1+\frac{2^{4n-5}(n-2)(n-1)q^2 [(n-1)v]^{2-2n}}{\beta ^2}}\right\} .\nonumber \\ \end{aligned}$$
(43)

There would be no \(P\)–\(V\) criticality because \(P\) monotonically decreases with \(v\).

Thirdly, we would discuss the \(k=-1\) case corresponding to hyperbolic topology. The equation of state reads

$$\begin{aligned} P&= \frac{T}{v}-\frac{32T\alpha }{(n-1)^2v^3}+ \frac{256T\alpha ^2}{(n-1)^4v^5}+\frac{(n-2)}{(n-1)\pi v^2}\nonumber \\&-\frac{16(n-4)\alpha }{(n-1)^3\pi v^4}+\frac{256(n-6)\alpha ^2}{3(n-1)^5\pi v^6} \nonumber \\&-\frac{\beta ^2}{4\pi }\left\{ 1\!-\!\sqrt{1+\frac{2^{4n-5} (n\!-\!2)(n\!-\!1)q^2[(n-1)v]^{2-2n}}{\beta ^2}}\right\} \!.\nonumber \\ \end{aligned}$$
(44)

Numerical solutions of Eqs. (29) and (30) are listed in Table 4 and we also plot the \(P\)–\(v\) diagram in Fig. 6b, in which a similar strange behavior is also observed. Note that the entropy analysis also holds because the entropy in Eq. (17) is independent of \(\beta \). So we would not repeat the analysis here.

Table 4 Critical values for different dimensions for \(k=-1,n=6\)
Full size table

5 Conclusions

Topological AdS black holes in Lovelock–Born–Infeld gravity are investigated in the extended phase space. The black hole solutions are reviewed while their thermodynamics is further explored in the extended phase space. We calculate the entropy by integration and find that the result in the previous literature [18] was incomplete. Treating the cosmological constant as pressure, we rewrite the first law of thermodynamics for the specific case in which the second order and the third order Lovelock coefficients are related by the Lovelock coefficient \(\alpha \). The quantity conjugated to the Lovelock coefficient and the Born–Infeld parameter, respectively, are calculated. Comparing our results of the above quantities with those in previous literature of Gauss–Bonnet black holes [40], we find that there exist extra terms due to third order Lovelock gravity. In order to make the phase transition clearer, the Gibbs free energy is also calculated.

To figure out the effect of third order Lovelock gravity on \(P\)–\(V\) criticality, a detailed analysis of the limit case \(\beta \rightarrow \infty \) has been performed. Since the entropy is convergent only when \(n>5\), our investigation is carried out in the case of \(n=6\), corresponding to the seven-dimensional black holes. It is shown that, for the spherical topology, \(P\)–\(V\) criticality exists even when \(q=0\). The critical physical quantities can be analytically solved and they vary with the parameter \(\alpha \). However, the ratio of \(\frac{P_cv_c}{T_c}\) is independent of the parameter \(\alpha \). Our results demonstrate again that the charge is not an indispensable condition of \(P\)–\(V\) criticality. It may be attributed to the effect of higher derivative terms of the curvature because a similar phenomenon was also found for Gauss–Bonnet black holes [40]. For \(q\ne 0\), it is shown that the physical quantities at the critical point, \(T_c, v_c,P_c\), depend on both the charge and the parameter \(\alpha \). With the increasing of \(\alpha \) or \(q\), both \(T_c\) and \(P_c\) decrease while \(v_c\) increases. However, the ratio \(\frac{P_cv_c}{T_c}\) decreases with \(\alpha \) but increases with \(q\). Similar behaviors as for the van der Waals liquid–gas phase transition can be observed in the \(P\)–\(v\) diagram and the classical swallow tail behaviors can be observed in both the two-dimensional and the three-dimensional graph of the Gibbs free energy. These observations indicate that a phase transition between small black holes and large black holes takes place when \(k=1\). For \(k=0\), no critical point can be found and there would be no \(P\)–\(V\) criticality. Interesting findings occur in the case \(k=-1\), in which positive solutions of critical points are found for both the uncharged and the charged case. However, the \(P\)–\(v\) diagram is very strange. For the uncharged case, the isotherms below or above the critical temperature both behave as the coexistence phase which is similar to the behaviors of the van der Waals liquid–gas system below the critical temperature. For the charged case, the “phase transition” picture is quite the reverse of the van der Waals liquid–gas phase transition. Above the critical temperature the behavior is “van der Waals like” while the behavior is “ideal gas like” below the critical temperature. This process is achieved by lowering the temperature rather than increasing the temperature. To check whether these findings are physical, we perform an analysis on the non-negative definiteness condition of the entropy. It is shown that, for any nontrivial value of \(\alpha \), the entropy is always positive for any specific volume \(v\). We relate the findings in the case \(k=-1\) with the peculiar property of third order Lovelock gravity. Because the entropy in third order Lovelock gravity consists of extra terms which are absent in the Gauss–Bonnet black holes, the critical points satisfy the constraint of non-negative definiteness condition of the entropy. We also check the Gibbs free energy graph and “swallow tail” behavior can be observed.

Moreover, the effect of nonlinear electrodynamics is included in our work. Similar observations are made as the limit case \(\beta \rightarrow \infty \) and only slight differences can be observed when we choose different values of \(\beta \). That may be attributed to the parameter region we choose. More interesting findings concerning “Schwarzschild like” behaviors can be found in the previous literature [32] and we will not repeat them here, because our main motivation is to investigate the impact of third order Lovelock gravity on \(P\)–\(V\) criticality in the extended phase space.