Oscillator-based optimization: design, emulation, and implementation

Abstract

The emergence of digital computers has profoundly reshaped our interactions with technology and the processing of information. Despite excelling in data processing and arithmetics, these computers face limitations in tackling complex nondeterministic-polynomial (NP) problems. In response, researchers have started searching for new computational paradigms that possess the natural tendency of solving these problems. Oscillator-based optimizers are one such paradigm, where the idea is to exploit the parallelism of oscillators networks in order to efficiently solve NP problems. This involves a process of mapping a given optimization task to a quadratic unconstrained binary optimization program and then mapping the resulting program onto an inter-oscillator coupling circuit encoding its coefficients. This paper presents a comprehensive approach to constructing oscillator-based optimizers, offering both the rationale for employing oscillator networks and formulas for linking optimization coefficients to inter-oscillator coupling. Here, we cover most aspects of oscillator-based optimization starting from the design of the network up to its technical implementation. Moreover, we provide a platform-independent wave digital algorithm, which allows for emulating our network’s behavior in a highly parallel fashion.

Graphical Abstract

1 Introduction

Digital computers, based on the von Neumann architecture [1], excel at many things such as complex calculations and data processing. However, when it comes to optimization there remain some challenges when dealing with certain problems, such as nondeterministic-polynomial (NP) problems. These are optimization problem that can not be efficiently solved in polynomial time using classical algorithmic approaches [2]. As a result, researchers have explored alternative computational paradigms, such as quantum computers [3, 4] and optical computers [5, 6], which hold promise in tackling these computationally difficult tasks.

A more recent approach for dealing with NP problems, lies in mapping them onto “the energy” of a network of electrical oscillators and allowing the network to run and naturally solve the problem. Here, the underlying assumption is that the network has the natural tendency of minimizing its “energy” consumption, although the term energy is not clearly defined but is to be understood in terms of a “generalized energy” such as the one appearing in Lyapunov’s direct method [7]. An optimization program based on a network of electrical oscillators is what we refer to as oscillator-based optimization in this paper. In literature, these types of machines are usually referred to as oscillator-based Ising machines for reasons that we explain later on. To our utmost knowledge, the notion of oscillator-based optimizers has been first presented in the preprint of Wang and Roychowdury [8]. In their published works [9, 10], the authors discuss the functionality of LC-oscillator networks as optimizers using the theory of phase macromodels [11], which, in the case of LC-oscillators, degenerate to the well-established Kuramoto model [12]. This led to a series of publications, where different authors have attempted to explain the functionalities of oscillator-based optimizers in more detail using different phase models [13,14,15]. Interestingly, it has also been shown that phase macromodels can be reliably used for simulated annealing [14,15,16,17]. Over the years, many hardware implementations of oscillator-based optimizers have emerged of which we can only list a few [13, 18,19,20,21]. Most implementations are based on ring oscillators due to their simplicity and CMOS-compatibility [22, 23].

The oscillator-based optimization that we deal with in this work can be explained in three steps:

• 1. A given optimization task is mapped onto a quadratic unconstrained binary optimization problem (QUBO):

  $$\begin{aligned} \min _{\varvec{x}} \, \varvec{x}^{\textrm{T}} {\varvec{Q}} \varvec{x} + \varvec{r}^{\textrm{T}} \varvec{x}\,, \quad \text {with} \quad {\varvec{Q}} = {\varvec{Q}}^{\textrm{T}} \,. \end{aligned}$$

  (1a)

  Here $x_{\nu }\in \{0,1\}$ are binary optimization variables resulting from the solution of the problem, ${\varvec{Q}} \in {\mathbb {R}}^{n \times n}$ and $\varvec{r} \in {\mathbb {R}}^{n}$ represent a matrix and vector of optimization coefficients, respectively.

• 2. The QUBO is reformulated in terms of the so-called Ising Hamiltonian:

  $$\begin{aligned} H(\varvec{s}) = -\varvec{s}^{\textrm{T}} {\varvec{J}} \varvec{s} - \varvec{h}^{\textrm{T}}\varvec{s} \,, \quad \quad \text {with} \quad {\varvec{J}} = {\varvec{J}}^{\textrm{T}}\,, \end{aligned}$$

  (1b)

  where $s_{\nu } \in \{\pm 1\}$ are equivalent binary optimization variables that are usually referred to as spins. Here, the bijective mapping,

  $$\begin{aligned} \varvec{s} = 2\varvec{x} - {\varvec{\mathbbm {1}}}\quad \Leftrightarrow \quad \varvec{x} = [\varvec{s} - {\varvec{\mathbbm {1}}}]/2 \,, \end{aligned}$$

  (1c)

  where ${\varvec{\mathbbm {1}}}$ denotes a vector of ones, allows for reformulating every QUBO (1a) as a minimization of (1b) with:

  $$\begin{aligned} {\varvec{J}} = -{\varvec{Q}} \quad \text {and} \quad \varvec{h} = 2{\varvec{Q}} {\varvec{\mathbbm {1}}}- 2\varvec{r}\,. \end{aligned}$$

  (1d)

  In the following, we refer to the entries of ${\varvec{Q}}$ as quadratic optimization coefficients and the entries of $\varvec{h}$ as linear optimization coefficients.

• 3. The optimization coefficients are mapped onto the couplings of an oscillator network. The optimizer then runs and solves the problem. The solution can be decoded from the phase configuration that the network settles to. A (relative) phase shift of 0 ($\pi$) corresponds to $s=1$ ($s=-1$).

In a previous work [15], we have discussed how general QUBOs, whose formulations are far more sophisticated than (1a), can be mapped onto the Ising Hamiltonian (1b). Together with the works of [24,25,26,27], which discuss the mapping of NP-problems onto QUBOs, steps 1 and 2 of the oscillator-based optimization program can be achieved. The third step assumes the existence of an oscillator network with the natural tendency of minimizing the Ising Hamiltonian (1b); this is also the reason why oscillator-based optimizers are referred to as Ising machines [9, 10].

The aim of this paper is to extensively discuss the third step of oscillator-based optimization. This involves the design of an oscillator network, which naturally tends to minimize the Ising Hamiltonian (1b). Contrary to most works, which attempt to explain the functionality of oscillator-based optimizers based on phase models, we explain their functionality based on the concepts of synchronization and power minimization. Our approach is motivated by the fact that phase models only represent an approximation of the network’s actual dynamics [28], and while they enhance our understanding of network dynamics, they do not explain the functionality of oscillator-based optimizers on a circuit level. Furthermore, our approach will allow us to draw a clear relation between the optimization coefficients of a QUBO problem and the inter-oscillator coupling circuit that is to be used. Another major advantage of our study is that we cover the entire third step of oscillator-based optimization. Most works on literature only partially cover this step by either discussing the modeling, hardware implementation, or mapping, separately. Therefore a clear relation between theory and practice has never been drawn in one work.

Besides modeling and implementation, a large portion of our work deals with the emulation of the proposed oscillator-based optimizer. Here, we make use of the wave digital (WD) concept as a powerful emulation tool [29,30,31]. A major benefit of WD algorithms is the fact that they can be massively parallelized, when dealing with structurally identical circuits [16, 32,33,34,35,36]. This is especially beneficial for oscillator-based optimizers, as they are composed of many oscillators of the same topology. Thus, we can exploit the concept of vector-valued wave digital models in order to efficiently emulate large networks on any platform in a highly parallel fashion.

In total, the main contributions of this paper can be summarized as follows:

I:

We give a constructive guide for building oscillator-based optimizers;

II:

We give a physical justification for why oscillator networks can be utilized as optimizers;

III:

We explain the relationship between the Ising Hamiltonian (1b) and the synchronization tendencies of oscillator networks. Here, we also present a formula for mapping the coefficients of the Ising Hamiltonian onto the inter-oscillator coupling;

IV:

We provide a compact electrical model for our oscillator-based optimizers;

V:

We derive a massively parallel WD algorithm for emulating our oscillator-based optimizer with an arbitrary number of oscillators and inter-oscillator couplings; and

VI:

We provide a technical blueprint of our in-house optimizer, based on the theoretical model discussed in this work.

The remainder of this paper is divided into three sections. Section 2 discusses the design of oscillator-based optimizers (I–IV). Section 3 derives a wave digital algorithm for our proposed oscillator-based optimizer (V). Section 4 presents the technical implementation of our in-house optimizer (VI). Finally Sect. 5 summarizes the contributions of our work and provides an outlook on future research in this context.

2 Designing an oscillator-based optimizer

This section establishes the theoretical foundation for the oscillator-based optimizer, whose implementation is discussed in Sect. 4. We start by introducing our oscillator model of choice, which constitutes the core of our network. To understand how optimization problems can be mapped to an oscillator network, we then discuss general synchronization tendencies of coupled oscillators. Furthermore, we explain how (necessary) optimization constraints can be set. Finally, we present an electrical model that serves as a compact description for our oscillator-based optimizer.

2.1 Oscillator model

Our oscillator of choice is the FitzHugh-Nagumo oscillator (FNO) [37] depicted in Fig. 1. From a theoretical point of view, this oscillator has the advantage that it can be implemented in hardware. Furthermore, it only contains one active nonlinear component that is responsible for generating self-sustaining oscillations, which makes the overall oscillator accessible from a mathematical point of view.

Fig. 1

Top: circuit schematic of the FitzHugh-Nagumo oscillator. Bottom: (i, u)-curve of the cubic nonlinearity $i_{\textrm{n}}(u)$ in the blue dashed box

The FNO can be described by the following set of algebraic-differential equations:

$$\begin{aligned} C \frac{\textrm{d}u}{\textrm{d}t}&= i_{\textrm{p}}(u) - i - i_{\textrm{n}}(u) - i_{\textrm{c}} \,, \end{aligned}$$

(2a)

$$\begin{aligned} L \frac{\textrm{d}i}{\textrm{d}t}&= u - R_{0} i \,, \end{aligned}$$

(2b)

$$\begin{aligned} R_{\textrm{n}} i_{\textrm{n}}(u)&= u^3/[3U_{0}^2] - u \,, \end{aligned}$$

(2c)

$$\begin{aligned} R_{\textrm{p}}i_{\textrm{p}}(u)&= e_{\textrm{p}}-u \,. \end{aligned}$$

(2d)

Here, u and i denote the capacitor voltage and inductor current, respectively. The electrical components $R_{0}$, L, and C constitute the oscillator’s RLC-tank. The current $i_{\textrm{c}}$ is an external coupling current that results from the oscillator’s interaction with other circuits/oscillators. The cubic nonlinearity $i_{\textrm{n}}(u)$, with the fitting parameters $R_{\textrm{n}}$ and $U_{0}$, represents an active electrical component with a negative differential resistance $-R_{\textrm{n}}<0$ that is used to maintain a constant energy landscape in order to generate self-sustaining oscillations. The activeness of the component can be verified from its (i, u)-curve, which is depicted on the bottom of Fig. 1. Finally, the perturbation voltage source $e_{\textrm{p}}$ with the internal resistance $R_{\textrm{p}}$ is used to set optimization constraints, as we explain in Sect. 2.4. Note, the oscillator parameters given in Table 1 lead to an oscillation period of $T_{0} \approx 11.7\,\textrm{ms}$.

Table 1 FitzHugh-Nagumo oscillator simulation parameters

Fig. 2

Graphical representation of two coupled oscillators, which are represented by the gray dashed boxes titled ${\mathcal {N}}_{1}$ and ${\mathcal {N}}_{2}$. Left: two oscillators coupled over a resistor with the conductance $G_{12}^{-}$, tend to synchronize in-phase through their interaction. Right: using the same type of coupling as the left side but inverting one oscillator output leads to anti-phase synchronization

2.2 Synchronization tendency of coupled oscillators

Now that we have covered our oscillator model, we make use of it to demonstrate a general tendency observed in resistively coupled oscillator networks. To this end, consider two oscillators ${\mathcal {N}}_{1}$ and ${\mathcal {N}}_{2}$ with the outputs voltages $u_{1}$ and $u_{2}$, respectively. Let us assume the oscillators to be coupled over a resistor $G_{12}^{-}$, as depicted on the left side of Fig. 2. In general, the conductance $G_{12}^{-}$ is proportional to the coupling strength between ${\mathcal {N}}_{1}$ and ${\mathcal {N}}_{2}$. If the coupling strength is chosen to be sufficiently strong, then the oscillators will always interact and have the tendency to synchronize, see the bottom left plot in Fig. 2. This general tendency is always present between coupled nonlinear oscillators regardless of the number of oscillators within the network. To our utmost knowledge, there is no formal mathematical proof showing the necessity of this behavior. However, we can justify it from a physical perspective: Synchronization minimizes power dissipation. To understand this statement, let us write out the equations governing the electrical coupling depicted on the left side of Fig. 2:

$$\begin{aligned} i_{12}^{-} = G_{12}^{-} v_{12}^{-} \,, \quad \text {with} \quad v_{12}^{-} = u_{1} - u_{2} \,. \end{aligned}$$

(3a)

The instantaneous (dissipated) power reads:

$$\begin{aligned} p_{12}(t) = v_{12}^{-} i_{12}^{-} = G_{12}^{-} [u_{1} - u_{2}]^2 \,. \end{aligned}$$

(3b)

As can be seen from (3b), the instantaneous power p(t) is proportional to the squared voltage difference $[v_{12}^{-}]^2$. Therefore, we conclude that p(t) is minimized when $[v_{12}^{-}]^2$ is minimized, i.e. for $u_{1}=u_{2}$, the case where the both oscillators are synchronized. Overall, this lead us to the hypothesis that our oscillator network has the natural tendency of minimizing dissipated power by minimizing the amount of interaction (interchanged power) between oscillators. In physics, such tendencies have been hinted at for a long time. The tendency of a complex network to minimize a certain energy functional is referred to as the principle of least energy dissipation [38,39,40], which was first postulated by Onsager [41].

Fig. 3

Coupling circuit for encoding optimization coefficients. The dashed gray boxes ${\mathcal {N}}_{\mu }$ and ${\mathcal {N}}_{\nu }$ represent two arbitrary adjacent oscillators with the output voltages $u_{\mu }$ and $u_{\nu }$, respectively. The top coupling circuit can be used to give a preference for anti-phase synchronization. The bottom coupling circuit can be used to give a preference for in-phase synchronization

It is noteworthy to state that the network’s tendency to minimize power dissipation greatly depends on the magnitude of the coupling conductance $G_{12}^{-}$. For small values of $G_{12}^{-}$, the oscillator network may not minimize power dissipation due to the (already) minimal interaction caused by the high resistance. Hence, our hypothesis only holds, when $G_{12}^{-}$ is chosen in a suitable manner. We cover this aspect again later on.

2.3 Mapping quadratic unconstrained binary optimization problems to synchronization tendencies

The state of synchronization only encodes the statement that two oscillators have reached a state of ”agreement”. To encode binary optimization problems, such as a general QUBO (1a), we also require the opposite, a state of ”disagreement”. The simplest way to encode the latter is by letting one oscillator experience a perspective change. If, for example, ${\mathcal {N}}_{1}$ only perceives the inverted output of ${\mathcal {N}}_{2}$, then ${\mathcal {N}}_{1}$ would synchronize with the inverted signal, again, due to principle of least energy dissipation [41]. This idea is depicted on the right side of Fig. 2. The bottom plot shows the oscillators asymptotically assuming an anti-phase configuration, which corresponds to a state of ”disagreement”. With reference to equations (1a) 1b, we associate agreement with $x=1$ ($s=1$) and disagreement with $x=0$ ($s=-1$).

2.3.1 Quadratic optimization coefficients

Up to this point, we have only discussed how oscillators can be brought to a phase of agreement or disagreement. However, when mapping optimization problems onto oscillator networks, we have no prior knowledge about the states resulting from the solution of the encoded problem. Instead, we must draw a relation between the coefficients of the problem and the tendencies of the network. To this end, let us consider a version of (1b) with two coupled spins and no linear optimization coefficients ($\varvec{h}={\textbf{0}}$):

$$\begin{aligned} H(\varvec{s}) = - \left[ \!\begin{array}{cc} s_{1}&s_{2} \end{array}\!\right] \left[ \!\begin{array}{cc} 0 &{} J_{12} \\ J_{12} &{} 0 \end{array}\!\right] \left[ \!\begin{array}{c} s_{1} \\ s_{2} \end{array}\!\right] \,. \end{aligned}$$

(4a)

By varying the coupling coefficient $J_{12}$, we obtain the two implications:

$$\begin{aligned} J_{12} < 0 \quad \Rightarrow \quad \arg \left\{ \min _{\varvec{s}} \{ H(\varvec{s}) \} \right\}&= \pm [1, 1]^{\textrm{T}} \,, \end{aligned}$$

(4b)

$$\begin{aligned} J_{12} > 0 \quad \Rightarrow \quad \arg \left\{ \min _{\varvec{s}} \{ H(\varvec{s}) \} \right\}&= \pm [1, -1]^{\textrm{T}} \,. \end{aligned}$$

(4c)

Hence, a negative coupling coefficient $J_{12} < 0$ implies that the minimum of $H(\varvec{s})$ is achieved, when the spins $s_{1}$ and $s_{2}$ have the same value. Meanwhile, a positive coupling coefficient $J_{12}>0$ implies that the minimum of $H(\varvec{s})$ is achieved, when the spins have different values. In the context of coupled oscillators, this means that $J_{12}>0$ and $J_{12}<0$ should ideally correspond to anti- and in-phase synchronization, respectively. To promote this behavior in our oscillator network, we can actively pick between the circuits depicted in Fig. 2.

Fig. 4

Circuit for encoding linear optimization coefficients. The voltage $u_{\textrm{ref}}$ denotes the voltage of a reference oscillator ${\mathcal {N}}_{\textrm{ref}}$. The latter is (unidirectionally) resistively coupled to every oscillator ${\mathcal {N}}_{\mu }$ via a controlled voltage source

To map the value of the coefficients in addition to their polarity, we start by normalizing all coefficients $J_{\mu \nu }$, so they are in the interval $[-1,1]$. Thus, we assume in the following that $J_{\mu \nu } \in [-1;1]$, where $J_{\mu \nu } \in {\mathbb {R}}$. With reference to our earlier discussion, $J_{\mu \nu }=1$ should promote in-phase synchronization, hence we would utilize the coupling circuit on the left side of Fig. 2. Meanwhile, the opposite case $J_{\mu \nu }=-1$ should promote anti-phase synchronization, such that we would use the coupling circuit on the right side of Fig. 2. We can map coefficients in the interval $J_{\mu \nu }^2 < 1$ by considering the superposition of the two coupling schemes depicted in Fig. 2, i.e. by utilizing the parallel connection of both circuits as presented in Fig. 3. The electrical relation governing this coupling reads:

$$\begin{aligned} \varvec{i}_{\textrm{c}}&= [{\varvec{G}}^{+} + {\varvec{G}}^{-}]\varvec{u} \,,&\varvec{i}_{\textrm{c}}&= \left[ \!\begin{array}{c} i_{\textrm{c},\mu } \\ i_{\textrm{c},\nu } \end{array}\!\right] \,, \quad \varvec{u} = \left[ \!\begin{array}{c} u_{\mu } \\ u_{\nu } \end{array}\!\right] \,, \end{aligned}$$

(5a)

$$\begin{aligned} {\varvec{G}}^{+}&= \left[ \!\begin{array}{cc} 1 &{} 1 \\ 1 &{} 1 \end{array}\!\right] \frac{G_{\mu \nu }^{+}}{2} \,,&{\varvec{G}}^{-}&= \left[ \!\begin{array}{cc} 1 &{} -1 \\ -1 &{} 1 \end{array}\!\right] \frac{G_{\mu \nu }^{-}}{2} \,. \end{aligned}$$

(5b)

Here, the relation between the coupling conductances $G_{\mu \nu }^{\pm }$ and the optimization coefficients $J_{\mu \nu }$ is given by

$$\begin{aligned} G_{\mu \nu }^{\pm } = \frac{G_{\textrm{b}}}{2} {\left\{ \begin{array}{ll} 1 \mp J_{\mu \nu } \,, &{} J_{\mu \nu } \ne 0 \\ 0 \,, &{} J_{\mu \nu } = 0 \end{array}\right. } \,, \quad R_{\textrm{b}} G_{\textrm{b}} = 1 \,, \end{aligned}$$

(5c)

where $G_{\textrm{b}}=1/R_{\textrm{b}}$ is a multiplicative bias with the physical unit of a conductance. It can be used to adjust the global coupling strength between oscillators, refer to the discussion at the end of Sect. . As can be seen, the extreme cases $J_{\mu \nu }=1$ and $J_{\mu \nu }=-1$ lead to $G_{\mu \nu }^{+} = 0$ and $G_{\mu \nu }^{-}=0$, respectively. In the first case, we promote in-phase synchronization, since we effectively obtain the coupling circuit on the left side of Fig. 2. In the second case, we are promoting an anti-phase tendency, as we effectively have the coupling circuit on depicted on the right side of Fig. 2. For all values of $J_{\mu \nu }^2 <1$, we are giving a preference for one of the two synchronization states. For $J_{\mu \nu } > 0$ we are encoding a preference for in-phase synchronization:

$$\begin{aligned} J_{\mu \nu }> 0 \quad \Rightarrow \quad G_{\mu \nu }^{-} > G_{\mu \nu }^{+} \,. \end{aligned}$$

This allows more current to flow through the coupling conductances $G_{\mu \nu }^{-}$, hence giving a preference for in-phase synchronization. Evidently, in the other case, we are giving a preference for anti-phase synchronization. Thus, we have now developed a concept for mapping optimization coefficients onto the coupling circuit of our network.

2.3.2 Linear optimization coefficients

The Ising Hamiltonian (1b) contains two terms. In Sect. 2.3 we have covered how the quadratic term $\varvec{s}^{\textrm{T}}{\varvec{J}}\varvec{s}$ can be mapped onto the oscillator network at hand. In this section, we discuss, how the second term $\varvec{h}^{\textrm{T}}\varvec{s}$, sometimes referred to as the Zeeman term [24], can be mapped to the network as well. To this end, we start out by rewriting the Ising Hamiltonian (1b) as:

$$\begin{aligned} H(\varvec{s}) = \varvec{s}_{\textrm{e}}^{\textrm{T}} {\varvec{J}}_{\textrm{e}} \varvec{s}_{\textrm{e}} \,, \quad {\varvec{J}}_{\textrm{e}} = \left[ \!\begin{array}{cc} {\varvec{J}} &{} \varvec{h}/2 \\ \varvec{h}^{\textrm{T}}/2 &{} 0 \end{array}\!\right] \,, \quad \varvec{s}_{\textrm{e}} = \left[ \!\begin{array}{c} \varvec{s} \\ 1 \end{array}\!\right] \,. \end{aligned}$$

(6)

Interpreting this equation, we see that a linear term $\varvec{h}^{\textrm{T}}\varvec{s}$ can be treated just like a quadratic one in case a slack variable with a fixed value $s_{\textrm{ref}}=1$ is appended to the vector of spins $\varvec{s}$ such that:

$$\begin{aligned} \varvec{s}_{\textrm{e}} = \left[ \!\begin{array}{cc} \varvec{s}^{\textrm{T}}&s_{\textrm{ref}} \end{array}\!\right] ^{\textrm{T}} \,, \quad \text {where} \quad s_{\textrm{ref}} = 1 \,. \end{aligned}$$

In terms of our networks this means that we must expand it by one oscillator ${\mathcal {N}}_{\textrm{ref}}$ with a fixed phase and couple that oscillator to the $\mu$-th oscillator in case $h_{\mu } \ne 0$. The sign of $h_{\mu }$ determines whether we must give a preference to in- or anti-phase synchronization. This type of coupling can be realized by the coupling circuit depicted in Fig. 4, where we make use of a controlled voltage source to couple ${\mathcal {N}}_{\textrm{ref}}$ to the $\mu$-th oscillator ${\mathcal {N}}_{\mu }$. The advantage of this coupling scheme is that ${\mathcal {N}}_{\textrm{ref}}$ does not perceive any feedback or load from its coupling with the other oscillators ${\mathcal {N}}_{\mu }$. Removing feedback is important so that the phase of ${\mathcal {N}}_{\textrm{ref}}$ is kept fixed. Besides the controlled voltage source, the coupling is resistive and identical to the one in Fig. 3. Here, the coupling current $i_{\mu ,\textrm{ref}}$ in Fig.  is given by

$$\begin{aligned} i_{\mu ,\textrm{ref}} = \frac{G_{\mu ,\textrm{ref}}^{-}}{2} [u_{\mu } - u_{\textrm{ref}}] + \frac{G_{\mu ,\textrm{ref}}^{+}}{2} [u_{\mu } + u_{\textrm{ref}}] \,, \end{aligned}$$

(7a)

which is essentially identical to the coupling current in (5). The coupling conductances $G_{\mu ,\textrm{ref}}^{\pm }$ can be calculated in a similar fashion as (5c):

$$\begin{aligned} G_{\mu ,\textrm{ref}}^{\pm } = \frac{\textrm{G}_{\textrm{b}}}{2} {\left\{ \begin{array}{ll} 1 \mp h_{\mu }/2 \,, &{} h_{\mu } \ne 0 \\ 0 \,, &{} h_{\mu } = 0 \end{array}\right. } \,. \end{aligned}$$

(7b)

Here, we are implicitly working with normalized coefficients $h_{\mu } \in [-1;1]$ similar to Sect. 2.3. Note, it is important to normalize both the entries ${\varvec{J}}$ and $\varvec{h}$ by the same value. In other words, we are normalizing the entries of ${\varvec{J}}_{\textrm{e}}$ from (6). Thus, we are now able to fully map a QUBO problem of the form (1) to our oscillator network.

Fig. 5

Left: three coupled oscillators solving an optimization problem with the coefficients $J_{\mu \nu }=-1$. Center: output voltage $u_{\mu }$ of the oscillators over time. Right: dissipated power p(t) over time

2.4 Optimization constraints

The most fundamental property of QUBOs, that makes them especially difficult to deal with, is their discrete solution space. In other words, our optimization variables $x_{\nu }$ are only allowed to assume two discrete values $x_{\nu } \in \{0,1\}$. Although we have shown that two oscillators can be brought to a state of agreement or disagreement, which resembles the two discrete states of a QUBO problem, we have yet to discuss whether a network composed of more than two oscillators would also naturally (only) assume these two discrete states. In fact, since our hypothesis only states that coupled oscillators attempt to minimize dissipated power, there may be other phase configurations besides the two discrete states of agreement/disagreement that minimize the dissipated power even more.

To understand this statement, consider the network depicted on the left of Fig. 5, which presents an oscillator network composed of three oscillators. Here, the oscillators are coupled via the circuit presented in Fig. 3. The optimization task is assumed to have the coefficients $J_{\mu \nu }=-1$. This way, the coupling circuit of Fig. 3 degenerates to the one presented on the right side of Fig. 2. This type of coupling imposes all three oscillators to assume an anti-phase configuration, which, in this case, leads to a contradiction. The solution of the underlying NP problem is for two (arbitrary) oscillators to be in-phase, while the last one is in anti-phase w.r.t. the other two. The oscillator voltages $u_{\mu }$ are presented in the center of Fig. 5. Here, we see that the network is able to find the actual solution of the problem for $20\,\textrm{ms}< t < 80\,\textrm{ms}$. However, it eventually leaves this state for $t>80\,\textrm{ms}$ and assumes a three-phase configuration. To interpret this behavior, we have plotted the (overall) power,

$$\begin{aligned} p(t) = \sum _{\mu < \nu } p_{\mu \nu }(t) \,, \quad p_{\mu \nu }(t) = G_{\mu \nu }^{-} [u_{\mu }(t) + u_{\nu }(t)]^2 \,, \end{aligned}$$

(8)

dissipated by the coupling network on the right side of Fig. 5. Here, we see that the three-phase configuration ($t>110\textrm{ms}$) leads to even lower power dissipation than the solution of the underlying NP problem.

This simple example shows us one important property of oscillator-based optimizers. Even though they tend to naturally minimize the dissipated energy p(t), there is no guarantee that the minimum of p(t) coincides with the minimum of (1b). In the following subsection, we will demonstrate how we can enforce binary constraints such that the oscillators are forced to achieve either in-phase our anti-phase synchronization.

Since we have shown the general problem with performing oscillator-based optimization without binary constraints, we now shed some light on how oscillator phases can be binarized. Here, we present the general methodology for introducing this kind of constraint and present a method that can be used to check, whether the constraints are enforced effectively.

The basic idea for applying a binarization constraint is to perturb the oscillator by an external sinusoidal signal, whose frequency is approximately double that of the oscillator’s eigenfrequency. The eigenfrequency $f_{0}$ is defined as the inverse of the oscillation’s period $T_{0}$, i.e. $f_{0}=1/T_{0}$. This type of perturbation is referred to as subharmonic injection locking (SHIL) [42, 43] and has, for example, been shown to lead to bi-stable phase behavior in coupled metronomes [44] or even in general LC oscillators [43]. For relaxation-type oscillators, whose output voltages are generated by charging and discharging a capacitor, a perturbation can be achieved by injecting a source current at the node of the capacitor. In this work, we have already pre-built an external perturbation source $e_{\textrm{p}}$ into our oscillator, see Fig. 1, which can be used to inject the SHIL signal defined as:

$$\begin{aligned} e_{\textrm{SHIL}}(t) = {\hat{e}}_{\textrm{SHIL}} \sin (2\Omega _{0}t) + {\hat{e}}_{\textrm{b}} \,, \quad \Omega _{0} = 2\pi /T_{0} \,. \end{aligned}$$

(9)

Here, ${\hat{e}}_{\textrm{SHIL}}$ denotes the amplitude of the SHIL signal, while ${\hat{e}}_{\textrm{b}}$ is a bias voltage relating to the strength of the SHIL signal. Both these values must be chosen in a suitable manner in order to observe any effect.

Fig. 6

Top: perturbation voltage $e_{\textrm{p}}(t)$, which is composed of SHIL and short voltage pulses. Center: oscillator output voltage u after being perturbed by the top signal (dashed black) and a reference oscillation (blue). Bottom: output voltages $u_{\mu }$ when solving the problem depicted in Fig. 5 but with SHIL

Table 2 SHIL parameters that have been used for obtaining the results in Fig. 6

Let us now consider the results depicted in Fig. 6 based on the parameters in Table 2. The top plot shows the perturbation signal $e_{\textrm{p}}(t)$. Here, $e_{\textrm{p}}(t)$ is by a composition of the SHIL signal $e_{\textrm{SHIL}}$ defined in (9) and two short voltage pulses that are intended to demonstrate the bi-stable phase behavior. The central plot presents the oscillator’s output voltage (dashed black) against a reference signal (blue) that is perturbed by SHIL but not by the two voltage pulses. This plot illustrates the influence of SHIL on the oscillator’s output:

• 1. $t < 40\,\textrm{ms}$: When an oscillator is perturbed by SHIL but not by any other external signal, we can observe a slightly distorted version of the oscillator’s output compared to the case when it is not perturbed by SHIL, compare Figs. 2 and 6.

• 2. $40\,\textrm{ms}< t < 110\,\textrm{ms}$: When the oscillator is perturbed by an external signal, in this case a short voltage pulse, we see a phase jump of $180^{\circ }$.

• 3. $t > 110\,\textrm{ms}$: When the oscillator is, again, disturbed by a short voltage pulse, the phase of the voltage again jumps by $180^{\circ }$, such that it effectively returns to case 1.

We would like to highlight that this experiment also serves as a guideline for testing SHIL in hardware. Essentially, we can try to replicate these three cases in hardware in order to calibrate the SHIL signal for our specific setup.

Using the SHIL signal, we solved the same problem depicted in Fig. 5. Our results are presented at the bottom of Fig. 6. Here, we see that SHIL forces the oscillator network to seek out a phase configuration from the discrete solution space of the QUBO problem. Indeed, we obtain the optimal solution for the mapped problem. Thus, we conclude that SHIL can be used to enforce binary constraints on the oscillator network.

2.5 Compact electrical model

In this section, we provide a compact electrical model describing a network composed of $n+1$ oscillators solving QUBO problems of the form (1). This model serves as the fundamental for the wave digital model derived in the next section and can also be used to simulate the network with standard numerical integrators. To this end, we start by introducing the state voltage and current vector

$$\begin{aligned} \varvec{u} = \left[ \!\begin{array}{cccc} u_{1}&\dots&u_{n}&u_{\textrm{ref}} \end{array}\!\right] ^{\textrm{T}} \quad \text {and} \quad \varvec{i} = \left[ \!\begin{array}{cccc} i_{1}&\dots&i_{n}&i_{\textrm{ref}} \end{array}\!\right] ^{\textrm{T}} \end{aligned}$$

(10a)

comprising the capacitor voltages and inductor current of every oscillator, respectively. The $[n+1]$-th entry of each vector represents the quantities of the reference oscillator ${\mathcal {N}}_{\textrm{ref}}$. Hence, our network is composed of n oscillators representing the problem and one reference oscillator for implementing linear optimization coefficients. Similar to the two state vectors, we also introduce a vector of perturbation voltages and a vector of perturbation currents, given by:

$$\begin{aligned} \varvec{e}_{\textrm{p}} = e_{\textrm{p}} {\varvec{\mathbbm {1}}}\quad \text {and} \quad \varvec{i}_{\textrm{p}} = \left[ \!\begin{array}{cccc} i_{\textrm{p},1}&\dots&i_{\textrm{p},n}&i_{\textrm{p},\textrm{ref}} \end{array}\!\right] ^{\textrm{T}} \,. \end{aligned}$$

(10b)

The vector $\varvec{e}_{\textrm{p}}$ is a scaled vector of ones, because we are assuming that only one voltage source is used to perturb with an SHIL signal for the sake of efficiency. Furthermore, we introduce a vector-valued function $\varvec{i}_{\textrm{n}}(\varvec{u}) : {\mathbb {R}}^{n+1} \mapsto {\mathbb {R}}^{n+1}$, defined as:

$$\begin{aligned} \varvec{i}_{\textrm{n}}(\varvec{u}) = \left[ \!\begin{array}{cccc} i_{\textrm{n}}(u_{1})&\dots&i_{\textrm{n}}(u_{n})&i_{\textrm{n}}(u_{\textrm{ref}}) \end{array}\!\right] ^{\textrm{T}} \,. \end{aligned}$$

(10c)

This function evaluates the cubic nonlinearity (2c) for every entry of $\varvec{u}$ and returns a corresponding $[n+1]$-dimensional vector. To accommodate for all the introduced vectors, we now introduce the following parameter matrices:

$$\begin{aligned} {\varvec{C}}&= {{\,\mathrm{\varvec{\textrm{diag}}}\,}}(C_{1},\dots ,C_{n},C_{\textrm{ref}}) \,, \end{aligned}$$

(10d)

$$\begin{aligned} {\varvec{L}}&= {{\,\mathrm{\varvec{\textrm{diag}}}\,}}(L_{1},\dots ,L_{n},L_{\textrm{ref}}) \,, \end{aligned}$$

(10e)

$$\begin{aligned} {\varvec{R}}_{0}&= {{\,\mathrm{\varvec{\textrm{diag}}}\,}}(R_{0,1},\dots ,R_{0,n},R_{0,\textrm{ref}}) \,, \end{aligned}$$

(10f)

$$\begin{aligned} {\varvec{R}}_{\textrm{p}}&= {{\,\mathrm{\varvec{\textrm{diag}}}\,}}(R_{\textrm{p},1},\dots ,R_{\textrm{p},n}, R_{\textrm{p},\textrm{ref}}) \,, \end{aligned}$$

(10g)

where ${{\,\mathrm{\varvec{\textrm{diag}}}\,}}(\cdot )$ denotes the diag operator. The $\mu$-th diagonal entry of each of these matrices represents the electrical parameter of the $\mu$-th oscillator. Thus, if all oscillators are assumed to be identical, they simplify to

$$\begin{aligned} {\varvec{C}}&= C {\textbf{1}}\,,&{\varvec{L}}&= L {\textbf{1}}\,,&{\varvec{R}}_{0}&= R_{0} {\textbf{1}}\,,&{\varvec{R}}_{\textrm{p}}&= R_{\textrm{p}} {\textbf{1}}\,, \end{aligned}$$

(10h)

where ${\textbf{1}}$ denotes the unit matrix. Although not necessary, we will work with the assumption of identical oscillators in the following section. Using all introduced quantities, we can now rewrite (2) for the case of $n+1$ coupled oscillators:

$$\begin{aligned} {\varvec{C}} \frac{\textrm{d}\varvec{u}}{\textrm{d}t}&= \varvec{i}_{\textrm{p}}(\varvec{u}) - \varvec{i} - \varvec{i}_{\textrm{n}}(\varvec{u}) - \varvec{i}_{\textrm{c}} \,, \end{aligned}$$

(11a)

$$\begin{aligned} {\varvec{L}} \frac{\textrm{d}\varvec{i}}{\textrm{d}t}&= \varvec{u} - {\varvec{R}}_{0} \varvec{i} \,, \end{aligned}$$

(11b)

$$\begin{aligned} {\varvec{R}}_{\textrm{p}}\varvec{i}_{\textrm{p}}(\varvec{u})&= \varvec{e}_{\textrm{p}}-\varvec{u} \,. \end{aligned}$$

(11c)

Here, we make use of a vector of coupling currents

$$\begin{aligned} \varvec{i}_{\textrm{c}} = \left[ \!\begin{array}{cccc} i_{\textrm{c},1}&\dots&i_{\textrm{c},n}&i_{\textrm{c},\textrm{ref}} \end{array}\!\right] ^{\textrm{T}} \,, \end{aligned}$$

(11d)

whose entries are given by

$$\begin{aligned} i_{\textrm{c},\mu } = \frac{1}{2}\sum _{\mu ,\nu } G_{\mu \nu }^{+}[u_{\mu }+u_{\nu }] + G_{\mu \nu }^{-}[u_{\mu }-u_{\nu }] \,, \end{aligned}$$

(11e)

for every pair of coupled oscillator with the index $\mu$ and $\nu$. Using the two matrices ${\varvec{G}}^{\pm } = [{\varvec{G}}^{\pm }]^{\textrm{T}} \in {\mathbb {R}}^{n \times n}$, with the entries $G_{\mu \nu }^{\pm }$ defined in (5c), and the vectors $\varvec{g}_{\textrm{ref}}^{\pm } \in {\mathbb {R}}^{n}$ with the entries $G_{\mu ,\textrm{ref}}^{\pm }$ defined in (7b), we introduce the coupling matrices

$$\begin{aligned} {\varvec{G}}_{\textrm{c}}^{\pm } = \frac{1}{2} \left[ \!\begin{array}{cc} {\varvec{G}}^{\pm } &{} \varvec{g}_{\textrm{ref}}^{\pm } \\ {\textbf{0}}^{\textrm{T}} &{} 0 \end{array}\!\right] \,, \end{aligned}$$

(11f)

where ${\textbf{0}}$ denotes a vector of zeros. Here, the unidirectional coupling depicted in Fig. 4 is reflected by the last zero row. Using these coupling matrices, we can now give a compact formulation for the coupling relation:

$$\begin{aligned} \begin{aligned} \varvec{i}_{\textrm{c}}&= {\varvec{G}}_{\textrm{c}} \varvec{u} \,,\\ {\varvec{G}}_{\textrm{c}}&= [{{\,\mathrm{\varvec{\textrm{diag}}}\,}}({\varvec{G}}_{\textrm{c}}^{+}{\varvec{\mathbbm {1}}}) + {\varvec{G}}_{\textrm{c}}^{+}] + [{{\,\mathrm{\varvec{\textrm{diag}}}\,}}({\varvec{G}}_{\textrm{c}}^{-}{\varvec{\mathbbm {1}}}) - {\varvec{G}}_{\textrm{c}}^{-}] \,. \end{aligned} \end{aligned}$$

(11g)

Fig. 7

Left: a port-wise decomposed equivalent circuit for the electrical model given in (11). For $\varvec{i}_{\textrm{c}}={\textbf{0}}$, the circuit represents n uncoupled FNOs, see Fig. 1. A multi-port resistor associated with the conductance matrix ${\varvec{G}}_{\textrm{c}}$ is used to represent the resistive coupling between oscillators (orange box). Right: corresponding wave digital model. The coupling network translates to a scattering relation in the wave digital domain (orange box). The block with the letter $\tau$ (purple dashed box) represents an iterator for solving (algebraic) directed delay-free loops

3 Wave digital emulation

This section utilizes the compact electrical model presented in Sect. 2.5 to derive a real-time capable wave digital (WD) algorithm for emulation purposes. This algorithm serves as a tool for deriving parameters for the optimizer’s technical implementation, which we discuss in the next section. It can therefore be used for designing and testing the optimizer prior to its actual production in order to seek out potential problems or derive suitable parameters. This section is divided into three subsections. The first subsection briefly recapitulates the WD concept. The second subsection derives a highly parallel WD algorithm for emulation purposes. Finally, the third subsection presents emulation results, where we have solved NP problems using the derived WD algorithm.

3.1 Wave digital concept

The WD concept is a powerful tool for the emulation of electrical circuits [29, 31]. The idea lies in mapping a reference circuit onto a recursive digital structure known as the WD model. The platform-independent WD algorithm is then obtained from iteratively emulating the latter. To derive the WD model, we start by decomposing the reference circuit into a set of one- and multi-ports. A port is defined as a pair of terminals, where the in-flowing current is equal to the out-flowing current. It is characterized by three quantities, the port voltage u, the port current i, and the port resistance $R>0$. A general m-port is assigned m port resistances $R_{\mu }>0$ and governed by a constitutive relationship relating the port voltage $u_{\mu }$ to the port current $i_{\mu }$ at the $\mu$-th port, where $\mu =1,\dots ,m$. If we comprise all port voltages $u_{\mu }$, port currents $i_{\mu }$, and port resistances $R_{\mu }$ into a voltage vector $\varvec{u} \in {\mathbb {R}}^{m}$, a current vector $\varvec{i} \in {\mathbb {R}}^{m}$, and a port resistance matrix ${\varvec{R}} = {{\,\mathrm{\varvec{\textrm{diag}}}\,}}(R_{\mu })\in {\mathbb {R}}^{m \times m}$, respectively, we can translate any m-port into the WD domain by applying the bijective transformation:

$$\begin{aligned} \left[ \!\begin{array}{c} \varvec{a} \\ \varvec{b} \end{array}\!\right] = \left[ \!\begin{array}{cr} {\textbf{1}}&{} {\varvec{R}} \\ {\textbf{1}}&{} -{\varvec{R}} \end{array}\!\right] \left[ \!\begin{array}{c} \varvec{u} \\ \varvec{i} \end{array}\!\right] \quad \Leftrightarrow \quad \left[ \!\begin{array}{c} \varvec{u} \\ \varvec{i} \end{array}\!\right] = \frac{1}{2} \left[ \!\begin{array}{cr} {\textbf{1}}&{} {\textbf{1}}\\ {\varvec{G}} &{} -{\varvec{G}} \end{array}\!\right] \left[ \!\begin{array}{c} \varvec{a} \\ \varvec{b} \end{array}\!\right] \,, \end{aligned}$$

(12)

where ${\varvec{R}}{\varvec{G}} = {\textbf{1}}$. In the WD domain, the port-wise structure of a circuit is retained. However, electrical m-ports translate to WD structures, where voltages $u_{\mu }$ and currents $i_{\mu }$ are replaced by incident waves $a_{\mu }$ and reflected waves $b_{\mu }$. Here, a suitable choice of the port resistance $R_{\mu }$ can greatly simplify the resulting WD structure. Now, we comprise all wave quantities $a_{\mu }$ and $b_{\mu }$ into a vector of incident wave $\varvec{a} \in {\mathbb {R}}^{m}$ and a vector of reflected waves $\varvec{b} \in {\mathbb {R}}^{m}$, respectively. The constitutive equation relating $\varvec{u}$ and $\varvec{i}$ in the electrical domain translates to a scattering equation,

$$\begin{aligned} \varvec{b} = {\varvec{S}} \varvec{a} \,, \quad \text {with} \quad {\varvec{S}} \in {\mathbb {R}}^{m \times m} \,, \end{aligned}$$

(13)

relating the reflected wave vector $\varvec{b}$ to the incident wave vector $\varvec{a}$ in the case of a memoryless m-port. Electrical components with memory, such as capacitors or inductors, are governed by differential equations. These elements must first be discretized via a numerical integration method [29] before the bijective transformation (12) is applied. Here, we make use of the trapezoidal rule [29].

3.2 Wave digital model of oscillator-based optimizer

The electrical model derived in Sect. 2.5 can be equivalently represented by the port-wise decomposed circuit on the left side of Fig. 7. Let us briefly assume $\varvec{i}_{\textrm{c}} = {\textbf{0}}$. In this case, the circuit on the left side of Fig. 7 would describe n uncoupled FNOs, see Fig. 1. Hence, this circuit can be (virtually) thought of as a vector of FNOs and we generally refer to it as a vector-valued circuit. To allow for an interaction between the entries of this virtual vector, we incorporate the coupling relation defined in (11g), which leads to the multi-port resistor associated with the conductance matrix ${\varvec{G}}_{\textrm{c}}$ (highlighted in orange on the left side of Fig. 7). Translating our vector-valued circuit into the WD domain will also result in a vector-valued WD model, which allows for a massive parallelization of the associated WD algorithm. We refer the interested reader to [32] for a great exposition on the parallelization of WD algorithms.

In order to obtain a WD model, the general procedure is to individually translate each electrical component into the WD domain and interconnect them according to the topology of the reference circuit via so-called WD adaptors. These are signal flow diagrams that result from translating Kirchhoff interconnections into the WD domain. For example, a series (parallel) connection translates to a series (parallel) adaptor, which is symbolized by the squared box containing the () symbol in Fig. 7.

A common phenomenon occurring in WD algorithms are so-called directed delay-free loops. These are implicit relationships, which hinder the evaluation of the WD model. There are generally two ways to deal with such loops depending on their type:

• 1. Topological loops occur when a reflected wave depends on its corresponding incident wave without any delay in between. To resolve such loops, we can make use of reflection-free ports [29]. Every WD adaptor is allowed to have exactly one reflection-free port, which is indicated by a T-shaped symbol in Fig. 7. This essentially eliminates the relationship between the incident and reflected wave (at the reflection-free port) but has the restriction that the corresponding port resistance is determined as a function of the other port resistances.

• 2. Algebraic loops occur due to the presence of algebraic dependencies that make the incident wave depend on its corresponding reflected wave with no delay separating the two; usually this type of loop occurs when dealing with nonlinear elements [45]. Here, we can make use of iterative methods, such as a fixed-point iteration, to solve such implicit relationships in the WD model, cf. [45].

Although, we have yet to discuss our WD model, we would like to mention that we have already optimally distributed reflection-free ports in Fig. 7 in order to avoid topological loops. To achieve this, we have made every port interconnecting two adaptors reflection-free from left to right. Moreover, we have inserted an iterator element, symbolized by the box containing the letter $\tau$, in order to deal with an algebraic loop that we cover at the end of this subsection.

Let us now individually translate all electrical components into the WD domain, cf. [29].

• 1. The inductors and capacitors associated with the inductance matrix ${\varvec{L}}$ and the capacitance matrix ${\varvec{C}}$ translate to a delay element with and without a sign inversion, respectively. Their port resistance matrices are given by:

  $$\begin{aligned} {\varvec{R}}_{C} = \frac{T}{2}{\varvec{C}}^{-1} \quad \text {and} \quad {\varvec{R}}_{L} = \frac{2}{T} {\varvec{L}} \,, \end{aligned}$$

  (14)

  where T denotes the sampling period of the WD algorithm.

• 2. Real voltage sources generally translate to reflective wave sources. However, in case their port resistances can be chosen freely, they can be made non-reflective. We have exploited this degree of freedom for the perturbation source with the supply voltage $\varvec{e}_{\textrm{p}}$. Hence, it translates to a wave source supplying with the incident wave $\varvec{a}_{\textrm{p}}=\varvec{e}_{\textrm{p}}$ in Fig. .

• 3. Resistances can be thought of as degenerate cases of real voltage sources, where the supply voltage is zero. Thus, they also generally translate to reflective wave sources in the WD domain. In the case of the resistances associated with the resistance matrix ${\varvec{R}}_{0}$, we have also matched their port resistances matrix to their resistance value, such that they translates to a wave source supplying the reflected wave $\varvec{b}_{R_{0}} = {\textbf{0}}$.

• 4. The coupling relation of the multi-port resistor (11g) is associated with the conductance matrix ${\varvec{G}}_{\textrm{c}}$, see the orange box on the left side of Fig. 7. The constitutive relation of a general multi-port resistor translates to a simple scattering equation (13). In this case, we have:

  $$\begin{aligned} \varvec{b}_{\textrm{c}}&= {\varvec{S}}_{\textrm{c}} \varvec{a}_{\textrm{c}} \,, \quad \text {with} \quad \end{aligned}$$

  (15a)
  $$\begin{aligned} {\varvec{S}}_{\textrm{c}}&= [{\textbf{1}}+ {\varvec{G}}_{\textrm{c}}{\varvec{R}}_{\textrm{c}}]^{-1} [{\textbf{1}}- {\varvec{G}}_{\textrm{c}}{\varvec{R}}_{\textrm{c}}] \quad \text {and} \quad \end{aligned}$$

  (15b)
  $$\begin{aligned} {\varvec{R}}_{\textrm{c}}&= [{\varvec{R}}_{\textrm{n}}^{-1} + [{\varvec{R}}_{\textrm{p}}^{-1}+{\varvec{R}}_{C}^{-1}] ]^{-1} \,. \end{aligned}$$

  (15c)

  Here, (15c) is a consequence of our choice of reflection-free ports.

It remains to translate the cubic nonlinearity $\varvec{i}_{\textrm{n}}(u)$ into the WD domain. Here, it is modeled as an ideal controlled current source, see the left side of Fig. 7. This is necessary, because the nonlinearity is formulated in terms of an (i, u)-curve and not in terms of a varying resistance. Ideal current sources translate to reflective wave sources in the WD domain, which, in this case, is governed by the following relation:

$$\begin{aligned} \varvec{a}_{\textrm{n}} = \varvec{b}_{\textrm{n}} - 2{\varvec{R}}_{\textrm{n}}\varvec{i}_{\textrm{n}}(\varvec{u}) \,, \quad \text {with} \quad \varvec{u} = \frac{\varvec{a}_{\textrm{n}}+\varvec{b}_{\textrm{n}}}{2} \,. \end{aligned}$$

(16)

This relationship is implicit, because the calculation of $\varvec{a}_{\textrm{n}}$ depends on the voltage vector $\varvec{u}$, which is a function of $\varvec{a}_{\textrm{n}}$ itself. This type of implicit relationship is what is referred to as an algebraic loop [45]. To resolve this implicitness, we make use of a fixed-point iteration to approximate the value of $\varvec{a}_{\textrm{n}}$ at every time instant. The use of an iteration method is indicated by the iterator symbol on the right handside of Fig. 7.

3.3 Emulation results and discussion

In this subsection, we present emulation results where we have solved two optimization problems utilizing the wave digital model derived in the previous subsection. All our computations were performed on a lab computer in MATLAB. The first problem is the so-called max-cut problem, which asks us to partition a given graph into two subgraphs, such that the number of edges connecting the two graphs is maximal. According to [9, 15, 24], the max-cut problem can be mapped to the Ising Hamiltonian by using the coefficients:

$$\begin{aligned} {\varvec{J}} = -{\varvec{A}} \quad \text {and} \quad \varvec{h} = {\textbf{0}}\,, \end{aligned}$$

(17)

where ${\varvec{A}}$ denotes the adjacency matrix of the underlying graph. We will not cover how these coefficients can be derived from the baseline formulation of the optimization problem, but refer the interested reader to [15, 24] for a good exposition on this topic. Besides the max-cut problem, we solve the so-called minimal vertex cover problem. This problem asks us to find the minimal number of vertices that need to be marked, such that every edge in the graph is incident to one of the marked vertices.

Fig. 8

The Tutte–Coxeter graph [46]

Fig. 9

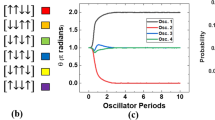
Emulation results of the max-cut (top) and vertex cover (bottom) problem belonging to the graph in Fig. 8. Left column: oscillation voltages $u_{\mu }$ over time. Central column: approximation of oscillation phases $\varphi _{\mu }$ over time. Right column: cut size over time with reference to the max-cut (top) and Hamiltonian belonging to vertex cover problem over time (bottom)

To map this problem onto the Ising machine, we choose the coefficients:

$$\begin{aligned} {\varvec{J}} = -{\varvec{A}} \quad \text {and} \quad \varvec{h} = \left[ 2{\varvec{A}} - 4 {\textbf{1}}\right] {\varvec{\mathbbm {1}}}\,. \end{aligned}$$

(18)

Contrary to the max-cut problem, the minimal vertex cover problem also requires a vector of linear optimization coefficients $\varvec{h}$. We make use of this problem to prove the validity of our mapping approach, when it comes to linear optimization coefficients. Note, both problems are based on the graph depicted in Fig. 8. Also, we have used the oscillator parameters provided in Table 1 and the network parameters provided in Table 3 for both problems.

Our emulation results are depicted in Fig. 9. The top row presents our results for the max-cut problem, while the bottom row presents our results for the minimal vertex cover problem. Let us first consider the max-cut problem and hence the first row of Fig. 9. The left plot depicts the oscillator voltages $u_{\mu }$ over time. Here, we see that the oscillator voltages quickly converge to steady-state phase configuration encoding the solution of the problem after just about $20\,\textrm{ms}$. In the center, we have attempted to extract the oscillation phases denoted by $\varphi _{\mu }$. This plot clearly demonstrates the influence of the SHIL signal, which enforces a bi-stable phase behavior with a phase shift of $\pi$. The right plot uses the phases $\varphi _{\mu }$ to approximate the cut size over time. Here, a phase of $\varphi _{\mu }=0$ is associated with a spin value of $s_{\mu }=1$, while a phase of $\varphi _{\mu }=\pi$ is associated with a spin value of $s_{\mu }=-1$. The graph in Fig. 8 has a maximal cut of 45 edges. As can be seen, the max-cut is successfully determined by the optimizer after just about $10\,\textrm{ms}$.

The Ising Hamiltonian encoding the minimal vertex cover problem consists of two terms [15, 24]:

$$\begin{aligned} H = H_{0} + H_{1} \,. \end{aligned}$$

(19)

The first term $H_{0} \ge 0$ represents a counter that counts the number of vertices that have been marked by the optimizer. The second term $H_{1} \ge 0$ is a penalty term. This term can only reach zero if all edges are incident to a vertex from the solution set. Thus, H is only minimized, when a valid vertex cover is found (imposed by $H_{1}$) that is also minimal (imposed by $H_{0}$). Looking at the bottom row of Fig. 9, we see that the oscillator voltages, again, quickly converge to a steady-state phase configuration after just about $20\,\textrm{ms}$. By extracting the phase values $\varphi _{\mu }$ out of the oscillation voltage $u_{\mu }$, we were able to depict the values of $H_{0}$ and $H_{1}$ over time in the right plot. Here, we also mark the size of the minimal vertex cover using a black dashed line, which, in this case, is 15. Both the Hamiltonian $H_{0}$ and $H_{1}$ converge to a constant value once the solution is found. Since a valid vertex cover is found, the penalty term $H_{1}$ converges to zero. Meanwhile, the counter $H_{0}$ converges to its optimal/minimal value $H_{0,\textrm{opt}}=15$, which is the size of the minimal vertex cover.

Fig. 10

Simulations of an oscillator-based optimizer solving the max-cut problem depicted on the left side. The solution of the problem is given by two partitions composed of two and three arbitrary oscillators, respectively. Plots a, b showcase the effects of using inadequate optimization parameters. a High values of $G_{\textrm{b}}$ lead to a strong coupling, which does not allow the network to settle to one phase configuration. b Low values of $G_{\textrm{b}}$ lead to the oscillators getting stuck in a certain phase configuration, usually determined by their initial values. c Similar to b, a strong SHIL signal leads to the oscillators getting stuck in a certain phase configuration and not correctly solving the problem. d Weak SHIL does not lead to bi-stable phase behavior, which (often) does not allow the network to settle to one binary phase configuration

Overall, we have shown that the oscillator network designed in this section indeed serves as an optimizer for QUBO problems. How different problems can be mapped to this optimizer is a question that has been extensively discussed in [15, 24]. Note that the wave digital model presented in the previous section can be used to simulate arbitrarily large network. In Appendix A, we demonstrate the runtime of the associated wave digital algorithm for different network sizes.

We would now like to briefly comment on one important aspect of our oscillator-based optimizer. Like every other optimizer, our device has a set of parameters that must be suitably chosen in order to obtain good solutions:

• 1. The multiplicative bias $G_{\textrm{b}}=1/R_{\textrm{b}}$, appearing in (5c) 7b, needs to be chosen adequately, being neither too high nor too low. In the first case, the interaction is too strong, such that the oscillators are usually unable to settle to one phase configuration. In the second, case, the oscillators are effectively uncoupled, such that the power exchange between them is too weak for optimization purposes. Here, the network usually converges to a suboptimal solution. These two cases are illustrated in Fig. 10a, b.

• 2. The SHIL signal has two parameters, namely the amplitude ${\hat{e}}_{\textrm{SHIL}}$ and the bias ${\hat{e}}_{\textrm{b}}$, see (9). Both these parameters need to be chosen adequately. When the amplitude and bias are too high, the oscillators tend to lock (or even get stuck) to their current phases. These parameters must be chosen so a perturbation can have the chance to influence the oscillator’s phase, as shown in Sect. 2.4. The consequences of strong and weak SHIL are illustrated in Fig. 10c, d, respectively.

• 3. A good balance between the multiplicative bias and the SHIL signal must be found. At first glance, these parameters seem independent of each other. However, if, for example, the SHIL signal is too strong, then this effect can be mitigated by increasing $G_{\textrm{b}}$, as this would lead to a greater perturbation by adjacent oscillators that may be enough for the oscillator to escape its current phase. Conversely, if the multiplicative bias is too high, the interaction between the oscillators may be too strong such that the bi-stable phase behavior is lost. In this case, increasing SHIL may restore bi-stability.

Table 3 Emulation parameters that have been used for the results in Fig. 9

The emulation parameters in Table 3, which have been used to solve the optimization tasks presented in this section, have been chosen on the basis of this discussion. Here, the wave digital algorithm was used as a flexible tool to test and find the correct parameters. In Sect. 4, this tool is also used to determine the parameters of the implemented circuit.

4 Technical implementation

The third and final part of this work discusses the technical implementation of our oscillator-based optimizer. This section is divided into three subsections. The first subsection discusses the technical implementation of the FNO. Here, we also present a method for enhancing the wave digital model of the oscillator, so it can emulate the real oscillator in a more accurate fashion. The second subsection discusses the different circuits used for problem mapping. This also includes the circuits required for setting optimization constraints. Finally, the third subsection provides measurements from our in-house oscillator-based optimizer, where we solve different small-sized optimization problems to validate the findings of this manuscript.

Fig. 11

Technical implementation of the FNO depicted in Fig. 1

4.1 Oscillator circuit

Our FNO implementation is depicted in Fig. 11. The circuit is composed of the same two elements as in Fig. 1: the cubic nonlinearity and the RLC-tank. For the sake of efficiency, the perturbation source $e_{\textrm{p}}$ is not embedded into the oscillator itself. Instead, we make use of one common signal generator for all oscillators in the network. We cover this aspect in more detail in the next section. The RLC-tank is composed of the resistor $R_{0}$, the capacitor C and inductor L just like in Fig. . However, the inductor is realized with the help of a capacitive gyrator. A gyrator is an ideal lossless two-port with the ability of inverting current-voltage characteristics [47]. With reference to Fig. 12, a capacitive gyrator is able to emulate an inductor described by:

$$\begin{aligned} L\frac{\textrm{d}i}{\textrm{d}t}= u \,, \quad \text {with} \quad L = R_{\textrm{g}}^2C_{\textrm{g}} \,, \end{aligned}$$

(20a)

where $R_{\textrm{g}}$ is the so-called gyration resistance. Thus, a gyrator allows for emulating large inductances with small capacitors by adequately adjusting the gyration resistance. This is important for our oscillator implementation, because the oscillation frequency of the unperturbed FNO is mainly determined by the inductance L of its RLC-tank. The larger L is, the slower the frequency will be. Slow frequencies, on the other hand, are helpful for circuit testing, as they eliminate most parasitic high frequency effects. The capacitive gyrator in Fig. 11 has two resistances $R_{\textrm{g},1}$ and $R_{\textrm{g},2}$. These resistances relate to the gyration resistance in (20a) as follows [48]:

$$\begin{aligned} R_{\textrm{g}} = \sqrt{R_{\textrm{g},1}R_{\textrm{g},2}} \end{aligned}$$

(20b)

Thus, for a desired inductance L, we require a capacitor

$$\begin{aligned} C_{\textrm{g}} = \frac{L}{R_{\textrm{g}}^2} = \frac{L}{R_{\textrm{g}_{1}}R_{\textrm{g},2}} \,, \end{aligned}$$

(20c)

where the latter equality is a direct consequence of (20b).

Fig. 12

An inductor can be realized by a capacitive gyrator

Fig. 13

Realization of the coupling depicted in Fig. 3 in hardware. The gray boxes titled ${\mathcal {N}}_{\mu }$ and ${\mathcal {N}}_{\nu }$ are used to compactly represent two FNOs just as in Fig. 11. Here, we only draw the capacitors to clearly demonstrate the coupling node. Both oscillators are equipped with a unity gain buffer and an inverter. The coupling circuit used in Fig. 3 can be found in the yellow box

The cubic nonlinearity is realized by the parallel interconnection of a negative impedance converter (NIC) and a diode clipper, see the blue box in Fig. 11. The negative impedance converter is used to produce a negative resistance:

$$\begin{aligned} i_{\textrm{NIC}} = -G_{\textrm{n}}u \,, \quad \text {with} \quad G_{\textrm{n}}R_{\textrm{n}} = 1 \,. \end{aligned}$$

(21a)

In combination with the diode clipper, we obtain

$$\begin{aligned} i_{\textrm{n}}(u)&= i_{\textrm{d}_{1}}(u) - i_{\textrm{d}_{2}}(u) + i_{\textrm{NIC}} \,, \end{aligned}$$

(21b)

where $i_{\textrm{d}_\nu }$ denotes the currents flowing through the diodes $\textrm{d}_{\nu }$. The diode clipper effectively limits the amount of voltage that is perceived by the NIC. Combining the negative resistance of the latter with the rectification of the diode clipper, we obtain an N-shaped (i, u)-curve with the negative differential resistance $R_{\textrm{n}}$, see Fig. . Here, we see that the N-shaped nonlinearity is able to approximate the characteristics of the original cubic nonlinearity (2c).

Fig. 14

Original cubic nonlinearity (2c) (dashed black), N-shaped nonlinearity produced by the circuit in Fig. 11 (solid blue), and the (i, u)-curve of the model (21) based on the fitted Shockley equation (dashed red)

Table 4 Parameters of the FNO circuit in Fig. 11

To enhance our wave digital model, we suggest modeling the diodes by the Schockley equation

$$\begin{aligned} i_{\textrm{d}_{1/2}}(u)&= I_{\textrm{s}}\left[ \exp \left( \pm \, u/U_{T} \right) -1 \right] \,, \end{aligned}$$

(21c)

with the scale current $I_{\textrm{s}}=20\textrm{nA}$ and the thermal voltage constant $U_{T}=51.8\,\textrm{mV}$. By fitting the latter, we were able to obtain good fit for our model (21) using the parameters in Table , see Fig. 14. Hence, for achieving more accurate results with the wave digital model of Sect. , we recommend replacing (2c) with (21) in the electrical model (11), which effectively modifies (16). For the sake of completeness, we would like to mention that our technical implementation uses the op-amp model TL071 and the diode model 1N4148.

Fig. 15

Realization of the coupling depicted in Fig. 4 in hardware. The gray boxes titled ${\mathcal {N}}_{\mu }$ and ${\mathcal {N}}_{\textrm{ref}}$ are used to compactly represent an arbitrary oscillator ${\mathcal {N}}_{\mu }$ and the reference oscillator ${\mathcal {N}}_{\textrm{ref}}$, respectively, just like in Fig. 4. The controlled voltage source in Fig. 4 is realized by the unity gain buffer highlighted in red, while the resistive coupling circuit is highlighted in yellow

4.2 Problem mapping

In this subsection, we demonstrate how the circuits presented in Sect. 2 translate to hardware in order to build an oscillator-based optimizer. The first part of this section discusses the mapping of optimization coefficients $J_{\mu \nu }$. The second part explains the injection of SHIL. The third and final part discusses the mapping of linear optimization coefficients.

4.2.1 Quadratic optimization coefficients

In order to map optimization coefficients onto our in-house optimizer, we make use of the circuit depicted in Fig. 13. Here, we see a coupling between two arbitrary oscillators ${\mathcal {N}}_{\mu }$ and ${\mathcal {N}}_{\nu }$, which are (compactly) represented by the gray filled boxes with the capacitances $C_{\mu }$ and $C_{\nu }$. Essentially, every oscillator can be considered to have two outputs ports, the first being the one parallel to the capacitor and the second being an inverted output. The latter is realized by interconnecting the upper capacitor node to a unity gain buffer and inverter, which invert the output voltages $u_{\mu }$ and $u_{\nu }$, see the blue shaded boxes. In practice, these components are necessary, as all lower capacitor nodes are connected to the ground, such that a signal inversion, like in Fig. 3, via a cross-over circuit is not possible. Using these two outputs, we can now interconnect the two oscillators in the same was as in Fig. 3, i.e. the non-inverted output of ${\mathcal {N}}_{\mu }$ is connected to the non-inverted output of ${\mathcal {N}}_{\nu }$ via a resistor with the conductance $G_{\mu \nu }^{-}$, while the inverted outputs of ${\mathcal {N}}_{\mu }$ and ${\mathcal {N}}_{\nu }$ are each cross-coupled to the non-inverted output via a resistor with the conductance $G_{\mu \nu }^{+}$. Contrary to the coupling in Fig. 3, the coupling conductances in Fig. 13 are halved in their value. This is because, the lower capacitor nodes in Fig. 3 are assumed to have different potentials, while the nodes in Fig. 13 are connected to the ground. This way, the two coupling schemes can only be identical, when the conductances are halved, such that the coupling currents $i_{\textrm{c},\mu }$ and $i_{\textrm{c},\nu }$ are the same as in (5).

4.2.2 Linear optimization coefficients

As we have seen in Fig. 4, the linear constraints can be essentially implemented in the same way as all other optimization coefficients. However, as explained in Sect. 2.3.2, the coupling must be unidirectional, i.e. the reference oscillator ${\mathcal {N}}_{\textrm{ref}}$ must perceive no load/feedback from the rest of the circuit in order to retain a fixed phase. The simplest solution to eliminate feedback is to make use of a unity gain buffer, whose output voltage is then used to couple the reference oscillator to all other oscillators. We have depicted this type of coupling in Fig. 15 on the example of our reference oscillator ${\mathcal {N}}_{\textrm{ref}}$ being coupled to one arbitrary oscillator ${\mathcal {N}}_{\mu }$. The unity gain buffer is highlighted in red. As can be seen in this figure, both outputs of the reference oscillator are connected to a unity gain buffer, which decoupled it from the rest of the circuit. This way, ${\mathcal {N}}_{\textrm{ref}}$ perceives no load allowing its output voltage $u_{\textrm{ref}}$ to retain a fixed oscillation phase.

Fig. 16

Circuit schematic demonstrating SHIL injection at the capacitor node. The voltage source $e_{\textrm{p}}$ represents a signal generator supplying (9). The gray dashed boxes entitled ${\mathcal {N}}_{\mu }$ are a compact version of the oscillators depicted in Fig. 11

4.2.3 Optimization constraints

In order to implement binary constraints, we have used SHIL in Sect. 2.4. Here, SHIL current was injected using the perturbation source that we have pre-built into the oscillator model depicted in Fig. 1. However, from a practical standpoint, this type of implementation is inefficient, as it necessitates one signal generator per oscillator. To reduce the number of components, we suggest injecting SHIL by using a common signal generator, see Fig. 16. Here, one voltage source $e_{\textrm{p}}$ is used to perturb all oscillators at the same time. The currents $i_{\textrm{p},\nu }$ then result as a result of the current divider law.

4.3 Results and discussion

The set up for the measurements can be seen in Fig. 17. The printed circuit board (PCB) consists of 20 oscillators of which only the necessary amount is used for each measurement. The PCB is screwed onto an aluminum plate that is grounded to reduce the noise. To couple the oscillators additional bread boards are used with variable resistances. The SHIL signal is supplied to the oscillators via a function generator (Keysight 33500B) and the oscillator voltages are measured with a Pico Scope and the corresponding computer program (Fig. 17).

Fig. 17

Photograph of the experimental set up. On the left side the complete set up is shown with the printed circuit board (PCB) and bread boards placed on a grounding plate. The PCB is connected to voltage sources and a function generator (used for SHIL). For data logging a Pico Scope is used with the according computer software. The PCB shown from above on the right side contains 20 oscillators which get coupled via resistors on separate bread boards. On the breadboard is an additional unity gain buffer placed that is necessary to decouple the reference oscillator in the Vertex Cover Problem

With the laboratory setup in Fig. 17 and the parameters in Table 5, we have solved the four optimization problems depicted in the left column in Fig. 18. Here, every node ${\mathcal {N}}_{\mu }$ represents a FNO, as depicted in Fig. 11, while every edge represents a resistive connection as depicted in Fig. 13. Problems (a) and (b) are used as simple benchmarks to reaffirm the discussions of Sects. 2.2 and 2.3. Problems (c) and (d), on the other hand, are small-sized examples for demonstrating the behavior of our oscillator-based optimizer. The middle column in Fig. 18 depicts the output voltages $u_{\mu }$ over time. Here, a red line is used to indicate the time instant at which SHIL is turned on. The right column in Fig. 18 shows the instantaneous power p(t) over time. This signal is not measured but rather reconstructed by using the known coupling matrix ${\varvec{G}}_{\textrm{c}}$, the measured voltage vector $\varvec{u}(t)$, and the coupling relation (11g):

$$\begin{aligned} p(t) = \varvec{u}^{\textrm{T}}(t) \varvec{i}_{\textrm{c}}(t) = \varvec{u}^{\textrm{T}}(t) {\varvec{G}}_{\textrm{c}} \varvec{u}(t) \,. \end{aligned}$$

(22)

Note that all results in the central column of Fig. 18 represent extracts of our measurements, i.e. the time instant $t=0$ only denotes the time at which the recording has been started.

Let us first consider problem (a) in Fig. 18, which is a simple max-cut problem with two coupled oscillators. According to (17), we have $J_{12}=-1$. Therefore, we use the coupling circuit depicted on the right side of Fig. 2 in order to promote anti-phase synchronization. Looking at the voltages $u_{\mu }$ in Fig. 18a, we observe that the oscillators achieve anti-phase synchronization even without the use of SHIL. According to our hypothesis, this outcome is natural, since anti-phase synchronization minimizes power dissipation, which is evident from the right plot in Fig. 18a. Once SHIL is turned on for $t > 60\,\textrm{ms}$, we see an interesting phenomenon. Prior to turning on the SHIL signal, the voltage signals are symmetrical about the t-axis. This allows for a destructive superposition of the two signals, such that $u_{1}+u_{2}=0$, when anti-phase synchronization is achieved; this also implies no power dissipation such that $p(t)=0$. Once SHIL is turned on, we can observe a slight distortion in the voltage signals; they are now asymmetric about the t-axis. In this case, the two signals can not sum to zero, such that $p(t)=0$ is not possible anymore. Therefore, we observe higher power dissipation, when SHIL is used. However, since anti-phase synchronization still minimizes power dissipation, we see that the oscillators assume this states nonetheless. This phenomenon is very important and has not been pointed out in literature so far. Depending on the problem, we see that SHIL can greatly influence the tendencies of coupled oscillators. This can even mean that the optimal solution of the considered problem does not map to the phase configuration minimizing the dissipated power p(t) anymore, when SHIL is active. Also, this analysis reveals that it may be beneficial to use oscillators with symmetric oscillations for oscillator-based optimization, since this guarantees that the optimal solution of the considered problem is mapped to the minimum of p(t), when the mapping of Sect. 2.3 is used.

Table 5 Parameters of the laboratory setup in Fig. 17

Fig. 18

Measurement results of four different optimization problems (a–d). The left column depicts the graph associated with the optimization task. The central column depicts the measured oscillator voltages $u_{\mu }$ over time, where the signal colors are correlated to the boundary colors of the nodes of the graphs in the left column. For all time instants preceding the red line, no SHIL signal is used. Afterwards SHIL is turned on. The right column depicts the dissipated power p(t) over time

Let us now consider problem (b) in Fig. 18. Here, we attempted to recreate the theoretical scenario depicted in Fig. 5. Again, we have $J_{12}=J_{13}=J_{23}=-1$, as in Fig. 5. As has been pointed out in that section, this type of coupling leads to a contradiction, as there is no binary phase configuration that can lead to $p(t)=0$. Therefore, the oscillators actively search for other phase configurations that minimize p(t), which are not binary. The same results depicted in Fig. 5 can be clearly observed in our voltage measurements in Fig. 18b. The oscillators assume a three-phase configuration, when SHIL is turned off ($t < 60 \,\textrm{ms}$). However, due to parameter mismatches (leading to a frequency mismatch between the oscillators), the oscillators do not fully lock to this state, but rather lock to it for short time intervals and oscillate around it otherwise. Once SHIL is turned on, the optimizer is now forced to search for binary solutions, and it successfully finds the same solution as in Fig. 5, which indeed corresponds to the problem’s solution. In the right plot of Fig. 18b, we again see that the three-phase configuration minimizes the dissipated power p(t) even more than the solution of the mapped problem, just like in Fig. 5.

The third problem depicted in Fig. 18c is an unweighted max-cut problem with a maximal cut size of 6 edges. There are multiple partitions that can lead to an optimal solution and we were able to achieve every one of these partitions using our oscillator-based optimizer. In the graph of Fig. 18c, we have depicted one of the optimal partitions that have been found by our optimizer. We would like to point out that the edge connecting ${\mathcal {N}}_{5}$ and ${\mathcal {N}}_{6}$ is grayed out, because is does not belong to solution of the problem, since we only count the edges that connect the two partitions, refer to Sect. 3.3. Looking at the central plot in Fig. 18c, we see that the optimizer finds this optimal partition even before the SHIL signal is turned on. In other words, we can clearly see that the optimal partition has been successfully minimized to the phase configuration minimizing the dissipated power. In order to clearly decode the solution, we turn on SHIL at $t=60\,\textrm{ms}$. Here, we see that the optimizer simply reassumes the solution of the problem. However, due to SHIL, the oscillation phases are exactly locked to 0 or $\pi$, which allows us to easily decode the solution. The right plot in Fig. 18c shows the same phenomenon observed in Fig. 18a: turning on SHIL leads to more power dissipation due to the distorted voltage signals.

Our final measurement is depicted in Fig. 18d. Here, we attempted to solve a minimal vertex cover problem with 6 nodes. As pointed out in Sect. (see equation (18)), the minimal vertex cover problem contains a Zeeman term, hence we require a seventh reference oscillator in order to implement the coefficients $h_{\mu }$. This problem is used as a proof-of-concept in order to show that our oscillator-based optimizer can also deal with problems containing the Zeeman term. We would like to point out that the graphs depicted in Fig. 18c, d are isomorphic. The minimal vertex cover problem, however, has a different solution than the max-cut problem. Specifically, we require at least four nodes in order to color every edge in the graph, while the max-cut problem requires two or three nodes in order to achieve the largest possible cut size. The four nodes representing the solution of the problem (${\mathcal {N}}_{1}$, ${\mathcal {N}}_{4}$, ${\mathcal {N}}_{5}$, ${\mathcal {N}}_{6}$) are drawn as a partition in the graph of Fig. 18d. We would like to point out that we have colored the edges in the same color as the incident nodes belonging to the solution of the problem. Prior to turning on the SHIL signal, the solution of the problem can not be identified from the output voltages $u_{\mu }$ depicted in the center of Fig. 18d. However, once the SHIL signal is turned on, the optimizer successfully finds the optimal solution, which translates to the graphical solution depicted on the left of Fig. 18d. The right plot in Fig. 18d, again, shows that the binary solution corresponds to a state of higher power dissipation, when compared against the state the oscillators assumed prior to turning on the SHIL signal. If we compare the right plots in Fig. 18c, d, however, we see that the solution of the vertex cover problem dissipates less power than that of the max-cut problem. This proves that adding a seventh reference oscillator with adequate coupling weights indeed reformulates the original max-cut problem as a minimal vertex cover problem. This observation is very important since the matrix ${\varvec{J}}$ is identical in problems (c) and (d), compare equations (17, 18).

5 Conclusion and outlook

In this work, we have covered the fundamental aspects of oscillator-based optimization. We started by explaining the theoretical design of oscillator-based optimizers with the goal of solving quadratic unconstrained binary optimization (QUBO) problems. Here, we propose to build an oscillator-based optimizer using resistively coupled FitzHugh-Nagumo oscillators. The resistive coupling results as a natural consequence of the synchronization tendencies of coupled oscillators. The main hypothesis supporting it is that a network of coupled oscillators has the natural tendency of minimizing interactions, as this minimizes power dissipation. In addition to explaining how QUBOs can be mapped onto the resistive couplings of our network, we have also discussed the enforcement of optimization constraints. In the second part of our work, we derived a real-time capable wave digital algorithm, which allows for emulating our proposed optimizer. This algorithm serves as a testing tool for seeking out potential problems prior to implementing the network. The third and final part of this work presents our own in-house oscillator-based optimizer. Here, the theoretical circuitry presented in the first part of this work is fully implemented in analog hardware. The resulting circuit is then tested on four different optimization problems, which validate our proposed methodology for building oscillator-based optimizers.

In future works, we plan to enhance the circuit implementation presented in this work by reducing the number of active components both in the coupling as well as in the oscillator itself. Besides that, we aim to explore the use of memristors for dynamic topology formation [49]. Memristors are resistors with memory that remember the last state they are programmed to. Usually, these devices are built, so they switch between a high- and low-ohmic state. By coupling the oscillators using memristors instead of resistors, we can thus implement a dynamic connection, which allows us to ”rewire” the network when dealing with new problems. When the memristor is in the high-ohmic state, the oscillators are effectively uncoupled. Otherwise, if the memristor is in the low-ohmic state, then the oscillators are coupled.

A Simulation time

In Fig. 19, we recorded the simulation runtime as a function of the network size. For every network size, we construct a complete network, in which every oscillator is connected to every other oscillator. The resulting network maps a max-cut problem of a complete graph for a given network size. All simulations were carried out on a lab computer (in MATLAB) with an Intel Core i7 processor running at 2.9 GHz, using 32GB of RAM and Windows 10.

As can be seen from Fig. 19, the wave digital concept allows for simulating large networks with up to 4500 oscillators with a reasonable runtime of about 3 min. At this point, we would like so stress that the wave digital concept is a platform-independent tool. By programming the wave digital algorithm in low-level programming languages such as C or C++, a significant improvement can be made. In other words, the simulation runtime of a wave digital algorithm is strongly dependent on the platform that it is programmed on.

Fig. 19

Simulation runtime of the wave digital algorithm as a function of the network size. In every simulation, a complete graph is considered, where every oscillator is connected to every other oscillator