1 Introduction

In today’s society, we are increasingly reliant on information devices in every aspect of our lives. The remarkable progress in information technology has been largely driven by the advancements in semiconductor technology, specifically the scaling law known as Moore’s law [1]. However, the pace of Moore’s law slows down due to physical and economic limitations [2].

The modern era of information processing has been largely dominated by the von Neumann architecture, a paradigm that has served as the backbone of general-purpose computing for decades. However, von Neumann machines have inherent limitations when solving certain types of problems, such as those involving combinatorial optimization. These problems have a wide spectrum of applications in the real world, including machine learning, computer vision, circuit wiring, route planning, and resource allocation [3,4,5,6].

Recognizing these challenges, there has been a growing interest in non-silicon-based, non-von Neumann architectures. These architectures, which admit massively parallel, asynchronous, and in-memory operations, are different from traditional general-purpose computing devices/models and are designed specifically to tackle these complex problems more effectively. These architectures, which include quantum computers, neuromorphic computers, and Ising machines, among others, offer promising alternatives for the advancement of next-generation information processing [7, 8].

Many combinatorial optimization problems can be translated into a problem of physics: finding the ground state of an Ising model, a system of interacting binary spins. Ising machines are physical systems specifically designed to find the ground states of Ising models [9]. Ising machines have been implemented using various physical systems, such as superconducting qubits, optical parametric oscillators, dedicated digital CMOS devices, memristors, and photonic simulators [10,11,12,13,14,15].

Oscillations are ubiquitous phenomena observed across the fields of natural science and engineering [16, 17]. Coupled oscillator systems, which can be realized through various physical phenomena, possess diverse information processing capacity and hold promise for building ultra energy efficient, high frequency and density scalable computing architecture [18, 19] (see [18, Table 1] for a comparison of several building block physical rhythmic elements). While the state of an oscillator is represented by a continuous phase value, sub-harmonic injection locking phenomena can be used to realize discrete states, as proposed since the time of von Neumann and Goto [20, 21]. These discrete states can be utilized to implement Ising spins, a principle that led to the foundation of oscillator-based Ising machines (OIMs) [22, 23]. OIMs have been experimentally demonstrated using various physical systems, such as analog electronic, insulator-to-metal phase transition, and spin oscillators [22, 24,25,26].

In this Chapter, we discuss the fundamentals and working mechanisms of the OIMs. We also numerically investigate the relationship between their performance and their properties, including some unexplored effects regarding driving stochastic process and higher harmonics, which have not been addressed in the existing literature.

2 Ising Model and Ising Machines

The Ising model, proposed by E. Ising in the early 20th century, is a theoretical model used to describe a system of interacting binary spins [27]. The model is specified by a collection of discrete variables, the “spins,” \((s_i)_{i=1}^N\in \{-1,1\}^N\), where N is the number of spins, and a cost function, or “Hamiltonian,” \(H: \{-1,1\}^N \rightarrow \mathbb {R}\), which specifies how the spins interact. The Ising Hamiltonian is given by:

$$\begin{aligned} H = -\dfrac{1}{2}\sum _{i=1}^N\sum _{j=1}^N J_{ij} s_i s_j - \sum _i^N h_i s_i\;, \end{aligned}$$
(1)

where \(J_{ij}\in \mathbb {R}\) is the interaction coefficient between the ith and jth spins, and \(h_i\in \mathbb {R}\) is the external magnetic field for the ith spin. Many combinatorial optimization problems can be mapped onto the problem of finding the ground state of the Ising model, with instances of these problems specified by the symmetric adjacency matrix \(\boldsymbol{J}\) and vector \(\boldsymbol{h}\). The problem is to find the spin configuration \(\boldsymbol{s}\) that minimizes the above Hamiltonian. In this chapter, we limit to consider the Ising models with no external field:

$$\begin{aligned} H = -\dfrac{1}{2}\sum _{i=1}^N\sum _{j=1}^N J_{ij} s_i s_j\;. \end{aligned}$$
(2)

These models still encompass various important combinatorial optimization problems [28], called NP-complete problems, which can be computationally intractable for the traditional von Neumann architecture machines.

Ising machines are physical systems that are designed to efficiently explore the ground state of the Ising Hamiltonian. Various Ising machines have been proposed, using approaches including classical, quantum, classical-quantum hybrid, and quantum-inspired classical [9]. Also, these machines have been realized through various physical systems, such as superconducting qubits, optical parametric oscillators, dedicated digital CMOS devices, memristors, and photonic simulators [10,11,12,13,14,15]. Among these, the focus of this Chapter is on the classical ones. A classical physical system subjected to thermal fluctuation exhibits a stationary distribution \(p_\textrm{s}\), known as the Boltzmann distribution, which takes the following form [29]:

$$\begin{aligned} p_\textrm{s}(\boldsymbol{x}) = \mathcal {N}\exp {(-V(\boldsymbol{x})/D)}\;, \ x \in \Omega \;, \end{aligned}$$
(3)

where \(\boldsymbol{x}\) is the state of the physical system, \(\Omega \) is the phase space, \(\mathcal {N}\in \mathbb {R}\) is the normalization constant, \(V(\boldsymbol{x}) \in \mathbb {R}\) is the energy of the state \(\boldsymbol{x}\) and \(D\in \mathbb {R}\) is the strength of the thermal fluctuation. The Boltzmann distribution tells us that the lower energy states appear with higher probability, and the probability of obtaining the ground state increases as the fluctuation strength is lowered. While reducing the fluctuation strength can increase the probability of obtaining the ground state, it’s not always advantageous to simply diminish the fluctuation. If the fluctuation is too weak, the system may become trapped in local minima of the potential and be unable to escape, which significantly increases the time it takes for the system to reach a stationary distribution. To address this challenge, a process known as annealing is often employed. In this process, the strength of the fluctuation is gradually reduced in order to achieve a balance between reaching a stationary distribution and enhancing the probability of finding the ground state. The discussion above leads to the following idea of a class of Ising machines: if we implement a physical gradient system with the potential V subject to the following conditions, and apply appropriate fluctuations to it, we can find the ground state of the Ising Hamiltonian and thus solve combinatorial optimization problems:

  • There exists a set in the phase space \(\Omega \) that can be regarded as spin configurations,

  • The Ising Hamiltonian H is represented as the potential V evaluated at these spin configurations,

  • The minimum value of V coincides with the minimum value of H.

Even continuous-state dynamical systems can be harnessed in the implementation of Ising machines. The Hopfield-Tank neural network [30] being a classical example, and coherent Ising machines [11] implemented using optical parametric oscillators and OIMs also belong to this group. Also, in addition to the method of utilizing thermal fluctuations as discussed above, other approaches utilizing deterministic chaotic fluctuations to implement Ising machines using classical continuous-state dynamical systems have been proposed [31, 32].

3 Oscillator-Based Ising Machines

Oscillations are ubiquitous phenomena observed across the fields of natural science and engineering [16, 17]. Coupled oscillator systems, which can be realized through various physical phenomena, possess diverse information processing capacity and hold promise for building ultra energy efficient, high frequency and density scalable computing architecture [18, 19].

In this section, we will discuss the background of the operating principle of oscillator-based Ising machines (OIMs) [22, 23]. This is summarized as follows: Under the assumption that the interaction and external forcing are sufficiently weak, network-coupled self-excited oscillators can universally be described using the Kuramoto model, which consists of network-coupled phase oscillators. Given certain symmetries in the topology and scheme of interaction, the Kuramoto model becomes a gradient system. Moreover, sub-harmonic injection allows for the introduction of spin configurations as a stable synchronized state within the phase space of the phase oscillator system.

These properties suggest that a broad class of network-coupled self-excited oscillator systems can be used to implement OIMs. OIMs have been experimentally demonstrated using various physical systems, such as analog electronic, insulator-to-metal phase transition, and spin oscillators [22, 24,25,26].

3.1 Phase Oscillators

In this Subsection, we introduce the notion of the phase for a stable self-excited oscillator and explain how its dynamics, when subjected to sufficiently weak fluctuation, can be reduced to a one-dimensional dynamics of a phase oscillator.

Consider a smooth autonomous dynamical system of \(N_\textrm{d}\)-dimensional state \(\boldsymbol{x}(t)\in \mathbb {R}^{N_\textrm{d}}\):

$$\begin{aligned} \dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t))\;, \quad \boldsymbol{x}(t) \in \mathbb {R}^{N_\textrm{d}}\;, \end{aligned}$$
(4)

which has an exponentially stable limit-cycle \(\chi : \tilde{\boldsymbol{x}}_0(t)\) with a natural period T and frequency \(\omega = 2\pi / T\), satisfying \(\tilde{\boldsymbol{x}}_0(t)=\tilde{\boldsymbol{x}}_0(t+T)\). We first introduce a phase \(\theta (\boldsymbol{x}) \in [0, 2\pi )\) on \(\chi \), where 0 and \(2\pi \) are considered identical. We can choose an arbitrary point \(\tilde{\boldsymbol{x}}_0(0)\) on \(\chi \) as the origin of phase, i.e., \(\theta (\tilde{\boldsymbol{x}}_0(0))=0\), and define the phase of \(\tilde{\boldsymbol{x}}_0(t)\) as \(\theta (\tilde{\boldsymbol{x}}_0(t))=\omega t \ (\textrm{mod} \ 2\pi )\). In the following, we reparametrize a point on \(\chi \) using \(\theta \) instead of t. Specifically, we define \(\boldsymbol{x}_0(\theta ):=\tilde{\boldsymbol{x}}_0(t)\) for subsequent discussions. Apparently, \(\boldsymbol{x}_0(\theta ) = \boldsymbol{x}_0(\theta +2\pi )\) holds.

To describe the dynamics when the system deviates from the periodic orbit \(\chi \) due to perturbation, we extend the definition of the phase beyond \(\chi \). Here, it’s important to note that \(\dot{\theta } = \omega \) holds as long as \(\boldsymbol{x}\) evolves on \(\chi \). Let us extend the definition of the phase such that \(\dot{\theta } = \omega \) holds. With this extension, the phase difference between two solutions of (4) starting from different initial conditions should remain constant over time. The basin of attraction \(\mathcal {B} \subset \mathbb {R}^{N_\textrm{d}}\) is the set of initial conditions that converge to \(\chi \). For smooth, exponentially stable limit-cycling system, the following holds [33]: For any point \(\boldsymbol{x}_* \in \mathcal {B}\), there exists a unique initial condition \(\boldsymbol{x}_0(\theta _*)\) on the periodic orbit, which yields a solution that maintains a constant phase difference of zero with the solution starting from \(\boldsymbol{x}_*\). Thus we can introduce a phase function \(\theta (\boldsymbol{x}) : \mathcal {B} \rightarrow [0, 2\pi )\) that maps the system state to a phase value as

$$\begin{aligned} \theta (\boldsymbol{x}_*) = \theta (\boldsymbol{x}_0(\theta _*))=\theta _*\;. \end{aligned}$$
(5)

For smooth systems, the phase function \(\theta \) is also smooth, and thus

$$\begin{aligned} \boldsymbol{F}(\boldsymbol{x}) \cdot \nabla \theta (\boldsymbol{x}) = \omega \;, \quad \forall \boldsymbol{x} \in B\;, \end{aligned}$$
(6)

holds due to the chain rule.

When an impulsive and sufficiently weak perturbation \(\epsilon \boldsymbol{k} \ (|\epsilon | \ll 1)\) is given to the system at \(\boldsymbol{x}_0(\theta _*)\), the response of the phase can be linearly approximated by neglecting higher-order terms in \(\epsilon \) as

$$\begin{aligned} \theta ( \boldsymbol{x}_0(\theta _*) + \epsilon \boldsymbol{k} ) - \theta _*= \nabla \theta ( \boldsymbol{x}_0(\theta _*) ) \cdot \epsilon \boldsymbol{k}\;. \end{aligned}$$
(7)

Thus, the gradient \(\nabla \theta ( \boldsymbol{x}_0(\theta _*) )\) of \(\theta \), evaluated at \(\boldsymbol{x} = \boldsymbol{x}_0(\theta _*)\) characterizes linear response property of the oscillator phase to weak perturbations. \(\nabla \theta ( \boldsymbol{x}_0(\theta _*) )\) is called the phase sensitivity function (a.k.a. infinitesimal phase resetting curve, perturbation projection vector) [34,35,36,37]. The phase sensitivity function plays central roles in analyzing synchronization dynamics of oscillatory systems. In the following, we denote the phase sensitivity function as \(\boldsymbol{Z}(\theta _*) := \nabla \theta ( \boldsymbol{x}_0(\theta _*) )\).

Consider a limit-cycle oscillator subjected to a weak perturbation, described by the equation:

$$\begin{aligned} \dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t)) + \epsilon \boldsymbol{p}(\boldsymbol{x},t)\;, \quad \boldsymbol{p}(\boldsymbol{x},t) \in \mathbb {R}^{N_\textrm{d}}\;, \end{aligned}$$
(8)

where \(\epsilon \boldsymbol{p}\) represents a small perturbation of magnitude \(\epsilon \), i.e., \(|\epsilon | \ll 1\). The dynamics of the phase \(\theta (\boldsymbol{x}(t))\) can be obtained using the chain rule:

$$\begin{aligned} \dot{\theta }(\boldsymbol{x}(t))= \nabla \theta (\boldsymbol{x}(t)) \cdot \{ \boldsymbol{F}(\boldsymbol{x}(t)) + \epsilon \boldsymbol{p}(\boldsymbol{x},t) \} = \omega + \epsilon \nabla \theta (\boldsymbol{x}(t)) \cdot \boldsymbol{p}(\boldsymbol{x},t)\;. \end{aligned}$$
(9)

This equation is not yet closed in phase \(\theta \) because \(\nabla \theta (\boldsymbol{x})\) depends on \(\boldsymbol{x}\). In order to obtain an equation for \(\theta \), we used the fact that the perturbation is small and \(O(\epsilon )\), implying that the deviation of the state \(\boldsymbol{x}\) from \(\chi \) is also small and \(O(\epsilon )\), i.e., \(\boldsymbol{x}(t) = \boldsymbol{x}_0(\theta _*) + O(\epsilon )\), where \(\theta _* = \theta (\boldsymbol{x}(t))\). The gradient \(\nabla \theta \) at \(\boldsymbol{x}\) can then be expressed as \(\nabla \theta (\boldsymbol{x}(t)) = \nabla \theta (\boldsymbol{x}_0(\theta _*)) + O(\epsilon )\) and by substituting into (9), we obtain an approximate phase equation for \(\theta \),

$$\begin{aligned} \dot{\theta }(t) = \omega + \epsilon \boldsymbol{Z}(\theta ) \cdot \boldsymbol{p}(\boldsymbol{x}_0(\theta ),t)\;, \end{aligned}$$
(10)

by neglecting the terms of \(O(\epsilon ^2)\). This phase equation is now closed in \(\theta \) and can be solved for \(\theta \) when the phase sensitivity function \(\boldsymbol{Z}\) and perturbation \(\epsilon \boldsymbol{p}\) are given. Thus the \(N_\textrm{d}\)-dimensional nonlinear dynamics of the oscillator is successfully reduced the one-dimensional phase dynamics.

When the model of a dynamical system is known, a convenient method for calculating the phase sensitivity function is the adjoint method [38,39,40]. The adjoint method involves solving

$$\begin{aligned} \omega \frac{d}{d\theta } \boldsymbol{Y}(\theta ) = - \textrm{D} \boldsymbol{F}^\top ( \boldsymbol{x}_0(\theta ) ) \boldsymbol{Y}(\theta )\;, \quad \boldsymbol{Y}(\theta ) \in \mathbb {R}^{N_\textrm{d}}\;, \end{aligned}$$
(11)

where \(\textrm{D} \boldsymbol{F}\) is the Jacobian matrix of \(\boldsymbol{F}\) and \(\top \) denotes the transposition. This equation is solved backward in time with an initial condition \(\boldsymbol{Y}(0)\) such that \( \boldsymbol{F}(\boldsymbol{x}_0(0)) \cdot \boldsymbol{Y}(0)\ne 0\). It then converges to a periodic solution. Normalizing this solution using the condition \( \boldsymbol{F} ( \boldsymbol{x}_0(\theta ) ) \cdot \boldsymbol{Y}(\theta )= \omega \), which corresponds to (6), gives rise to the phase sensitivity function. While this is a simple method, it requires the calculation of the Jacobian matrix, which can often be challenging to use for high-dimensional oscillatory systems. Therefore, methods to avoid the calculation of the Jacobian matrix have also been proposed [41, 42].

The phase sensitivity functions can also be measured experimentally in model-free manners [43,44,45,46,47]. Furthermore, the phase function (and thus its gradient) can also be characterized by an eigenfunction of the associated Koopman operator for dynamical systems [48]. The Koopman operator allows for a data-driven spectral decomposition method, known as dynamic mode decomposition, which is a rapidly evolving field of study [49].

3.2 Second-Harmonic Injection Locking

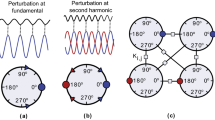
An oscillator with a frequency \(\omega \) can be entrained by an external periodic signal having a frequency close to \((l/k)\omega \), where k and l are natural numbers. This is phenomenon is known as synchronization of order k : l. If \(k < l\) (resp. \(k > l\)), the locking is referred to as sub-harmonic (resp. superharmonic) [16, 17]. The term “second-harmonic injection locking” refers to 1 : 2 sub-harmonic synchronization. Furthermore, when an oscillator is perturbed by an external second-harmonic injection signal, the phase difference between the oscillator and the injection signal settles down to one of two values, separated by \(\pi \). This allows for the encoding of a spin state of an Ising model into the phase difference, using the two steady states to represent the spin down or up, respectively.

Let us provide a concrete discussion of this scenario. Consider a limit-cycle oscillator with the frequency \(\omega \) subjected to a weak, almost second-harmonic perturbation of frequency \(\omega _\textrm{s} \approx 2\omega \), described by the equation:

$$\begin{aligned} \dot{\boldsymbol{x}}(t) = \boldsymbol{F}(\boldsymbol{x}(t)) + \epsilon \boldsymbol{p}(t)\;. \end{aligned}$$
(12)

We define \(\omega -\omega _\textrm{s}/2 = \Delta \omega \) and the phase difference \(\psi \) between the oscillator and the forcing as

$$\begin{aligned} \psi :=\theta - \frac{1}{2}\omega _\textrm{s}t\;. \end{aligned}$$
(13)

The evolution of the phase difference is then given by

$$\begin{aligned} \frac{\textrm{d} \psi }{\textrm{d} t}=\Delta \omega +\boldsymbol{Z}\left( \frac{1}{2} \omega _\textrm{s} t+\psi \right) \cdot \epsilon \boldsymbol{q}\left( \omega _\textrm{s} t\right) \;, \end{aligned}$$
(14)

where \(\boldsymbol{q}\left( \omega _\textrm{s} t\right) := \boldsymbol{p}(t)\). From the assumptions \(\omega _\textrm{s} \approx 2\omega , |\epsilon | \ll 1\), the right-hand side of (14) is very small, and \(\psi \) varies slowly. Hence, the averaging method [50] provides an approximate dynamics of (14) as

$$\begin{aligned} \dfrac{\textrm{d} \psi }{\textrm{d} t} = \Delta \omega + \epsilon \Gamma (\psi )\;, \end{aligned}$$
(15)
$$\begin{aligned} \Gamma (\psi )=\dfrac{1}{2 \pi } \int \limits _0^{2 \pi } \textrm{d} \theta \boldsymbol{Z}(\theta +\psi ) \cdot \boldsymbol{q}(2 \theta )\;. \end{aligned}$$
(16)

Consider the Fourier series expansions of \(\boldsymbol{Z}\) and \(\boldsymbol{q}\):

$$\begin{aligned} \boldsymbol{Z}(\phi )=\left[ \sum _{k=-\infty }^{\infty }{Z_{1,k}e^{ik\phi }}, \sum _{k=-\infty }^{\infty }{Z_{2,k}e^{ik\phi }}, \cdots , \sum _{k=-\infty }^{\infty }{Z_{N_\textrm{d},k}e^{ik\phi }}, \right] ^\top \;, \end{aligned}$$
(17)
$$\begin{aligned} \boldsymbol{q}(\phi )=\left[ \sum _{l=-\infty }^{\infty }{q_{1,l}e^{il\phi }}, \sum _{l=-\infty }^{\infty }{q_{2,l}e^{il\phi }}, \cdots , \sum _{l=-\infty }^{\infty }{q_{N_\textrm{d},l}e^{il\phi }}, \right] ^\top \;. \end{aligned}$$
(18)

Then,

$$\begin{aligned} \Gamma (\psi ) = \sum _{m=1}^{N_\textrm{d}}\sum _{l=-\infty }^{\infty }{Z_{m,-2l}q_{m,l}e^{-2il\psi }}\;. \end{aligned}$$
(19)

If \(\epsilon \boldsymbol{p}(t)\) is a second-harmonic injection, i.e., \(q_{m,l}=0\) for any \(|l|\ne 1\), (19) simplifies to

$$\begin{aligned} \Gamma (\psi ) = 2.0\sum _{m=1}^{N_\textrm{d}}\textrm{Re}\left( Z_{m,-2}q_{m,1}e^{-2i\psi }\right) \;. \end{aligned}$$
(20)

This equation represents a second-harmonic wave. Therefore, when the mismatch in the 1 : 2 frequency relation \(\Delta \omega \) is sufficiently small, the dynamics of the phase difference (15) exhibits two stable and two unstable equilibria, each of which are separated \(\pi \). These stable equilibria can be utilized as the spin state of an Ising model.

Even if \(\boldsymbol{q}\) is not a purely second-harmonic, as long as the frequency mismatch condition is met, the DC component of \((q_{m,0})_{m=1}^{N_\textrm{d}}\) is small, and \(Z_{m,-2l}q_{m,l} \ (|l|\ge 2)\) do not create new equilibria, there continue to be only two stable equilibria separated by \(\pi \). This separation can again be utilized to represent the spin states.

3.3 Kuramoto Model

In this Subsection, we derive a variant of the Kuramoto model from a general system of weakly coupled, weakly heterogeneous oscillators subjected to second-harmonic forcing.

Consider

$$\begin{aligned} \dot{\boldsymbol{x}_i}(t) = \boldsymbol{F}(\boldsymbol{x}_i(t)) + \tilde{\boldsymbol{f}}_i(\boldsymbol{x}_i(t)) + \sum _{j=1}^N{J_{ij}\tilde{\boldsymbol{g}}_{ij}(\boldsymbol{x}_i(t),\boldsymbol{x}_j(t))} + \boldsymbol{p}(t)\;. \end{aligned}$$
(21)

Here, \(\boldsymbol{F}\) has a “standard” oscillator with a periodic orbit \(\tilde{\boldsymbol{x}}_0\) of frequency \(\omega \), while \(\tilde{\boldsymbol{f}}_i\) characterizes the autonomous heterogeneity of the ith oscillator. \(\boldsymbol{J}=(J_{ij})\) is the adjacency matrix of the coupling connectivity, and \(\tilde{\boldsymbol{g}}_{ij}\) represents the interaction from oscillator j to i. \(\boldsymbol{p}\) is the almost second-harmonic injection of frequency \(\omega _\textrm{s} \approx 2\omega \). We assume that the magnitudes of \(\tilde{\boldsymbol{f}}\), \(\tilde{\boldsymbol{g}}_{ij}\), and \(\boldsymbol{p}\) are sufficiently small. We introduce phase functions \(\theta _i\) for the ith oscillator using the standard oscillator. We define \(\Delta \omega \) and \(\psi _i\) as in (13). Then we obtain

$$\begin{aligned} {} & {} \dot{\psi _i}(t) = \Delta \omega + \boldsymbol{Z}\left( \dfrac{1}{2} \omega _\textrm{s} t+\psi _i\right) \cdot \nonumber \\ {} & {} \left[ \boldsymbol{f}_i\left( \dfrac{1}{2} \omega _\textrm{s} t+\psi _i\right) + \sum \limits _{j=1}^N{J_{ij}\boldsymbol{g}_{ij}\left( \dfrac{1}{2} \omega _\textrm{s} t+\psi _i,\dfrac{1}{2} \omega _\textrm{s} t+\psi _j \right) } + \boldsymbol{q}\left( \omega _\textrm{s} t\right) \right] \;, \end{aligned}$$
(22)

where \(\boldsymbol{x}_0(\theta ):=\tilde{\boldsymbol{x}}_0(t)\), \(\boldsymbol{f}_i(\theta _*) := \tilde{\boldsymbol{f}}_i(\boldsymbol{x}_0(\theta _*))\), \(\boldsymbol{g}_{ij}(\theta _*,\theta _{**}) := \tilde{\boldsymbol{g}}_{ij}(\boldsymbol{x}_0(\theta _*), \boldsymbol{x}_0(\theta _{**}))\), \(\boldsymbol{q}\left( \omega _\textrm{s} t\right) := \boldsymbol{p}(t)\). Given the assumptions above, the right-hand side of (22) is very small and the averaging approximation leads to

$$\begin{aligned} \dot{\psi _i}(t) = \Delta \omega _i + \sum _{j=1}^N{J_{ij}\Gamma _{ij}(\psi _i-\psi _j)} + \Gamma (\psi _i)\;, \end{aligned}$$
(23)

where \(\Delta \omega _i := \Delta \omega + \delta \omega _i\) and

$$\begin{aligned} \delta \omega _i = \dfrac{1}{2 \pi } \int \limits _0^{2 \pi } \textrm{d} \theta \boldsymbol{Z}(\theta +\psi _i) \cdot \boldsymbol{f}_i(\theta +\psi _i)\;, \end{aligned}$$
(24)
$$\begin{aligned} \Gamma _{ij}(\psi _i-\psi _j) = \dfrac{1}{2 \pi } \int \limits _0^{2 \pi } \textrm{d} \theta \boldsymbol{Z}(\theta +\psi _i) \cdot \boldsymbol{g}_{ij}(\theta +\psi _i,\theta +\psi _j)\;, \end{aligned}$$
(25)
$$\begin{aligned} \Gamma (\psi _i) = \dfrac{1}{2 \pi } \int \limits _0^{2 \pi } \textrm{d} \theta \boldsymbol{Z}(\theta +\psi _i) \cdot \boldsymbol{q}(2 \theta )\;. \end{aligned}$$
(26)

Thus, the system of weakly coupled, weakly heterogeneous oscillators subjected to second-harmonic forcing (21) can be universally reduced to the variant of Kuramoto phase oscillator system (23). This type of Kuramoto model, which has an external field term \(\Gamma \), is called the active rotator model [51,52,53].

3.4 Gradient Structure of the Kuramoto Model

In this Subsection, given certain assumptions about symmetries in the topology and the scheme of interaction, we show that the Kuramoto model (23) is a gradient system. Our discussion draws heavily on the material presented in Appendix C of [22], but we slightly relax the assumption therein and extend the result.

We assume that \(J_{ij}=J_{ji}, \Gamma _{ij}=\Gamma _{ji}\) and its antisymmetricity:

$$\begin{aligned} \Gamma _{ij}(x) = -\Gamma _{ij}(-x)\;. \end{aligned}$$
(27)

Such antisymmetry appears when the interaction \(\boldsymbol{g}_{ij}\) is diffusive, i.e.,

$$\begin{aligned} \boldsymbol{g}_{ij}(\psi _i,\psi _j) = - \boldsymbol{g}_{ij}(\psi _j,\psi _i)\;. \end{aligned}$$
(28)

Note that, in [22], it is assumed that \(\Gamma _{ij}=\Gamma _{kl}\), i.e., the interaction scheme is uniform. We only assume its symmetricity instead.

Let us introduce a potential function L as

$$\begin{aligned} L(\boldsymbol{\psi })& :=\dfrac{1}{2}\sum _{i=1}^N{\sum _{j=1}^N{\left\{ \dfrac{-1}{N}\left[ \Delta \omega _i \psi _i + \Delta \omega _j \psi _j \right] \right. }} \nonumber \\ {} & {{\left. +\dfrac{1}{2N}\left[ I_\textrm{s}(2\psi _i)+I_\textrm{s}(2\psi _j)\right] +J_{ij}I_{ij}(\psi _i-\psi _j)\right\} }}\;, \end{aligned}$$
(29)

where

$$\begin{aligned} I_{ij}(x) := -\int \limits _0^x{\Gamma _{ij}(y)\textrm{d}y}+C_{ij} \;, \end{aligned}$$
(30)
$$\begin{aligned} I_\textrm{s}(x) := -\int \limits _0^x{\Gamma (y)\textrm{d}y} \;. \end{aligned}$$
(31)

Here \(C_{ij}\in \mathbb {R}\) is a constant. Then we have

$$\begin{aligned} \dfrac{\partial }{\partial \psi _l}\Bigg \{\sum \limits _{i=1}^N \sum \limits _{j=1}^N{} & {} \dfrac{-1}{N}\left[ \Delta \omega _i \psi _i+\Delta \omega _j \psi _j\right] \Bigg \} =-\dfrac{1}{N} \sum \limits _{i=1}^N \sum \limits _{j=1}^N\left[ \Delta \omega _i \delta _{i l}+\Delta \omega _j \delta _{j l}\right] \nonumber \\ ={} & {} -\dfrac{1}{N} \sum \limits _{j=1}^N \sum \limits _{i=1}^N \Delta \omega _i \delta _{i l}-\dfrac{1}{N} \sum \limits _{i=1}^N \sum \limits _{j=1}^N \Delta \omega _j \delta _{j l} \nonumber \\ {} & {} =-\dfrac{1}{N} \sum \limits _{j=1}^N \Delta \omega _l-\dfrac{1}{N} \sum \limits _{i=1}^N \Delta \omega _l =-2 \Delta \omega _l\;, \end{aligned}$$
(32)

where \(\delta _{ij}\) is the Kronecker delta. Also,

$$\begin{aligned} &\qquad \dfrac{\partial }{\partial \psi _l} \left\{ \sum \limits _{i=1}^N \sum \limits _{j=1}^N \dfrac{1}{2 N}\left[ I_s\left( 2 \psi _i\right) +I_s\left( 2 \psi _j\right) \right] \right\} \nonumber \\ &\quad =-\dfrac{1}{2 N} \sum \limits _{i=1}^N \sum \limits _{j=1}^N\left[ 2 \delta _{i l} \Gamma \left( 2 \psi _i\right) +2 \delta _{j l} \Gamma \left( 2 \psi _j\right) \right] \nonumber \\ & =-\dfrac{1}{N} \sum \limits _{j=1}^N \sum \limits _{i=1}^N \delta _{i l} \Gamma \left( 2 \psi _i\right) -\dfrac{1}{N} \sum \limits _{i=1}^N \sum \limits _{j=1}^N \delta _{j l} \Gamma \left( 2 \psi _j\right) \nonumber \\ &\;\; =-\dfrac{1}{N} \sum \limits _{j=1}^N \Gamma \left( 2 \psi _l\right) -\dfrac{1}{N} \sum \limits _{i=1}^N \Gamma \left( 2 \psi _l\right) =-2 \Gamma \left( 2 \psi _l\right) \;, \end{aligned}$$
(33)
$$\begin{aligned} &\qquad \qquad \qquad \qquad \dfrac{\partial }{\partial \psi _l}\left\{ \sum \limits _{i=1}^N \sum \limits _{j=1}^N J_{i j} I_{ij}\left( \psi _i-\psi _j\right) \right\} \nonumber \\ &\qquad \qquad \qquad =-\sum \limits _{i=1}^N \sum \limits _{j=1}^N\left[ J_{i j}\left( \delta _{i l}-\delta _{j l}\right) \Gamma _{ij}\left( \psi _i-\psi _j\right) \right] \nonumber \\ & =-\left[ \sum \limits _{j=1}^N \sum \limits _{i=1}^N \delta _{i l} J_{i j} \Gamma _{ij}\left( \psi _i-\psi _j\right) -\sum \limits _{i=1}^N \sum \limits _{j=1}^N \delta _{j l} J_{i j} \Gamma _{ij}\left( \psi _i-\psi _j\right) \right] \nonumber \\ &\qquad \quad =-\left[ \sum \limits _{j=1}^N J_{l j} \Gamma _{lj}\left( \psi _l-\psi _j\right) -\sum \limits _{i=1}^N J_{i l} \Gamma _{il}\left( \psi _i-\psi _l\right) \right] \nonumber \\ &\qquad \quad =-\left[ \sum \limits _{j=1}^N J_{l j} \Gamma _{lj}\left( \psi _l-\psi _j\right) +\sum \limits _{j=1}^N J_{l j} \Gamma _{lj}\left( \psi _l-\psi _j\right) \right] \nonumber \\ &\qquad \qquad \qquad \qquad \left( \because (27) \text{ and } J_{i l}=J_{l i}, \Gamma _{i l}=\Gamma _{l i}\right) \nonumber \\ &\qquad \qquad \qquad \qquad \; =-2 \sum \limits _{j=1}^N J_{l j} \Gamma _{lj}\left( \psi _l-\psi _j\right) \;. \end{aligned}$$
(34)

Thus the Kuramoto model (23) is a gradient flow of L:

$$\begin{aligned} \dot{\boldsymbol{\psi }} = -\nabla L(\boldsymbol{\psi })\;. \end{aligned}$$
(35)

3.5 Working Principle of OIMs

In this Subsection, we explain how an OIM explores the ground state of the Ising Hamiltonian.

Consider a coupled oscillator system, where noisy fluctuation is introduced into (23), as follows:

$$\begin{aligned} \dot{\psi _i}(t) = \Delta \omega _i - K\sum _{j=1}^N{J_{ij}\Gamma _{ij}(\psi _i-\psi _j)} - K_\textrm{s}\Gamma (\psi _i) + K_\textrm{n}\xi _i(t)\;, \end{aligned}$$
(36)

where \(\xi _i(t)\) is a white Gaussian noise with zero mean and unit variance, and \(K, K_\textrm{s}, K_\textrm{n}\) represent the strength of each term. We interpret the stochastic integral of the Langevin equation (36) in the Strantonovich sense, as we are considering real and physical noises [54]. We assume that the symmetry assumptions (27), \(J_{ij}=J_{ji}, \Gamma _{ij}=\Gamma _{ji}\) so that the associated deterministic system has a potential function:

$$\begin{aligned} {} & {} \;L(\boldsymbol{\psi }):=\dfrac{1}{2}\sum _{i=1}^N{\sum _{j=1}^N{\left\{ \dfrac{-1}{N}\left[ \Delta \omega _i \psi _i + \Delta \omega _j \psi _j \right] \right. }} \nonumber \\ {} & {} {{\left. -\dfrac{K_\textrm{s}}{2N}\left[ I_\textrm{s}(2\psi _i)+I_\textrm{s}(2\psi _j)\right] -KJ_{ij}I_{ij}(\psi _i-\psi _j)\right\} }}\;. \end{aligned}$$
(37)

As discussed in Subsect. 3.2, the second-harmonic injection aids in creating two stable equilibria that are separated by \(\pi \). Without loss of generality, we can consider these equilibria as 0 and \(\pi \). This is because \(\psi \) represents the phase difference with respect to the second-harmonic injection, and the origin of the phase of the injection can be chosen arbitrarily. Assuming small phase mismatches \(\Delta \omega _i\) and that all \(\psi _i\) have settled to either 0 or \(\pi \), the potential energy can be approximated as

$$\begin{aligned} L(\boldsymbol{\psi }) \approx -\dfrac{NK_\textrm{s}}{2}I_\textrm{s}(0) - \dfrac{1}{2}\sum _{i=1}^N{\sum _{j=1}^N{KJ_{ij}I_{ij}(\psi _i-\psi _j) }} \;. \end{aligned}$$
(38)

We used the fact that \(I_\textrm{s}(0)=I_\textrm{s}(2\pi )\). As \(\Gamma _{ij}\) is antisymmetric, \(I_{ij}\) is symmetric, hence \(I_{ij}(\pi )=I_{ij}(-\pi )\). Thus, if we can choose \(C_{ij}\) in (30) such that

$$\begin{aligned} I_{ij}(0) = - I_{ij}(\pi ) = C\;, \end{aligned}$$
(39)

where \(C\in \mathbb {R}_{\ge 0}\) is a constant independent of i, j, we obtain

$$\begin{aligned} L(\boldsymbol{\psi }) \approx -\dfrac{NK_\textrm{s}}{2}I_\textrm{s}(0) - \dfrac{KC}{2}\sum _{i=1}^N\sum _{j=1}^N {J_{ij}\tilde{s}(\psi _i)\tilde{s}(\psi _j)} \;, \end{aligned}$$
(40)

where \(\tilde{s}(0)=1, \tilde{s}(\pi )=\tilde{s}(-\pi )=-1\). Thus, the potential function evaluated at \(\pi \)-separated stable equilibria created by second-harmonic injection matches the Ising Hamiltonian (2), up to a constant offset and a constant scaling factor. Since the deterministic part of (36) has the gradient structure, the stationary distribution for \(\boldsymbol{\psi }\) is given by the Boltzmann distribution:

$$\begin{aligned} p_\textrm{s}(\boldsymbol{\psi }) = \mathcal {N}\exp {\left( -\dfrac{2}{K_\textrm{n}^2}L(\boldsymbol{\psi }) \right) }\;. \end{aligned}$$
(41)

In this stationary distribution, states with lower potential energy are more likely to occur. Therefore, when the second-harmonic injection establishes \(\pi \)-separated equilibria, the OIM effectively searches for the ground state of the Ising Hamiltonian.

4 Experiments

In this Section, we conduct numerical investigations to explore the relationship between the performance and properties of OIMs. Our focus is on the MAX-CUT problem, an important problem that is straightforwardly mapped onto the Ising model and is classified as NP-complete. Additionally, we delve into some aspects related to higher harmonics and time discretization, which have remained unexplored thoroughly in the existing literature.

4.1 MAX-CUT Problem

The MAX-CUT problem asks for the optimal decomposition of a graph’s vertices into two groups, such that the number of edges between the two groups is maximized. The MAX-CUT problem is NP-complete for non-planar graphs [55].

In this Chapter, we consider the MAX-CUT problem for unweighted, undirected graphs. The problem can be formulated as follows: Given a simple graph \(G = (V, E)\), where V is the set of vertices and E is the set of edges. Find a partition of V into two disjoint subsets \(V_1\) and \(V_2\) such that the number of edges between \(V_1\) and \(V_2\) is maximized. Let us assign each vertex \(i \in V\) a binary variable \(s_i \in \{-1, 1\}\). If \(i \in V_1\) (resp. \(V_2\)), we set \(s_i = 1\) (resp. \(s_i = -1\)). The term \(1 - s_i s_j\) is 2 if vertices i and j are in different subsets (and thus contribute to the cut), and 0 otherwise. Then, the sum of \((1 - s_i s_j)/2\) over the graph provides the cut value:

$$\begin{aligned} c := \dfrac{1}{4}\sum _{i\in V}\sum _{j\in V}{A_{ij}(1 - s_i s_j)} = \dfrac{|E|}{2} - \dfrac{1}{4}\sum _{i\in V}\sum _{j\in V} A_{ij}s_i s_j\;. \end{aligned}$$
(42)

Therefore, the MAX-CUT problem can be written as \(\max _{\boldsymbol{s}}\lbrace - \frac{1}{2}\sum _{i\in V}\sum _{j\in V} A_{ij}s_i s_j\rbrace \), which is eqivalent to

$$\begin{aligned} \min _{\boldsymbol{s}}\left\{ - \dfrac{1}{2}\sum _{i\in V}\sum _{j\in V} J_{ij}s_i s_j\right\} \;, \end{aligned}$$
(43)

by setting \(\boldsymbol{J}:=-\boldsymbol{A}\). Thus, by defining \(\boldsymbol{J}:=-\boldsymbol{A}\), the MAX-CUT problem is mapped to the Ising model (2).

In this work, we use MAX-CUT problems associated with Möbius ladder graphs in order to demonstrate the performance and characteristics of OIMs. Figure 1(a) depicts a Möbius ladder graph of size 8 along with its MAX-CUT solution. Möbius ladder graphs are non-planar and have been widely employed as benchmarking Ising machines [9, 11, 13, 14, 22, 24,25,26, 32]. Note that the weighted MAX-CUT problem on Möbius ladder graphs has recently been classified as “easy,” falling into the complexity class P (NP-completeness does not imply all instances are hard) [56]. However, our focus is not on the qualitative side, such as the pursuit of polynomial scaling of required time to reach optimal or good solutions for NP-complete problems. Instead, by understanding the impact of the quantitative physical properties of OIMs, particularly the magnitudes and schemes of interaction and injection denoted by \(\Gamma _{ij}\) and \(\Gamma \), we aim to lay the groundwork that could eventually lead to the derivation of effective design principles for physical rhythm elements, thus potentially enhancing the performance of OIMs.

The computational capability of OIMs for MAX-CUT problems, such as experimentally observed polynomial scaling, has been somewhat explained by exploring connections with rank-2 semidefinite programming (SDP) relaxation of MAX-CUT problems [57]. In this regard, the construction of physical coupled oscillator systems that could effectively integrate with randomized rounding [58] would be an intriguing research direction.

Fig. 1
figure 1

(a) Möbius ladder graph of size 8 and its MAX-CUT solution. (b–e) Time evolution of the OIM state (top panel) and the corresponding cut value (bottom panel). The parameters for each plot are as follows: (b) \((K_\textrm{s},K_\textrm{n}) = (0.1, 0.01)\); (c) \((K_\textrm{s},K_\textrm{n}) = (13.5, 0.01)\); (d) \((K_\textrm{s},K_\textrm{n}) = (13.5, 1.25)\); (e) \((K_\textrm{s},K_\textrm{n}) = (13.5, 1.85)\); and (f) \((K_\textrm{s},K_\textrm{n}) = (13.5, 5.27)\)

Full size image

4.2 Experimental Setting and Evaluation Metrics

Unless otherwise specified, (36) is integrated over time using the Euler-Heun method [59] under the parameters listed in Table 1.

Table 1 Default parameters for the numerical integration of an OIM
Full size table

The waveforms of \(\Gamma _{ij}\) and \(\Gamma \) are normalized so that

$$\begin{aligned} \int \limits _0^{2\pi }{|\Gamma _{ij}(\psi )|\textrm{d}\psi } = \int \limits _0^{2\pi }{|\sin {\psi }|\textrm{d}\psi }\;, \ \int \limits _0^{2\pi }{|\Gamma (\psi )|\textrm{d}\psi } = \int \limits _0^{2\pi }{|\sin {2\psi }|\textrm{d}\psi }\;, \end{aligned}$$
(44)

hold.

We define how to interpret the phase difference \(\psi \) as a spin state when it takes values other than \({0, \pi }\). We extend the definition of \(\tilde{s}(\psi )\) in (40) to \([0, 2\pi )\) as \(\tilde{s}(\psi ) := \text {sign}(\cos (\psi ))\).

Figure 1(b–e) illustrates the time evolution of the state of OIMs solving the MAX-CUT problem and the corresponding cut values. (b) corresponds to weak coupling and weak noise. (c–f) are related to a moderate level of coupling, where (c) represents tiny noise, (d) somewhat weak noise, (e) moderate noise, and (f) excessively strong noise. In situations like (e), characterized by moderate coupling and noise intensity, it has been observed that even if the initial conditions do not lead to the spin configuration of the ground state (in this case, with a cut value of 10), the system can effectively navigate to the ground state due to the noise, subsequently sustaining this state for a certain time interval. Excessively strong noise (f) can also guide the OIM toward an instantaneous realization of the ground state. If we were to consider this as an achievement of the ground state, it would imply that the search performance could be infinitely improved by conducting exploration with pure white noise with unbounded strength and using unbounded frequency measurements, independent of the dynamical properties of OIMs. This is of course unphysical. In this study, we explore the performance of OIMs within the range where the dynamical characteristics of them matter. Specifically, when an OIM reaches a particular value of an Ising Hamiltonian and remains at that value for a time duration of \(\tau _\textrm{duration}\) or more, we determine that this Ising Hamiltonian value has been achieved. We set \(\tau _\textrm{duration} = \pi /4\) in this study.

We examine the performance of OIMs using Monte Carlo experiments with randomly generated initial conditions. We define the cut value for each trial as

$$\begin{aligned} \max {\{\mathrm{cut \ value} \ | \ \mathrm{cut \ value \ persists \ for \ a \ time \ duration \ of} \ \tau _\textrm{duration} \ \mathrm {or \ more}\}}\;. \end{aligned}$$
(45)

Note that we do not merely use the cut value at the end point of the time integration interval.

Time-to-solution (TTS) metric is a standard quantitative measure of performance used for Ising machines [9]. TTS is introduced as follows: Consider a Monte Carlo experiment where the time taken for a single trial is denoted by \(\tau \). Assume that, after r trials, it is found that an acceptable performance can be achieved with probability \(p_\textrm{acc}\). The probability that an acceptable performance is achieved at least once in r trials can be estimated as \(1-(1-p_\textrm{acc})^r\). Let us denote the number of trials required to achieve a desired probability, typically set to 99%, as \(r_*\). TTS refers to the time required to conduct \(r_*\) trials, represented as \(\tau r_*\), and can be expressed as follows:

$$\begin{aligned} \textrm{TTS}(\tau ) = \dfrac{\ln {0.01}}{\ln {(1-p_\textrm{acc})}}\tau \;. \end{aligned}$$
(46)

TTS metric exhibits a nonlinear dependence on \(\tau \) due to the nonlinear relationship of \(p_\textrm{acc}\) with \(\tau \). Therefore, in practice, TTS is defined to be

$$\begin{aligned} \textrm{TTS} = \min _{\tau }{\textrm{TTS}(\tau )}\;. \end{aligned}$$
(47)

In this study, a trial is deemed to exhibit an acceptable performance if it yields a cut value greater than 0.9 times the best cut value discovered in the experiment. For the Möbius ladder graph of size 8, the maximum cut value is 10. Therefore, in this case, the acceptance probability corresponds to the ground state probability of the Ising model.

4.3 Effect of Properties of Noisy Fluctuation and Coarse Time Discretization

Figure 2(a) (resp. (d)) shows the color maps of the mean cut value of the OIM (resp. acceptance probability \(p_\textrm{acc}\)) when changing the ratio of injection strength to coupling strength \(K_\textrm{s}/K\) and noise intensity \(K_\textrm{n}\), for a time discretization step of \(\textrm{d}t = 0.01\). Figure 2(c, f) depicts those for a default time discretization step of \(\textrm{d}t = 0.1\). It is observable that the mean cut values and acceptance probabilities have significantly improved by coarsening the time discretization step. Table 2 shows that by coarsening the time discretization step, the maximum of acceptance probabilities has improved by more than four times.

Discussing factors such as the coarsening of the time discretization step might initially appear artificial and tangential for physically implemented Ising machines. However, if we are able to identify a physical equivalent to this coarsening effect, these insights could serve as valuable guides to enhance the efficiency of OIMs.

Figure 2(b, e) plots the color maps for the OIM for a fine time discretization step of \(\textrm{d}t = 0.01\), driven by random pulse inputs at coarse time intervals \(\textrm{d}\tilde{t}=0.1\) instead of the Wiener process. Here, each pulse follows an independent normal distribution, and its variance is taken to be \(K_\textrm{n}^2\textrm{d}\tilde{t}\), that is, identical to the quadratic variation of the Wiener process at the coarse time interval \(\textrm{d}\tilde{t}\). Similar to the case where the time discretization step was coarsened, an improvement in performance can be observed.

In this way, it is conceivable that a solver with effects similar to coarsening the time discretization step can be physically implemented. Given its physical relevance, in this research, we have chosen to default to a coarser time discretization step.

Interestingly, performance improvements through coarsening the time discretization step have also been reported for Ising machines utilizing not stochastic fluctuation but deterministic chaotic fluctuations [60]. It is intriguing to explore effects equivalent to such coarse-graining from both deterministic and probabilistic perspectives.

Fig. 2
figure 2

(a) (resp. (d)) the mean cut value of the OIM (resp. acceptance probability \(p_\textrm{acc}\)) when varying the ratio of injection strength to coupling strength \(K_\textrm{s}/K\) and noise intensity \(K_\textrm{n}\), for a time discretization step of \(\textrm{d}t = 0.01\). (b) (resp. (e)) the same metrics for the OIM subjected to random pulse inputs at coarse time intervals \(\textrm{d}\tilde{t}=0.1\) instead of the Wiener process of the identical variance, with a fine time discretization step of \(\textrm{d}t = 0.01\). (c) (resp. (f)) these measures for the OIM with a coarse time discretization step \(\textrm{d}t = 0.1\). The horizontal and vertical axes of the color map are presented in a logarithmic scale

Full size image
Table 2 Maximum mean cut value and maximum acceptance probability obtained from each simulation setting presented in Fig. 2
Full size table

4.4 Effect of Injection and Noise Strength

Figure 3 shows color maps of the mean cut value, the best cut value, the acceptance probability \(p_\textrm{acc}\), and the time to solution when altering the ratio of injection strength to coupling strength \(K_\textrm{s}/K\) and noise intensity \(K_\textrm{n}\), using the default parameter setting.

In situations where the relative injection strength is small, the best cut value does not reach the maximum cut value 10, indicating that the OIM does not converge to the ground state. Increasing the injection strength stabilizes the ground state, allowing the OIM to reach the ground state without requiring noise, if the initial condition is set within its basin of attraction (as shown in Fig. 1(c)).

However, once the ground state is stabilized, if the noise strength remains low, noise-driven exploration occurs infrequently (as depicted in Fig. 1(d)). Figure 3(c, d) shows that, within certain ranges of \(K_\textrm{n}\), both \(p_\textrm{acc}\) and TTS show no significant improvement. There is an optimal level of noise magnitude that optimizes performance (as shown in Fig. 1(e)). Increasing the noise beyond this optimal level results in an inability to maintain the quasi-steady state, as observed in Fig. 1(f).

Fig. 3
figure 3

Performance measures of the OIM when varying the ratio of injection strength to coupling strength \(K_\textrm{s}/K\) and noise intensity \(K_\textrm{n}\) using the default parameter setting. The horizontal and vertical axes of the color map are presented in a logarithmic scale. (a) Mean cut value. (b) Best cut value. (c) Acceptance probability. (d) Time to solution

Full size image

It should be noted that an excessively strong injection strength stabilizes all possible spin configurations [57], thereby degrading the performance of OIMs.

4.5 Effect of Higher Harmonics in Coupling and Injection Schemes

In [22], it was reported that the performance of the OIMs improves when a square wave type coupling function \(\Gamma _{ij}\) is used. However, there has been no comprehensive study investigating which types of coupling functions \(\Gamma _{ij}\) are effective, nor has there been research into the effectiveness of various injection schemes \(\Gamma \).

Figure 4 shows performance metrics of the OIM when either the coupling scheme, the injection scheme, or both are implemented as square waves. The overall trend remains similar to that in Fig. 3. However, when the coupling scheme is implemented as a square wave, it is observed that the ground state becomes stable even when the injection strength is small (as shown in Fig. 4(d, f)), and there is a significant improvement in performance metrics at optimal parameters, as shown in Table 3. In particular, TTS remains almost invariant over various magnitudes of noise intensity, and thus is largely dominated by whether the initial conditions belong to the attraction region of the ground state. However, when the coupling scheme is a square wave and the injection scheme is a sine wave, it can be observed that there is an improvement in TTS due to noise exploration, as shown in Table 3. This minimum TTS is attained at \(K_\textrm{s}/K=15, K_\textrm{n}=1.43\).

Fig. 4
figure 4

(a, d, g) Performance metrics of the OIM with a square wave coupling scheme and second-harmonic sinusoidal injection scheme. (b, e, h) The same metrics for the OIM with a sinusoidal coupling scheme and square wave injection scheme. (c, f, i) The corresponding metrics for the OIM with both square wave coupling and injection schemes

Full size image
Table 3 Optimal performance metrics obtained from each simulation setting presented in Figs. 3 and 4
Full size table

To explore how optimal the square wave coupling is and what constitutes a good injection scheme, we conducted the following experiments using the parameter set \(K_\textrm{s}/K=15, K_\textrm{n}=1.43\). We consider the following coupling and injection schemes:

$$\begin{aligned} \Gamma _{ij}(\psi ) = \mathcal {N}_\textrm{c}\left[ \sin {\psi } + \sum _{k=2}^5{\dfrac{l_k}{k}\sin {k\psi }} \right] , \quad \boldsymbol{l} \in \{-1,0,1\}^4\;, \end{aligned}$$
(48)
$$\begin{aligned} \Gamma (\psi ) = \mathcal {N}_\textrm{s}\left[ \sin {2\psi } + \sum _{k=2}^5{\dfrac{l_k}{2k}\sin {2k\psi }} \right] , \quad \boldsymbol{l} \in \{-1,0,1\}^4\;, \end{aligned}$$
(49)

where \(\mathcal {N}_\textrm{c}, \mathcal {N}_\textrm{s}\) are normalization constants to satisfy (44). Figure 5 shows TTS calculated for all combinations of the above coupling and injection schemes. The results are plotted against the cosine similarity between each scheme and a square wave. No clear correlation is observed between the similarity to a square wave and the performance of the coupling/injection scheme. Furthermore, a number of schemes demonstrate a TTS smaller than that achieved with a square wave coupling scheme, suggesting that the square wave scheme is not optimal. Most notably, we observed combinations of schemes that reached the ground state in every trial, resulting in a TTS of zero. Figure 6 shows the coupling and injection schemes that achieved a zero TTS. The results suggest that a sawtooth wave is more suitable as the coupling scheme than a square wave, and a triangular wave is effective for the injection scheme.

Fig. 5
figure 5

TTS against the cosine similarity between a square wave and (a) the coupling scheme, and (b) the injection scheme

Full size image
Fig. 6
figure 6

(a) The coupling scheme, and (b) the injection scheme that achieved a zero TTS

Full size image

5 Summary

Oscillations are ubiquitous phenomena observed across various fields of natural science and engineering. Coupled oscillator systems, manifested through diverse physical phenomena, exhibit significant information processing capabilities. These systems hold potential for the development of ultra energy efficient, high frequency, and density scalable computing architectures.

Oscillator-based Ising machines (OIMs) have shown great versatility, offering new paradigms for information processing. Although the inherent nonlinearity in spontaneously oscillating systems presents challenges in analysis and optimization, the application of phase reduction techniques can simplify the analysis and facilitate the optimization of the performance of the system.

The key to designing effective OIMs lies in several factors:

  1. (i)

    Tuning the strengths of coupling, injection, and noise.

  2. (ii)

    Designing good coupling and injection schemes: The choice of coupling and injection schemes, especially their higher harmonics, can greatly affect the performance of OIMs.

  3. (iii)

    Properties of the driving stochastic process: The choice of the stochastic process, beyond the Wiener process, can have a significant impact on the performance of the OIM.

Related to (iii), exploring the physical implementations of performance-enhancing effects, which emerge from the coarse-graining of time discretization, in both deterministic and probabilistic aspects, presents an intriguing research direction. While not discussed in this Chapter, it is known that heterogeneity in the frequency of oscillators can degrade the performance of OIMs [22]. Additionally, performing appropriate annealing is also important [22, 24]. These factors highlight the complexity of designing effective OIMs and the need for a comprehensive approach that considers all these aspects.

These advancements together form the foundation for further improvements and innovations in the development of efficient computing architectures in a versatile manner using coupled oscillator systems.