Heat transfer in granular media consisting of particles in humid air at low confining pressure

Abstract

I study the heat transfer in systems of weakly interacting particles at low confining pressure in the normal atmosphere. The particles have surface roughness with self-affine fractal properties, as expected for mineral particles produced by fracture, e.g., by crunching brittle materials in a mortar. I show that for small particles (say $<10 \ \mathrm{\mu m}$) with hydrophilic surfaces, at large humidity water capillary bridges dominate the heat transfer, while for big particles heat transfer via the air dominates. This differs from vacuum conditions where the propagating electromagnetic (EM) waves give the dominant heat transfer for large particles, while for small particles both the evanescent EM-waves and the phononic contribution from the area of real contact are most important.

1 Introduction

Granular materials can be described as homogeneous media in the continuum approximation, on length scales much larger than the particle sizes (diameter 2R). The effective thermal conductivity K is an important property of granular materials which may be very different from the thermal conductivity $K_0$ of a solid block made from the same material [1, 2]. Thus K depends on not only $K_0$ but on the size and shape of the particles, on the nature of the particle contact regions, and on the fraction of the total volume occupied by the particles, the so-called filling factor. It also depends on the environment such as temperature, gas pressure and humidity.

In this study, we will assume that $K<<K_0$. This is always the case for granular solids in a vacuum where there is no gas or fluid which could facilitate the heat transfer between the particles, but is often the case also in the normal atmosphere. In this case, if all the particles are small enough, the temperature in each particle may be nearly constant but the temperature change slightly from one particle to a nearby particle. The effective thermal conductivity is determined by the heat transfer between the particles and from dimensional arguments one expect $K \approx G/R$, where G is the thermal contact conductance relating to the heat transfer rate between two particles to the temperature difference $\dot{Q} = G(T_0-T_1)$.

Most studies of heat transfer in granular materials have assumed spherical particles without surface roughness. However, all solids have surface roughness [3, 4] which affect all contact mechanical [5, 6], electrical [7, 8] and thermal properties [9,10,11,12,13]. In this paper we will study the influence of surface roughness on the heat transfer between particles in the normal atmosphere where heat flow in the air and in water capillary bridges are important. In an earlier paper [14] we have studied particles in vacuum where the heat transfer involves the (propagating or evanescent) EM field, and phonon transfer in the area of real contact.

2 Heat diffusion in particle systems

We assume that the heat transfer between the particles is so slow that the temperature in each particle is approximately constant in space. We assume for simplicity that all the particles are spherical with equal radius R and forming a simple cubic lattice, and that the temperature depends only on the x-coordinate. The heat transfer rate from the particle at $x-\Delta x$ into the particle at x is $G [T(x-\Delta x)-T(x)]$ and the heat flow rate out of the particle at x to the particle at $x+\Delta x$ is $G [T(x)-T(x+\Delta x)]$, where G is the (thermal) contact conductance (see Fig. 1). The net heat flow into the particle at x is

$$\begin{aligned} \dot{Q}&= G [T(x-\Delta x)-T(x)]- G [T(x)-T(x+\Delta x)]\\&\approx G {\partial ^2 T\over \partial x^2} \Delta x^2 \end{aligned}$$

This will give rise to a change in the temperature in the particle determined by

$$\begin{aligned} \rho C V {\partial T \over \partial t} = \dot{Q} \end{aligned}$$

where $\rho$ is the particle mass density, C the heat capacity per unit mass and $V=4 \pi R^3/3$ the volume of the particle. Thus we get

$$\begin{aligned} \rho C V {\partial T \over \partial t} \approx G {\partial ^2 T\over \partial x^2} \Delta x^2 \end{aligned}$$

Using that $\Delta x = 2 R$ we get the heat diffusion equation

$$\begin{aligned} \rho C {\partial T \over \partial t} = K {\partial ^2 T\over \partial x^2} \end{aligned}$$

where the effective heat conductivity

$$\begin{aligned} K={3\over \pi } {G\over R}. \end{aligned}$$

(1)

The prefactor $\gamma =3/\pi$ was derived for a simple cubic arrangements of the particles. Other arrangements of the spheres result in similar expressions for K, but with a different prefactor $\gamma$ (of order unity).

Fig. 1

Heat transfer between particles at different temperatures

Here we will not discuss the geometrical distribution of the particles in granular materials (the packing geometry). This topic has been discussed in several papers (see Ref. [15] for a review). Particular important are the number of contact points and liquid bridges formed between the particles as these quantities influence the contribution to the heat transfer from the area of real contact and from the fluid in the capillary bridges.

The derivation of (1) is only valid as long as $K<<K_0$. When this inequality is not obeyed but still $K_1<<K_0$, where $K_1$ is the thermal conductivity of the fluid (gas or liquid) surrounding the particles, K will depend non-linearly on G. This is discussed in Appendix C (see also Sect. 6).

Note that the effective heat conductivity K has a factor 1/R. Thus, since for small particles with rough surfaces capillary bridges dominate the heat transfer, and since this contribution is nearly independent of the radius of the particles (see Sect. 5), K will increase as the size of the particles decrease. For big enough particles heat diffusion in the air will dominate, and since it gives a contribution to G roughly proportional to $R\textrm{ln}R$ (see Sects. 3 and 5) the effective heat conductivity K will increase very weakly as $\textrm{ln}R$ with increasing particle radius.

Fig. 2

(a) The heat transfer between two particles in vacuum occurs via lattice vibrations (phonons) in the area of real contact (white arrows) or by electromagnetic radiation (photons) in the non-contact area (blue arrows). (b) In normal (humid) atmosphere, in addition to the processes in (a), heat transfer occur in the atmospheric gas (red arrows) and in water capillary bridges (white arrows)

3 The thermal contact conductance G

Natural mineral particles, e.g., stone powder produced by crunching (involving fracture), are not perfect spherical but have very rough surfaces (see Fig. 2). This will drastically influence the heat contact conductance. In the most general case the heat transfer between two particles can occur via several different interfacial processes (see Fig. 2):

• (a) Contribution from the area of real contact. For insulators, this corresponds to heat transfer via phonons (lattice vibrations) which can propagate from one solid to the other via the area of real contact.

• (b) Heat radiation. Here one must in general consider both the propagating electromagnetic (EM) waves, which correspond to the normal black-body radiation, and the evanescent EM-waves, which decay exponentially with the distance from the surfaces of the solids. The latter will dominate the heat transfer at short surface separation and will be very important for small particles.

• (c) Heat transfer can occur in the surrounding atmosphere by heat conduction (or convection) in the gas.

• (d) In the normal atmosphere fluid capillary bridges may form and heat diffusion in the fluid bridges will contribute to the heat transfer. In fact, even in laboratory ultrahigh vacuum experiments mobile contamination molecules occur on most surfaces which can accumulate in regions where the surface separation is small and result in thermal conductance values many orders of magnitude larger than otherwise expected [16, 17]. This is, in fact, a subject of current research [18].

In the present study, we neglect heat transfer via convection. This is a good approximation for systems of densely packed small particles as the ratio between the convective and diffusive heat currents scales with the particle radius as $R^3$ (see Appendix A).

In an earlier publication, we studied the heat flow in asteroids and in these case there is no atmospheric gas and no capillary bridges so only processes (a) and (b) where relevant. Here we are interested in heat transfer in the normal atmosphere on earth and in these cases processes (c) and (d) are most important unless the temperature is very high, where the EM-wave contribution may dominate.

Fig. 3

The heat current at a water capillary bridge. In the solid most of the thermal resistance occur in a volume element of linear size w at the junction giving the resistance $\sim w/(K_0 w^2) = 1/(K_0 w)$ where $K_0$ is the thermal conductivity. This resistance act in series with the resistance of the capillary (fluid) bridge $R_\textrm{c}=1/G_\textrm{c}$

The phonon heat transfer through the area of real contact, or the heat transfer in narrow capillary bridges, involves a constriction resistance, see Fig. 3. The constriction resistance arises from the localization of the heat flow current in a region of lateral size w (see Ref. [7, 19]). The thermal resistance of a cylinder of width and height w can be obtained from the expression for the heat current: $J= K_0 \Delta T /w$ giving $\dot{Q} = w^2 J = K_0 w \Delta T$ and the constriction conductance $G= K_0w$ and the constriction resistance $1/G = 1/(K_0 w)$. The constriction resistance act in series with these interfacial heat resistances. Thus, for example, the capillary bridge will result in an effective heat conductance $G_\textrm{c}^*$ given by

$$\begin{aligned} {1\over G_\textrm{c}^*} = {1\over G_\textrm{c}} + {1\over K_0 w}, \end{aligned}$$

(2)

where w is the width of the capillary bridge. A similar equation determines the effective area of real contact conductance $G_\textrm{a}^*$. For the heat transfer due to an atmospheric gas between the particles, the constriction resistance is not well-defined because in this case the width of the heat flow region is of order the particle diameter. We note that in some cases the constriction resistance will dominate the heat transfer resistance, but to determine it one must know the width w of the heat transfer region. Thus even if the interfacial heat resistance can be neglected compared to the constriction resistance, the width w of the heat transfer region must be known.

Contribution to G from the atmospheric gas

Consider two flat and parallel surfaces separated by the distance u and surrounded by a gas with molecular mass m. When the surface separation $u>> \lambda _\textrm{g}$, where $\lambda _\textrm{g}$ is the gas molecule mean free path, the heat flow depends on the gas heat conductivity $K_\textrm{g}$, and the heat current

$$\begin{aligned} J= K_\textrm{g} {\Delta T \over u} \end{aligned}$$

where $\Delta T = T_1-T_2$ is the temperature difference between the two solids. In this (diffusive) limit a gas molecules makes many collisions with other gas molecules before colliding with a wall.

When $u<< \lambda _\textrm{g}$ one can neglect collisions between the gas molecules. In this (ballistic) limit the heat transfer depends on the nature of the collisions between the gas molecules and the solid walls. As shown in Appendix B we can interpolate between heat conductance per unit surface area, $\alpha _\textrm{g} = J/\Delta T$, in the diffusive limit and the ballistic limit using

$$\begin{aligned} \alpha _\textrm{g} = {K_\textrm{g} \over u+ a \lambda _\textrm{g}}, \end{aligned}$$

(3)

where a depends on the so-called thermal accommodation coefficient $\alpha$ (see Appendix B). In the numerical calculations below we assume $\alpha = 0.5$ giving $a\approx 3.3$.

Consider now the contact between a sphere and a flat surface, both without surface roughness. The separation u(x, y) can be approximated by $u\approx r^2/2R$ for $r<<R$. Using (3) we get

$$\begin{aligned} G_\textrm{g} \approx \int d^2x {K_\textrm{g} \over u+ a \lambda _\textrm{g}} = 2 \pi \int _0^{r_0} dr \ r {K_\textrm{g} \over u+ a \lambda _\textrm{g}} \end{aligned}$$

where we have introduced a cut-off radius $r_0<R$. Changing the integration variable to u using $r dr = R du$ gives

$$\begin{aligned} G_\textrm{g} \approx 2 \pi R \int _0^{u_0} du {K_\textrm{g} \over u+ a \lambda _\textrm{g}}= 2\pi R K_\textrm{g} \textrm{ln} \left( 1+{u_0\over a \lambda _\textrm{g}}\right) \end{aligned}$$

where $u_0 = r_0^2/2R$. To obtain the total heat conductance we need to choose $r_0$ to be of order R. Hence $u_0$ will be proportional to R, or $u_0 = \kappa R$, and we can write

$$\begin{aligned} G_\textrm{g} = 2\pi R K_\textrm{g} \textrm{ln} \left( 1+{R\over R_0}\right) , \end{aligned}$$

(4)

where $R_0 = a \lambda _\textrm{g}/\kappa$.

For big enough particles $R>> R_0$, $G_\textrm{g}$ will be proportional to $R\textrm{ln}(R/R_0)$ and the effective heat conductivity $K = \gamma G/R \sim \textrm{ln}(R/R_0)$.

For small particles where $R/R_0<< 1$ we get from (4):

$$\begin{aligned} G_\textrm{g} \approx 2\pi R K_\textrm{g} {R\over R_0}, \end{aligned}$$

which scales as $\sim R^2$ with the particle radius and hence $K \sim R$.

Equation (4) was derived for a sphere without surface roughness. We will show below that surface roughness has only a relative small influence on $G_\textrm{g}$. This is in contrast to the huge influence of surface roughness on other quantities such as the contribution to the heat conductance from capillary bridges.

For particles with surface roughness the heat conductance, which is obtained by integrating $\alpha _\textrm{g}$ over the particle surface, can only be obtained by numerical methods. In the study below we only include a circular region centered at the point of contact and with radius $r_0 = 0.5 R$. For a smooth sphere the surface separation for $r=0.5R$ is $u\approx R/8$ and hence $\kappa = 1/8$. Heat exchange will also occur in the region $R/2< r <R$, but it will increase the heat conductance by a factor less than 2, which we will neglect. Neglecting this contribution is particularly good approximation when $R>> \lambda _\textrm{g}$ (where $G_\textrm{gas}$ depends on $R\textrm{ln}R$), i.e. for large enough particles. We also note that the heat transfer from the region $r>R/2$ must be studied using a more accurate approach as the small slope approximation is not valid, and one cannot expect the heat flow to occur in the same way as between parallel surfaces at the local separation given by u(x, y) as is implicit in using (3). Finally we note that using (1) and (4) gives

$$\begin{aligned} K= 2\pi \gamma K_\textrm{g} \textrm{ln} \left( 1+{R\over R_0}\right) \end{aligned}$$

In order for the effective heat conductivity to be given by (1) one must assume $K<<K_0$ or

$$\begin{aligned} 2\pi \gamma \textrm{ln} \left( 1+{R\over R_0} \right)<< {K_0\over K_\textrm{g}} \end{aligned}$$

(5)

For silica particles surrounded by atmospheric gas at room temperature $K_0/K_\textrm{g} \approx 40$ where we have used $K_0 \approx 1 \ \mathrm{W/Km}$ and $K_\textrm{g} \approx 0.025 \ \mathrm{W/Km}$. Since typically $\gamma \approx 0.6$ (see Sect. 6) the inequality (5) is satisfied for particles with radius which obey $\textrm{ln}(R/R_0)<< 10$, giving $R<< 10^5 R_0$. At room temperate where $\lambda _\textrm{g} \approx 60 \ \textrm{nm}$ and hence $R_0 = a \lambda _\textrm{g}/\kappa \approx 1.6 \ \mathrm{\mu m}$. Thus, the inequality $K<<K_0$, which is required in order for the temperature to be nearly constant in each particle, is satisfied only if $R< 1 \ \textrm{mm}$. For quartz particles $K_0 \approx 8 \ \mathrm{W/Km}$ the condition $K<<K_0$ will be obeyed for almost all particle sizes. The gas heat transfer occur over most of the particle surface and in this case there is no constriction modification of the gas contact conductance.

If the gas is replaced by a fluid (e.g. oil or water) with the thermal conductivity $K_1$ the assumption $K<<K_0$ may not be satisfied for any particle radius. Here one must consider two different cases: If the condition $K_1<<K_0$ is satisfied the heat transfer will still be a function of the heat conductance G but the effective conductivity cannot be calculated assuming a constant temperature in the particles, i.e., (1) is not valid and K will depend nonlinear on G (see Appendix C). If the inequality $K_1<<K_0$ is not obeyed a different approach, e.g., an effective medium theory, is needed for determining the effective thermal conductivity [25].

Contribution to G from capillary bridges

In a humid atmosphere, for hydrophilic particles water capillary bridges form in regions between particles where the surface separation is small enough. Here we assume that the fluid (water) wets the solid surfaces. Following Ref. [26], we put water at the interface in all surface regions where the surface separation u(x, y) is below the critical separation $h_\textrm{c}$, where $h_\textrm{c}$ depends on the humidity and is given by the Kelvin equation [27,28,29,30,31].

The (macroscopic) Kelvin equation relates the equilibrium curvature of the liquid–vapor interface with the vapor pressure, as derived by equating the chemical potentials between two bulk phases:

$$\begin{aligned} {1\over r_\textrm{eff}} = {k_\textrm{B} T \over v_0 \gamma } \textrm{ln} {P_\textrm{S}\over P} \end{aligned}$$

where $r_\textrm{eff}$ is the mean radius of curvature such that $1/r_\textrm{eff} =1/r_1+1/r_2$ (where $r_1$ and $r_2$ are the two surface principal radius of curvatures) for the liquid meniscus. Here $k_\textrm{B}$ is the Boltzmann constant, T is the temperature, $\gamma$ the surface tension of water, $v_0=V/N$ the volume of a water molecule in water and $P/P_\textrm{S}$ the relative humidity ($P_\textrm{S}$ and P are the saturated and actual water vapor pressure, respectively). For water $v_0 \approx 29.7 \ \mathrm{\text{\AA }^3}$ and $\gamma \approx 0.072 \ \mathrm{J/m^2}$.

One radius of curvature, say $r_1$, is of the meniscus in the direction normal to the interface and will in general be much smaller than $r_2$. We will denote it with $r_\textrm{c}$ in what follows. The separation $h_\textrm{c} \approx r_\textrm{c} (\textrm{cos}\theta _0+\textrm{cos}\theta _1 )$ where $\theta _0$ and $\theta _1$ are the water contact angle on the two solid surfaces. As an example for water assuming complete wetting ($\theta _0 = \theta _1 = 0$) and room temperature, at the relative humidity $P/P_\textrm{S}=0.5$ for water $h_\textrm{c} \approx 1.5 \ \textrm{nm}$.

The heat flow per unit surface area is given by

$$\begin{aligned} \alpha _\textrm{c} = {K_\textrm{w} \over u+ b \lambda _\textrm{w}}, \end{aligned}$$

(6)

where $K_\textrm{w}$ is the thermal conductivity of water and $\lambda _\textrm{w}$ the mean free path of a water molecule which is an atomic distance of order $0.3\ \textrm{nm}$, and b a number of order unity.

The contribution to the thermal conductance from capillary bridges is obtained by integrating (6) over the wet surface area. For a sphere in contact with a flat surface (no surface roughness) we get

$$\begin{aligned} G_\textrm{c} = \int d^2 x {K_\textrm{w} \over u+ b \lambda _\textrm{w}} = 2 \pi \int _{r_\textrm{c}}^{r_0} dr r {K_\textrm{w} \over u+ b \lambda _\textrm{w}} \end{aligned}$$

where $r_0$ is the radius of the circular wet region centered at the contact point, and $r_\textrm{c}$ a cut-off length where the surface separation if of order the size of a water molecule. Using $u\approx r^2/2R$ we get

$$\begin{aligned} G_\textrm{c}= & {} 2\pi R K_\textrm{w} \int _{u_\textrm{c}}^{h_\textrm{c}} du {1 \over u+ b \lambda _\textrm{w}}\nonumber \\= & {} 2\pi R K_\textrm{w} \textrm{ln} \left( {h_\textrm{c}+b \lambda _\textrm{w} \over u_\textrm{c} +b \lambda _\textrm{w}}\right) . \end{aligned}$$

(7)

The thermal conductivity of water at $T=20^\circ \textrm{C}$ is $K_\textrm{w}=0.598 \ \mathrm{W/m K}$, while the atmosphere gas thermal conductivity is $\sim 20$ times smaller, $K_\textrm{g} =0.025 \ \mathrm{W/m K}$. At $T=20^\circ \textrm{C}$ and $1 \ \textrm{bar}$ the air molecule mean free part is about $\lambda _\textrm{g} \approx 60 \ \textrm{nm}$, while we will use for water $\lambda _\textrm{w} \approx 0.3 \ \textrm{nm}$.

As an example, for the relative humidity $P/P_\textrm{S} =0.5$ we get at $T=20^\circ \textrm{C}$ the height of the capillary bridge $h_\textrm{c} \approx 1.5 \ \textrm{nm}$ and with $u_\textrm{c} = 0.3 \ \textrm{nm}$ and $b \lambda _\textrm{w} \approx 1 \ \textrm{nm}$ we get from (7)

$$\begin{aligned} G_\textrm{c} \approx 2\pi R K_\textrm{w} \textrm{ln} (2.5/1.3) \approx 4 R K_\textrm{w} \end{aligned}$$

or $G_\textrm{c} \approx 2 \times 10^{-6} \ \mathrm{W/K}$ for a $R=1 \ \mathrm{\mu m}$ particle. For particles with large surface roughness the lateral size of the capillary bridge will be smaller than for particles without surface roughness. Thus we will show in Sect. 5 (see Fig. 9) that for a granite particle at $P/P_\textrm{S} =0.5$ the thermal conductance due to water capillary bridges (neglecting the constriction resistance) is $G_\textrm{c} \approx 5\times 10^{-8} \ \mathrm{W/K}$ independent of the particle radius for $R>0.1 \ \mathrm{\mu m}$. The lateral size of the capillary bridges are relatively small and the heat conductance $G_\textrm{c}$ need to be corrected by the constriction contribution, $G_\textrm{c} \rightarrow G_\textrm{c}^*$ (see Sect. 5).

In Ref. [14] we have studied the contribution to the thermal conductance from phonon transfer in the area of real contact and from the electromagnetic field, and here we will only briefly review the main results.

Contribution to G from the area of real contact

Heat transfer between two particles can occur by phonon transfer in the area of real contact. There are two contributions to the thermal resistance, which act in series, associated with this process. One is the constriction resistance and is usually assumed to dominate. However, this assumes that the material at the interface interact as strongly as in the bulk. This may be the case in many practical (engineering) applications where the material in the contact regions are plastically deformed and where (for metals) cold-welded regions form. However, here we are interested in the contact between brittle mineral particles at low contact pressure where the particle-particle interaction is very weak. In this case, most of the contact resistance may be due to the weak coupling between the solids at the interface. In Ref. [14] we have shown that this is the case assuming there is no external force squeezing the particles together, but they are kept together only by the Van der Waals interaction. Assuming an atomic-sized contact in Ref. [14] we showed for silica particles that the interfacial heat conductance $G_\textrm{a} \approx 3.8\times 10^{-11} \ \mathrm{W/K}$ and the contact resistance $R_\textrm{a} = 1/G_\textrm{a} \approx 2.6 \times 10^{10} \ \mathrm{K/W}$.

In Ref. [14] we showed that the interfacial resistance is larger than the constriction resistance $1 /(a_\textrm{c} K_0)$ where $K_0 \approx 1 \ \mathrm{W/Km}$ is the silica thermal conductivity and $a_\textrm{c} \approx d_0 \approx 0.3 \ \textrm{nm}$ the diameter of the contact area. Thus $1/(a_\textrm{c} K_0 ) \approx 3\times 10^{9} \ \mathrm{K/W}$. Since the constriction resistance and the interfacial resistance $R_\textrm{a}$ act in series they add together. We will show below that for particle systems located in the atmospheric gas the heat transfer in the area of real contact can be neglected compared to the contribution from the gas heat transfer.

We note that the assumption of negligible squeezing pressure is a good approximation for the first $1 \ \textrm{cm}$ layer of particles in asteroids, but on earth there will always be an external force (e.g. the gravitational force) which will squeeze particles together. We will address the role of the squeezing pressure on the thermal conductance in another paper.

Contribution to G from the EM field

The heat flux per unit area between two black-bodies with flat surfaces (of area $A_0 \propto R^2$) separated by d is given by the Stefan-Boltzmann law [32]

$$\begin{aligned} J= \sigma \left( T_1^4-T_0^4\right) \end{aligned}$$

(8)

where $T_1$ and $T_0$ are the temperatures of solids $\textbf{1}$ and $\textbf{0}$, respectively. The Stefan-Boltzmann constant

$$\begin{aligned} \sigma = {\pi ^2 k_\textrm{B}^4 \over 60 \hbar ^3 c^2} \end{aligned}$$

where $\hbar$ the reduced Planck’s constant and c the light velocity. Note that (8) is only valid if the surface separation d is larger than the wavelength $\lambda$ of the emitted radiation. Since $c k = \omega$ where the wavenumber $k=2 \pi /\lambda$ we get $\lambda = 2\pi c /\omega =2 \pi c \hbar /\hbar \omega \approx 2 \pi c \hbar /k_\textrm{B}T$ where we have used that a typical photon energy $\hbar \omega$ is of order $k_\textrm{B}T$. At $T=273 \ \textrm{K}$ we get $d_T = c \hbar /k_\textrm{B}T \approx 10 \ \mathrm{\mu m}$.

We assume $T_1-T_0 = \Delta T<< T_0$ and expand J to first order in $\Delta T$:

$$\begin{aligned} J = \sigma 4 T_0^3 \Delta T \end{aligned}$$

Hence the radiative heat transfer coefficient

$$\begin{aligned} \alpha _\textrm{r} =4 \sigma T_0^3 \end{aligned}$$

and the interfacial heat conductance $G_\textrm{r} \approx \alpha _\textrm{r} A_0$.

In this limiting case, the heat transfer between the bodies is determined by the propagating electromagnetic (EM) waves radiated by the bodies and does not depend on the separation d between the bodies. Electromagnetic waves (or photons) always exist outside any body due to thermal or quantum fluctuations of the current density inside the body. The EM-field created by the fluctuating current density exists also in the form of evanescent waves, which are damped exponentially with the distance away from the surface of the body. For an isolated body, the evanescent waves do not give a contribution to the energy radiation. However, for two solids separated by $d < d_{T}$, the heat transfer may increase by many orders of magnitude due to the evanescent EM-waves; this is often referred to as photon tunneling [33]. In the present case, the heat transfer is associated with thermally excited optical (surface) phonons. That is, the electric field of a thermally excited optical phonon in one solid excites an optical phonon in the other solid, leading to energy transfer. The excitation transfer occurs in both directions but if one solid is hotter than the other, there will be a net transfer of energy from the hotter to the colder solid.

In Ref. [14] we have studied the role of the EM field for the heat transfer between particles in a vacuum with applications to asteroids. The same treatment is approximately valid if the particle system is located in atmospheric gas. For room temperature the EM heat transfer is negligible compared to the heat transfer by the atmospheric gas and water capillary bridges (see Fig. 7 below).

4 Surface roughness power spectra of fractured mineral stones

All surfaces of solids have surface roughness and mineral particles produced by fracture have usually large roughness which exhibit self-affine fractal behavior. This implies that if a surface area is magnified new (shorter wavelength) roughness is observed which appear very similar to the roughness observed at smaller magnification, assuming the vertical coordinate is scaled with an appropriate factor.

The roughness profile $z=h(\textbf{x})$ of a surface can be written as a sum of plane waves $\textrm{exp}(i\textbf{q}\cdot \textbf{x})$ with different wave vectors $\textbf{q}$. The wavenumber $q=|\textbf{q}| = 2 \pi /\lambda$, where $\lambda$ is the wavelength of one roughness component. A self-affine fractal surface has a two-dimensional (2D) power spectrum $C(q)\sim q^{-2(1+H)}$ (where H is the Hurst exponent related to the fractal dimension $D_\textrm{f} = 3-H$), which is a strait line with the slope $-2(1+H)$ when plotted on a log–log scale. Most solids have surface roughness with the Hurst exponent $0.7< H <1$ (see Ref. [3]).

The most important information about the surface topography of a rough surface is the surface roughness power spectrum. For a one-dimensional (1D) line scan $z=h(x)$ the power spectrum is given by

$$\begin{aligned} C_\textrm{1D} (q) = {1\over 2 \pi } \int _{-\infty }^\infty dx \ \langle h(x) h(0) \rangle e^{i q x} \end{aligned}$$

where $\langle .. \rangle$ stands for ensemble averaging. For surfaces with isotropic roughness the 2D power spectrum C(q) can be obtained directly from $C_\textrm{1D} (q)$ as described elsewhere [34, 35].

Contact mechanics theory [36] shows that the (elastic) contact between two solids with different surface roughness $h_1(\textbf{x})$ and $h_2(\textbf{x})$, and different elastic properties (Young’s modulus $E_1$ and $E_2$, and Poisson ratio $\nu _1$ and $\nu _2$) can be mapped on a problem of the contact between an elastic half space (with the effective modulus $E_{\textrm{eff}}$ and Poisson ratio $\nu =0$) with a flat surface, and a rigid solid with a combined surface roughness $h(\textbf{x}) = h_1(\textbf{x})+h_2(\textbf{x})$. If the surface roughness on the two surfaces are uncorrelated then the surface roughness power spectrum of the rigid surface

$$\begin{aligned} C(q)=C_1(q)+C_2(q), \end{aligned}$$

where $C_1(q)$ and $C_2(q)$ are the power spectra of the original surfaces. The effective modulus of the elastic solid is determined by

$$\begin{aligned} {1\over E_\textrm{eff}} = {1-\nu _1^2\over E_1}+{1-\nu _2^2\over E_2} \end{aligned}$$

If both particles are made of the same material and produced the same way (e.g. by crunching) then $C(q)=2C_1(q)$ and $E_\textrm{eff}= E_1/[2(1-\nu _1^2)]$.

Fig. 4

The stones 1–13 used for the calculations of the power spectra shown in Fig. 5. The stones (in German) 1 sodalith, 2 rosenquartz, 3 hämatit, 4 onyx, 5 roter jaspis, 6 bergcristall, 7 leopardit, 8 feuercalcit, 9 amazonit, 10 schlangenjaspis, 11 orangencalcit, 12 obsidian, 13 gabbro, was bought on amazon.de and was used as they arrived. The stones have diameters $\sim 3-4 \ \textrm{cm}$

Fig. 5

The surface roughness power spectrum as a function of the wave number (log–log scale) for a fractured granite stone surface 0 (thick red line) and for the stones 1–13 shown in Fig. 4. Note that the stones 2,5,7 and 12 shows similar roughness power spectra as for granite, while the stone 4 (onux) has a power spectrum nearly a factor of 100 smaller than for the granite surface, corresponding to the scaling factor $s=0.1$ in the theory calculations

For randomly rough surfaces, all the (ensemble averaged) information about the surface is contained in the power spectrum C(q). For this reason the only information about the surface roughness which enter in contact mechanics theories (with or without adhesion) is the function C(q). Thus, the (ensemble averaged) area of real contact, the interfacial stress distribution and the distribution of interfacial separations, are all determined by C(q) [37,38,39].

Note that moments of the power spectrum determine standard quantities which are the output of most stylus instruments and are often quoted. Thus, for example, the mean-square roughness amplitude $\langle h^2 \rangle$ and the mean-square slope $\langle (\nabla h)^2\rangle$ are easily obtained as integrals involving $C(\textbf{q})$. We will denote the root-mean-square (rms) roughness amplitude with $h_\textrm{rms}$ and the rms slope with $\xi$. For isotropic roughness, the 2D mean-square roughness amplitude is the same as the 1D mean-square roughness amplitude, but the mean-square slope is a factor of 2 larger in the 2D case.

Using an engineering stylus instrument we measured the roughness profile $z=h(x)$ of 14 mineral stones, namely granite and the 13 mineral stones shown in Fig. 4. The topography measurements were performed using Mitutoyo Portable Surface Roughness Measurement Surftest SJ-410 with a diamond tip with the radius of curvature $R=1 \ \mathrm{\mu m}$, and with the tip-substrate repulsive force $F_\textrm{N} = 0.75 \ \textrm{mN}$. The scan length $L=10 \ \textrm{mm}$ and the tip speed $v=50 \ \mathrm{\mu m/s}$.

Figure 5 shows the surface roughness power spectrum as a function of the wave number (log–log scale) for a fractured granite stone surface 0 (thick red line) and for (in German) 1 sodalith, 2 rosenquartz, 3 hämatit, 4 onyx, 5 roter jaspis, 6 bergcristall, 7 leopardit, 8 feuercalcit, 9 amazonit, 10 schlangenjaspis, 11 orangencalcit, 12 obsidian, and 13 gabbro. Note that the stones 2,5,7 and 12 shows similar roughness power spectra as for granite, while the stone 4 (onux) has a power spectrum nearly a factor of 100 smaller than for the granite surface, corresponding to the scaling factor $s=0.1$ in the theory calculations. See Fig. 4 for pictures of the mineral stones $1-13$.

5 Gas and capillary contribution to G: numerical results

We have calculated the heat contact conductance using the same approach as used to study the adhesion between particles with random surface roughness in Ref. [6]. No two natural stone particle have the same surface roughness, and the heat transfer between two particles will depend on the particles used. To take this into account we have generated particles (with linear size $L=2R$) with different random surface roughness but with the same surface roughness power spectrum. That is, we use different realizations of the particle surface roughness but with the same statistical properties. We first generate a smooth particle with radius R (or radius of curvature R) and add the surface roughness h(x, y) which has zero mean height, $\langle h \rangle =0$.

For each particle size, we have generated 60 particles using different set of random numbers. The surface roughness was generated as described in Appendix A of Ref. [4] by adding plane waves with random phases $\phi _\textbf{q}$ and with the amplitudes determined by the power spectrum:

$$\begin{aligned} h(\textbf{x}) = \sum _\textrm{q} B_\textbf{q} e^{i (\textbf{q} \cdot \textbf{x} + \phi _\textbf{q})} \end{aligned}$$

where $B_\textbf{q} = (2\pi /L) [C(\textbf{q})]^{1/2}$. We assume isotropic roughness so $B_\textbf{q}$ and $C(\textbf{q})$ only depend on the magnitude of the wavevector $\textbf{q}$.

We have used nominally spherical particles with 7 different radii, where the radius increasing in steps of a factor of 2 from $R=78 \ \textrm{nm}$ to $R=5.06 \ \mathrm{\mu m}$. The longest wavelength roughness which can occur on a particle with radius R is $\lambda \approx 2R$ so when producing the roughness on a particle we only include the part of the power spectrum between $q_0< q < q_1$ where $q_0 = \pi /R$ and where $q_1$ is a short distance cut-off corresponding to atomic dimension (we use $q_1 = 1.4\times 10^{10} \ \mathrm{m^{-1}}$). We will refer to these particles as granite particles because the power spectra used are linear extrapolation to larger wavenumber of the measured granite power spectrum. For more details about the numerical procedure see Ref. [6].

We will now present numerical results for the heat conductance of granite particles. We will also consider particles with the same sizes as above but with larger and smaller surface roughness, obtained by scaling the height h(x, y) for the granite particles with scaling factors $s=0$ (smooth surface), 0.1, 0.2, 0.4, 1 and 2. Note that scaling h(x, y) by a factor of s will scale the power spectrum with a factor of $s^2$ but it will not change the slope of the C(q) relation on the log–log scale so the Hurst exponent (and the fractal dimension) is unchanged.

We assume that the heat current depends on the surface separation u(x, y) as $J(x,y)= K_\textrm{g} \Delta T/(u+a\lambda _\textrm{g} )$ in the dry surface area, and $J(x,y)= K_\textrm{w} \Delta T/(u+b\lambda _\textrm{w} )$ in the surface area filled with water. This holds accurately only in the small slope approximation (for a discussion of the accuracy of this method, see Ref. [10]). The total heat conductance $G_\textrm{tot}$ is obtained by integrating $J(x,y)/\Delta T$ over the surface area (see Fig. 6). We obtain the capillary $G_\textrm{c}$ and the gas $G_\textrm{g}$ heat conductance by integration of $J(x,y)/\Delta T$ over the wet and dry surface area, respectively. The capillary contribution needs to be corrected by the constriction contribution so that $G_\textrm{c} \rightarrow G_\textrm{c}^*$ and $G_\textrm{tot} = G_\textrm{c}^* +G_\textrm{g}$.

Fig. 6

Heat transfer between a rigid particle in contact with a rigid flat surface in a humid atmosphere. The particle has surface roughness and is in contact with a smooth surface in one point. The heat transfer occurs between the solids by heat transfer (diffusive or ballistic) in the surrounding atmospheric gas and in the water capillary bridges. The capillary bridges are in thermal (kinetic) equilibrium with the surrounding gas of water molecules

Fig. 7

The cumulative probability for the heat conductance due to the evanescent electromagnetic (EM) waves (in vacuum), and due to heat conduction in water capillary bridges (in the normal atmosphere at the relative humidity $\textrm{RH} = 0.5$). For silica particle ($s=1$) at $T=20^\circ \textrm{C}$ and for many particle radius from $R=0.08 \ \mathrm{\mu m}$ to $5.06 \ \mathrm{\mu m}$. The probability distributions are obtained from 60 simulations for each particle radius. The 60 simulations use 60 different realizations of the particle surfaces topography but with the same power spectra. The calculations are for the granite surface (scaling factor $s=1$, Hurst exponent $H=1$) at 293 K, parameter R is effective particle radius

Consider now the contact between silica particles ($s=1$) in the normal atmosphere (gas pressure $p=1 \ \textrm{bar}$) at the relative humidity $\textrm{RH} = 0.5$. Figure 7 shows the cumulative probability for the heat conductance due to heat conduction in the water capillary bridges for many particle radius from $R=0.08 \ \mathrm{\mu m}$ to $5.06 \ \mathrm{\mu m}$. The probability distributions are obtained from 60 simulations for each particle radius. The 60 simulations use 60 different realizations of the particle surfaces topography but with the same power spectra. Note that the heat conductance is nearly the same independent of the particle radius. This is not the case for the heat conductance from heat flow in the gas which increases with the particle radius faster than linear (see Fig. 9).

In Fig. 7 we also show the heat conductance due to the evanescent electromagnetic (EM) waves (in vacuum) which was studied in Ref. [14]. Note that the heat transfer in the capillary bridges is much more important that the EM wave contribution, i.e. we expect much larger heat conductance in the normal atmosphere than in vacuum.

Figure 8 shows the contribution to the heat conductance from the heat flow in (a) the water capillary bridges, $G_\textrm{c}$, and in (b) the gas, $G_\textrm{g}$, for particles in the normal atmosphere ($p=1 \ \textrm{bar}$ gas pressure) at the relative humidity $\textrm{RH} = 0.5$. Results are shown for smooth particles ($s=0$), and for particles with the granite particle roughness scaled by the factor of s. The conductance is obtained by averaging over 60 realizations of the surface roughness for each particle radius. The $s=0$ line in (a) is given by (7) and has the slope 1 corresponding to a linear increase in $G_\textrm{c}$ with increasing particle radius R.

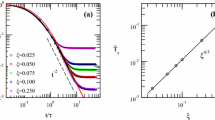
For smooth spherical particles ($s=0$) the heat conductance contribution from the capillary bridges increases linearly with the particle radius, but for $s=1$ and $s=2$ the heat conductance is independent of the particle radius. The contribution from heat transfer in the gas increases with the particle radius as $\sim R^2$ for small particle radius while for larger radius than used here it increases nearly linearly with R (or as $\sim R \textrm{ln} R$). The cross-over from $G_\textrm{g} \sim R^2$ to a $\sim R \textrm{ln} R$ with increasing particle radius is due to the switching from ballistic to diffusive gas motion dominating the heat transfer. Note that $G_\textrm{g}$ is only weakly dependent on the particle surface roughness, compared to the strong dependency of $G_\textrm{c}$ on the roughness parameter s.

To illustrate how the heat transfer depends on the relative humidity, consider again silica particles ($s=1$) in the normal atmosphere ($p=1 \ \textrm{bar}$) as we increases the humidity from $P/P_\textrm{0} = 0.1$ to 0.95. Figure 9 shows the contribution to the heat conductance from heat transfer in the capillary bridges and in the atmospheric gas as a function of the logarithm of the particle radius. Note that for large enough particles the contribution to the heat conductance from the heat flow in the gas will dominate the total conductance.

Figure 10 shows the heat conductance due to heat transfer in the atmospheric gas as a function of the logarithm of the particle radius for dry air (relative humidity $P/P_\textrm{0} = 0$). We show results for the gas pressure $p=0.001$, 0.01, 0.1 and $1 \ \textrm{bar}$.

We now consider the role of constriction resistance. This requires determining the lateral size of the water-filled region, and of the gas filled region. Figure 11 shows the heat flow current $\partial J(x,y,T)/\partial T$ in the water capillary bridge in the xy plane. The center of the square region is at the point where the particle makes contact with the plane. The result is for (a) $s=1$ (granite particle) and (b) for $s=0.1$, with the particle radius $R=0.32 \ \mathrm{\mu m}$ at the relative humidity $\textrm{RH}=0.71$.

Fig. 8

The thermal conductance due to (a) water capillary bridges, $G_\textrm{c}$, and due to (b) heat transfer in the air, $G_\textrm{g}$. For the relative humidity $\textrm{RH} = 0.5$ and at $p=1 \ \textrm{bar}$ gas pressure. Results are shown for smooth particles ($s=0$) and for particles with the granite particle roughness scaled by the factor of s. The results are averages of 60 simulations for each particle radius using 60 different realizations of the particle surfaces topography but with the same power spectra

Fig. 9

The heat conductance due to heat transfer in capillary bridges and in the atmospheric gas as a function of the logarithm of the particle radius. For several relative humidity’s from $P/P_\textrm{0} = 0.1$ to 0.95. For the temperature $T = 20^\circ \textrm{C}$ and the gas pressure $p=1 \ \textrm{bar}$. The results are averages of 60 simulations for each particle radius using 60 different realizations of the particle surfaces topography but with the same power spectra

Fig. 10

The heat conductance due to heat transfer in the atmospheric gas as a function of the logarithm of the particle radius. For the relative humidity $P/P_\textrm{0} = 0$, the temperature $T = 20^\circ \textrm{C}$ and for gas pressures increasing from $p=0.001$ to $1 \ \textrm{bar}$. The results are averages of 60 simulations for each particle radius using 60 different realizations of the particle surfaces topography but with the same power spectra

Fig. 11

The heat flow current $\partial J(x,y,T)/\partial T$ in the water capillary bridge in the xy plane, centered at the point where the particle makes contact with the plane. For (a) a granite particle ($s=1$) and (b) for $s=0.1$, with the radius $R=0.32 \ \mathrm{\mu m}$ and the gas pressure $p=1 \ \textrm{bar}$, the temperature $T=20^\circ \textrm{C}$ and the relative humidity $\textrm{RH}=0.71$. The black region at the center of the capillary bridge [very small in (a) but big in (b)] is a region where the surface separation $u< u_\textrm{c} = 0.3 \ \textrm{nm}$ where we assume no water molecules occur

Fig. 12

The logarithm of the heat flow current $\partial J(x,y,T)/\partial T$ in the water capillary bridge (red) and in the atmospheric gas (blue) along the x-axis through the point where the particle makes contact with the plane. For granite particle ($s=1$) with the radius $R=0.32 \ \mathrm{\mu m}$ and the gas pressure $p=1 \ \textrm{bar}$, the temperature $T=20^\circ \textrm{C}$ and the relative humidity $\textrm{RH}=0.71$

Fig. 13

The effective radius $r_\textrm{wet} = (A_\textrm{wet}/\pi )^{1/2}$ of the region occupied by water (capillary bridges) as a function of the particle radius (log–log scale). For several relative humidity’s from $P/P_\textrm{0} = 0.1$ to 0.95. For the temperature $T = 20^\circ \textrm{C}$ and the gas pressure $p=1 \ \textrm{bar}$. The results are averages of 60 simulations for each particle radius using 60 different realizations of the particle surfaces topography but with the same power spectra

For the same system as in Fig. 11(a) in Fig. 12 we show the logarithm of $\partial J(x,y,T)/\partial T$ in the water capillary bridge (red), and in the atmospheric gas (blue), along the x-axis through the point where the particle make contact with the plane. Note that the heat flow in the water capillary bridge extends laterally of order [see Fig. 11(a)] $a_\textrm{w} \sim 30 \ \textrm{nm}$ giving the constriction contribution to the contact resistance $\approx 1/(K_0 a_\textrm{w}) \approx 3 \times 10^7 \ \mathrm{K/W}$ where we have used the silica heat conductivity $K_0 \approx 1 \ \mathrm{W/m K}$. This is similar but larger than the (water) capillary heat contact resistance (see Fig. 9) $R_\textrm{c} = 1/G_\textrm{c} \approx 1\times 10^7 \ \mathrm{K/W}$. Since these resistances act in series the contact conductance is dominated by constriction contribution $G \approx K_0 a_\textrm{w} \approx 3 \times 10^{-8} \ \mathrm{W/K}$. Note that this is true for all radius of the particles because the size of the wet region is nearly independent of the radius of the particle for the rough particles considered here (granite, $s=1$). The physical reason for this is that the surface roughness, rather than the particle radius of curvature, determine the region where the surfaces are close enough to form the capillary bridge.

As the relative humidity increases the effective diameter of the water-filled region will increase, but this will reduce both the constriction resistance and the capillary bridge resistance. Thus for $\textrm{RH}=0.95$ the width of the water-filled region is about (see Fig. 13) $a_\textrm{w} \approx 250 \ \textrm{nm}$ giving the constriction resistance $\approx 1/(K_0 a_\textrm{w}) \approx 4 \times 10^6 \ \mathrm{K/W}$. In this case, the water contact resistance is (see Fig. 9) $R_\textrm{c} = 1/G_\textrm{c} \approx 6 \times 10^5 \ \mathrm{K/W}$ i.e. the constriction resistance will still dominate. Note that even if the capillary bridge heat resistance can be neglected, the lateral size of the capillary bridge is needed to calculate the constriction resistance.

At very high humidity the water occupies a region with a radius of order the size of the particle. In this limit the constriction resistance looses its meaning, and the thermal conductivity of the system is determined by the heat flow in a composite system consisting of particles immersed in the fluid.

For the particle sizes we have studied above, the gas constriction resistance can be neglected. This follows from the fact that at least for small particles the gas heat transfer does not decrease very much with the distance from the contact point between the particle and the flat (see Fig. 12), while at the same time the gas heat resistance is rather high because of the low thermal conductivity of the gas as compared to the particles. Thus even for the biggest particle with $R \approx 5\times 10^{-6} \ \textrm{m}$ we have (see Fig. 8) $G_\textrm{g} \approx 10^{-6} \ \mathrm{W/K}$ and hence $R_\textrm{g} \approx 10^{6} \ \mathrm{K/W}$, while the constriction resistance $\approx 1/(K_0 2 R) \approx 10^5 \ \mathrm{K/W}$. Thus the gas contact conductance is mainly determined by the heat transfer through the gas giving $G \approx G_\textrm{g} \approx 10^{-6} \ \mathrm{W/K}$.

Fig. 14

The calculated heat conductivity K as a function of the logarithm of the particle radius. We have used $K=\gamma G_\textrm{g}/R$ with $\gamma = 0.6$. The thermal heat conductance due to gas conduction (gas pressure $p=1 \ \textrm{bar}$, relative humidity $\textrm{RH}=0$), $G_\textrm{g}$, are calculated for the surface roughness scaling factor $s=1$ (red line), 0.7 (blue line), 0.5 (green line), 0.3 (pink line), 0.1 (yellow line, below the black line) and 0 (black line). The dashed lines are extrapolations to larger particle radius

6 Discussion

Figure 9 shows that for particles with large roughness ($s=1$), even at the relative humidity $\textrm{RH}=0.95$, the air heat transfer will dominate the total heat conductance if the particle radius $R>10 \ \mathrm{\mu m}$. The effective heat conductivity of quartz sand has been studied as a function of the particle size and the water content [40]. For dry sand, the heat conductivity depends very weakly on the sand particle radius, roughly as $\textrm{ln} R$ for $R> 10 \ \mathrm{\mu m}$, as expected from theory.

When $K<<K_0$ the temperature in each particle can be considered as constant and then $K\approx \gamma G/R$ (see Sect. 2). The parameter $\gamma$ depends on the arrangements of the particles (e.g. random or ordered), on the particle surface roughness, and on the porosity (void volume over total volume). Loosely packed sand has a porosity between $0.4-0.5$ which gives $\gamma$ between 0.4 and 0.7 depending on the model used for the arrangements of the particles (see, e.g., Fig. 20 in Ref. [14]). In Fig. 14 we show the thermal conductivity calculated for dry particles using $K=\gamma G/R$ with $\gamma = 0.6$ assuming only heat transfer in the air gas surrounding the particles. The rapid variation in the slope of the K curve with decreasing particle radius for small particle radius is due to the transition from diffusive to ballistic gas heat transfer when the surface separation decreases below the gas molecule mean free path [see Eq. (13)]. The dashed curves show extrapolated results to typical sand particle diameters $\sim 0.1-1 \ \textrm{mm}$, and gives thermal conductivity’s in the range $K=0.2-0.5 \ \mathrm{W/Km}$ typically observed for loosely packed dry quartz sand [41, 42]. The thermal conductivity of quartz is about $K_0\approx 8 \ \mathrm{W/Km}$ so the condition $K<<K_0$ is approximately obeyed. (Note: quartz is crystalline $\mathrm{Si O_2}$ while silica is amorphous $\mathrm{Si O_2}$; the phonon mean free path is higher in the crystalline state than in the amorphous state, and this is the origin of the much larger thermal conductivity of quartz than of silica where $K_0\approx 1 \ \mathrm{W/Km}$.)

Fig. 15

When the effective thermal conductivity K of a particle system is not much smaller than the thermal conductivity $K_0$ of the solid particles, then the temperature in the particles will not be constant but will drop in the heat flow direction. In this case the temperature change at the interface between the particles $\Delta T= T_\textrm{b}-T_\textrm{c}$ (which will vary over the interface) will be smaller than in the difference $T_1-T_0$ in the average particle temperatures. This will reduce the heat flow and hence the effective thermal conductivity from what would be the case when the temperature in the particles would be uniform

We note that sand particles, e.g., beach sand, are usually “polished” because the wind, or the ocean waves, move particles so that they rub against each other, wearing down rough edges and smoothing surfaces. Thus sand particles may have a power spectra much smaller than that for the granite surface ($s=1$) produced by crunching (fracture), but the heat transfer in the air is not strongly dependent on the particle surface roughness. However, the contribution from capillary bridges depends strongly on the surface roughness.

For wet sand, I am not aware of any studies where the sand is in thermal (or kinetic) equilibrium with humid air at typical humidity’s. Instead the sand is mixed with water but the amount of water is so high as to effectively correspond to almost $100\%$ humidity. In this case the fraction of the total mass (or volume) occupied by water is determined by measuring the weight of the dry and wet sand. As the water content increase from 0 to saturated water content (all cavities filled with water), the heat conductivity for quartz sand in one (typical) study [42] increases from $K \approx 0.3 \ \mathrm{W/Km}$ to $3 \ \mathrm{W/Km}$, i.e., by a factor of $\approx 10$. In this case the condition $K<<K_0$ is no longer satisfied, and the expression $K\approx \gamma G/R$ is not valid. This is the reason (see Fig. 15) for why K increases less than otherwise expected, given by the ratio of the thermal conductivity of water and air, which equals $0.6/0.025 \approx 24$.

In Appendix C I propose a formula for the effective thermal conductivity, valid approximately for any $K/K_0$ as long as $K_1<<K_0$, given by

$$\begin{aligned} K= \gamma {G\over R} \ {1\over 1+\gamma ' G/(RK_0)}, \end{aligned}$$

(9)

where $\gamma$ and $\gamma '$ are of order unity but depend on the porosity, particle surface roughness and the arrangements of the particles. The ratio between the thermal conductivity’s for the water-filled and the gas-filled quartz particle systems depends on the ratio $\gamma '/\gamma$, which can be chosen so as to reproduce the observed ratio $K(\textrm{water})/K(\textrm{gas}) \approx 10$ (see Appendix C).

In this study, we have assumed that there is no applied pressure squeezing the particle system. If an applied pressure occur, and if large enough, the particles will deform plastically (or by brittle fracture) in the particle-particle contact regions, and the area of real contact will increase and the particle will approach each other which will affect both the heat transfer via the atmospheric gas and the capillary bridges. We will study the influence of an applied pressure in another paper.

7 Summary and conclusion

We have studied the heat transfer in weakly interacting particle systems in the normal atmosphere. The particles have surface roughness with self-affine fractal properties, as expected for mineral particles produced by fracture, e.g., by crunching brittle materials in a mortar. The surface topography of several types of mineral stones was studied and the power spectra calculated.

For small particles (say $<10 \ \mathrm{\mu m}$) with hydrophilic surfaces, at large humidity water capillary bridges dominate the heat transfer, while for big particles heat transfer via the air dominates. This differs from vacuum conditions where the propagating electromagnetic (EM) waves give the dominant heat transfer for large particles, while for small particles the evanescent EM-waves and the phononic contribution from the area of real contact are most important.

The calculated effective conductivity was compared to experimental data for quartz sand particles. The observed magnitude and the dependency of the conductivity on the particle radius is in rough agreement with the theory predictions for dry sand. For wet sand no detail comparison of theory with experiment is possible since no equilibrium between the water gas phase and the water capillary bridges occur, and hence the relative humidity is not well defined or known. In addition, for the high water content typically used in experiments the thermal conductivity K is so large that $K<<K_0$ no longer holds accurately, but for this limit we have proposed an approximate formula [see Eq. (9)].

Appendices

Appendix A: Convective heat transfer in small particle systems

Thermal energy can be transferred from hot places to cold places by convection. Convection occurs when warmer areas of a liquid or gas rise to cooler areas in the liquid or gas. In the present study the liquid (water) forms capillary bridges and no convective heat flow can occur in the liquid. However (atmospheric) gas occurs in the cavity regions between the particles and convective heat (and mass) flow could occur in the gas.

Here we are interested in the spontaneous or natural convection of heat driven by the gravity force resulting from the mass density difference between the cold and warm fluid (or gas). This process is in general unimportant for the heat transfer in (densely packed) small particle systems where the cavity regions between the particles have the linear size of the order of particle radius R. If $\Delta T$ is the temperature difference in the fluid over the cavity distance R then the difference in the fluid mass density is $\Delta \rho \approx \beta \Delta T$, where $\beta$ is the thermal expansion coefficient. Thus fluid in the upper half of the cavity region is more heavy than the bottom half by an amount that scales as $\Delta m \sim \Delta \rho R^3$ which gives the gravity force $\Delta F = g \Delta m \sim g \Delta \rho R^3$, where g is the gravity constant. The fluid pressure $\Delta p\sim \Delta F/R^2 \sim g \Delta \rho R$. In a stationary state (constant fluid flow velocity) this pressure difference must be balanced by the friction stress from the viscosity of the fluid which scales as $\eta v/R$ giving $v \sim g \Delta \rho R^2/\mu = g \beta \Delta T R^2 /\mu$. The heat transfer due to the thermal conductivity scales as $J_\textrm{diff} \sim \kappa \Delta T/R$, where $\kappa$ is the fluid heat conductivity. The convective heat flow current $J_\textrm{conv} \sim \rho v C_\textrm{V} \Delta T$, where $C_V$ is the fluid heat capacity, giving $J_\textrm{conv}/J_\textrm{diff} \sim \rho v C_\textrm{V} R/\kappa = (g \beta C_V/\mu \kappa ) \rho \Delta T R^3$. Thus the convective heat transfer, driven by gravity, divided by the diffusive heat transfer scales as $\sim R^3$, so the convective heat transfer will be unimportant for systems of (densely packed) small particles.

Appendix B: Diffusive and ballistic gas contribution to G

Consider two flat and parallel surfaces separated by the distance u and surrounded by gas with molecular mass m. When the surface separation $u>> \lambda$, where $\lambda$ is the gas molecule mean free path, the heat flow depends on the gas heat conductivity $K_\textrm{g}$, and the heat current

$$\begin{aligned} J= K_\textrm{g} {\Delta T \over u} \end{aligned}$$

where $\Delta T = T_1-T_2$ is the temperature difference between the two solids. In this (diffusive) limit a gas molecules makes many collisions with other gas molecules before colliding with a wall.

The kinetic theory of gases gives [20, 21]

$$\begin{aligned} K_\textrm{g} = {1\over 3} C_V {\bar{v}} \lambda _\textrm{g}, \end{aligned}$$

(B1)

where ${\bar{v}}$ is an average gas molecule velocity (see below), and $\lambda _\textrm{g}$ the gas molecule mean free path due to collisions with other gas molecules. In (B1) $C_V$ is the heat capacity per unit volume which for a diatomic gas is given by

$$\begin{aligned} C_V \approx {1\over 2} (3+2) {N\over V} k_\textrm{B} = {5\over 2} {N\over V} k_\textrm{B}, \end{aligned}$$

(B2)

where we have assumed that only the 3 translations and the 2 rotations are thermally activated (the vibration mode has too high energy to be thermally activated). Using (B1) and (B2) gives

$$\begin{aligned} K_\textrm{g}= {5\over 6} {N\over V} k_\textrm{B} {\bar{v}} \lambda _\textrm{g} \end{aligned}$$

(B3)

Using $PV=N k_\textrm{B} T$ we can write

$$\begin{aligned} K_\textrm{g} = {5\over 6} {P \over T} {\bar{v}} \lambda _\textrm{g} \end{aligned}$$

The mean free path [20, 21]

$$\begin{aligned} \lambda _\textrm{g} = {V \over N \sigma \surd 2} \end{aligned}$$

(B4)

where $\sigma$ is a molecular cross section. From (B3) and (B4) we get

$$\begin{aligned} K_\textrm{g} = {5\over 6} {k_\textrm{B} {\bar{v}} \over \sigma \surd 2} \end{aligned}$$

The average velocity

$$\begin{aligned} {\bar{v}} = \left( {8 k_\textrm{B} T \over \pi m} \right) ^{1/2} \end{aligned}$$

Hence $K_\textrm{g}$ is independent of the gas pressure but scales as $T^{1/2}$ with the gas temperature. From (B4) the mean free path

$$\begin{aligned} \lambda _\textrm{g} = {k_\textrm{B} T \over P \sigma \surd 2} \end{aligned}$$

depends on both the gas pressure and the temperature.

When $u<< \lambda _\textrm{g}$ one can neglect collisions between the gas molecules. In this (ballistic) limit the heat transfer depends on the nature of the collisions between the gas molecules and the solid walls. If we assume that the gas molecules stick to a wall when colliding with it, and if they fully thermalize before desorbing, then it is trivial to estimate the energy transfer between the walls. Thus the average kinetic energy of a molecule desorbing from a wall at temperature T is $U=(5/2) k_\textrm{B} T$ (2 rotations plus 3 translations). The average velocity ${\bar{v}}_z = {\bar{v}}/2$, where ${\bar{v}} = \langle v \rangle = (8 k_\textrm{B}T/\pi m)^{1/2}$, and the heat flow current $J\approx (N/V) (\bar{v}/2) (5/2) k_\textrm{B}T$. If the two walls have the temperatures $T_1$ and $T_2$, respectively, the net heat flow will be

$$\begin{aligned} J=J_1-J_2 \approx {5\over 4} {N {\bar{v}} \over V} k_\textrm{B} \Delta T, \end{aligned}$$

where we have assumed that $\Delta T = T_1-T_2<< T_1$. Note that from ideal gas law $PV = N k_\textrm{B}T$ so that

$$\begin{aligned} J\approx {5\over 4} {P {\bar{v}} \over T} \Delta T \end{aligned}$$

(B5)

In general, a gas molecule may not completely thermalize when colliding with a wall, and to describe this the thermal accommodation coefficient is defined by [22]

$$\begin{aligned} \alpha = {E_\textrm{in}-E_\textrm{re} \over E_\textrm{in}-E_\textrm{th}}, \end{aligned}$$

where $E_\textrm{in}$ and $E_\textrm{re}$ are the (average) energy of a molecule before and after colliding with a wall, and $E_\textrm{th}$ the energy of a gas molecule fully thermalized with the wall. Note that $0<\alpha <1$, where $\alpha =1$ correspond to the fully thermalized case, and $\alpha =0$ to the case where there is no energy exchange between the wall and the molecule, where the heat current J must vanish. The heat current for $u<< \lambda _\textrm{g}$ and arbitrary $\alpha$ is given by [23, 24]

$$\begin{aligned} J\approx {1\over 4} {P{\bar{v}} \over T} \left( {\alpha _1\over 2-\alpha _1} +{\alpha _2\over 2-\alpha _2}\right) \left( 1+{f \over 4}\right) \Delta T, \end{aligned}$$

(B6)

where $\alpha _1$ and $\alpha _2$ are the accommodation coefficients for the two different walls and f the number of internal degrees of freedom equal to $f=2$ for a diatomic molecule (two rotation modes; the vibration mode is assumed to be not thermally activated). Assuming $f=2$, and that both solids are of the same material so that $\alpha _1 = \alpha _2 = \alpha$, we get

$$\begin{aligned} J\approx {3\over 4} {P{\bar{v}} \over T} {\alpha \over 2-\alpha } \Delta T \end{aligned}$$

(B7)

Note that for $\alpha =0$ there is, as expected, no heat transfer between the walls, while for $\alpha =1$ (B7) reduces to (B5) except for a numerical factor 3/5 due to inaccuracy in the derivation of (B5) (one need to calculate $\langle v_z U\rangle$ rather than $\langle v_z \rangle \langle U\rangle$ and they differ by a factor of 3/5).

We can interpolate between heat conductance per unit surface area, $\alpha _\textrm{g} = J/\Delta T$, in the diffusive limit and in the ballistic limit using

$$\begin{aligned} \alpha _\textrm{g} = {K_\textrm{g} \over u+ a \lambda _\textrm{g}}, \end{aligned}$$

(B8)

where we choose a so that $J=\alpha _\textrm{g} \Delta T$ reduces to (B6) for $u<<\lambda _\textrm{g}$. Using (B8) and (B5) for $u<<\lambda _\textrm{g}$ we get

$$\begin{aligned} \alpha _\textrm{g} = {K_\textrm{g} \over a \lambda _\textrm{g}} = {5\over 6 a} {P\over T} {\bar{v}}. \end{aligned}$$

(B9)

Comparing (B6) with (B9) gives

$$\begin{aligned} {1\over a}= {3\over 10} \left( {\alpha _1\over 2-\alpha _1} +{\alpha _2\over 2-\alpha _2}\right) \left( 1+{f \over 4}\right) \end{aligned}$$

(B10)

Using $f =2$ and $\alpha _1=\alpha _2=\alpha$ gives

$$\begin{aligned} a= {10 (2-\alpha )\over 9 \alpha } \end{aligned}$$

In the numerical calculations below we assume $\alpha = 0.5$ giving $a\approx 3.3$.

Fig. 16

Heat flow in a simple cubic lattice of cubic blocks (particles). The heat transfer in the gap region (separation u) is assumed proportional to the temperature difference $T_\textrm{b}-T_\textrm{c}$ at the interface

Appendix C: Approximate formula for the heat conductivity

The derivation of (1) is only valid as long as $K<<K_0$. When this inequality is not obeyed but still $K_1<<K_0$, where $K_1$ is the thermal conductivity of the fluid (gas or liquid) surrounding the particles, the temperature will not be constant in the particles and K will depend non-linearly on G.

Consider the heat flow in a simple cubic lattice of cubic blocks (side of length L), and separated by a small distance u, see Fig. 16. The temperature in the blocks decreases linearly with the distance between the two surfaces in the heat flow direction. Thus the heat current

$$\begin{aligned} J=K_0 {T_\textrm{a}-T_\textrm{b} \over L} \end{aligned}$$

(A1)

The heat flow between the blocks is assumed proportional to the temperature difference $T_\textrm{b}-T_\textrm{c}$ between the two surfaces of the blocks at the interface:

$$\begin{aligned} \dot{Q} = J L^2 = G (T_\textrm{b}-T_\textrm{c}) \end{aligned}$$

(A2)

The effective heat conductivity K of the block system is defined by

$$\begin{aligned} J= K \ {T_\textrm{a}-T_\textrm{c}\over L+u} \end{aligned}$$

(A3)

Using (A1)-(A3) gives

$$\begin{aligned} K= {G \over L} \ {1+u/L \over 1+G/(LK_0)} \end{aligned}$$

(A4)

To generalize this to particles with the (average) radius R we first choose $L=2R$ to get

$$\begin{aligned} K= {G \over 2R} \ {1+u/(2R) \over 1+G/(2 R K_0)} \end{aligned}$$

and more generally we write

$$\begin{aligned} K \approx \gamma {G\over R} \ {1\over 1+ \gamma ' G/(R K_0)} \end{aligned}$$

(A5)

where $\gamma$ and $\gamma '$ are numbers of order unity which depends on the geometrical parameters (the spatial arrangement and the shape of the particles). For $K_0 \rightarrow \infty$ from (A5) we get $K\approx \gamma G/R$ while for $K_0 \rightarrow 0$ we get $K\approx 0$. This latter result is not strictly true because even when the thermal conductivity of the particles vanish it is possible for heat to diffuse in the fluid (liquid or gas) surrounding the particles because the fluid is assumed to percolate. However, this involves heat flow in the fluid in regions far from the particle-particle contact region, which we have neglected in our study (see Sect. 3). For $G\rightarrow 0$ we get $K\rightarrow 0$ as expected, and for $G\rightarrow \infty$ we get $K\rightarrow K_0 \gamma /\gamma '$. In this limit, we expect $K>K_0$ which imply $\gamma >\gamma '$.

We can determine $\gamma '/\gamma$ so that (A5) gives the observed ratio $K (\textrm{water})/K (\textrm{gas}) \approx 10$ between the thermal conductivity of water saturated and dry quartz sand. Thus using

$$\begin{aligned} K (\textrm{gas}) \approx \gamma {G_\textrm{g}\over R}, \end{aligned}$$

(A6)

and

$$\begin{aligned} K (\textrm{water}) \approx \gamma {G_\textrm{w}\over R} \ {1\over 1+ \gamma ' G_\textrm{w}/(R K_0)}, \end{aligned}$$

(A7)

where we have assumed the same arrangements of the particles in the dry and in the wet state so $\gamma$ is unchanged, we get

$$\begin{aligned} {K (\textrm{water}) \over K (\textrm{gas})} \approx {G_\textrm{w}\over G_\textrm{g}} \ {1\over 1+ \gamma ' G_\textrm{w}/(R K_0)} \end{aligned}$$

(A8)

Using that

$$\begin{aligned} {G_\textrm{w}\over R K_0} = {G_\textrm{w}\over G_\textrm{g}} {G_\textrm{g}\over R K_0}= {G_\textrm{w}\over G_\textrm{g}} {1\over \gamma } {K(\textrm{gas})\over K_0} \end{aligned}$$

we can write (A8) as

$$\begin{aligned} {K (\textrm{water}) \over K (\textrm{gas})} ={G_\textrm{w}\over G_\textrm{g}} \ {1\over 1+ (\gamma '/\gamma ) (G_\textrm{w}/G_\textrm{g}) (K(\textrm{gas})/K_0)} \end{aligned}$$

Using $K (\textrm{water}) / K (\textrm{gas}) \approx 10$, $G_\textrm{w}/ G_\textrm{g} = K_\textrm{w}/K_\textrm{g} \approx 24$ and $K(\textrm{gas})/K_0 \approx 0.3/8$ gives $\gamma '/\gamma \approx 1.56$, which does not obey the condition $\gamma > \gamma '$. This indicate that $K_0$ may be smaller than the ideal (perfect lattice) quartz thermal conductivity $\approx 8 \ \mathrm{W/m}$. Thus, for example, using $K_0 = 4 \ \mathrm{W/m}$ would give $\gamma '/\gamma \approx 0.78$. Alternatively, the arrangements of the particles in the dry and wet state are different, and the $\gamma$ in (A6) and (A7) differ.