Octupole shape phase transitions and critical points in neutron rich actinides

Abstract

The evolution of octupole shapes and shape phase transitions in neutron rich actinides is studied within the covariant density functional framework. Octupole constrained energy surfaces, and spectroscopic observables of four isotopic chains of: Cm, Cf, Fm and No with neutron numbers $186\le N \le 200$ are analysed using a collective quadrupole–octupole Hamiltonian (QOCH). The parameters of the Hamiltonian are determined by axially reflection-asymmetric relativistic Hartree–Bogoliubov calculations based on the energy density functional DD-PC1, and a finite-range pairing interaction. The results suggest quantum phase transitions from non-octupole to octupole deformed shapes and to octupole vibrations with increasing neutron number. $^{288}$Cm is possibly close to the critical point of a simultaneous phase transition from spherical to prolate deformed and from non-octupole to stable octupole deformed configurations.

1 Introduction

The evolution of equilibrium nuclear shapes is one of the most extensively explored properties of atomic nuclei. Most nuclei in their ground state configuration are non-spherical. In many cases, they manifest deformed shapes, due to strong proton–neutron correlations in open-shell nuclei. Less often, nuclei are characterized by octupole “pear-like” shapes (stable or dynamical) due to spontaneous breaking of their intrinsic reflection symmetry. Reflection-asymmetric shapes in nuclei are due to the long-range octupole–octupole correlations that depend on the coupling of orbitals with $\Delta j = \Delta l = 3$ in the vicinity of the Fermi surface [1]. Regions of the nuclear chart that this condition is fulfilled are for proton Z and neutron numbers N close to 34, 56, 88, and 134 [1,2,3,4]. In the case of actinides ($Z \approx 96$ and $N \approx 196$) the coupling of the neutron orbitals h11/2 and k17/2, and that of the proton single-particle states f7/2 and i13/2, can lead to octupole deformations. Stable octupole deformation is characterized by the formation of the so called “octupole band” consisting of level sequences with alternating parities, and enhanced electric dipole and octupole transitions. In the case of octupole vibrations the negative-parity levels are systematically at higher energy than the ones in the y-rast configuration, forming a separate collective band.

In some regions of the nuclear chart the evolution of the equilibrium shapes with the variation of nucleon number can be sudden and phenomena such as shape coexistence and quantum phase transitions may occur. Phase transitions in the ground state configurations of nuclei correspond to first- and second order quantum phase transitions (QPT) between competing ground-state phases induced by variation of a non-thermal control parameter (number of nucleons) at zero temperature [5]. Thorough theoretical and experimental efforts were performed investigating the phenomena of phase transitions in even–even nuclei near shell closures. Most of them focus on transitions between quadrupole collective degrees of freedom and only recently transitions from stable to dynamical octupole shapes have been considered. Nuclear structure models that have been used in theoretical studies of this type of transitions are algebraic (interacting boson) models [6,7,8,9,10,11,12,13,14,15,16], phenomenological collective models [17,18,19,20,21,22,23,24,25,26], cluster models [27,28,29,30] and, self-consistent mean-field models [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46].

The majority of these studies have been focused on the regions corresponding to $Z \approx 88$ and $N \approx 134$, and $Z \approx 56$ and $N \approx 88$. A systematic search for axial octupole deformation in the region of actinides and superheavy nuclei with proton numbers $Z =$ 88–126 and neutron numbers from the two-proton drip line up to $N = 210$ within the covariant density functional theory (DFT) was performed in [44]. The existence of a region of octupole deformed nuclei around $Z \approx 96$ and $N \approx 196$ was confirmed in this study, in agreement with other studies in this region based on the Skyrme DFT [47] and microscopic–macroscopic [48] calculations. In Ref. [45] reflection-asymmetric relativistic mean-field plus BCS (RMF+BCS) model, with the effective interaction in the particle-hole channel defined by the relativistic density functional PC-PK1 and an EDF-based quadrupole–octupole collective Hamiltonian was applied in a systematic analysis of octupole phase transition in eight neutron-rich isotopic chains - Ra, Th, U, Pu, Cm, Cf, Fm, and No.

In this work the axially reflection-asymmetric implementation of the relativistic Hartree–Bogoliubov (RHB) model [41, 43, 45], and the quadrupole–octupole collective Hamiltonian [41, 43, 51] constructed to calculate the excitation spectra and observables that can be related to quantum order parameters, are used. Shape phase transitions and critical points in the octupole deformed neutron-rich actinides: Cm, Cf, Fm and No are analysed and a microscopic realization of a QPT from non-octupole to stable octupole deformation and to octupole vibrations is presented.

2 Potential energy surfaces

The RHB model provides a unified description of particle-hole (ph) and particle-particle (pp) correlations on a mean-field level. In the present analysis, the mean-field potential is determined by the relativistic density functional DD-PC1 [49] in the ph channel, and a separable pairing force [50] is used in the pp channel. DD-PC1 denotes a parametrization for the covariant nuclear energy density functional with non-linear point-coupling interactions, that was adjusted in a fit to ground-state properties of 64 axially deformed nuclei in the mass regions $A \approx 150-180$ and $A \approx 230-250$ [49]. The DD-PC1 functional has been successfully applied to various properties of finite nuclei, such as the phenomena of quantum phase transitions [10, 52,53,54,55] and shape coexistence [56, 57]. Constrained, axially reflection-asymmetric RHB calculations for the entire energy surface are performed to compute the microscopic input, collective potential and inertia parameters for the quadrupole–octupole collective Hamiltonian as function of the quadrupole $\beta _2$ and octupole $\beta _3$ deformation parameters.

Fig. 1

Microscopic DD-PC1 self-consistent relativistic Hartree–Bogoliubov axially symmetric energy surfaces of the nuclei $^{282-296}$Cm in the ($\beta _2, \beta _3$) plane. The contours join points on the surface with the same energy and the separation between neighboring contours is 0.5 MeV

Fig. 2

Same as Fig. 1 for $^{284-298}$Cf

Fig. 3

Same as Fig. 1 for $^{286-300}$Fm

Fig. 4

Same as Fig. 1 for $^{288-302}$No

Figures  1, 2 and 3 display the contour plots of deformation energy surfaces in the ($\beta _2, \beta _3$) plane for the isotopes of Cm, Cf, Fm and No, respectively, calculated in the constrained RHB model with the DD-PC1 density functional in the particle-hole channel and a separable pairing force. The contours join points on the surface with the same energy; successive contours differ in energy by 0.5 MeV. Already at the mean-field level the RHB model predicts a very interesting structural evolution with transitions from non-octupole to pronounced octupole deformations and to shallow $\beta _3$ potentials. In the case of $^{282}$Cm, $^{284}$Cf, and $^{286}$Fm the potential energy surfaces (PESs) are softer, with the energy minimum at $\beta _2, \beta _3 \approx (0,0)$. With the increase of neutron number more pronounced quadrupole and octupole deformations develop. For $^{288}$Cm, $^{290}$Cf, and $^{292}$Fm with $N=192$ the energy minimum is found in the non-zero octupole deformation region, located at $(\beta _2, \beta _3) \approx (0.09$–0.15, 0.14). The potentials for Cm, Cf and Fm isotopes with $N > 196$ start to become more rigid in $\beta _2$ and softer in $\beta _3$. The maximum gain in binding energy due to octupole deformation [$\Delta E_{oct}=E^{oct}(\beta _2,\beta _3)-E^{quad}(\beta _2',\beta '_3=0)$, cf. Ref. [42, 44]] is found in $^{292}$Cm, $^{294}$Cf, and $^{296}$Fm at neutron number $N=196$. In the isotopic chain of No the deformation energy surfaces are very shallow in both $\beta _2$ and $\beta _3$ for nuclei with $N=186-190$ and a distinct octupole deformed minimum appears in the PES of $^{294}$No. In isotopes with $N \ge 194$ the $\beta _2-\beta _3$ potentials are shallow in the $\beta _3$ direction denoting possible octupole vibrations. The results are in agreement with the ones in Refs.  [44, 45] in which the calculations with the DD-PC1 functional predicts a maximum binding energy gain at $N \approx 196$ in Cm, Cf and Fm and at $N \approx 192$ in No. The PC-PK1 functional predicts the octupole minimum at slightly higher neutron number $N \approx 198$.

3 Spectroscopic properties

To quantitatively study shape transitions and critical point phenomena one must go beyond a simple Kohn–Sham approximation and take into account the restoration of broken symmetries at the mean-field level, and fluctuations in the collective coordinates. Spectroscopic properties relevant for the characterization of shape transitions are investigated using a quadrupole–octupole collective Hamiltonian [41, 43, 51] that is a gamma rigid axially symmetric version of the general quadrupole–octupole Bohr Hamiltonian. The constrained self-consistent solutions of the relativistic Hartree–Bogoliubov equations at each point on the energy surface determine the mass parameters $B_{2 2}$, $B_{2 3}$, $B_{3 3}$, the three moments of inertia $\mathcal {I}_k$, and the zero-point energy corrections as functions of the deformation parameters $\beta _2$ and $\beta _3$. The moments of inertia are calculated according to the Inglis-Belyaev formula [58, 59] and the mass parameters are calculated in the perturbative cranking approximation [43, 60]. The collective potential is obtained by subtracting the zero-point energy corrections [60] from the total energy that corresponds to the solution of self-consistent mean field (SCMF) calculations. The diagonalization of the resulting Hamiltonian yields the low-energy excitation spectrum, collective wavefuctions, and reduced transitions probabilities of even–even nuclei. In Figs. 5, 6 ,7, 8 and 9 the evolution with neutron number (which serves as the control parameter) of several observables that can be related to order parameters obtained with the quadrupole–octupole collective Hamiltonian are analyzed.

Figures  5 and 6 display the systematics of the low-energy excitation spectra of the positive-parity band ($K^{\pi } = 0^+_1$) and the lowest negative-parity band ($K^{\pi } = 0^-_1$), respectively, in the isotopic chains of Cm, Cf, Fm and No. As shown in Fig. 5, the excitation energies of the $\pi =+$ even-spin states in the ground state band decrease with neutron number. The energy levels of isotopes with $N=186-190$ that are close to the neutron shell closure at $N=184$ are equidistant indicating a quadrupole vibrational structure with $E(4^+_1)/E(2^+_1) \approx 2$, whereas for heavier nuclei with $N>194$ it is of rotational type $L(L+1)$ with $E(4^+_1)/E(2^+_1) \approx 3.33$. For all isotopes, the calculated excitation energies exhibit a pronounced decrease from $N = 190$ to $N=192$ indicating the onset of increased quadrupole deformation. In the case of $^{288}$Cm$_{192}$ the $E(4^+_1)/E(2^+_1)$ ratio is equal to 2.7 which is close to the value 2.71 predicted by the X(4) model introduced in Ref. [61] indicating a critical point of a quadrupole phase transition between spherical and quadrupole-deformed prolate shapes. The discrepancy could be due to missing triaxial correlations in the QOCH.

The calculated spectra of the $\pi =-$ odd-spin states as functions of N are shown in Fig. 6. Similarly to the positive-parity ground state energies [cf. Fig. 5], the calculated energy levels in the negative-parity band exhibit a sudden drop from $N=190$ to $N=192$, whereas for $N=192-196$ a weak dependence with neutron number is observed. A local minimum in the excitation spectra is observed in all isotopic chains that in Cm, Cf and Fm occurs at $N\approx 196$, while in No at $N\approx 192$. Starting from $N=198$ ($N=194$ in No), the energies of the $\pi =-$ odd-spin states systematically increase and the band becomes more compressed. This behavior correlates with the systematics of SCMF calculations of the PESs [cf. Figs. 1, 2, 3, 4] in which the octupole deformed minimum developes at $N=192$ becomes more pronounced at $N=196$ and the surfaces become softer in $\beta _3$ from $N > 196$ in the three isotopes of Cm, Cf and Fm, whereas in No the maximum gain in binding due to octupole deformation is observed at $N=192$ and an octupole vibrational behavior is observed for $N \ge 194$. The softness of the potential in the $\beta _3$ direction and the systematics of the calculated $\pi =-$ odd-spin states indicate the development of a rotational-like collective band based on the octupole vibrational $1^-_1$ state. The results signify shape phase transitions from non-octupole to stable octupole deformations and to octupole vibrations as a function of the control parameter – the neutron number. The relevant calculations using the quadrupole–octupole collective Hamiltonian based on the constrained self-consistent RMF+BCS solutions with the functional PC-PK1 and a $\delta$-force pairing predict the minimum at neutron number $N \approx 198$ [45]. The discrepancies between the two theoretical results could be attributed to differences in the underlying shell structure and/or the different pairing strength in the two models.

Fig. 5

Isotopic dependence of the excitation energies of levels of the positive-parity ground-state band ($K^{\pi } = 0^+_1$) for a $_{96}$Cm, b $_{98}$Cf, c $_{100}$Fm, and d $_{102}$No

Fig. 6

Isotopic dependence of the excitation energies of levels of the lowest negative-parity band ($K^{\pi } = 0^-_1$) for a $_{96}$Cm, b $_{98}$Cf, c $_{100}$Fm, and d $_{102}$No

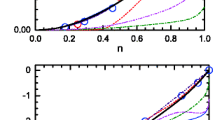
Further evidence of the phase transitions from non-octupole to octupole deformation and octupole vibrations for shallow $\beta _3$ potentials is provided by the odd-even staggering in the energy ratio $E(J^{\pi })/E(2^+_1)$ with $\pi = +$ for even-spin and $\pi = -$ for odd-spin yrast states. In the case of an alternating-parity rotational band the energy ratio would depend quadratically on J. If the even-spin and odd-spin yrast states form a separate rotational band built on the octupole vibration the ratio is expected to show a pronounced odd-even-spin staggering. Figure  7 displays the ratios $E(J^{\pi })/E(2^+_1)$ for both positive- and negative-parity yrast states of $^{282-296}$Cm, $^{284-298}$Cf, $^{286-300}$Fm and $^{288-302}$No as functions of the angular momentum J. One can see that in all isotopic chains the odd-even staggering is negligible for $N \le 190$, with the $\pi =+$ and $\pi =-$ states lying close in energy meaning they merge into a single band. The staggering only becomes more pronounced starting at $N = 192$, indicating the onset of octupole vibrations that is the negative-parity band is a seperate rotational band build on the octupole bandhead. The energy ratio $E(J^{\pi })/E(2^+_1)$ for $\pi =-$ (odd-spin) states could be considered as an order parameter for the octupole shape transition. The results are in consistency with the ones in [45] with the RMF+BCS model.

Fig. 7

Theoretical energy ratios $E(J)/E(2^+_1)$ of the yrast states of a $^{282-296}$Cm, b $^{284-298}$Cf, c $^{286-300}$Fm and d $^{288-302}$No, including both positive (J even) and negative (J odd) parity, as functions of the angular momentum J

The rapid transition and critical behavior is also clearly illustrated by the probability density distributions for the ground state $0^+_1$ and the lowest negative – parity state $1^-_1$ of $^{284,288,292,296}$Cm in the $\beta _2-\beta _3$ plane, plotted in the left and right panels, respectively in Fig. 8. The $0^+_1$ probability densities in $^{284}$Cm and $^{292}$Cm show a peak at ($(\beta _2, \beta _3)\approx (0,0)$) and stable quadrupole–octupole deformed shapes ($(\beta _2, \beta _3)\approx (0.15,0.14)$), respectively. In $^{288}$Cm and $^{296}$Cm the positive-parity yrast bandhead wavefunctions are extended along both $\beta _2$ and $\beta _3$. This is consistent with the systematics of the SCMF calculations of the PESs in the $\beta _2-\beta _3$ plane [cf. Fig. 1] of $^{284,288,292,296}$Cm that indicate a rapid shape transition between $N = 188$ and $N = 192$, from non-octupole to pronounced octupole deformations and between $N = 196$ and $N = 200$ from octupole deformation to octupole vibrations. The collective wave functions for the $1^-_1$ states are concentrated at the same values of $\beta _2$ and $\beta _3$ as the corresponding ground states.

Fig. 8

Probability density distributions for the ground states $0^+_1$ (left panels) and $1^-_1$ states (right panels) of $^{284,288,292,296}$Cm in the $\beta _2-\beta _3$ plane

Fig. 9

Evolution of a $B(E1; 1^-_1 \rightarrow 0^+_1)$, b $B(E2; 2^+_1 \rightarrow 0^+_1)$ and c $B(E3; 3^-_1 \rightarrow 0^+_1)$ values (in W.u. units) as functions of the neutron number in Cm, Cf, Fm and No isotopes

The isotopic dependence of $B(E1; 1^-_1 \rightarrow 0^+_1)$, $B(E2; 2^+_1\rightarrow 0^+_1)$ and $B(E3; 3^-_1 \rightarrow 0^+_1)$ reduced transition probabilities (in units W.u.) are shown in Fig.  9 for the isotopes of Cm, Cf, Fm and No. The theoretical values are obtained using the collective wave functions of $K^{\pi } = 0^+$ and $K^{\pi } = 0^-$ states from the QOCH calculation. The $B(E2; 2^+_1 \rightarrow 0^+_1)$ values (middle panel (b) in Fig. 9) exhibit a sharp increase from $N=190$ to $N=192$ reflecting the shift of the quadrupole deformation $\beta _2$ from nearly zero to $\beta _2 \approx 0.2$ in the SCMF deformation energy surfaces [cf. Figs. 2, 3, 4]. A raise of the $B(E3; 3^-_1 \rightarrow 0^+_1)$ transition rates is connected with increased octupole collectivity and is expected to be larger in octupole deformed nuclei. In Fig.  9 lower panel (c) the large B(E3) values in all four isotopes with $N \ge 192$ indicate an enhanced octupole collectivity that is consistent with the emergence of octupole deformation at these neutron numbers in $\beta _2-\beta _3$ energy surfaces [cf. Figs. 2, 3, 4]. In Cm, Cf and Fm isotopes the higher B(E3) values occur between $N=194$ and $N=198$ and in No at $N=192$ in consistency with the systematics of the calculated energy levels in the negative-parity band. The $B(E1; 1^-_1 \rightarrow 0^+_1)$ rates are also related to octupole deformed shapes. In the upper panel (a) in Fig. 9 large $B(E1; 1^-_1 \rightarrow 0^+_1)$ values are observed in Cf, Fm and No isotopes with neutron numbers $190 \le N\le 196$ having a peak at $N \approx 192$, whereas in Cm the $B(E1; 1^-_1 \rightarrow 0^+_1)$ rates are larger in the heavier isotopes with $N \ge 198$. The systematics of the calculated B(E1) reduced transition probabilities are different from the evolution of the B(E3) ones. One should note that the E1 transitions are more of single-particle nature compared to the E2 and E3 ones; hence the collective model does not necessarily provide accurate predictions for the B(E1) values.

4 Summary and conclusions

Octupole collectivity and critical points of four isotopic chains of: Cm, Cf, Fm and No with neutron numbers $186<N<200$ have been investigated within the microscopic framework of nuclear DFT.

Deformation constrained SCMF calculations have been performed with the relativistic Hartree–Bogoliubov method based on the universal energy density functional DD-PC1 and a separable pairing interaction. At the mean field level the constrained $\beta _2-\beta _3$ energy surfaces, suggest phase transitions from non-octupole to octupole deformed shapes and to octupole vibrations with the critical points at neutron numbers at $N=192$ and $N=196$, respectively.

A collective quadrupole–octupole Hamiltonian withparameters determined by self-consistent mean-field calculations has been used to calculate the low-energy spectra of even–even isotopes. The energy levels of the positive-parity ground-state band of the isotopes under consideration exhibit a decrease with neutron number manifesting a structural change from spherical vibrators to quadrupole deformed rotors. The states in the lowest negative-parity band display a parabolic dependence with increasing neutron number with the deepest minima at $N \approx 196$ in Cm, Cf, and Fm and $N=192$ in No that correspond to stable octupole deformations, consistent with the evolution of the microscopic energy surfaces (Figs.  1, 3, 4).

The odd–even staggering, the probability density distributions for the ground states $0^+_1$ and the $1^-_1$ states and the calculated B(E2) and B(E3) reduced transition probabilities confirm the structural change from spherical vibrators to deformed rotors and from octupole deformated configurations to octupole vibrators with increasing neutron number. The systematics presented here are in consistency with the ones in Ref.  [45] however the differences in the treatment at the mean-field level of the pp and ph correlations result in shifting the critical points. In the RHB (DD-PC1) model treated in this work the critical point for the transition between octupole deformation and octupole vibrations appears at $N \approx 196$ while in the RMF+BCS (PC-PK1) at $N \approx 198$.

In the isotopic chain of Cm the calculations signify the onset of a double phase transition from spherical to quadrupole-deformed and from non-octupole to octupole-deformed shapes, with $^{288}$Cm being closest to the critical point. The neutron-rich actinides considered here appear to have a complex structure with octupole and triaxially deformed shapes. A more complete description of their properties would require extensions of the model in such a way that it simultaneously handles the reflection asymmetric degree of freedom and the triaxial deformation. Experimental studies in this region would help identify any deficiencies of the model, i.e. missing degrees of freedom, description of the underlying shell structure and/or pairing correlations.