Ab Initio Prediction of the Structural, Elastic and Thermodynamic Properties Under Hydrostatic Pressure of the Ternary Tetragonal Phosphides XRh₂P₂ (X = Ca, Ba) for Superconducting Application

Abstract

This study uses density functional theory calculations to study the impact of pressure on the structural, elastic, and thermodynamic properties of CaRh₂P₂ and BaRh₂P₂ compounds. The equilibrium structural parameters closely match the experimental values. CaRh₂P₂ shows a greater reduction in lattice parameter “a” under pressure, while BaRh₂P₂ shows the opposite trend. The single-crystal elastic constants calculated for both compounds meet the criteria for mechanical stability under varying pressures up to 18 GPa. The study extends to polycrystalline elastic properties, including bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, and related properties, under pressures up to 18 GPa. The Pugh ratio, Cauchy pressure, and Poisson’s ratio indicate the ductile behavior of the title compounds. BaRh₂P₂ exhibits superconducting characteristics, unlike CaRh₂P₂, confirmed by interlayer PP bond length calculations. Debye’s quasi-harmonic model explores the temperature dependencies of various properties, with results that align well with elastic constant data, thus validating the results.

1 Introduction

Advancements in modern technology and industry have seen an increasing reliance on superconducting materials in recent years. Notably, the discovery of high-temperature superconductors in 1986 sparked a revolutionary transformation, opening up possibilities for practical applications in diverse fields, including energy transfer, energy storage, and medical imaging [1, 2]. Among these materials, layered ternary intermetallic compounds with the ThCr₂Si₂-type (also known as 122-type) structure have been extensively investigated due to their intriguing and diverse physical phenomena [3]. Researchers have been particularly drawn to these materials because of their noteworthy properties, such as low-temperature superconductivity [4, 5], as well as the ability to exhibit high-temperature superconductivity under the influence of chemical doping and external pressure [6]. Additionally, these compounds exhibit other intriguing characteristics, such as heavy fermion behavior, unique magnetic ordering, and quantum criticality [3, 7,8,9]. The origins of the ThCr₂Si₂-type structure can be traced back to 1965 when Ban and Sikirica first reported it [10]. Subsequently, in 1996, Just and Paufler conducted an extensive geometric analysis of nearly 600 compounds with ThCr₂Si₂-type structure [11]. These compounds are typically represented by the chemical formula AB₂X₂, where A can be alkali, alkaline earth, or rare earth metals, B represents transition metals, and X includes elements from groups 13 to 15 of the periodic table [12, 13]. The 122-type ternary compounds exist in two distinct structures, depending on temperature conditions. The first structure, with a primitive tetragonal arrangement, is exemplified by CaBe₂Ge₂ (space group P4/nmm). The second structure, characterized by a body-centered tetragonal arrangement, is represented by ThCr₂Si₂ (space group I4/mmm) [14]. The ThCr₂Si₂-type structure corresponds to space group I4/mmm (no. 139) and has been identified in over seven hundred compounds [15]. The synthesis of iron-based superconductors with ThCr₂Si₂-type structure, such as AFe₂As₂ (A = Ca, Ba, Sr, Eu), showcasing high critical temperatures of up to 49 K, marked a remarkable breakthrough and played a pivotal role in advancing current technology [16]. However, due to challenges in manufacturing iron-based superconducting materials, researchers have directed their efforts toward exploring alternative ternary intermetallic ThCr₂Si₂-type materials with promising superconducting properties.

Hoffmann and Zheng [17] performed band structure calculations to elucidate the bonding and anti-bonding characteristics of the interlayer P-P bond in the ThCr₂Si₂ structure, which explains the noticeable variation in bond length. The length of the interlayer P-P bond has been identified as a crucial factor in the occurrence of superconductivity in the 122-type phosphides [18]. Theoretical considerations propose a critical interlayer P-P bond length of approximately 2.8 Å (d_P−P ≈ 2.8 Å) for the formation of a covalent bond. Hence, to achieve a superconducting compound within the 122-type series, the interlayer P-P bond length needs to be greater than 2.8 Å [19]. Due to their intriguing superconductive properties at remarkably low temperatures (Tc below 3 K), ThCr₂Si₂-type compounds, such as CaPd₂Ge₂ (Tc = 1.98 K) [20], BaNi₂P₂ (Tc ≈ 3.0 K) [21], YIr₂Si₂ (Tc = 2.52 K) [22], BaIr₂P₂ (Tc = 2.1 K), BaRh₂P₂ (Tc = 1.0 K) [23], have attracted significant interest from researchers. It is evident that 122-type superconducting materials have played a crucial role in the advancement of modern technology. Therefore, the primary objective of this current study is to explore some fundamental physical properties of superconducting materials XRh₂P₂ (X = Ba, Ca). To achieve this, we have conducted ab initio calculations through the Density Functional Theory (DFT)-based pseudopotential plane wave (PP-PW) method. These calculations aim to determine the structural, elastic, and thermodynamic properties of the ternary phosphides BaRh₂P₂ and CaRh₂P₂. The paper is structured as follows: Section 2 provides a detailed explanation of the methodology and the specific calculation parameters employed. In Section 3, we present the analysis and discussion of the physical property results obtained from the calculations. Finally, Section 4 highlights the key findings of the study.

2 Calculational Approches and Settings

Our theoretical investigation was conducted using the pseudopotential plane wave (PP-PW) approach based on density functional theory (DFT) as implemented in the CASTEP program [24]. The exchange-correlation interactions were described using the PBEsol version of the generalized gradient approximation, known as GGA-PBEsol [25]. To model the Coulomb interactions between valence electrons (Ba-5s²5p⁶6s², Rh-4d⁸5s¹, P-3s23p³, and Ca-3s²3p⁶4s²) and the ionic core, Vanderbilt-type ultrasoft pseudopotentials [26] were employed. For the basis set in the plane-wave approach, cut-off energy of 610 eV was chosen for BaRh₂P₂ and CaRh₂P₂. To sample the irreducible Brillouin zone, the Monkhorst-Pack scheme [27] was utilized with a grid of 8 × 8 × 11 k-points. The structural parameters were optimized using the BFGS (Broyden-Fletcher-Goldfarb-Shanno) technique [28]. Convergence tolerances were set as follows: the total energy convergence was within the limit of $5.06 \times {10^{ - 6}}eV/atom$, the maximum Hellmann–Feynman force is within the limit of 0.01 eV / Å, the maximum displacement is within the limit of 5.0 × 10^-4 Å, and the maximum stress is within the limit of $0.0{\text{2 GPa}}$. The elastic constants (denoted as C_ij) are ascertained through the meticulous execution of two distinct and specialized modes of finite lattice distortions. By subjecting the lattice to these deliberate deformations, the resultant strain-stress linear relationship is diligently analyzed and subsequently employed as the foundational basis for the derivation of the elastic constants [29]. Temperature and pressure dependencies of certain macroscopic thermodynamic parameters, such isobaric and isochoric heat capacities, thermal volume expansion coefficient and Debye temperature, of the studied materials were explored using the quasi-harmonic Debye model implemented in the GIBBS program [30].

3 Results and Discussion

3.1 Structural Properties

CaRh₂P₂ and BaRh₂P₂ materials adopt a tetragonal crystal structure known as the ThCr₂Si₂-type, characterized by the space group I4/mmm (No. 139) [31]. In the conventional unit cell (shown in Fig. 1), there are two formula units, housing a total of 10 atoms, while the primitive unit cell contains only one chemical formula, consisting of five atoms. The positions of these atoms are as follows: Ca (or Ba) atoms occupy the 2a site at coordinates (0,0,0), Rh atoms occupy the 4d site at coordinates (0,1/2,1/4), and P atoms are located at the 4e site with coordinates (0,0,z_P). The internal parameter z_P determines the z-coordinate of the P atom in the unit cell [18, 31]. The crystal structures of CaRh₂P₂ and BaRh₂P₂ can be conceptualized as alternating infinite layers. These layers consist of Rh atoms bonded with P atoms, forming RhP chains that are stacked along the crystallographic c-axis, the longest axis of the tetragonal lattice. These RhP chains are separated by the Ca (or Ba) atoms, which give rise to the overall structure. To determine the equilibrium lattice parameters a₀ and c₀, as well as the z_P fractional coordinate that correspond to the minimum total energy of the XRh₂P₂ compounds (X = Ca, Ba), all free structural parameters, namely a, c and z_P, have been fully relaxed. The resulting values for these parameters are presented in Table 1, along with previously reported values for the title compounds [18, 31] and for other compounds having the 122-type crystal structure [32,33,34,35,36]. The calculated equilibrium lattice parameters (a₀ and c₀) as well as the internal coordinate parameter z_P for the XRh₂P₂ compounds, where X can be Ca or Ba, closely match the experimental counterparts available in the literature [18, 31]. This congruence between the computed and experimental data enhances the reliability and validity of the computational methods used to analyze the crystal structures of these materials. Such accurate alignment between theory and experiment is of significant importance in the field of solid-state physics and materials science, as it reaffirms the precision and predictive capability of computational techniques for investigating the structural properties of complex compounds like XRh₂P₂. The volume of the unit cell of BaRh₂P₂ is bigger than that of BaRh₂P₂, with values of V = 192.51 ų and V = 158.64 ų, respectively. The sole distinction between these two compounds lies in the Ba and Ca atoms. Consequently, the observed variation in unit cell volume can be ascribed to the higher radius of the Ba atom compared to that of the Ca atom.

The length of the interlayer P-P bond plays a crucial role in determining the occurrence of superconductivity in 122-type phosphides [18]. This parameter, denoted as d_P−P, serves as an indicator of the presence or absence of interlayer P-P covalent bonds. A critical length of the interlayer P-P bond of approximately 2.8 Å (d_P−P ≈ 2.8 Å) is considered essential for the formation of interlayer P-P covalent bonds, and any value of d_P−P greater than 2.8 Å indicates the absence of such a bond at the P-P interface, which is associated with the emergence of superconductivity. Upon calculating the interlayer P-P bond lengths for both CaRh₂P₂ and BaRh₂P2 (as listed in Table 1), interesting findings emerge. For CaRh₂P₂, the computed value of d_P−P is 2.23 Å, falling below the critical threshold of 2.8 Å. This indicates the formation of a P-P covalent bond in CaRh₂P₂. On the other hand, for BaRh₂P₂, the calculated d_P−P value is 3.8 Å, surpassing the critical limit. Consequently, no interlayer P-P covalent bond is formed in BaRh₂P₂. These results provide an explanation for the differing superconducting behaviors observed in CaRh₂P₂ and BaRh₂P₂. As the interlayer P-P covalent bond is absent in BaRh₂P₂ due to its larger d_P−P value, this compound exhibits superconductivity. In contrast, the presence of a P-P covalent bond in CaRh₂P₂, owing to its smaller d_P−P value, prevents superconductivity from occurring. It is worth to remark that the distinctive difference between CaRh₂P₂ and BaRh₂P₂ is located in the Ba and Ca atoms. Thus the fact the interlayer P-P covalent bond in BaRh₂P₂ is bigger than that in CaRh₂P₂ may be attributed the fact that the atomic radius of Ba is larger than that of Ca.

Fig. 1

The tetragonal unit cell of BaRh₂P₂ crystal. The BaRh₂P₂ structure can be viewed alternating layers of RhP connected via the Ba atom. d_P−P is the length of the interlayer P-P bond

Table 1 Calculated equilibrium lattice parameters (a₀ and c₀, in Å), z-coordinate of the P atom (z_P), bulk modulus (B, in GPa), interlayer P-P bond length (d_P−P, in Å) and the enthalpies of formation ($\Delta H$, in eV/atom) for XRh₂P₂ (X = Ca, Ba) in comparison with those of certain isostructural compounds

We conducted an investigation into the pressure dependencies of the unit cell volume (V) and the lattice parameters (a and c). To analyze the behavior of these parameters under varying pressure conditions, we utilized normalized values. The normalized unit cell volume (V/V₀) represents the ratio of the unit cell volume at a certain pressure (V) to its value at zero pressure (V₀). Similarly, the normalized lattice parameters, a/a₀ and c/c₀, indicate the ratios of the lattice parameters (a and c) at pressure P to their respective values at zero pressure (a₀ and c₀). Second-order polynomials were employed to fit the variations of the normalized unit cell volume (V/V₀) and the normalized lattice parameters (a/a₀ and c/c₀) under hydrostatic pressure. The fitting process allowed for a more precise representation of the relationships between the crystal lattice’s structural parameters and the applied pressure as follows:

$${\text{CaR}}{{\text{h}}_{\text{2}}}{{\text{P}}_{\text{2}}}\left\{ \begin{gathered} \frac{a}{{{a_0}}}=1 - 2.35 \times {10^{ - 3}}P+2.58 \times {10^{ - 5}}{P^2} \hfill \\ \frac{c}{{{c_0}}}=1 - 1.68 \times {10^{ - 3}}P+1.86 \times {10^{ - 5}}{P^2} \hfill \\ \frac{V}{{{V_0}}}=1 - 6.33 \times {10^{ - 3}}P+7.66 \times {10^{ - 4}}{P^2} \hfill \\ \end{gathered} \right.$$

(1)

$${\text{BaR}}{{\text{h}}_{\text{2}}}{{\text{P}}_{\text{2}}}\left\{ \begin{gathered} \frac{a}{{{a_0}}}=1 - 2.27 \times {10^{ - 3}}P+3.60 \times {10^{ - 5}}{P^2} \hfill \\ \frac{c}{{{c_0}}}=1 - 5.49 \times {10^{ - 3}}P+6.44 \times {10^{ - 5}}{P^2} \hfill \\ \frac{V}{{{V_0}}}=1 - 9.92 \times {10^{ - 3}}P+1.47 \times {10^{ - 4}}{P^2} \hfill \\ \end{gathered} \right.$$

(2)

From the data presented in Fig. 2a, it is evident that as the pressure increases, the normalized structural parameters diminish. In order to quantify this behavior, linear compressibility values along the 𝑎 and 𝑐 directions were estimated and found to be β_a = $2.35 \times {10^{-3}}$ GPa⁻¹ ($2.27 \times {10^{-3}}$ GPa⁻¹) and β_c = $1.68 \times {10^{-3}}$ GPa⁻¹ ($5.49 \times {10^{-3}}$GPa⁻¹) for CaRh₂P₂ (BaRh₂P₂). Further examination of the data reveals that under the influence of pressure, a distinct behavior is observed in the variation of lattice parameters “a” and “c” for the CaRh₂P₂ compound compared to the BaRh₂P₂ compound. Specifically, for the CaRh₂P₂ compound, the lattice parameter “a” experiences a more pronounced reduction in response to applied pressure, whereas the lattice parameter “c” exhibits a comparatively less substantial decrease. This indicates an anisotropic response of the crystal lattice to pressure, with the “a” direction being more sensitive to compression compared to the “c” direction. In contrast, the BaRh₂P₂ compound demonstrates a converse trend. Here, under pressure, the lattice parameter “c” displays a more significant decrease compared to the lattice parameter “a” This signifies a differing response to pressure, with the “c” direction being more susceptible to compression than the “a” direction in this particular compound. It is important to mention that, despite the higher size of the unit cell of BaRh₂P₂ compared to CaRh₂P₂ at zero pressure, the lattice parameter “a” in BaRh₂P₂ is smaller than that in CaRh₂P₂, but the parameter “c” in BaRh₂P₂ is significantly larger than that in CaRh₂P₂. Consequently, the bond lengths along the a-axis in BaRh₂P₂ are shorter compared to those in CaRh₂P₂, indicating that the bonds along the a-axis in BaRh₂P₂ possess greater strength than the corresponding bonds in CaRh₂P₂. In contrast, the bonds along the c-axis in CaRh₂P₂ exhibit greater strength compared to the analogous bonds in BaRh₂P₂. The stronger the bond, the less sensitive it is to the pressure impact. This behavior may elucidate the observed inverse correlation between the lattice parameters “a” and “c” with respect to the pressure effect in CaRh₂P₂ and BaRh₂P₂.

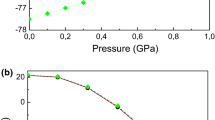
To estimate the bulk moduli (B) of the XRh₂P₂ compounds, where X can be Ca or Ba, two different approaches were employed for data fitting. Firstly, the total energy versus unit cell volume (E(V)) data was fitted to the third-order Birch-Murnaghan equation of state (BM-EOS) [37]. Secondly, the hydrostatic pressure versus unit cell volume (P(V)) data was fitted to the third-order Vinet equation of state (V-EOS) [38]. These fittings are illustrated in Fig. 2b and c. The obtained bulk modulus (B) values are presented in Table 1. Remarkably, there was a notable agreement between the values of B obtained through the BM-EOS and V-EOS approaches, thus affirming the consistency and reliability of the results. It is observed that the B value of BaRh₂P₂ is smaller than that of CaRh₂P₂, which is consistent with the established relationship: $B\sim 1/V$, where V represents the unit cell volume.

Fig. 2

a Pressure dependencies of a/a₀, c/c₀, and V/V₀, and b total energy (Energy (eV)) as function of primitive cell volume (V) and c hydrostatic pressure (P) as function of primitive cell volume (V) for XRh₂P₂ (X = Ca, Ba). The subscript “0” denotes the parameter value at zero pressure. The symbols are the results obtained from the first principles calculations and the solid lines are the fits. b fit of the E–V data to the Birch–Murnaghan (BM) EOS, and c fit of the P–V data to Vinet EOS

To ensure the structural stability of the XRh₂P₂ compounds (where X can be either Ca or Ba), we performed an estimation of the formation enthalpy (∆H) using a specific expression [39, 40]:

$$\Delta H=\frac{1}{{{n_X}+{n_{Rh}}+{n_P}}}\left[ {E_{{Tot}}^{{XR{h_2}{P_2}}} - \left( {{n_X}E_{{Tot}}^{{X(solid)}}+{n_{Rh}}E_{{Tot}}^{{Rh(solid)}}+{n_P}E_{{Tot}}^{{P(solid)}}} \right)} \right]$$

(3)

In this context, $E_{{Tot}}^{{XR{h_2}{P_2}}}$ represents the total energy of the primitive cell of XRh₂P₂ (X = Ca, Ba), and $E_{{Tot}}^{{X(solid)}}$, $E_{{Tot}}^{{Rh(solid)}}$, and $E_{{Tot}}^{{P(solid)}}$ represent the total energies per atom of the solid state of the pure elements X (Ca or Ba), Rh, and P, respectively. n_X, n_Rh, and n_P are the numbers of X, Rh, and P atoms in the primitive cell, respectively. Applying this methodology, we obtained the enthalpies of formation given in Table 1 for XRh₂P₂ (X = Ca, Ba). Notably, upon examining Table 1, it becomes evident that the XRh₂P₂ compounds, whether X is Ca or Ba, exhibit negative formation enthalpies. This negative value indicates that these compounds are thermodynamically stable in their structural configuration.

3.2 Elastic Properties

3.2.1 Single-crystal Elastic Constants

Single-crystal elastic constants (C_ij) play a crucial role in providing essential insights into various properties of materials, such as their bonding characteristics, how they respond to external stress, their mechanical stability, and overall stiffness [41]. In addition, the elastic constants are closely related to various fundamental physical properties, such as specific heat, melting point, Debye temperature, thermal expansion coefficient. In the context of a tetragonal system, there are six independent elastic constants that are of particular importance. These constants are denoted as C₁₁, C₁₂, C₁₃, C₃₃, C₄₄, and C₆₆. Table 2 presents the values of these six elastic constants for the XRh₂P₂ (X = Ca, Ba) tetragonal systems and those of some isostructural compounds [32, 35, 42]. Comparing these values with those from other related compounds helps in understanding the similarities and differences in the properties of these materials, thus contributing to the broader understanding of their behavior and applications. We can make some observations from the calculated elastic constants in XRh₂P₂ (X = Ca, Ba) compounds:

• (i) One notable observation from the calculated elastic constants (C_ij) in XRh₂P₂ compounds (where X = Ca, Ba) is that C₁₁ (which represents the linear compression resistance along the a-axis) is greater than C₃₃ (which characterizes the linear compression resistance along the c-axis) in BaRh₂P₂. However, in CaRh₂P₂, C₁₁ is smaller than C₃₃. This finding suggests that the linear compressibility along the a-direction should be lower than that along the c-direction in BaRh₂P₂, while the opposite trend should be observed in the case of CaRh₂P₂. These results are consistent with the pressure dependence of lattice parameters “a” and “c” that we have already studied in Section 3.1.

• (ii) The C_ij values show a decreasing trend from CaRh₂P₂ to BaRh₂P₂, demonstrating a decrease in C_ij values as the unit cell volume increases.

• (iii) In the compound BaRh₂P₂, the value of C₁₁ is greater than C₃₃. However, in the compound CaRh₂P₂, the value of C₁₁ is smaller than C₃₃. This observation aligns with the controversies responses of “a” and “c” to changes in pressure in CaRh₂P₂ and BaRh₂P₂, as stated in Section 3.1.

• (iv) Another significant observation pertains to C₄₄, which characterizes the material’s resistance against shear distortion in the (100) plane, and C₆₆, which characterizes the resistance to shear in the <110> direction. The calculated values indicate that C₄₄ is greater than C₆₆, suggesting that XRh₂P₂ compounds (X = Ca, Ba) are more competent in resisting shear distortion along the <110> direction compared to the (100) plane [43].

• (v) The elastic constants C₁₁ and C₃₃ are somewhat larger than C₄₄ and C₆₆. This finding implies that XRh₂P₂ compounds (X = Ca, Ba) should be more resistant to unidirectional compression than to shear deformation.

• (vi) The Cauchy pressure (C₁₂–C₄₄) is an important indicator of material ductility or brittleness. When the Cauchy pressure is negative, the material tends to be brittle, whereas a positive value indicates ductility [43]. In the case of both XRh₂P₂ compounds (X = Ca, Ba), the Cauchy pressure (C₁₂–C₄₄) is positive, indicating that they are ductile materials.

• (vii) The linear compressibility along the a-direction (β_a) and c-direction (β_c) in a tetragonal crystal can be represented as follows [44]: β_a = S₁₁ + S₁₂ + S₁₃, and β_c = S₃₃ + 2S₁₃, where S_ij are the compliance constants The calculated values of β_a and β_c for CaRh₂P₂ (BaRh₂P₂) are found to be $2.4 \times {10^{-3}}$ GPa⁻¹ ($2.5 \times {10^{-3}}$ GPa⁻¹) and $1.7 \times {10^{-3}}$ GPa⁻¹ ($5.9 \times {10^{-3}}$ GPa⁻¹), respectively. These values are very close to the linear compressibilities obtained from the pressure dependence of the lattice parameters a and c studied in Section 3.1, and reflect well the fact that the linear compressibility along the a-direction is greater than that along the along the c-direction in CaRh₂P₂, while the compound BaRh₂P₂ exhibits an opposite trend. This close agreement supports the reliability of the calculated elastic constants.

• (viii) It is interesting to note that the values of the elastic constants (C_ij) increase when the Ba atom in BaRh₂P₂ is replaced by the Ca atom, leading to a decrease in stiffness when transitioning from CaRh₂P₂ to BaRh₂P₂.

• (ix) In the realm of materials science, the critical parameter known as the melting temperature (T_m) assumes considerable significance, as it defines the temperature at which a given material undergoes a transformative shift from its solid state to a liquid state. The quantification of this pivotal parameter can be accomplished through the application of the following mathematical relationship [45]:

  $$T_m=354+[4.5(2C_{11}+C_{33})/3]$$

  (4)

  The computed values od T_m for the considered compounds are presented in Table 2.

• (x) Lastly, it is crucial to consider the mechanical stability requirements at zero pressure. In this regard, the calculated values of the single-crystal elastic constants satisfy the required conditions for mechanical stability [46]:

  $${C_{11}}>0;\; {C_{33}}>0;\; {C_{44}}>0;\; {C_{66}}>0;\; {C_{11}}+{C_{33}} - 2{C_{13}}>0;\; {C_{11}} - {C_{12}}>0;\; 2\left( {{C_{11}}+{C_{12}}} \right)+4{C_{13}}+{C_{33}}>0$$

  (5)

His indicates the mechanical stability of the XRh₂P₂ (X = Ca, Ba) compounds.

Table 2 The calculated elastic constants (C_ij, in GPa), compliances constants (S_ij, in GPa⁻¹) and melt temperature (T_m, in K) for XRh₂P₂ (X = Ca, Ba) along with previous calculations for some isostructural compounds

The graph presented in Fig. 3 illustrates the variations of C_ij as a function of pressure within the range of 0 to 18 GPa. It is noteworthy that the calculated values of Cij at specific pressures (C_ij(P)), namely 0, 3, 6, 9, 12, 15, and 18 GPa, fulfill the necessary conditions for mechanical stability under hydrostatic pressure [47, 48]:

$$(C_{11}-C_{12})>0;\; (C_{11}+C_{33}-2C_{13})>0;\; C_{ii}>0;\:(2C_{11}+C_{33}+2C_{12}+4C_{13})>0$$

(6)

In this context, $C_{\alpha\alpha}=C_{\alpha\alpha}-P\;(\alpha=1,\;2,\;3,\;4,\;5,\;6)$, $C_{12}=C_{12}+P$, and $C_{13}=C_{13}+P$. This demonstrates that the materials XRh₂P₂ (where X can be either Ca or Ba) are mechanically stable under hydrostatic pressure. Furthermore, it has been observed that C_ij exhibit a quadratic relationship with pressure. As the pressure increases, the elastic constants increase in accordance with the following quadratic polynomials:

$${\mathrm{CaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}C_{11}=239.40+6.23P\mathit-0.02P^{\mathit2}\\\begin{array}{l}C_{33}=261.00+7.83P\mathit-0.01P^{\mathit2}\\C_{44}=79.36+1.55P\mathit-0.01P^{\mathit2}\\C_{66}=100.22+4.58P\mathit-0.05P^{\mathit2}\\C_{12}=90.96+3.44P-0.03P^2\\C_{\mathit{13}}=108.08+5.20P\mathit-0.07P^{\mathit2}\end{array}\end{array}\right.$$

(7)

$${\mathrm{BaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}C_{\mathit{11}}=188.11+6.70P\mathit-1.5\times10^{-3}\;P^{\mathit2}\\\begin{array}{l}C_{\mathit{33}}=118.99+5.24P\mathit-6.3\times10^{-2}\;P^{\mathit2}\\C_{\mathit{44}}=37.94+2.96P\mathit-1.9\times10^{-2}\;P^{\mathit2}\\C_{\mathit{66}}=100.30+4.27P\mathit-5.6\times10^{-2}\;P^{\mathit2}\\C_{\mathit{12}}=73.19+4.83P\mathit-3.1\times10^{-3}\;P^{\mathit2}\\C_{\mathit{13}}=57.67+3.93P\mathit-1.4\times10^{-2}\;P^{\mathit2}\end{array}\end{array}\right.$$

(8)

 

3.2.2 Polycrystalline Elastic Moduli

The elastic properties of polycrystalline aggregates can be characterized by a pair of isotropic elastic moduli, namely the bulk and shear moduli (B and G). The polycrystalline bulk and shear moduli (B and G) can be determined from the single-crystal elastic constants (C_ij) via the Voigt-Reuss-Hill approaches [49,50,51]. The Reuss [49] and Voigt [50] approximations are employed to obtain the extreme values of B (B_R, B_V) and G (G_R, G_V) for polycrystalline samples. The subscript “R” or “V” serves as a denotation that the adopted approximation pertains to the Reus or Voigt approximation, correspondingly. In the case of a tetragonal system, the polycrystalline elastic moduli B_R, B_V, G_R, and G_V are expressed as functions of C_ij as follows [52]:

$${B_V}=\frac{1}{9}\left( {2({C_{11}}+{C_{12}})+{C_{33}}+4{C_{13}}} \right);\;{G_V}=\frac{1}{{30}}\left( {M+3{C_{11}} - 3{C_{12}}+12{C_{44}}+6{C_{66}}} \right);\;{B_R}={C^2}/M;\;{G_R}=15{\left\{ {\left( {\frac{{18{B_V}}}{{{C^2}}}} \right)+\left[ {\frac{6}{{\left( {{C_{11}} - {C_{12}}} \right)}}} \right]+\left( {\frac{6}{{{C_{44}}}}} \right)+\left( {\frac{3}{{{C_{66}}}}} \right)} \right\}^{ - 1}}$$

(9)

In this context, $M=({C_{11}}+{C_{12}})+2{C_{33}} - 44{C_{13}}$, and ${C^2}=\left( {{C_{11}} - {C_{12}}} \right){C_{33}} - 2C_{{13}}^{2}$. According to the Hill approximation, the effective values of the bulk and shear moduli (B_H and G_H) are given by the arithmetic mean of the Voigt and Reuss limits [51]:

$${B_H}=\left( {{B_V}+{B_R}} \right)/2;\;{G_H}=\left( {{G_V}+{G_R}} \right)/2$$

(10)

Another pair of polycrystalline elastic moduli, namely Young’s modulus (E) and Poisson’s ratio (σ), can be calculated from B and G using the following relationships:

$$\textit{E}=\frac{9\textit{BG}}{\left(3\textit{B}+\textit{G}\right)};\;\sigma=\frac{\left(3\textit{B}-2\textit{G}\right)}{\left(6\textit{B}+2\textit{G}\right)}$$

(11)

Additionally, to quantify the hardness of a material, the Vickers hardness (H_V) is commonly used as a powerful tool to describe the hardness of solids. Chen et al. [53, 54] proposed an expression for the Vickers hardness (H_V) based on the obtained elastic moduli B and G, using the following relationship:

$${H_{\text{V}}}=2{\left( {{K^2}G} \right)^{0.585}} - 3$$

(12)

Here, $K=G/B$. The predicted values of the polycrystalline moduli: B_V, B_R, G_V, G_R, G_H, E_H, σ_H, and H_V, for the considered tetragonal crystals XRh₂P₂ (X = Ca, Ba) are listed in Table 3. This table also includes results from the literature for certain isostructural compounds [32, 37, 42]. From the data presented in Table 3, several significant conclusions can be drawn:

• (i) The bulk modulus (B) values obtained through the equation of state (EOS) fits for CaRh₂P₂ (B = 148.2 GPa) and BaRh₂P₂ (B = 91.8 GPa) closely align with those calculated from the single-crystal elastic constants, namely B = 149.6 GPa for CaRh₂P₂ and B = 93.9 GPa for BaRh₂P₂. This concordance between the two independent methods serves as strong evidence of the reliability and accuracy of the computed single elastic constants.

• (ii) The determination of a material’s brittleness or ductility holds considerable importance, as ductile materials are known for their ease of machinability and resilience to thermal shock. Poisson’s ratio (σ) and Pugh’s ratio (B/G) have proven to be effective indicators in distinguishing between ductile and brittle materials. When Poisson’s ratio is higher (or lower) than 0.26, the material is identified as ductile (or brittle) [43]. Similarly, if the B/G ratio exceeds (or is lower than) 1.75, the material exhibits ductile (or brittle) behavior [55, 56]. Based on the values listed in Table 3, it is evident that both CaRh₂P₂ and BaRh₂P₂ possess Poisson’s ratios greater than 0.26 and Pugh’s ratios larger than 1.75, pointing out their ductile behavior across various pressures (0, 3, 6, 9, and 18 GPa).

• (iii) A comparative analysis of the bulk modulus (B), shear modulus (G), and Young’s modulus (𝐸) between CaRh₂P₂ and BaRh₂P₂ reveals that the values of aforementioned elastic moduli of CaRh₂P₂ are consistently higher than those of BaRh₂P₂. This suggests that CaRh₂P₂ exhibits greater resistance to deformations, implying that the chemical bonds in CaRh₂P₂ possess a degree of strength superior to those in BaRh₂P₂.

• (iv) The Vickers hardness (H_V) value in CaRh₂P₂ surpasses that of BaRh₂P₂, providing concrete evidence that CaRh₂P₂ possesses a higher hardness level than BaRh₂P₂.

• (v) Isotropic sound wave velocities, specifically the longitudinal, transverse, and mean sound wave velocities (denoted as V_L, V_T, and V_m), are fundamental and noteworthy physical parameters due to their intricate interrelation with various thermodynamic properties. These properties encompass the Debye temperature, thermal conductivity, heat capacity, and melting temperature. The quantities V_L, V_T, and V_m can be evaluated through explicit formulations using the isotropic bulk and shear moduli (designated as B and G, respectively), as articulated below:

  $$V_T=\left(\frac G\rho\right)^{1/2};\;V_L=\left(\frac{3B+4G}{3\rho}\right)^{1/2};\;V_m=\left[\frac13\left(V_L^{-3}+2V_T^{-3}\right)\right]^{-1/3}$$

  (13)

The mass density ρ plays a pivotal role. The resulting V_L, V_T, and V_m values for the materials under scrutiny are documented within Table 3. The Debye temperature (symbolized as θ_D), an imperative thermodynamic parameter, is amenable to computation via the average sound wave velocity (V_m) in accordance with the ensuing expression [57,58,59]:

$$\theta_D=\frac h{k_B}\left[\frac{3n}{4\pi}\frac{N_A\rho}M\right]^{1/3}\;V_m$$

(14)

Here, the constants h, N_A, k_B, M, and n embody the Planck constant, Avogadro number, Boltzmann constant, molecular weight, and the count of atoms within the molecule, respectively. The computed θ_D values for the compounds of interest are thoughtfully juxtaposed with those belonging to some isostructural compounds [32, 35, 42], within the tabular arrangement denoted as Table 3. In the endeavor to comprehend the efficacy of heat propagation within materials, the parameter of thermal conductivity denoted as K_min assumes paramount importance. This parameter’s significance is underscored by its intimate and direct correlation with high-temperature materials [60]. The lattice thermal conductivity K_min for the XRh₂P₂ compounds where X stands for Ca and Ba has been calculated utilizing an established relationship [61]:

$$K_{\text{min}}=k_BV_m\left(M/n\rho N_A\right)^{-2/3}$$

(15)

Table 3 Calculated bulk and shear modulus values via Voigt approximation (B_V, G_V, in GPa), Reuss approximation (B_R, G_R, in GPa), and Hill approximation (B_H, G_H, in GPa), Hill Young’s modulus (E_H, in GPa), Hill Poisson’s ratio (σ_H, dimensionless), Vickers hardness (H_V, in GPa), density of mass (ρ, in g.cm⁻³), isotropic longitudinal, transverse and average sound velocities (V_l; V_t; V_m, in m.s⁻¹), Debye temperatures (θ_D, in K), minimum thermal conductivity (K_min, in W.m⁻¹.K⁻¹) and melting temperature (T_m, in K) for CaRh₂P₂ and BaRh₂P₂ materials as well as available results of certain isostructural compounds

The plot shown in Fig. 3 illustrates the changes in polycrystalline elastic moduli, including bulk modulus (B_H), shear modulus (G_H), and Young’s modulus (E_H), for both CaRh₂P₂ and BaRh₂P₂ as a function of applied pressure. To describe the relationship between these moduli and pressure, second-order polynomial equations were employed, which resulted in good fits to the calculated data. These polynomial equations effectively capture the variations of the moduli with increasing pressure.

$${\mathrm{CaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}B=149.6+5.26P-1.82\times10^{-2}\;P^2\\\begin{array}{l}G=79.9+1.81P-3.26\times10^{-2}\;P^2\\E=203.46+4.99P-3.91\times10^{-3}\;P^2\end{array}\end{array}\right.$$

(16)

$${\mathrm{BaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}B\mathit\;=93.9+4.83P\mathit-1.89\times10^{-2}\;P^{\mathit2}\\\begin{array}{l}G=51.9+2.42P\mathit-2.96\times10^{-2}\;P^{\mathit2}\\E=131.5+6.25P-6.9\times10^{-2}\;P^2\end{array}\end{array}\right.$$

(17)

Figure 4 shows that in the case of both examined compounds there exists a nearly linear augmentation of the longitudinal (V_L), transversal (V_T) and average (V_m) sound wave velocities with a rise in pressure. The alterations in V_L, V_T, and V_m exhibit a strong conformity with the mathematical representation of second-order polynomial equations:

$${\mathrm{CaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}\begin{array}{l}V_t=3458.8+27.64P-0.11P^2\\\begin{array}{l}V_l=6196.0+70.57P-0.58P^2\\V_m=3850+31.79P-0.14P^2\end{array}\end{array}\end{array}\right.$$

(18)

$${\mathrm{BaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}V_t=2725.5+45.5P-0.86P^2\\\begin{array}{l}V_l=4832.2+87.7P-1.30P^2\\V_m=3031.8+51.0P-0.95P^2\end{array}\end{array}\right.$$

(19)

The impact of pressure on key thermodynamic properties, namely the melting temperature (T_m), minimum thermal conductivity (K_min), and Debye temperature (θ_D), for the compounds CaRh₂P₂ and BaRh₂P₂ is illustrated in Fig. 4. It is evident that these entire aforementioned parameters exhibit a consistent upward trend as pressure is incrementally augmented. The discernment is reinforced by the data in Table 3, wherein the Debye temperature for BaRh₂P₂ is notably lower compared to that of CaRh₂P₂. This discrepancy can be attributed to the inherent mechanical rigidity disparity between the two compounds, with CaRh₂P₂ demonstrating greater stiffness in comparison to BaRh₂P₂. The resultant polynomial expressions that represent the relationships for melting temperature (Tm), minimum thermal conductivity (Kmin), and Debye temperature (θD) pertaining to the XRh₂P₂ (X = Ca, Ba) compounds are enumerated as follows:

$${\mathrm{CaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}\theta_D=461.8+4.82P-0.02P^2\\K_{\text{min}}=0.86+0.01P-4.76\times10^{-5}\;P^2\\T_m=1463.7+30.44P-0.07P^2\end{array}\right.$$

(20)

$${\mathrm{BaRh}}_2{\mathrm P}_2\left\{\begin{array}{l}\theta_D=336.7+6.89P-0.11P^2\\K_{\text{min}}=0.58+1.4\times10^{-2}\;P-2.06\times10^{-4}\;P^2\\T_m=1096.8+27.69P-0.09P^2\end{array}\right.$$

(21)

Fig. 3

Pressure-dependence of the single-crystal elastic constants (C_ij), and polycrystalline elastic moduli: isotropic bulk modulus B_H, shear modulus G_H, Young’s modulus E_H for CaRh₂P₂ and BaRh₂P₂. The symbols are the calculated results, while the lines represent the fit curves

Fig. 4

Calculated pressure-dependence of the transverse, longitudinal and average sound wave velocities (V_t, V_l and V_m) (a), Debye temperature (θ_D) (b), minimum thermal conductivity (K_min) (c), and melting temperature (T_m) (d) for CaRh₂P₂ and BaRh₂P₂. The symbols are the calculated results, while the lines represent the fit curves

3.2.3 Elastic Anisotropy

The assessment of elastic anisotropy in crystals holds paramount significance due to its intimate relationship with various phenomena and material properties. Notably, it plays a pivotal role in understanding the development of plastic deformation in crystals [62], the stability and configuration of dislocations in materials, the texture of nanoscale shape-memory alloys [63], and the initiation of microcracks [64]. To quantitatively estimate the extent of elastic anisotropy in crystals, several metrics have been developed. In our study, we employed four distinct metrics to estimate the degree of elastic anisotropy exhibited by the compounds under investigation. By utilizing these metrics, we aim to gain comprehensive insights into the anisotropic behavior of the studied materials.

• (i) The evaluation of elastic anisotropy in crystals commonly relies on the calculation of percent anisotropy in shear (${A_{Shear}}=\frac{{{G_V} - {G_R}}}{{{G_V}+{G_R}}} \times 100$) and compression (${A_{Comp}}=\frac{{{B_V} - {B_R}}}{{{B_V}+{B_R}}} \times 100$) [65, 66]. Specifically, ${A_{Shear}}$ is defined as the ratio of shear modulus (G), while ${A_{Comp}}$ is the ratio of bulk modulus (B). These metrics serve as useful measures to quantify the extent of anisotropy in shear and compression within a crystal structure. The degree of anisotropy in shear and compression is reflected by the deviation of ${A_{Shear}}$ and ${A_{Comp}}$, respectively, from zero. Higher values of ${A_{Shear}}$ or ${A_{Comp}}$ indicate a more pronounced anisotropic behavior, while values closer to zero imply a more isotropic crystal. In Table 4, we present the calculated values of ${A_{Shear}}$ and ${A_{Comp}}$ for the studied tetragonal XRh₂P₂ (X = Ca, Ba) compounds. It is evident from these results that these materials exhibit a notable degree of anisotropy in shear and compression. This finding highlights the structural anisotropy in these crystals.

• (ii) To investigate the elastic anisotropy in crystals, researchers often employ the universal anisotropic index, denoted as A^U, which is defined as ${A^U}=5\frac{{{G_V}}}{{{G_R}}}+\frac{{{B_V}}}{{{B_R}}} - 6$ [67, 68]. This index serves as a valuable metric for quantifying the degree of elastic anisotropy in a crystal structure. For isotropic crystals, the universal index equals zero, signifying a balanced distribution of elastic properties in all directions. However, for anisotropic crystals, the index deviates from zero, indicating the presence of varying degrees of anisotropy in the material’s response to shear and compression. In Table 4, we present the calculated values of the universal anisotropic index for the studied tetragonal XRh₂P₂ (X = Ca, Ba) compounds. The results confirm the presence of strong elastic anisotropy in both materials. This finding underscores the significant variation in their elastic properties along different crystallographic directions.

• (iii) The assessment of shear anisotropy factors A₁ $({A_1}={A_{\left\{ {100} \right\}}}=4{C_{44}}/\left( {{C_{11}}+{C_{33}} - 2{C_{13}}} \right))$ along the {100} shear planes and A₃ $({A_3}={A_{\left\{ {001} \right\}}}=2{C_{66}}/\left( {{C_{11}} - {C_{12}}} \right))$ along the {001} shear planes [69, 70] plays a crucial role in evaluating the degree of anisotropy in the bonding between atoms in different crystal planes. In the context of a tetragonal structure, the anisotropic shear factors 𝐴₁ and 𝐴₃ are expected to have values equal to unity for an isotropic crystal. Hence, any deviation from unity reflects the extent of elastic anisotropy. In Table 4, we present the calculated values of 𝐴₁ and 𝐴₃ for the title materials. The results indicate significant shear anisotropy along the {100} and {001} shear planes. This finding underscores the pronounced variation in bonding strengths and mechanical responses of atoms in different crystallographic directions.

• (iv) In a tetragonal system, the crystal direction-dependent Young’s modulus (E) and linear compressibility (β) can be expressed in the spherical coordinate system as follows [44]:

  $$\left\{\begin{array}{l}\frac1E=\left(l_1^4+l_2^4\right)S_{11}+l_3^4S_{33}+2l_1^2l_2^2S_{12}+2\left(l_1^2l_3^2+2l_2^2l_3^2\right)S_{13}+\left(l_2^2l_3^2+l_1^2l_3^2\right)S_{44}+l_1^2l_2^2S_{66}\\\begin{array}{l}\beta=\left(S_{11}+S_{12}+S_{13}\right)-\left(S_{11}+S_{12}-S_{13}-S_{33}\right)l_3^2\end{array}\end{array}\right.$$

  (22)

Here, l₁, l₂, and l₃ are the direction cosines, and S_ij are the components of the compliance matrix. An elastic modulus isotropic with respect to crystal directions in 3D is represented by a closed surface that assumes a perfect spherical configuration. This is because the elastic modulus is the same in all directions for an isotropic material, and a sphere is the only shape that has the same radius in all directions. Therefore, the degree of deviation of the shape of this closed surface from its spherical shape reflects the degree of anisotropy of the represented elastic modulus. Figure 5 show the 3D contours of E and β as well as their cross-sections (2D contours) in the (001), (010), and (001) crystalline planes for the considered compounds. As can be seen, the 3D representations (2D representations) of the Young’s modulus deviate considerably from the spherical shape (circular form), indicating that this property is noticeably anisotropic for both studied compounds. In CaRh₂P₂ (CaRh₂P₂), the minimum value of E (E_min) is 184 GPa (94 GPa) along the [001] direction, and the maximum value (E_max) is 219 GPa (203 GPa) along the [110] direction. Similarly, the 3D-representations (2D-representations) of the linear compressibility of CaRh₂P₂ and BaRh₂P₂ deviate considerably from the spherical shape (circular form), indicating that this property is also noticeably anisotropic. In CaRh₂P₂ (BaRh₂P₂), the minimum value of β (β_min) is 0.0018 GPa⁻¹ (0.0025 GPa⁻¹) along the [001] direction (along any direction in the (001) plane), and the maximum value (β_max) is 0.0024 GPa⁻¹ (0.0060 GPa⁻¹) along any direction in the (001) plane (along the [001] direction) direction. This is consistent with the statement that has already been drawn from the elastic constants C₁₁, and C₃₃. The consistent difference between E_max (β_max) and E_min (β_min) indicates the strong anisotropy of the Young’s modulus (linear compressibility) in the considered compounds.

Table 4 Calculated universal anisotropic index (A^U), percent anisotropy (A_comp and A_shear) and shear anisotropic factors (A₁ and A₂) for BaRh₂ × ₂ (X = P, As) compounds as well as the results of previous calculations for some isostructural compounds

Fig. 5

Direction-dependent Young’s modulus E and linear compressibility β as well as the corresponding cross-sections in the (100)/(010), (001) and planes for CaRh₂P₂ and BaRh₂P₂ crystals

3.3 Thermodynamic Properties

The thermodynamic characteristics of the materials under investigation were subjected to comprehensive analysis through the utilization of the quasi-harmonic Debye approximation [71], and executed using the specialized computational framework known as the Gibbs software [30]. Within the scope of this particular investigation, a thorough exploration was conducted into the temperature-dependent behavior of several key material physical parameters. These physical parameters encompass the lattice parameter, bulk modulus, thermal expansion coefficient, heat capacity, and Debye temperature. The temperature range scrutinized spanned from absolute zero up to 600 K, and this analysis was conducted under controlled pressures held at fixed values of 0, 4, 8, 12, and 16.

Figure 6a illustrates the change in the lattice parameter “a” with change in temperature at the fixed pressures 0, 4, 8, 12, and 16 GPa. The lattice parameter increases as the temperature rises, while in contrast, it decreases with increasing pressure, proving the contrasting effects of temperature and pressure on the lattice parameter. Our computations indicate that at zero pressure and T = 300 K, the lattice parameter is 4.2698 Å for CaRh₂P₂, and 4.6112 Å for BaRh₂P₂.

Figure 6b illustrates the variation of the bulk modulus (B) as it responds to temperature alterations, all while being subjected to a series of unchanging pressures, namely 0, 4, 8, 12, and 16 GPa. Notably, the observed trend demonstrates a decline in the bulk modulus magnitude with the escalation of temperature. Furthermore, it becomes evident that an increase in pressure corresponds to an augmentation in the bulk modulus magnitude. Upon closer examination, it becomes evident that, under the conditions of zero pressure and a temperature of 300 K, the calculated bulk modulus values stand at 123.17 GPa for CaRh₂P₂ and 80.6 GPa for BaRh₂P₂. These numerical results distinctly indicate that CaRh₂P₂ exhibits a considerably greater resistance to deformation in comparison to BaRh₂P₂, implying a higher degree of structural rigidity and stability.

Thermal expansion (α), a phenomenon caused by the inherent mobility of the constituent atoms or molecules of a material, refers to the propensity of a substance to undergo volumetric expansion upon exposure to high temperatures. Figure 6c visually elucidates the nuanced trajectory of the coefficient of thermal expansion as a function of temperature and pressure changes. Notably, this diagram depicts a clear trend in which the coefficient of thermal expansion (α) experiences an accelerated increase as temperatures rises from zero to about 200 K. Beyond this temperature threshold, a more moderate and essentially linear progression characterizes his growth. Conversely, a noticeable decrease in the coefficient of thermal expansion is noticeable with increasing pressure, a trend evident in both composite materials. The coefficient of volumetric thermal expansion, evaluated at zero pressure and at a temperature of 300 K, amounts to $5.98636\times10^{-5}\mathrm K^{-1}$ for CaRh₂P₂ and $6.36372\times10^{-5}\mathrm K^{-1}$ for BaRh₂P₂, respectively.

Figure 6d and e shows the relationship between temperature and heat capacity, both at constant volume (C_V) and constant pressure (C_P), at the fixed pressures of 0, 4, 8, and 16 GPa. In the lower temperature steps, precisely covering the interval from 0 to 200 K, the values of C_V and C_P unquestionably follow a proportional relationship with the cubic power of temperature (T³). With increasing temperature, the increase in C_V follows a gradual trajectory, gradually aligning with the eminent Dulong-Petit limit (${\text{124}}{\text{0.66 J}}{\text{.mo}}{{\text{l}}^{-1}}{{\text{.K}}^{ - 1}}$). In contrast, the C_P constantly progresses in a linear fashion as the temperature increases. It is important to note that C_V and C_P tend to decrease as pressure increases. At a perfect intersection of zero pressure and a fixed temperature of 300 K, the estimated value of C_V (C_P) add up to 112.54 J.mol^-1 .K^-1 (118.76 J.mol^-1 .K^-1) for CaRh₂P₂ and $118.19\;\mathrm J.\mathrm{mol}^{-1}\;.\mathrm K^{-1}$ $\left(123.98\;\mathrm J.\mathrm{mol}^{-1\;}.\mathrm K^{-1}\right)$ for BaRh₂P₂.

The temperature dependence of the Debye temperature (θ_D) for the studied compounds at fixed pressures of 0, 4, 8, 12 and 16 GPa is illustrated in Fig. 6f. θ_D remains practically constant below 100 K, but then decreases gradually with increasing temperature. With increasing pressure, θ_D shows a noticeable increase, from ${\text{448}}.{\text{1 K}}\left( {{\text{322}}.{\text{6 K}}} \right)$ at zero pressure to $550.8\;\mathrm K\;\left(423.1\mathrm K\right)$ at 16 GPa for CaRh₂P₂ (BaRh₂P₂). This increase in θ_D with pressure is due to the increase in the velocities of elastic waves, which in turn is caused by the increase in the interatomic forces. At zero pressure and 300 K, the approximate value of θ_D is 250 K for CaRh₂P₂ and 280 K for BaRh₂P₂. These values are in good agreement with the corresponding values derived from the elastic constants, which provides further confirmation of the reliability of the obtained results.

Fig. 6

Temperature dependence of the lattice parameter (a) bulk modulus; B (b), thermal expansion coefficient; α (c), heat capacity at constant volume; C_V (d) heat capacity at constant pressure; C_P (d) and Debye temperature; θ (f) of CaRh₂P₂ and BaRh₂P₂ compounds at fixed pressures of 0, 4, 8, 12 and 16 GPa

4 Conclusion

The first-principles PP-PW method with the GGA-PBE exchange–correlation functional was used to calculate the effect of pressure on the structural, elastic, and thermodynamic properties of the tetragonal XRh₂P₂ (X = Ca, Ba) compounds. The main conclusions are as follows:

• (i) The computed ground state structural parameters are in good agreement with the experimental counterparts. The values obtained for the interlayer P-P bond distance reveal that BaRh₂P₂ is superconducting, while CaRh₂P₂ is not superconducting.

• (ii) The predicted values of the single-crystal elastic constants for the considered materials at zero-pressure as well as under hydrostatic pressure up to 18 GPa satisfy the mechanical stability conditions, and show high uniaxial elastic anisotropy.

• (iii) Pugh’s ratio, Cauchy pressure, and Poisson’s ratio indicate that XRh₂P₂ (X = Ca, Ba) are ductile materials. The XRh₂P₂ (X = Ca, Ba) compounds are expected to resist to shear distortion in the <110> more than in the (100) plane.

• (iv) The shear and bulk moduli (B, and G), Poisson’s ratio (σ), and Young’s modulus (E) increase with increasing pressure. The Vickers hardness, Debye temperature, sound wave velocity, melting temperature, and minimum thermal conductivity values were predicted in the pressure range from 0 to 18 GPa.

• (v) The temperature-dependency of the lattice parameter, bulk modulus, Debye temperature, volume thermal expansion coefficient, and isobar and isochoric heat capacities at the fixed pressures of 0, 4, 8, 12, and 16 GPa were successfully determined via the quasi-harmonic Debye model.

To conclude, there are no experimental studies regarding the thermodynamic and elastic properties of the tetragonal XRh₂P₂ (X = Ca, Ba) compounds to be compared to our results. Therefore, we expect that this study will stimulate further theoretical and experimental research activities.