Efficient emulator for solving three-nucleon continuum Faddeev equations with chiral three-nucleon force comprising any number of contact terms

Abstract

We demonstrate a computational scheme which drastically decreases the required time to get theoretical predictions based on chiral two- and three-nucleon forces for observables in three-nucleon continuum. For a three-nucleon force containing N short-range terms all workload is reduced to solving N+1 Faddeev-type integral equations. That done, computation of observables for any combination of strengths of the contact terms is done in a flash. We demonstrate on example of the elastic nucleon-deuteron scattering observables the high precision of the proposed emulator and its capability to reproduce exact results.

1 Introduction

Since the birth of nuclear physics the nuclear force problem has been at the centre of experimental and theoretical studies. Extensive efforts based on purely phenomenological approaches or incorporating the meson-exchange picture have led to numerous nucleon-nucleon (NN) potentials, able to describe a vast amount of available data [1] with high precision. A major breakthrough occurred with the emergence of the effective field theory (EFT) concept [2], which paved the way for developing precise nuclear forces [3,4,5,6]. The progress in constructing nuclear forces within the EFT approach is presently documented by the availability of numerous high precision NN potentials developed by the Bochum-Bonn [7, 8], Idaho-Salamanca [9], and Bochum [10] groups. These forces provide a very good description of the NN data set.

Applications of the EFT approach in the form of chiral perturbation theory (ChPT) have resulted not only in the theoretically well grounded NN potentials but also for the first time have given a possibility to apply in practical calculations NN forces augmented by consistent 3N interactions, derived within the same formalism. Understanding of nuclear spectra and reactions based on these consistent chiral two- and many-body forces has become a hot topic of present day few-body studies [11].

The first nonvanishing contributions to the 3N force (3NF) appear at next-to-next-to-leading order of chiral expansion (N$^2$LO) [3, 12] and comprise in addition to the $2\pi$-exchange term two contact contributions with strength parameters $c_D$ and $c_E$ [13]. The chiral 3NF at N$^3$LO was derived in [14, 15]. At that order three components of long-range character [14] supplemented by the short-range terms [15] contribute to 3NF. The 3NF at N$^3$LO order does not involve any new unknown low-energy constants and depends only on two parameters, $c_D$ and $c_E$, that parameterize the leading one-pion-contact term and the 3N contact term present already at N$^2$LO. The $c_D$ and $c_E$ values need to be then fixed at this order, as at N$^2$LO, from a fit to few-nucleon data. At the higher order, N$^4$LO, in addition to long- and intermediate-range interactions generated by pion-exchange diagrams [16, 17], the chiral N$^4$LO 3NF involves thirteen purely short-range operators, which have been worked out in [18, 19].

Since the advent of numerically exact three-nucleon continuum Faddeev calculations the elastic nucleon-deuteron (Nd) scattering and the deuteron breakup reaction have been a powerful tool to test modern models of the nuclear forces [20,21,22] and the question about the importance of 3NF has developed into the main topic of 3N system studies. That issue has been given a new impetus by the ChPT-based achievements and the possibility to apply consistent two- and many-body nuclear forces, derived within this framework, in 3N continuum calculations.

Using chiral 3NF in 3N continuum requires numerous time consuming computations with varying strengths of the contact terms in order to establish their values. They can be determined for example from the $^3$H binding energy and the minimum of the elastic Nd scattering differential cross section at the energy ($E_{lab}\approx 70$ MeV), where the effects of 3NF start to emerge in elastic Nd scattering [23, 24]. Specifically at N$^2$LO, after establishing the so-called ($c_D,c_E$) correlation line, which for a particular chiral NN potential combined with a N$^2$LO 3NF gives pairs of ($c_D,c_E$) values reproducing the $^3$H binding energy, a fit to experimental data for the elastic Nd cross section is performed to determine the $c_D$ and $c_E$ strengths. Fine-tuning of the 3N Hamiltonian parameters requires an extensive analysis of available 3N elastic Nd scattering and breakup data. That ambitious goal calls for a significant reduction of computer time necessary to solve the 3N Faddeev equations and to calculate the observables. Thus finding an efficient emulator for exact solutions of the 3N Faddeev equations seems to be essential and of high priority.

In Ref. [25] we proposed such an emulator which enables us to reduce significantly the required time of calculations. We tested its efficiency as well as ability to accurately reproduce exact solutions of 3N Faddeev equations. In the present study we introduce a new computational scheme, based on the perturbative approach of [25], which even by far more reduces the computer time required to obtain the observables in the elastic nucleon-deuteron scattering and deuteron breakup reactions at any energy, and which is well-suited for calculations with varying strengths of the contact terms in a chiral 3NF.

2 The new emulator

Before presenting this new emulator, for the reader’s convenience we shortly outline the main points of the 3N Faddeev formalism and of the perturbative treatment of Ref. [25]. For details of the formalism and numerical performance we refer to [20, 26,27,28].

Neutron-deuteron (nd) scattering with nucleons interacting via NN interactions $v_{NN}$ and a 3NF $V_{123}=V^{(1)}+V^{(2)}+V^{(3)}$, is described in terms of a breakup operator T satisfying the Faddeev-type integral equation [20, 26, 27]

$$\begin{aligned} T\vert \phi \rangle= & {} t P \vert \phi \rangle + (1+tG_0)V^{(1)}(1+P)\vert \phi \rangle + t P G_0 T \vert \phi \rangle \nonumber \\&+ (1+tG_0)V^{(1)}(1+P)G_0T \vert \phi \rangle \, . \end{aligned}$$

(1)

The 2N t-matrix t is the solution of the Lippmann-Schwinger equation with the interaction $v_{NN}$. $V^{(1)}$ is the part of a 3NF which is symmetric under the interchange of nucleons 2 and 3: $V_{123}=V^{(1)}(1+P)$. The permutation operator $P=P_{12}P_{23} + P_{13}P_{23}$ is given in terms of the transposition operators, $P_{ij}$, which interchange nucleons i and j. The initial state $\vert \phi \rangle = \vert \mathbf {q}_0 \rangle \vert \phi _d \rangle$ describes the free motion of the neutron and the deuteron with the relative momentum $\mathbf {q}_0$ and contains the internal deuteron wave function $\vert \phi _d \rangle$. $G_0$ is the free three-body resolvent. The amplitude for elastic scattering leading to the final nd state $\vert \phi ' \rangle$ is then given by [20, 27]

$$\begin{aligned} \langle \phi ' \vert U \vert \phi \rangle= & {} \langle \phi ' \vert PG_0^{-1} \vert \phi \rangle + \langle \phi '\vert V^{(1)}(1+P)\vert \phi \rangle \nonumber \\&+ \langle \phi ' \vert V^{(1)}(1+P)G_0T\vert \phi \rangle + \langle \phi ' \vert PT \vert \phi \rangle ~, \end{aligned}$$

(2)

while the amplitude for the breakup reaction reads

$$\begin{aligned} \langle \mathbf {p} \mathbf {q} \vert U_0 \vert \phi \rangle= & {} \langle \mathbf {p} \mathbf {q} \vert (1 + P)T\vert \phi \rangle , \end{aligned}$$

(3)

where the free breakup channel state $\vert \mathbf {p} \mathbf {q} \rangle$ is defined in terms of the Jacobi (relative) momenta $\mathbf {p}$ and $\mathbf {q}$.

We solve Eq. (1) in the momentum-space partial-wave basis $\vert p q {\tilde{\alpha }} \rangle$, determined by the magnitudes of the Jacobi momenta p and q and a set of discrete quantum numbers ${\tilde{\alpha }}$ comprising the 2N subsystem spin, orbital and total angular momenta s, l and j, as well as the spectator nucleon orbital and total angular momenta with respect to the center of mass (c.m.) of the 2N subsystem, $\lambda$ and I:

$$\begin{aligned} \vert p q {\tilde{\alpha }} \rangle \equiv \Bigg \vert p q (ls)j \left( \lambda \frac{1}{2}\right) I (jI)J \left( t \frac{1}{2}\right) T \Bigg \rangle ~. \end{aligned}$$

(4)

The total 2N and spectator angular momenta j and I as well as isospins t and $\frac{1}{2}$, are finally coupled to the total angular momentum J and isospin T of the 3N system. In practice a converged solution of Eq. (1) using partial wave decomposition in momentum space at a given energy E requires taking all 3N partial wave states up to the 2N angular momentum $j_{max}=5$ and the 3N angular momentum $J_{max}=\frac{25}{2}$, with the 3N force acting up to the 3N total angular momentum $J=7/2$. The number of resulting partial waves (equal to the number of coupled integral equations in two continuous variables p and q) amounts to 142. The required computer time to get one solution on a personal computer is about $\approx 2$ h. In the case when such calculations have to be performed for a big number of varying 3NF parameters, time restrictions become prohibitive. Fortunately, the perturbative approach of Ref. [25] leads to a significant reduction of the required computational time.

Let us consider a chiral 3NF at a given order of chiral expansion with variable strengths of its contact terms. The 3NF at N$^2$LO has one parameter-free term (2$\pi$-exchange contribution) and two short-range terms with strength parameters $c_D$ and $c_E$. At N$^3$LO there are more contributing parameter-free parts but again only two contact terms. At N$^4$LO parameter-free contributions are supplemented by fifteen short-range terms with strengths: $c_D$, $c_E$, $c_{E_1}$, ..., $c_{E_{13}}$. All these contact terms are restricted to small 3N total angular momenta and to only few partial wave states for a given total 3N angular momentum J and parity $\pi$. For example for $J^{\pi }=7/2^{\pm }$ all matrix elements $< p q {\tilde{\alpha }} \vert V^{(1)} \vert p' q' \tilde{\alpha }'>$ proportional to $c_{E_1}$ and $c_{E_7}$ vanish, while the $c_D$ and $c_E$ terms are nonzero only for a restricted number of ${\tilde{\alpha }}, {\tilde{\alpha }}'$ pairs (mostly these containing $^1S_0$ and $^3S_1-^3D_1$ quantum numbers) [12, 13]. Bearing that in mind and taking into account the fact that contact terms yield a small contribution to the 3N potential energy compared to the leading, parameter-free part, it is possible to apply a perturbative approach in order to include the contact terms.

We split the $V^{(1)}$ part of a 3NF into a parameter-free term $V(\theta _0)$ and a sum of N contact terms $c_i \varDelta V_i$ with strengths $c_i$:

$$\begin{aligned} V^{(1)}= & {} V(\theta _0) + \varDelta V(\theta ) = V(\theta _0) + \sum _{i=1}^N c_i \varDelta V_i ~, \end{aligned}$$

(5)

with $\theta _0=(c_i=0,i=1,\dots ,N)$ and $\theta =(c_i,i=1,\dots ,N)$ being the sets of contact terms strength values, for which we would like to find solution of Eq. (1).

We divide the 3N partial wave states ${\tilde{\alpha }}$ into two sets: $\beta$ and the remaining one, $\alpha$. The $\beta$ set contains states with nonvanishing elements of $\varDelta V(\theta )$ and states most strongly coupled to them through the permutation operator P. This set of states is sufficient for the convergence of $\varDelta T(\theta )$ in the second equation (7), also in the intermediate states. Introducing $T(\theta _0)$ and $\varDelta T(\theta )$ such that $T \equiv T(\theta )=T(\theta _0) + \varDelta T(\theta )$, and using the fact, that $\varDelta V(\theta )$ has nonvanishing elements only for channels $\vert \beta \rangle$, one gets from Eq. (1) (omitting the Jacobi momenta in notation of partial wave states) two separate equations for $\langle \alpha \vert T (\theta _0) \vert \phi \rangle$ and $\langle \alpha \vert \varDelta T (\theta ) \vert \phi \rangle$ [25]:

$$\begin{aligned} \langle \alpha \vert T (\theta _0) \vert \phi \rangle&= \langle \alpha \vert t P \vert \phi \rangle + \langle \alpha \vert (1+tG_0) V(\theta _0) (1+P)\vert \phi \rangle \nonumber \\&\quad + \langle \alpha \vert t P G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&\quad + \langle \alpha \vert (1+tG_0) V (\theta _0) (1+P)G_0T(\theta _0) \vert \phi \rangle \nonumber \\ \langle \alpha \vert \varDelta T (\theta ) \vert \phi \rangle&= \langle \alpha \vert t P G_0 \varDelta T(\theta ) \vert \phi \rangle \nonumber \\&\quad + \langle \alpha \vert (1+tG_0) V (\theta _0) (1+P)G_0 \varDelta T(\theta ) \vert \phi \rangle ~, \end{aligned}$$

(6)

as well as for $\langle \beta \vert T (\theta _0) \vert \phi \rangle$ and $\langle \beta \vert \varDelta T (\theta ) \vert \phi \rangle$:

$$\begin{aligned} \langle \beta \vert T (\theta _0) \vert \phi \rangle= & {} \langle \beta \vert t P \vert \phi \rangle + \langle \beta \vert (1+tG_0) V(\theta _0) (1+P)\vert \phi \rangle \nonumber \\&+ \langle \beta \vert t P G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) V (\theta _0) (1+P)G_0T(\theta _0) \vert \phi \rangle \nonumber \\ \langle \beta \vert \varDelta T (\theta ) \vert \phi \rangle= & {} \langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)\vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) V (\theta _0) (1+P)G_0 \varDelta T(\theta ) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)G_0 \varDelta T(\theta ) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert t P G_0 \varDelta T(\theta ) \vert \phi \rangle ~. \end{aligned}$$

(7)

The first equations in (6) and (7) are the Faddeev equations (1) for $T(\theta _0)$. The second equation in the set (7) for $\langle \beta \vert \varDelta T (\theta ) \vert \phi \rangle$ can be solved within the set of channels $\vert \beta \rangle$ only. Using this solution, $\langle \alpha \vert \varDelta T (\theta ) \vert \phi \rangle$ is then computed by:

$$\begin{aligned} \langle \alpha \vert \varDelta T (\theta ) \vert \phi \rangle= & {} \left\langle \alpha \vert t P G_0 \sum _{\beta } \int _{p'q'} \vert p' q' \beta \right\rangle \langle p' q' \beta \vert \varDelta T(\theta ) \vert \phi \rangle \nonumber \\&+ \langle \alpha \vert (1+tG_0) V (\theta _0) (1+P)G_0 \nonumber \\&\sum _{\beta } \int _{p'q'} \vert p'q' \beta \rangle \langle p' q' \beta \vert \varDelta T(\theta ) \vert \phi \rangle ~, \end{aligned}$$

(8)

and finally, $\langle {\tilde{\alpha }} \vert T (\theta ) \vert \phi \rangle$ is calculated.

The outlined above procedure constitutes the perturbative approach of Ref. [25]. In short, one solves the 3N Faddeev equation (1) exactly with the NN potential combined with the 3NF restricted to the parameter free term (set $\theta _0=(0,\dots ,0)$). The solution with the $\theta _0$ set forms a starting point in the perturbative treatment of Eqs. (6–8) and has to be calculated only once, regardless of how many variations of strength parameters are required. In the next step, the proper perturbative treatment is performed, solving first the second equation in set (7). Having determined $\langle \alpha \vert \varDelta T (\theta ) \vert \phi \rangle$ from Eq.(8) the emulator solution $\langle {\tilde{\alpha }} \vert T (\theta ) \vert \phi \rangle$ is calculated (in the following this emulator will be denoted by $E\varDelta T$). That allows one to reduce the required computation time and to reproduce surprisingly well the exact predictions for neutron-deuteron (nd) elastic scattering as well as for nd breakup observables [25]. To be specific, taking set $\vert \beta \rangle$ which includes all 2N states with the total 2N angular momenta $j\le 2$, leads to a reduction of the computing time by a factor of approximately 4 in comparison to the exact calculations. Note that it takes approximately 30 minutes on a personal computer to solve Eq. (1), provided that the $V(\theta _0) (1+P)$ and $V(\theta _i) (1+P)$ kernels, acting in $(1+tG_0) V (\theta ) (1+P)G_0T(\theta ) \vert \phi \rangle$ term of Eq. (1), are prepared in advance, with the strengths $\theta _i=(c_i=1, c_{k\ne i}=0)$.

In spite of such a large reduction, the computational time can be even further decreased and calculation of 3N continuum observables made in a flash. This notion is based on the observation that among three kernel-terms in the second equation of set (7), it is possible (because of the smallness of $\varDelta V(\theta )$) to neglect the term $\langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)G_0 \varDelta T(\theta ) \vert \phi \rangle$. The resulting integral equation for $\langle \beta \vert \varDelta T (\theta ) \vert \phi \rangle$:

$$\begin{aligned} \langle \beta \vert \varDelta T (\theta ) \vert \phi \rangle= & {} \langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)\vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) \varDelta V(\theta ) (1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) V (\theta _0) (1+P)G_0 \varDelta T(\theta ) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert t P G_0 \varDelta T(\theta ) \vert \phi \rangle ~, \end{aligned}$$

(9)

permits one to transfer the linear dependence on the strengths $c_i$ from the $\varDelta V(\theta )$ on the $\varDelta T(\theta )$. Namely, let $\langle \beta \vert \varDelta T_i \vert \phi \rangle$ be a solution of Eq. (9) for a set $\theta _i=(c_i=1, c_{k \ne i}=0)$:

$$\begin{aligned} \langle \beta \vert \varDelta T_i \vert \phi \rangle\equiv & {} \langle \beta \vert (1+tG_0) \varDelta V_i (1+P)\vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) \varDelta V_i (1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&+ \langle \beta \vert (1+tG_0) V (\theta _0) (1+P)G_0 \varDelta T_i \vert \phi \rangle \nonumber \\&+ \langle \beta \vert t P G_0 \varDelta T_i \vert \phi \rangle ~. \end{aligned}$$

(10)

Multiplying (10) by $c_i$ and summing over i one gets:

$$\begin{aligned}&\langle \beta \vert \sum _i c_i \varDelta T_i \vert \phi \rangle \nonumber \\&\quad \equiv \langle \beta \vert (1+tG_0) \sum _i c_i \varDelta V_i (1+P)\vert \phi \rangle \nonumber \\&\qquad + \langle \beta \vert (1+tG_0) \sum _i c_i \varDelta V_i (1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&\qquad + \langle \beta \vert (1+tG_0) V (\theta _0) (1+P)G_0 \sum _i c_i \varDelta T_i \vert \phi \rangle \nonumber \\&\qquad + \langle \beta \vert t P G_0 \sum _i c_i \varDelta T_i \vert \phi \rangle ~, \end{aligned}$$

(11)

and the solution of Eq. (9) is given by:

$$\begin{aligned} \langle \beta \vert \varDelta T(\theta ) \vert \phi \rangle= & {} \sum _{i=1}^N c_i \langle \beta \vert \varDelta T_i \vert \phi \rangle ~. \end{aligned}$$

(12)

In this way at a given energy the computation of observables in the elastic Nd scattering and deuteron breakup reaction for any combination of strengths $c_i$ of contact terms is reduced to solving once $N+1$ Faddeev equations: one equation for $T(\theta _0)$ and N equations for $\varDelta T_i$. In the first step, solution for $\langle \alpha (\beta ) \vert T (\theta _0) \vert \phi \rangle$ is found. Then Eq. (10) is solved for $\langle \beta \vert \varDelta T_i \vert \phi \rangle$, from which the $\langle \alpha \vert \varDelta T_i \vert \phi \rangle$ is calculated using Eq. (8). The above computations need to be done only once and then for any combination of the strengths $c_i$ the amplitude $\langle {\tilde{\alpha }} \vert T(\theta =(c_i,i=1,\dots ,N) ) \vert \phi \rangle$ is obtained by trivial summation.

For a calculation of elastic scattering observables the required sum of the second and the third term in Eq. (2) is obtained by:

$$\begin{aligned}&\langle \beta \vert V^{(1)}(\theta )(1+P)\vert \phi \rangle + \langle \beta \vert V^{(1)}(\theta )(1+P)G_0T(\theta ) \vert \phi \rangle \nonumber \\&\quad = \langle \beta \vert V(\theta _0)(1+P)\vert \phi \rangle + \langle \beta \vert V(\theta _0)(1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&\qquad + \sum _i c_i [ \langle \beta \vert \varDelta V_i(1+P) \vert \phi \rangle \nonumber \\&\qquad + \langle \beta \vert \varDelta V_i(1+P)G_0 T(\theta _0) \vert \phi \rangle \nonumber \\&\qquad + \langle \beta \vert V(\theta _0) (1+P)G_0 \varDelta T_i \vert \phi \rangle ] \nonumber \\&\qquad + \sum _{i,k} c_i c_k \langle \beta \vert \varDelta V_i (1+P)G_0 \varDelta T_k \vert \phi \rangle ~. \end{aligned}$$

(13)

It is interesting to note that while the breakup amplitude (3) is linear in 3N contact strengths, the elastic scattering amplitude contains, as a consequence of the third term present in Eq. (2), also terms quadratic in these strengths.

3 Results and discussion

The above computational scheme forms the new emulator, which will be denoted in the following by $E\varDelta T_i$. To check its quality and efficiency as well as to compare it with $E\varDelta T$ we have chosen, as in Ref. [25], the SMS N$^4$LO$^+$ chiral potential of the Bochum group [10], with the regularization cutoff $\varLambda = 450$ MeV, and combined it with the chiral N$^2$LO 3NF. We solved the 3N Faddeev equation (1) exactly at two incoming neutron energies $E=70$ and 190 MeV with that combination as well as with this NN potential supplemented with the parameter free $2\pi$-exchange term of the N$^2$LO 3NF (set $\theta _0=(c_D=0, c_E=0)$). The first energy was taken from a region where 3NF effects start to appear in 3N continuum observables and the second one from a range with well-developed 3NF effects [23, 24]. The solution with the $\theta _0$ set together with solutions $\langle \beta \vert \varDelta T_i \vert \phi \rangle$ of N integral equations (10) with the set of 3N channels $\vert \beta \rangle$, comprising all 2N states with the total angular momentum $j\le 2$, form a starting point in the proposed computational scheme and have to be calculated only once. Also $\langle \alpha \vert \varDelta T_i (\theta ) \vert \phi \rangle$ is computed only once according to Eq. (8), and, in parallel with those calculations, all terms in Eq. (13) independent from $c_i$. Based on these quantities we calculated the emulator solution $\langle {\tilde{\alpha }} \vert T (\theta ) \vert \phi \rangle$. Our new scheme performed for $N=2$ leads to reduction by a factor of $\approx 50$ of the computer time required by the perturbative approach of Ref. [25]. Computation of all elastic scattering observables or observables in one exclusive breakup geometry for a particular set of strengths $\theta =(c_i, i=1,\dots ,N)$, in the perturbative approach requires $\approx 8$ minutes of a personal computer time, while the new scheme requires only $\approx 10$ seconds. Since the calculation of $\langle {\tilde{\alpha }} \vert T (\theta ) \vert \phi \rangle$ from $\langle {\tilde{\alpha }} \vert T (\theta _0) \vert \phi \rangle$ and $\langle {\tilde{\alpha }} \vert \varDelta T_i (\theta ) \vert \phi \rangle$ takes practically no time, the drastic reduction of time in the new scheme is independent from the number of the contact terms N.

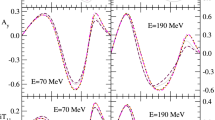
The emulators $E \varDelta T_i$ and $E \varDelta T$ are approximations of the exact results. To estimate the quality of these approximations we show in Fig. 1 at both energies the distributions of percentage deviations from exact results $O_{exact}$ predictions of both emulators $O_{appr}$: $\varDelta = {(O_{appr}-O_{exact})} / {O_{exact}} \times 100.0$, for all nonvanishing nd elastic scattering observables O (cross section, nucleon and deuteron analyzing powers as well as spin correlation and spin transfer coefficients between all participating particles, altogether 51 observables). They were calculated on a uniform grid of 73 c.m. angles $\theta _{c.m.} \in (0^o,180^o)$. These distributions encompass six sets of strengths values $(c_D,c_E)=(1, 1), (2, 1), (4, 1)$, (6, 1), (8, 1), and (10, 1) (according to the notation of Refs. [12, 13]). The precision of both emulators at both energies is similar and amounts to $\approx 1-2$ %, with $E \varDelta T$ being slightly more precise than $E \varDelta T_i$.

Fig. 1

Histograms of percentage deviations from exact results of the predictions by the emulator $E\varDelta T$ (red lines) or $E\varDelta T_i$ (blue lines), for 51 nonvanishing observables of the elastic nd scattering and 6 sets of $(c_D,c_E)$ strengths. For details see text

To demonstrate the power of the new emulator we show in Fig. 2 the color map of $\chi ^2$ values in the plane of strengths ($c_D,c_E$) for elastic scattering cross section at $E=70$ MeV. That map was obtained with about 5000 values of strength combinations, both varied in step of 0.1. The minimum of $\chi ^2$ valley is indicated by black squares. It crosses with $\chi ^2$ values for the $^3$H correlation line, shown by yellow dots, in their minimum. The resulting values of strengths and their errors are $c_D=2.910 \pm 0.140$ and $c_E=0.385 \pm 0.015$. Using these strengths we demonstrate in Fig. 3 importance of contributions to the cross section from individual terms of the N$^2$LO 3NF. We show percentage changes in the cross section values calculated solely with the NN potential by adding the parameter-free term itself, and by the combination of that term with the D- or E-terms. The 2$\pi$-exchange contribution as well as the short-range D-term are important at both energies. The contribution of the E term is negligible at $E=70$ MeV but clearly visible at 190 MeV.

Fig. 2

The color map of $\chi ^2$ values for nd elastic scattering cross section at $E=70$ MeV, in the plane of strengths ($c_D,c_E$) of N$^2$LO 3NF contact terms. It was obtained with the $E\varDelta T_i$ emulator for combination of chiral NN N$^4$LO$^+$ potential and N$^2$LO 3NF and computed from about 5000 strengths combinations. The proton-deuteron cross section data were taken from [29] and $\chi ^2$ calculated for c.m. angles in the range $\theta _{c.m.} \in (62.18^o,158.33^o)$. The (black) squares show the position of the $\chi ^2$-minimum at given $c_E$-value and (yellow) dots depict the $^3$H correlation line

Fig. 3

The (red) solid lines show percentage changes of the nd elastic scattering cross section at $E=70$ and 190 MeV, predicted with SMS N$^4$LO$^+$ NN potential, induced by N$^2$LO 3NF with strengths of the contact terms $c_D=2.910$ and $c_E=0.385$. The (blue) dashed lines correspond to changes caused by a 3NF parameter-free term, while the (black) dash-dotted and (magenta) dash-double-dotted curves to changes by a 3NF parameter free + D and parameter free + E terms, respectively

4 Summary and conclusions

In summary, we presented a new powerful calculational scheme which enables us to take efficiently into account any number of contact terms of a chiral 3NF in the 3N continuum Faddeev calculations. That approach facilitates a reduction of the time required to compute observables for a given set of strengths to seconds and is thus especially suited to repeated calculations with varying strengths of contact terms. We demonstrated that the proposed emulator reproduces very well the exact predictions for 3N continuum observables. It is conceivable that with the help of the constructed emulator of the exact solutions of the 3N Faddeev equation fine tuning of a 3N Hamiltonian parameters based on available 3N scattering data is feasible. To that aim not only existing neutron-deuteron elastic scattering and breakup data but also more abundant and precise proton-deuteron data should be used. However, before using the proton-deuteron data they should be corrected for the effects of the proton-proton Coulomb force acting in the proton-deuteron system. Such procedure involving estimation of the Coulomb corrections through the difference of calculations with and without Coulomb force included [21, 30,31,32] have been already applied for example in [12].