Abstract
Ultrafine grained (UFG) metallic materials obtained by severe plastic deformation (SPD) typically exhibit very high strength properties, whose values are much higher than those predicted by the well-known Hall–Petch relation. Our studies show that the basis for this to occur is that SPD not only forms the UFG structure, but also leads to the formation of other nanostructural features, such as dislocation substructures, nanotwins, and nanosized precipitates of second phases, which additionally contribute to strengthening of materials. At the same time, this analysis of hardening mechanisms indicates that the structure and condition of grain boundaries, namely, their nonequilibrium state and the presence of grain boundary segregations, also substantially contribute to hardening. Taking this into consideration, approaches are discussed to achieve very high strengths in metallic materials by SPD.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
It is well known that the strength properties of pure metals and alloys are determined by several factors, but the average grain size frequently plays a key role [1, 2]. In particular, the dependence of the strength of various polycrystalline materials on the average grain size d is usually described by the well-known Hall–Petch formula, according to which the yield strength σy has the form of
where σ0 is the lattice friction stress, kHP is the Hall–Petch coefficient, and d is the average grain size. According to Eq. (1), the strength of the material increases with a decrease in the average grain size.
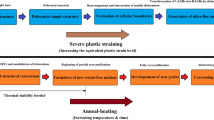
In this regard, the strength of pure metals and alloys can be substantially increased due to the formation of (i) the ultrafine grained (UFG) structure in their volume with an average grain size of less than 1 μm and (ii) predominantly high-angle boundaries, which can be achieved by severe plastic deformation (SPD) [3‒5]. At present, the most popular SPD methods for this purpose are equal channel angular pressing (ECAP), high-pressure torsion (HPT), and a number of other methods. The deformation treatment of materials by SPD methods was a key step that marked the beginning of comprehensive studies of the mechanical properties of bulk nanomaterials and now serve as a basis for numerous studies of various nanostructured metallic materials (see recent reviews and books on this topic [5–10]). The above studies were devoted to investigating the mechanisms of hardening and plasticity and ways to increase them, as well as to enhancing their fatigue, impact strength, and other operation-related properties.
Over the past 2 decades, the effect of refinement of the grain size to the nanometer range on the strength of materials has been investigated in sufficient detail in a number of studies (see, for example, [3–10]). As a rule, increased strengths in many studies were observed with a decrease in the grain size in accordance with Eq. (1). However, this formula is often violated for nanosized grains (less than 50–100 nm), so that the Hall–Petch curve deviates from a linear relationship, and its slope kHP becomes negative (Fig. 1, curve 1) (see, for example, [5]). This problem has been extensively analyzed in many experimental and theoretical studies. In addition, several recent studies have shown that UFG materials can exhibit substantially higher strengths than those predicted by the Hall–Petch relation for the range of ultrafine grains (see Fig. 1, curve 2) [11, 12]. The reason for such superstrength can be associated with the influence of various nanostructural features observed in the metals and alloys subjected to SPD and located both in the bulk of grains (dislocation substructures, nanosized particles of secondary phases, and nanotwins) and along their boundaries (nanoclusters and segregations) [10].
Therefore, an analysis of the origin of superstrength in UFG materials and an investigation of the action of various hardening mechanisms, including both known ones that are associated with the presence of nanoparticles and other indicated nanostructural features and new ones that are associated with the influence of grain boundary structures in UFG materials are urgent problems that have been considered in this study.
EXPERIMENTAL OBSERVATIONS
In the past decade, a number of studies have been devoted to the strength properties of various nanostructured metals and alloys, including Al alloys [13, 14], steels [15, 16], and titanium materials [17]. In all cases, a substantial increase in the strength of materials was observed after microstructure refinement by SPD methods, while the yield strength values substantially exceeded the values calculated from the Hall–Petch relation. This situation is illustrated in Fig. 2 [13], from which one can see that the yield strength values of the UFG Al alloys 1570 and 7475 with a grain size of about 100 nm are much higher than those predicted by the Hall–Petch formula for similar Al alloys with a similar grain size.
The dependence of the yield strength on the average grain size for the Al alloys 1100 and Al–3% Mg and the yield strength values for the UFG alloys 1570 and 7475 [13].
Next, we more closely analyze the results of experiments on achieving a high-strength state in commercially pure titanium Grade 4 processed by ECAP and HPT techniques. This material (composition, wt %: Fe 0.5, O 0.4, C 0.08, N 0.05, H2 0.015, and a Ti base) is very important for medical applications in the manufacture of implants. At the same time, an increase in its strength is important for creating implants with an improved design and increased osseointegration [18]. A detailed description of the processing of commercially pure titanium by the ECAP and HPT techniquesto form a UFG structure was published in previous studies [17–19]. The microstructure of the samples after SPD treatment was studied by transmission electron microscopy (TEM), X‑ray diffraction, and scanning electron microscopy with electron backscatter diffraction (EBSD). Tensile tests were carried out on an Instron 5982 testing machine at room temperature after HPT on small specimens with a size of 1 × 0.25 × 3 mm at a strain rate of 3 × 10–4 s–1 [10, 13] and on standard cylindrical specimens with a diameter of 3 mm and a length of 15 mm after ECAP processing.
The study results show that ECAP or HPT processing can provide the formation of various types of grain boundaries (GBs). After a small number of ECAP passes or the first revolutions during HPT, a large number of low-angle boundaries appear in the structure. With an increase in the number of passes, the proportion of low-angle boundaries decreases [5]. In particular, the proportion of high-angle boundaries with a misorientation angle of more than 15° in commercially pure titanium subjected to HPT with five turns is about 80% compared to 20–30% HPT with one turn. In this case, the average grain size in titanium subjected to HPT is about 120 nm. This UFG structure is stable when heated up to 300°C.
An interesting example of high-strength UFG Ti obtained by combined SPD processing in the shape of long rods intended for the subsequent manufacture of medical implants is studied. This original technology for manufacturing bars up to 8 mm in diameter and up to 3 m in length from UFG Ti includes the ECAP procedure followed by thermomechanical treatment (TMT) [20].
Such a combined SPD treatment leads to the formation of an UFG structure in the bars, which consists of equiaxed grains smaller than 150 nm in size (Fig. 3), although there are also grains elongated in the longitudinal direction with a substructure inside. Measurements of grain boundary misorientation using EBSD analysis showed that the fraction of high-angle boundaries in this state is less than 40%. At the same time, a substantial decrease in substructural units and an increase in the proportion of high-angle boundaries up to 80% with preservation of the average grain size were achieved by varying the deformation modes and performing TMT at 300–350°C.
The microstructure of commercially pure titanium of Grade 4 (a) in the initial hot-rolled state and (b, c) after ECAP + TMT according to (a, b) optical microscopy and (c) transmission electron microscopy [20].
The technology for producing nanotitanium rods has been improved in recent years, and the original ECAP-Conform die-set installation is used at present to obtain pilot batches of nanotitanium rods for producing medical implants for dentistry and maxillofacial surgery [18].
Recently, the processing of Grade 4 titanium was studied in detail, including the HPT with ten revolutions and annealing procedures in different regimes [19]. Table 1 shows the structural parameters of titanium after these treatments.
In addition, Table 2 shows data on the mechanical properties of titanium after these treatments. It follows from the results that the formation of an UFG structure in commercially pure titanium by HPT leads to an increase in the microhardness HV to (353 ± 7) HV (Table 2). Subsequent annealing at 700°C for 30 min (HPT + 700°C) leads to softening of the material due to the development of recrystallization processes, which is accompanied by a decrease in hardness to 266 ± 5 HV. After additional treatment (HPT + 700°C + HPT), the double contribution to the strength from the formed ω phase and the resulting UFG structure provide an even greater increase in the microhardness HV to 423 ± 8 HV, and subsequent annealing at 350°C for 30 min (HPT + 700°C + HPT + 350°C) to relieve stress in the material allows retaining the achieved microhardness parameters at a very high level of 433 ± 3 HV. Figure 4 shows the engineering curves of the dependence of the flow (yield) stresses on the degree of tensile strain of the studied samples. In the initial state, the behavior of the curve is typical of hot-rolled materials. After reaching the yield point, a gradual increase in stresses to maximum values is observed with a subsequent decrease due to the strain localization. Severe plastic deformation by torsion (HPT) substantially changes the behavior of the curve. A decrease in the uniform strain, a substantial increase in the strength parameters, and a decrease in the plasticity are observed. High-temperature annealing in the deformed state leads to further developing the recrystallization processes and leveling the hardening effect out due to the formation of the UFG structure and crystal lattice distortions. Repeated HPT leads to a sharp increase in the strength of the material, but a substantial loss of plasticity. However, subsequent stress-relieving annealing at 350°C provides an increase in the plasticity with preservation of high strength.
ANALYSIS OF HARDENING MECHANISMS
To determine the main mechanisms of hardening after combined deformation–heat treatment of commercially pure titanium of Grade 4 and to understand the nature of its superstrong strength state, we analyze the contributions of various microstructural parameters to the overall strength of the material. For this purpose, we applied an approach that takes additive contributions of hardening mechanisms into account, such as the grain boundary (σgb), dislocation (σd), solid solution (σss), and dispersion (σor) types of hardening, to the flow (yield) stress in accordance with [1, 6, 9, 21], as follows:
where σ0 ≈ 80 MPa is the friction stress of the crystal lattice in titanium [17, 22].
Grain Boundary Hardening (Hall–Petch Effect)
The grain boundary hardening can be calculated using the Hall–Petch equation (1) [1, 2, 21, 22]. As was shown in [6, 22], the value of the Hall–Petch coefficient (kHP) for commercially pure titanium can noticeably decrease when its structure is refined in size to the UFG state. Following the published data [22], two kHP values were used: 0.45 MPa m1/2 for coarse grained Ti and 0.12 MPa m1/2 for UFG Ti.
Data on the average grain sizes of Grade 4 titanium in various states are given in Table 1. The calculated data on σgb are given in Table 3. For Grade 4 titanium in the initial state, the contribution of the grain boundary hardening was about 140 MPa. Subsequent processing by the HPT method with ten revolutions leads to a substantial increase in this parameter to values of approximately 350 MPa due to a strong refinement of the grain structure. Subsequent annealing at 700°C for 30 min leads to recrystallization of the structure and, consequently, to grain growth; as a result, the grain boundary hardening decreased to a value of 200 MPa. The combined processing according to the HPT + annealing at 700°C + HPT regime made it possible to obtain a structure with an even smaller grain size, which led, as a result, to an increase in the grain boundary hardening value up to 400 MPa. The use of annealing at 350°C for 30 min after the combined deformation–heat treatment led to a slight coarsening of the grain structure and, consequently, to a change in the grain boundary hardening value to about 340 MPa.
Dislocations-Related Hardening
The contribution of dislocations to the hardening of a material is usually described using the Taylor formula [1, 2, 21]:
where α1 is the dislocation hardening constant equal to 0.2 for Ti [22], b = 0.347 nm is the Burgers vector, G = 45.6 GPa is the shear modulus, M = 3 is the Taylor factor, and ρ is the total dislocation number density.
Data on the dislocation number density of Grade 4 titanium in various states are given in Table 1. The results of calculations of σd are given in Table 3. For samples in the initial state, the calculated contribution to the strength is 150 MPa. After the HPT treatment, an increase in the dislocation number density is observed; the dislocation hardening calculated from these data is 440 MPa. Subsequent annealing at 700°C leads to recrystallization of the structure and, accordingly, to annihilation of defects in the crystal lattice; the calculated contribution of dislocations-related hardening decreases to 140 MPa. A sufficiently high dislocation number density is observed after combined deformation–heat treatment according to the following regime: HPT + annealing 700°C + HPT. In this case, the dislocation hardening is 380 MPa. Subsequent annealing at 350°C leads to intense annihilation of defects in the crystal lattice, which gives rise to a substantial decrease in the dislocation number density. In this state, the hardening from dislocations is 150 MPa.
Solid Solution Hardening
The solid solution hardening is proportional to the square root of the concentration of impurities O, Nb, and C in Ti, and is determined using the following formula [22, 23]:
where c is the oxygen equivalent in atomic percents, which is defined as O + 20N + \(\frac{3}{4}\)C.
The proportion of O, N, and C in Grade 4 titanium in the initial state was determined using an optical emission spectrometer. The σss value calculated from the obtained oxygen equivalent is given in Table 3. In the initial state, the solid solution hardening of Grade 4 titanium was 110 MPa. According to [23], a change in the concentration of impurity elements in commercially pure titanium after deformation–heat treatments has a small effect on the hardening. In this regard, the solid solution hardening of Grade 4 titanium after deformation–heat treatments can be taken approximately equal to the σss value for this material in the initial state.
Dispersion Hardening
Dispersion hardening due to the influence of dispersed particles is usually estimated using the Orowan equation, which is expressed as follows [21, 23]:
where r is the particle radius and λ is the average distance between particle centers, which is determined by the relationship [21, 23]
where f is the volume fraction of particles.
The sizes of intermetallic nanoparticles and their volume fraction are given in Table 1. The largest particles are observed in the state after HPT + annealing at 700°C. Calculations with use of the Orowan equation demonstrate that these particles make an additional contribution of about 70 MPa to the strengthening of titanium after HPT + annealing at 700°C. The largest volume fraction of nanosized particles is observed in the state after treatments HPT + annealing at 700°C + HPT + annealing at 350°C. The calculations performed using the Orowan equation demonstrate an additional contribution of 150 MPa to the strengthening of Grade 4 titanium in this state. In the hot-rolled state and after HPT the dispersion hardening is not taken into account due to the small fraction of precipitated particles and the difficulty of their detection in TEM images. In the case of the state after treatments HPT + annealing at 700°C + HPT, an additional contribution to hardening is made by the metastable ω phase (σSL), which is formed as a result of this HPT, as further studies have shown.
The calculated hardening of Grade 4 titanium after HPT + annealing at 700°C + HPT due to the additional contribution of the ω phase was 200 MPa.
Table 3 compares the calculated types of hardening of Grade 4 titanium in various states with the experimental results of mechanical tests. As can be seen from the data given in Table 3, different hardening mechanisms contribute to the strength of UFG titanium. However, the total contribution from the considered hardening mechanisms in the state with the highest strength (σy = 1340 MPa) is much less than this value. This discrepancy indicates that another hardening mechanism also operates during deformation of UFG titanium in this state. Similar conclusions have been previously drawn in the studies of our laboratory staff and colleagues for other UFG metal materials, namely, Al alloys [13, 14] and a number of steels [15, 16]. Such a hardening mechanism can be associated with the state of grain boundaries in UFG materials, their nonequilibrium structure containing grain boundary dislocations, and the presence of grain boundary segregations of alloying elements [10, 23].
Recent model calculations performed in [24] have shown that the formation of segregations of impurities or alloying elements at grain boundaries can substantially slow the generation of dislocations at grain boundaries and contribute to additional hardening of UFG materials. At the same time, the computer simulation data [25, 26] and experimental study results [13, 14, 16] provide convincing evidence of the formation of grain boundary segregations during the formation of UFG structures in metallic materials by the SPD methods, while their nature and morphology are closely related to the treatment regimes.
CONCLUSIONS
The results of recent studies show that the strength values of UFG materials obtained by SPD methods are traditionally much higher than those predicted from the Hall–Petch relation. The physical origin of this phenomenon is related to the fact that the strength properties of UFG materials are determined not only by the presence of ultrafine grains, but also by other nanostructural features, such as the formation of a subgrain dislocation structure, nanotwins, and nanosized segregations of second phases, as well as the structure of grain boundaries, i.e., their nonequilibrium state and the presence of grain boundary segregation of impurities or alloying elements. The last factor is newly discovered, but very important, since it can make a substantial contribution to the strength of UFG materials. Moreover, segregations at grain boundaries can also have an effect on the ductility of these kinds of metals and alloys. In particular, it has recently been shown that the presence of Zn grain boundary segregations in Al alloys with ultrafine grains even ensures the manifestation of superplasticity at low temperatures [25]. It can be expected that the study of hardening mechanisms and their control using SPD methods in the coming years will become an important research direction in the development of metallic materials that exhibit not only very high strength, but also ductility and other enhanced mechanical properties.
REFERENCES
M. A. Shtremel’, Strength of Alloys. Part II. Deformation (MISiS, Moscow, 1997) [in Russian].
M. I. Gol’dshtein, V. S. Litvinov, and B. M. Bronfin, Metal Physics of High-Strength Alloys (Metallurgiya, Moscow, 1986) [in Russian].
R. Z. Valiev, R. K. Islamgaliev, and I. V. Alexandrov, “Bulk nanostructured materials from severe plastic deformation,” Prog. Mater Sci. 45, 103–189 (2000).
R. Z. Valiev and I. V. Aleksandrov, Bulk Nanostructured Metallic Materials (Akademkniga, Moscow, 2007) [in Russian].
R. Z. Valiev, A. P. Zhilyaev, and T. G. Langdon, Bulk Nanostructured Materials: Fundamentals and Applications (TMS-Wiley, Hoboken, 2014).
E. V. Kozlov, A. M. Glezer, N. A. Koneva, N. A. Popova, and I. A. Kurzina, Fundamentals of Plastic Deformation of Nanostructured Materials (Fizmatlit, Moscow, 2016) [in Russian].
Z. Horita and K. Edalati, “Severe plastic deformation for nanostructure controls,” Mater. Trans. 61, 2241–2247 (2020).
K. Edalati, A. Bachmaier, V. A. Beloshenko, Y. Beygelzimer, V. D. Blank, W. J. Botta, K. Bryła, J. Čížek, S. Divinski, N. A. Enikeev, Y. Estrin, G. Faraji, R. B. Figueiredo, M. Fuji, T. Furuta, T. Grosdidier, J. Gubicza, A. Hohenwarter, Z. Horita, J. Huot, Y. Ikoma, M. Janeček, M. Kawasaki, P. Král, S. Kuramoto, T. G. Langdon, D. R. Leiva, V. I. Levitas, A. Mazilkin, M. Mito, H. Miyamoto, T. Nishizaki, R. Pippan, V. V. Popov, E. N. Popova, G. Purcek, O. Renk, A. Révész, X. Sauvage, V. Sklenicka, W. Skrotzki, B. B. Straumal, S. Suwas, L. S. Toth, N. Tsuji, R. Z. Valiev, G. Wilde, M. J. Zehetbauer, X. Zhu, “Nanomaterials by severe plastic deformation: review of historical developments and recent advances,” Mater. Res. Lett. 10, 163–256 (2022).
I. A. Ovid’ko, R. Z. Valiev, and Y. T. Zhu, “Review on superior strength and enhanced ductility of metallic nanomaterials,” Prog. Mater Sci. 94, 462–540 (2018).
R. Z. Valiev, B. Straumal, and T. G. Langdon, “Using severe plastic deformation to produce nanostructured materials with superior properties,” Annu. Rev. Mater. Res. 52, 357–382 (2022).
R. Z. Valiev, N. A. Enikeev, and T. G. Langdon, “Towards superstrength of nanostructured metals and alloys, produced by SPD,” Kovove Mater. 49, 1–9 (2011).
S. A. Firstov, T. G. Rogul, and O. A. Shut, “Transition from microstructures to nanostructures and ultimate hardening,” Funct. Mater. 16, 364–373 (2009).
R. Z. Valiev, N. A. Enikeev, M. Yu. Murashkin, V. U. Kazykhanov, and X. Sauvage, “On the origin of extremely high strength of ultrafine–grained Al alloys produced by severe plastic deformation,” Scr. Mater. 63, 949–952 (2010).
P. V. Liddicoat, X. Z. Liao, Y. Zhao, Y. Zhu, M. Y. Murashkin, E. J. Lavernia, R. Z. Valiev, and S. P. Ringer, “Nanostructural hierarchy increases the strength of aluminium alloys,” Nat. Commun. 1, 63 (2010).
M. V. Karavaeva, S. K. Kiseleva, A. V. Ganeev, E. O. Protasova, M. M. Ganiev, L. A. Simonova, and R. Z. Valiev, “Superior strength of carbon steel with an ultrafine-grained microstructure and its enhanced thermal stability,” J. Mater. Sci. 50, 6730–6738 (2015).
J. G. Kim, N. A. Enikeev, J. B. Seol, M. M. Abramova, M. V. Karavaeva, R. Z. Valiev, C. G. Park, and H. S. Kim, “Superior strength and multiple strengthening mechanisms in nanocrystalline TWIP steel,” Sci. Rep. 8, 11200 (2018).
I. Semenova, G. Salimgareeva, CostaG. Da, W. Lefebvre, and R. Valiev, “Enhanced strength and ductility of ultrafine-grained Ti processed by severe plastic deformation,” Adv. Eng. Mater. 12, 803–807 (2010).
R. Z. Valiev, I. Sabirov, E. G. Zemtsova, E. V. Parfenov, L. Dluhoš, and T. C. Lowe, “Nanostructured commercially pure titanium for development of miniaturized biomedical implants,” in Titanium in Medical and Dental Applications (Woodhead, 2018), pp. 393–417.
L. R. Rezyapova, R. R. Valiev, V. D. Sitdikov, and R. Z. Valiev, “Study of second phase precipitates in nanostructured commercially pure titanium,” Lett. Mater. 11, 345–350 (2021).
R. Valiev, I. P. Semenova, E. Jakushina, V. V. Latysh, H. J. Rack, T. C. Lowe, J. Petruželka, L. Dluhoš, D. Hrušák, and J. Sochová, “Nanostructured SPD processed titanium for medical implants,” Mater. Sci. Forum 584, 49–54 (2008).
N. Balasubramanian and T. G. Langdon, “The strength–grain size relationship in ultrafine-grained metals,” Metall. Mater. Trans. A 47, 5827–5838 (2016).
P. Luo, Q. Hu, and X. Wu, “Quantitatively analyzing strength contribution vs grain boundary scale relation in pure titanium subjected to severe plastic deformation,” Metall. Mater. Trans. A 47, 1922–1928 (2016).
R. Z. Valiev, “Superior strength in ultrafine-grained materials produced by SPD processing,” Mater. Trans. 55, 13–18 (2014).
S. V. Bobylev, N. A. Enikeev, A. G. Sheinerman, and R. Z. Valiev, “Strength enhancement induced by grain boundary solute segregations in ultrafine-grained alloys,” Int. J. Plast. 123, 133–144 (2019).
N. Q. Chinh, M. Y. Murashkin, E. V. Bobruk, J. L. Lábár, J. Gubicza, Z. Kovács, V. Maier-Kiener, and R. Z. Valiev, “Ultralow-temperature superplasticity and its novel mechanism in ultrafine-grained Al alloys,” Mater. Res. Lett. 9, 475–482 (2021).
M. V. Petrik, A. R. Kuznetsov, N. A. Enikeev, Yu. N. Gornostyrev, and R. Z. Valiev, “Peculiarities of interactions of alloying elements with grain boundaries and the formation of segregations in Al–Mg and Al–Zn alloys,” Phys. Met. Metallogr. 119 (7), 607–612 (2018).
Funding
This study was supported by a grant from the Russian Science Foundation (project no. 22-19-00445) and by the Ministry of Science and Higher Education of the Russian Federation, contract 075-15-2021-709, unique identifier of project RF-2296.61321X0037 (methodological guidelines).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflicts of interest.
Additional information
Translated by O. Kadkin
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Valiev, R.Z., Usmanov, E.I. & Rezyapova, L.R. The Superstrength of Nanostructured Metallic Materials: Their Physical Nature and Hardening Mechanisms. Phys. Metals Metallogr. 123, 1272–1278 (2022). https://doi.org/10.1134/S0031918X22601627
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0031918X22601627