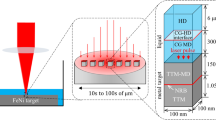
Ablation in liquid is numerically simulated with molecular dynamics and hydrodynamics codes. Laser radiation passes through a transparent liquid, illuminates a metal target, and is absorbed in it and reflected from it. The range of absorbed fluences Fabs about 1 J/cm2 is considered, which is of technological interest: the number of nanoparticles formed per laser pulse below these values is small, whereas the optical breakdown of the liquid occurs above them. A theory is developed to estimate the mass and composition of nanoparticles formed by laser radiation using simulation data and thermodynamic information (equation of state of matter).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 INTRODUCTION
Great attention is paid to the production of nanoparticles (NPs) by means of laser ablation in liquid. The current status of the corresponding studies can be found in the materials of recent conferences:
(i) 6th International Conference on Advanced Nanoparticle Generation & Excitation by Lasers in Liquids (ANGEL), June 2021, China, http://angel-conference.org;
(ii) https://www.cecam.org/workshop-details/1068 Flagship Workshop: Multi-Approach Modeling of Alloy Nanoparticles: from Non-equilibrium Synthesis to Structural and Functional Properties, July 2021 (Centre Européen de Calcul Atomique et Moléculaire).
The finest approaches to increase the yield of NPs and to control their composition and internal structure are proposed in numerous experimental physicochemical works. In particular, core–shell NPs are fabricated for applications in medicine and nanotechnologies [1–4]. To control the composition of NPs, alloy targets are used or NPs are postprocessed in a solution of specially selected salts. In particular, to fabricate NPs from metals М1 and М2, a target of their alloy is irradiated or a nanolaminate of alternating layers of М1 and М2 is processed. In another approach, М1 is used as a target and М2 is present in the composition of dissolved salt.
The initial stages are certainly decisive for the subsequent events. In these stages, laser radiation is absorbed, the target and liquid are heated, and the surface layer begins to move toward the liquid. Heating, motion, and cooling result in the initial composition of NPs. Processes of further transformation of NPs occur in later stages.
In [5–9], the first numerical calculations were performed to quantitatively describe the initial stages (see also [10] and review [11]). Before these works, qualitative characteristics were discussed, including the formation and evolution of plasma (luminescence was detected, spectra were determined [4, 12]) and, then, nucleation, expansion, and oscillations of a cavitation bubble [12–14]. It was unclear how the appearance of NPs is related to a plasma burst and bubble. Even studies with the pulsed X-ray radiography of the plasma region and the bubble nucleus [15] did not provide complete understanding. X-ray radiography [15] was performed in a rather late stage (after 10 μs) when the size of the bubble reached fractions of a millimeter, whereas decisive thermomechanical processes proceed at times of 0.1–10 ns.
In this work, we develop an approach with numerical hydrodynamic and molecular dynamics simulations. The equations of thermodynamic state of substances and phase diagrams are used to understand how the material of the surface layer is separated into a part that is transformed in NPs and a part that remains on the target.
The dynamics of ablation significantly depends on the duration of the pulse. There are two qualitatively different regimes: “spallation” (short pulses) and “nonspallation” (long pulses). In the first regime, tensile stresses exceed the strength of the material; consequently, the nucleation of cavities, cavitation, expansion of the foam layer, and separation of the surface layer occur [16]. A flow appears and covers two regions of a continuous material that are separated by a two-phase mixture (foam); these regions are the separated layer and the remainder of the target. The thermal conductivity of the foam is low [16] and heat release in the liquid is small (the thermal conductivity of the liquid is low); for this reason, the entropy of the separated layer decreases slowly. In the second regime, the continuity of the target is not broken. This regime is considered below.
The amplitude of tensile stresses increases with the absorbed fluence Fabs and decreases with an increase in the duration of the pulse τL. The time dependence of the intensity of the pulse is approximated by a Gaussian I ~ exp(–t2/\(\tau _{{\text{L}}}^{{\text{2}}}\)). Nucleation begins if Fabs exceeds the threshold Fa. In works concerning laser actions, this threshold is called the thermomechanical ablation threshold. The threshold Fa(τL) and depth dnucl(τL) at which the first nuclei (cavities) appear depend on the duration of the pulse τL.
It is known that the relation between the acoustic scale ts = dT/cs, where dT is the thickness of the heated layer and cs is the speed of sound, and the duration τL determines whether nucleation causes the breaking of the material. Depending on a particular metal, ts ~ 5–50 ps. The largest value ts ≈ 50 ps is achieved in gold, where the thermal conductivity is high, electron–ion heat exchange is slow (hence, the thickness dT is large), and the speed of sound is low. Femtosecond impacts certainly belong to the case with spallation: τL < 1 ps and ts ~ 5–50 ps.
As will be seen below, the situation with a nanosecond pulse is of interest. Our calculations for the system consisting of gold and water show that the nucleation of vapor cavities in gold is absent at τL = 0.5 ns and longer. Impacts with the fluence Fabs ~ 1 J/cm2 during the pulse transfers gold in the surface layer to states above the critical point in temperature and pressure.
2 NANOSECOND IMPACT
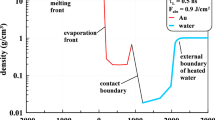
As illustration, Fig. 1 shows instantaneous spatial distributions of parameters in the gold–water system at τL = 0.5 ns and the times t = 0.3, 1, and 3 ns, when the metal absorbs 80, 99.8, and 100% of the fluence Fabs = 0.9 J/cm2, respectively. The absorbed intensity, which is specified by a Gaussian as mentioned above, is maximal at the time t = 0. Beginning the calculation at the time –3τL instead of –∞ we lose 10–5 of Fabs. Before the beginning of the action of the laser pulse, the contact between gold and water is at the point x = 0 (see Fig. 1) and the system is heated to room temperature.
(Color online) (a) Density and pressure profiles at the time t = 0.3 ns over the entire flow field, where m marks the melting front. (b) Pressure and velocity profiles near the contact cb at the time t = 1 ns, where m marks the melting front. (c) Velocity and density profiles near the contact cb at the time t = 3 ns. Gold to the right of the point cc is dense and is almost at rest.
The vertical straight line cc (meaning the condensation curve) in Fig. 1c marks the point on the gold profile that is on the condensation curve at a given time (see also Fig. 2b). The vertical straight lines ch, cb, and a indicate the cold/hot water interface, the gold–water contact (contact boundary), and the “upper” boundary of the “atmosphere.” Water at room temperature is referred to as cold water. The upper boundary of the atmosphere is defined with respect to the effective gravitational acceleration vector g in a noninertial coordinate system associated with the contact cb. The vector g is opposite to the deceleration vector of the contact boundary cb.
(Color online) Phase states of gold at the times t = (a) 0.3 and (b) 1 ns. The evolution of the phase state is accompanied by the descent of the point cb toward the condensation curve because of the expansion and cooling of the near-contact gold layer. Orange lines beginning at the point cb are the profiles of gold that are obtained by excluding the x coordinate from the parametric dependences p(x, t) and ρ(x, t). The green line is the binodal of gold, c.p. is the critical point, and black line Scr is the isentrope passing through the critical point. Water is not shown.
We use the term atmosphere in the sense introduced in [7], where the action of the ultrashort pulse with the duration τL = 100 fs on gold was studied. In this case, gold near the contact was strongly decelerated by water after the initial sharp acceleration to a high velocity of expansion in water [7]. It appeared that the deceleration g of the boundary cb under the nanosecond impact is comparable with that in the case of τL = 100 fs and is about the gravitational acceleration on the surface of a neutron star. In the calculation shown in Fig. 1, the maximum velocity of the contact 490 m/s is reached at a time of 70 ps, and the maximum deceleration g = 8 × 1013 сm/s2 is at the time t = 620 ps (see also Fig. 3 and Section 8). The velocity of the contact cb at a time of 1 ns shown in Fig. 1b is reduced to 63 m/s owing to the deceleration g(t).
(Color online) Time dependences of (black line) the position of the contact and (red line) the intensity. Under heating, the contact xcb(t) begins to move towards water (cf. Fig. 1). After the end of laser irradiation, the contact turns back at a time of 1.2 ns under the action of pressure in the hot water layer. The contact stops at a time of 3.2 ns because of the disappearance of the gas part of the gold profile: the point cb in diagrams shown in Fig. 2 descends below the condensation curve; see the main text.
The field g strongly reduces the pressure in the atmospheric layer with the thickness d between the boundaries cb and a. In Fig. 1b, a decrease in the pressure on the atmosphere owing to the weight of above layers is approximately 0.3 GPa = 3000 atm. This value is about the hydrostatic pressure difference ρa-tmgd on the atmosphere, where ρatm is the density of hot gold in the atmosphere. In this case, the thickness d and the deceleration g are such that the spatial scale of the atmosphere h = \(c_{{\text{s}}}^{{\text{2}}}\)/g, where cs is the speed of sound in gold on the boundary cb, is an order of magnitude larger than the thickness d. Consequently, the density varies slightly on the thickness d (see Fig. 2, where the boundaries of the atmosphere cb and a are indicated). The deceleration of water does not affect gold to the right of the boundary a in Figs. 1a and 1b, and gold in this region expands as in the case of expansion in vacuum.
The role of the absorption of radiation and thermal conductivity under nanosecond impact is significant. It is easier to take into account absorption in the case of femtosecond pulses of a moderate intensity. Absorption occurs in an almost static skin layer. It is necessary to take into account changes in the reflection coefficient caused by the excitation of the electron subsystem. It is appropriate to use the effective absorption coefficient that refers to the entire femtosecond pulse and is taken from experiments.
The significant displacement of the boundary cb between gold and water during the nanosecond pulse is taken into account when describing absorption within our model. The density of gold on the contact during the duration τL = 0.5 ns of the pulse decreases to about the thermodynamic critical density. The thickness Δxcrit of the layer with such a density varies from ~10 to ~100 nm during the action of the main part of the pulse. In our calculations (Fig. 1), the thickness of the absorption layer is not varied over the layer with a nearly critical density. Approximation with absorption in the skin layer is used. The variation of the thickness of the skin layer in the range of 15–30 nm hardly affects the results because the thickness Δxcrit is small. The model of thermal conductivity κ of gold is taken from [17], where the dependence of κ on the temperature and density is taken into account. The thermal conductivity of water is taken from [18, 19].
3 PHASE TRANSITIONS
Figure 2 shows the instantaneous phase diagrams at times of 0.3 and 1 ps corresponding to the profiles in Figs. 1a and 1b, respectively. The equations of state of gold and water are taken according to the broadband multiphase representation [20–23]. Orange lines beginning at the point cb in Fig. 2 are the profiles of gold that are obtained by excluding the x coordinate from the parametric dependences p(x, t) and ρ(x, t). Water is located to the left of the contact cb in Fig. 1 and is not shown in Fig. 2.
The green line in Fig. 2 is the line of coexistence (binodal) of the condensed and vapor phases. This line to the left of the critical point is called the line of condensation. The part of the binodal between the critical and triple points is the line of boiling. The line of sublimation is below the triple point. The melting front m on the profile from Fig. 1 is represented in the form of the horizontal segment m in Fig. 2. In this segment, melting leads to a decrease in the density by approximately 10%. Solidus sol and liquidus liq bound the band of melting.
The pressure is much lower than the bulk modulus of gold of 1.8 Mbar (see Fig. 1). For this reason, a part of the profile (orange line) corresponding to relatively cold gold (entropy below the critical value) in Fig. 2a closely approaches the line of boiling. The entire atmosphere cb–a in Fig. 2a is beyond the binodal. A part of the atmosphere in Fig. 2b begins to enter the two-phase region through the line of condensation. The other part of the atmosphere cb–cc remains in the region of gas-like gold. Furthermore, after the acceleration of the contact cb toward the target induced by the pressure of hot water stops, the atmosphere disappears completely at a time of 3.2 ns (see Fig. 3 and Sections 4 and 8).
4 DISAPPEARANCE OF GAS-LIKE STATES IN GOLD
The deceleration g mentioned above reduces the velocity of expansion of gold in water. The deceleration g is due to the pressure gradient: the pressure on the contact cb is higher than that in gold near the surface after the penetration of the acoustic wave deep into the gold target. Owing to the pressure gradient, the motion of the contact toward water is decelerated, stops, and is reversed. Thus, the trajectory of the contact cb is turned back (see Fig. 3).
It is seen in Figs. 1 and 2 that the density and temperature at the contact cb (the end point of the orange line in Fig. 2) decrease with time. The thermal conductivities of gold and water are taken into account; for this reason, the entropy of gold at the point cb decreases. The point cb moves approximately along an isentrope. This isentrope is located far to the left of the isentrope Scr in Fig. 2 because Scb(t) is larger than Scr. Thus, upon expansion and cooling, the point cb descends on the line of condensation.
The pressure in the hot water layer ch–cb (Fig. 1) both expands this layer and pushes the contact cb to the right. This is seen from the velocity profile shown by the blue line in Fig. 1c. Since dense gold is at rest, the thickness of the remnant cb–cc, which is in the gas-like state above the line of condensation, decreases (see Figs. 1c and 2b). The remnant cb–cc disappears completely at a time of 3.2 ns. After that, the hot water layer is already adjacent to static dense condensed gold. For this reason, the expansion of the hot water layer toward gold ceases and, correspondingly, the contact cb stops (see Fig. 3).
5 STAGE WITH ZERO SURFACE TENSION
The surface tension of strongly rarefied supercritical gold on the boundary cb with water is zero when the point cb is above the line of condensation (see Fig. 2). In this gas-like state of gold, the contact cb is a mechanical contact between two gases rather than between the condensed and gas phases. Therefore, the surface energy barrier on the contact cb is absent, gold atoms are not evaporated but freely diffuse to water gas, and water molecules diffuse to gold gas.
At our parameters of laser impact, gas-like gold exists for about 3 ns.
6 ESTIMATE OF THE MASS OF GOLD ATOMS IN THE DIFFUSE LAYER
The accepted numerical hydrodynamic scheme involves the division into a chain of Lagrangian sites. Water and gold sites are located to the left and right of the point cb in Fig. 1. The diffusion mixing spreading the boundary cb is absent in this scheme.
Let us estimate the coefficient of diffusion of gold atoms in hot water. The mean free path is l = 1/(nσ), where σ = π(rAu + rwt)2; here, rwt is the average radius of water molecules and products of their dissociation (temperatures in the hot layer are high enough for the partial dissociation of molecules). The radii are rAu = 0.17 nm, \({{r}_{{{{{\text{H}}}_{2}}{\text{O}}}}} = 0.15\) nm, rH = 0.12 nm, and \({{r}_{{{{{\text{O}}}_{2}}}}} = \) 0.15 nm. The concentration of water molecules and products of their dissociation is estimated in terms of the density of water in the hot layer, which is approximately 0.05 g/cm3 (see Fig. 1c). Substituting the thermal velocity vT of gold atoms at temperatures under consideration, we obtain D = \(l{{v}_{T}}{\text{/}}3\) = 3 × 10–3 cm2/s.
The thickness of the diffusion layer formed in \({{t}_{{{\text{diff}}}}} = 3\) ns is \({{d}_{{{\text{diff}}}}} = 2\sqrt {D{{t}_{{{\text{diff}}}}}} \) = 60 nm. Consequently, the yield of nanoparticles at the density of the gold fluid of 1–2 g/cm3 (see Fig. 1) on the boundary cb in the time interval when the surface barrier is absent is equal to 10–5 g/cm2. Under the assumption that the average size of nanoparticles is 5–10 nm (the process of condensation is described below), the yield of nanoparticles per irradiation event is about 1012 NPs/cm2.
7 CONDENSATION OF GOLD ATOMS
Figure 4 shows the process of condensation of gold (Au) according to the molecular dynamics simulation for 2.5 × 106 particles in the x × y × z calculation parallelepiped with the dimensions 40 × 200 × 100 nm. The x, y, and z axes are directed along the horizontal, vertical, and normal to the plane of Fig. 4, respectively. The dimensions of the parallelepiped are much longer than the mean free path. The dimension in the x axis increases with time; its initial value is indicated above.
The diffusion of atoms in the hot Au–water binary mixture was simulated with three different potentials describing the Au–Au, water–water, and Au–water interactions. Water is considered in our simulation as a monatomic system for which an ЕАМ (embedded atom method) potential was developed (see [7, 24]). The water–water potential ensures the correct mechanical properties of liquid water, including the density, speed of sound, and shock (Hugoniot) adiabat.
Because of lack of information on the interaction between gold atoms and water molecules, the description of this interaction is significantly simplified to the pair Au–water potential. To construct this potential, we used the van der Waals radii of 0.166 and 0.152 nm for gold and oxygen atoms, respectively, and assumed that a strong repulsion proportional to r–11 exists between particles.
The calculation parallelepiped is a small part of the diffusion mixing layer. The entire mixing layer cannot be covered because of limited computational resources. In the calculation shown in Fig. 4, the 50 : 50 mixture of gold atoms and water is expanded along the x axis. The rate of expansion was chosen in terms of the gradient of the hydrodynamic velocity \(\partial u{\text{/}}\partial x\) in the hot water layer (see Fig. 1). The gradient decreases gradually with time. We are interested in times about 10 ns, when nanoparticles are formed. The rate of expansion in the calculation shown in Fig. 4 was taken to be 2 m/s. The volume of the mixture to a time of 25.7 ns is more than doubled: 2 m/s × 25.7 ns = 51.4 nm; the initial x dimension of the parallelepiped is 40 nm.
Periodic boundary conditions are imposed on the faces of the x × y × z parallelepiped perpendicular to the y and z axes. Movable rigid walls perpendicular to the x axis are described in the molecular dynamics simulation by means of the wall potential reflecting particles. The reflection of particles from moving walls uniaxially expanding the parallelepiped is accompanied by the adiabatic cooling of the mixture because of reflection with a slightly lower velocity. The rate of expansion of the parallelepiped is much lower than thermal velocities.
Gold atoms in the parallelepiped in the initial state are slightly above the line of condensation (see Fig. 2). Their density of 0.516 g/cm3, temperature of 6.1 kK, and pressure of 936 atm approximately correspond to the situation on the phase diagram at a time of 3 ns. In the end of the calculation t = 25.7 ns shown in Fig. 4, the density, temperature, and pressure of the mixture decrease to 0.226 g/cm3, 5.2 kK, and 324 atm, respectively. The temperature of the two-phase system is still much higher than the melting temperature. Therefore, gold nanoparticles remain in the liquid state.
After diffuse Au atoms intersect the line of condensation, the formation of gold clusters begins at a certain distance under it. The evolution of the mixture is shown in Fig. 4. Condensation into clusters occurs first and the coagulation of clusters and nanoparticles then begins. The calculation shows that the temperatures of nanoparticles and the surrounding atomic medium are approximately the same; i.e., intense heat exchange occurs in a sufficiently dense medium. The dependence p(ρ) becomes less steep after the beginning of condensation (the effective heat capacity ratio decreases) because of the release of a large evaporation energy upon condensation.
Figure 4 demonstrates the picture along the z axis perpendicular to the plane of the figure. The thickness of the parallelepiped in this direction is 100 nm. The field in Fig. 4 is composed of the x × y grid of pixels. Each pixel represents information on the potential energy averaged along the z axis. The lighter the green color, the lower the potential energy. Light green spots correspond to NPs. Indeed, bound gold atoms in NPs have a lower potential energy than free atoms. The diameters of NPs in the late stage become about 10 nm.
8 DIFFUSION AND RAYLEIGH–TAYLOR INSTABILITY
The path \(s = \int_{t1}^{t3} d\tau \int_{t1}^\tau g(t)dt\) = \(\left( {\int_{t1}^{t2} + \int_{t2}^{t3} } \right)v(\tau )d\tau \) lost compared to the rectilinear motion is collected in two segments. The first segment is associated with the deceleration of the contact cb in the time interval from t1 = 0.07 ns to t2 = 1.2 ns. At the time t1 = 0.07 ns, the maximum velocity on the trajectory cb is reached and the trajectory xcb(t) is bent (see Fig. 3). The boundary cb stops at the time t2 = 1.2 ns (see Fig. 3). The contribution to the lost path on the first segment is approximately 200 nm.
In the second time interval t2 < t < t3 = 3.2 ns, the contact moves back (see Fig. 3). The acceleration g(t) is determined by the inertia of displaced water and by the pressure in the expanded hot water layer ch–cb (see Fig. 1). The acceleration g on the second segment is lower than that on the first segment, but it acts for a longer time. As a result, the contribution to the lost path on the second segment is also approximately 200 nm.
On both segments, the effective gravitational acceleration (weight) in the noninertial coordinate system connected with the contact cb is directed from the heavy material (gold) to the light one (water). Correspondingly, the boundary cb is Rayleigh–Taylor unstable on these segments [6, 7, 9]. In the absence of stabilizing factors (surface tension, viscosity, diffusion), the thickness of the hydrodynamically mixed layer (owing to instability) will be 5–10% of the path s, i.e., 20–40 nm [7].
This thickness is about the thickness of the diffusion-induced mixing layer (see Section 6). Consequently, large nanoparticles are not formed in the case of the nanosecond pulse because of instability in contrast to the case of the femtosecond pulse considered in [6, 7, 9], where such nanoparticles with a diameter of several tens of nanometers determined by the capillary scale are formed. In our case, the surface tension appears after a time of 3.2 ns, when the gas-like segment of the gold profile disappears. However, the deceleration/acceleration of the boundary cb stops just at this time (see Fig. 3).
9 CONCLUSIONS
(a) Ablation in liquid and the formation of primary nanoparticles in the case of nanosecond pulses have been analyzed. Such pulses are used in modern technologies to produce nanoparticles. It has been shown that the material near the boundary of the target at fluences of about 1 J/cm2 passes to the supercritical fluid state. In this case, the boundary loses the capillary tension and the surface barrier preventing the free diffusion of atoms of the target to the hot liquid layer. This circumstance sharply increases the yield of nanoparticles per laser burst.
(b) Diffusion determining the subsequent appearance of nanoparticles has been studied. Gold atoms are emitted diffusely to water from the end (point cb) of the orange line on the phase diagram in Fig. 2. Intense emission occurs until the point cb is above the line of condensation.
The supercritical stage in the ablation flow when intense diffusion occurs is limited in time for hydrodynamic reasons. The pressure difference in hot water and condensed gold and the immobility of condensed gold lead to the back hydrodynamic motion of the contact cb. As a result, the gas-like section of the gold profile disappears in a finite time interval and the point cb descends under the line of condensation.
(c) The process of condensation in the diffusely mixed layer of atoms of the target and molecules/atoms of the liquid has been studied. The kinetics of condensation of supercooled vapor is studied in some works, e.g., in important work [25] concerning the condensation of gold. However, these works are far from our formulation with the dynamic intersection of the line of saturation and the subsequent (after a certain delay) condensation in the adiabatic expanding volume. A buffer gas with a maintained temperature is usually used, starting from supercooled vapor in a fixed volume. These formulations are far from our problem with ablation in liquid.
Change history
27 November 2022
An Erratum to this paper has been published: https://doi.org/10.1134/S002136402234001X
REFERENCES
Ch.-Y. Shih, Ch. Chen, Ch. Rehbock, A. Tymoczko, U. Wiedwald, M. Kamp, U. Schuermann, L. Kienle, S. Barcikowski, and L. V. Zhigilei, J. Phys. Chem. C 125, 2132 (2021).
A. A. Nastulyavichus, S. I. Kudryashov, N. A. Smirnov, A. A. Rudenko, A. Yu. Kharin, N. I. Busleev, D. A. Zayarny, A. A. Ionin, D. A. Kirilenko, and P. N. Brunkov, Laser Phys. Lett. 16, 096002 (2019).
V. Amendola, S. Scaramuzza, F. Carraro, and E. Cattaruzza, J. Colloid Interface Sci. 489, 18 (2017).
N. Tarasenka, A. Nominé, A. Nevar, M. Nedelko, H. Kabbara, S. Bruyère, J. Ghanbaja, C. Noel, A. Krasilin, G. Zograf, V. Milichko, N. Kulachenkov, S. Makarov, Th. Belmonte, and N. Tarasenko, Phys. Rev. Appl. 13, 014021 (2020).
M. E. Povarnitsyn and T. E. Itina, Appl. Phys. A 117, 175 (2014).
Ch.-Y. Shih, R. Streubel, J. Heberle, A. Letzel, M. V. Shugaev, Ch. Wu, M. Schmidt, B. Gokce, S. Barcikowski, and L. V. Zhigilei, Nanoscale 10, 6900 (2018).
N. A. Inogamov, V. V. Zhakhovskii, and V. A. Khokhlov, J. Exp. Theor. Phys. 127, 79 (2018).
N. A. Inogamov, V. A. Khokhlov, Yu. V. Petrov, and V. V. Zhakhovsky, Opt. Quantum Electron. 52, 63 (2020).
Ch.-Yu. Shih, M. V. Shugaev, Ch. Wu, and L. V. Zhigilei, Phys. Chem. Chem. Phys. 22, 7077 (2020).
N. A. Inogamov, S. A. Romashevskiy, V. V. Zhakhovsky, A. I. Ignatov, V. A. Khokhlov, E. M. Eganova, E. A. Pershina, and S. I. Ashitkov, JETP Lett. 113, 75 (2021).
S. I. Anisimov, V. V. Zhakhovsky, N. A. Inogamov, K. P. Migdal, Yu. V. Petrova, and V. A. Khokhlov, J. Exp. Theor. Phys. 129, 757 (2019).
K. Sasaki and N. Takada, Pure Appl. Chem. 82, 1317 (2010).
D. Amans, W. Cai, and S. Barcikowski, Appl. Surf. Sci. 488, 445 (2019).
X. Song, X. Q. Wu, K. L. Xiao, C. Li, H. Y. Wang, and M. Q. Jiang, Philos. Mag. 100, 2708 (2020).
S. Reich, J. Göttlicher, A. Ziefuss, R. Streubel, A. Letzel, A. Menzel, O. Mathon, S. Pascarelli, T. Baumbach, M. Zuber, B. Gökce, S. Barcikowski, and A. Plech, Nanoscale 12, 14011 (2020).
I. Milov, B. Ziaja, D. Ilnitsky, E. Louis, F. Bijkerk, I. Makhotkin, K. Migdal, N. Inogamov, N. Medvedev, V. Zhakhovsky, V. Medvedev, V. Khokhlov, V. Lipp, and Y. Petrov, Appl. Surf. Sci. 528, 14652 (2020).
S. I. Ashitkov, P. S. Komarov, V. V. Zhakhovsky, Yu. V. Petrov, V. A. Khokhlov, A. A. Yurkevich, D. K. Ilnitsky, N. A. Inogamov, and M. B. Agranat, J. Phys.: Conf. Ser. 774, 012097 (2016).
E. W. Lemmon, M. O. McLinden, and D. G. Friend, NIST Chemistry WebBook, NIST Standard Reference Database Number 69 (Gaithersburg MD, 2019), p. 20899.
Calculation of Thermophysical Properties of Water and its Vapor Using. http://www.ivpromenergo.ru/page/programs/watersteamcalculator.php.
A. V. Bushman and V. E. Fortov, Sov. Phys. Usp. 26, 465 (1983).
A. V. Bushman, G. I. Kanel’, A. L. Ni, and V. E. Fortov, Intense Dynamic Loading of Condensed Matter (Taylor Francis, Washington, D.C., 1993).
K. V. Khishchenko, S. I. Tkachenko, P. R. Levashov, I. V. Lomonosov, and V. S. Vorobev, Int. J. Thermophys. 23, 1359 (2002).
I. V. Lomonosov, Laser Part. Beams 25, 567 (2007).
Development of Interatomic EAM Potentials. https://www.researchgate.net/project/Developmentof-interatomic-EAM-potentials.
D. I. Zhukhovitskii and V. V. Zhakhovsky, J. Chem. Phys. 152, 224705 (2020).
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (agreement no. 075-15-2020-785 on September 23, 2020, with the Joint Institute for High Temperatures, Russian Academy of Sciences).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflicts of interest.
Additional information
Translated by R. Tyapaev
The original online version of this article was revised: Due to a retrospective Open Access order.
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Inogamov, N.A., Zhakhovsky, V.V. & Khokhlov, V.A. Physical Processes Accompanying Laser Ablation in Liquid. Jetp Lett. 115, 16–22 (2022). https://doi.org/10.1134/S002136402201009X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S002136402201009X