Abstract
Uncertainty is an inherent aspect of the open-pit mine production scheduling problem (MPSP); however, little is reported in the literature about solution methods for the stochastic versions of the problem. In this paper, two variants of a variable neighbourhood descent algorithm are proposed for solving the MPSP with metal uncertainty. The proposed methods are tested and compared on actual large-scale instances, and very good solutions, with an average deviation of less than 3% from optimality, are obtained within a few minutes up to a few hours.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1. Introduction
Production scheduling of open-pit mining operations is a challenging and critical issue for mining companies, a key factor in determining returns on investments in the order of hundreds of millions of dollars. In scheduling mine production, the mineral deposit is represented as a three-dimensional array of blocks. Each block has a weight and a metal content estimated using information obtained from drilling. To recover the metal, the block is first mined from the ground and then processed in a mill. These operations are termed mining and processing, respectively.
Blocks are classified as ore or waste according to their metal content. Ore blocks are those that have a selling revenue greater than their processing costs, while waste blocks have a total metal content whose selling revenue is less than the processing costs. Both ore and waste blocks must be mined in order to gain access to all the ore blocks. Any block that must be mined in order to reach another block is called the predecessor of the second block.
Decisions on block scheduling are subject to various types of constraints. The production schedule not only must respect the limits on extraction capacity (mining constraints) and the capacity of the processor (processing constraints) at each period of the life of the mine, but also must take into consideration the order in which blocks can be removed from the orebody to ensure that a block is not mined before any of its predecessors (slope constraints). In addition, any block can be mined only once (reserve constraints). The problem is to determine which blocks to extract and when to extract them (mining sequence) in order to maximize the net present value (NPV) of the mine while respecting the various constraints.
A major complexity in the open-pit mine production scheduling problem (MPSP) is that the number of blocks is large, in general in the order of tens to hundreds of thousands, yielding a large-scale optimization problem. Another factor adding to the complexity of the mine scheduling problem is metal uncertainty, for the metal content of the blocks is not known precisely at the time decisions are made but is inferred from limited drilling information. Up to now, most methods developed to solve the MPSP either ignore the metal uncertainty issue or are not able to solve large-scale instances in which metal uncertainty is accounted for.
Indeed, the MPSP has been frequently studied since the 1960s (Newman et al, 2010). Different methods have been applied to solve the deterministic version of the problem, which assumes that all the problem parameters are well known. These methods can be classified into three categories: exact methods (Dagdelen and Johnson, 1986; Caccetta and Hill, 2003; Ramazan, 2007; Boland et al, 2009; Bley et al, 2010), heuristic and metaheuristic methods (Gershon, 1987; Denby and Schofield, 1994; Ferland et al, 2007; Chatterjee et al, 2010), and hybrid methods (Tolwinski and Underwood, 1996; Sevim and Lei, 1998; Moreno et al, 2010). However, the uncertain nature of the problem is ignored in the deterministic version of the MPSP, resulting in misleading assessments (Ravenscroft, 1992; Dowd, 1994; Dimitrakopoulos et al, 2002; Godoy and Dimitrakopoulos, 2004). Studies that compare stochastic to deterministic approaches (Godoy and Dimitrakopoulos, 2004; Menabde et al, 2007; Albor and Dimitrakopoulos, 2009, 2010; Asad and Dimitrakopoulos, 2013) indicate that stochastic approaches show major improvements in NPV, on the order of 20% to 30%, substantially reduce risk in meeting production forecasts, and find pit limits larger than the ones found by deterministic approaches, contributing to the sustainable utilization of mineral resources.
In the stochastic versions of the problem, a scenario approach is usually used to handle the metal uncertainty. The scenarios are specified from estimates in the continuous space without any underlying scenario tree structure. Consequently, the multistage approach commonly used in stochastic programming cannot be used. Three different approaches are used in the literature. The first involves formulations maximizing the expected NPV over the scenarios describing the metal uncertainty while satisfying the production targets in an average sense (Menabde et al, 2007). The second involves formulations maximizing the expected NPV and minimizing deviations from production targets for each individual scenario (Ramazan and Dimitrakopoulos, 2007; Albor and Dimitrakopoulos, 2010; Ramazan and Dimitrakopoulos, 2013). The third approach, illustrated in Boland et al (2008), takes into account the metal uncertainty via a multistage stochastic programming approach where the missing interdependency between scenarios and the decisions (ie, the missing tree structure) is simulated using conditional non-anticipativity constraints.
While different stochastic models have been developed, solution methods have received relatively less attention. Furthermore, most of the solution methods developed have been able to deal only with instances of relatively small size (typically, up to 20 000 blocks). The stochastic models proposed in the studies by Menabde et al (2007), Ramazan and Dimitrakopoulos (2007, 2013), and Boland et al (2008) are solved using the mixed integer programming solver CPLEX. The method used in Albor and Dimitrakopoulos (2010) consists of generating a set of nested pits, grouping these pits into pushbacks, and then generating a schedule based on the pushback designs obtained, while the method used in Lamghari and Dimitrakopoulos (2012) is based on Tabu search.
In this paper, we propose an efficient solution method to deal with large instances of the MPSP with metal uncertainty, where the uncertainty is addressed using a two-stage stochastic programming approach. Specifically, we introduce a metaheuristic method based on a variable neighbourhood descent (VND) procedure (Hansen and Mladenovic, 2001). To generate the initial solution to be improved by this procedure, we consider two different alternatives. Both are based on a decomposition approach separating the problem into a series of sub-problems, each associated with one period. They differ in the method used to solve the sub-problems. In the first alternative, the sub-problems are solved exactly, while in the second one, the sub-problems are solved approximately with a greedy heuristic. We evaluate and compare the performance of the two variants of the proposed solution method on large-scale instances with up to 97 307 blocks. The results indicate that both variants generate very good solutions in reasonable computational times. The first variant, where the sub-problems are solved exactly, slightly outperforms the second one in terms of solution quality, while the second variant, where the sub-problems are solved with a heuristic, requires in general significantly less computational time.
The remainder of the paper is organized as follows: In Section 2, the approach used to deal with metal uncertainty is outlined, and a mathematical formulation of the problem is introduced. The following section briefly describes the methods used to generate the initial solution. Section 4 summarizes the variable neighbourhood procedure used to improve the initial solution. Computational results on real-life data are reported and discussed in Section 5. Finally, some conclusions are drawn in Section 6.
2. Mathematical formulation
Referring to the description given in the previous section, the problem can be formulated as a two-stage stochastic programming model (Birge and Louveaux, 1997). In the first stage, one determines a set of blocks to be mined at each period in order to satisfy the reserve constraints, the slope constraints, and the mining constraints. The metal content of each block, determining whether the block is ore or waste, is uncertain at this stage. In the second stage, when the blocks are mined, the metal content becomes known. In some periods, the ore blocks available, requiring processing, may have a total weight exceeding the mill capacity (ie, the processing constraints may be violated). To deal with such a situation, some recourse actions are available, but they induce a cost. The problem is then to identify a schedule that maximizes the expected NPV of the mining operation minus the expected recourse costs incurred due to the violation of the processing constraints.
The following notation is used to formulate the mathematical model:
-
T: the number of periods over which blocks are being scheduled (horizon).
-
t: period index, t=1, …, T.
-
W t: maximum amount of rock (ore and waste) that can be mined during period t (mining capacity in tons).
-
Θt: maximum amount of ore that can be processed in the mill during period t (processing capacity in tons).
-
N: the number of blocks considered for scheduling.
-
i: block index, i=1, …, N.
-
 : the set of predecessors of block i; that is, blocks that have to be mined to have access to block i.
: the set of predecessors of block i; that is, blocks that have to be mined to have access to block i. -
 : the set of direct predecessors of block i; that is,
: the set of direct predecessors of block i; that is, 
-
Γ i : the set of successors of block i; that is, γ∈Γ i if i∈P γ . Figure 1 gives a two-dimensional illustration of the sets
 and Γ
i
.
and Γ
i
. -
w i : the weight of block i (in tons).
-
v i : the economic value of block i. It is a random variable depending on the metal content of the block.
-
 : the discounted economic value of block i if mined during period t (d
1 being the discount rate per period). Note that it is assumed that ore blocks are processed during the same period when they are mined and that the profit is also generated during that period.
: the discounted economic value of block i if mined during period t (d
1 being the discount rate per period). Note that it is assumed that ore blocks are processed during the same period when they are mined and that the profit is also generated during that period. -
θ i : a random variable indicating if block i is an ore or a waste block

It is a random variable because the metal content of a block determines whether the block is ore or waste.
-
 : unit surplus cost incurred if the total weight of ore blocks mined during period t exceeds the processing capacity, Θt (c being the undiscounted surplus cost, and d
2 represents the risk discount rate).
: unit surplus cost incurred if the total weight of ore blocks mined during period t exceeds the processing capacity, Θt (c being the undiscounted surplus cost, and d
2 represents the risk discount rate).
The variables used to formulate the problem are as follows:
-
A binary variable is associated with each block i for each period t:

This means that if block i is mined in period τ, then x i t=0 for all t−1, …, τ−1 and x i t=1 for all t=1, …, T. If i is not mined during the horizon, then x i t=0 for all t=1, …, T.
-
A random variable d t is associated with each period t. It measures the surplus in ore mined during period t.
The mathematical model can be summarized as follows:

(M) Subject to








The objective function (1) includes two terms to maximize the expected NPV of the mining operation and to minimize the expected recourse costs incurred whenever the processing constraints are violated due to metal uncertainty. Constraints (2) guarantee that each block i is mined at most once during the horizon (reserve constraints). The mining precedence (slope constraints) is enforced by constraints (3). Constraints (4) and (5) impose an upper bound W t on the amount of rock (ore and waste) mined during each period t (mining constraints). Constraints (6) and (7) are related to the requirements on the processing levels (processing constraints). The target is to have the total amount of ore mined during any period t be smaller than Θt; otherwise, the surplus penalty cost is equal to c t d t. The model is a two-stage stochastic programming model. The variables x i t specifying the mining sequence are the first-stage decision variables, and the random variables d t measuring the surplus in ore production are the second-stage decision variables. d t depend on both the realization of the metal content and the first-stage decisions.
To transform this stochastic model into an equivalent deterministic one, assume that S possible scenarios are available where each scenario s specifies the metal content of each block. Furthermore, assume that the probability of occurrence of scenario s is π
s
, with  . Let v
is
t, θ
is
, and d
s
t denote respectively a realization of the random variables v
i
t, θ
i
, and d
t. Then, the original model (1)–(9) can be reformulated as follows:
. Let v
is
t, θ
is
, and d
s
t denote respectively a realization of the random variables v
i
t, θ
i
, and d
t. Then, the original model (1)–(9) can be reformulated as follows:

(DE) Subject to
Constraints (2), (3), (4) and (5), (8), and



The model (DE) utilizes a limited number of scenarios, each specifying the metal content of each block, which then are used to calculate the corresponding economic value. A natural question to address is how to choose the number of scenarios to consider. This is a well-studied topic in stochastic optimization (Dupacova et al, 2003) and other fields (Scheidt and Caers, 2009). The case studies presented in this paper use 20 scenarios because past work, such as the work in Albor and Dimitrakopoulos (2009), indicates that after about 15 simulated representations of an orebody, stochastic schedules converge to a stable final physical schedule as well as stable forecasts of production performance. This behaviour is not surprising; while simulated scenarios represent a mineral deposit at the support-scale of mining blocks, each with a volume of a few cubic meters, a mine’s production schedule represents a grouping of a few thousand of these mining blocks in just one time (mining) period under various constraints. Thus, as the support-scale of a mine’s schedule is orders of magnitude larger than that of the simulated representations of the mineral deposit being scheduled, the stochastic schedule becomes insensitive to additional scenarios after a relatively small number of scenarios. In this paper, the set of sufficient scenarios is provided, and the objective is to design an efficient method to solve the proposed mathematical model.
If the mining and the processing constraints are eliminated, and if the scheduling horizon reduces to a single period, then the model (DE) reduces to the classical maximum closure problem. This problem is reducible to the minimum-cut problem (Picard, 1976), and thus it can be solved efficiently using any of the known polynomial maximum-flow algorithms. However, as Bienstock and Zuckerberg (2010) note on page 3, ‘it can be shown by reduction from max clique that adding a single cardinality constraint to a maximum closure problem is enough to make it NP-hard’. Because the MPSP is more complex than a constrained maximum closure problem, and as real-world MPSP instances are very large, having typically tens to hundreds of thousands blocks, it is most likely not appropriate to solve these large-scale realistic instances using an exact method. Instead, we propose a metaheuristic solution method where an initial feasible solution is first obtained and then improved with a VND procedure. The methods used to generate the initial solution as well as the VND procedure are described in the following sections.
3. Generating the initial solution
We propose to generate the initial solution using two different heuristics based on a decomposition approach where the global problem is divided into smaller sub-problems, each associated with a period t (t=1, …, T). The sub-problems are solved sequentially in increasing order of t, and their solutions are combined to generate the initial solution. The heuristics differ in the method used to deal with the sub-problems. In the first one, the sub-problems are solved exactly, while in the second one, the sub-problems are solved approximately with a greedy heuristic. Note that since the sub-problems are smaller than the global problem, an exact method can be used to solve them.
3.1. Sub-problem formulation
The sub-problem associated with period t consists of determining a set of blocks  to be mined in period t. Let us denote by
to be mined in period t. Let us denote by  the set of blocks not mined yet (if t=1, then
the set of blocks not mined yet (if t=1, then  otherwise,
otherwise,  ). In order to satisfy the reserve constraints, the blocks to be included in
). In order to satisfy the reserve constraints, the blocks to be included in  should be selected from
should be selected from  The sub-problem associated with period t can then be summarized as follows:
The sub-problem associated with period t can then be summarized as follows:

(SP t) Subject to





where

Recall that if block i is mined in period t, then x i τ=0 for all τ=1, …, t−1 and x i τ=1 for all τ=1, …, T.
Logical implications of the constraints are used to generate valid inequalities to strengthen the formulation above and make the sub-problems easier to solve. To be more specific, consider any block  On the one hand, the slope constraints require that to include i in
On the one hand, the slope constraints require that to include i in  we must also include all blocks
we must also include all blocks  (the set of blocks that are predecessors of i and not mined yet). On the other hand, i should not be included in
(the set of blocks that are predecessors of i and not mined yet). On the other hand, i should not be included in  if
if  because this would lead to violation of the mining constraints. Hence, we add the following constraints to the model (SP
t):
because this would lead to violation of the mining constraints. Hence, we add the following constraints to the model (SP
t):

where e i is a parameter equal to 1 if the extraction of block i will not lead to violation of the mining constraints and 0 otherwise; that is,

3.2. Sub-problem solution methods
Two different methods are introduced to solve the sub-problems. In the first method, the formulation (14)–(20) is solved using the branch-and-cut algorithm (BC) implemented in the mixed integer programming solver CPLEX.
The second method is a sequential greedy heuristic procedure (GH) where at each iteration we try to include in the set  an inverted cone formed by a ‘base’ block in
an inverted cone formed by a ‘base’ block in  and all its predecessors not mined yet. Let us analyse a typical iteration.
and all its predecessors not mined yet. Let us analyse a typical iteration.
Let  and
and  be the residual mining capacity and the residual processing capacity under scenario s, respectively. For each block
be the residual mining capacity and the residual processing capacity under scenario s, respectively. For each block  we denote:
we denote:
-
 the set formed by block i and all its unmined predecessors (ie, the inverted cone whose base is i).
the set formed by block i and all its unmined predecessors (ie, the inverted cone whose base is i). -
 : the total weight of blocks in Ω
i
.
: the total weight of blocks in Ω
i
. -
 : the total weight of ore blocks in Ω
i
under scenario s.
: the total weight of ore blocks in Ω
i
under scenario s. -
 : the total expected discounted economic value of blocks in Ω
i
.
: the total expected discounted economic value of blocks in Ω
i
. -
 : the total contribution of blocks in Ω
i
to the objective function (14).
: the total contribution of blocks in Ω
i
to the objective function (14).
Consider the set  of blocks
of blocks  whose weight plus the weight of their predecessors not mined yet does not exceed the residual mining capacity. Clearly, only cones having blocks in
whose weight plus the weight of their predecessors not mined yet does not exceed the residual mining capacity. Clearly, only cones having blocks in  as their base can be added to
as their base can be added to  while satisfying the slope constraints and the mining constraints. Select the block i*∈
while satisfying the slope constraints and the mining constraints. Select the block i*∈ maximizing the value of ξ
i
. Ties are broken up randomly. Remove all blocks k∈Ω
i* from
maximizing the value of ξ
i
. Ties are broken up randomly. Remove all blocks k∈Ω
i* from  add them to
add them to  and update
and update 
 for each s=1, …, S, and the set
for each s=1, …, S, and the set  This process is repeated until the mining constraints are approximately satisfied; that is, until
This process is repeated until the mining constraints are approximately satisfied; that is, until

where δ is a random number in the interval [δ 1, δ 2], and δ 1 and δ 2 are parameters of the procedure in [0,1].
Note that choosing blocks along with their predecessors (an inverted cone at each iteration) allows a look ahead feature generating better solutions than the myopic approach of choosing blocks one by one.
4. Improving the initial solution
As mentioned before, the initial solution  is improved by applying an adaptation of the VND method proposed by Hansen and Mladenovic (2001). The basic idea of VND is to combine different descent heuristics based on different neighbourhood structures to escape from local optima. In the following, we first describe the neighbourhood structures used in our adaptation of the VND method. Next, we outline the procedure used to improve the solution x.
is improved by applying an adaptation of the VND method proposed by Hansen and Mladenovic (2001). The basic idea of VND is to combine different descent heuristics based on different neighbourhood structures to escape from local optima. In the following, we first describe the neighbourhood structures used in our adaptation of the VND method. Next, we outline the procedure used to improve the solution x.
4.1. Neighbourhood structures
Three neighbourhood structures are used in our adaptation of the VND method. The first structure tries to swap two blocks scheduled in consecutive periods. For example, a waste block scheduled to be mined in period 1 and having no successors scheduled in period 1 could be left behind to be mined in period 2. In its place, an ore block scheduled to be mined in period 2 could be mined in period 1 provided that its predecessors are scheduled in period 1. The mining capacity should not be exceeded in either period as a result of the swap. The second and third structures try to make room for new blocks in a given period by scheduling some blocks to be mined in that period backward or forward while satisfying the slope and the mining constraints. A more formal description of the three neighbourhood structures as well as an outline of the strategy used to explore them is given below.
-
N 1 (Exchange or Swap): Let i and j be two blocks mined in periods t and (t+1), respectively. An exchange consists of replacing
 and
and  by (
by ( and (
and ( respectively. The exchange of two blocks is feasible if the resulting solution is feasible; that is, only if it satisfies the slope and the mining constraints. Figure 2 gives a two-dimensional illustration of an exchange move involving two blocks, i and j, with T=2.
respectively. The exchange of two blocks is feasible if the resulting solution is feasible; that is, only if it satisfies the slope and the mining constraints. Figure 2 gives a two-dimensional illustration of an exchange move involving two blocks, i and j, with T=2. -
N 2 (Shift-after): Let i be a block mined in period t, and let
 denote the set including i and its successors mined in the same period. A shift-after consists of replacing
denote the set including i and its successors mined in the same period. A shift-after consists of replacing  and
and  by
by  and
and  respectively. Clearly, the slope constraints are satisfied in the resulting solution since the blocks are moved along with their successors. However, the mining constraints must be satisfied in period (t+1) in order to allow this shift-after. Figure 3 illustrates the Shift-after move where block i and its successors mined in period 1 are moved to period 2.
respectively. Clearly, the slope constraints are satisfied in the resulting solution since the blocks are moved along with their successors. However, the mining constraints must be satisfied in period (t+1) in order to allow this shift-after. Figure 3 illustrates the Shift-after move where block i and its successors mined in period 1 are moved to period 2. -
N 3 (Shift-before): Let i be a block mined in period t, and let
 denote the set including i and its predecessors mined in the same period. A shift-before consists of replacing
denote the set including i and its predecessors mined in the same period. A shift-before consists of replacing 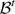 and
and 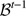 by
by  and
and 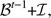 respectively. As for the Shift-after neighbourhood, the slope constraints are necessarily satisfied, but the mining constraints in period (t−1) must be satisfied in order to allow this shift-before. Figure 4 illustrates the Shift-before move where block i and its predecessors mined in period 2 are moved to period 1.
respectively. As for the Shift-after neighbourhood, the slope constraints are necessarily satisfied, but the mining constraints in period (t−1) must be satisfied in order to allow this shift-before. Figure 4 illustrates the Shift-before move where block i and its predecessors mined in period 2 are moved to period 1.
Note that the operators Shift-after and Shift-before motivate the introduction of constraints (21) when applying the greedy heuristic procedure (GH) to generate the initial solution. Indeed, if the value of δ were fixed to 1 at each iteration, then it would be more difficult to find a feasible neighbour solution when applying these operators.
The strategy to explore the first neighbourhood N 1 is as follows: Periods t=1, …, (T−1) are considered sequentially in increasing order. Given a period t, all feasible exchanges involving pairs of blocks mined in t and (t+1) are systematically considered. The best exchange is selected. We apply the selected exchange if it leads to a better solution or to a solution of the same value as the current solution (in order to escape from the current local optimum). The process is iterated with the new solution. When no feasible exchange exists to further improve the solution or to get a solution of equal value, the next period (t+1) is considered; that is, exchanges involving pairs of blocks mined in periods (t+1) and (t+2) are evaluated.
A similar exploration strategy is used when considering the Shift-after neighbourhood N 2 except that periods t=1, …, (T−1) are considered in decreasing order. For the Shift-before neighbourhood N 3, periods t=2, …, T are considered in increasing order.
4.2. Variable neighbourhood descent procedure
The rules of a basic VND are applied. Start by exploring the Exchange neighbourhood (N 1). When the search of N 1 is completed (ie, for all t=1, …, (T−1), no feasible exchange between pairs of blocks mined in periods t and (t+1) exists to further improve the solution or to get a solution of equal value), restart a new search using the Shift-after neighbourhood (N 2). Once the search of N 2 is completed, if the solution has been improved, return to N 1; otherwise, use the Shift-before neighbourhood (N 3). This process terminates when no move in any of the three neighbourhoods improves the value of the objective function. Note that the order in which the neighbourhoods are explored follows from preliminary tests.
5. Numerical results
Numerical tests were completed on three different problems based on actual instances from different mines. Problem P 1 is generated from an actual copper deposit where all blocks i are 20 × 20 × 10 meters in size and weigh w i =10 800 tons each. Problem P 2 is from an actual gold deposit where all blocks i are 15 × 15 × 10 meters in size and weigh w i =5625 tons each. Finally, problem P 3 is also from a gold deposit but where blocks i are 10 × 10 × 5 meters in size and weigh w i =1250 tons each. The economic parameters used to compute the block economic values and the recourse costs are also based on real-life data, and they are summarized in Table 1.
Each problem is characterized by a number of blocks N and a number of periods T, specified in Table 2. Note that N corresponds to the number of blocks within the pit limits obtained by solving the maximum closure problem (to maximize the expected profit from the mining operation but accounting only for the slope constraints). Each period is one year long, as this is the case in practice and in the literature related to the MPSP. The number of periods is set to  The number of scenarios S is equal to 20. The scenarios are equiprobable (ie, π
s
=1/S ∀s=1, …, S), and they were generated from a limited amount of drilling information using the geostatistical techniques of conditional simulation (Goovaerts, 1997; Scheidt and Caers, 2009; Boucher and Dimitrakopoulos, 2012). These techniques can be seen as a complex Monte Carlo simulation framework. They reproduce all available data and information as well as spatial statistics of the data. Note that some authors use only 5–10 scenarios to model metal uncertainty (Menabde et al, 2007; Boland et al, 2008).
The number of scenarios S is equal to 20. The scenarios are equiprobable (ie, π
s
=1/S ∀s=1, …, S), and they were generated from a limited amount of drilling information using the geostatistical techniques of conditional simulation (Goovaerts, 1997; Scheidt and Caers, 2009; Boucher and Dimitrakopoulos, 2012). These techniques can be seen as a complex Monte Carlo simulation framework. They reproduce all available data and information as well as spatial statistics of the data. Note that some authors use only 5–10 scenarios to model metal uncertainty (Menabde et al, 2007; Boland et al, 2008).
Additional parameters to specify the problems are as follows: For each problem, the production capacities are identical in all periods and emulate those in real-world problems. For each period t, the mining capacity W
t is set to  (ie, total amount of rock/number of periods plus a margin of 20%). The processing capacity Θt is set to
(ie, total amount of rock/number of periods plus a margin of 20%). The processing capacity Θt is set to  (ie, total expected amount of ore/number of periods plus a margin of 5%).
(ie, total expected amount of ore/number of periods plus a margin of 5%).
All the numerical experiments were performed on an Intel® Xeon® CPU X7350 computer (2.93 GHz) with 64 GB of RAM running under Linux. Version 12.2 of CPLEX was used to solve the mathematical model (SP t) introduced in Section 3.1. To fix the values of the parameters of the greedy heuristic in Section 3.2, some preliminary numerical experimentations were completed with problem P 2 and a set of other four smaller problems. We considered 15 values for the interval [δ 1, δ 2] ([0.3, 0.35], [0.35, 0.4],…, [0.95, 1] and [1, 1]). The best results are obtained with the interval [0.9, 0.95]. Hence, we complete the rest of the numerical tests using these values for δ 1 and δ 2.
The linear relaxation of the model (DE) in Section 2 was solved using CPLEX 12.2 to obtain an upper bound Z LR on the optimal value, which is used to assess the quality of the solutions produced with the two variants of the proposed solution method, denoted BC-VND and GH-VND.
Since GH and VND include random choices, each problem was solved 10 times. The results are summarized in Table 3, where
-
%
 : the value of the relative gap between the value Z
best of the best solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the value Z
best of the best solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation. -
%
 : the value of the relative gap between the value Z
worst of the worst solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the value Z
worst of the worst solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation. -
%
 : the value of the relative gap between the average value Z
average of the 10 solutions obtained by the variants and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the average value Z
average of the 10 solutions obtained by the variants and the optimal value Z
LR of the linear relaxation. -
Ave CPU: the average solution time in minutes.
The first three criteria do not apply to CPLEX as indicated by ‘–’. The last criterion indicates also the CPU time required by CPLEX to solve the linear relaxation of the problems.
The following observations can be derived from Table 3:
-
The two variants are very efficient in the sense that for each problem the value of %Min Gap is less than 5% away from the upper bound provided by CPLEX.
-
The length of the interval [%Min Gap, %Max Gap] indicates the robustness of the variants. In all cases (considering the three problems and the 10 runs of each variant) the gap between the solution generated and the upper bound provided by CPLEX is smaller than 6%, and in 96.66% of cases, it is smaller than 5%.
-
The computational time required by the variants is very reasonable. For instance, CPLEX may require almost 16 days to solve the linear relaxation of problem P 2, while very good feasible solutions for this problem are obtained in 16 min and 3.5 h by GH-VND and BC-VND, respectively.
-
When comparing the two variants, we observe that BC-VND provides the best gaps. GH-VND is, however, generally the best in terms of computational time.
Next, the ability of the VND procedure to improve the initial solutions provided by BC and GH is evaluated. Table 4 summarizes the value Ave Iter VND of the average number of VND major iterations performed (a major iteration is when the three neighbourhoods have been explored), as well as the value %Impr defined as follows:

where Z average is as defined above (the average value of the solutions generated in the 10 runs) and Z init is the average value of the initial solutions generated using either BC or GH. The last column Ave CPU shows the average solution time in minutes (same values as in Table 3).
The results indicate that the BC procedure using the branch-and-cut algorithm is very efficient at generating very good solutions that VND fails to improve or improves very slightly. However, BC requires significantly longer computational times than the greedy heuristic, GH. Although the initial solutions generated by GH are of low quality when compared with those generated by BC, VND improves them to the point that they are close to those generated by BC, and these improved solutions are obtained in significantly less computational time, indicating the benefits of VND when the initial solution is of low quality.
In summary, both variants outperform CPLEX. They offer an excellent compromise between solution quality and computational effort. On the one hand, with respect to solution quality, the results indicate that, for the tested problems, the variant BC-VND is slightly better. On the other hand, solution times are in general significantly reduced when using GH-VND.
6. Conclusions
Production scheduling is a challenging and critical issue for mining companies exploiting open-pit mines. Determining the block mining sequence is a crucial step in maximizing the NPV of the mining operation. Decisions on block scheduling are subject to various types of constraints, typically slope constraints, bounds on mining, and bounds on processing. Furthermore, the open-pit mine production scheduling is even more difficult because the number of blocks is large and because the metal content of the blocks is not known precisely at the time decisions are made. This yields a large-scale stochastic optimization problem.
We have addressed metal uncertainty using a two-stage stochastic programming approach and we have proposed a metaheuristic approach to solve the problem. An initial feasible solution is first generated using either an exact method or a greedy heuristic to solve sequentially a sub-problem for each period. A VND procedure is then applied to improve the solution. Upper bounds provided by CPLEX were used to evaluate the efficiency of the two variants of the proposed solution method, specified according to the process used for generating the initial solution. Tests were conducted on realistic actual large-scale instances, and their results indicate that the two variants generate solutions of very good quality, with an average deviation of less than 3% from optimality, within a few minutes up to a few hours. When comparing the two variants, the results indicate that the variant based on an exact method slightly outperforms the one based on a greedy heuristic as far as the solution quality is concerned, but its average computational time is two times larger. The results also indicate that the VND procedure can substantially improve initial solutions of low quality.
Future research will be devoted to extending the proposed approach to account for additional operational constraints and to developing other efficient approaches for these more complex versions of the problem. One approach we are investigating consists of solving the linear relaxation of the problem using an efficient algorithm and then using an LP-rounding procedure to generate an integer solution.
References
Albor F and Dimitrakopoulos R (2009). Stochastic mine design optimization based on simulated annealing: Pit limits, production schedules, multiple orebody scenarios and sensitivity analysis. IMM Transactions, Mining Technology 118 (2): 80–91.
Albor F and Dimitrakopoulos R (2010). Algorithmic approach to pushback design based on stochastic programming: Method, application and comparisons. IMM Transactions, Mining Technology 119 (2): 88–101.
Asad M and Dimitrakopoulos R (2013). Implementing a parametric maximum flow algorithm for optimal open pit mine design under uncertain supply and demand. Journal of the Operational Research Society 64 (2): 185–197.
Bienstock D and Zuckerberg M (2010). Solving LP relaxations of large-scale precedence constrained problems. Integer Programming and Combinatorial Optimization. Lecture Notes in Computer Science 6080: 1–14.
Birge J and Louveaux F (1997). Introduction to Stochastic Programming. New York: Springer.
Bley A, Boland N, Fricke C and Froyland G (2010). A strengthened formulation and cutting planes for the open pit mine production scheduling problem. Computers & Operations Research 37 (9): 1641–1647.
Boland N, Dumitrescu I and Froyland G (2008). A multistage stochastic programming approach to open pit mine production scheduling with uncertain geology. Optimization Online, http://www.optimization-online.org/DB_FILE/2008/10/2123.pdf, accessed 31 January 2012.
Boland N, Dumitrescu I, Froyland G and Gleixner AM (2009). LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity. Computers & Operations Research 36 (4): 1064–1089.
Boucher A and Dimitrakopoulos R (2012). Multivariate block-support simulation of the Yandi iron ore deposit, Western Australia. Mathematical Geosciences 44 (4): 449–468.
Caccetta L and Hill SP (2003). An application of branch and cut to open pit mine scheduling. Journal of Global Optimization 27 (2–3): 349–365.
Chatterjee S, Lamghari A and Dimitrakopoulos R (2010). A two-phase heuristic method for constrained pushback design. In: R Castro, X Emery and R Kuyvenhoven (eds). Proceedings of MININ 2010, Conference on Mining Innovation. Santiago, Chile: Gecamin, pp 195–204.
Dagdelen K and Johnson TB (1986). Optimum open pit mine production scheduling by lagrangian parameterization. In: RV Ramani (ed). Proceedings of 19th International APCOM Symposium. Littleton, CO, pp 127–142.
Denby B and Schofield D (1994). Open-pit design and scheduling by use of genetic algorithms. Transactions of the Institution of Mining and Metallurgy 103: A21–A26.
Dimitrakopoulos R, Farrelly C and Godoy M (2002). Moving forward from traditional optimization: Grade uncertainty and risk effects in open pit mine design. Mining Technology 111 (1): 82–88.
Dowd P (1994). Risk assessment in reserve estimation and open-pit planning. Transactions of the Institution of Mining and Metallurgy 103: A148–A154.
Dupacova J, Growe-Kuska N and Romisch W (2003). Scenario reduction in stochastic programming: An approach using probability metrics. Mathematical Programming 95 (3): 493–511.
Ferland JA, Amaya J and Djuimo MS (2007). Application of a particle swarm algorithm to the capacitated open pit mining problem. In: S Mukhopadhyay and G Sen Gupta (eds). Autonomous Robots and Agents. Berlin Heidelberg: Springer-Verlag, pp 127–133.
Gershon M (1987). Heuristic approaches for mine planning and production scheduling. International Journal of Mining and Geological Engineering 5 (1): 1–13.
Godoy M and Dimitrakopoulos R (2004). Managing risk and waste mining in long-term production scheduling of open-pit mines. Society for Mining, Metallurgy & Exploration (SME) Transactions 316: 43–50.
Goovaerts P (1997). Geostatistics for Natural Resources Evaluation. New York: Oxford University Press.
Hansen P and Mladenovic N (2001). Variable neighborhood search: Principles and applications. European Journal of Operational Research 130 (3): 449–467.
Lamghari A and Dimitrakopoulos R (2012). A diversified tabu search approach for the open-pit mine production scheduling problem with metal uncertainty. European Journal of Operational Research 222 (3): 642–652.
Menabde M, Froyland G, Stone P and Yeates G (2007). Mining schedule optimisation for conditionally simulated orebodies. Orebody Modelling and Strategic Mine Planning, The Australasian Institute of Mining and Metallurgy, Spectrum Series 14: 379–384.
Moreno E, Espinoza D and Goycoolea M (2010). Large-scale multi-period precedence constrained knapsack problem: A mining application. Electronic Notes in Discrete Mathematics 36: 407–414.
Newman AM, Rubio E, Caro R, Weintraub A and Eurek K (2010). A review of operations research in mine planning. Interfaces 40 (3): 222–245.
Picard C (1976). Maximal closure of a graph and applications to combinatorial problems. Management Science 22 (11): 1268–1272.
Ramazan S (2007). The new fundamental tree algorithm for production scheduling of open pit mines. European Journal of Operational Research 177 (2): 1153–1166.
Ramazan S and Dimitrakopoulos R (2007). Stochastic optimization of long term production scheduling for open pit mines with a new integer programming formulation. Orebody Modelling and Strategic Mine Planning, The Australasian Institute of Mining and Metallurgy, Spectrum Series 14: 359–365.
Ramazan S and Dimitrakopoulos R (2013). Production scheduling with uncertain supply: A new solution to the open pit mining problem. Optimization and Engineering 14 (2): 361–380.
Ravenscroft P (1992). Risk analysis for mine scheduling by conditional simulation. Transactions of the Institution of Mining and Metallurgy, Section A: Mining Technology 101: A104–A108.
Scheidt C and Caers J (2009). Representing spatial uncertainty using distances and kernels. Mathematical Geosciences 41 (4): 397–419.
Sevim H and Lei D (1998). The problem of production planning in open pit mines. INFOR 36 (1–2): 1–12.
Tolwinski B and Underwood R (1996). A scheduling algorithm for open pit mines. IMA Journal of Mathematics Applied in Business & Industry 7 (3): 247–270.
Acknowledgements
The work in this paper was funded by Natural Science and Engineering Research Council of Canada CRDPJ 411270-10, Discovery Grant DGP 8212-2011, and the industry members of the COSMO Stochastic Mine Planning Laboratory: AngloGold Ashanti, Barrick, BHP Billiton, De Beers, Newmont, and Vale.
Author information
Authors and Affiliations
Additional information
after one revision
The online version of this article is available Open Access
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Lamghari, A., Dimitrakopoulos, R. & Ferland, J. A variable neighbourhood descent algorithm for the open-pit mine production scheduling problem with metal uncertainty. J Oper Res Soc 65, 1305–1314 (2014). https://doi.org/10.1057/jors.2013.81
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jors.2013.81





 : the set of predecessors of block i; that is, blocks that have to be mined to have access to block i.
: the set of predecessors of block i; that is, blocks that have to be mined to have access to block i. : the set of direct predecessors of block i; that is,
: the set of direct predecessors of block i; that is, 
 and Γ
i
.
and Γ
i
.
 , and
, and  .
. : the discounted economic value of block i if mined during period t (d
1 being the discount rate per period). Note that it is assumed that ore blocks are processed during the same period when they are mined and that the profit is also generated during that period.
: the discounted economic value of block i if mined during period t (d
1 being the discount rate per period). Note that it is assumed that ore blocks are processed during the same period when they are mined and that the profit is also generated during that period.
 : unit surplus cost incurred if the total weight of ore blocks mined during period t exceeds the processing capacity, Θt (c being the undiscounted surplus cost, and d
2 represents the risk discount rate).
: unit surplus cost incurred if the total weight of ore blocks mined during period t exceeds the processing capacity, Θt (c being the undiscounted surplus cost, and d
2 represents the risk discount rate).
 the set formed by block i and all its unmined predecessors (ie, the inverted cone whose base is i).
the set formed by block i and all its unmined predecessors (ie, the inverted cone whose base is i). : the total weight of blocks in Ω
i
.
: the total weight of blocks in Ω
i
. : the total weight of ore blocks in Ω
i
under scenario s.
: the total weight of ore blocks in Ω
i
under scenario s. : the total expected discounted economic value of blocks in Ω
i
.
: the total expected discounted economic value of blocks in Ω
i
. : the total contribution of blocks in Ω
i
to the objective function (14).
: the total contribution of blocks in Ω
i
to the objective function (14). and
and  by (
by ( and (
and ( respectively. The exchange of two blocks is feasible if the resulting solution is feasible; that is, only if it satisfies the slope and the mining constraints.
respectively. The exchange of two blocks is feasible if the resulting solution is feasible; that is, only if it satisfies the slope and the mining constraints. 
 while the white area delimited by the thick lines represents the set of blocks to be mined in period 2
while the white area delimited by the thick lines represents the set of blocks to be mined in period 2 
 denote the set including i and its successors mined in the same period. A shift-after consists of replacing
denote the set including i and its successors mined in the same period. A shift-after consists of replacing  and
and  by
by  and
and  respectively. Clearly, the slope constraints are satisfied in the resulting solution since the blocks are moved along with their successors. However, the mining constraints must be satisfied in period (t+1) in order to allow this shift-after.
respectively. Clearly, the slope constraints are satisfied in the resulting solution since the blocks are moved along with their successors. However, the mining constraints must be satisfied in period (t+1) in order to allow this shift-after. 
 while the white area delimited by the thick lines represents the set of blocks to be mined in period 2
while the white area delimited by the thick lines represents the set of blocks to be mined in period 2 
 denote the set including i and its predecessors mined in the same period. A shift-before consists of replacing
denote the set including i and its predecessors mined in the same period. A shift-before consists of replacing 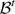 and
and 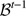 by
by  and
and 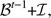 respectively. As for the Shift-after neighbourhood, the slope constraints are necessarily satisfied, but the mining constraints in period (t−1) must be satisfied in order to allow this shift-before.
respectively. As for the Shift-after neighbourhood, the slope constraints are necessarily satisfied, but the mining constraints in period (t−1) must be satisfied in order to allow this shift-before. 
 while the white area delimited by the thick lines represents the set of blocks to be mined in period 2
while the white area delimited by the thick lines represents the set of blocks to be mined in period 2 
 : the value of the relative gap between the value Z
best of the best solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the value Z
best of the best solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation. : the value of the relative gap between the value Z
worst of the worst solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the value Z
worst of the worst solution obtained by the variants in the 10 runs and the optimal value Z
LR of the linear relaxation. : the value of the relative gap between the average value Z
average of the 10 solutions obtained by the variants and the optimal value Z
LR of the linear relaxation.
: the value of the relative gap between the average value Z
average of the 10 solutions obtained by the variants and the optimal value Z
LR of the linear relaxation.