Introduction

It is already well-established that the mechanical (and functional) properties of crystalline materials depend critically on their microstructure, which can be tailored during the manufacturing process in order to optimize the performance of a material with a given chemistry and a given application. The search for sustainable materials with improved properties is a longstanding challenge of material science and engineering. The task of finding solutions which maximizing one or more specified objectives while satisfying all constraints is of utmost importance. Solving an optimization problem involving a single objective function such as strength, corrosion resistance, oxidation resistance, etc. has been the prime focus of engineers and this usually results in a single optimal solution. In such cases, all the other properties are ignored and often considered to be unimportant. In reality, however, several conflicting objectives are simultaneously sought and a single optimal solution may be non-existent. A multi-objective optimization problem has to be solved in order to identify the set of possibilities with different trade-offs. In such cases, the Pareto-optimal solutions, or non-dominated solutions are what is sought [2]. Although a whole locus of Pareto-optimal solutions exists, in practice, only one of these solutions will be selected, based on additional technical or practical considerations.

Effective multi-objective optimization in context of the materials design involves knowledge of chemistry–processing–structure–properties–performance (CPSPP) relationships of the integrated computational materials engineering (ICME) framework [3]. However, a great deal of materials design seems to focus almost exclusively on chemistry [4,5,6,7,8]. In the present work, a framework to obtain the microstructure that maximizes the strength, ductility, and toughness for dual-phase, composite type metallic alloys, is described. The strategy integrates a physics-based crystal plasticity model, which accounts for damage evolution in the reinforcing phase, and a genetic algorithm-based optimization routine. The Pareto-optimal set of solutions for strength–ductility trade-off is investigated and linkages between microstructure and mechanical properties are obtained, which will allow engineers to evaluate how close their present microstructures are to the Pareto frontier and how to alter the microstructures to obtain the optimal properties. This will help remove the Edisonian nature that process engineering can take and provide helpful guidance.

While some of the results and conclusions presented here may appear obvious in retrospect, the authors contend that hindsight is 20–20, and no straightforward answer to the questions, “What microstructures would place a dual-phase alloy on the Pareto frontier of strength and ductility, and which specific microstructure would yield the highest toughness, here defined as the product of tensile strength & uniform elongation (vis a vis Considère criterion)?” exists. The present work aims to provide straightforward answers to these questions. This is the second part of a two-series paper. The companion paper primarily focuses on establishing the connections between the constitutive response of the individual phases and the aggregate behavior, without considering damage. This work considers cracking of the reinforcing phase and highlights the role that microstructure has on the strength–ductility trade-off.

Modeling Framework

The single-crystal elasto-viscoplastic constitutive models for a ductile, face-centered cubic (FCC) structured matrix and a strong, intermetallic reinforcing phase, as well as the choice of material parameters are described in detail in the first part of this two-series paper [1]. The aggregate response of a polycrystal comprises 1000 grains of the matrix and 1000 grains of the reinforcement phase, weighted to represent the crystallographic texture of each of the phases, is computed using the elasto-viscoplastic self-consistent (EVPSC) algorithm introduced by Molinari [9, 10] and extended to cases of finite strain by Wang et al. [11]. The particular FORTRAN95 implementation employed was written by Calhoun [12] and the dislocation density-based hardening law of Beyerlein and Tome [13] was introduced for the present work. Table 1 summarizes the various model parameters used in this work.

Table 1 Description, symbol, and magnitude of the model parameters used in this study
Full size table

A genetic algorithm-based optimization approach is used to examine four different types of strain hardening responses of the matrix. The dislocation density on slip system \(\alpha\), \({\rho }^{\alpha }\), evolves according to the Kocks–Mecking relation: \({\text{d}}{\rho }^{\alpha }={k}_{1}^{\alpha }\sqrt{{\rho }^{g}}{\text{d}}{\gamma }^{\alpha }-{k}_{2}^{\alpha }\left(\dot{\varepsilon },T\right){\rho }^{\alpha }{\text{d}}\Gamma\), where the accumulated shear strain in a grain \({\text{d}}\Gamma =\sum_{\beta }{\text{d}}{\gamma }^{\beta }\). \({k}_{1}^{\alpha }\) is the athermal storage coefficient and \({k}_{2}^{\alpha }\left(\dot{\varepsilon },T\right)\) is the temperature- and rate-dependent dynamic recovery term, given by \({k}_{2}^{\alpha }\left(\dot{\varepsilon },T\right)=\frac{\chi {k}_{1}^{\alpha }{b}^{\alpha }}{{g}^{\alpha }}\left(1-\frac{kT}{{D}^{\alpha }{{b}^{\alpha }}^{3}}{\text{ln}}\left(\frac{\dot{\varepsilon }}{{\dot{\varepsilon }}_{0}}\right)\right)\) [13, 14]. The reader is referred to the companion paper [1] for details of the model. For all cases, the normalized activation energy for dynamic recovery, \(g\), is kept constant at 0.08 in order to minimize the number of variables since changing the drag stress, D, can have a similar effect as changing \(g\). For instance, decreasing D is the same as decreasing \(g\), both lead to an increase in the dynamic recovery term \({k}_{2}\). An additional set of parameters (#5) was used for demonstrating the effect of fracture strength on toughness (Table 2). The initial hardening rate \({\theta }_{0}\) and the saturation stress \({\tau }_{1}\) of the individual slip systems of the FCC matrix are calculated using the well-known relationships: \({\theta }_{0}=\frac{1}{2}\chi \mu {b}^{\alpha }{k}_{1}\) and \({\tau }_{1}=\frac{\chi \mu {b}^{\alpha }{k}_{1}}{{k}_{2}}\). The flow curves of these five different matrix material as well as that of the intermetallic hard phase (all for a grain size of 50 μm) are shown in Fig. 1a.

Table 2 Strain hardening parameters related to the accumulation and recovery of dislocations
Full size table
Fig. 1
figure 1

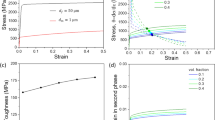
a The flow curves of five matrix materials with different strain hardening behavior as detailed in Table 1, as well as that of the intermetallic hard phase, all for a grain size of 50 μm. b Backscattered electron micrograph of a 6Al–10Cr–40Fe–5Mn–3Mo–30Ni–6Ti (in at.%) corrosion-resistant compositionally complex alloy comprises of an FCC matrix reinforced with L21 Heusler phase, showing evidence of fracture of the L21 phase after tensile loading. c Cumulative Weibull distribution showing the probability of fracture vs. stress for two different characteristic stresses S = 2.5 and 3.0 GPa

Full size image

Damage Model for Reinforcement

It is reasonable to assume that hard phase-induced damage evolution plays the dominant role in heterogeneous materials consisting of a hard phase embedded within a soft ductile matrix, since the latter typically has a higher damage tolerance. Whether second-phase fracture or interface decohesion dominates depends on several factors such as the exact values of the matrix/reinforcement interface strength, the fracture strength of the particles, the size and the volume fraction of the second phase [15], as well as the strain hardening behavior of the matrix [16]. Note that the specific form of damage which is considered (cracking of the reinforcing phase) is posited to dominate, in general, as the size and the volume fraction of reinforcement are increased [15, 17]. For instance, in dual-phase steels, it was found that martensite fracture dominates for volume fractions greater than 15% for martensite sizes of 1–3 μm [15]. Figure 1b shows a backscattered electron micrograph of a 6Al–10Cr–40Fe–5Mn–3Mo–30Ni–6Ti (in at.%) alloy, comprising of an FCC matrix reinforced with L21 Heusler phase. This alloy has been proposed as a relatively low cost, lightweight, corrosion-resistant material with adequate strength and ductility, which is of interest for the overall project [18]. The micrograph provides evidence of fracture of the L21 phase after tensile loading, which supports the choice of the damage model employed in this work. Notably, this alloy system shows fracture of the second phase at a relatively low second-phase volume fraction of ~ 6% and particle sizes < 10 μm suggesting that the damage model employed is appropriate for the ranges of grain sizes and volume fractions explored in this work.

The basics of the damage model for the reinforcing phase have been described briefly in an overview paper [18]. A stress-based fracture criterion is employed in which the contribution of both the hydrostatic mean stress, \({\sigma }_{{\text{m}}}\), and the equivalent stress, \({\sigma }_{{\text{eq}}}\), are taken into account, i.e., damage initiates when \({\sigma }_{{\text{eq}}}\left(1+\frac{{\sigma }_{{\text{m}}}}{{\sigma }_{{\text{eq}}}}\right)={\sigma }_{{\text{c}}}\) [19, 20]. The damage in the second phase is assumed to occur stochastically according to the cumulative Weibull distribution function:

$${P}_{{\text{r}}}=1-{\text{exp}}\left[-\frac{V}{{V}_{0}}{\left(\frac{{\sigma }_{{\text{eq}}}\left(1+\frac{{\sigma }_{{\text{m}}}}{{\sigma }_{{\text{eq}}}}\right)}{S}\right)}^{m}\right],$$

where \(S\) represents the stress at which the probability for cracking is 1 − 1/e = 63% (see Fig. 1c). For simplicity, V/V0 is assumed to be 1 [21, 22]. In order to account for the fact that some load transfer from the matrix to the fractured particles still occurs via shear of the lateral particle sides, the so-called ‘Vanishing Cracked Particle’ (VCP) model is employed [23, 24]. In this model, it is assumed that the load carried by the cracked second-phase particle is approximately equal to that carried by an equal volume of the matrix.

Genetic Algorithm-Based Optimization

Using Considére criterion, \(\frac{{\text{d}}\sigma }{{\text{d}}\varepsilon }=\sigma\), the uniform elongation, \({\varepsilon }_{{\text{u}}}\), and the ultimate tensile stress, \({\sigma }_{{\text{u}}}\), are obtained from the stress–strain data generated by the crystal plasticity model. The toughness T is defined as \({\sigma }_{{\text{u}}}{\varepsilon }_{{\text{u}}}\) and is chosen as the objective function, which can be stated as \({\mathbf{x}}^{*}={\text{argmax}}T(\mathbf{x}),\) where x is a set of design variables, \({\mathbf{x}}^{\boldsymbol{*}}\) is the combination of the design variables that leads to maximum T. For a given microstructure optimization, three quantities viz. the volume fraction of the second phase, \({v}_{{\text{f}}}\), the FCC matrix and the second-phase grain sizes (\({d}_{{\text{m}}}\) , and \({d}_{{\text{f}}}\) , respectively) are chosen as the design variables. The lower and upper bounds of the design variables were chosen as \(0.01\le {v}_{{\text{f}}}\le 0.40 {\text{ and }} 1\le {d}_{{\text{m}}}={d}_{{\text{f}}}\le 50 \mathrm{\mu m}\), in order to restrict attention to microstructures which are practically achievable via conventional thermomechanical processing [25]. While a genetic algorithm (GA)-based optimization strategy using the GA function in MATLAB [26] is used to obtain \({\mathbf{x}}^{*}\), it is to be noted that any other strategies such as grid search methods, particle swarm, or simulated annealing algorithms can also be employed.

A population size of 158 was used and the initial population is generated using the default gacreationuniform function which creates a random population with a uniform distribution. The raw fitness scores (toughness values) are scaled based on the rank of each individual using the default fitscalingrank function. For instance, an individual with rank n has scaled score proportional to 1/√n. In order to choose the parents for the next generation, the default selection function, selectionstochunif, is used where the probability that a parent is selected is proportional to its scaled score. The fraction of population which comprises crossover children, CrossoverFraction, was set to 0.6, and was generated using the default crossoverscattered function which creates a random binary vector and chooses the genes of the parents based on the binary vector values and combines them to form the child. EliteCount which specifies how many individuals in the present generation are guaranteed to survive to the next generation was set to 5% of the population size. The default mutation function mutationgaussian was chosen which adds a random number to each entry of the parent to make small changes in the individuals in the population to create mutation children and increase the diversity. Convergence is achieved if the average relative change in the best fitness function value over MaxStallGenerations (set to 15) is less than or equal to the FunctionTolerance (set to 0.1). A Slurm-based parallel computing framework, where 4 nodes with 40 processes (tasks) per node are employed. Each EVPSC simulation takes ~ 20 min. A run of the GA optimization with the given population size takes ~ 15 generations to converge in ~ 10 h.

Pareto Frontier

The strength–ductility Pareto frontier is the locus of all microstructural states (phase fractions and grain sizes) which cannot be tailored to further improve the strength without sacrificing the ductility. In this work, the Pareto frontier is constructed using the simulations performed by the GA-based optimization routine. The GA routine runs ~ 2500 simulations before converging. Using a custom MATLAB function, the \({\sigma }_{{\text{u}}}\), the \({\varepsilon }_{{\text{u}}}\) , and the toughness values are calculated for all these simulation runs, and the Pareto frontier is calculated using the following algorithm. First, the data are sorted in one of the coordinate dimensions (e.g., ductility). Then, in order of decreasing ductility, each point (a microstructural state and the corresponding \({\sigma }_{{\text{u}}}\), \({\varepsilon }_{{\text{u}}}\), and toughness values) is tested to determine whether the strength of the current point is greater than the maximum strength of any previously processed point. If it is, then the current point is considered as on the frontier. The final output is a set of maximal or non-dominated points where there is no other point in the total set whose strength and ductility values are both greater than or equal to the corresponding values of this maximal set. A line is fitted to these maximal points to obtain the Pareto frontier. The slope of the Pareto frontier (the rate of decrease in strength with increasing ductility) will prove significant in what follows. To summarize, a schematic showing the microstructure-based mechanical property optimization framework, highlighting the connections between microstructure, crystal plasticity model accounting for damage in the reinforcing phase, and the GA-based optimization strategy to obtain optimal microstructures and the Pareto frontier is shown in Fig. 2.

Fig. 2
figure 2

A schematic showing the microstructure-based mechanical property optimization framework. The material microstructure is used as input to a crystal plasticity model which accounts for damage evolution within the reinforcement through a “vanishing cracked particle” model that is governed by Weibull statistics, to predict the stress–strain response of the aggregate. Considere criterion is employed to determine the uniform elongation, εunif, and the ultimate tensile stress, σUTS, from the aggregate stress–strain data. A genetic algorithm-based optimization routine is employed, which varies the design variables, in order to maximize the design objective “toughness,” defined as σUTS × εunif. The Pareto-optimal set of solutions for strength–ductility trade-off is constructed using the simulations performed by the GA-based optimization routine

Full size image

Results and Discussion

Role of Damage of the Second Phase

Figure 3a shows the effect of the hard phase’s fracture strength on the toughness of the two-phase aggregate. The matrix behavior is given according to case #5 (Table 2). Three different fracture strengths are considered: infinite fracture strength, 3.0 GPa, and 2.5 GPa. The latter two correspond to \(\frac{S}{{\tau }_{{\text{m}}}}\) = 30 and 25, respectively, where the matrix critical resolved shear stress (CRSS), \({\tau }_{{\text{m}}}\) = 0.1 GPa. The case of infinite fracture strength was detailed in the companion paper [1], and it was shown that the overall toughness can be improved with increasing volume fraction of reinforcement, provided it has sufficiently high strength and the matrix has sustained strain hardening behavior. The present results show that, even with reinforcing materials of finite fracture strength, the overall toughness can be maintained or even improved. For instance, adding 10% reinforcing phase with a fracture strength \(\frac{S}{{\tau }_{{\text{m}}}}\) = 30 leads to an improvement in the toughness as compared to that of the matrix. At the limit of weak reinforcements (here \(\frac{S}{{\tau }_{{\text{m}}}}\) = 25), the toughness monotonically decreases with reinforcement addition, suggesting that no second-phase addition is beneficial. Figure 3b shows the fraction of fractured second-phase grains as a function of strain. As the volume fraction of second phase increases (from 0.1 to 0.4), the fraction fractured also increases. At a given volume fraction and applied strain, a stronger reinforcement is less prone to fracture, as expected.

Fig. 3
figure 3

a The effect of hard phase’s fracture strength on toughness of two-phase aggregate illustrated using three different fracture strengths: infinite fracture strength, S/τm = 30 and 25, where the matrix CRSS τm = 0.1 GPa. The plot shows that even with reinforcements of finite fracture strength, the overall toughness can be improved as compared to the matrix. b The fraction of fractured second-phase grains as a function of strain, for S/τm = 25 and 30, for different volume fractions (0.1–0.4) of the second phase

Full size image

Genetic Algorithm-Based Optimum Microstructures

Cases #1–4 with a reinforcement fracture strength of \(\frac{S}{{\tau }_{{\text{m}}}}\) = 25 were used for the GA-based optimization. When each of these “pure phase” material is combined to produce an aggregate, the GA-based optimal microstructure that lead to the highest toughness value is shown in Table 3. It is evident that, depending on the strain hardening response of the matrix material, a wide range of microstructures will lead to the optimum properties. More importantly, the maximum toughness that one can achieve strongly depends on the behavior of the matrix. For instance, as the strain hardening rate of the matrix material increases, the maximum achievable toughness value increases from ~ 200 to ~ 300 MPa.

Table 3 The optimal microstructure obtained by the GA-based routine, i.e., volume fraction (\({v}_{{\text{f}}})\), matrix (\({d}_{{\text{m}}}\), in μm), and reinforcement grain sizes (\({d}_{{\text{f}}}\), in μm) for the types of matrix material
Full size table

Figure 4 shows the dependence of toughness on the second-phase volume fraction for all grain sizes. The scatter in the results is due to the grain size effect and it is evident that the volume fraction is the key factor that determines the toughness of the aggregate. It has already been shown that grain sizes only have a second-order effect which results in the few outliers [18]. The plots also show that when the matrix strain hardening rate is high, a lower volume fraction of the reinforcing phase is predicted to result in maximum toughness, whereas for a low matrix strain hardening rate, a higher volume fraction of the reinforcing phase results in the maximum toughness, and in the limit, any reinforcement addition is detrimental for the toughness (Case #3). As the second-phase content increases, a larger amount of strain (stress) is partitioned to the second phase, which either leads to yielding (plastic flow) or damage in the second phase, leading to toughness degradation. Lower hardening rate leads to lower overall stress levels in the aggregate, meaning the strength contrast between the two phases does not rapidly decrease. In such situations, the addition of a higher amount of hard phase is beneficial because of the increase in strength associated with this phase. The situation is opposite for a high hardening matrix.

Fig. 4
figure 4

The dependence of toughness on the second-phase volume fraction for all grain sizes for cases #1–4 (Table 2)

Full size image

On the other hand, if the matrix has a sustained strain hardening response akin to alloys which exhibit TRIP/TWIP behavior, then much higher toughness values ~ 650 MPa can be achieved with reinforcement addition. In such scenarios, the sustained hardening rate of the matrix compensates (up to a point) for the decrease in the hardening rate associated with a higher amount of strain partitioning in the second phase. This implies that a matrix that exhibits TRIP/TWIP effects, leading to a sustained strain hardening rate, will promote higher toughness values than can be achieved with a matrix which exhibits the typical saturation type strain hardening response stemming from dislocation–dislocation interactions alone.

It is worth restating that the exact values of the optimal microstructural variables and the corresponding properties will vary with the choice of parameters. For instance, the optimal volume fraction would be lower for a reinforcement having a lower fracture strength. For the chosen set of parameters, the toughness values are relatively insensitive to the reinforcement grain size since only a small amount of the strain is partitioned to the second phase. Regardless of details, the approach provides guidance for alloy and microstructure design.

Pareto Frontier

Figure 5 shows the strength–ductility Pareto frontier for case #4. (One can consider each case as being comprised of a particular matrix and reinforcement material combination, though the grain sizes and phase fractions are free variables.) The red points on the frontier are instances of Pareto-optimal choices. Materials researchers are well-acquainted with the concept of “the banana curve” for steels [27, 28] where an increase in strength is accompanied by a decrease in ductility. Indeed, many papers in the literature are concerned with developing materials (especially compositions) whose properties are in “the white space” which lies “beyond the banana curve” e.g., [29, 30].

Fig. 5
figure 5

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by case #4 (Table 2). The red points on the frontier are instances of Pareto-optimal choices of strength and ductility. Points denoted by orange × are examples of points which lie below the frontier, i.e., they are not Pareto-efficient, since there exist points on the frontier which dominate them. These non-optimal points can be pushed to the frontier by optimizing the microstructure as illustrated for points 1 and 3. The resulting optimal points are denoted as 1′, 1″ and 3′, 3″, respectively (Color figure online)

Full size image

There are three important points of distinction in the present work. First, the shape of the Pareto frontier shown in Fig. 5, which is discussed further below, is unlike that of the typical “banana curve.” Second, it is not possible to “go beyond” this curve unless the fundamental, governing assumptions are proven false, because this is the locus of truly optimal microstructures. Third, this curve is not a collection of all possibilities. Rather, there are an infinite number of points which lie below the frontier, such as the few examples shown in orange. These orange points are not Pareto-efficient, since there exist points on the frontier which dominate them. In other words, the strength–ductility combinations resulting from these microstructures are not optimized. The aim of this paper and what should be the aim of materials designers and process engineers is to insure that the materials we produce lie on the frontier. Table 4 shows the values of the microstructural variables that lead to these non-optimal points. A couple of these are used for illustration. Let us consider point #1. If a similar level of \({\varepsilon }_{{\text{u}}}\) is desired, reducing the matrix grain size from ~ 40 to 8 μm leads to a higher strength which will make the point lie on the frontier, without changing the reinforcement content. Conversely, if a higher \({\varepsilon }_{{\text{u}}}\) is desirable at the same strength level, then decreasing the reinforcement content from 39 to 26% and the reinforcement size from 39 to 5 μm will also push the point to the frontier. These optimal points 1′ and 1″ are shown in Fig. 5, and the corresponding microstructures that would move #1 to the Pareto frontier are shown in Table 5. Between these two scenarios, 1′ and 1″ lie an infinite number of routes via which the Pareto frontier can be reached, limited only by processing realities.

Table 4 The volume fraction (\({v}_{{\text{f}}})\), matrix (\({d}_{{\text{m}}}\), in μm) and reinforcement grain sizes (\({d}_{{\text{f}}}\), in μm) and uniform elongation (\({\varepsilon }_{{\text{u}}}\)), ultimate tensile strength (\({\sigma }_{{\text{u}}}\), in MPa), and toughness (in MPa), defined as \({\varepsilon }_{{\text{u}}}\times {\sigma }_{{\text{u}}}\), of six non-optimal points shown in orange in Fig. 5, for matrix strain hardening behavior given by #4 in Table 2
Full size table
Table 5 The microstructures that would push points #1 and #3 (Table 4) to the Pareto frontier (1′, 1″, 3′ and 3″ in Fig. 5) and the corresponding \({\varepsilon }_{{\text{u}}}\), \({\sigma }_{{\text{u}}}\), and toughness values
Full size table

Now let us consider point #3. By increasing the reinforcement content from 1 to 37%, as well as by increasing the grain sizes of both the phases (from ~ 1 to 19 and 44 μm, respectively), this point can be pushed to the frontier, by maintaining a similar level of \({\varepsilon }_{{\text{u}}}\). Alternatively, if the strength level is held constant, then by increasing the reinforcement content to ~ 19%, and the grain sizes of both the phases to ~ 40 μm, this point can be made to lie on the frontier. These two optimal points 3′ and 3″ are shown in Fig. 5 and the corresponding microstructures that would move #3 to the Pareto frontier are shown in Table 4. In many cases, a simultaneous increase in the second-phase fraction and matrix grain size would have enabled simultaneous increase in both tensile strength and uniform elongation, thus pushing closer the Pareto frontier. It is notable that larger matrix grain size has been determined to promote optimal combinations of tensile strength and uniform elongation in an era where so much emphasis has been placed on nanostructuring [31, 32] There are practical bounds to the present design predictions. Very large grain sizes relative to component sizes could lead to undesirable, inhomogeneous deformation. That said, the grain size dependence of strength becomes quite weak at grain sizes larger than about 50 μm.

Depending on the matrix strain hardening behavior, the Pareto frontier exhibits two different shapes. The curve may be convex, as shown in Fig. 5, which is replotted together with the corresponding microstructural variables and toughness in Fig. 6. Cases #2 and #3 exhibit a similar shape (Figs. 7 and 8, respectively), albeit with a different degree of convexity. As the matrix hardening rate decreases, the level of convexity also decreases, such that for case #2, the Pareto frontier is only slightly convex (Fig. 7). Starting from the pure matrix material (which exhibits the highest ductility and the lowest strength), the tensile strength dramatically increases for a given reduction in ductility (e.g., going from A to B in Fig. 6a) as second-phase reinforcement is added. At higher levels of reinforcement, the rate of reduction in ductility for a given increase in strength diminishes (e.g., going from C to D). This is also reflected in Fig. 6c, which shows the variation of toughness along the Pareto frontier, and shows that the highest toughness is associated with a coarse matrix. Note, that for the present linear hardening case #4, one can achieve a single position on the frontier with very different grain sizes (Fig. 6b). In other words, a wide range of matrix grain sizes can be employed to achieve a singular position (combination of ultimate strength and ductility) on the frontier by varying other microstructure attributes (i.e., phase fraction). The situation is different for cases #3 and #2, where the highest toughness results from a finer matrix grain size (Figs. 7b, 8b). For case #3, the optimal volume fraction is 0.01 essentially suggesting that the matrix material provides the highest toughness and any reinforcement addition is detrimental. For case #2, the optimal volume fraction is 0.13 which is intermediate to cases #3 and #4.

Fig. 6
figure 6

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by case #4 (Table 2). The microstructure that gives rise to the frontier is shown a dependence on the reinforcement volume fraction, b dependence on the matrix grain size, and c the values of toughness given by εu × σu, along the frontier

Full size image
Fig. 7
figure 7

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by case #3 (Table 2). The microstructure that gives rise to the frontier is shown a dependence on the reinforcement volume fraction, b dependence on the matrix grain size, and c the values of toughness given by εu × σu, along the frontier

Full size image
Fig. 8
figure 8

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by case #2 (Table 2). The microstructure that gives rise to the frontier is shown a dependence on the reinforcement volume fraction, b dependence on the matrix grain size, and c the values of toughness given by εu × σu, along the frontier

Full size image

Upon further reduction of the matrix hardening rate (i.e., below #2), the Pareto frontier shape changes to concave up for case #1 (Fig. 9). This shape implies that as one moves from high to low uniform elongation, there is a larger rate of increase in strength associated with a similar level of reduction in ductility. This situation arises when the rate of increase in tensile strength for a given increment in second-phase content (or grain size reduction) increases for a nearly constant level of ductility reduction. Note, a finer matrix grain size is advantageous in this case (Fig. 9b), which is similar to cases #2 and #3 but contrary to #4, suggesting that finer matrix grains are preferred, for a matrix that exhibits parabolic strain hardening response stemming from dislocation–dislocation interactions alone, whereas for a matrix exhibiting sustained hardening rate, a coarser matrix grain size is preferable to maintain a high strength contrast between the phases. Finally, although the toughness only marginally increases, it does show a maximum around the highest strength portion of the Pareto frontier. The other possibility, which is not reflected here, is the linear Pareto frontier which reflects the situation where the increase in strength is balanced by the reduction in ductility such that the slope remains constant.

Fig. 9
figure 9

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by case #1 (Table 2). The microstructure that gives rise to the frontier is shown a dependence on the reinforcement volume fraction, b dependence on the matrix grain size, and c the values of toughness given by εu × σu, along the frontier

Full size image

Given a particular strength–ductility Pareto frontier, the criterion which determines whether there is an optimum in the toughness is derived as follows. The total differential of the toughness, \(T=T\left({\sigma }_{{\text{u}}}{,\varepsilon }_{{\text{u}}}\right)\), is \({\text{d}}T=\frac{\partial T}{\partial {\sigma }_{{\text{u}}}}{\text{d}}{\sigma }_{{\text{u}}}+\frac{\partial T}{\partial {\varepsilon }_{{\text{u}}}}{\text{d}}{\varepsilon }_{{\text{u}}}\). The total derivative of toughness with respect to uniform elongationFootnote 1 is, \(\frac{{\text{d}}T}{{\text{d}}{\varepsilon }_{{\text{u}}}}=\frac{\partial T}{\partial {\sigma }_{{\text{u}}}}\frac{{\text{d}}{\sigma }_{{\text{u}}}}{{\text{d}}{\varepsilon }_{{\text{u}}}}+\frac{\partial T}{\partial {\varepsilon }_{{\text{u}}}}\). Let the slope of the Pareto frontier \(\frac{{\text{d}}{\sigma }_{{\text{u}}}}{{\text{d}}{\varepsilon }_{{\text{u}}}}=m\), and since toughness \(T={\sigma }_{{\text{u}}}{\varepsilon }_{{\text{u}}}\), \(\frac{\partial T}{\partial {\sigma }_{{\text{u}}}}={\varepsilon }_{{\text{u}}}\) and \(\frac{\partial T}{\partial {\varepsilon }_{{\text{u}}}}={\sigma }_{{\text{u}}}\). Therefore, a maximum to occur, \(\frac{{\text{d}}T}{{\text{d}}{\varepsilon }_{{\text{u}}}}={\varepsilon }_{{\text{u}}}m+{\sigma }_{{\text{u}}}=0\) and \(\frac{{{\text{d}}}^{2}T}{{\text{d}}{\varepsilon }_{{\text{u}}}^{2}}<0\), which implies that the maximum toughness is obtained when \(m=-\frac{{\sigma }_{{\text{u}}}}{{\varepsilon }_{{\text{u}}}}\). The maximum toughness occurs for the microstructure which leads to a strength–ductility combination which satisfies this condition. Figure 10 shows this criterion for cases #1 and #4. The predicted combination of strength and ductility that leads to the highest toughness closely matches with the simulation results. The slightly discrepancy, particularly for #4, stems from the numerical uncertainties in fitting which underestimates the slope of the Pareto frontier and thereby the location of the toughness maximum.

Fig. 10
figure 10

The strength–ductility Pareto frontier of a two-phase aggregate, where the matrix hardening behavior is described by a case #1 and b case #4 (Table 2). Also shown are the toughness values, slope of the frontier \(\frac{{\text{d}}{\varepsilon }_{{\text{u}}}}{{\text{d}}{\sigma }_{{\text{u}}}}=m,\) and \(-\frac{{\sigma }_{{\text{u}}}}{{\varepsilon }_{{\text{u}}}}\). The maximum in toughness is predicted to occur when \(m=-\frac{{\sigma }_{{\text{u}}}}{{\varepsilon }_{{\text{u}}}}\), denoted by dotted red line (Color figure online)

Full size image

Conclusions

A strategy which integrates physics-based crystal plasticity model, damage evolution in the reinforcement, and a genetic algorithm-based optimization routine is employed to obtain the optimal microstructure that maximizes the toughness. The results undergird the following conclusions:

  1. (1)

    The overall toughness of an alloy can be maintained or even improved by adding a strong reinforcing phase, even if the particles have a finite fracture strength.

  2. (2)

    A matrix that exhibits a sustained strain hardening rate, such as is observed for so-called transformation- or twinning-induced plasticity (TRIP/TWIP) scenarios, always leads to higher toughness values as compared to a matrix which exhibits the typical saturation type strain hardening response stemming from dislocation–dislocation interactions alone.

  3. (3)

    For the latter case, as the strain hardening rate of the matrix increases, the optimal volume fraction of reinforcement decreases. This is attributed to increasing stress levels which promote strain partitioning and damage of the reinforcement which leads to rapid plastic instability of the aggregate.

  4. (4)

    It is shown that the addition of a fine-grained hard reinforcing phase is preferred in most cases. For cases where the stress levels are low (due to low matrix strain hardening), finer matrix grains are preferred, whereas a coarser matrix grain size is preferable for a matrix exhibiting sustained hardening rate, in order to maintain a high strength contrast between the phases.

  5. (5)

    It is shown that by modifying the individual phase properties, the shape of the strength–ductility Pareto frontier can be modified. For matrix exhibiting parabolic hardening rates, the shape of the Pareto frontier changes from convex to concave up, as the hardening rate is decreased. For matrices with sustained hardening rates, the Pareto frontier shape is convex.

  6. (6)

    The link between microstructure and the Pareto frontier is highlighted, and it is demonstrated that there are infinite routes, limited only by processing realities, via which the Pareto frontier can be reached, thus providing a novel approach to design multiphase materials.

  7. (7)

    An analytical criterion which determines whether there is an optimum in the toughness within the bounds of the independent variables (rather than at the limits) is derived, which adequately matches that observed in the simulations.