Abstract
The seagull optimization algorithm (SOA) is a meta-heuristic algorithm proposed in 2019. It has the advantages of structural simplicity, few parameters and easy implementation. However, it also has some defects including the three main drawbacks of slow convergence speed, simple search method and poor ability of balancing global exploration and local exploitation. Besides, most of the improved SOA algorithms in the literature have not considered the drawbacks of the SOA comprehensively enough. This paper proposes a hybrid strategies based algorithm (ISOA) to overcome the three main drawbacks of the SOA. Firstly, a hyperbolic tangent function is used to adjust the spiral radius. The spiral radius can change dynamically with the iteration of the algorithm, so that the algorithm can converge quickly. Secondly, an adaptive weight factor improves the position updating method by adjusting the proportion of the best individual to balance the global and local search abilities. Finally, to overcome the single search mode, an improved chaotic local search strategy is introduced for secondary search. A comprehensive comparison between the ISOA and other related algorithms is presented, considering twelve test functions and four engineering design problems. The comparison results indicate that the ISOA has an outstanding performance and a significant advantage in solving engineering problems, especially with an average improvement of 14.67% in solving welded beam design problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many problems in real life could be converted into optimization problems subject to complex constraints. These optimization problems are often accompanied by multiple constraints and massive computation, so that traditional optimization approaches are unable to cope with such problems [1]. To overcome the limitations of traditional methods, such as obtaining only local optimal solution and relying too much on gradient information of objective functions, researchers have proposed a new optimization method, the metaheuristic algorithm. The meta-heuristic algorithm is featured as non-derivative, high efficiency and low computation cost. It provides an efficient solution for NP-hard problems, by obtaining the optimal solution or suboptimal solution within an acceptable running time.
Due to no free lunch (NFL) theorem [2], no single optimization algorithm can be used to solve all constrained optimization problems, so it is essential to constantly explore new algorithms and improve existing ones. In recent decades, a variety of flexible and versatile metaheuristic algorithms has been put forward to solve the increasingly complicated optimization problems in various areas. For example, some standard algorithms proposed by early researchers include: genetic algorithm (GA) derived from the law of natural selection in the biosphere [3], simulated annealing algorithm (SA) based on solid annealing principle [4], ant colony optimization algorithm (ACO) inspired by the ants foraging paths [5], particle swarm optimization algorithm (PSO) proposed by simulating the foraging actions of birds [6], gravitational search algorithm (GSA) inspired by the law of gravity and Newton's second law [7], and cuckoo search algorithm (CS) which is proposed by simulating the breeding habits of cuckoo [8]. In recent years, based on previous studies, many new standard optimization algorithms have been developed. For instance, grey wolf optimization algorithm (GWO) is proposed based on the hierarchy and predation behavior of grey wolf population [9], ant lion optimization algorithm (ALO) simulates the mechanism of ant lion predation on ants [10], whale optimization algorithm (WOA) is based on the mechanism of whale rounding up prey [11], sparrow search algorithm (SSA) simulates the foraging and anti-predatory actions of sparrows [12], and butterfly optimization algorithm (BOA) is based on the behaviors of butterflies feeding on nectar and mating in nature [13].
Besides, researchers have put forward different strategies to enhance the optimization performance of the standard algorithms. For instance, introducing the mechanism of nelder-mead local search algorithm to the WOA, an algorithm named HWOANM is proposed to speed up the convergence of the WOA and to solve engineering optimization problems [14]. A new hybrid algorithm (HPSOGWO) is proposed by effectively combining PSO and GWO [15]. The negative correlation search algorithm is introduced to GSA to achieve the differentiation of search behaviors, and the test results show that the optimization accuracy of GSA is enhanced [16]. A memory-based grey wolf optimization algorithm (mGWO) is proposed to enhance the ability of balancing global and local search [17]. To overcome the disadvantages of sine and cosine search algorithm (SCA), Ref. [18] proposed the m-SCA algorithm, which introduces reverse learning strategy and self-adaptation strategy.
The seagull optimization algorithm (SOA) is proposed by Dhiman and Kumarti, simulating the migration and aggressive behavior of seagulls [19]. The SOA has the merits of simple parameter setting, easy and flexible adjustment and easy implementation. It has been studied and improved by many scholars, and been applied to different fields. Like other optimization algorithms, it also has the defects of low population diversity, easily plunging into local optimum, and weak convergence [20].
In the literature, the SOA is investigated mainly from two aspects: one is to study the optimization process of the SOA, and improve the algorithm by changing the population initialization, parameters, convergence factor or position updating method; the other is to apply the SOA to the parameter optimization of other algorithms or to some practical fields. For example, an improvement of the SOA was made by replacing the convergence factor with a nonlinear dynamic factor and using lévy flight mechanism to increase the randomness [21]. Parameters and attack angle \(\uptheta \) in the SOA were adjusted and dynamic reverse learning strategy was utilized, with an application to the PID controller model [22]. The levy-flight mechanism was added to the search method of the SOA to improve the convergence rate. Then it was applied to the optimization model of the PEMFC system [23]. Ref. [24] combined the shrink-wrap mechanism of WOA with the spiral search mode of SOA, to avoid premature convergence and improve the convergence accuracy. Three strategies were introduced to improve the convergence capability of the SOA, with an application to the blind source separation [25]. The SOA was utilized to calculate the threshold points for threshold segmentation of otsu images to achieve better segmentation effect [26]. The heat transfer formula of the heat exchange optimization algorithm (TEO) was used to improve the attack formula of the SOA, providing solutions to the feature selection problems [27]. Natural selection mechanism was introduced to the SOA to avoid trapping in the local optimum, and was used to solve the dynamic optimization problems together with the unequal division method [28].
Although the researches enhanced the performance of the SOA in a way, most of them have not considered the drawbacks of the SOA comprehensively enough. At this point, this paper proposes hybrid strategies to enhance the convergence of the SOA, working on the three main drawbacks of slow convergence, poor ability to balance global and local search, and single search mode. Firstly, the helical coefficient of the SOA is improved, so that the helical radius of seagulls attacking can change with the number of iterations, and the local search ability is enhanced; secondly, an adaptive weight factor is added to the position updating method to balance the global and local search in the optimization process; finally, the chaotic local strategy is used to update the seagull position twice to prevent falling into a local optimum. In the experimental simulation, 12 test functions are utilized. Experimental comparison of solution results and convergence curves with other recent related optimization algorithms shows that the ISOA has stronger searching ability and faster convergence. In addition, four engineering optimization problems with constraints are solved by the ISOA. The results indicate that the proposed algorithm (ISOA) has strong competitiveness compared with other algorithms.
The rest of this paper is structured as follows: Sect. 2 describes the principle and optimization mechanism of the standard SOA, and analyzes the problems existing in the SOA; Sect. 3 puts forward the improvement strategies and describes the optimization procedure of the ISOA; In Sect. 4, experimental comparative analysis is carried out to validate the performance of the ISOA; Sect. 5 applies the ISOA to four engineering design problems; Sect. 6 concludes the paper, and proposes further research.
2 Seagull Optimization Algorithm and Shortcomings
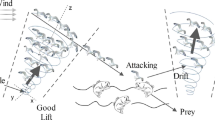
The main inspiration for the SOA is the migration and aggressive behavior of seagulls in nature. Migration is the seasonal movement of seagulls in search of the richest food source to provide sufficient energy. During migration, seagulls are supposed to keep from colliding with each other, and each seagull updates the position with the best one in the population. Then, seagulls assault prey in a spiral trajectory through the air. The migration is the global exploration phase of the SOA, while the attack denotes the local exploitation phase. The SOA is to constantly adjust the positions of seagulls to seek an optimal solution by imitating the two behaviors.
2.1 Migration Behavior
During the migration phase, the algorithm simulates how a flock of seagulls moves from one location to another. Every search agent needs to meet three conditions: avoid colliding with each other, move in the direction of the best search agent, and update the position with the best search agent.
1. Avoid collision: To avoid the mutual collision, the variable A is introduced into the algorithm to evaluate the updated position of search agents.
where \({\overrightarrow{C}}_{s}\) represents the location where the seagull does not collide with another individual; \({\overrightarrow{P}}_{s}(t)\) is the current position of the search agent; \({\text{t}}\) indicates the number of iterations; \({\text{A}}\) represents the movement behavior of seagulls in the feasible region.
where \({T}_{maxitera}\) is the maximum number of iterations, \(\mathrm{t }=\mathrm{ 1,2},...,{T}_{maxitera}\), the hyper parameter \({f}_{c}\) is used to control the size of the variable A, \({f}_{c}\) is set to 2, and the variable A decreases linearly from \({f}_{c}\) to 0.
2. Move in the direction of the best search agent: The seagulls will move to the best search agent when there is no collision between individuals.
where \({\overrightarrow{M}}_{s}\) represents the position of the seagull moving toward the best search agent; \({\overrightarrow{P}}_{best}(t)\) is the current position of the best search agent, which has a small fitness value; \({\text{B}}\) is a random number, which is used to balance global exploration and local exploitation; \({\text{rd}}\) is a random number between 0 and 1.
3. Update the position with the best search agent: After the convergence direction is determined, the seagull constantly approaches the best search agent.
where \({\overrightarrow{D}}_{s}\) denotes the distance between the search agent and the best one.
2.2 Attack Behavior
During attacking, seagulls constantly change the angle and speed, and they use their wings and weight to maintain their hovering altitude. When attacking prey, seagulls move through the air in a spiral motion. Their behavior is described below in terms of x, y and z coordinates:
where, \({\text{r}}\) is the spiral radius of each turn; \(\uptheta \) is a random number in \([\mathrm{0,2\pi }]\). \({\text{u}}\) and \({\text{v}}\) are constants; e is the base of the natural logarithm. In the standard SOA, u and v are both 1. Equations (6)–(9) are used to figure out the updated position of a seagull as shown below:
where \({\overrightarrow{P}}_{s}\left(t+1\right)\) is the updated position of the search agents.
2.3 Shortcomings
The SOA has the following shortcomings: (a) slow convergence. According to the position updating method of the SOA, the spiral radius \({\text{r}}\) determines the size of the search range of the seagulls. However, r is determined by the coefficients \({\text{u}}\) and \({\text{v}}\) that are constants. As a result, the search radius is too large in the later stage, causing an oscillation near the optimal solution and a failure to achieve fast convergence. (b) Poor ability of balancing global and local search. From Eq. (10), the position of the current best individual has strong influence on the position of the seagulls. The influence is supposed to vary with different stages of the algorithm. However, in the standard SOA, the weight value given to the best individual is always 1 in both early and late stages, which leads to a poor ability of balancing the global and local search. (c) Single search mode, causing a local optimal. The standard SOA has only one position updating method, as a result, search agents can only search in one way, reducing the diversity of species. This makes the algorithm susceptible to the local optimization, particularly for the multi-peak test functions.
3 Improved Seagull Optimization Algorithm
To overcome the drawbacks existing in the SOA, this paper proposes three optimization strategies: The spiral coefficient v is improved by using the hyperbolic tangent function (Tanh) to speed up the convergence; the adaptive weight factor is introduced to strengthen the ability of balancing global and local search; the chaotic local strategy is introduced to increase the diversity of search methods to improve the convergence accuracy. Finally, the solving procedure of the ISOA is provided.
3.1 Improvement of Helical Coefficient \(\mathbf{v}\)
From the iterative process of the SOA, when the search agent launches the attack behavior, the spiral radius r affects the size of attack range, thus has a deep impact on the optimization accuracy of the SOA. According to Eq. (9), the spiral radius r is determined by the values of the spiral coefficients u and v. In the standard SOA, the values of u and v are set to 1. As a result, the size of the spiral shape is constant and cannot be adjusted continuously with the iterations. Especially, in the later stage of the algorithm, the spiral radius cannot be decreased, even causing a failure to converge to the optimum value. At this point, the Tanh is introduced to improve the helix coefficient v.
Figure 1 is the curve of the Tanh expressed by Eq. (11), indicating that Tanh is a continuous and increasing function. Equation (12) is the improved spiral coefficient v, performed by telescopic translation of the Tanh function. From Fig. 2, it can be seen that the value of v gradually approaches 0 with the iteration. In this way, in the early stage of the algorithm, the search agent can search with a large radius, enhancing the global exploration ability; in the later stage, the spiral radius decreases gradually, which allows the algorithm converge to the optimal solution rapidly and enhances the local search ability.
where, \({T}_{maxitera}\) is the maximum number of iterations, \({\text{t}}=\mathrm{1,2},...,{T}_{maxitera}\).
3.2 Adaptive Weight Factor Strategy
The adaptive weight factor is one of the essential factors used in optimization algorithms to balance global exploration and local exploitation [29,30,31]. As illustrated in Sect. 2.3, the current best individual is supposed to have greater influence on the early stage of the SOA search than on the late one. So, a larger weight should be given to the current best search agent in the early stage to speed up the convergence to the neighbor of global optimal solution; in the late stage, a smaller weight value should be chosen to refrain from falling into the local optimum caused by an excessively fast convergence, thus to enhance the capability of local search. Therefore, the adaptive weight factor, expressed by Eq. (13), is utilized to improve the position updating method, as shown in Eq. (14).
where, \({\overrightarrow{D}}_{s}\), \(x\), \(y\), \(z\) and \({\overrightarrow{P}}_{best}(t)\) have the same meaning as in Eq. (10).
The iterative curve of the adaptive weight ω(t) is shown in Fig. 3a, which indicates that the value range of \(\upomega \) reduces from 2 to 0. The weight value given to the best individual in the early stage is greater than 1; the weight value in the late stage decreases rapidly and gradually approaches 0. To further prove the validity of the proposed adaptive weight factor \(\upomega \), comparison of \(\upomega \),\({\upomega }_{1}\),\({\upomega }_{2}\) will be made in what follows, where \({\upomega }_{1}\),\({\upomega }_{2}\) are the weight factors proposed in [30] and [31], as expressed by Eqs. (15) and (16) respectively and shown in Fig. 3a.
where, the values of \({\upomega }_{{\text{max}}}\) and \({\upomega }_{{\text{min}}}\) are the same as in Ref. [30].
When Eq. (10) in the SOA is changed to Eq. (14), we obtain a new algorithm and name it SOA-\(\upomega \). Similarly, SOA-\({\omega }_{1}\) and SOA-\({\omega }_{2}\) are the new algorithms obtained by replacing \(\upomega \) in Eq. (14) with \({\upomega }_{1}\), \({\upomega }_{2}\) respectively. Three test functions F1, F4 and F7 are randomly selected for convergence comparison of SOA-\(\upomega \), SOA-\({\omega }_{1}\) and SOA-\({\omega }_{2}\). As can be seen from Fig. 3b and Fig. 3c, the SOA-\(\upomega \) is nearer to the optimal solution than the other two, i.e., it has higher convergence accuracy. According to Fig. 3d, although the SOA-\(\upomega \) converges to the same optimal solution as SOA-\({\omega }_{1}\) and SOA-\({\omega }_{2}\), it has the fastest convergence rate. In summary, the adaptive weight factor proposed is effective for balancing the global search and local search of the SOA.
3.3 Chaotic Local Search Strategy
The chaotic local search strategy uses chaotic systems to generate chaotic variables. Due to the random and uniform distribution of chaotic variables, an algorithm can perform two searches near the optimal individual, which reduces the possibility of plunging into the local optimum. Moreover, the chaotic local strategy has been introduced into other algorithms, and the experiments have proved that it can effectively improve the performance [32, 33]. The standard SOA has only one spiral position search mode, which both reduces the diversity of the search agent and limits the search scope. It easily falls into local optimal, especially on the multi-peak functions. Therefore, to overcome the limitation of single search mode, an improved chaotic local strategy is introduced into the search process. Equations (17)–(18) describe the mathematical formulation of the improved chaotic local search.
where, \({X}^{\prime}(t)\) is the position of an individual, \({\text{z}}({\text{t}})\) represents the chaotic variable mapped through the chaotic system; \({\overrightarrow{X}}_{best}(t)\) is the current position of the best individual; \({\text{ub}}\) and \({\text{lb}}\) describe the boundaries of the search space; \(r(t)\) is the radius of chaotic search; Eq. (18) describes how the chaotic search radius is updated, and the initial value is set as 0.01. In this paper, the strategy is adjusted and applied to the position updating method of the SOA to form a mechanism of secondary updating, as shown in Eqs. (19)–(21), so as to increase the diversity of the population.
where, \({P}_{s}^{\prime}(t)\) is the position of a seagull obtained by the improved chaotic local strategy, and \({\overrightarrow{P}}_{s}(t)\) is the position obtained by Eq. (14). The logistic chaotic mapping model is adopted in this paper, as shown in Eq. (20), \({\text{z}}({\text{t}})\) is a chaotic variable whose initial value is 0.152, and \(\upmu \) is 4. Finally, the position \({P}_{s}^{\prime}(t)\) is compared with \({\overrightarrow{P}}_{s}(t)\) in terms of fitness. If the fitness of \({P}_{s}^{\prime}(t)\) is less than that of \({\overrightarrow{P}}_{s}(t)\), maintain the current position \({P}_{s}^{\prime}(t)\); otherwise, \({P}_{s}^{\prime}(t)\) will be abandoned, as expressed by Eq. (21).
3.4 Pseudo-Code and Flowchart of ISOA
In this section, the pseudocode of the ISOA is provided based on the improvement strategies of the previous three sections. And the flowchart of the ISOA is shown in Fig. 4.

4 Experimental Simulation and Result Analysis
Section 4 consists of five parts. Section 4.1 introduces the basic information of the test functions and the experimental environment; A comparison of the ISOA with the standard SOA and other standard optimization algorithms is in Sect. 4.2; In Sect. 4.3, the ISOA is compared with other improved seagull optimization algorithms, including ISOA-1 (introducing strategy (1), ISOA-2 (introducing strategy 1 and strategy (2), BSOA [23] and WSOA [24]. Section 4.4 makes a comparison of convergence curves of all the algorithms. In Sect. 4.5, a comparison of MAE of the algorithms is presented to further verify the optimization ability and stability of the ISOA.
4.1 Experimental Environment and Benchmark Functions
Twelve benchmark functions are utilized in this paper. F1–F4 are single-peak test functions mainly utilized to test the search ability and convergence velocity of an algorithm. F5–F12 are multi-peak test functions, among which F9–-F12 are fixed-dimensional. The multi-peak test functions have many local minimums in the search space and are used to verify the ability of an algorithm to jump out of the local minima. Table 1 illustrates the basic information about the test functions. The population size (N) for all algorithms is 30 and the maximum number of iterations (\({T}_{maxitera}\)) is 500. Each algorithm is independently run 30 times to obtain four indexes: the minimum (Best), the maximum (Worst), average (Ave) and standard deviation (Std). The experiments were performed in MATLAB R2020b and on a computer having an Intel(R) Core (TM) i5-7200U CPU, 8 GB of RAM, and 64-bit Windows 10 operating system.
4.2 Comparison with Standard Optimization Algorithms
We compare the ISOA with the ant lion optimization algorithm (ALO), butterfly optimization algorithm (BOA), grey wolf optimization algorithm (GWO), whale optimization algorithm (WOA) and standard SOA. The parameter settings are the same as in the corresponding references, listed in Table 2. Table 3 shows the comparison results on 12 test functions. The value in bold indicates the best result in a row.
According to Table 3, only the ISOA can converge to the theoretical optimum values in the F1–F4 tests among all the algorithms, moreover, it has the smallest standard deviations. This demonstrates that the ISOA has a great global optimization capability and stability in solving single-peak functions. Among the multi-peak functions, the ISOA performs the best in the F5, F7, F8, F10 and F12 tests, in terms of the four indexes. Both the ISOA and WOA converge to the theoretical optimum in the F6 test. The running result of the ISOA is slightly inferior to WOA and GWO in the F9 test. In the F11 test, although the ISOA has a slightly worse standard value than GWO, it performs better in terms of the other indexes, especially Ave. In general, the ISOA has better optimization ability and stronger stability than the other algorithms.
4.3 Comparison with Improved Seagull Optimization Algorithms
To further validate the effectiveness of the algorithm, the ISOA is compared experimentally with other improved seagull optimization algorithms, including ISOA-1, ISOA-2, BSOA and WSOA. The ISOA-1 is the algorithm improved only by the strategy proposed in Sect. 3.1. The ISOA-2 is the algorithm improved by the strategies in Sects. 3.1 and 3.2. BSOA and WSOA are recent related algorithms proposed in Refs. [23] and [24] respectively. Table 4 illustrates the test results of the algorithms. The value in bold indicates the best result in a row.
According to Table 4, the ISOA has better performance than the SOA, ISOA-1, and ISOA-2 on all the functions except for F8, and ranks second on the function F8, while the SOA has the worst performance among the four algorithms. This also implies that each of the strategies proposed in this paper is valid in improving the optimization performance of the SOA. Especially, the ISOA-1 can reach the theoretical optimum in the F6 test. The ISOA-2 can converge to the optimal values in the F1–F4 and F6 tests. The ISOA can reach the theoretical optimum values in the F1–F6, F10, and F12 tests.
The ISOA performs better in the F1–F4, F7–12 tests than the BSOA and WSOA. And the three algorithms perform nearly the same in the F6 test. In the F5 test, the ISOA converges to the theoretical optimal solution in terms of the index Best, while ranks second in the Ave and Std. On the whole, the ISOA has strong competitiveness in search ability and stability.
4.4 Comparison of Convergence Curves
The convergence curves of all algorithms in the F1–F12 tests are shown in Fig. 5. From Fig. 5, the ISOA has the fastest convergence rate and the highest convergence accuracy in the F1–F4 tests. In particular, the ISOA can converge to the optimum within about 380 iterations in the F1 test. In the F5–F12 tests, the ISOA still converges dramatically faster than the comparison algorithms except for function F8. In the F8 test, the ISOA performs slightly worse in the early part of the test, but better in the later part. Especially in the F10–F12 tests, ISOA converges to the optimal value within less than 200 iterations. It can also be found in Fig. 5 that the comparison algorithms such as BSOA and WSOA easily fall into the local optimums, and their capability to jump out of the local optimums is worse than ISOA’s. All above shows that the ISOA has faster convergence speed and stronger global exploration and local exploitation ability.
4.5 Sorting by Mean Absolute Error (MAE)
Now the ISOA is compared with the published algorithms from Sects. 4.2 and 4.3 in terms of MAE. The MAE is an indicator used to describe the gap between the actual optimum value of an algorithm and the theoretical optimum value, which is expressed as follows.
where, \({\text{N}}\) is the number of test functions selected;\({{\text{F}}}_{{\text{i}},{\text{best}}}\) is the average value of the results acquired by running algorithms for 30 times on the i-th test function; and \({\overline{{\text{F}}} }_{{\text{i}}}\) is the theoretical optimal value in the i-th test function. Table 5 shows the sorted MAE values. The ISOA has the smallest MAE value, i.e., the optimization result of the ISOA is the closest to the theoretical optimal value. This further indicates that the ISOA has better convergence accuracy.
5 Engineering Applications
This section verifies the advantages of the ISOA in optimizing four engineering design problems with different complexities. Two types of algorithms are selected for comparison tests, including the standard algorithms and improved algorithms. All algorithms are run independently 30 times, with the population size and the number of iterations set to 30 and 1000 respectively, and all the comparisons are based on the best-case results.
5.1 Three-bar Truss Design Problem
The three-bar truss design problem [34] is a typical problem in engineering applications, whose optimization objective is to minimize the volume of the truss structure under certain conditions. Figure 6 shows the model structure diagram of the three-bar truss. The model uses two variables \({A}_{1}\) and \({A}_{2}\) to modify the cross-sectional area of the rods. The cross-sectional area of the two sides is \({A}_{1}\), and the cross-sectional area of the middle rod is \({A}_{2}\). The objective function and constraint conditions are as follows:
Consider \(x=[{x}_{1} {x}_{2}]=[{A}_{1} {A}_{2}]\),
where, \(0<{x}_{1},{x}_{2}<1\), other parameters: \(l=100\) cm, \(p=2KN/{cm}^{2}\), \(\delta =2KN/{cm}^{2}\).
The ISOA is compared with other algorithms proposed in recent years, including ALO [10], WOA [11], AOA [35], SCA [18], HHO [36], MFO [37], m-SCA [18], MMPA [38], GSA-GA [39], AGWO [40], BWOA [41], NCCO [42], PSO-DE [43], DEDS [44] and ESOA [20]. As shown in Table 6, the convergence result of the ISOA is the best, and the ISOA has stronger optimization accuracy. The optimal solution is 263.8956 and the corresponding optimum variable is \(x=[0.78812, 0.4098\)]. Figure 7 gives the convergence curve of the ISOA, indicating that it takes only 400 iterations to converge to the optimum value, and the ISOA has a fast convergence speed.
5.2 Pressure Vessel Design Problem
The optimization objective of the pressure vessel design problem [45] is to minimize the total manufacturing cost consisting of material cost, molding cost and welding cost of cylindrical vessel under four constraints. Figure 8 shows the structure diagram of the pressure vessel model. This design problem involves four optimization variables, which are the thickness of the shell (\({T}_{s}\)), the thickness of the side of the head (\({T}_{h}\)), cylinder radius (\({\text{R}}\)) and the length of the cylindrical shell (\({\text{L}}\)), where R and L are both continuous variables. The specific mathematical expressions are as follows:
Consider \(x=[{x}_{1} {x}_{2} {x}_{3} {x}_{4}]=[{T}_{s} {T}_{h} R L]\),
In tackling this problem, the ISOA is compared with the standard optimization algorithms, including PSO [6], SOA [18], GWO [9], WOA [11], AOA [35], and SOS [46], and other recent related improved optimization algorithms, including ESOA [20], WSOA [24], RCSA [47], IDARSOA [48], TLMPA [49], EEGWO [50], hHHO-SCA [51], MMPA [38] and ASOINU [52]. According to Table 7, the lowest manufacturing cost for the pressure vessel solved by the ISOA is 5805.7158, and the corresponding optimum variable value is \(x=[0.7735698, 0.3679545, 41.59672, 182.9594]\). The ISOA has the best result among all the algorithms, showing its strong competitiveness in searching optimal solution. As shown by the convergence curve of the ISOA in Fig. 9, the ISOA converges rapidly in the initial stage, jumps out of the local optimum within only about 400 iterations, and reaches the optimal solution within only about 480 iterations.
5.3 Welded Beam Design Problem
The optimization objective of the welded beam design problem [53] is to minimize the manufacturing cost subject to seven constraint conditions. This design problem involves four variables, which are weld thickness (h), cleat length (l), beam height (t) and beam thickness (b), as illustrated in Fig. 10. It also involves four functions \(\uptau \), \(\upsigma \), \(\updelta \),\({ P}_{c}\), which denote the beam bending stress, shear stress of the welded beam, the deflection at the end of the beam, and bar buckling load respectively. The following is the mathematical model of the problem:
Consider \(x=[{x}_{1} {x}_{2} {x}_{3} {x}_{4}]=[h l t b]\),
where, \(0.1\le {x}_{1}\le 2, 0.1\le {x}_{2}\le 10, 0.1\le {x}_{3}\le 10, 0.1\le {x}_{4}\le 2\),
The ISOA is compared with the algorithms proposed recently, including HWOANM [14], WSOA [24], IDARSOA [48], BFOA [54], hHHO-SCA [51], GSA [7], SCA [18], SBO [55], HHO [36], T-cell [56], HEAA [57], Random [58] and Coello [59], and the experimental results are illustrated in Table 8. The optimization result of the ISOA is superior to the others except for HWOANM, with an average improvement of 14.67%. Although the ISOA ranks second in optimization result, it converges to the optimal solution within only about 500 iterations, while the HWOANM takes 2300 iterations [14], as shown by the convergence curve in Fig. 11. The ISOA also has advantage in addressing the complex engineering problem.
5.4 Speed Reducer Design Problem
The speed reducer design problem [60] is a classical engineering optimization problem. The optimization objective of this problem is to minimize the weight of a reducer under inequality constraints. The constraints are with respect to bending stress of the gear, surface pressure, lateral deflection of the shaft and pressure in the shaft, and involve 7 optimization variables, including the width (\({\text{b}}\)), the tooth module (\({\text{m}}\)), the number of teeth in the pinion (\({\text{p}}\)), the length of the first shaft between the bearings (\({l}_{1}\)), the length of the second shaft (\({l}_{2}\)), the diameter of the first shaft (\({d}_{1}\)) and the second shaft (\({d}_{2}\)), where the number of teeth (\({\text{p}}\)) is an integer. The model structure diagram is in Fig. 12. The mathematical description of this problem is shown below:
Consider \(x=[{x}_{1} {x}_{2} {x}_{3} {x}_{4} {x}_{5} {x}_{6} {x}_{7}]=[{b m p {l}_{1} {l}_{2} d}_{1} {d}_{2}]\),
where,\(2.6\le {x}_{1}\le 3.6,\) \(0.7\le {x}_{2}\le 0.8,\) \(17\le {x}_{3}\le 28,\) \(7.3\le {x}_{4}\le 8.3,\) \(7.3\le {x}_{5}\le 8.3,\) \(2.9\le {x}_{6}\le 3.9,\) \(5.0\le {x}_{7}\le 5.5\).
The ISOA is compared with both the standard algorithms and the latest algorithms, including PSO [6], SOA [18], GWO [9], AOA [35], SHO [61], CA [62], ESOA [20], hHHO-SCA [51], IAFOA [63], IPSO [64], IDARSOA [48], QOCSOS [52], ASOINU [52] and ISCA [65]. The solution to this design problem by the ISOA is 2973.91750, the optimum variables is \(x=[3.40385, 0.7, 17, 7.74585, 7.76495, 3.32186, 5.25780]\). From Table 9, the ISOA provides lighter weight of the speed reducer compared to other algorithms. Moreover, the ISOA has fast convergence speed, converging to the optimal solution within only 170 iterations, as shown by the convergence curve in Fig. 13. The ISOA has strong competitiveness in solving complex engineering design problems.
6 Conclusions and Future works
This paper presented an improved seagull optimization algorithm named ISOA, by combining a variety of improvement strategies to overcome the drawbacks of slow convergence, poor ability to balance global and local search, and single search mode. Firstly, the strategy of adding spiral factor to the spiral radius in the attack stage enables search agents to adjust the search radius with the increase of the iteration number, so that the ISOA can not only converge quickly in the early stage but also avoid missing the optimal solution in the late stage caused by an excessively large radius. The second strategy of utilizing dynamic adaptive weight factors adjusts the proportion of best individuals to achieve equal emphasis on global exploration and local exploitation. Finally, the chaotic local search strategy is added to update the algorithm twice, expanding the search scope, and improving the capability to jump out of the local optimal.
The comprehensive comparative experiments on 12 benchmark test functions, including single-peak and multi-peak functions, show that the ISOA has greatly enhanced the optimization accuracy and convergence rate of the original SOA, and has strong competitiveness among the recent related optimization algorithms. Moreover, the ISOA solves 4 engineering optimization problems of the three-bar truss design, pressure vessel design, welded beam design and speed reducer design. The experimental results show that the ISOA generally offers better solutions, and has a fast convergence speed.
In future works, the proposed ISOA and strategies will be applied to solve optimization problems in practical fields, such as UAV path planning, inventory control and resource allocation. For instance, one of our ongoing work is to apply ISOA to multi-scenario and multi-obstacle UAV path planning, and we have made some progress. In addition, another research direction worth being further explored is an application of ISOA to data science such as differential privacy.
Data Availability
Not applicable.
References
Yang, X.S.: Nature-inspired optimization algorithms: challenges and open problems. J. Comput. Sci. 46, 101104 (2020). https://doi.org/10.1016/j.jocs.2020.101104
Wolpert, D.H., Macready, W.G.: No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1(1), 67–82 (1997). https://doi.org/10.1109/4235.585893
Dziwinski, P., Bartczuk, L.: A new hybrid particle swarm optimization and genetic algorithm method controlled by fuzzy logic. IEEE Trans. Fuzzy Syst. 28, 1140–1154 (2019). https://doi.org/10.1109/TFUZZ.2019.2957263
Steinbrunn, M., Moerkotte, G., Kemper, A.: Heuristic and randomized optimization for the join ordering problem. VLDB J. 6(3), 8–17 (1997). https://doi.org/10.1007/s007780050040
Dorigo, M., Birattari, M., Stutzle, T.: Ant colony optimization. IEEE Comput. Intell. Mag. 1, 28–39 (2006). https://doi.org/10.1109/MCI.2006.329691
Kennedy, J., Eberhart, R.: Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks. 4, 1942–1948(1995). https://doi.org/10.1109/ICNN.1995.488968
Rashedi, E., Nezamabadi-pour, H., Saryazdi, S.: GSA: a gravitational search algorithm. Inform. Sci. 179(13), 2232–2248 (2009). https://doi.org/10.1016/j.ins.2009.03.004
Gandomi, A.H., Yang, X.S., Alavi, A.H.: Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng. Comput. 29(1), 17–35 (2013). https://doi.org/10.1007/s00366-011-0241-y
Mirjalili, S., Mirjalili, S.M., Lewis, A.: Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61 (2014)
Mirjalili, S.: The ant lion optimizer. Adv. Eng. Softw. 83, 80–98 (2015). https://doi.org/10.1016/j.advengsoft.2015.01.010
Mirjalili, S., Lewis, A.: The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67 (2016). https://doi.org/10.1016/j.advengsoft.2016.01.008
Xue, J., Shen, B.: A novel swarm intelligence optimization approach: sparrow search algorithm. Syst. Sci. Control Eng. 8(1), 22–34 (2020). https://doi.org/10.1080/21642583.2019.1708830
Arora, S.: Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. A Fusion Found. Methodol. Appl. 23(3), 715–734 (2019). https://doi.org/10.1007/s00500-018-3102-4
Yildiz, A.R.: A novel hybrid whale-nelder-mead algorithm for optimization of design and manufacturing problems. Int. J. Adv. Manuf. Technol. 105, 5091–5104 (2019). https://doi.org/10.1007/s00170-019-04532-1
Dahmani, S., Yebdri, D.: Hybrid algorithm of particle swarm optimization and grey wolf optimizer for reservoir operation management. Water Resour. Manage 34, 4545–4560 (2020). https://doi.org/10.1007/s11269-020-02656-8
Chen, H., Peng, Q., Li, X., et al.: An efficient negative correlation gravitational search algorithm. In: 2018 IEEE International Conference on Progress in Informatics and Computing (PIC), pp. 73–79 (2018). https://doi.org/10.1109/PIC.2018.8706274
Gupta, S., Deep, K.: A memory-based grey wolf optimizer for global optimization tasks. Appl. Soft Comput. 93, 106367 (2020). https://doi.org/10.1016/j.asoc.2020.106367
Gupta, S., Deep, K.: A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst. Appl. 119, 210–230 (2019). https://doi.org/10.1016/J.ESWA.2018.10.050
Dhiman, G., Kumar, V.: Seagull optimization algorithm: theory and its applications for large- scale industrial engineering problems. Knowl.-Based Syst. 165(2), 169–196 (2019). https://doi.org/10.1016/j.knosys.2018.11.024
Che, Y., He, D.: An enhanced seagull optimization algorithm for solving engineering optimization problems. Appl. Intell. 52, 13043–13081 (2022). https://doi.org/10.1007/s10489-021-03155-y
Weina, Q., Damin, Z., Dexin, Y., et al.: Seagull optimization algorithm based on nonlinear inertia weight. J. Chin. Comp. Syst. 43(01), 10–14 (2022). https://doi.org/10.3969/j.issn.1000-1220.2022.01.002
Aijun, Y., Kaicheng, H.: Improvement strategy and its application to improve the optimization ability of seagull optimization algorithm. Inform. Control. 51(6), 688–698 (2022). https://doi.org/10.13976/j.cnki.xk.2022.1438
Cao, Y., Li, Y., Zhang, G., et al.: Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Rep. 5, 1616–1625 (2019). https://doi.org/10.1016/j.egyr.2019.11.013
Che, Y., He, D.: A hybrid whale optimization with seagull algorithm for global optimization problems. Math. Probl. Eng. 2021, 1–31 (2021). https://doi.org/10.1155/2021/6639671
Xia, Q., Ding, Y., Zhang, R., et al.: Optimal performance and application for seagull optimization algorithm using a hybrid strategy. Entropy 24(7), 973 (2022). https://doi.org/10.3390/e24070973
Yuyin, W.: Otsu image threshold segmentation method based on seagull optimization Algorithm. J. Phys: Conf. Ser. 1650(3), 032181 (2020). https://doi.org/10.1088/1742-6596/1650/3/032181
Jia, H., Xing, Z., Song, W.: A new hybrid seagull optimization algorithm for feature selection. IEEE Access. 7, 49614–49631 (2019). https://doi.org/10.1109/ACCESS.2019.2909945
Xu, L., Mo, Y., Lu, Y., et al.: Improved seagull optimization algorithm combined with an unequal division method to solve dynamic optimization problems. Processes. 9(6), 1037 (2021). https://doi.org/10.3390/pr9061037
Dingli, C., Hong, C., Xvguang, W.: Whale optimization algorithm based on adaptive weight and simulated annealing. Acta Electron. Sin. 47(05), 992–999 (2019). https://doi.org/10.3969/j.issn.0372-2112.2019.05.003
Rong, D., Jianling, G., Qian, Z.: Bald eagle search algorithm combining adaptive inertia weight and cauchy variation. J. Chin. Comput. Syst. (2022). https://doi.org/10.20009/j.cnki.21-1106/TP.2021-0748
Jingsen, L., Mengmeng, Y., Fang, Z.: Global search-oriented adaptive leader salp swarm algorithm. Control Decis. 36(09), 2152–2160 (2021). https://doi.org/10.13195/j.kzyjc.2020.0090
Yu, H., Yu, Y., Liu, Y., et al.: Chaotic grey wolf optimization. In: 2016 International Conference on Progress in Informatics and Computing (PIC), pp. 103–113 (2016). https://doi.org/10.1109/PIC.2016.7949476
Ji, S., Gao, S., Wang, Y., et al.: Self-Adaptive gravitational search algorithm with a modified chaotic local search. IEEE Access. 5, 17881–17895 (2017). https://doi.org/10.1109/ACCESS.2017.2748957
Ray, T., Saini, P.: Engineering design optimization using a swarm with an intelligent information sharing among individuals. Eng. Optim. 33(6), 735–748 (2001). https://doi.org/10.1080/03052150108940941
Abualigah, L., Diabat, A., Mirjalili, S., et al.: The arithmetic optimization algorithm. Comp. Methods Appl. Mech. Eng. 376, 113609 (2021). https://doi.org/10.1016/j.cma.2020
Heidari, A., Mirjalili, S., Farris, H., et al.: Harris hawks optimization: algorithm and applications. Futur. Gener. Comput. Syst. 97, 849–872 (2019). https://doi.org/10.1016/j.future.2019.02.028
Mirjalili, S.: Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 89, 228–249 (2015). https://doi.org/10.1016/j.knosys.2015.07.006
Fan, Q., Huang, H., Chen, Q., et al.: A modified self-adaptive marine predators algorithm: framework and engineering applications. Eng. Comp. 38, 3269–3294 (2022). https://doi.org/10.1007/S00366-021-01319-5
Garg, H.: A hybrid GSA-GA algorithm for constrained optimization problems. Inf. Sci. 478, 499–523 (2019). https://doi.org/10.1016/J.INS.2018.11.041
Cheng, Z., Song, H., Wang, J., et al.: Hybrid firefly algorithm with grouping attraction for constrained optimization problem. Knowl.-Based Syst. 220, 106937 (2021). https://doi.org/10.1016/j.knosys.2021.106937
Chen, H., Xu, Y., Wang, M., et al.: A balanced whale optimization algorithm for constrained engineering design problems. Appl. Math. Model. 71, 45–59 (2019). https://doi.org/10.1016/j.apm.2019.02.004
Galvez, J., Cuevas, E., Hinojosa, S., et al.: A reactive model based on neighborhood consensus for continuous optimization. Expert Syst. Appl. 121, 115–141 (2019). https://doi.org/10.1016/j.eswa.2018.12.018
Liu, H., Cai, Z., Wang, Y.: Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 10, 629–640 (2010). https://doi.org/10.1016/j.asoc.2009.08.031
Zhang, M., Luo, W., Wang, X.: Differential evolution with dynamic stochastic selection for constrained optimization. Inf. Sci. 178, 3043–3074 (2008). https://doi.org/10.1016/j.ins.2008.02.014
Askari, Q., Younas, I., Saeed, M.: Political optimizer: a novel socio-inspired meta-heuristic for global optimization. Knowl.-Based Syst. 195, 105709 (2020). https://doi.org/10.1016/j.knosys.2020.105709
Cheng, M.Y., Prayogo, D.: Symbiotic organisms search: a new metaheuristic optimization algorithm. Comput. Struct. 139, 98–112 (2014). https://doi.org/10.1016/j.compstruc.2014.03.007
Thirugnanasambandam, K., Prakash, S., Subramanian, V., et al.: Reinforced cuckoo search algorithm-based multimodal optimization. Appl. Intell. 49(6), 2059–2083 (2019). https://doi.org/10.1007/s10489-018-1355-3
Yu, H., Qiao, S., Heidari, A.A., et al.: Individual disturbance and attraction repulsion strategy enhanced seagull optimization for engineering design. Mathematics. 10(2), 276 (2022). https://doi.org/10.3390/math10020276
Zhong, K., Luo, Q., Zhou, Y., et al.: TLMPA: teaching-learning-based marine predators algorithm. AIMS. Math. 6(2), 1395–1442 (2021). https://doi.org/10.3934/math.2021087
Long, W., Jiao, J., Liang, X., et al.: An exploration enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 68, 63–80 (2018). https://doi.org/10.1016/j.engappai.2017.10.024
Kamboj, V.K., Nandi, A., Bhadoria, A., et al.: An intensify Harris hawks optimizer for numerical and engineering optimization problems. Appl. Soft Comput. 89, 106018 (2020). https://doi.org/10.1016/j.asoc.2019.106018
Pu, S.A., Hao, L.B., Yong, Z.A., et al.: An intensify atom search optimization for engineering design problems. Appl. Math. Model. 89, 837–859 (2021). https://doi.org/10.1016/j.apm.2020.07.052
Kabir, M.I., Bhowmick, A.K.: Applicability of North American standards for lateral torsional buckling of welded i-beam. J. Constr. Steel Res. 147, 16–26 (2018). https://doi.org/10.1016/j.jcsr.2018.03.029
Mezura-Montes, E., Hernández-Ocana, B.: Modified bacterial foraging optimization for engineering design. Proc. Artif. Neural Netw. Eng. Confer. 19, 357–364 (2009). https://doi.org/10.1115/1.802953.paper45
Moosavi, S., Bardsiri, V.K.: Satin bowerbird optimizer: a new optimization algorithm to optimize anfis for software development effort estimation. Eng. Appl. Artif. Intell. 60, 1–15 (2017). https://doi.org/10.1016/j.engappai.2017.01.006
Aragón, V.S., Esquivel, S.C., Coello, C.: A modified version of a t-cell algorithm for constrained optimization problems. Int. J. Numer. Meth. Eng. 84(3), 351–378 (2010). https://doi.org/10.1002/nme.2904
Wang, Y., Cai, Z., Zhou, Y., et al.: Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique. Struct. Multidiscip. Optim. 37(04), 395–413 (2009). https://doi.org/10.1007/s00158-008-0238-3
Ragsdell, K.M., Phillips, D.T.: Optimal design of a class of welded structures using geometric programming. ASME. J. Eng. Ind. 98(3), 1021–1025 (1976). https://doi.org/10.1115/1.3438995
Coello, C.: Theoretical and numerical constraint handling techniques used with evolutionary algorithms: a survey of the state of the art. Comput. Methods Appl. Mech. Eng. 191(11–12), 1245–1287 (2002). https://doi.org/10.1016/S0045-7825(01)00323-1
Sadollah, A., Bahreininejad, A., Eskandar, H., et al.: Mine blast algorithm: a new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 13(5), 2592–2612 (2013). https://doi.org/10.1016/j.asoc.2012.11.026
Dhiman, G.: ESA: a hybrid bio-inspired metaheuristic optimization approach for engineering problems. Eng. Comput. 37(1), 323–353 (2021). https://doi.org/10.1007/S00366-019-00826-W
Canayaz, M., Karci, A.: Cricket behaviour-based evolutionary computation technique in solving engineering optimization problems. Appl. Intell. 44(2), 362–376 (2016). https://doi.org/10.1007/S10489-015-0706-6
Wu, L., Liu, Q., Tian, X.: A new improved fruit fly optimization algorithm IAFOA and its application to solve engineering optimization problems. Knowl.-Based Syst. 144, 153–173 (2017). https://doi.org/10.1016/J.KNOSYS.2017.12.031
Machado-Coelho, T.M., Machado, A.M.C., Jaulin, L., et al.: An interval space reducing method for constrained problems with particle swarm optimization. Appl. Soft Comput. 59, 405–417 (2017). https://doi.org/10.1016/j.asoc.2017.05.022
Gupta, S., Deep, K., Moayedi, H., et al.: Sine cosine grey wolf optimizer to solve engineering design problems. Eng. Comp. 37, 3123–3149 (2021). https://doi.org/10.1007/s00366-020-00996-y
Acknowledgements
The authors thank the anonymous reviewers for their thoughtful suggestions and comments.
Funding
This work was partly supported by the National Natural Science Foundation of China under Grant Nos. 12371508, 11701370.
Author information
Authors and Affiliations
Contributions
PH and JL provided the main concept of this work. PH and FN wrote the main script text. PH and LZ made the experiments. All authors reviewed the manuscript. Corresponding author: Correspondence to JL.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hou, P., Liu, J., Ni, F. et al. Hybrid Strategies Based Seagull Optimization Algorithm for Solving Engineering Design Problems. Int J Comput Intell Syst 17, 62 (2024). https://doi.org/10.1007/s44196-024-00439-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44196-024-00439-2