1 Introduction

The study of numerical solutions is important, which is an approximation to the solution of a mathematical equation, often used where analytical solutions are hard or impossible to find. Numerical solutions to linear and non-linear Robin BVPs and Bratu-type equations play a significant role in contemporary mathematics research. Computer systems are constructed by analyzing BVPs and Bratu-type equations, calculating numerical solutions, and identifying convergent alternatives. Recently, many methods have been submitted to find numerical solutions, you can read these papers [1,2,3,4,5].

Lately, Chebyshev polynomials have emerged as an extremely powerful approximation for numerical analysis under orthogonality constraints. Chebyshev polynomials play an important role in approximation theory due to their minimality properties and direct linkages to the Laurent and Fourier series with continuous and discrete orthogonality in function spaces [6,7,8,9,10,11,12]. This research proposes the numerical solution to linear and non-linear for Bratu-type equations and Robin BVPs applying shifted Chebyshev tau and collocation methods. The tau and collocation methods are easily applicable to solve any Differential equations with their types. You can see that in [13,14,15].

Spectral methods become one of the greatest popular numerical algorithms employed to solve many forms of differential equations. These methods have certain advantages over other ways. The spectral approach has a pair of basis functions: test and trial functions. These two types of functions are frequently described in terms of appropriate orthogonal polynomials or a combination of them. The test and trial functions are selected based on the method used. Finite-difference approaches involve approximating the function and its derivatives with a local polynomials interpolant, whereas spectral methods are global. Spectral approaches can yield exponential convergence with solutions, making them useful in chemical and physical applications that demand solutions that have several decimal places of accuracy. These papers [16,17,18] describe some of the major applications of spectral techniques. The spectral Galerkin methodology selects two coincident pairs of polynomials that fulfill the problem’s fundamental conditions. The Galerkin approach is based on establishing certain combinations of orthogonal polynomials that accomplish the differential equation’s initial or boundary conditions, and then forcing the residual to be orthogonal with the chosen basis functions. This method is particularly good at dealing with linear boundary value problems, and systems that result from its use can be easily and efficiently inverted. In this paper, we apply shifted and modified shifted Chebyshev polynomials as bases to get an approximate solution of Bratu-type equations and Robin boundary value problems, respectively.

The Robin problem, sometimes known as the third boundary value problem, is a combination of the Neumann and Dirichlet conditions, which are fundamental BVPs that exists in complex analysis. There are many authors solving BVPs with Robin conditions, such as in [19] which used the Adomian decomposition method, and others in [20,21,22,23]. Robin boundary conditions occur in a variety of applications, including heat transport and electromagnetic problems, these Robin conditions are known as impedance and convective boundary conditions, respectively, as discussed within [24]. The Galerkin approximation and Bernoulli polynomial for resolving Robin boundary condition (BC) problems with linear and non-linear were investigated in [25]. The diagonal block approach for solving differential equations has been extensively investigated in prior publications. These involve discussions on how to resolve first-order differential equations within [26]. In [27], also the authors used the diagonal block approach to solve ordinary differential equations of second order.

Bratu-type equations often serve to compare and evaluate numerical solutions like polynomial pseudospectral algorithms [28], the homotopy analysis method [29], Laplace transform decomposition algorithms [30, 31], Derivative Legendre spectral method [32], and an Adomian decomposition technique [33,34,35] can be efficiently used on non-linear equations of this kind.

The Bratu’s BVP with one-dimensional planar coordinates is represented as

$$\begin{aligned} \mathcal {L}''(\chi )+\sigma \, e^{\mathcal {L}(\chi )}=0, \quad \chi \in [0,1], \end{aligned}$$
(1)

based on BCs:

$$\begin{aligned} \mathcal {L}(1)=\mathcal {L}(0)=0, \end{aligned}$$
(2)

analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=\ln {\left( \frac{\cosh {\left( \frac{\nu \,\chi }{2}-\frac{\nu }{4}\right) }}{\cosh {(\frac{\nu }{4})}}\right) ^{-2}}, \end{aligned}$$
(3)

where \(\nu\) is distributed as

$$\begin{aligned} \nu =\sqrt{2\,\sigma }\,\cosh {\left(\frac{\nu}{4}\right) },\quad \quad \sigma > 0. \end{aligned}$$
(4)

This equation was applied for modeling the fuel explosion in the thermal combustion theory, a combustion problem in a numerical slab, and Chandrasekhar model of the universe’s expansion. It promotes a thermal reaction operating in a hard material, which is dependent on an equilibrium of chemically produced heat and heat transport via conduction [35,36,37,38].

A problem of two-dimensional Bratu represents an elliptic partial differential equation, applicable to homogeneous Dirichlet BCs. This problem forms as

$$\begin{aligned} \nabla ^2 \mathcal {L} (\chi ,\tau )+\mu \,\mathcal {L} (\chi ,\tau )=f(\chi ,\tau ), \quad \zeta =[0,1]\times [0,1], \end{aligned}$$
(5)

where the boundary conditions:

$$\begin{aligned} \mathcal {L} (\chi ,\tau )=0, \quad on \, \partial \zeta , \end{aligned}$$
(6)

where \(\zeta\) is a restricted domain about a boundary \(\partial \zeta\).

Several numerical and analytical methods were used to tackle problems (1) and (5). For problem (1), the authors in [39] turn this problem into the non-linear starting value problem, which they then solve using the Lie-group shooting approach. In [40], the authors give a numerical method that uses the decomposition technique to deal with a type of non-linear BVPs encompassing Bratu one-dimensional and Troesch problems. The analytical solution to problem (5) is unknown. Thus, a numerical method for a solution is required.

This paper has been organized as follows: Sect. 2 provides an overview of Chebyshev polynomials about the second-kind and their fundamental features. In Sect. 3, the linear and non-linear Robin BVPs are solved numerically using the spectral tau method. Also, elliptic partial differential equations are solved in Sect. 4. Section 5 analyses the convergence and error of the suggested approach. Section 6 proposes numerical results and comparisons to validate our proposed method. Section 7 includes a small outline paper.

2 Overview of the Chebyshev polynomials about the second-kind

This section provides an overview of the shifted and modified shifted Chebyshev polynomials about the second-kind, as well as several helpful relations and power forms.

The Polynomials of Chebyshev of the second-kind \(\vartheta _{\iota }(\chi )\) are famous polynomials given in the interval \([-1,1]\) with the relation [41]:

$$\begin{aligned} \vartheta _{\iota }(\chi )=\frac{\sin {(\iota \,\nu +\nu )}}{\sin {\nu }}, \quad 0\le \nu \le \pi \quad and \quad \chi =\cos {\nu }. \end{aligned}$$
(7)

The polynomials \(\vartheta _{\iota }(\chi )\) are created via the basic recurrence relations

$$\begin{aligned} \vartheta _{\iota -1}(\chi )=2\, \chi \,\vartheta _{\iota -2}(\chi )-\vartheta _{\iota -3}(\chi ), \quad \iota =3,\,4,\,\dots , \end{aligned}$$
(8)

when the initial polynomials are provided as

$$\begin{aligned} \vartheta _{0}(\chi )=1, \quad \vartheta _{1}(\chi )=2\, \chi . \end{aligned}$$
(9)

The weight function about the second-kind Chebyshev \(\varphi (\chi )\) presented by

$$\begin{aligned} \varphi (\chi )=\sqrt{1-\chi ^2}, \end{aligned}$$
(10)

then the orthogonality of \(\vartheta _{\iota }(\chi )\) is

$$\begin{aligned} \displaystyle \int _{-1}^{1} \vartheta _{\iota }(\chi )\,\vartheta _{j}(\chi )\,\varphi (\chi )\,d\chi = {\left\{ \begin{array}{ll}\frac{\pi }{2},&{} \iota =j,\\ 0,&{} \iota \ne j.\\ \end{array}\right. } \end{aligned}$$
(11)

The power form of \(\vartheta _{\iota }(\chi )\) is

$$\begin{aligned} \vartheta _{\iota }(\chi )=\displaystyle \sum _{s=0}^{\lceil \frac{\iota }{2}\rceil }\frac{(-1)^s\,(\iota -s)!}{s!\,2^{2\,s-\iota }\,(\iota -2\,s)!}\, \chi ^{\iota -2\,s}, \quad \iota > 0, \end{aligned}$$
(12)

such that \(\lceil \frac{\iota }{2}\rceil\) is the lowest integer larger than or equal to the specified value of \((\frac{\iota }{2})\).

Theorem 1

[42] For Chebyshev polynomials about the second-kind, the first derivative yields by

$$\begin{aligned} \vartheta _{\iota }'(\chi )= \displaystyle \sum _{\begin{array}{c} z=0 \\ \, (z+\iota )\, odd \end{array}}^{\iota -1} 2\,(z+1)\, \vartheta _{z}(\chi ), \quad \iota \ge 0. \end{aligned}$$
(13)

In our work, we use the polynomials about the second-kind Chebyshev on the interval [0, 1] where we transform \(\chi\) into \(2\,\chi -1\), so the polynomial becomes \(\vartheta ^{*}_{\iota }(\chi )\)

$$\begin{aligned} \vartheta ^{*}_{\iota }(\chi )=\vartheta _{\iota }\left( 2\,\chi -1\right) , \end{aligned}$$
(14)

or for the polynomials of the second-kind Chebyshev on the interval [a, b], we have

$$\begin{aligned} \vartheta ^{*}_{\iota }(\chi )=\vartheta _{\iota }\left( \frac{2\,\chi -a-b}{b-a}\right) . \end{aligned}$$
(15)

Shifted Chebyshev polynomials are polynomials that are orthogonal for a weight function \(\varphi ^{*}(\chi )\)

$$\begin{aligned} \displaystyle \int _{0}^{1} \vartheta ^{*}_{k}(\chi )\,\vartheta ^{*}_{l}(\chi )\,\varphi ^{*}(\chi )\,d\chi = {\left\{ \begin{array}{ll}\frac{\pi }{8},&{} k=l,\\ 0,&{} k\ne l,\\ \end{array}\right. } \end{aligned}$$
(16)

where

$$\begin{aligned} \varphi ^{*}(\chi )=\sqrt{\chi -\chi ^{2}}. \end{aligned}$$
(17)

The recurrence relation of shifted Chebyshev polynomials for the second-kind is defined as

$$\begin{aligned} \vartheta ^{*}_{\iota }(\chi )=\frac{1}{4\,\chi -2}\left( \vartheta ^{*}_{\iota +1}(\chi )+\vartheta ^{*}_{\iota -1}(\chi )\right) , \quad \iota =1,\,2,\,\dots , \end{aligned}$$
(18)

in addition to the initial conditions

$$\begin{aligned} \vartheta ^{*}_{0}(\chi )=1, \quad \vartheta ^{*}_{1}(\chi )=2\,(2\,\chi -1). \end{aligned}$$
(19)

The second-kind for shifted Chebyshev polynomials’ power form is denoted by

$$\begin{aligned} \vartheta ^{*}_{\iota }(\chi )=\displaystyle \sum _{s=0}^{\iota }\frac{(-1)^s\,(2\,\iota -s+1)!}{s!\,2^{2\,s-2\,\iota }\,(2\,\iota -2\,s+1)!}\, \chi ^{\iota -s}, \quad i > 0, \end{aligned}$$
(20)

and its explicit inversion formula is as follows

$$\begin{aligned} \chi ^{s}=\frac{4\,\Gamma \left( s+\frac{3}{2}\right) }{\sqrt{\pi }}\,\displaystyle \sum _{k=0}^{s}\frac{s!\,(k+1)!}{k!\,(s-k)!\,(2+s+k)!}\, \vartheta ^{*}_{k}(\chi ), \quad s \ge 0. \end{aligned}$$
(21)

Theorem 2

[42] For shifted Chebyshev polynomials about the second-kind, the first derivative yields by

$$\begin{aligned} \left( \vartheta _{\iota }^{*}(\chi )\right) ^{(1)}= \displaystyle \sum _{\begin{array}{c} z = 0 \\ \, (z+\iota )\, odd \end{array}}^{\iota -1} 4\,(z+1)\, \vartheta ^{*}_{z}(\chi ), \quad \iota \ge 0. \end{aligned}$$
(22)

3 Linear and non-linear Robin BVPs

In this section, we introduce an overview of the Robin linear and non-linear BVPs and how to use the modified shifted Chebyshev about the second-kind polynomials to solve them.

3.1 Second-order linear BVPs involving robin conditions

We consider the following form of the second-order linear differential equation [43]

$$\begin{aligned} \mathcal {L}''(\chi )+p(\chi )\,\mathcal {L}'(\chi )+q(\chi )\, \mathcal {L}(\chi )=r(\chi ), \quad a\le \chi \le b, \end{aligned}$$
(23)

managed by non-homogeneous Robin BCs:

$$\begin{aligned} \alpha _{0}\,\mathcal {L}(a)+\beta _{0}\,\mathcal {L}'(a)=\gamma _{0}, \quad \alpha _{1}\,\mathcal {L}(b)-\beta _{1}\,\mathcal {L}'(b)=\gamma _{1}, \end{aligned}$$
(24)

or

$$\begin{aligned} \alpha _{0}\,\mathcal {L}(a)-\beta _{0}\,\mathcal {L}'(a)=\gamma _{0}, \quad \alpha _{1}\,\mathcal {L}(b)+\beta _{1}\,\mathcal {L}'(b)=\gamma _{1}, \end{aligned}$$
(25)

where \(\alpha _{0}\), \(\alpha _{1}\), \(\beta _{0}\), and \(\beta _{1}\) are non-negative constants, \(\alpha _{0}+\beta _{0} > 0\), \(\alpha _{1}+\beta _{1} > 0\), \(\alpha _{0}+\alpha _{1} > 0\), and \(\gamma _{0}\), \(\gamma _{1}\) are both finite constants.

In this article, we apply modified shifted Chebyshev polynomials \(\aleph _{p}(\chi )\) to the Robin BVP, where

$$\begin{aligned} \omega (\chi )=\aleph _{p}(\chi )=\varphi _{p}(\chi )\,\vartheta ^{*}_{p}(\chi ), \quad p=0,\,1,\,2,\,\dots , \end{aligned}$$
(26)

such that \(\varphi _{p}(\chi )\) establishes the form

$$\begin{aligned} \varphi _{p}(\chi )=\frac{1}{p+1}\,\left( \chi ^{2}+A_{p}\,\chi +B_{p}\right) , \end{aligned}$$
(27)

where \(A_{p}\) and \(B_{p}\) constitute distinct constants that make \(\aleph _{p}(\chi )\) satisfies the Conditions (24) or (25). Substituting \(\aleph _{p}(\chi )\) through (24) or (25) yields two separate linear equations with two unknowns \(A_{p}\) and \(B_{p}\)

$$\begin{aligned}{} & {} \left( \frac{\alpha _{0}\,\left( a^{2}+A_{p}\,a+B_{p}\right) }{p+1} \right) \,\vartheta ^{*}_{p}(a)+\beta _{0}\,\left( \left( \frac{2a+A_{p}}{p+1}\right) \,\vartheta ^{*}_{p}(a) + \left( \frac{a^{2}+A_{p}\,a+B_{p}}{p+1}\right) \, \vartheta ^{*\,(1)}_{p}(a) \right) =\gamma _{0}, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \left( \frac{\alpha _{1}\,\left( b^{2}+A_{p}\,b+B_{p}\right) }{p+1} \right) \,\vartheta ^{*}_{p}(b)- \beta _{1}\,\left( \left( \frac{2b+A_{p}}{p+1}\right) \,\vartheta ^{*}_{p}(b) + \left( \frac{b^{2}+A_{p}\,b+B_{p}}{p+1}\right) \, \vartheta ^{*\,(1)}_{p}(b) \right) =\gamma _{1}, \end{aligned}$$
(29)

or

$$\begin{aligned}{} & {} \left( \frac{\alpha _{0}\,\left( a^{2}+A_{p}\,a+B_{p}\right) }{p+1} \right) \,\vartheta ^{*}_{p}(a)-\beta _{0}\,\left( \left( \frac{2a+A_{p}}{p+1}\right) \,\vartheta ^{*}_{p}(a) + \left( \frac{a^{2}+A_{p}\,a+B_{p}}{p+1}\right) \, \vartheta ^{*\,(1)}_{p}(a) \right) =\gamma _{0}, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \left( \frac{\alpha _{1}\,(b^{2}+A_{p}\,b+B_{p})}{p+1} \right) \,\vartheta ^{*}_{p}(b)+ \beta _{1}\,\left( \left( \frac{2b+A_{p}}{p+1}\right) \,\vartheta ^{*}_{p}(b) + \left( \frac{b^{2}+A_{p}\,b+B_{p}}{p+1}\right) \, \vartheta ^{*\,(1)}_{p}(b) \right) =\gamma _{1}, \end{aligned}$$
(31)

which ((28) and (29)) or ((30) and (31)) immediately yields

$$\begin{aligned} A_{p}= & {} \frac{1}{\eta } \, \left( 2\,\beta _{0}\,(3\,L\,(b\,p\,S+a\,(3+p\,S))\,\alpha _{1}+2\,T\,p\,S\,(3+p\,S)\,\beta _{1}) \right. \nonumber \\- & {} \left. 3\,L\,\alpha _{0}\,(3\,L\,T\,\alpha _{1}+2\,(a\,p\,S+b\,(3+p\,S))\,\beta _{1} \right) , \end{aligned}$$
(32)

and

$$\begin{aligned} B_{p}= & {} \frac{1}{\eta } \,\left( \beta _{0}\,(3\,b\,L\,(3\,b-2\,a\,Y)\,\alpha _{1}-2\,(-3\,L^{2}+4\,a\,b\,p+2\,a\,b\,p^{2})\,Y\beta _{1}) \right. \nonumber \\- & {} \left. 3\,a\,L\,\alpha _{0}\,(-3\,L\,b\,\alpha _{1}+(3\,a-2\,b\,Y)\,\beta _{1})\right) , \end{aligned}$$
(33)

where \(\eta =\beta _{0}\,(-3\,L\,(3+2\,p\,S)\, \alpha _{1}-4\,p\,S\,(3+p\,S)\,\beta _{1})-3\,L\, \alpha _{0}\,(-3\,L\,\alpha _{1}-(3+2\,p\,S)\,\beta _{1})\ne 0\), \(S=2+p\), \(L=b-a\), \(Y=3+p\,S\), \(C=1+p\), and \(T=b+a\). In a particular case of (24) or (25), homogeneous Dirichlet conditions are established by setting \(\alpha _{0}\) = \(\alpha _{1}\) = 1, \(\beta _{0}\) = \(\beta _{1}\) = 0, and \(\gamma _{0}\) = \(\gamma _{1}\) = 0. We can define \(\aleph _{p}(\chi )\) as

$$\begin{aligned} \aleph _{p}(\chi )=\left( \frac{\chi ^{2}-T\,\chi +a\,b}{C} \right) \,\vartheta ^{*}_{p}(\chi ), \quad p=0,\,1,\,2,\,\dots . \end{aligned}$$
(34)

In case of (24), so that \(\alpha _{0}\) = \(\alpha _{1}\) = 0, \(\beta _{0}\) = 1, and \(\beta _{1}\) = -1 or in case of (25), where \(\alpha _{0}\) = \(\alpha _{1}\) = 0, \(\beta _{0}\) = -1, and \(\beta _{1}\) = 1 there are both defined as homogeneous Neumann conditions with \(\gamma _{0}\) = \(\gamma _{1}\)= 0 and that can be considered a specific case of the Robin conditions, which yields

$$\begin{aligned} \aleph _{p}(\chi )=\left( \frac{\chi ^{2}-T\,\chi +B_{p}}{C} \right) \,\vartheta ^{*}_{p}(\chi ), \quad B_{p}=\frac{2\,a\,b\,p^{2}+4\,a\,b\,p-3\,L^2}{2\,p\,S},\quad p=1,\,2,\,\dots . \end{aligned}$$
(35)

Now, we shall create an operational matrix for derivatives of modified shifted Chebyshev polynomials about the second-kind \(\aleph _{p}(\chi )\) with the Robin BCs

$$\begin{aligned} \begin{aligned}&D\aleph _{0}(\chi )=2\,\chi +A_{0},\\&D\aleph _{1}(\chi )=\frac{(S-3)\,\left( a^2+b^2\right) +2\,a\,b\,(6+S)-6\,S\,T\,\chi +6\,S\,\chi ^2}{S\,L}. \end{aligned} \end{aligned}$$
(36)

These allow us to declare and establish the main theorems, which introduce derivatives of the modified shifted Chebyshev about the second-kind polynomials.

Theorem 3

For all \(p\ge 0\), the first and second derivatives of a modified shifted Chebyshev for the second-kind polynomials are denoted as

$$\begin{aligned} \begin{aligned}&D\aleph _{p}(\chi )= \frac{-1}{2}\,\left( L\,\vartheta ^{*}_{p-1}(\chi )+ \frac{(T\,S-2\,S\,\chi )\,\vartheta ^{*}_{p}(\chi )}{C} \right) ,\\&D^{2}\aleph _{p}(\chi )= \frac{-\,\left( L\,C\,(T-2\,\chi )\, \vartheta ^{*}_{p+1}(\chi )+\left( S\,\left( a^2\,+b^2\right) -2\,a\,b\,\left( 2+p(3+2p)\right) +4\,p\,C\,\left( T\,\chi -\chi ^2\right) \right) \,\vartheta ^{*}_{p}(\chi ) \right) }{4\,C\,(a-\chi )\,(b-\chi )}. \end{aligned} \end{aligned}$$
(37)

Proof

Using the relation (34), the first derivative for \(\aleph _{p}(\chi )\) is represented by

$$\begin{aligned} \begin{aligned} D\aleph _{p}(\chi )=&\, \left( \frac{\chi ^{2}-T\,\chi +a\,b}{C} \right) \,D\vartheta ^{*}_{p}(\chi )+ \left( \frac{2\,\chi -T}{C} \right) \,\vartheta ^{*}_{p}(\chi )\\ =&\, \left( \frac{\chi ^{2}-T\,\chi +a\,b}{C} \right) \,\left( \frac{-\,\left( L\,C\,\vartheta ^{*}_{p-1}(\chi ) + p\,(T-2\,\chi )\,\vartheta ^{*}_{p}(\chi ) \right) }{2\,(a-\chi )\,(b-\chi )}\right) + \left( \frac{2\,\chi -T}{C} \right) \,\vartheta ^{*}_{p}(\chi )\\ =&\,\frac{-1}{2}\,\left( L\, \vartheta ^{*}_{p-1}(\chi ) + \frac{p\,(T-2\,\chi )\,\vartheta ^{*}_{p}(\chi )}{C} \right) +\left( \frac{2\,\chi -T}{C} \right) \,\vartheta ^{*}_{p}(\chi )\\ =&\, \frac{-1}{2}\,\left( L\, \vartheta ^{*}_{p-1}(\chi ) + (\frac{(T-2\,\chi )\,\vartheta ^{*}_{p}(\chi )}{C})\, (p+2)\right) \\ =&\, \frac{-1}{2}\,\left( L\,\vartheta ^{*}_{p-1}(\chi )+ \frac{(T\,S-2\,S\,\chi )\,\vartheta ^{*}_{p}(\chi )}{C} \right) . \end{aligned} \end{aligned}$$
(38)

The second derivative can be obtained from the last relation of the first derivative for \(\aleph _{p}(\chi )\), which is provided by

$$\begin{aligned} D^{2}\aleph _{p}(\chi )= & {} \frac{-1}{2}\,D\left( L\,\vartheta ^{*}_{p-1}(\chi )+ \frac{(T\,S-2\,S\,\chi )\,\vartheta ^{*}_{p}(\chi )}{C}\right) \nonumber \\= & {} \frac{-1}{2}\,\left( L\,D\vartheta ^{*}_{p-1}(\chi )+ \frac{(T\,S-2\,S\,\chi )\,D\vartheta ^{*}_{p}(\chi )-2\,S\,\vartheta ^{*}_{p}(\chi )}{C}\right) \nonumber \\= & {} \frac{-1}{2}\,\left( L\,\left( \frac{L\,p\,\vartheta ^{*}_{p-2}(\chi )-\frac{(p-1)\,(T-2\,\chi )\,\vartheta ^{*}_{p-1}(\chi )}{L}}{2\,(a-\chi )\,(b-\chi )}\right) \right. \nonumber \\- & {} \left. \frac{(T\,S-2\,S\,\chi )\,\left( \frac{L\,(1+p)\,\vartheta ^{*}_{p-1}(\chi )+p\,(T-2\,\chi )\,\vartheta ^{*}_{p}(\chi )}{2\,(a-\chi )\,(b-\chi )}\right) -2\,S\,\vartheta ^{*}_{p}(\chi )}{C}\right) \nonumber \\= & {} \frac{-\,\left( L\,C\,(T-2\,\chi )\, \vartheta ^{*}_{p+1}(\chi )+\left( S\,(a^2\,+b^2)-2\,a\,b\,(2+p(3+2p))+4\,p\,C\,(T\,\chi -\chi ^2)\right) \,\vartheta ^{*}_{p}(\chi ) \right) }{4\,C\,(a-\chi )\,(b-\chi )}. \qquad \end{aligned}$$
(39)

□

Theorem 4

In the special situations of (35), the first and second derivatives of the modified shifted Chebyshev for the second-kind polynomials are designated as

$$\begin{aligned} D\aleph _{p}(\chi ) = \, & {} \frac{-1}{p+1}\,\left( \frac{(3\,L^{2}-2\,p\,(a\,b\,S+S\,\chi \,(\chi -T)))\, \left( S\,D\,\vartheta ^{*}_{p}(\chi )+L\,B\,\vartheta ^{*}_{p+1}(\chi ) \right) }{p\,S\,(D-L)\,(D+L)}+D\,\vartheta ^{*}_{p}(\chi ) \right) , \nonumber \\ D^2\aleph _{p}(\chi ) = \, & {} \frac{-1}{8\,p\,B\,J^2\,G^2}\, \left( (O+2\,a\,X)\,\vartheta ^{*}_{p}(\chi ) \right. \nonumber \\{} & {} \left. + \,\frac{L\,B\,D\,(9\,L^2+4\,a\,b\,p+2\,a\,b\,p^2-2\,T\,p\,S\,\chi +2\,p\,S\,\chi ^2)\,\vartheta ^{*}_{p+1}(\chi )}{S} \right) , \end{aligned}$$
(40)

\(\forall \, p\ge 0\),

$$\begin{aligned} where {\left\{ \begin{array}{ll} W=8+p,\\ R=9+8\,p,\\ E=3+4\,p,\\ V=a^2+b^2,\\ C=1+p,\\ H=18+p\,(8+p\,R),\\ J=a-\chi ,\\ G=b-\chi ,\\ A=p\,W\,G-18\,\chi ,\\ Q=18+p\,(8-p\,E),\\ I=18+p\,W,\\ F=3+2\,p,\\ N=-b^2\,(9+2\,p\,(8+p\,F))+b\,H,\\ D=T-2\,\chi ,\\ O=9\,V+2\,a^3\,A-2\,b^3\,I\,\chi +2\,b^2\,Q\,\chi ^2+16\,b\,p^2\,B\,\chi ^3-8\,p^2\,B\,\chi ^4+2\,a^2\,N\,\chi +Q\,\chi ^2,\\ X=b^3\,p\,W+b^2\,H\,\chi -2\,b\,H\,\chi ^2+8\,p^2\,B\,\chi ^3. \end{array}\right. } \end{aligned}$$
(41)

Proof

That’s simple to demonstrate. The procedures are the same as in the earlier proof.□

The numerical formula to (23) is

$$\begin{aligned} \mathcal {L}_M(\chi )=\displaystyle \sum _{\iota =0}^M k_\iota \,\aleph _\iota (\chi )={\textbf {K}}^T\, \varvec{\aleph }(\chi ), \end{aligned}$$
(42)

such that

$$\begin{aligned} {\textbf {K}}={[k_0,\, k_1,\, \dots ,\, k_{M}]}^T, \quad \varvec{\aleph }(\chi )=[\aleph _0(\chi ),\, \aleph _1(\chi ),\, \dots ,\, \aleph _{M}(\chi )]^T. \end{aligned}$$
(43)

The residual of the given problem (23) is obtained as

$$\begin{aligned} R_{M}(\chi )=\displaystyle \sum _{\iota =0}^M k_\iota \,\aleph ^{''}_\iota (\chi )+p(\chi )\,\displaystyle \sum _{\iota =0}^M k_\iota \,\aleph ^{'}_\iota (\chi )+q(\chi )\,\displaystyle \sum _{\iota =0}^M k_\iota \,\aleph _\iota (\chi )-r(\chi ), \end{aligned}$$
(44)

then employ the spectral methods, Specifically tau method

$$\begin{aligned} \displaystyle \int _0^1 R_{M}(\chi )\,\aleph _p(\chi )\,\varphi ^{*}(\chi )\,d\chi =0, \quad p=0,\, 1, \,\dots ,\, M-q, \end{aligned}$$
(45)

with the numerical Robin conditions ((28) and (29)) or ((30) and (31)).□

3.2 Second-order of non-linear BVPs with robin Conditions

The next non-linear BVPs of second-order form

$$\begin{aligned} \mathcal {L}^{''}(\chi )=f\left( \mathcal {L}^{'}(\chi ), \,\mathcal {L}(\chi ),\, \chi \right) , \end{aligned}$$
(46)

adapted to the Robin non-homogeneous boundary conditions (24) or (25).

The residual of Eq. (46) is provided by

$$\begin{aligned} R_M(\chi )=\mathcal {L}^{''}(\chi )-f\left( \mathcal {L}^{'}(\chi ), \,\mathcal {L}(\chi ),\, \chi \right) . \end{aligned}$$
(47)

We now apply the collocation method to the residual, and the next relation yields (M+1) equations

$$\begin{aligned} R_{M} \left( \frac{1+\cos ({\frac{(i+1)\,\pi }{M+2}})}{2} \right) =0, \qquad i=0,\,1,\,\dots ,\, M, \end{aligned}$$
(48)

with the numerical Robin conditions ((28) and (29)) or ((30) and (31)). Then we solve these equations by any suitable method to get the unknowns K.

Algorithm 1
figure a

Our Method’s Coding Algorithm for Robin BVPs

Full size image

4 Elliptic partial differential equation

This section discusses two dimensions of linear elliptic equation (5), as well as how to solve them using our method.

An approximate solution is provided by

$$\begin{aligned} \mathcal {L}_M(\chi ,\,\tau )=\displaystyle \sum _{\iota =0}^M \,\displaystyle \sum _{j=0}^M z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau ), \end{aligned}$$
(49)

where \(\Upsilon _\iota (\chi )\) shifted Chebyshev for the second-kind polynomials is supplied as

$$\begin{aligned} \Upsilon _\iota (\chi )=(3+\iota )\, \vartheta ^{*}_{\iota }(\chi ) -(1+\iota )\,\vartheta ^{*}_{\iota +2}(\chi ), \end{aligned}$$
(50)

and

$$\begin{aligned} {\textbf {Z}}={[z_0,\, z_1,\, \dots ,\, z_{M}]}^T, \quad \varvec{\Upsilon }(\chi )=[\Upsilon _0(\chi ),\, \Upsilon _1(\chi ),\, \dots ,\, \Upsilon _{M}(\chi )]^T. \end{aligned}$$
(51)

Theorem 5

The orthogonality of \(\Upsilon _\iota (\chi )\) w.r.t \(\varphi ^{*}(\chi )\) could be obtained as

$$\begin{aligned} \displaystyle \int _{0}^{1} \Upsilon _\iota (\chi )\,\Upsilon _j(\chi )\,\varphi ^{*}(\chi )\,d\chi = {\left\{ \begin{array}{ll}\frac{\pi }{4}\,(4+\iota +j),&{} \iota =j,\\ 0,&{} \iota \ne j.\\ \end{array}\right. } \end{aligned}$$
(52)

Proof

Substituting \(\Upsilon _\iota (\chi )\) in the left side of relation (52). So, we acquire the next

$$\begin{aligned}{} & {} \displaystyle \int _{0}^{1} \Upsilon _\iota (\chi )\,\Upsilon _j(\chi )\,\varphi ^{*}(\chi )\,d\chi \nonumber \\= & {} \displaystyle \int _{0}^{1} \left( (3+\iota )\, \vartheta ^{*}_{\iota }(\chi ) -(1+\iota )\,\vartheta ^{*}_{\iota +2}(\chi )\right) \,\left( (3+j)\, \vartheta ^{*}_{j}(\chi ) -(1+j)\,\vartheta ^{*}_{j+2}(\chi )\right) \,\varphi ^{*}(\chi )\,d\chi \nonumber \\ {}= & {} \displaystyle \int _{0}^{1} \, ((3+\iota )\,(3+j)\,\vartheta ^{*}_{\iota }(\chi )\,\vartheta ^{*}_{j}(\chi )\,\varphi ^{*}(\chi )-(3+\iota )\,(1+j)\,\vartheta ^{*}_{\iota }(\chi )\,\vartheta ^{*}_{j+2}(\chi )\,\varphi ^{*}(\chi ) \nonumber \\ {}- & {} (1+\iota )\,(3+j)\,\vartheta ^{*}_{\iota +2}(\chi )\,\vartheta ^{*}_{j}(\chi )\,\varphi ^{*}(\chi )-(1+\iota )\,(1+j)\,\vartheta ^{*}_{\iota +2}(\chi )\,\vartheta ^{*}_{j+2}(\chi )\,\varphi ^{*}(\chi ))\,d\chi , \end{aligned}$$
(53)

from the orthogonality form in (16), we obtain

$$\begin{aligned}{} & {} \displaystyle \int _{0}^{1} \Upsilon _\iota (\chi )\,\Upsilon _j(\chi )\,\varphi ^{*}(\chi )\,d\chi \nonumber \\= & {} {\left\{ \begin{array}{ll}\displaystyle \int _{0}^{1}\, ((3+\iota )\,(3+j)\,\vartheta ^{*}_{\iota }(\chi )\,\vartheta ^{*}_{j}(\chi )\,\varphi ^{*}(\chi )- (1+\iota )\,(1+j)\,\vartheta ^{*}_{\iota +2}(\chi )\,\vartheta ^{*}_{j+2}(\chi )\,\varphi ^{*}(\chi )) \,d\chi ,&{} \iota =j,\nonumber \\ 0,&{} \iota \ne j, \\ \end{array}\right. }\\= & {} {\left\{ \begin{array}{ll}\frac{\pi }{4}\, (4+\iota +j),&{} \iota =j, \\ 0,&{} \iota \ne j.\\ \end{array}\right. } \end{aligned}$$
(54)

□

Equation (5) has the residual form supplied by

$$\begin{aligned} \begin{aligned} R(\chi ,\tau )&=\nabla ^2 \mathcal {L} (\chi ,\tau )+\mu \,\mathcal {L} (\chi ,\tau )-f(\chi ,\tau )\\&=\displaystyle \sum _{\iota =0}^M\,\displaystyle \sum _{j=0}^M z_{\iota j}\,\nabla ^2 \left( \Upsilon _{\iota }(\chi )\,\Upsilon _{j}(\tau )\right) +\mu \,\displaystyle \sum _{\iota =0}^M \,\displaystyle \sum _{j=0}^M z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau )-f(\chi ,\tau ), \end{aligned} \end{aligned}$$
(55)

using the Galerkin technique, we generate a system of equations from the residual as

$$\begin{aligned} R\left( \frac{\iota +1}{3+M},\, \frac{j+1}{3+M}\right) =0, \quad \iota ,\,j=0,\, 1, \,\dots ,\, M. \end{aligned}$$
(56)

The relation (56) constructs (M + 1) equations as a linear system with unknowns \({\textbf {Z}}\). Finally, we employ any algebraic method to solve this system.

Algorithm 2
figure b

Our Method’s Coding Algorithm for Elliptic Partial Differential Equation

Full size image

5 Convergence analysis for the suggested polynomials

This section contains an error estimate and convergence analysis for the method employed to solve the Robin BVPs and Bratu-type equations. To apply the theory on orthogonal polynomials (shifted and modified shifted Chebyshev polynomials about the second-kind).

Theorem 6

Let \(\mathcal {L}_M(\chi ),\,\mathcal {L}_M(\chi ,\tau )\le \xi\), \(\xi \ge 1\), The coefficients \(k_j\) and \(z_{ij}\) can be computed as follows:

$$\begin{aligned} |k_j|\lesssim \frac{\pi \,(j-1)}{384}, \end{aligned}$$
(57)

and

$$\begin{aligned} |z_{\iota j}|\lesssim \frac{9\,\pi }{16\,(4+\iota +j)}. \end{aligned}$$
(58)

Proof

Multiplying each side of the relation (42) with \(\aleph _j(\chi )\) and \(\varphi ^{*}(\chi )\) yields

$$\begin{aligned} \displaystyle \int _{0}^{1} \mathcal {L}_M(\chi )\,\aleph _j(\chi )\,\varphi ^{*}(\chi )\,d\chi =\displaystyle \int _{0}^{1}\,\displaystyle \sum _{\iota =0}^M k_\iota \,\aleph _j(\chi )\,\aleph _\iota (\chi )\,\varphi ^{*}(\chi )\,d\chi . \end{aligned}$$
(59)

Then the constant \(k_\iota\) will be supplied by

$$\begin{aligned} \begin{aligned} |k_{j}|&= \,\displaystyle \int _{0}^{1} \mathcal {L}_M(\chi )\,\aleph _j(\chi )\,\varphi ^{*}(\chi )\,d\chi \\&= \displaystyle \int _{0}^{1} \left( \frac{\chi ^{2}-T\,\chi +B_{j}}{j+1} \right) \,\vartheta ^{*}_{j}(\chi )\,\varphi ^{*}(\chi )\,d\chi \\&= \displaystyle \int _{0}^{1} \left( \frac{\chi ^{2}-T\,\chi +B_{j}}{j+1} \right) \,\left( \displaystyle \sum _{s=0}^{j}\frac{(-1)^s\,(2\,j-s+1)!}{s!\,2^{2\,s-2\,j}\,(2\,j-2\,s+1)!}\, \chi ^{j-s} \right) \,\left( \sqrt{\chi -\chi ^{2}} \right) \,d\chi , \end{aligned} \end{aligned}$$
(60)

Now, we evaluate the integration and then estimate the result to get the next value

$$\begin{aligned} |k_{j}|\lesssim \frac{\pi \,(j-1)}{384}. \end{aligned}$$
(61)

Now, we will prove the second relation as follows:

$$\begin{aligned} \mathcal {L}_M(\chi ,\tau )=\displaystyle \sum _{\iota =0}^M \,\displaystyle \sum _{j=0}^M z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau ), \end{aligned}$$
(62)

multiplying each side of the last relation by \(\Upsilon _\iota (\chi )\), \(\Upsilon _j(\tau )\), \(\varphi ^{*}(\chi )\), and \(\varphi ^{*}(\tau )\), then integrating with respect to \(\chi\) and \(\tau\) from 0 to 1. As well as applying the relation (50) in the integration with the orthogonality (52), we have

$$\begin{aligned} \begin{aligned} |z_{\iota j}|&=\frac{4}{\pi \,(4+\iota +j)}\,\displaystyle \int _{0}^{1}\,\displaystyle \int _{0}^{1} \mathcal {L}_M(\chi ,\tau )\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau )\,\varphi ^{*}(\chi )\,\varphi ^{*}(\tau )\,d\chi \,d\tau \\&= \frac{4}{\pi \,(4+\iota +j)}\,\displaystyle \int _{0}^{1}\,\displaystyle \int _{0}^{1} \left( (3+\iota )\, \vartheta ^{*}_{\iota }(\chi ) -(1+\iota )\,\vartheta ^{*}_{\iota +2}(\chi )\right) \,\\&\times \left( (3+j)\, \vartheta ^{*}_{j}(\tau ) -(1+j)\,\vartheta ^{*}_{j+2}(\tau )\right) \,\varphi ^{*}(\chi )\,\varphi ^{*}(\tau )\,d\chi \,d\tau \\&\lesssim \frac{4}{\pi \,(4+\iota +j)}\left( \,\frac{9\,\pi ^2}{64}\right) \\&= \frac{9\,\pi }{16\,(4+\iota +j)}. \end{aligned} \end{aligned}$$
(63)

□

Theorem 7

For \(\iota \ge 0\), the modified shifted and shifted of Chebyshev polynomials satisfy the estimates below, respectively

$$\begin{aligned} |\aleph _{\iota }(\chi )|\lesssim \frac{2\,(\iota +2)}{3}, \quad \quad |\Upsilon _{\iota }(\chi )|\lesssim (2\,\iota +1)^{2}. \end{aligned}$$
(64)

Proof

Equation (26) provides

$$\begin{aligned} \left| \aleph _{\iota }(\chi )\right| =\left| \frac{\left( \chi ^{2}+A_{\iota }\,\chi +B_{\iota }\right) \,\vartheta ^{*}_{\iota }(\chi )}{\iota +1}\right| , \end{aligned}$$
(65)

where \(\vartheta ^{*}_{\iota }(\chi )\) can be estimated as follows:

$$\begin{aligned} |\vartheta ^{*}_{\iota }(\chi )|= \left| \displaystyle \sum _{s=0}^{\lceil \frac{\iota }{2}\rceil }\frac{(-1)^s\,2^{\iota -2\,s}\,(\iota -s)!}{s!\,(\iota -2\,s)!}\, (2\,\chi -1)^{\iota -2\,s} \right| \lesssim \iota +2. \end{aligned}$$
(66)

Then we’re given the next estimate

$$\begin{aligned} \begin{aligned} |\aleph _{\iota }(\chi )|&\lesssim \left| \frac{\left( \chi ^{2}+A_{\iota }\,\chi +B_{\iota }\right) \,(\iota +2)}{\iota +1}\right| \\&\lesssim \frac{2\,(\iota +2)}{3}. \end{aligned} \end{aligned}$$
(67)

For shifted to second-kind Chebyshev polynomials is provided by

$$\begin{aligned} |\Upsilon _{\iota }(\chi )|= & {} \left| (3+\iota )\, \vartheta ^{*}_{\iota }(\chi ) -(1+\iota )\,\vartheta ^{*}_{\iota +2}(\chi )\right| \nonumber \\= & {} \left| (3+\iota )\,\displaystyle \sum _{s=0}^{\lceil \frac{\iota }{2}\rceil }\frac{(-1)^s\,2^{\iota -2\,s}\,(\iota -s)!}{s!\,(\iota -2\,s)!}\, (2\,\chi -1)^{\iota -2\,s} \right. \nonumber \\- & {} \left. (1+\iota )\,\displaystyle \sum _{s=0}^{\lceil \frac{\iota +2}{2}\rceil }\frac{(-1)^s\,2^{\iota +2-2\,s}\,(\iota +2-s)!}{s!\,(\iota +2-2\,s)!}\,(2\, \chi -1)^{\iota +2-2\,s} \right| \nonumber \\\lesssim & {} \left| (8+2\,\iota )^2\,\displaystyle \sum _{s=0}^{\lceil \frac{\iota +1}{2}\rceil }\frac{(-1)^s\,2^{\iota +1-2\,s}\,(\iota +1-s)!}{s!\,(\iota +1-2\,s)!}\, (2\,\chi -1)^{\iota +1-2\,s} \right| \nonumber \\\lesssim & {} (2\,\iota +1)^{2}. \end{aligned}$$
(68)

□

Theorem 8

The absolute error \(|e_M(\chi )|\) and \(|e_M(\chi ,\tau )|\) are estimated employing these relations:

$$\begin{aligned} \begin{aligned}&|e_M(\chi )| \lesssim \frac{4\,\pi }{576}\, e^{(1+\iota )}\,\left( 1-\frac{\Gamma (M+1,\iota +1)}{\Gamma (M+1)}\right) ,\\&|e_M(\chi ,\tau )|\lesssim \frac{9\,\pi }{16}\, e^{(2+2\,\iota +j)}\,\left( 1-\frac{\Gamma (M+1,1+2\,\iota )}{\Gamma (M+1)}\right) \,\left( 1-\frac{\Gamma (M+1,j+1)}{\Gamma (M+1)}\right) . \end{aligned} \end{aligned}$$
(69)

Proof

The definition of absolute error can be stated as

$$\begin{aligned} \begin{aligned} |e_M(\chi )|&= \left| \displaystyle \sum _{\iota =0}^{\infty } \,k_{\iota }\,\aleph _\iota (\chi )\,-\displaystyle \sum _{\iota =0}^M \, k_{\iota }\,\aleph _\iota (\chi )\,\right| \\&= \left| \displaystyle \sum _{\iota =M+1}^{\infty } \, k_{\iota }\,\aleph _\iota (\chi )\right| \\&\le \displaystyle \sum _{\iota =M+1}^{\infty } \, |k_{\iota }|\,|\aleph _\iota (\chi )|. \end{aligned} \end{aligned}$$
(70)

Implementing relations in (57) and (64), we generate

$$\begin{aligned} \begin{aligned} |e_M(\chi )|&\lesssim \displaystyle \sum _{\iota =M+1}^{\infty } \, \frac{1}{576}\,(2+\iota )\,(\iota -1)\,\pi \\&\lesssim \frac{4\,\pi }{576}\,\displaystyle \sum _{\iota =M+1}^{\infty } \, \frac{(1+\iota )^\iota }{\iota !}\\&\lesssim \frac{4\,\pi }{576}\, e^{(1+\iota )}\,\left( 1-\frac{\Gamma (M+1,\iota +1)}{\Gamma (M+1)}\right) . \end{aligned} \end{aligned}$$
(71)

We will now prove the second relation of the absolute error in (69)

$$\begin{aligned} \begin{aligned} |e_M(\chi ,\tau )|=&\left| \displaystyle \sum _{\iota =0}^{\infty } \displaystyle \sum _{j=0}^{\infty }\,z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau )-\displaystyle \sum _{\iota =0}^M \,\displaystyle \sum _{j=0}^M z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau )\right| \\ =&\left| \displaystyle \sum _{\iota =M+1}^{\infty } \, \displaystyle \sum _{j=M+1}^{\infty }\,z_{\iota j}\,\Upsilon _\iota (\chi )\,\Upsilon _j(\tau )\right| , \end{aligned} \end{aligned}$$
(72)

with hypotheses (58) and (64), we find

$$\begin{aligned} \begin{aligned} |e_M(\chi ,\tau )|&\lesssim \displaystyle \sum _{\iota =M+1}^{\infty } \, \displaystyle \sum _{j=M+1}^{\infty }\,\left( \frac{9\,\pi \,(2\,\iota +1)^{2}}{16\,(4+\iota +j)} \right) \\&\lesssim \frac{9\,\pi }{16}\, \displaystyle \sum _{\iota =M+1}^{\infty } \, \displaystyle \sum _{j=M+1}^{\infty }\, \frac{(1+2\,\iota )^\iota }{\iota !}\,\frac{(1+j)^j}{j!}\\&\lesssim \frac{9\,\pi }{16}\, e^{(2+2\,\iota +j)}\,\left( 1-\frac{\Gamma (M+1,1+2\,\iota )}{\Gamma (M+1)}\right) \,\left( 1-\frac{\Gamma (M+1,j+1)}{\Gamma (M+1)}\right) , \end{aligned} \end{aligned}$$
(73)

where \(\Gamma (\eth ,\jmath )\) indicates an upper incomplete gamma function.□

6 Discussion of numerical results

This section explores the second-kind of shifted Chebyshev polynomials on the Bratu-type equation and Robin BVPs. All the next examples were solved to evaluate the maximum absolute error, where

$$\begin{aligned} \displaystyle \max (e_M)=\displaystyle \max \left| \mathcal {L}(\chi )-\mathcal {L}_M(\chi ) \right| ,\quad \,0 \le \chi \le 1, \end{aligned}$$
(74)

or with two variables are given as

$$\begin{aligned} \displaystyle \max (e_M)=\displaystyle \max |\mathcal {L}(\chi ,\tau )-\mathcal {L}_M(\chi ,\tau )|,\quad \,0 \le \chi ,\,\tau \le 1. \end{aligned}$$
(75)

All results were obtained by using the Mathematica program of version 11 by a PC with those specifications: Processor: Intel(R) Core(TM) i7-4790 CPU @ 3.60GHz; installed memory: 16.0 GB.

Example 1

[44, 45] Consider the following is a second-order non-linear BVP:

$$\begin{aligned} 8\,\mathcal {L}''(\chi )+4\,(\mathcal {L}'(\chi ))^{2}+e^{-2\,\mathcal {L}(\chi )}=0, \quad 0\le \chi \le 1, \end{aligned}$$
(76)

applied in the non-homogeneous Robin BCs:

$$\begin{aligned} \mathcal {L}(0)-2\,\mathcal {L}'(0)=-1, \quad \mathcal {L}(1)+2\,\mathcal {L}'(1)= \log {\left( \frac{3}{2}\right) }+\frac{2}{3}. \end{aligned}$$
(77)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=\log {\left( \frac{\chi }{2}+1 \right) }. \end{aligned}$$
(78)

In Table 1, by using our method, we compare both exact and approximate solutions at \(M=2\) and \(M=4\). As we increase the value of M, we observe how the numerical solution approaches the exact solution. The maximum absolute error for our method, the compact finite difference method (CFDM), and the Direct two-point diagonal block method of order four (2PDD4) is compared with \(M=8\) and \(M=16\) in Table 2. Figure 1 presents the absolute error with \(M=18\). As well as to Fig. 2, we explain the absolute error for various values of M.

Table 1 Comparison among the approximate and exact solutions of Example 1
Full size table
Table 2 Comparison about \(e_M\) in Example 1
Full size table
Fig. 1
figure 1

Absolute error with \(M=18\) of Example 1

Full size image
Fig. 2
figure 2

Absolute error for \(M=2:2:12\) of Example 1

Full size image

Example 2

[44,45,46] Assume the non-linear Bratu-type BVP shown below:

$$\begin{aligned} \mathcal {L}''(\chi )-\pi ^{2}\, e^{\mathcal {L}(\chi )}=0, \quad 0\le \chi \le 1, \end{aligned}$$
(79)

through the Robin BCs:

$$\begin{aligned} \mathcal {L}(0)+2\,\mathcal {L}'(0)=-2\, \pi , \quad 2\,\mathcal {L}(1)-\mathcal {L}'(1)= -\pi . \end{aligned}$$
(80)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=-\left( \ln {(2)}+2\, \ln {\left(\cos {\pi \,(\frac{\chi }{2}-\frac{1}{4})}\right)}\right) .\end{aligned}$$
(81)

We estimate in Table 3 the maximum absolute error with across various h and then compare our results to those of other methods (CFDM, 2PDD4, and QBSCM), where QBSCM is the Quintic B-spline collocation method. Figure 3 illustrates the absolute error to our method in \(M=50\). Finally, we compare the exact solution with approximate solutions about (\(M=10\), 15, 20, and 40) as shown in Fig. 4.

Table 3 Maximum absolute error to Example 2 with a variety of h
Full size table
Fig. 3
figure 3

Absolute error with \(M=50\) of Example 2

Full size image
Fig. 4
figure 4

Comparison of exact and approximate answers with distinct values of M in Example 2

Full size image

Example 3

[44] Consider the next is the non-linear Robin BVP:

$$\begin{aligned} 2\,e^{\chi }\,\mathcal {L}''(\chi )-\left( \mathcal {L}(\chi ))^2-(\mathcal {L}'(\chi )\right) ^2=0, \quad \chi \in [0,1], \end{aligned}$$
(82)

based on the Robin BCs:

$$\begin{aligned} \mathcal {L}(0)-\mathcal {L}'(0)=0, \quad \mathcal {L}(1)+\mathcal {L}'(1)= 2\,e. \end{aligned}$$
(83)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=e^{\chi }. \end{aligned}$$
(84)

We use the provided method in 3 with different values of h and M, the maximum absolute error to our method is better than CFDM in [44] as shown in Table 4. Figure 5 shows the behavior of absolute error in shifted Chebyshev polynomials to solve the non-linear Robin BVP with \(M=24\). For a variety of M, we present Fig. 6 to illustrate the difference between approximate and exact solutions. From this figure, we note that the exact solution is very close to the approximate solution at small values of M.

Table 4 Maximum absolute error over Example 3 for various h values
Full size table
Fig. 5
figure 5

Absolute error at \(M=24\) for Example 3

Full size image
Fig. 6
figure 6

Comparison between the exact and approximate solutions involving various values at M of Example 3

Full size image

Example 4

[25, 47,48,49] Considering a non-linear BVP about Robin’s conditions:

$$\begin{aligned} 2\,\mathcal {L}''(\chi )-\left( 1+x+\mathcal {L}(\chi )\right) ^3=0, \quad \chi \in [0,1], \end{aligned}$$
(85)

according to the Robin BCs:

$$\begin{aligned} \mathcal {L}(0)-\mathcal {L}'(0)=0.5, \quad \mathcal {L}(1)+\mathcal {L}'(1)= 1. \end{aligned}$$
(86)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=-\chi \, \left( \frac{\chi -1}{\chi -2} \right) . \end{aligned}$$
(87)

In the beginning, we provide a comparison with both exact and approximate solutions at M =5, 10, and 15 as shown in Table 5. In which there isn’t a difference between them. With different values of h in Table 6, we make a comparison in the maximum absolute error by our method with the following methods:

  • 2PDD5: The [47] paper proposes a direct two-point diagonal block approach of order five.

  • 2PDAM5: The direct two-step Adams Moulton block approach of order five, as described in [48].

  • DAM5: The direct Adams Moulton technique of order five, as described in [49].

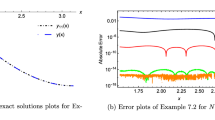
For \(M=8\) and \(M=10\), we compare the maximum absolute error between our technique and Bernoulli polynomials (BPs) [25] in Table 7. Figure 7 shows the behavior of the absolute error with \(M=6\) by our method. Finally, Fig. 8 illustrates the plot of absolute error for various M values.

Table 5 Our method’s approximate solutions with different M values for Example 4
Full size table
Table 6 Maximum absolute error to Example 4 in different values of h
Full size table
Table 7 Maximum absolute error to Example 4
Full size table
Fig. 7
figure 7

Absolute error with M = 25 of Example 4

Full size image
Fig. 8
figure 8

Absolute error with \(M=5:5:25\) of Example 4

Full size image

Example 5

[47,48,49] Considering a linear Robin BVP:

$$\begin{aligned} \mathcal {L}''(\chi )-\mathcal {L}(\chi )+4\,\chi \,e^{\chi }=0, \quad \chi \in [0,1], \end{aligned}$$
(88)

through the Robin BCs:

$$\begin{aligned} \mathcal {L}(0)-\mathcal {L}'(0)=-1, \quad \mathcal {L}(1)+\mathcal {L}'(1)= -e^{\chi }. \end{aligned}$$
(89)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi )=\chi \,(1-\chi )\,e^{\chi }. \end{aligned}$$
(90)

With \(h=0.1,\, 0.05, \, and \, \, 0.01\) at different M, we compared the maximum absolute error between our technique and some authors [47,48,49] in Table 8. In Table 9, we describe the results of the approximate solution \((M=15)\) obtained by our method and compare these with the exact solution, then there isn’t a difference between them. Figure 9 describes the log(maximum absolute error) of our method with \(M=3,\, 5,\, 7,\, 9,\, and\, 11\).

Table 8 Maximum absolute error in Example 5 with various values of h and M
Full size table
Table 9 The approximate solution employing our method via \(M=15\) for Example 5
Full size table
Fig. 9
figure 9

For \(M=3,\, 5,\, 7,\, 9,\, and\, 11\), this figure refers to Example 5’s log (maximum error)

Full size image

Example 6

[50] Evaluate a subsequent linear elliptic equation:

$$\begin{aligned} \nabla ^2 \mathcal {L} (\chi ,\tau )-2\,\mathcal {L}(\chi ,\tau )+4\,(\chi +\tau )\,(1-\chi )\,(1-\tau )\,e^{-\chi -\tau }=0, \quad 0 \le \chi ,\,\tau \le 1, \end{aligned}$$
(91)

ruled with the homogeneous BCs:

$$\begin{aligned} \begin{aligned} \mathcal {L}(0,\tau )= 0, \quad \mathcal {L}(1,\tau )= 0,\\ \mathcal {L}(\chi ,0)= 0, \quad \mathcal {L}(\chi ,1)= 0. \end{aligned} \end{aligned}$$
(92)

Analytical solution:

$$\begin{aligned} \mathcal {L}(\chi ,\tau )=\tau \,\chi \,(1-\tau )\,(1-\chi )\,e^{-(\tau +\chi )}.\end{aligned}$$
(93)

In Tab. 10, we compare maximum absolute error between of our technique with others when \(M=3,\,6,\, and \, 9\). Used methods in [50] are shifted third-kind about Chebyshev Petrov-Galerkin method (S3CPGM) and the shifted fourth-kind about Chebyshev Petrov-Galerkin method (S4CPGM). When \(M=9\), we compare exact and approximate solutions. In that case, the approximate solution equals the exact solution stated in Tab. 11. Figure 10 demonstrates the absolute error when \(M=9\).

Table 10 Maximum absolute error to Example 6 with \(M=3,\,6,\,and \,9\)
Full size table
Table 11 Comparison of exact and approximate solutions at \(M=9\) in Example 6
Full size table
Fig. 10
figure 10

When \(M=9\), this figure refers to Example 6’s absolute error

Full size image

7 Conclusions

In this study, numerical solutions of two-dimensional Bratu-type equations and Robin BVPs were obtained by applying suitable spectral methods in conjunction with shifted and modified shifted Chebyshev polynomials about the second-kind, and then we converted the residual of those two problems to equations. These equations are solved numerically using two algorithms. We demonstrated the superiority of the suggested method over a few other methods. If the remainder of the modes of the approximation expansions are modest, we have acquired more accurate errors. The proposed approximate expansion’s convergence analysis was examined by proving certain estimations related to the second-kind shifted and modified shifted Chebyshev polynomials.