Skip to main content
SpringerLink
Log in

The RKHS method for numerical treatment for integrodifferential algebraic systems of temporal two-point BVPs

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

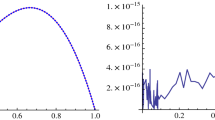
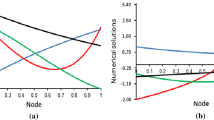
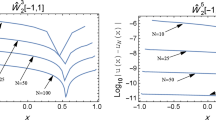
Abstract

Many problems arising in different fields of sciences and engineering can be reduced, by applying some appropriate discretization, either to a system of integrodifferential algebraic equations or to a sequence of such systems. The aim of the present analysis is to implement a relatively recent computational method, reproducing kernel Hilbert space, for obtaining the solutions of integrodifferential algebraic systems of temporal two-point boundary value problems. Two extended inner product spaces W[0, 1] and H[0, 1] are constructed in which the boundary conditions of the systems are satisfied, while two smooth kernel functions R t (s) and r t (s) are used throughout the evolution of the algorithm in order to obtain the required grid points. An efficient construction is given to obtain the numerical solutions for the systems together with an existence proof of the exact solutions based upon the reproducing kernel theory. In this approach, computational results of some numerical examples are presented to illustrate the viability, simplicity, and applicability of the algorithm developed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Ascher UM, Petzold LR (1998) Computer methods for ordinary differential equations and differential-algebraic equations. SIAM, Philadelphia

    Book  Google Scholar 

  2. Brenan KE, Campbell SL, Petzold LR (1996) Numerical solution of initial-value problems in differential-algebraic equations (classics in applied mathematics). SIAM, Philadelphia

    MATH  Google Scholar 

  3. Hairer E, Wanner G (2004) Solving ordinary differential equations II: stiff and differential algebraic problems (series in computational mathematics). Springer, Berlin

    MATH  Google Scholar 

  4. Kunkel P, Mehrmann V (2006) Differential-algebraic equations: analysis and numerical solution (EMS textbooks in mathematics). European Mathematical Society, Switzerland

    Book  Google Scholar 

  5. Lamour R, März R, Tischendorf C (2013) Differential-algebraic equations: a projector based analysis (differential-algebraic equations forum). Springer, Berlin

    Book  Google Scholar 

  6. Pytlak R (1999) Numerical methods for optimal control problems with state constraints. Springer-Verlag, Berlin

    Book  Google Scholar 

  7. Kubicek M, Hlavacek V (2008) Numerical solution of nonlinear boundary value problems with applications. Dover Publications, New York

    MATH  Google Scholar 

  8. Lawder MT, Ramadesigan V, Suthar B, Subramanian VR (2015) Extending explicit and linearly implicit ODE solvers for index-1 DAEs. Comput Chem Eng 82:283–292

    Article  Google Scholar 

  9. Celik E, Bayram M (2004) Numerical solution of differential-algebraic equation systems and applications. Appl Math Comput 154:405–413

    MathSciNet  MATH  Google Scholar 

  10. Huang J, Jia J, Minion M (2007) Arbitrary order Krylov deferred correction methods for differential algebraic equations. J Comput Phys 221:739–760

    Article  MathSciNet  Google Scholar 

  11. Celik E, Bayram M (2005) The numerical solution of physical problems modeled as a systems of differential-algebraic equations (DAEs). J Franklin Inst 342:1–6

    Article  MathSciNet  Google Scholar 

  12. Celik E (2004) On the numerical solution of chemical differential-algebraic equations by Pade series. Appl Math Comput 153:13–17

    MathSciNet  MATH  Google Scholar 

  13. Celik E, Bayram M (2003) Arbitrary order numerical method for solving differential-algebraic equation by Padé series. Appl Math Comput 137:57–65

    MathSciNet  MATH  Google Scholar 

  14. Ascher UM, Petzold LR (1991) Projected implicit Runge–Kutta methods for differential-algebraic equations. SIAM J Numer Anal 28:1097–1120

    Article  MathSciNet  Google Scholar 

  15. Trent A, Venkataraman R, Doman D (2004) Trajectory generation using a modified simple shooting method In: Aerospace Conference, Proceedings: 2004 IEEE, vol 4, pp 2723–2729

  16. Holsapple RW, Venkataraman R, Doman D (2004) New, fast numerical method for solving two-point boundary-value problems. J Guid Control Dyn 27:301–304

    Article  Google Scholar 

  17. Zhao J (2007) Highly accurate compact mixed methods for two point boundary value problems. Appl Math Comput 188:1402–1418

    MathSciNet  MATH  Google Scholar 

  18. Cash JR, Wright MH (1991) A deferred correction method for nonlinear two-point boundary value problems: implementation and numerical evaluation. SIAM J Sci Stat Comput 12:971–989

    Article  MathSciNet  Google Scholar 

  19. Cash JR, Moore DR, Sumarti N, Daele MV (2003) A highly stable deferred correction scheme with interpolant for systems of nonlinear two-point boundary value problems. J Comput Appl Math 155:339–358

    Article  MathSciNet  Google Scholar 

  20. Jankowski T (2003) Samoilenko’s method to differential algebraic systems with integral boundary conditions. Appl Math Lett 16:599–608

    Article  MathSciNet  Google Scholar 

  21. Amodio P, Mazzia F (1997) Numerical solution of differential algebraic equations and computation of consistent initial/boundary conditions. J Comput Appl Math 87:135–146

    Article  MathSciNet  Google Scholar 

  22. Abu Arqub O (2016) Approximate solutions of DASs with nonclassical boundary conditions using novel reproducing kernel algorithm. Fundam Inform 146:231–254

    Article  MathSciNet  Google Scholar 

  23. Abu Arqub O (2016) The reproducing kernel algorithm for handling differential algebraic systems of ordinary differential equations. Math Methods Appl Sci 39:4549–4562

    Article  MathSciNet  Google Scholar 

  24. Kumar S, Kumar A, Argyros IK (2016) A new analysis for the Keller–Segel model of fractional order. Numer Algorithms. doi:10.1007/s11075-016-0202-z

    Article  MATH  Google Scholar 

  25. Kumar S, Kumar A, Baleneu D (2016) Two analytical methods for time-fractional nonlinear coupled Boussinesq–Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn 85:699–715

    Article  MathSciNet  Google Scholar 

  26. Yin XB, Kumar S, Kumar D (2015) A modified homotopy analysis method for solution of fractional wave equations. Adv Mech Eng 7:1–8

    Google Scholar 

  27. Kumar S, Kumar D, Singh J (2016) Fractional modelling arising in unidirectional propagation of long waves in dispersive media. Adv Nonlinear Anal 5:383–394

    MathSciNet  MATH  Google Scholar 

  28. Alquran M, Al-Khaled K, Chattopadhyay J (2015) Analytical solutions of fractional population diffusion model: residual power series. Nonlinear Stud 22:31–39

    MathSciNet  MATH  Google Scholar 

  29. Alquran M, Al-Khaled K, Sarda T, Chattopadhyay J (2015) Revisited Fisher’s equation in a new outlook: a fractional derivative approach. Phys A 438:81–93

    Article  MathSciNet  Google Scholar 

  30. Jaradat HM, Awawdeh F, Al-Shara’ S, Alquran M, Momani S (2015) Controllable dynamical behaviors and the analysis of fractal burgers hierarchy with the full effects of inhomogeneities of media. Rom J Phys 60:324–343

    Google Scholar 

  31. Alquran M, Jaradat HM, Al-Shara’ S, Awawdeh F (2015) A new simplified bilinear method for the N-soliton solutions for a generalized FmKdV equation with time-dependent variable coefficients. Int J Nonlinear Sci Numer Simul 16:259–269

    MathSciNet  MATH  Google Scholar 

  32. Lin Y, Cui M, Yang L (2006) Representation of the exact solution for a kind of nonlinear partial differential equations. Appl Math Lett 19:808–813

    Article  MathSciNet  Google Scholar 

  33. Zhoua Y, Cui M, Lin Y (2009) Numerical algorithm for parabolic problems with non-classical conditions. J Comput Appl Math 230:770–780

    Article  MathSciNet  Google Scholar 

  34. Yang LH, Lin Y (2008) Reproducing kernel methods for solving linear initial-boundary-value problems. Electron J Differ Equ 2008:1–11

    MathSciNet  MATH  Google Scholar 

  35. Wang WY, Han B, Yamamoto M (2013) Inverse heat problem of determining time-dependent source parameter in reproducing kernel space. Nonlinear Anal Real World Appl 14:875–887

    Article  MathSciNet  Google Scholar 

  36. Jiang W, Lin Y (2011) Representation of exact solution for the time fractional telegraph equation in the reproducing kernel space. Commun Nonlinear Sci Numer Simul 16:3639–3645

    Article  MathSciNet  Google Scholar 

  37. Wang Y, Du M, Tan F, Li Z, Nie T (2013) Using reproducing kernel for solving a class of fractional partial differential equation with non-classical conditions. Appl Math Comput 219:5918–5925

    MathSciNet  MATH  Google Scholar 

  38. Jiang W, Lin Y (2010) Approximate solution of the fractional advection–dispersion equation. Comput Phys Commun 181:557–561

    Article  MathSciNet  Google Scholar 

  39. Jiang W, Chen Z (2014) A collocation method based on reproducing kernel for a modified anomalous subdiffusion equation. Numer Methods Partial Differ Equ 30:289–300

    Article  MathSciNet  Google Scholar 

  40. Geng FZ, Cui M (2012) A reproducing kernel method for solving nonlocal fractional boundary value problems. Appl Math Lett 25:818–823

    Article  MathSciNet  Google Scholar 

  41. Li X, Wu B (2015) Approximate analytical solutions of nonlocal fractional boundary value problems. Appl Math Model 39:1717–1724

    Article  MathSciNet  Google Scholar 

  42. Abu Arqub O, Maayah B (2016) Solutions of Bagley-Torvik and Painlevé equations of fractional order using iterative reproducing kernel algorithm. Neural Comput Appl. doi:10.1007/s00521-016-2484-4

    Article  Google Scholar 

  43. Abu Arqub O, Al-Smadi M, Momani S, Hayat T (2016) Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput 20:3283–3302

    Article  Google Scholar 

  44. Abu Arqub O, Al-Smadi M, Momani S, Hayat T (2016) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput. doi:10.1007/s00500-016-2262-3

    Article  MATH  Google Scholar 

  45. Abu Arqub O (2015) Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm–Volterra integrodifferential equations. Neural Comput Appl. doi:10.1007/s00521-015-2110-x

    Article  MATH  Google Scholar 

  46. Jiang W, Chen Z (2013) Solving a system of linear Volterra integral equations using the new reproducing kernel method. Appl Math Comput 219:10225–10230

    MathSciNet  MATH  Google Scholar 

  47. Yang LH, Shen JH, Wang Y (2012) The reproducing kernel method for solving the system of the linear Volterra integral equations with variable coefficients. J Comput Appl Math 236:2398–2405

    Article  MathSciNet  Google Scholar 

  48. Abu Arqub O, Al-Smadi M, Shawagfeh N (2013) Solving Fredholm integro-differential equations using reproducing kernel Hilbert space method. Appl Math Comput 219:8938–8948

    MathSciNet  MATH  Google Scholar 

  49. Abu Arqub O, Al-Smadi M (2014) Numerical algorithm for solving two-point, second-order periodic boundary value problems for mixed integro-differential equations. Appl Math Comput 243:911–922

    MathSciNet  MATH  Google Scholar 

  50. Geng FZ, Qian SP (2013) Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers. Appl Math Lett 26:998–1004

    Article  MathSciNet  Google Scholar 

  51. Geng FZ, Qian SP, Li S (2014) A numerical method for singularly perturbed turning point problems with an interior layer. J Comput Appl Math 255:97–105

    Article  MathSciNet  Google Scholar 

  52. Geng FZ, Qian SP (2015) Modified reproducing kernel method for singularly perturbed boundary value problems with a delay. Appl Math Model 39:5592–5597

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors express their thanks to unknown referees for the careful reading and helpful comments.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Al-Balqa Applied University, Salt, 19117, Jordan

    Omar Abu Arqub

  2. Department of Computer Science, P.A.B.G Faculty of Information Technology, Al-Balqa Applied University, Salt, 19117, Jordan

    Hasan Rashaideh

Authors
  1. Omar Abu Arqub
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hasan Rashaideh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Omar Abu Arqub.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abu Arqub, O., Rashaideh, H. The RKHS method for numerical treatment for integrodifferential algebraic systems of temporal two-point BVPs. Neural Comput & Applic 30, 2595–2606 (2018). https://doi.org/10.1007/s00521-017-2845-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-017-2845-7

Keywords

Search

Navigation