1 Introduction / background

Tropical ecosystems are undergoing rapid land use and land cover (LULC) changes from increased pressures for agricultural land expansion and human settlement (FAO, 2019). The human population is projected to reach 9.5 billion, where more than half will be living in cities by the year 2050 (Arof et al., 2020). Expanding urban settlements create novel microclimates (1–104 m2) that often differ significantly from the regional climatic means (Lembrechts et al., 2020; Zhou et al., 2020). Moreover, the synoptic conditions recorded in a standard meteorological station may be unrepresentative of the range of microclimates within an area (Zellweger et al., 2019).

Predictions show that all African capital cities are likely to experience unusually hot days (heat waves) in the future with respect to the rest of the world (Ceccherini et al., 2017). The combination of local and regional warming trends, attributed to changes in land surface physics and effects of greenhouse gas emissions respectively, have significantly altered ecosystem processes and weather patterns (Shukla et al., 2019; Thorne et al., 2018), and threaten food production systems that millions of people depend on (Myers et al., 2017). One of the major impacts of global warming in Africa is increased frequencies of heat waves, that not only impair food production systems but also affect the health of urban residents (Ceccherini et al., 2017).

Urban heat island (UHI) is undesirable property in tropical areas since the cooling energy expenditures could be exorbitant and unaffordable to many of the residents (Wonorahardjo et al., 2020). The UHI intensity, the temperature difference of each urban cell relative to measurement from the rural reference station, can be attributed to differences in thermal mass (the thermal properties such as heat capacity) (Zhou et al., 2020). Moreover, the biogeophysical attributes that contributes to UHI include extent of built-up environment on sensible and latent heat flux, and other ecosystem processes such as evapotranspiration (Vlassova et al., 2014). For instance, the skin temperature of exposed surface soils may be significantly different from that of an adjacent vegetated surface (Zhou et al., 2020). The patterns, biogeophysical properties and extent of use of motorised transport tend to make urban areas warmer (UHI) than rural areas (Wonorahardjo et al., 2020). Although the Fifth Assessment Report of the Intergovernmental Panel on Climate Change concludes that there is unequivocal evidence of global warming (Pachauri et al., 2014), accurate characterization of conditions under which weather records are obtained is needed to improve reliability of future climate predictions (Thorne et al., 2018). Moreover, the use of temperature data derived from urban weather stations to assess historical climate series attributable to global warming may present a warm bias since temperatures are usually elevated in urban areas (Stewart and Oke, 2012).

Majority of literature on urban heat island studies fail to give quantitative metadata of site exposure or land cover and instead rely on the so-called urban and rural qualifiers to describe the local landscapes of their measurements (Stewart and Oke, 2012). However, Stewart and Oke (2012) developed a classification scheme of urban and rural field sites based on logical division for heat island assessment using quantifiable physiographic properties that can be related to surface thermal climate at the local scale (i.e., hundreds of meters to several kilometers). Within this classification scheme, the surface structure (height and spacing of buildings and trees) and surface cover (pervious or impervious) is considered because of its influence on NST (screen-height temperature). In addition, the surface structure also modifies local climate through changes in airflow, atmospheric heat transport, and shortwave and longwave radiation balances. On the other hand, surface cover modifies the albedo, moisture availability, and heating/cooling potential of the ground. The clustering of these properties tends to create spatially distinctive microclimates (hereafter referred to as ‘local climate zones’). Oke and Stewart (2012) define local climate zones (LCZs) as regions of uniform surface cover, structure, material, and human activity that span hundreds of meters to several kilometers in horizontal scale. Further, this classification scheme presents quantifiable physiographic attributes such as; geometric and surface cover properties (i.e. sky view factor, aspect ratio, building surface fraction, impervious surface fraction, pervious surface fraction, height of roughness elements, and terrain roughness class), and thermal, radiative, and metabolic properties (i.e. surface admittance, surface albedo, anthropogenic heat output) that can be related to NST temperature observations.

The relationship between satellite land surface temperature (LST) and near surface temperature (NST) is essential in estimating NST measurements, especially in areas where meteorological stations are absent (Good et al., 2017). However, uncertainties in generating climate predictions result from a number of factors including reliability of weather instruments, locations of weather stations, land use attributes (e.g., degree of urbanization), and non-standard approaches in weather records (Thorne et al., 2018). When weather stations are scarcely distributed, interpolating temperature values between them creates large uncertainties because of heterogeneities created by biophysical attributes of landscape features (Zellweger et al., 2019). Satellite-based LST estimates can fill the gaps in temperature data in absence of weather stations, although satellite-based LSTs incorporate temperatures of both the ground surface as well as above surface that includes; the uppermost parts of trees and buildings (Good et al., 2017). Additionally, time-synchronized fixed site and in situ traverse air temperature measurements are gaining popularity as accurate methods of characterizing micro-environments (Tsin et al., 2016; Zhou et al., 2020). Traverse walk or vehicular traverse measurements have proved reliable in obtaining spatial trends in near-surface air temperature patterns within urbanized environments (Zhou et al., 2020). Moreover, these traverse measurements can act as ‘ground truth’ data for validating satellite-based temperature observations, and also provide base data for generating projections of future surface and near-surface temperature estimates (Zhou et al., 2020). In fact, air temperatures alone are inadequate in explaining the higher temperatures encountered in urban areas compared to the adjacent rural areas (Koopmans et al., 2020). Since the thermal source area for a temperature measurement ("foot print" or "circle of influence") is a function of instrument height, surface geometry, and boundary layer wind and stability conditions (Stewart and Oke, 2012), ancillary variables describing the local environment are required. In this regard, biophysical attributes (e.g., topography, vegetation cover, and surface characteristics) contribute to the offset between land surface temperature (LST) and near-surface atmospheric temperature particularly during the day through differential solar heating, vegetation transpiration, and surface turbulence (Aalto et al., 2018). Therefore, the relationship between LST, NST, and biophysical variables are needed in order to exploit satellite-based LST estimates. Moreover, land cover, vegetation fraction, and elevation had a significant influence on ΔT (LST-T2m) values.

Given that urban environments in arid/semi-arid regions contain more than one third of the world's human population mapping urban microclimate patterns is essential in thermal conditions that urbanized residents are exposed to (Zhou et al. 2020). This study sought to; explore the microclimatic patterns in a tropical peri-urban environment and determine the biogeophysical factors driving the observed patterns. The specific objectives of the study were; (i) figure out if the use of fixed and mobile temperature sensors in time-synchronized in situ traverses can yield statistically significant temperature gradients (ΔT) attributable to landscape features, (ii) find out how time of the day influences NST gradients, (iii) determine how NST clusters compare to LST values derived from analysis of ‘cloud-free’ Landsat 8 OLI (Operational Land Imager) satellite image, and (iv) determine how NST and LST values are related to biophysical properties of land cover features. This study sought to find out how diurnal NST temperature gradients are related to properties of land surface features during the dry season and what time of the day yields the most significant temperature gradients. This paper serves as a baseline on evaluating future changes in LST and NST attributable to changes in urban development and global climate change.

2 Methodology

2.1 Study area

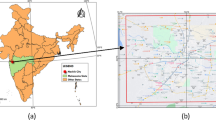
This study was conducted at a section of Kenyatta University Main Campus located between 36.20° to 36.96° East and -1.72° to -1.19° South, covering an area of about 10.6 ha (Fig. 1). The campus occurs within a peri-urban area with a humid highland sub-tropical climate with distinct dry and wet seasons. The bimodal rainfall occurs between March and May, and October and December, intervened by dry seasons. The aggregate annual precipitation and the mean annual temperature are about 1065 mm and 18.9 ℃, respectively. The maximum temperature averages at about 24.9 ℃, occurring in January to February, while the minimum temperature averages at about 13.0 ℃ occurring in July to August. The study area has a wide range of landcover and land use types that together with other physiographic attributes potentially contain a wide range of microclimates.

Fig. 1
figure 1

The study area map showing the road networks downloaded from OpenStreetMap (https://www.openstreetmap.org/) and buildings digitized from Google Earth® Imagery

Full size image

2.2 Near-surface air temperature measurements

The temperature records were obtained from a fixed HOBO Pendant® Temp/Light 8 K loggers (UA-002–64, Onset Computer Corporation, MA, USA) with a resolution of 0.14 °C and accuracy of ± 0.53 °C during the dry season when soils are dry, sky clear, and winds are minimum. In order to assess the reliability of air temperature measurements using the loggers, an experiment was set up to determine the effectiveness of solar radiation shields on diurnal air temperature variations within the weather station. Four air temperature records were obtained from four sensors (Table 1) as shown in Fig. 2.

Table 1 Description of the sensors used in recording temperatures
Full size table
Fig. 2
figure 2

The experimental set-up at Kenyatta University weather station; a – unshielded and shielded (in a fabricated radiation shield), b – a HOBO Pendant logger inside the Stevenson screen, and c – automatic weather station (model Envilog GP5W-Shell sensor, ecoTech, Germany). The HOBO Pendant logger are indicated by the red circle

Full size image

2.3 Traverse walk

We used HOBO Pendant loggers to record air temperatures in the weather station (fixed logger) (located at 1.183761° S, 36.928603° E, 1545 m mean sea level [MSL]) and across the traverse (mobile logger) at 30 s intervals. For the traverse walks, we chose the days with clear weather condition (no overcast conditions) and dry weather conditions. We conducted the first in situ traverse walk on 8th January 2018 in the late afternoon (between 4:06 pm and 5:35 pm) and the second in situ traverse walk on 18th February 2021 in the morning (between 10:00 am and 10:47 am) (Fig. 3). During the walks, the logger was suspended on a string within a fabricated radiation shield (see Fig. 4). We also took several photos to help in interpreting the results. During the walk, Garmin GPSMAP® 64S (Garmin Ltd.) Global Positioning System (GPS) receiver was used to collect the geographical coordinates along the traverse, whereupon the time-stamps of the GPS records and Hobo Pendant logger records were used to produce time-synchronized geographical coordinates and temperature records, respectively. The walk traverse was designed to pass through various cover types (tarmac road, concrete pavements, earthen field, forests, etc.). An attempt was made to maintain a constant speed during the walk to avoid temperature fluctuations caused by stagnation, given our interest in the spatial rather than temporal variability of air temperature.

Fig. 3
figure 3

Part of Kenyatta University Main Campus (study area) showing the background Google Earth ® image (dated 31st January 2020). In situ traverses used to collect air temperature data on are illustrated. The first in situ traverse walk (8th January 2018) and second in situ traverse walk (18th February 2021) is shown on the top and bottom map respectively

Full size image
Fig. 4
figure 4

A fabricated (‘rocket type’) radiation shield containing the Hobo Pendant temperature logger that was used in traverse walk around campus. The radiation shield was developed from 160 mm PVC pipe and white melamine bowls

Full size image

2.4 Temperature data analysis

2.4.1 Evaluating the effectiveness of solar radiation shield on air temperature records

To evaluate the effectiveness of fabricated shield in controlling for solar radiation, comparative temperature data was generated from all the four sensors (i.e. unshielded logger, and shielded logger in a fabricated radiation shield, logger inside the Stevenson screen, and Envilog GP5W-Shell logger in the automatic weather station).

2.4.2 Evaluating the spatial profiles in air temperature records across the traverses

The temperature difference (ΔT) was computed from time-synchronized temperature records of the fixed sensor positioned inside a Stevenson’s screen and the mobile sensor used in traverse walk on study area (Eq. 1):

$$\Delta T={TM}_{air}-{TF}_{air}$$
(1)

where ΔT is the difference in the temperature readings of mobile (TMAir) and fixed (TFAir) logger, respectively. In this case, negative ΔT values would indicate fixed logger had recorded a higher air temperature than that of the mobile logger. The converse is also true.

2.5 Hotspot analysis

Hotspot analysis of ΔT values was used to identify thermal hot and cold spots for the study region using Arc GIS 10.8® (ESRI Inc.). Getis–Ord Gi*, a geostatistical tool was used for identifying statistically significant hot and cold spot concentration using Eqs. 2, 3 and 4 (Daramola et al., 2018).

$${G}_{i}^{*}=\frac{\sum_{j=i}^{n}{w}_{i,j}{x}_{j}-\overline{X}\sum_{j=i}^{n}{w}_{i,j}}{\sqrt[S]{\left[n\sum_{j=i}^{n}{{w}^{2}}_{i,j}-{\left(\sum_{j=i}^{n}{w}_{i,j}\right)}^{2}\right]/(n-1)}}$$
(2)
$$\overline{X}=\frac{\sum_{j=i}^{n}{x}_{j}}{n}$$
(3)
$$S=\sqrt{\frac{\sum_{j=i}^{n}{x}_{j}^{2}}{n}-{\left(\overline{X}\right)}^{2}}$$
(4)

where xj is the ΔT values for feature j, wi,j is the spatial weight between feature i and j, n is the total number of sample points.

2.6 Retrieving Land Surface Temperatures (LST) and landscape metrics from Landsat 8 OLI

Cloud-free Landsat 8 OLI Collection 2 Level-2 imagery was downloaded from USGS-Earth Explorer on 30th December 2020. The details of the Landsat scene are shown in Table 2.

Table 2 Details of Landsat bands used in radiometric correction
Full size table

LST was retrieved from the thermal infrared band of Landsat 8 OLI/TIRS (band 10) using ENVI 5.3 software. The procedure for retrieving the LST involved, converting the digital number (DN).

into top-of-atmosphere (TOA) radiance, converting radiance values to brightness temperature (BT) values, and then modifying the BT values through integration of the emissivity of different land covers as outlined in Fig. 5.

Fig. 5
figure 5

Methodological flow chart of retrieving LST from Landsat 8 OLI

Full size image

2.6.1 Top of atmospheric spectral radiance

Thermal infrared Band 10 was used to retrieve the top of atmospheric (TOA) spectral radiance (Lλ) as given in Eq. 5 (Barsi et al., 2014):

$${L}_{\lambda }={M}_{L}*{Q}_{cal}+{A}_{L}-{O}_{i}$$
(5)

where ML represents the band-specific multiplicative rescaling factor, Qcal is the Band 10 image, AL is the band-specific additive rescaling factor, and Oi is the correction for Band 10 (Table 3).

Table 3 Metadata of the satellite images
Full size table

For OLI bands, Radiometric correction of Multispectral and Thermal bands was performed using Model-Based (FLAASH—Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes) in ENVI 5.3 software using mono window algorithm as per Eq. 6.

$${L}_{\lambda }=\left(\frac{{L}_{MAX}-{L}_{MIN}}{{QCAL}_{MAX}-{QCAL}_{MIN}}\right)*\left(DN-{QCAL}_{MIN}\right)+{L}_{MIN}$$
(6)

where; DN is the digital number of each pixel, LMAX and LMIN are calibration constants, QCALMAX and QCALMIN are the highest and lowest range of values for rescaled radiance in DN obtained from the metadata.

2.6.2 Conversion of radiance to at-sensor temperature

After the digital numbers (DNs) are converted to reflection, the TIRS band data should be converted from spectral radiance to BT (also known as blackbody temperatures) which is derived from Plank's law (Dash et al., 2002) using the thermal constants provided in the metadata file. The conversion of reflectance to BT is shown in Eq. 7:

$$\mathrm{BT}=\frac{{K}_{2}}{ln(\frac{{K}_{1}}{{L}_{\lambda }}+1)}+273.15$$
(7)

where:

BT – at satellite brightness temperature (Kelvin);

Lλ – top-of-atmosphere (TOA) spectral radiance;

K1 – Band-specific thermal conversion constant;

K2—Band-specific thermal conversion constant (from the metadata).

The values for Landsat 8 were as follows, band 10: K1 = 774.89, K2 = 1321.08; band 11: K1 = 480.89, K2 = 1201.14.

Lλ is the spectral radiance for the thermal band. LST in Kelvin and therefore was converted to Celsius. The parameters used in this calculation were obtained from Landsat 8 OLI Metadata file (Table 4) while the conversion formulations may be obtained from Landsat 8 (Landsat N.A.S.A 2019).

Table 4 Landsat 8 OLI parameters from metadata file
Full size table

2.7 Normalized Difference Vegetation Index (NDVI) method for emissivity correction

Landsat visible and near-infrared bands were used for calculating the Normal Difference.

Vegetation Index (NDVI) (Eq. 8). NDVI is needed in calculating emissivity because, the proportion of the vegetation (PV) is highly related emissivity (ε) should be calculated:

$$NDVI=\frac{{p}^{NIR}-{p}^{Red}}{{p}^{NIR}+{p}^{Red}}$$
(8)

where pNIR and pRed represent the surface reflectance values of the near-infrared (corresponding to Band 5 of Landsat 8 OLI) and the red wavelengths (corresponds to band 4 of Landsat 8 OLI), respectively.

Proportion of NDVI (PVNDVI) is then computed to adjust emissivity for different land cover features, whereby pixels with NDVI less than 0.2 are considered as bare soil or rock, pixels with values between 0.2 and 0.5 are considered a mixture of bare soil and vegetation, and pixels with values greater than 0.5 are considered fully vegetated (Sekertekin and Bonafoni, 2020; Urmambetova, 2017) (Eq. 9).

$${P}_{v}NDVI=\left(\frac{NDVI-{NDVI}_{s}}{{NDVI}_{v}-{NDVI}_{s}}\right)$$
(9)

where NDVIV and NDVIs, are NDVI values for vegetation that are equal to 0.5 and 0.2 respectively. Thus, the emissivity (ελ) of bare soil or rock is considered to be 0.966 while that of a fully vegetated pixel is considered 0.986 (Urmambetova, 2017).

2.8 Mapping Land Use and Land Cover (LULC)

LULC was generated through manual digitalization over Google Earth images (Fig. 6) and resulting KML files imported into Arc GIS 10.8 ® (ESRI Inc.).

Fig. 6
figure 6

Detailed illustrations of a section of the study area indicating how tree canopies (left) and buildings (right) were extracted from Google Earth® image. Other features (i.e. roads, parking lots, bare soils, and grass cover) was obtained in a similar way

Full size image

2.9 Selection of explanatory biophysical variables

In examining the relationship between the spectral indices and LST as well as NST, Normalized Difference Built-up Index (NDBI), Modified Normalized Difference Water Index (MNDWI), Albedo, and Normalized Difference Vegetation index (NDVI) were selected as ancillary biophysical variable (Table 5). These spectral indices were selected based on their reported performance in other studies (e.g., Daramola et al., 2018). NDBI highlights urban areas with high reflectance of short-wave radiation, and is based on reflectance measurements in the red and mid-infrared (MIR) portion of the spectrum (Liu and Zhang, 2011). MNDWI enhances water features and improves contrast between the built-up land and water (Xu, 2006). NDVI highlights areas covered by vegetation, with high values signifying high vegetation cover (Tucker, 1979). Albedo highlights differences in reflectivity between features within the visible electromagnetic spectrum. The short-wave albedo was estimated with an empirical formula (Eq. 8) previously developed for the Landsat Thematic Mapper/Enhanced Thematic Mapper Plus (TM/ETM +) sensor (Liang  2000):

Table 5 Spectral indices selected as explanatory variables of LST and NST
Full size table
$${\alpha }_{short}={0.356\alpha }_{1}+0.13{\alpha }_{2}+{0.373\alpha }_{3}+{0.085\alpha }_{4}+{0.072\alpha }_{5}-0.0018$$
(10)

where \({\alpha }_{1}\),\({\alpha }_{2},\) \({\alpha }_{3}\), \({\alpha }_{4}\), and \({\alpha }_{5}\), correspond to the Top of Atmosphere (TOA) reflectance in Landsat‐8 spectral bands 2 (0.45–0.515 μm), 3 (0.525–0. 60 μm), 4 (0.63–0.68 μm), 5 (0.845–0.885 μm), 6 (1.560–1.660 μm), and 7 (2.1–2.3 μm), respectively. The average albedo values of each 90 m grid cell were found to range from 0.11 to 0.53. Albedo ranges between 0 and 1.

2.10 Evaluating statistical relationships between LST and biophysical variables

In order LST, NST, and spectral indices for statistical analysis, to samples A fishnet corresponding to the study area was created in ArcGIS with a spatial resolution of 30 m × 30 m to match the resolution of Landsat 8 OLI image. Then, ΔT values of the traverse were obtained using spatial join tool of ArcGIS overlay toolbox. Similarly, spectral indices (Albedo, MNDWI, NDBI, and NDVI) were also obtained using values for statistical analysis.

Ordinary Least Square (OLS) regression analysis was done using Spatial analysis Toolbox in ArcGIS 10.8® (ESRI Inc.) to determine how Albedo, MNDWI, NDBI, and NDVI account for the observed LST and ΔT patterns. OLS is a global regression that assumes spatial stationarity (i.e., the processes triggering the observed patterns in temperature are spatially invariable such that the selected predictors trigger the same response throughout the study area) (Chen et al., 2020; Li et al., 2020; Wang et al., 2020). The coefficient of determination (R2), the global Moran’s I of the residuals, and the Akaike Information Criterion (AIC), were used to evaluate the performances of global regression models with respect to the goodness-of-fit and residual spatial autocorrelation.

We then performed an Ordinary Least Square regression between the NST (dependent variable) and the independent variables selected (Albedo, MNDWI, NDBI, and NDVI). All assumptions of least square regression were checked, including spatial autocorrelation.

In examining the relationship between the spectral indices and land surface temperature, statistical analysis was performed.

3 Results

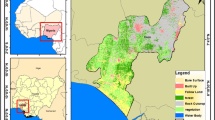
There were seven (7) major land use land cover (LULC) classes in the study area (Fig. 7). land cover classes were generally Among the land cover classes, tree cover had the largest proportion (37%) while water had the least proportion (0.7%) (Table 6).

Fig. 7
figure 7

Land Use Land Cover Map of Kenyatta University, manually digitized from Google Earth Imagery dated 31st January 2020

Full size image
Table 6 The proportion of various land cover classes in the study area
Full size table

3.1 Clustering patterns of NST records in relation to landscape features

The Getis–Ord Gi* statistics of ΔT values of the in situ traverse show spatial clustering with statistically significant hot and cold spot (Fig. 7). The results indicate spatial clustering, with statistically significant spatial clusters of high values (hot spots) and low values (cold spots). The higher (or lower) the z-score, the more intense the clustering. There is a correspondence between high temperature regions and low temperature regions in LST (Fig. 6) to the ‘hot spot’ and ‘cold spot’ regions observed from the temperature traverse (Fig. 8).

Fig. 8
figure 8

The Getis–Ord Gi* statistics of ΔT values of the in situ traverse showing statistically significant hot and cold spot categorized into confidence level bin in ± 3 bins, ± 2 bins, and ± 1 bins corresponding to 99 percent, 95 percent, and 90 percent confidence level (Gi_Bin). The cold spots and hot spots for the late afternoon traverse walk (8th January 2018) and morning traverse walk (18th February 2021) is shown on the top and bottom map respectively

Full size image

3.2 How time of the day influenced NST gradients

The experimental data evaluating effect of solar radiation on NST measurements reveals the fabricated shield did not significantly block solar radiation and showed that shielded HOBO Pendant logger recorded temperature variations were comparable to the unshielded sensor (Fig. 9). On the other hand, the HOBO Pendant logger situated inside the Stevenson screen and Envilog GP5W-Shell logger in the automatic weather station) showed comparable results, that were significantly lower than temperature records of HOBO Pendant logger in the fabricated shield and the unshielded sensor.

Fig. 9
figure 9

Air temperature time-trends gathered from Hobo Pendant sensors (in Outdoor shield, Open air – unshielded, and in Stevenson’s screen) and an Envilog GP5W-Shell sensor (ecoTech, Germany) indicating differences in daytime sensor temperature records on 12/10/2020 between 6:00 AM to 6:00 PM. Temperature measured by unshaded HOBO Pendant (red line), shaded HOBO Pendant using fabricated radiation shield (green line), shaded HOBO Pendant using Stevenson’s screen (blue line), and shaded using Envilog GP5W-Shell radiation shield (brown line) over the experimental period

Full size image

There were significant differences in temperature gradients (ΔT) between morning and evening measurements (Fig. 10). Considering ΔT profiles as a function of distance from the start of the traverse, the late afternoon in situ traverse walk (8th January 2018) showed a greater range in ΔT values and more significant peaks that morning in situ traverse walk (18th February 2021). Furthermore, the clustering patterns of ΔT values for the morning traverse yielded anomalous clusters that covered several land cover classes (Fig. 7).

Fig. 10
figure 10

Histograms of NST record and the corresponding traverse profile for the first in situ traverse walk (8th January 2018) (top panel) and the second in situ traverse walk (18th February 2021) (bottom panel) respectively. The late afternoon traverse (8th January 2018) showed a greater variability in ΔT values that followed a relatively normal distribution than the evening traverse (18th February 2021)

Full size image

Based on ground-truth observations, the combination of landscape elements (e.g., tree cover, paved surfaces, building heights, etc.) create a suite of microclimates that generate temperature gradients observed in this study. However, the significant ‘hot-spots’ and ‘cold spots’ (Figs. 11 and 12) can be attributed to three land cover classes as illustrated in Table 7.

Fig. 11
figure 11

Temperature differences between fixed and mobile sensor (ΔT) for the late afternoon traverse undertaken on 5th January 2018. The various land cover types encountered are represented in red lines numbered 1 – 3. The corresponding description the landscape features are shown in Table 7

Full size image
Fig. 12
figure 12

LST Map of the study area showing areas of low temperature (in blue and cyan) and areas of high temperature (in red and yellow) and late afternoon in situ traverse, as well as the location of weather station where the fixed temperature sensor was located are indicated. The location of significant ΔT clusters coinciding with cold and hots spots are illustrated in enclosed boxes with numbers coinciding with landcover classes described in Table 7

Full size image
Table 7 Description of land cover features encountered during the traverse walks
Full size table

The LST maps (Fig. 12) shows that areas with a high tree cover and close to the stream have low surface temperatures, while built up areas of low tree cover have high surface temperatures. The spectral indices (NDBI, NDVI, NDWI, and albedo) that were generated as explanatory biophysical variables for LST and NST patterns are shown in Fig. 13.

Fig. 13
figure 13

Spectral indices of biophysical variables (NDBI, NDVI, NDWI, and albedo) used to explain LST and NST patterns

Full size image

3.3 Results of ordinary linear regression

NDVI was found to have a high VIF (> 7.5) and was removed from the regression model. The resulting OLS regression model indicates that ΔT values are positively correlated with MNDWI, and NDBI but negatively correlated with albedo. Probability and Robust Probability (Robust_Pr) indicates a coefficient of MNDWI and NDBI are statistically significant (p < 0.01) (Table 8). However, these explanatory variables were only able to explain 15% of the variation in the observed ΔT patterns (Multiple R-Squared = 0.15).

Table 8 Summary of ordinary least square regression of ΔT (dependent variable) and Albedo, MNDWI, and NDBI (independent variables) results. Asterisk (*) indicates a coefficient is statistically significant (p < 0.01)
Full size table

4 Discussion

Proper shielding is critical for NST measurements, given the potentially large variations observed in daytime temperature records among the sensors (Fig. 9). The early morning and early evening temperature records are comparable across all the temperature sensors indicating that solar radiation is the main driver of the observed differences in daytime temperature records of the sensors. The use of ‘rocket-type’ fabricated shield did not significantly reduce the radiative effect (total and reflected radiation) on NST records (i.e. the day-time NST records of sensors inside the fabricated shield relatively similar to those of the shielded sensor) (Fig. 9). Since the fabricated sensor was passively ventilated, poor air circulation, and albedo effect of the white PVC material housing the sensor are known to contribute to poor performance of radiation shields (Tarara and Hoheisel, 2007). On the other hand, the day-time temperature records of the sensor inside Stevenson’s screen were comparable to that of the Envilog GP5W-Shell® sensor (ecoTech, Germany), which were significantly lower than those of unshielded and sensor in fabricated shield (Fig. 9). The experimental data on temperature sensors therefore indicate that the Stevenson’s screen and radiation shield of Envilog GP5W-Shell® sensor were effective in blocking solar radiation, hence providing reference values (‘true values’) of near-surface temperature. However, low-cost fabricated solar radiation shields are still necessary given that the-state-of-the art shielded temperature sensors are still largely unavailable in most poor developed countries such as Kenya.

Comparisons between mobile and fixed site air temperatures indicated that mobile measurements were generally higher than time-synchronized fixed site measurements. The delay in temperature response with time (‘memory effect’) was assumed to be negligible (not evaluated) given the steady walking pace and 30 s time interval used to record NST that we considered sufficient to reduce the effect of such micro‐scale turbulence. However, this ‘memory effect’ is known to vary from sensor to sensor, with a potential to lose spatial detail (Burt and Podesta, 2020). Unlike vehicular traverses (e.g., Zhou et al., 2020), walking traverse is not limited to paved roads. Rather, walking traverse allows one to navigate through a wider variety of land cover types and also provides for adequate response time for the sensors to capture and record the temperature including transient turbulence.

It is evident that there is an effect of time on the ΔT values (Fig. 9). Histogram of evening records showed relatively normal distribution and greater range in ΔT values compared to the morning records. Given that the coldest time of the day occurs at sunrise (6:00 to 6:30 AM) when the interference of solar radiation on NST and LST patterns would be minimal (Fig. 10), the differences in ΔT values may be attributed to effects of both direct and diffuse solar radiation as well as ground heating. Moreover, hot and cold regions of Landsat-based LST map (Fig. 10) are suggestive of thermal properties of the surface features, owing to the fact that the Landsat image was acquired in the morning (07:43:21 AM) (Table 4) when radiation effects are minimal. Since surfaces radiates heat throughout the night, those surfaces that have high heat capacity would retain more thermal energy than those with lower heat capacity. Indeed, the clustering of ΔT values of the in situ traverse (cold spots and hot spots) for the late afternoon traverse walk (8th January 2018) are more significant than the morning traverse walk (18th February 2021) (Fig. 8). Consequently, in a clear sunny day, NST records collected in the afternoons would be more appropriate for characterizing spatial temperature variability as opposed to those collected in the morning.

The temperature difference between NST ‘cold spots’ and ‘hot spot’ in the study area (Fig. 11) may be attributed to a suite of thermal properties and aerodynamic conditions created by the landscape elements (e.g., tarmac, bare soil, buildings, pavements, and grasslands, etc.), although these were not evaluated in this study. The location of significant ΔT clusters coincide with cold and hots spots (Fig. 11) coincide with landcover classes (dense trees lightly built areas with tall and relatively dense tree cover, and paved areas made up of asphalt with no tree cover) (Table 7). The statistically significant coefficient of MNDWI, and NDBI (p < 0.01) (Table 8) can only explain 15% of the variation in the observed ΔT patterns. On the other hand, the coefficients of albedo, MNDWI, and NDBI could explain 46% of the variations in LST patterns (Table 9). On examination of the MNDWI spectral grid (Fig. 13), water bodies were over-estimated especially in areas that appear dark such as roads and pavements made up of asphalt (Fig. 7), an observation that has been made by other workers (e.g., Yang et al. 2018). Such artifacts may partially account for the poor performance of spectral indices in explaining the ΔT patterns. Simultaneous measurements of biophysical variables and NST records should be considered in future studies to capture the thermal source area for a temperature measurement ("foot print") and enhance reliability of the predictor variables. Indeed, biogeophysical variables (e.g., soil moisture or vegetation state) are ephemeral (can vary seasonally) and have been shown to contribute to the soil-atmosphere temperature offset (ΔT) (Aalto et al., 2018).and Studies show that tree cover control microclimates through shading (the difference between outside-forest radiation and within-canopy radiation), cooling and humidifying effects that significantly differ from synoptic weather conditions (Lindén et al., 2016; Wang et al., 2018). Humidifying effects occur through transpiration whereby, trees transfer sensible heat to latent heat, thereby leading to cooling effect and buffering of diurnal amplitude of air temperature (Lindén et al., 2016). Considering that many landscapes in tropical environments are physically heterogeneous, accurate characterizations of spatial variability in temperature conditions, may help identify microenvironments that significantly differ from synoptic weather conditions and evaluate the causes of such variations. Given the worsening conditions created by anthropogenic climate change and urban development, more ground-based peri-urban microclimate monitoring campaigns are needed to enrich our understanding of the complex land surface‐atmosphere interaction, for proper adaptive and mitigation measures.

Table 9 Table Summary of ordinary least square regression of LST (dependent variable) and Albedo, MNDWI, and NDBI (independent variables) results
Full size table

5 Conclusion

The study established that; (i) the use of fixed and mobile temperature sensors in time-synchronized in situ traverses under clear sky during the dry season can yield statistically significant temperature gradients (ΔT) attributable to landscape features, (ii) late afternoons (3:00 –5:00 PM local solar time) yield the most statistically significant ΔT (LST-T2m) clusters (hot spots and cold spots), (iii) only statistically significant NST clusters (hot spots and cold spots) compared to LST estimates from ‘cloud-free’ Landsat 8 OLI (Operational Land Imager) satellite image, and (iv) the selected satellite indices of surface properties (MNDWI and NDBI) can explain 15% of ΔT variation, while albedo, MNDWI, and NDBI can explain 46% of the variations in LST patterns. Our results suggest that under clear sky, Landsat-based LST and late afternoon NST values relate to spatial arrangement of landscape elements and their properties during dry season. Simultaneous characterization of biophysical attributes of sites along the traverse may provide additional explanatory variables for evaluate the contribution of various landscape elements on thermal variability, therefore improve regression models for urban thermal ecology.