Neural network-based adaptive sliding mode control for underactuated dual overhead cranes suffering from matched and unmatched disturbances

Abstract

To improve transportation capacity, dual overhead crane systems (DOCSs) are playing an increasingly important role in the transportation of large/heavy cargos and containers. Unfortunately, when trying to deal with the control problem, current methods fail to fully consider such factors as external disturbances, input dead zones, parameter uncertainties, and other unmodeled dynamics that DOCSs usually suffer from. As a result, dramatic degradation is caused in the control performance, which badly hinders the practical applications of DOCSs. Motivated by this fact, this paper designs a neural network-based adaptive sliding mode control (SMC) method for DOCS to solve the aforementioned issues, which achieves satisfactory control performance for both actuated and underactuated state variables, even in the presence of matched and mismatched disturbances. The asymptotic stability of the desired equilibrium point is proved with rigorous Lyapunov-based analysis. Finally, extensive hardware experimental results are collected to verify the efficiency and robustness of the proposed method.

1 Introduction

Single overhead crane systems (SOCSs) are widely used in harbors, factories, and workshops. As typical underactuated systems, cranes have fewer control inputs than their degrees of freedom, making the controller design task a very challenging problem. Moreover, according to the transportation requirements, the control goal of crane systems includes accurate trolley positioning and fast payload swing suppression. Specifically, the swing angles need to be suppressed as small as possible during the transportation, so that the payload can be transported to the desired position stably. To achieve such requirements, the couplings between the unactuated states (i.e., payload swing angles) and the actuated states (i.e., trolley positions) need to be enhanced appropriately, which often requires elaborate analysis and design. In recent decades, many scholars have developed abundant effective controllers for SOCS to solve the above-mentioned open and challenging problems, including input shapers [1], trajectory planning algorithms [2–4], adaptive control [5–7], SMC [8–12], energy-based control [13–15], optimal control [16], intelligent control [17–19], and so forth.

Nevertheless, with the advancement of manufacturing, the cargos become larger and heavier, which can no longer be regarded as a mass point. Besides, the transportation capacity of a single crane (i.e., SOCS) is not enough to handle complex transportation tasks. Therefore, two cranes are combined together to form a DOCS system, so as to simultaneously convey a single large cargo efficiently, which plays a more and more important role in the modern cargo transportation industry. Furthermore, in addition to the issues existed in SOCS, DOCS is of more complex couplings and stronger nonlinearities, which makes the controller design problem even more challenging. Specifically, compared with SOCS, DOCS has more degrees of freedom. Moreover, in addition to non-holonomic constraints, there are geometric constraints in DOCS, which makes the couplings between the system states more sophisticated. Recently, the above-mentioned open and challenging problems attract mounting scholars to study DOCS. Some scholars apply open-loop control algorithms to DOCS [20–23]. [24] proposes a modified extra-insensitive input shaper to suppress the payload swing and pitch in DOCS, which is validated by simulation and experimental results. In [25], an automatic path planning algorithm for dual-crane is designed that can quickly generate optimized lifting paths even under complex constraints. However, the control performance of these open-loop algorithms degrades drastically under various disturbances. For this reason, some closed-loop control algorithms have been developed [26, 27]. To achieve trajectory tracking of multiple mobile cranes, Qian, et al. [28] construct a robust iterative learning controller based on the linearization of the dynamics. Perig, et al. develop a series of linearization methods to linearize DOCS and then achieve optimal control in [29]. [30] designs an adaptive output feedback controller to achieve high-performance control of DOCS with payload hoisting/lowering ability.

Summarizing the existing results, some scholars have conducted preliminary research on DOCS and achieved phased results in certain aspects. However, the control of DOCS still presents many issues, which are drawn as follows:

• 1) Most controllers applied to DOCS are open-loop controllers. For example, the input shapers, similar to other open-loop algorithms, are less robust when the systems suffer from initial swing disturbances and other various disturbances, which is a nonnegligible drawback in practice. In addition, to address the closed-loop control problems of DOCS, linearizations or approximations are widely adopted, which cannot guarantee the stability of the system towards external disturbances.

• 2) Worse still, most existing results are based on exact model knowledge (i.e., some parameters of DOCS are involved in the controller law). In practice, the measurement of the precise value of the parameters will greatly reduce transportation efficiency. Furthermore, plant parameters (e.g., payload mass) vary from different transportation tasks frequently, which may greatly degrade the control performance of these methods.

• 3) Moreover, DOCSs are disturbed by matched disturbances persistently. For example, input dead zones of servo motors and frictions are piecewise discontinuous nonlinear functions, whose precise modeling is an open problem. To eliminate the swing, the trolley needs to move back and forth, which changes the direction of the friction force, making it even more difficult for the controller to achieve satisfactory anti-swing performance.

• 4) Presently, almost no robust algorithm for DOCS has been developed. For instance, SMC has achieved remarkable results on relatively simple underactuated systems [12]. However, DOCS presents higher degrees of freedom and stronger nonlinearities, thus it is quite difficult to design a sliding surface stabilizing all states simultaneously and complete stability analysis.

Based on these observations, this paper proposes an adaptive SMC method based on a neural network and a new sliding manifold to solve the above problems. Specifically, two groups of new auxiliary variables are constructed to transform DOCS into a cascade system. Based on these closely related variables, a new sliding surface is elaborately constructed with more swing-related information incorporated to suppress payload swing. Besides, a neural network is adopted to address parameter uncertainties, so that DOCS can deliver different masses and sizes payloads. Moreover, unmodeled dynamics, such as frictions and input dead zones of servo motors, are also compensated by the neural network. Finally, an adaptive SMC is designed to stabilize both actuated and unactuated states, even when DOCSs suffer from both matched and unmatched disturbances, which guarantees more reliable performance in practical application. The asymptotic stability of the desired equilibrium point is strictly guaranteed through Lyapunov technique without tuning to linearizations or approximations. Furthermore, extensive hardware experiments are collected to validate the efficiency and robustness of the proposed method.

The innovations and contributions in this paper are summarized as follows:

• 1) Based on two groups of new auxiliary variables, a new sliding surface is elaborately constructed with more swing-related information incorporated, which can stabilize both actuated and unactuated states and suppress swing quickly, even when DOCSs suffer from matched and unmatched disturbances.

• 2) A neural network is introduced into the SMC controller to address parameter uncertainties and unmodeled dynamics of DOCS and hence improve the system robustness, which better facilitates the practical application of the proposed method.

• 3) The asymptotic stability of the desired equilibrium point is demonstrated without turning to linearizations or approximations.

The rest of this article is structured as follows: Section 2 briefly introduces DOCS and the control problem. Section 3 depicts the design process of the adaptive sliding mode controller. In Sect. 4, the stability analysis is presented. Simulation results are shown in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Problem statement

To facilitate description, the following abbreviations are defined:

$$\begin{aligned}& s_{i}=\sin \theta _{i}, \qquad c_{i}=\cos \theta _{i},\qquad s_{i \pm j}=\sin (\theta _{i} \pm \theta _{j} ), \\& c_{i \pm j}=\cos (\theta _{i} \pm \theta _{j} ), \quad i, j=1, 2, 3\ (i \neq j). \end{aligned}$$

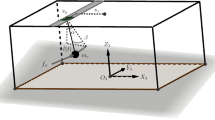
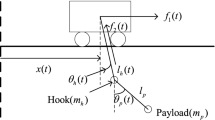
As shown in Fig. 1, a large/heavy payload is cooperatively transported by two cranes that run on the same rail. Each crane is connected to the payload through a hoisting rope (the two connection points are $A_{1}$, $A_{2}$), whose length is denoted by l (>0). The distance between $A_{1}$, $A_{2}$ is 2a. $m_{1}$, $m_{2}$, respectively, denote the masses of crane 1 and crane 2. The driving forces of two cranes are $F_{1}$, $F_{2}$, respectively. $x_{1}(t)$, $x_{2}(t)$ indicate the traveling displacements of crane 1 and crane 2. m stands for the mass of the payload. The payload inclination is $\theta _{3}$, while the swing angles of the two hoisting ropes are $\theta _{1}$, $\theta _{2}$, respectively. b depicts the vertical distance between the payload barycenter and the line $A_{1}A_{2}$.

Figure 1

Structure diagram of DOCS

It can be observed from Fig. 1 that the DOCS has the following geometric constraints:

$$ \begin{aligned} &l s_{1}-l s_{2}+2 a c_{3}- (x_{2}-x_{1} ) = 0, \\ &l c_{1}-l c_{2}+2 a s_{3} = 0. \end{aligned} $$

(1)

The input dead zones of the servo motors are expressed as

$$ Z(F_{i})\triangleq \textstyle\begin{cases} h_{r}(F_{i}-b_{r}), & F_{i}\ge b_{r}, \\ 0, & b_{l}< F_{i}< b_{r},\quad (i=1, 2), \\ h_{l}(F_{i}-b_{l}), & F_{i}\le b_{l}, \end{cases} $$

(2)

where $Z(F_{1})$ and $Z(F_{2})$ denote the real input forces of DOCS, and $h_{l}(*)$ and $h_{r}(*)$ represent the lower and upper bounds of the dead zone, respectively. To facilitate the design of the controller, $Z(F_{1})$ and $Z(F_{2})$ are redefined as $Z(F_{i})= F_{i} + \Delta F_{i}$, $i=1, 2$.

In this paper, Lagrange’s equation is utilized to establish the model of DOCS and a similar modeling process can also be found in [31], which is as follows:

$$\begin{aligned} \frac{d}{{dt}} \biggl( {\frac{{\partial L}}{{\partial {{\dot{q}}_{k}}}}} \biggr) - \frac{{\partial L}}{{\partial {q_{k}}}} = {Q_{k}}, \end{aligned}$$

(3)

where $L(t)=T(t)-U(t)$ indicates the Lagrange multiplier, $T(t)$ denotes the kinematic energy of the system, $U(t)$ represents the gravity potential energy of the system, and $q_{k}$ and $Q_{k}$ ($k = 1, 2$) denote the system states and generalized force, respectively.

After derivation, the explicit expression of the kinematic energy $T(t)$ can be arranged as follows:

$$\begin{aligned} T ={}& \biggl( {\frac{1}{2}{m_{1}} + \frac{1}{8}m} \biggr)\dot{x}_{1}^{2} + \biggl( {\frac{1}{2}{m_{2}} + \frac{1}{8}m} \biggr) \dot{x}_{2}^{2} + \frac{1}{4}m{{ \dot{x}}_{1}} {{\dot{x}}_{2}} \\ &{}+ \frac{1}{8}m{l^{2}} \dot{\theta }_{1}^{2} + \frac{1}{8}m{l^{2}} \dot{\theta }_{2}^{2}+ \frac{1}{2}m{b^{2}}\dot{\theta }_{3}^{2} + \frac{1}{4}m{l^{2}} {c_{1 - 2}} {{\dot{\theta }}_{1}} {{\dot{\theta }}_{2}} \\ &{}- \frac{1}{2}mbl{c_{1 + 3}} {{ \dot{\theta }}_{1}} {{\dot{\theta }}_{3}} - \frac{1}{2}mbl{c_{2 + 3}} {{ \dot{\theta }}_{2}} {{ \dot{\theta }}_{3}} \\ &{}+ \frac{1}{4}ml{c_{1}} {{\dot{\theta }}_{1}} ( {{{\dot{x}}_{1}} + {{ \dot{x}}_{2}}} ) + \frac{1}{4}ml{c_{2}} {{\dot{\theta }}_{2}} ( {{{\dot{x}}_{1}} + {{\dot{x}}_{2}}} ) \\ &{}- \frac{1}{2}mb{c_{3}} {{ \dot{\theta }}_{3}} ( {{{\dot{x}}_{1}} + {{\dot{x}}_{2}}} ). \end{aligned}$$

(4)

On the other hand, the gravity potential energy $U(t)$ of the system are calculated as follows:

$$\begin{aligned} U = mg \biggl( {\frac{l}{2}{c_{1}} + \frac{l}{2}{c_{2}} + b{c_{3}}} \biggr). \end{aligned}$$

(5)

Considering the DOCS suffering from both matched and unmatched disturbances and substituting (4) and (5) into (3), the dynamic equations of DOCS are described as follows:

$$\begin{aligned}& \quad \biggl(m_{1}+\frac{1}{4} m \biggr) \ddot{x}_{1}+\frac{1}{4} m \ddot{x}_{2}+ \frac{1}{4} m l c_{1} \ddot{\theta }_{1}+ \frac{1}{4} m l c_{2} \ddot{\theta }_{2} \\& \quad{}- \frac{1}{2} m b c_{3} \ddot{\theta }_{3}- \frac{1}{4} m l s_{1} \dot{\theta }_{1}^{2} -\frac{1}{4} m ls_{2} \dot{\theta }_{2}^{2}+ \frac{1}{2} m b s_{3} \dot{\theta }_{3}^{2} \\& =Z(F_{1})+d_{a1}=F_{1}+ \Delta F_{1}+d_{a1}, \end{aligned}$$

(6)

$$\begin{aligned}& \quad \frac{1}{4} m \ddot{x}_{1}+ \biggl(m_{2}+\frac{1}{4} m \biggr) \ddot{x}_{2}+ \frac{1}{4} m l c_{1} \ddot{\theta }_{1}+ \frac{1}{4} m l c_{2} \ddot{\theta }_{2} \\& \quad {}- \frac{1}{2} m b c_{3} \ddot{\theta }_{3}- \frac{1}{4} m ls_{1} \dot{\theta }_{1}^{2} -\frac{1}{4} m ls_{2} \dot{\theta }_{2}^{2}+ \frac{1}{2} m b s_{3} \dot{\theta }_{3}^{2} \\& =Z(F_{2})+d_{a2}=F_{2}+ \Delta F_{2}+d_{a2}, \end{aligned}$$

(7)

$$\begin{aligned}& \frac{1}{4} m l c_{1} \ddot{x}_{1}+ \frac{1}{4} m l c_{1} \ddot{x}_{2}+ \frac{1}{4} m l^{2} \ddot{\theta }_{1}+ \frac{1}{4} m l^{2} c_{1-2} \ddot{\theta }_{2} \\& \quad {}-\frac{1}{2} m b l c_{1+3} \ddot{\theta }_{3}+ \frac{1}{4} m l^{2} s_{1-2} \dot{\theta }_{2}^{2} \\& \quad {} +\frac{1}{2} m b l s_{1+3} \dot{\theta }_{3}^{2}+\frac{1}{2} m g l s_{1}=d_{u1}, \end{aligned}$$

(8)

$$\begin{aligned}& \frac{1}{4} m l c_{2} \ddot{x}_{1}+ \frac{1}{4} m l c_{2} \ddot{x}_{2}+ \frac{1}{4} m l^{2} c_{1-2} \ddot{\theta }_{1}+\frac{1}{4} m l^{2} \ddot{\theta }_{2} \\& \quad {}-\frac{1}{2} m b l c_{2+3} \ddot{\theta }_{3}- \frac{1}{4} m l^{2} s_{1-2} \dot{\theta }_{1}^{2} \\& \quad {} +\frac{1}{2} m b l s_{2+3} \dot{\theta }_{3}^{2}+\frac{1}{2} m g l s_{2}=d_{u2}, \end{aligned}$$

(9)

$$\begin{aligned}& -\frac{1}{2} m b c_{3} \ddot{x}_{1}- \frac{1}{2} m b c_{3} \ddot{x}_{2}- \frac{1}{2} m b l c_{1+3} \ddot{\theta }_{1}+m b^{2} \ddot{\theta }_{3} \\& \quad {}- \frac{1}{2} m b l c_{2+3} \ddot{\theta }_{2}+\frac{1}{2} m b l s_{1+3} \dot{\theta }_{1}^{2} \\& \quad {} +\frac{1}{2} m b l s_{2+3} \dot{\theta }_{2}^{2}+m g b s_{3}=d_{u3}, \end{aligned}$$

(10)

where ${d_{a1}}$, ${d_{a2}}$ denote matched disturbances, including frictions of the two trolleys and other unmodeled dynamics, and ${d_{u1}}$, ${d_{u2}}$, ${d_{u3}}$ represent unmatched disturbances.

To facilitate analysis, (6)–(10) are transformed into the following form:

$$ M(\boldsymbol{q}) \ddot{\boldsymbol{q}}+C({ \boldsymbol{q}}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+G(\boldsymbol{q}) = {\boldsymbol{u}}+{\boldsymbol{d}}, $$

(11)

where $\boldsymbol{q}(t)=[x_{1}(t)\enskip x_{2}(t)\enskip \theta _{1}(t)\enskip \theta _{2}(t)\enskip \theta _{3}(t)]^{\top }$ denotes the system state vector, $\boldsymbol{d}=[{d_{a1}},\ {d_{a2}}\, {d_{u1}},\ {d_{u2}},\ {d_{u3}}]^{\top }$ denotes the unknown disturbance vector, and $M(\boldsymbol{q}), C(\boldsymbol{q}, \dot{\boldsymbol{q}})\in \mathbb{R}^{5\times 5}$, $G( \boldsymbol{q})$, and q represent the inertia matrix, the centripetal-Coriolis matrix, the gravity vector, and the control input vector, respectively. The explicit expressions for the matrices in (11) are given as follows:

$$\begin{aligned}& M= \begin{bmatrix} m_{1}+\frac{1}{4} m & \frac{1}{4} m & \frac{1}{4} m l c_{1} & \frac{1}{4} m l c_{2} & -\frac{1}{2} m b c_{3} \\ \frac{1}{4} m & m_{2}+\frac{1}{4} m & \frac{1}{4} m l c_{1} & \frac{1}{4} m l c_{2} & -\frac{1}{2} m b c_{3} \\ \frac{1}{4} m l c_{1} & \frac{1}{4} m l c_{1} & \frac{1}{4} m l^{2} & \frac{1}{4}ml^{2}c_{1-2} & -\frac{1}{2}mblc_{1+3} \\ \frac{1}{4} m l c_{2} & \frac{1}{4} m l c_{2} & \frac{1}{4}ml^{2}c_{1-2} & \frac{1}{4} m l^{2} & -\frac{1}{2}mblc_{2+3} \\ -\frac{1}{2} m b c_{3} & -\frac{1}{2} m b c_{3} & -\frac{1}{2}mblc_{1+3} & -\frac{1}{2}mblc_{2+3} & m b^{2} \end{bmatrix}, \\& C= \begin{bmatrix} 0 & 0 & -\frac{1}{4} m l s_{1} \dot{\theta }_{1} & -\frac{1}{4} m l s_{2} \dot{\theta }_{2} & \frac{1}{2} m b s_{3} \dot{\theta }_{3} \\ 0 & 0 & -\frac{1}{4} m l s_{1} \dot{\theta }_{1} & -\frac{1}{4} m l_{2} \dot{\theta }_{2} & \frac{1}{2} m b s_{3} \dot{\theta }_{3} \\ 0 & 0 & 0 & \frac{1}{4} m l^{2} s_{1-2} \dot{\theta }_{2} & \frac{1}{2} m b l s_{1+3} \dot{\theta }_{3} \\ 0 & 0 & -\frac{1}{4} m l^{2} s_{1-2} \dot{\theta }_{1} & 0 & \frac{1}{2} m b l s_{2+3} \dot{\theta }_{3} \\ 0 & 0 & \frac{1}{2} m b l s_{1+3} \dot{\theta }_{1} & \frac{1}{2} m b l s_{2+3} \dot{\theta }_{2} & 0 \end{bmatrix}, \\& {G}= \begin{bmatrix} 0 \\ 0 \\ \frac{1}{2} m g l s_{1} \\ \frac{1}{2} m g l s_{2} \\ m g b s_{3} \end{bmatrix},\qquad {\boldsymbol{u}}= \begin{bmatrix} F_{1} +\Delta F_{1} \\ F_{2} +\Delta F_{2} \\ 0 \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

Due to physical constraints, the following assumptions are made for the DOCS.

Assumption 1

The swing angles of the payload and the payload inclination are all bounded, namely

$$ -\frac{\pi }{2}< \theta _{1}, \theta _{2}, \theta _{3}, ( \theta _{1}+\theta _{3} ), (\theta _{2}+\theta _{3} )< \frac{\pi }{2}. $$

(12)

Assumption 2

The disturbances ${d_{a1}}$, ${d_{a2}}$, ${d_{u1}}$, ${d_{u2}}$, and ${d_{u3}}$ have the following bounded property:

$$ \begin{aligned} &\bigl\vert d_{ai}(t) \bigr\vert \le {\bar{d}}_{ai}, \qquad \bigl\vert d_{uj}(t) \bigr\vert \le { \bar{d}}_{uj},\qquad \bigl\vert \dot{d}_{ai}(t) \bigr\vert < \bar{k}_{vi}, \\ &d_{uj}(t) \to 0, \quad \forall t \in {\mathbb{R} ^{+} }, i=1, 2, j=1, 2, 3, \end{aligned} $$

(13)

where ${\bar{d}_{a1}}$, ${\bar{d}_{a2}}$, ${\bar{k}_{v1}}$, ${\bar{k}_{v2}}$, ${ \bar{d}_{u1}}$, ${\bar{d}_{u2}}$, and ${\bar{d}_{u3}}$ denote the upper bounds of ${d_{a1}}$, ${d_{a2}}$, ${\dot{d}_{a1}}$, ${\dot{d}_{a2}}$, ${d_{u1}}$, ${d_{u2}}$, ${d_{u3}}$.

Remark 1

(12) is introduced to illustrate that the payload of crane systems cannot run above the rail, which are widely done by [8, 14, 26], and [30]. Besides, the disturbances in the real world are bound and similar assumption as (13) is utilized extensively by many related works [12, 32] and [33].

Symmetry widely exists in underactuated systems [34]. Specifically, the symmetry property $M(\boldsymbol{q})=M(\boldsymbol{q_{a}})$ ($\boldsymbol{q_{a}}$ denotes the actuated vector of DOCS) holds for DOCS, which is easily obtained from the expression of $M(\boldsymbol{q})$. Furthermore, underactuated systems can be transformed into cascaded forms by utilizing symmetry, which is convenient for the design of the controller. To achieve the transformation, and motivated by [34], the following two groups of auxiliary variables are constructed as

$$ \textstyle\begin{cases} \zeta _{1i}= \eta _{1i}-\eta _{1id}, \\ \zeta _{2i}= \eta _{2i}-\eta _{2id}, \\ \zeta _{3i}= \eta _{3i}-\eta _{3id}, \\ \zeta _{4i}= \eta _{4i}-\eta _{4id}, \quad i=1, 2, \end{cases} $$

(14)

where (6)–(9) are utilized, and $\eta _{1i}$, $\eta _{2i}$, $\eta _{3i}$, $\eta _{4i}$, $\eta _{1id}$, $\eta _{2id}$, $\eta _{3id}, \eta _{4id}, i=1, 2$ are defined as follow

$$\begin{aligned}& \textstyle\begin{cases} \eta _{11}= x_{1}+x_{2}+l\ln (\frac{1+s_{1}}{c_{1}})+ \frac{ls_{2-1}}{c_{1}}-\frac{2bs_{1+3}}{c_{1}}, \\ \eta _{21}= \dot{x}_{1}+\dot{x}_{2}+\frac{l}{c_{1}}\dot{\theta }_{1}+ \frac{lc_{1-2}}{c_{1}}\dot{\theta }_{2}-\frac{2bc_{1+3}}{c_{1}} \dot{\theta }_{3}, \\ \eta _{31}= (m_{1}+\frac{1}{4} m ) x_{1}+\frac{1}{4} m x_{2}+ \frac{1}{4} m ls_{1} \\ \hphantom{\eta _{31}={}}{}+\frac{1}{4} m ls_{2} -\frac{1}{2} mbs_{3}, \\ \eta _{41}= (m_{1}+\frac{1}{4} m ) \dot{x}_{1}+\frac{1}{4} m \dot{x}_{2}+\frac{1}{4} m l c_{1}\dot{\theta }_{1} \\ \hphantom{\eta _{41}={}}{}+\frac{1}{4} m l c_{2} \dot{\theta }_{2}-\frac{1}{2} mbc_{3} \dot{\theta }_{3}, \\ \eta _{11d}= x_{1d}+x_{2d}+l\ln (\frac{1+s_{1d}}{c_{1d}})+ \frac{ls_{2d-1d}}{c_{1d}}-\frac{2bs_{1d}}{c_{1d}}, \\ \eta _{21d}= \dot{x}_{1d}+\dot{x}_{2d}, \\ \eta _{31d}= (m_{1}+\frac{1}{4} m ) x_{1d}+\frac{1}{4} m x_{2d}+ \frac{1}{4} m l s_{1d}+\frac{1}{4} m ls_{2d}, \\ \eta _{41d}= (m_{1}+\frac{1}{4} m ) \dot{x}_{1d}+ \frac{1}{4} m \dot{x}_{2d}, \end{cases}\displaystyle \end{aligned}$$

(15)

$$\begin{aligned}& \textstyle\begin{cases} \eta _{12}=sx_{1}+x_{2}+l\ln (\frac{1+s_{2}}{c_{2}})+ \frac{ls_{1-2}}{c_{2}}-\frac{2bs_{2+3}}{c_{2}}, \\ \eta _{22}= \dot{x}_{1}+\dot{x}_{2}+\frac{lc_{1-2}}{c_{2}}\dot{\theta }_{1}+ \frac{l}{c_{2}}\dot{\theta }_{2}-\frac{2bc_{2+3}}{c_{2}}\dot{\theta }_{3}, \\ \eta _{32}= \frac{1}{4} mx_{1}+ (m_{2}+\frac{1}{4} m ) x_{2} +\frac{1}{4} m l s_{1} \\ \hphantom{\eta _{32}={}}{}+\frac{1}{4} m ls_{2} -\frac{1}{2} mbs_{3}, \\ \eta _{42}= \frac{1}{4} m\dot{x}_{1}+ (m_{2}+\frac{1}{4} m ) \dot{x}_{2}+\frac{1}{4} m l c_{1}\dot{\theta }_{1} \\ \hphantom{\eta _{42}={}}{}+\frac{1}{4} m l c_{2} \dot{\theta }_{2}-\frac{1}{2} mbc_{3} \dot{\theta }_{3}, \\ \eta _{12d}= x_{1d}+x_{2d}+l\ln (\frac{1+s_{2d}}{c_{2d}})+ \frac{ls_{1d-2d}}{c_{2d}}+\frac{2bs_{2d}}{c_{2d}}, \\ \eta _{22d}= \dot{x}_{1d}+\dot{x}_{2d}, \\ \eta _{32d}= \frac{1}{4} mx_{1d}+ (m_{2}+\frac{1}{4} m ) x_{2d} \\ \hphantom{\eta _{32d}={}}{}+ \frac{1}{4} m l s_{1d}+\frac{1}{4} m ls_{2d}, \\ \eta _{42d}= \frac{1}{4} m\dot{x}_{1d}+ (m_{2}+\frac{1}{4} m ) \dot{x}_{2d}, \end{cases}\displaystyle \end{aligned}$$

(16)

where $x_{d1}$, $x_{d2}$ denote the reference trajectories of crane 1 and crane 2, respectively, and the desired values for $\theta _{1}$, $\theta _{2}$ (i.e., $\theta _{1d}$, $\theta _{2d}$) are expressed as

$$ \theta _{1 d}=\arcsin \biggl(\frac{x_{d 2}-x_{d 1}-2 a}{2 l} \biggr)=- \theta _{2 d}. $$

(17)

Taking the time derivative of (14), the dynamic equations of DOCS in (11) can be transformed into the following cascade forms:

$$ \textstyle\begin{cases} \dot{\zeta }_{1i}= \zeta _{2i}+{\xi _{1i}}, \\ \dot{\zeta }_{2i}= \zeta _{3i}+{\xi _{2i}}-\frac{4d_{ui}}{mlc_{i}}+ \dot{\eta }_{2id}, \\ \dot{\zeta }_{3i}= \zeta _{4i}, \\ \dot{\zeta }_{4i}= F_{i}+\Delta F_{i}+d_{ai}+\dot{\eta }_{4id},\quad i=1, 2, \end{cases} $$

(18)

where (6)–(9) are utilized, and $\xi _{11}$, $\xi _{12}$, $\xi _{21}$, $\xi _{22}$, $\dot{\eta }_{21d}$ and $\dot{\eta }_{22d}$ are expressed as follows

$$ \begin{aligned} &{\xi _{11}}= -\frac{c_{2}}{c_{1}^{2}}\dot{ \theta }_{1}- \frac{c_{3}}{c_{1}^{2}}\dot{\theta }_{1},\qquad { \xi _{12}}=- \frac{c_{1}}{c_{2}^{2}}\dot{\theta }_{2}- \frac{c_{3}}{c_{2}^{2}} \dot{\theta }_{2}, \\ &\dot{\eta }_{21d}= \dot{\eta }_{22d}=\ddot{x}_{1d}+\ddot{x}_{2d}, \\ &\xi _{21}= -2g\tan \theta _{1} \\ &\hphantom{\xi _{21}={}}{}- \biggl( \frac{ls_{1}}{c_{1}^{2}}{ \dot{\theta }_{1}}+\frac{ls_{2}}{c_{1}^{2}}{\dot{ \theta }_{2}}+ \frac{2bs_{3}}{c_{1}^{2}}{\dot{\theta }_{3}} \biggr){\dot{\theta }_{1}}- \zeta _{31}, \\ &\xi _{22}= -2g\tan \theta _{2} \\ &\hphantom{\xi _{22}={}}{}- \biggl( \frac{ls_{1}}{c_{2}^{2}}{ \dot{\theta }_{1}}+\frac{ls_{2}}{c_{2}^{2}}{\dot{ \theta }_{2}}+ \frac{2bs_{3}}{c_{2}^{2}}{\dot{\theta }_{3}} \biggr){\dot{\theta }_{2}}- \zeta _{32}. \end{aligned} $$

(19)

Combining (14)–(16) and (18), the desired equilibrium point for the DOCS can be converted into the following form:

$$ \begin{aligned}[b] &\quad {[\zeta _{11}, \zeta _{12}, \zeta _{21}, \zeta _{22}, \zeta _{31}, \zeta _{32}, \zeta _{41}, \zeta _{42} ]}^{\top } \\ & = [\zeta _{11d}, \zeta _{12d},\zeta _{21d}, \zeta _{22d}, \zeta _{31d}, \zeta _{32d}, \zeta _{41d}, \zeta _{42d} ]^{\top } \\ &\qquad \Longleftrightarrow \quad [x_{1}, x_{2}, \theta _{1}, \theta _{2}, \theta _{3}, \dot{x}_{1}, \dot{x}_{2}, \dot{\theta }_{1}, \dot{\theta }_{2}, \dot{\theta }_{3} ]^{\top } \\ &\hphantom{\qquad \Longleftrightarrow \ \ } = [x_{d 1}, x_{d 2}, \theta _{1 d}, \theta _{2 d}, 0,0,0,0,0,0 ]^{\top }. \end{aligned} $$

(20)

The control objective of this paper is to drive DOCS to the desired equilibrium point (20) and improve the robustness of the system with fast swing elimination. To transport the payload to the desired position, the following property always holds for the reference trajectories:

$$ \lim_{t \to \infty } \dot{x}_{d 1}(t), \dot{x}_{d 2}(t), \ddot{x}_{d 1}(t), \ddot{x}_{d 2}(t)=0. $$

(21)

Remark 2

In [26], the geometric constraints (1) are incorporated into the dynamic equation (11) by utilizing implicit functions to obtain a lower-dimensional model, which facilitates the design and stability of the controller. However, the characteristics of the model are hidden and the couplings between states become more complicated, making the designed controller non-intuitive. In this paper, regarding the geometric constraints as constraints and couplings between states, the dynamic equation (11) is transformed into cascade forms (18) by utilizing the symmetry. Finally, the designed controller based on the cascade forms is concise and intuitive, as shown in Sect. 3.

3 Controller design

In this section, an adaptive sliding mode controller is designed for the DOCS to enhance its robustness. Specifically, a sliding surface based on the cascade forms is constructed. Besides, a neural network is introduced to estimate the unknown parts of the system dynamics.

Based on the newly obtained variables (14), the following sliding manifold is constructed:

$$ s_{i}={\lambda }_{1i}\zeta _{1i}+{\lambda }_{2i}\zeta _{2i}+{ \lambda }_{3i}\zeta _{3i}+\zeta _{4i},\quad i=1, 2, $$

(22)

where $\lambda _{1i}$, $\lambda _{2i}$, $\lambda _{3i}$, $i=1, 2$ are parameters to be determined. The explicit expressions of the time derivative of $s_{1}$ and $s_{2}$ are calculated as

$$ \begin{aligned}[b] \dot{s}_{i} ={}&\underbrace{{\lambda }_{1i} (\zeta _{2i}+\xi _{1i} )+{\lambda }_{2i}(\zeta _{3i}+{\xi _{2i}})+{\lambda }_{3i}\zeta _{4i} +\dot{\eta }_{4id}}_{h_{ i}(m,l,b,t)} \\ &{}+F_{i}+\Delta F_{i}+{\lambda }_{2i}\dot{ \eta }_{2id}+d_{ai}-{\lambda }_{2i} \frac{4d_{ui}}{mlc_{i}}, \\ & i=1, 2, \end{aligned} $$

(23)

where (18) is utilized and ${h_{ i}(m,l,b,t)}$ is the part of the controller related to the system parameters. ${h_{ i}(m,l,b,t)}$ is the nominal value, and the actual value of $h_{ i}$ is depicted as $h_{\Delta i} =h_{ i}+\Delta {h_{ i} }$. Therefore, the unknown parts of (23) can be rearranged as follows:

$$ \dot{s}_{i} =h_{ i}+F_{i}+{ \lambda }_{2i}\dot{\eta }_{2id}+D_{i}, \quad i=1, 2, $$

(24)

where $D_{1}$ and $D_{2}$ are the unknown parts of $\dot{s}_{1}$ and $\dot{s}_{2}$, which are rearranged into the following forms:

$$ D_{i}=d_{ai}-{\lambda }_{2i}\frac{4d_{ui}}{mlc_{i}}+ \Delta {h_{ i} }+\Delta F_{i},\quad i=1, 2. $$

(25)

The following neural networks are introduced to approximate the unknown parts $D_{1}$ and $D_{2}$:

$$ D_{1}=W_{1}^{\top } \sigma ( \boldsymbol{x} )+ { \epsilon _{1}},\qquad D_{2}=W_{2}^{\top } \sigma ( \boldsymbol{x} )+ { \epsilon _{2}}, $$

(26)

where $\boldsymbol{x} =[{x_{1}},{x_{2}},{\theta _{1}},{{\dot{x}}_{1}},{{\dot{x}}_{2}},{{ \dot{\theta }}_{1}},1]^{\top }$, $\sigma ( * ) =\frac{1}{1+e^{-*}}$ is an activation function, ${W_{1}}$, ${W_{2}}$ denote input and output weights, ${ \epsilon _{1}}$, ${\epsilon _{2}}$ are approximation errors, whose upper bounds are ${\bar{\epsilon }_{1}}$, ${\bar{\epsilon }_{2}}$.¹

Based on the above analysis, the following adaptive sliding mode controllers are designed:

$$ \begin{aligned}[b] F_{i}={}&{-}{\lambda }_{1i} ( \zeta _{2i}+\xi _{1i} )-{\lambda }_{2i}(\zeta _{3i}+{\xi _{2i}})-{\lambda }_{3i}\zeta _{4i}- \dot{\eta }_{4id} \\ &{}-{\lambda }_{2i}\dot{\eta }_{2id}-\hat{W}_{i}^{\top } \sigma ( \boldsymbol{x} )-K_{i}\operatorname{sgn}(s_{i}) \\ &{}-f_{i},\quad i=1, 2 \end{aligned} $$

(27)

with

$$ f_{i}=k_{\epsilon _{i}} \frac{s_{i}}{ \Vert s_{i} \Vert }, \quad i=1, 2, $$

(28)

where $K_{1}$, $K_{2}$ are positive control gains to be selected, $f_{1}$ and $f_{2}$ are introduced to provide robustness in the presence of estimating errors of the radial basis function neural network (RBFNN), and $k_{\epsilon _{1}}>{\bar{\epsilon }_{1}}$, $k_{\epsilon _{2}}>{ \bar{\epsilon }_{2}}$.

To construct the update laws of the neural network, the following estimation errors are first defined:

$$ \begin{aligned}[b] {\tilde{W}_{i}} &= {W_{i}} - {\hat{W}_{i}}, {{\Omega_{i}}} \\ &={W_{i}^{T} \sigma ( \boldsymbol{x} ) - \hat{W}_{i}^{T}\sigma ( \boldsymbol{x} ) + {\epsilon _{i}}}, \quad i=1, 2. \end{aligned} $$

(29)

The update laws of weights ${W_{1}}$, ${W_{2}}$ are elaborately designed as follows:

$$ \dot{\hat{W}}_{i}= a s_{i} \Gamma _{i}\sigma ( \boldsymbol{x} ),\quad i=1, 2, $$

(30)

where a is a positive parameter and $\Gamma _{1}$ and $\Gamma _{2}$ are positive diagonal parameter matrices. To illustrate the entire control system design process, a block diagram is provided in Fig. 2.

Figure 2

Block diagram for the closed-loop system

Remark 3

The RBFNN adopted in this paper is capable of universal approximation [37]. However, almost no neural network-based controller for underactuated system is robust to unmatched disturbances [19]. Based on elaborately designed sliding surface and neural network, the proposed method achieves the robust control while DOCS suffers form unmatched disturbances. Specifically, when the payload is disturbed, the cranes need to move back and forth to eliminate the swing, which requires appropriate swing-related feedbacks being incorporated into the sliding surface. Moreover, the friction force will change drastically during the process, and a large part of it can be compensated by the one-hidden-layer RBFNN with fast approximation capability.

Remark 4

Although the adopted neural network is able to compensate the frictions and the dead zones of the actuators, it is difficult to know the accuracy of the compensation because the frictions and the dead zones are hard to measure. Furthermore, the sliding mode controller is also robust to various disturbances and can partially conquer the frictions and the dead zones of the actuators. On the other hand, the frictions keep changing among the entire transportation. For neural networks, there will be a delay in compensating for signals that change quickly. Hence, once the system reaches the desired equilibrium point, it can be determined that the sliding mode controller and the neural network accurately compensate for frictions and other unmodeled dynamics together.

Remark 5

Although the sliding mode controller is known for strong robustness, the cost is that its control gain may be large, and the switching function will cause chattering problems to the motors and the mechanical systems. These factors hinder the application of the sliding mode controller. Hence, we adopt the neural network to compensate for various disturbances, thereby reducing the control gains of the sliding mode controller and weakening the chattering problem of the mechanical systems.

4 Stability analysis

Before carrying out analysis, the following property is introduced:

Property 1

If $H \in {\mathbb{R} ^{n \times n}}$ is a positive definite, symmetric matrix, the following property holds:

$$ {h_{1}} { \Vert \boldsymbol{x} \Vert ^{2}} \le { \boldsymbol{x}^{\top }}H\boldsymbol{x} \le {h_{2}} { \Vert \boldsymbol{x} \Vert ^{2}},\quad \forall \boldsymbol{x} \in {\mathbb{R} ^{n}}, $$

(31)

where ${h_{1}}$, ${h_{2}}$ denote the minimum and the maximum eigenvalues of H, respectively.

Theorem 1

For the underactuated DOCS (6)–(10), the designed controller (27) guarantees that the desired equilibrium point introduced in (20) is asymptotically stable.

Proof

For clarity, the proof of Theorem 1 is split into two steps. Specially, it first shows that the adaptive SMC can drive the system states to the sliding surface. After that, the asymptotic stability of the desired equilibrium point is demonstrated.

Step 1. First, choose the following Lyapunov function candidate:

$$ \begin{aligned}[b] V ( t ) ={}& \frac{1}{2}s_{1}^{2}+ \frac{1}{2}s_{2}^{2}+ \frac{1}{2{a}} \operatorname{Tr} \bigl( {\tilde{W}_{1}^{T}{\Gamma _{1} ^{ - 1}} {{ \tilde{W}}_{1}}} \bigr) \\ &{}+ \frac{1}{{2{a}}}\operatorname{Tr} \bigl( {\tilde{W}_{2}^{T}{ \Gamma _{2} ^{ - 1}} {{\tilde{W}}_{2}}} \bigr) . \end{aligned} $$

(32)

Taking the time derivative of $V ( t )$ yeilds

$$\begin{aligned} {{\dot{V}}}( t )={}& s_{1}\dot{s}_{1}+s_{2} \dot{s}_{2}+ \frac{1}{a}\operatorname{Tr} \bigl( { \tilde{W}_{1}^{T}{\Gamma _{1} ^{ - 1}} {{\dot{\tilde{W}}}_{1}}} \bigr) \\ &{}+ \frac{1}{{a}}\operatorname{Tr} \bigl( {\tilde{W}_{2}^{T}{ \Gamma _{2} ^{ - 1}} {{\dot{\tilde{W}}}_{2}}} \bigr) \\ ={}&s_{1} \bigl( h_{ 1}+F_{1}+{\lambda }_{21}\dot{\eta }_{21d}+W_{1}^{\top } \sigma ( \boldsymbol{x} ) \bigr) \\ &{}+s_{2}\bigl( h_{ 2}+F_{2} +{\lambda }_{22}\dot{\eta }_{22d}+W_{2}^{\top } \sigma ( \boldsymbol{x} )\bigr) \\ &{}- \frac{1}{a}\operatorname{Tr} \bigl( { \tilde{W}_{1}^{T}{\Gamma _{1} ^{ - 1}} {{\dot{\hat{W}}}_{1}}} \bigr) - \frac{1}{{a}}\operatorname{Tr} \bigl( { \tilde{W}_{2}^{T}{ \Gamma _{2} ^{ - 1}} {{\dot{\hat{W}}}_{2}}} \bigr) \\ ={}&{-}K_{1}s_{1} \operatorname{sgn}(s_{1})+s_{1} \tilde{W}_{1}^{\top }\sigma ( \boldsymbol{x} )- \frac{1}{a}\operatorname{Tr} \bigl( {\tilde{W}_{1}^{T}{ \Gamma _{1} ^{ - 1}} {{\dot{\hat{W}}}_{1}}} \bigr) \\ &{}+s_{1}\epsilon _{1}-s_{1}f_{1} \\ &{}-K_{2}s_{2} \operatorname{sgn}(s_{2})+s_{2} \tilde{W}_{2}^{\top }\sigma ( \boldsymbol{x} ) \\ &{}- \frac{1}{{a}}\operatorname{Tr} \bigl( {\tilde{W}_{2}^{T}{ \Gamma _{2} ^{ - 1}} {{\dot{\hat{W}}}_{2}}} \bigr) +s_{2}\epsilon _{2}-s_{2}f_{2} \\ ={}&{-}K_{1} \vert s_{1} \vert +\operatorname{Tr} \biggl[ \tilde{W}_{1}^{T} \biggl(s_{1} \sigma ( \boldsymbol{x} )-\frac{1}{a}\Gamma _{1} ^{ - 1}{{ \dot{\hat{W}}}_{1}} \biggr) \biggr] \\ &{}+s_{1}\epsilon _{1}-k_{\epsilon _{1}} \frac{s_{1}^{2}}{ \Vert s_{1} \Vert } \\ &{}-K_{2} \vert s_{2} \vert +\operatorname{Tr} \biggl[ \tilde{W}_{2}^{T} \biggl(s_{2} \sigma ( \boldsymbol{x} )-\frac{1}{a}\Gamma _{2} ^{ - 1}{{ \dot{\hat{W}}}_{2}} \biggr) \biggr] \\ &{}+s_{2}\epsilon _{2}-k_{\epsilon _{2}} \frac{s_{2}^{2}}{ \Vert s_{2} \Vert } \\ \le {}&{-}K_{1} \vert s_{1} \vert - \bigl(k_{\epsilon _{1}}- \Vert \epsilon _{1} \Vert \bigr) \Vert s_{1} \Vert \\ &{} -K_{2} \vert s_{2} \vert -\bigl(k_{\epsilon _{2}}- \Vert \epsilon _{2} \Vert \bigr) \Vert s_{2} \Vert \le 0, \end{aligned}$$

(33)

where (24), (25), (27), (28) and (30) are utilized. The following conclusion can be obtained

$$ \begin{aligned}[b] \dot{V}(t)\le 0&\quad \Rightarrow\quad {V}(t) \in {\mathcal{L}_{\infty }} \\ &\quad \Rightarrow\quad { \hat{W}_{1}}\in {\mathcal{L}_{\infty }}, \quad { \hat{W}_{2}}\in {\mathcal{L}_{\infty }}. \end{aligned} $$

(34)

The result in (33) indicates that ${\hat{W}_{1}}$ and ${\hat{W}_{2}}$ are all bounded as

$$ {{\Omega_{i}}}={W_{i}^{T} \sigma ( \boldsymbol{x} ) - \hat{W}_{i}^{T}\sigma ( \boldsymbol{x} ) + {\epsilon _{i}}} \le {{{{\bar{\Omega }}}}_{i}},\quad i=1, 2 , $$

(35)

where ${{\bar{\Omega }}_{1}}$, ${{\bar{\Omega }}_{2}}$ are the upper bounds of ${{\Omega_{1}}}$, ${{{{\Omega }}_{2}}}$.

To further analyze the convergence rate of the sliding manifold, another Lyapunov function candidate is given as follows:

$$ V_{1} ( t ) = \frac{1}{2}s_{1}^{2}+ \frac{1}{2}s_{2}^{2}. $$

(36)

The time derivative of $V_{1} ( t )$ can be expressed as

$$\begin{aligned} \dot{V}_{1} ( t ) \le {}&{-}K_{1} \vert s_{1} \vert -\bigl(k_{ \epsilon _{1}}- \Vert \epsilon _{1} \Vert \bigr) \Vert s_{1} \Vert +{\bar{\Omega }}_{1} \vert s_{1} \vert \end{aligned}$$

(37)

$$\begin{aligned} &{}-K_{2} \vert s_{2} \vert -\bigl(k_{\epsilon _{2}}- \Vert \epsilon _{2} \Vert \bigr) \Vert s_{2} \Vert +{\bar{\Omega }}_{2} \vert s_{2} \vert \end{aligned}$$

(38)

$$\begin{aligned} \begin{aligned} ={}&{-}(K_{1}-{\bar{\Omega }}_{1}) \vert s_{1} \vert -\bigl(k_{\epsilon _{1}}- \Vert \epsilon _{1} \Vert \bigr) \Vert s_{1} \Vert \\ &{}-(K_{2}-{\bar{\Omega }}_{2}) \vert s_{2} \vert \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned} &{}-\bigl(k_{\epsilon _{2}}- \Vert \epsilon _{2} \Vert \bigr) \Vert s_{2} \Vert \le -\gamma \sqrt{2V_{1}(t)}, \end{aligned}$$

(40)

where $\gamma \triangleq \min(K_{1}-{{\bar{\Omega }}_{1}}+k_{ \epsilon _{1}}-\|\epsilon _{1}\|, K_{2}-{{\bar{\Omega }}_{2}}+k_{ \epsilon _{2}}-\|\epsilon _{2}\|)$. The control gains ${K_{1}}$, ${K_{2}}$ in (27) are selected to satisfy the following conditions:

$$ {K_{1}} > {{\bar{\Omega }}_{1}} ,\qquad {K_{2}} > {{\bar{\Omega }}_{2}}. $$

(41)

Substituting the conditions (41) into (40), the following conclusion holds:

$$\begin{aligned} \dot{V}(t), \dot{V}_{1}(t)\le 0&\quad \Rightarrow\quad s_{i} = 0,\quad {\hat{W}_{i}} \in {\mathcal{L}_{\infty }} \\ &\quad \Rightarrow\quad \zeta _{4i}=-{\lambda }_{1i}\zeta _{1i}-{\lambda }_{2i} \zeta _{2i}-{\lambda }_{3i}\zeta _{3i} \\ &\quad \Rightarrow\quad \dot{s}_{i} = 0, \quad \forall t \ge {t_{f}}, i=1, 2, \end{aligned}$$

(42)

where $t_{f}\le \frac{\sqrt{2}}{\gamma }\sqrt{V_{1}(0)}$. Based on the above results, it can be concluded that the sliding surface will converge in a finite time $t_{f}$.

Step 2. Furthermore, the following auxiliary vector is constructed to proceed with the proof of Theorem 1:

$${\mathit{\zeta }}_{\mathit{a}\mathit{i}}={\left[\begin{array}{ccc}{\zeta }_{1i}& {\zeta }_{2i}& {\zeta }_{3i}\end{array}\right]}^{\mathrm{\top }},i=1,2.$$

(43)

Taking the time derivatives of ${\boldsymbol{\zeta _{a1}}}$ and ${\boldsymbol{\zeta _{a2}}}$ as

$$ \boldsymbol{\dot{\zeta }_{ai} }= A_{i}\boldsymbol{{\zeta _{ai}}} + { \boldsymbol{\xi _{i}}} + {\boldsymbol{\varsigma _{i}}},\quad i=1, 2, $$

(44)

where (18) and (42) are utilized, and $A_{i}, {\boldsymbol{\xi _{i}}}, {\boldsymbol{\varsigma _{i}}}$, $i=1, 2$ are expressed as follows,

$$ \begin{aligned}&A_{i} = \begin{bmatrix} 0&1&0 \\ 0&0&1 \\ { - {\lambda _{1i}}}& - {\lambda _{2i}}& - {\lambda _{3i}} \end{bmatrix}, \qquad {\boldsymbol{\xi _{i}}} = \begin{bmatrix} {\xi _{1i}} \\ {\xi _{2i}} \\ 0 \end{bmatrix}, \\ &\boldsymbol{\varsigma _{i}} = \begin{bmatrix} 0 \\ -\frac{4d_{ui}}{mlc_{i}}+\dot{\eta }_{2id} \\ 0 \end{bmatrix},\quad i=1, 2. \end{aligned} $$

(45)

It can be observed that $A_{1}$ and $A_{2}$ in (44) are quasi-linear systems. The stability of the quasi-linear system $A_{1}$ is analyzed first. To better deal with the linear part of (44), the following state transformation is made:

$$ \begin{aligned} \boldsymbol{{\mu }_{1}} = {{{P }_{1}}^{ - 1}} {\boldsymbol{\zeta _{a1}}} &\quad \Rightarrow \quad {\boldsymbol{\zeta _{a1}}} = {{P }_{1}} \boldsymbol{{\mu }_{1}} \\ &\quad \Rightarrow \quad \Vert {\boldsymbol{\zeta _{a1}}} \Vert \le \Vert {{P }_{1}} \Vert \cdot \Vert \boldsymbol{{\mu }_{1}} \Vert . \end{aligned} $$

(46)

Choose the following nonnegative Lyapunov function candidate:

$$ {V_{2}} ( t ) = {\boldsymbol{{\mu }_{1}} ^{\top }}\boldsymbol{{\mu }_{1}} = { \Vert \boldsymbol{{ \mu }_{1}} \Vert ^{2}} \ge 0. $$

(47)

Taking the time derivative of (47) produces

$$ {{\dot{V}}_{2}} ( t ) = - {{\boldsymbol{ \mu _{1} }} ^{ \top }} {{H_{1}}} {\boldsymbol{ \mu _{1} }} + 2{{\boldsymbol{\mu _{1} }} ^{\top }} {{{P _{1}}}^{ - 1}} {\boldsymbol{\xi _{1}}} + 2{{\boldsymbol{\mu _{1} }} ^{\top }} {{{P _{1}}}^{ - 1}} { \boldsymbol{\varsigma _{1}}}, $$

(48)

where

$$ {{{P }_{1}}^{ - 1}}A_{1}{{P }_{1}} = {{J}_{1}}, \qquad {H_{1} }={J_{1}^{ \top }}+J_{1}. $$

(49)

The upper bounds of the first two terms of (48) are unknown. To complete the proof, $\lambda _{1i}$, $\lambda _{2i}$, $\lambda _{3i}$, $i=1, 2$ are firstly selected to satisfy:

$$ {\lambda _{1i}} > 0,\qquad {\lambda _{2i}} > 0, \qquad {\lambda _{3i}} > 0,\quad i=1, 2. $$

(50)

Utilizing the Routh criterion, $A_{1}$, $A_{2}$ are Hurwitz. To facilitate analysis, all the roots of $A_{1}$ and $A_{2}$ are configured as $-k_{1}$ and $-k_{2}$. respectively, as long as

$$ {\lambda _{1i}} = k_{i}^{3},\qquad {\lambda _{2i}} = 3k_{i}^{2}, \qquad { \lambda _{3i}} = 3k_{i},\quad i=1,2. $$

(51)

To this end, ${H_{1} }$ is a Jordan Matrix as follows:

$$ J_{1}= \begin{bmatrix} -k_{1} & 1 & 0 \\ 0 & -k_{1} & 1 \\ 0 & 0 & -k_{1} \end{bmatrix}. $$

(52)

Moreover, to render ${H_{1} }$ positive, the minimum eigenvalue ${\lambda _{m1}}$ of ${H_{1}}$ is configured to satisfy

$$ {\lambda _{m1}} = 2k_{1} - \sqrt{2} > 0\quad \Rightarrow\quad k_{1} > \frac{{\sqrt{2} }}{2}. $$

(53)

Subsequently, the upper bounds of $\boldsymbol{\xi _{1}}$ and $\boldsymbol{\xi _{2}}$ are calculated as (please see the appendix for the explicit calculation):

$$ \Vert { {\boldsymbol{\xi _{1}}} } \Vert \le {\rho _{1}} { \Vert { \boldsymbol{\zeta _{a1}}} \Vert ^{2}}, \qquad \Vert { {\boldsymbol{\xi _{2}}} } \Vert \le {\rho _{2}} { \Vert {\boldsymbol{ \zeta _{a2}}} \Vert ^{2}}. $$

(54)

Using Property 1, the upper bound of (48) is calculated as

$$ \begin{aligned}[b] {{\dot{V}}_{2}} ( t ) \le{} & {-} {\lambda _{m1}} { \Vert {\boldsymbol{\mu _{1}}} \Vert ^{2}} + 2 \Vert {\boldsymbol{\mu _{1} }} \Vert \cdot \bigl\Vert {{\mathrm{{P _{1}}}^{ - 1}}} \bigr\Vert \cdot \bigl( \Vert {\boldsymbol{\xi _{1}}} \Vert + \Vert { \boldsymbol{\varsigma _{1}}} \Vert \bigr) \\ \le{} & {-} {\lambda _{m1}} { \Vert {\boldsymbol{\mu _{1} }} \Vert ^{2}} + 2{ \rho _{1}}\cdot \bigl\Vert {{ \mathrm{{P_{1} }}^{ - 1}}} \bigr\Vert \cdot { \Vert { \mathrm{{P_{1} }}} \Vert ^{2}} \cdot { \Vert { \boldsymbol{\mu _{1}}} \Vert ^{3}} \\ &{}+ 2 \Vert { \boldsymbol{\mu _{1}}} \Vert \cdot \bigl\Vert {{{ \mathrm{P _{1}}}^{ - 1}}} \bigr\Vert \cdot \Vert {\boldsymbol{ \varsigma _{1}}} \Vert \\ ={}& \Vert {\boldsymbol{\mu _{1} }} \Vert \bigl( {{L_{1}} {{ \Vert { \boldsymbol{\mu _{1} }} \Vert }^{2}} - {\lambda _{m1}} \Vert { \boldsymbol{\mu _{1} }} \Vert + {L_{2}}} \bigr) \\ ={}& \Vert {\boldsymbol{ \mu }} \Vert Q_{1}, \end{aligned} $$

(55)

where (54) and (46) are utilized, and ${\alpha _{1}}$, ${\alpha _{2}}$ are expressed as

$$ \alpha _{1}=2{\rho _{1}} \cdot \bigl\Vert {{\mathrm{{P_{1} }}^{ - 1}}} \bigr\Vert \cdot { \Vert {\mathrm{{P_{1} }}} \Vert ^{2}},\qquad { \alpha _{2}}=2 \bigl\Vert {{\mathrm{{P _{1}}}^{ - 1}}} \bigr\Vert \cdot \Vert {\boldsymbol{ \varsigma _{1}}} \Vert . $$

(56)

Noticing that $Q_{1}$ is a quadratic function going upwards, as long as

$$ \Delta = {\lambda _{m1}}^{2} - 4{\alpha _{1}} {\alpha _{2}} > 0, $$

(57)

there exists an interval Λ of $\|\boldsymbol{\mu }\|$ (>0) guaranteeing ${{\dot{V}}_{2}} ( t )\le \|\boldsymbol{\mu }_{1}\|Q_{1}<0$, which can be calculated as

$$ \Lambda = \biggl(\frac{{\lambda _{m1}} -\sqrt{\Delta }}{2{\alpha _{1}}}, \frac{{\lambda _{m1}}+ \sqrt{\Delta }}{2{\alpha _{1}}} \biggr). $$

If the initial value of $\|\boldsymbol{\mu }_{1}\|$ is set to satisfy $\|\boldsymbol{\mu }_{1}(0)\|\in \Lambda$, one can obtain that ${{\dot{V}}_{2}} ( t )\le 0$ and the following conclusion can be drawn:

$$ \lim_{t \to \infty } \Vert { \boldsymbol{ \mu _{1} }} \Vert = \frac{{\lambda _{m1}} -\sqrt{\Delta }}{2{\alpha _{1}}}. $$

(58)

Furthermore, combining (13) with (21), one can obtain

$$ \begin{aligned}[b] \Vert {\boldsymbol{\varsigma _{1}}} \Vert \to 0 &\quad \Rightarrow\quad \alpha _{2} \to 0 \quad \Rightarrow\quad \Delta \to { \lambda _{m1}}^{2} \\ &\quad \Rightarrow \quad \frac{{\lambda _{m1}} -\sqrt{\Delta }}{2{\alpha _{1}}} \to 0. \end{aligned} $$

(59)

Gathering the results in (58) and (59) gives rise to

$$ \begin{aligned}[b] &\lim_{t \to \infty } \Vert { \boldsymbol{\mu _{1} }} \Vert = 0 \\ &\quad \Rightarrow \quad \lim _{t \to \infty } {\boldsymbol{\mu _{1} }} = {{\mathbf{0}}} \quad \Rightarrow \quad \lim_{t \to \infty } { \boldsymbol{\zeta _{a1}}} = {{\mathbf{0}}} \\ &\quad \Rightarrow \quad \lim_{t \to \infty } \begin{bmatrix} {{\zeta _{11}}}&{{{\zeta _{21}}}}&{{\zeta _{31}}} \end{bmatrix} ^{\top } = \begin{bmatrix} 0&0&0 \end{bmatrix} ^{\top } \\ &\quad \Rightarrow\quad \lim_{t \to \infty } {\zeta _{41}} = {{\mathbf{0}}}, \end{aligned} $$

(60)

where (42) and (46) is utilized. For the system $\boldsymbol{{\dot{\zeta }_{a2}}}=A_{2}\boldsymbol{{\zeta _{a2}}} + {\boldsymbol{\xi _{2}}} + { \boldsymbol{\varsigma _{2}}}$, the proof process is similar to the above analysis, which will not be repeated here for brevity. Finally, Theorem 1 is proved as follows

$$ \begin{aligned}[b] &\quad \lim_{t \to \infty } [\zeta _{11}, \zeta _{12},\zeta _{21}, \zeta _{22}, \zeta _{31}, \zeta _{32}, \zeta _{41}, \zeta _{42} ]^{\top } \\ & = [\zeta _{11d}, \zeta _{12d},\zeta _{21d}, \zeta _{22d}, \zeta _{31d}, \zeta _{32d}, \zeta _{41d}, \zeta _{42d} ]^{\top }. \end{aligned} $$

(61)

 □

Remark 6

In fact, as a quasi-linear system, the performance of (44) mainly depends on the linear part of (44), i.e., the matrix $A_{1}$, $A_{2}$. Hence, if the parameters $\lambda _{1i}$, $\lambda _{2i}$, $\lambda _{3i}$, $i=1, 2$ of A are configured as the functions of k according to (51), the condition in (50) will be satisfied and then $A_{1}$, $A_{2}$ are Hurwitz. Moreover, further tuning $k_{1}$, $k_{2}$ within the range (53) by trial and error, the condition in (57) can be satisfied and the asymptotical stability of DOCS at the equilibrium point is guaranteed.

5 Hardware experimental results

The hardware experimental testbed has been explicitly described in [26], which is not introduced in this paper for brevity. The physical parameters of the testbed are as follows:

$$ \begin{aligned} &{m_{1}} = {m_{2}} = 4.6\mbox{ kg}, \qquad m = 4.12 \mbox{ kg}, l = 1 \mbox{ m}, \\ &a = 0.45 \mbox{ m}, \qquad b = 0.05 \mbox{ m}. \end{aligned} $$

(62)

Furthermore, the input dead zones of the two servo motors are $h_{r1}=h_{r2}=17.39~\mathrm{N}$ and $h_{l1}=h_{l2}=-17.39~\mathrm{N}$. The target positions of crane 1 and crane 2 are determined as 1.5 m and 2.4 m. The two cranes track the trajectories of the same shape to minimize the payload swing. According to the target positions, some smooth trajectories are introduced as follows:

$$ \begin{aligned} &{x_{1d}} ( t ) = 1.5 \bigl( {1 - {\mathrm{e}^{ - 0.0065{t^{3}}}}} \bigr), \\ &{x_{2d}} ( t ) = 1.5 \bigl( {1 - {\mathrm{e}^{ - 0.0065{t^{3}}}}} \bigr) + 0.9. \end{aligned} $$

(63)

The initial values of system states are set as

$$ {x_{1}} ( 0 ) = 0~\mathrm{m},\qquad {x_{2}} ( 0 ) = 0.9~\mathrm{m}. $$

(64)

The control gains of the proposed controller are tuned as

$$ \begin{aligned} &{K_{1}} = 5,\qquad {K_{2}} = 10,\qquad k{s_{1}} = 4,\qquad k{s_{2}} = 3, \\ &k{\epsilon _{1}} = k{\epsilon _{2}} = 10,\qquad a_{1} = 0.8,\qquad a_{2} = 1, \\ &\Gamma _{1}=\Gamma _{2}=\operatorname{diag}[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5]. \end{aligned} $$

(65)

It is worth pointing out that the control gains are not changed during the entire experimental process.

5.1 Experiment 1

In this group of experiments, the controller needs to overcome matched disturbances such as the dead zones of actuators and frictions. Specifically, the frictions and the dead zones of the actuators are both piecewise and discontinuous functions, which cause positioning errors of the two trolleys. Furthermore, the friction forces change with the positions and speeds, and the friction forces of the two trolleys are also different. As shown in Figs. 3 and 4, the proposed method can drive the two trolleys to the desired positions at about 10 s. Moreover, the swing angles of the payload also converge quickly at the same time. Meanwhile, the 2-norm of the output weights $W_{1}$ and $W_{2}$ vary diversely, which illustrates that the frictions of the two trolleys are different.

Figure 3

Experiment 1. The proposed control method (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 4

Experiment 1. The 2-norms of the neural network weights $W_{1}$, $W_{2}$ and the control inputs $F_{1}$, $F_{2}$

5.2 Experiment 2

In this experiments, the parameters of DOCS are changed to $m = 4.308\mbox{ kg}$, $l = 0.6\mbox{ m}$ to verify the robustness of the proposed method against parameter uncertainties. To better verify the robustness and anti-swing performance of the proposed control method, the classic coordination controller of DOCS in [26] and the neural network-based adaptive antiswing controller (NNAAC) in [19] are utilized as comparison in this experiments. The control gains of the NNAAC are elaborately tuned as follows:

$$ \begin{aligned} &{k_{1}} ={k_{2}} = 20,\qquad {k_{p1}} ={k_{p2}} = 10, \\ &k_{v1} = k_{v2} = 100,\qquad k_{\theta 1} =k_{\theta 2} = 10, \\ &\alpha =1,\qquad \beta _{1}=\beta _{2}=1,\qquad \gamma _{1}=\gamma _{2}=0.5, \\ &\Pi _{1}=\Pi _{2}=0.5, \qquad \Gamma _{1}=\Gamma _{2}=0.5. \end{aligned} $$

(66)

The control gains for the coordination controller are elaborately constructed as

$$ \begin{aligned} & \lambda =1,\qquad k=5,\qquad k_{p1}=1000, \qquad k_{d}=300, \\ & k_{a1}=400,\qquad \Delta =0.05, \qquad k_{p2}=800, \\ & k_{d}=300,\qquad k_{a1}=400. \end{aligned} $$

(67)

From Fig. 5, it can be seen that even when the payload mass and the length of the hoisting ropes are all changed, the proposed controller can still compensate uncertain parameters and unmodeled dynamics simultaneously. In contrast, as shown in Figs. 6 and 7, the coordination controller and the NNAAC fail to achieve parameters adaptation and friction compensation simultaneously. As a result, position errors and obvious residual payload swing are exhibited. Specifically, the position errors of two trolleys for the proposed method are $0.002~\mathrm{m}$ and $0.004~\mathrm{m}$, while the NNAAC has positioning errors of $0.012~\mathrm{m}$ and $0.01~\mathrm{m}$ and the trolleys of the coordination controller are still $0.029~\mathrm{m}$ and $0.033~\mathrm{m}$ away from the desired positions when they stop. Moreover, it can also be seen from Fig. 8 that the adopted RBFNN of the proposed method compensates most of the matching disturbances, but the network of the NNAAC has poor estimation ability for such large and varying disturbances.²

Figure 5

Experiment 2. The proposed control method (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 6

Experiment 2. The coordination controller in [26] (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 7

Experiment 2. The neural network-based adaptive antiswing controller in [19] (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 8

Experiment 2. The 2-norms of the neural network weights $W_{1}$, $W_{2}$, $V_{1}$, $V_{2}$ and the control inputs $F_{1}$, $F_{2}$ (blue solid lines: the proposed method, green chain lines: the coordination controller in [26], and red dash lines: the neural network-based adaptive antiswing controller in [19])

5.3 Experiment 3

In practical application, when the payloads are replaced, the payloads cannot be stabilized immediately. Hence, there will exist residual payload swing, which takes a long time to eliminate and thus badly reduces transportation efficiency. To test the performance and robustness of the controller under this working condition, initial swings are inflicted on the payload. As can be seen from Fig. 9, even when apparent initial swings exist, the proposed method still accomplishes accurate positioning and satisfactory anti-swing performance, which verifies the robustness of the proposed method. However, from Figs. 10 and 11, although the two comparison methods can drive the trolley to the desired position, there is still obvious residual swing afterward, which cannot be eliminated after 20 s.

Figure 9

Experiment 3. The proposed control method (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 10

Experiment 3. The coordination controller in [26] (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 11

Experiment 3. The neural network-based adaptive antiswing controller in [19] (black dashed lines: desired positions and blue solid lines: experimental results)

5.4 Experiment 4

To fully validate the robustness of the presented controller, external mismatched disturbances are exerted on the payload abruptly. As shown in Fig. 12, the maximum payload swing angle is up to about 7 deg at about 26 s. From Fig. 12, it can be observed that the system is re-stabilized quickly (in about 2.5 s) after being disturbed. For comparison, the NNAAC is also tested with an external disturbance. However, since the cooperative controller is similar to the PD (Proportion Differentiation) controller, the coordination controller is not robust in counteracting the sudden disturbances (see Fig. 13). On the other hand, because no swing-related information is incorporated into the sliding surface of the NNAAC, the trolleys fail to react to the swing motion and eliminate the swing (see Fig. 14).

Figure 12

Experiment 4. The proposed control method (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 13

Experiment 4. The coordination controller in [26] (black dashed lines: desired positions and blue solid lines: experimental results)

Figure 14

Experiment 4. The neural network-based adaptive antiswing controller in [19] (black dashed lines: desired positions and blue solid lines: experimental results)

6 Conclusions

Utilizing the symmetry property, the dynamic equations of DOCS are transformed into cascade forms and a new sliding manifold is constructed afterward. Based on the sliding mode surface and one-hidden-layer neural network, an adaptive SMC is proposed. Furthermore, the asymptotic stability of DOCS is guaranteed, even when DOCS suffers from both matched and unmatched disturbances. Simultaneously, the adopted neural network addresses the parameter uncertainties, frictions, input dead zones, and other unmodeled dynamics. Finally, a series of experimental results verify the effectiveness and the strong robustness of the proposed control scheme. In our future works, the hoisting and lowering of the payload and the actuators’ saturation problem will be considered.

Appendix

To prove the conclusion of (54), this part of the analysis is divided into the following two cases:

1. ${\boldsymbol{q}}, \boldsymbol{\dot{q}}\to 0$

The upper bounds of $\xi _{11}$, $\xi _{12}$, $\xi _{21}$ and $\xi _{22}$ in the case ${\boldsymbol{q}}, \boldsymbol{\dot{q}}\to 0$ are first analyzed. Utilizing (14) and (16), the following conclusion can be obtained

$$ \begin{aligned} &\zeta _{11} \to -\eta _{11d},\qquad \zeta _{21}\to -\eta _{21d}, \qquad \zeta _{31}\to - \eta _{31d}, \\ &\xi _{11} \to 0,\qquad \xi _{21}\to \eta _{31d}. \end{aligned} $$

(68)

Based on (43) and the resluts in (68), the upper bounds of $\xi _{11}$, $\xi _{21}$ are obtained

$$ \begin{aligned}[b] &\Vert \xi _{11} \Vert \le \Vert \zeta _{a1} \Vert ^{2}, \quad \Vert \xi _{21} \Vert \to \Vert \zeta _{31} \Vert \\ &\quad \Longrightarrow\quad \Vert \xi _{21} \Vert \le n_{1} \Vert \zeta _{a1} \Vert ^{2}, \end{aligned} $$

(69)

where $n_{1}$ is a sufficiently large positive. Substituting (68) into (45) yields

$$ \|\xi _{1}\|=\sqrt{ \Vert \xi _{11} \Vert ^{2}+ \Vert \xi _{21} \Vert ^{2}} \le n \Vert \zeta _{a1} \Vert ^{2}, $$

(70)

where n is a sufficiently large positive to satisfy the inequation (70).

2. ${\boldsymbol{q}}, \boldsymbol{\dot{q}}\to \infty$

Substituting ${\boldsymbol{q}}, \boldsymbol{\dot{q}}\to \infty$ into (14) and (16), and ignoring constant terms and low-order infinity terms, the following conclusion can be drawn

$$ \begin{aligned} &\Vert \xi _{11} \Vert = \biggl\Vert \frac{c_{2}+c_{3}}{c_{1}^{2}} \biggr\Vert \cdot \Vert \dot{\theta }_{1} \Vert \le \biggl\Vert \frac{c_{2}+c_{3}}{c_{1}^{2}} \biggr\Vert \Vert \boldsymbol{\dot{q}} \Vert , \\ &\Vert \xi _{21} \Vert =\left \Vert \begin{bmatrix} \frac{ls_{1}}{c_{1}^{2}} & \frac{ls_{2}}{c_{1}^{2}} & \frac{2bs_{3}}{c_{1}^{2}} \end{bmatrix} \right \Vert \cdot \left \Vert \begin{bmatrix} \dot{\theta }_{1} & \dot{\theta }_{2} & \dot{\theta }_{3} \end{bmatrix}^{\top }\right \Vert \\ &\hphantom{\Vert \xi _{11} \Vert ={}}{}\cdot \Vert \dot{\theta }_{1} \Vert \\ &\hphantom{\Vert \xi _{21} \Vert }\le \left \Vert \begin{bmatrix} \frac{ls_{1}}{c_{1}^{2}} & \frac{ls_{2}}{c_{1}^{2}} & \frac{2bs_{3}}{c_{1}^{2}} \end{bmatrix} \right \Vert \cdot \Vert \boldsymbol{\dot{q}} \Vert ^{2}, \\ &\Vert \zeta _{21} \Vert =\left \Vert \begin{bmatrix} 1 & 1 & \frac{l}{c_{1}} &\frac{lc_{1-2}}{c_{1}} & \frac{2bc_{1+3}}{c_{1}} \end{bmatrix} \right \Vert \cdot \Vert \boldsymbol{\dot{q}} \Vert . \end{aligned} $$

(71)

Because both $\|\xi _{1}\|$ and $\|\zeta _{21}\|$ are positive second-order infinite terms, there must be a positive number m satisfying the following inequation:

$$ \begin{aligned}[b] \Vert \xi _{1} \Vert ={}&\sqrt{ \Vert \xi _{11} \Vert ^{2}+ \Vert \xi _{21} \Vert ^{2}} \\ ={}& \Vert \xi _{21} \Vert \le m \Vert \zeta _{21} \Vert ^{2}\le m \Vert \boldsymbol{\zeta _{a1}} \Vert ^{2}. \end{aligned} $$

(72)

Apparently, it is very difficult to give a specific value of the upper bounds of the nonlinear items, only the shape can be obtained. Hence, combining (70) with (72), the upper bounds of $\|\xi _{1}\|$ are the quadratic function of $\|\boldsymbol{\zeta _{a1}}\|$ as

$$ \Vert \xi _{1} \Vert \le \rho _{1} \Vert \boldsymbol{\zeta _{a1}} \Vert ^{2}, $$

(73)

where $\rho _{1}$ is a bounded positive, which is sufficiently large to satisfy the above requirement. The proof process of the upper bound of $\|\xi _{2}\|$ is similar with $\|\xi _{1}\|$, which is not included here for brevity.