Introduction

Optimisation is a fundamental and multidisciplinary field that most generically aims to detect within a set of potential solution that one that satisfies the most one or more objectives. Within the plethora of possible optimisation methods, a clear distinction can be made between mathematical and heuristic optimisation:

  • mathematical optimisation: methods that, under some hypotheses, are guaranteed to rigorously detect the optimum [48];

  • heuristic optimisation: methods that, without requiring specific hypotheses on the problem, search for a solution that is close enough to the optimum [1,2,3, 13, 26].

Algorithms of mathematical optimisation are often iterative methods that are rigorously justified and endowed with proofs of convergence [48]. The software implementation of an algorithm of mathematical optimisation is thus a straightforward decodification of mathematical formulas.

Algorithms of heuristic optimisation are software procedures usually described by means of words and formulas and justified by means of metaphors, see [26, 40]. To ensure that a heuristic algorithm can be understood and reproduced by the reader and the community, modern articles provide pseudocode of their proposed algorithms.

However, whilst the pseudocode of modern heuristics can be effective to communicate the general idea of the proposed algorithm, they often do not capture all the implementation details due to their complexity. Although ideas can be generally understood and re-implemented, due to the lack of mathematical rigour, a misinterpretation of an idea can be implemented into an algorithm which still performs reasonably well on an optimisation problem. This is likely to be an experience common to any person who has attempted to implement a program based on the idea of a colleague.

The present article discusses the topic of potential ambiguity in heuristic optimisation and how algorithmic descriptions could be subject to misinterpretation with a specific reference to multi-objective problems. We chose this subfield since multi-objective problems are naturally hard to solve, e.g. to the difficulty of comparing candidate solutions belonging to the same non-dominated set, and heuristics are often fairly complex. More specifically, we pose the following question

Is the process of implementation of a multi-objective algorithm from its description straightforward and unambiguous?

To address this point we have performed an extensive experimental study. We have focussed on three popular algorithmic frameworks:

  • Non-dominated sorting genetic algorithm II (NSGA-II) [11].

  • Generalized differential evolution 3 (GDE3) [34].

  • Multi-objective evolutionary algorithm based on decomposition with dynamic resource allocation (MOEA/D-DRA) [57].

Each of these frameworks has been extensively implemented by multiple researchers and in various research software platforms such as jMetal [16]. We compared the behaviour and performance of the different implementations/interpretations of each framework. More specifically, five implementations of NSGA-II, five implementations of GDE3, and four implementations of MOEA/D-DRA are evaluated using the test functions provided by the ZDT, DTLZ and WFG test suites, see [12, 25, 59]. Furthermore, the source code of the tested implementations has been analysed to identify the differences in the implementation.

The article is organised as follows. Section “Basic Definitions and Notation” provides the reader with the basic definitions and notation which are used throughout the paper. Section “Algorithmic Frameworks in This Study” provides a description of NSGA-II, GDE3, and MOEA/D-DRA according to their original presentations but with the standardised notation used throughout the paper. Section “Software Implementations of the Algorithmic Frameworks” presents the software platforms where the three algorithmic frameworks under examination have been implemented. Section “Experimental Setup” describes the experimental design, including test problems, parameter settings, and methods used to perform the comparisons. Section “Experimental Results and Discussion” presents the numerical results of this study. Section “Differences in the Implementations” highlights the algorithmic and software engineering differences across the software platforms under consideration. Finally, section “Conclusion” presents the conclusion to this study.

Basic Definitions and Notation

Definition 1

(Multi-objective Optimisation Problem) A multi-objective optimisation problem can be defined as follows:

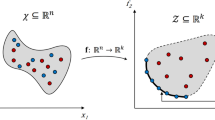
$$\begin{aligned} \begin{array}{lll} &{}\mathrm{maximise/minimise} &{}\mathbf {y}=(f_1 (\mathbf {x}), f_2 (\mathbf {x}), \ldots , f_n (\mathbf {x})) \\ &{}\mathrm{where } &{}\mathbf {x}=\left( x_1, \ldots ,x_d \right) \in \mathbf {X} \subset \mathbb {R}^n\ (\mathrm{decision\ vector}) \\ &{} &{}\mathbf {y}=\left( y_1, \ldots ,y_n \right) \in \mathbf {Y} \subset \mathbb {R}^k\ (\mathrm{objective\ vector}). \end{array} \end{aligned}$$

The sets \(\mathbb {R}^n\) and \(\mathbb {R}^k\) represent the decision space and the objective space, respectively (Fig. 1). The set \(\mathbf {X} \subseteq\)\(\mathbb {R}^n\) is also known as the feasible set and is associated with equality and inequality constraints.

The function \(f: \mathbb {R}^n \rightarrow \mathbb {R}^k\) represents a transformation from the decision space \(\mathbf {X}\) into the objective space \(\mathbf {Y}\) that can be used to evaluate the quality of each solution. The image of \(\mathbf {X}\) under the function f represents a subset of the function space known as the feasible set in the objective function space. It is denoted by \(\mathbf {Y}=f\left( \mathbf {X}\right)\) [37].

Fig. 1
figure 1

Illustration of the decision space and the objective space of a multi-objective optimisation problems

Full size image

Definition 2

(Pareto dominance) Unlike single-objective optimisation in which the relation \(\ge\) can be used to compare the quality of solutions, comparing solutions in multi-objective optimisation problems is not as straightforward (there is no order relation). A relation that is usually adopted to compare solutions to such problems is known as Pareto dominance.Footnote 1

Without loss of generality let us assume that all objectives need to be simultaneously maximised. For any two objective vectors

$$\begin{aligned} \begin{array}{l} \mathbf {y^1} = \left( y_1^1,\ldots ,y_n^1\right) \\ \mathbf {y^2} = \left( y_1^2,\ldots ,y_n^2\right) \end{array} \end{aligned}$$

and the corresponding decision vectors \(\mathbf {x^1}\) and \(\mathbf {x^2}\), it can be said that \(\mathbf {x^1} \succ \mathbf {x^2}\) (\(\mathbf {x^1}\) dominates \(\mathbf {x^2}\)) if no component of \(\mathbf {y^2}\) outperforms the corresponding component of \(\mathbf {y^1}\), and at least one component of \(\mathbf {y^1}\) outperforms the corresponding component of \(\mathbf {y^2}\):

$$\begin{aligned} \begin{array}{l} \forall k=1:n, y^1_k \ge y^2_k\\ \exists k {{{\backepsilon}}}`\,y^1_k > y^2_k. \end{array} \end{aligned}$$

In the event that \(\mathbf {x^1}\) does not dominate \(\mathbf {x^2}\) and \(\mathbf {x^2}\) does not dominate \(\mathbf {x^1}\), it can be said that the two vectors are indifferent \(\left( \mathbf {x^1} \sim \mathbf {x^2} \right)\).

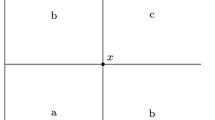
Figure 2 illustrates the concept of Pareto dominance. The blue rectangle represents the region of the objective space that dominates the objective vector \(\mathbf {B}\). All the objective vectors in that region have at least one objective value that outperforms the corresponding objective value of vector \(\mathbf {B}\) and the other objective is bigger than or equal to the objective of vector \(\mathbf {B}\). The red rectangle contains the objective vectors that are dominated by vector \(\mathbf {B}\), and the vectors that are not in one of the two rectangles are indifferent to vector \(\mathbf {B}\).

Fig. 2
figure 2

Illustration of the Pareto dominance relation

Full size image

Definition 3

(Pareto optimality) Pareto optimality is a concept that is based on Pareto dominance. A solution \(\mathbf {x^*} \in \mathbf {X}\) is Pareto optimal if there is no other solution \(\mathbf {x} \in \mathbf {X}\) that dominates it [37]. A Pareto optimal solution denotes that there does not exist another solution that can increase the quality of a given objective without decreasing the quality of at least one other objective [53].

Definition 4

(Pareto optimal set) Instead of having one optimal solution, multi-objective optimisation problems may have a set of Pareto optimal solutions. This set is also known as the Pareto optimal set. It is defined as follows:

$$\begin{aligned} P^*=\lbrace \mathbf {x} \in \mathbf {X}\ |\ \not \exists \ \mathbf {x^*} \in \mathbf {X} :\mathbf {x^*} \succeq \mathbf {x} \rbrace . \end{aligned}$$

Definition 5

(Pareto front) The Pareto front represents the image of the Pareto optimal set in the objective function space (Fig. 3). It can be defined as follows:

$$\begin{aligned} \mathrm{PF}^*=\lbrace f\left( \mathbf {x}\right) | \mathbf {x} \in P^* \rbrace . \end{aligned}$$
Fig. 3
figure 3

Illustration of the Pareto optimal set and the Pareto front

Full size image

Definition 6

(Approximation set) The main goal of multi-objective optimisation is to find the Pareto front of a given multi-objective optimisation problem. However, since Pareto fronts usually contain a large number of points, finding all of them might require an undefined amount of time and therefore a more practical solution is to find a good approximation of the Pareto front. This set approximating the Pareto is called approximation set. A good approximation set should be as close as possible to the actual Pareto front and should be uniformly spread over it, otherwise the obtained approximation of the Pareto front will not offer sufficient information for decision making [53].

Algorithmic Frameworks in This Study

The heuristic algorithms investigated in this study can all be considered under the umbrella name of evolutionary multi-objective optimisation (EMO) algorithms, see [31]. During the past decades, a wide variety of EMO algorithms have been proposed and applied to many different real-world problems.

Although EMO algorithms can differ by major aspects, they can still be considered to be members of the same family that is characterised by the general algorithmic structure outlined in Algorithm 1.

figure a

The following subsections introduce the three popular EMO algorithms under examination: the non-dominated sorting genetic algorithm II, the generalized differential evolution 3 algorithm, and the multi-objective evolutionary algorithm based on decomposition with dynamic resource allocation.

Non-dominated Sorting Genetic Algorithm II

The non-dominated sorting genetic algorithm II (NSGA-II) was proposed in [11] as an improvement to NSGA-I [49]. It addresses some of the main issues with the original version such as high-computational complexity of the non-dominated sorting algorithm, lack of elitism, and the need to specify a sharing parameter. Algorithm 2 illustrates the life cycle of NSGA-II.

figure b

NSGA-II starts by building a population of randomly generated candidate solutions. Each solution is then evaluated and assigned a fitness rank equal to its non-domination level (with 1 being the best level) using a fast non-dominated sorting algorithm. Binary tournament selection, recombination, and mutation operators are then applied to create an initial offspring population. In the original paper (as well as in many implementations thereafter), NSGA-II employs the simulated binary crossover (SBX) operator and polynomial mutation, see [19]. Then the generational loop begins. The parent population and the offspring population are combined. Since the best solutions from both the parent and offspring populations are included, elitism is ensured. The new combined population is then partitioned into fronts using the fast non-dominated sorting, see Algorithm 3.

figure c

The algorithm then iterates through the set of fronts (from best to worst), and adds their solutions to the population for the next generation until there is not enough space to accommodate all of the solutions of a given front. After the end of the procedure, if there are any places left in the new population, the solutions of the next front that could not be added are sorted in descending order based on their crowding distance and the best ones are added to the population until it is full. The new population is then used for selection, recombination and mutation to create an offspring population for the next generation. The algorithm uses the crowding distance during the selection process in order to maintain diversity in front by ensuring that each member stays a crowding distance apart which supports the algorithm in exploring the objective space [6]. Algorithm 4 shows how the crowding distance is calculated. The process is repeated until a termination condition is met.

figure d

Generalized Differential Evolution 3

The generalized differential evolution 3 (GDE3) algorithm was proposed by Kukkonen and Lampinen in [34]. It is the third version of the GDE algorithm. GDE3 achieves better performance than previous versions by employing a growing offspring population that can accommodate twice as many solutions as there are in the parent population, and non-dominated sorting with pruning of non-dominated solutions to reduce the size of the population back to normal at the end of each generation. This technique improves the diversity of the obtained solution set and makes the algorithm less reliant on the selection of control parameters. The execution life cycle of the algorithm can be seen in Algorithm 5.

figure e

Similar to other EMO algorithms, GDE3 starts by generating a population with N candidate solutions and evaluating their fitness. The main loop of the algorithm then begins. An empty offspring population with maximum size 2N is initialised. The algorithm then iterates through the initial population. At each position, differential evolution selection and differential evolution variation operators are used to select parents and generate a child solution. The fitness of the child solution is then evaluated. It is then compared to the solution at the current position of the population. If the two solutions are indifferent to each other, both are added to the offspring solution, otherwise only the dominating solution is added. After the algorithm is finished iterating through the initial population, the offspring population is sorted and pruned to form the population for the next generation.

The GDE3 algorithm has been successfully applied to many real-world problems from various fields such as molecular biology [33] and electronics [22].

Multi-objective Evolutionary Algorithm Based on Decomposition with Dynamic Resource Allocation

The multi-objective evolutionary algorithm based on decomposition (MOEA/D) was proposed in [57]. MOEA/D uses a decomposition method to decompose a multi-objective problem into a number of scalar optimisation sub-problems by means of several weight vectors. A sub-problem is optimised using information from its neighbouring sub-problems, which leads to lower computational complexity than NSGA-II. Different approaches to decomposition exist in the literature. Some of the most popular ones are the weighted sum approach [18, 30], the Tchebycheff approach [38], and the normal-boundary intersection approach [9]. The authors of the algorithm employed the Tchebycheff approach in the paper in which it was introduced, and MOEA/D outperformed or performed similarly to NSGA-II on a number of test functions.

Over the years, many different versions of MOEA/D have been proposed, see [32, 35, 41, 58]. One of the versions that has become very popular is MOEA/D with dynamic resource allocation (MOEA/D-DRA [58]. In the original version of MOEA/D, all of the sub-problems are treated equally and all of them receive equal computational effort. However, different sub-problems might have different computational difficulties and, therefore, they require different amount of computational effort. Because of this, MOEA/D-DRA introduces dynamic resource allocation which allows the algorithm to assign different amounts of computational effort to different sub-problems. The amount of computational resources each sub-problem i gets is based on the computation of a utility value \(\pi ^i\).

The basic principles of MOEA/D-DRA are described in Algorithm 6 which highlights the 5-step structure characterising the framework as highlighted in the paper that originally proposed it, see [58]. It must be observed that MOEA/D-DRA is a relatively complex framework and contains multiple heuristic rules and a problem-specific internal parameter setting as it was designed for entry in the IEEE CEC 2009 competition. Hence, for the sake of brevity, we omitted the details of some of the formulas in Algorithm 6 and refer the original paper for the interested reader.

figure f

Software Implementations of the Algorithmic Frameworks

In this article, we focus on five popular software platforms and libraries for heuristic optimisation:

  • jMetal-Java (version 4.5.2).

  • jMetal-.NET (version 0.5).

  • MOEA Framework (version 2.12)

  • Platypus (GitHub commit 723ad6763abff99b4f31305191b754c2c26867b0).

  • PlatEMO (version 2.8.0).

jMetal-Java jMetal-Java is a java-based framework introduced by Durillo and Nebro in 2006 [16]. The main goal of the framework is to provide an easy to use tool for developing heuristics (and metaheuristics) for solving multi-objective optimisation problems. It also provides implementations of many state-of-the-art EMO algorithms, test problems and performance indicators, and has been used in several experiments described in the literature [44,45,46,47, 50].

In 2011, the authors of the framework started a project to implement jMetal using C# and in present days, the C# version provides almost all of the features that can be found in the Java version. The latter version is known as jMetal.NET.

MOEA The MOEA Framework library (here referred to also as MOEA for brevity) is a Java-based open-source library for multi-objective optimisation introduced by Hadka in 2011 [23]. Similarly to jMetal, MOEA also provides means to quickly design, develop and execute EMO algorithms. It supports genetic algorithms, differential evolution, genetic programming, and more. A number of state-of-the-art EMO algorithms, test problems, and quality indicators are provided out-of-the-box and have been used in multiple experiment studies detailed in the EMO literature [5, 15, 52].

Platypus Platypus is a python-based framework for evolutionary computing, whose focus lays on EMO algorithms. It was developed by Hadka and was introduced in 2015 [24]. It also provides implementations of several state-of-the-art algorithms, test problems and quality indicators, and also supports parallel processing. The algorithm implementations provided by the library have been used for various experiments in the EMO literature [4, 39].

PlatEMO is a MATLAB platform for evolutionary multi-objective optimisation [54]. It contains implementations of multiple state-of-the-art EMO algorithms as well as numerous test problems.

These algorithmic frameworks under consideration are present in these software platforms according to the following scheme

  • NSGA-II \(\rightarrow\) jMetal-Java, jMetal.NET, MOEA, Platypus, PlatEMO.

  • GDE3 \(\rightarrow\) jMetal-Java, jMetal.NET, MOEA, Platypus,PlatEMO.

  • MOEA/D-DRA \(\rightarrow\) jMetal-Java, jMetal.NET, MOEA, PlatEMO.

Experimental Setup

The three algorithmic frameworks under consideration in the eleven above-mentioned implementations have been extensively tested on the test functions of the ZDT [59], DTLZ [12], and WFG [25] test suites.

The performance of the implementations is measured with the use of the Hypervolume indicator and Inverted Generational Distance+. In order to determine if there is a significant difference between different implementations of the same EMO algorithm, the experimental results have been tested with the Wilcoxon signed-rank test.

This section is organised as follows. The next subsection describes the test problems used in this study, and explicitly provides the reader with all the parameters associated with the problem followed by which the parameters that have been used by each EMO algorithmic framework are displayed. The final subsection describes in detail how the comparisons have been carried out.

Test Problems

ZDT The ZDT test suite was proposed by Zitzler, Deb and Thiele in 2000 [59]. It consists of six bi-objective synthetic test functions, five of which (ZDT1–ZDT4; ZD6) are real-coded and one (ZDT5) which is binary-coded. In this study, only the real-coded test problems were selected. ZDT5 was not selected due to its requirement for binary encoded problem variables. The parameter configuration of the ZDT test functions have been listed in Table 1.

Table 1 Parameter configurations for the ZDT test functions
Full size table

DTLZ The DTLZ test suite was proposed by Deb, Thiele, Laumanns and Zitzler in 2002 [12]. It contains seven scalable multi-objective test functions with diverse characteristics such as non-convex, multimodal, and disconnected Pareto fronts. In this study, two and three objectives are considered for each problem, and the number of decision variables is set to 7, 12 and 22 for DTLZ1, DTLZ2-6, and DTLZ7, respectively. The parameter configurations for the DTLZ test functions have been listed in Table 2.

Table 2 Parameter configurations for the DTLZ test functions
Full size table

WFG The WFG tool-kit was introduced by Huband, Hingston, Barone and While in 2006 [25]. The tool-kit makes it possible to construct synthetic test problems which incorporate common characteristics of real-world problems such as variable linkage and separability. To demonstrate its functionality, the authors constructed nine test problems (WFG1-9) with scalable variables and problem objectives. The proposed test functions are referred to as the WFG test suite. In this study, two and three objectives are considered for each problem. The full parameter configurations for each test problem can be seen in Table 3.

Table 3 Parameter configurations for the WFG test functions
Full size table

Parameter Setting

The parameters used to configure the implementations of the selected algorithms can be seen in Tables 4, 5 and 6. The implementations of NSGA-II and MOEA/D-DRA are configured with the parameters proposed by the authors of the algorithms, while GDE3 is configured with the parameters used in the experiment described in [17]. The maximum number of generations per execution is set to 500, with a sample size of 30 executions per test function.

Table 4 Parameter configurations of the chosen NSGA-II implementations
Full size table
Table 5 Parameter configurations of the chosen GDE3 implementations
Full size table
Table 6 Parameter configurations of the chosen MOEA/D-DRA implementations
Full size table

Comparison Method

In the last decades, various performance indicators have been proposed to assess the performance of EMO algorithms, see [27]. The most popular performance indicator amongst the EMO society in recent years has been the Hypervolume (HV) indicator [42] and the Inverted Generational Distance+ (IGD\(^+\)), see [27, 29, 51].

The HV indicator is a performance metric proposed by Zitzler and Thiele in [60]. It measures the volume of the objective space dominated by an approximation set (Fig. 4). The HV indicator is a popular choice for researchers as it does not require knowledge about the true Pareto optimal front, which is an important factor when working with multi-objective optimisation problems that are yet to be solved [43].

Fig. 4
figure 4

Illustration of the HV indicator in two-dimensional space with three solutions

Full size image

A reference point is required for the calculation of the HV indicator. When the HV indicator is used to compare EMO algorithms, the reference point must be the same otherwise the results will not be accurate or comparable. Selecting the reference point is an important issue and the difficulty of selecting such a point increases with the number of objectives [36]. The reference points used in the experimental study are selected by constructing a vector of the worst objective values contained in the union of the approximation sets generated by the algorithm implementations chosen for comparison. They have been listed in Tables 1, 2, and 3.

The IGD is a classical metric used to assess the quality of a non-dominated set, see [7] on the basis of the study reported in [8]. Let us consider a set of reference points \(Z=\lbrace \mathbf {z^1}, \mathbf {z^2}, \ldots \mathbf {z^r}\rbrace\) that approximate the Pareto set. Let us now consider the set of non-dominated points returned by an algorithm \(X=\lbrace \mathbf {x^1}, \mathbf {x^2}, \ldots , \mathbf {x^N} \rbrace\) and the corresponding set of objective vectors \(Y=\lbrace \mathbf {y^1}, \mathbf {y^2}, \ldots , \mathbf {y^N} \rbrace\). The IGD of the set Y is calculated as

$$\begin{aligned} \mathrm{IGD}_Z\left( Y\right) =\frac{1}{r}\left( \sum _{j=1}^r \min \lbrace d\left( \mathbf {z^j, y^k}\right) | \mathbf {y^k}\in Y \rbrace \right) \end{aligned}$$

where \(d\left( \mathbf {z^j, y^k}\right)\) is the Euclidean distance between \(\mathbf {z^j}\) and \(\mathbf {y^k}\):

$$\begin{aligned} d\left( \mathbf {z^j, y^k}\right) =\sqrt{\sum _{i=1}^n\left( z^j_i-y^k_i\right) ^2}, \end{aligned}$$

where n is the dimensionality of the objective space.

For the sake of clarity, IGD is obtained from Z and Y. At first, for each element of Z, the Euclidean distances between the element of Z and all the elements of Y are calculated. Then minimal distance is chosen. The average sum of all the minimal distances is the desired IGD, see [28].

The IGD\(^+\) corrects the IGD using the modified distance \(d^+\) instead of the Euclidean distance, [29]:

$$\begin{aligned} d^+\left( \mathbf {z^j, y^k}\right) =\sqrt{\sum _{i=1}^n\left( \max \lbrace 0, \left( z^j_i-y^k_i\right) \rbrace \right) ^2} \end{aligned}$$

and then uses in the IGD\(^+\) calculation

$$\begin{aligned} \mathrm{IGD}_Z^+\left( Y\right) =\frac{1}{r}\left( \sum _{j=1}^r \min \lbrace d^+\left( \mathbf {z^j, y^k}\right) | \mathbf {y^k}\in Y \rbrace \right) . \end{aligned}$$

To determine whether there is significant difference between the results of different implementations of a given EMO algorithm, it is necessary to carry out a statistical test. In this paper, the mean hypervolume and IGD\(^+\) results of the implementations used in the experiment are compared with the use of the Wilcoxon signed [14, 20, 21, 55, 61]to test for such statistical difference. The Wilcoxon test is a non-parametric test used to test for a difference in the mean (or median) of paired observations.

The results in tables are expressed as mean value ± and standard deviation \(\sigma\). For all the tables presented in this study, we have used jMetal-Java implementations as the reference for the Wilcoxon test. This choice has been made on the basis of the practical consideration that it is the most complete framework amongst those considered in this article. In each column of the Tables, a “+” indicates that the implementation in that column outperforms the jMetal counterpart, a “−” indicates that the implementation is outperformed by the jMetal-Java implementation, an “=” indicates that the two implementations have a statistically indistinguishable performance.

Experimental Results and Discussion

Table 7 displays the HV results for the five implementations of NSGA-II. Table 8 displays the HV results for the five implementations of GDE3. Table 9 displays the HV results for the five implementations of MOEA/D-DRA.

Table 7 Hypervolume results (mean value and standard deviation) from 30 executions of five versions of NSGA-II on two and three objective test functions after 500 generations
Full size table
Table 8 Hypervolume results (mean value and standard deviation) from 30 executions of five versions of GDE3 on two and three objective test functions after 500 generations
Full size table
Table 9 Hypervolume results (mean value and standard deviation) from 30 executions of the four versions available of MOEA/D-DRA on two and three objective test functions after 500 generations
Full size table

It can be observed that the HV results for DTLZ4 and DTLZ5 are missing in Tables 7, 8, 9. The lack of those results is due to a malfunctioning of the MOEA and Platypus platforms: there is a systematic crash in the system when any of the three algorithms under examination is executed. Hence, we decided to omit these results.

Numerical results in Tables 7, 8, 9 show that the implementations of the same algorithms on different platforms leads to dramatically different results. For example, with reference to Table 7, the NSGA-II implementations on jMetal-Java and MOEA platforms display very different performance, which is statistically different in about half of the problems. A macroscopic difference displayed in Tables 7, 8 and 9 is that PlatEMO significantly outperforms the other platforms on most of the problems, especially for NSGA-II and MOEA/D-DRA.

The results on this extensive data set confirm the intuition shown on the study on NSGA-II implementations published in [56]. It was suggested that different implementations of the same algorithm might perform significantly differently. This means that newly proposed algorithms might perform better than one implementation of the benchmark algorithm but worse than another one.

When proposing a new algorithm, however, researchers typically use only one implementation of the state-of-the-art algorithms chosen for benchmarking. Algorithms are often considered as conceptual paradigms which are associated with their performance. On the contrary, implementations are tasks of secondary importance which consist of communicating the conceptual paradigm expressed in equations and pseudocode to a machine. Furthermore, the use of multiple implementations while running tests is often overlooked since, besides being perceived as a repeated operation, it can be time consuming and onerous. However, the results in this paper show that different implementations of the same algorithm may perform significantly differently. Thus, the choice of the implementation/software platform may likely have an impact on the conclusion of research papers in algorithmics and on the performance of newly proposed algorithms.

To provide the reader with a graphical representation of the differences in HV performance across the platforms under consideration, we plotted the evolution of the HV indicator. Figure 5 depicts the three sets of trends for NSGA-II in Fig. 5a, GDE3 in Fig. 5b, and MOEA/D-DRA in Fig. 5c, respectively.

Fig. 5
figure 5

HV trends for the three algorithms and five software platforms under consideration for the WFG1 problem with two objectives

Full size image

The HV trends in Fig. 5 show that for each algorithm the various software implementations of the same algorithm may lead to different results. It is worth noting that jMetal-Java and jMetal-.NET lead to similar results. This is overall expected since jMetal-.NET is based on jMetal-Java and thus relies on the same interpretation of the algorithms. However, Fig. 5a shows that for NSGA-II, the two jMetal versions lead to different results. Furthermore, Fig. 5 shows that the performance on PlatEMO implementations are dramatically different.

Tables 10, 11, and 12 display the IGD\(^+\) results for NSGA-II, GDE3, and MOEA/D-DRA, respectively. For this set of results, we excluded PlatEMO since it does not have IGD\(^+\) among the metrics available. The IGD\(^+\) results clearly show that different software implementations can lead to extremely different performance values. For example, Table 10 shows that for ZDT4 the jMetal IGD\(^+\) values are about 100 times lower than those achieved by the MOEA and Platypus platforms. We conclude that an expert who analyses these results without knowing that they are allegedly produced by the same algorithm would think that they are produced by conceptually different algorithmic frameworks.

To give a graphical representation of the IGD\(^+\) results, Fig. 6 displays the IGD\(^+\) trends of the three algorithmic and the four software platforms under investigation in the case of WFG1 with two objectives. Figure 6a shows the results of the four NSGA-II software implementations, Fig. 6b shows the results of the four GDE3 software implementations and Fig. 6c shows the results of the three MOEA/D-DRA software implementations.

Table 10 Inverted generational distance+ results (mean value and standard deviation) from 30 executions of the four versions available of NSGA-II on two and three objective test functions after 500 generations
Full size table
Table 11 Inverted generational distance+ results (mean value and standard deviation) from 30 executions of the four versions available of GDE3 on two and three objective test functions after 500 generations
Full size table
Table 12 Inverted generational distance+ results (mean value and standard deviation) from 30 executions of the three versions available of MOEA/D-DRA on two and three objective test functions after 500 generations
Full size table
Fig. 6
figure 6

IGD\(^+\) trends for the three algorithms and four software platforms under consideration for the WFG1 problem with two objectives

Full size image

The results on IGD\(^+\) values confirm what was shown for HV values: the various trends appear distinct with a similarity between the two jMetal platforms.

Differences in the Implementations

To understand how the original papers, [11, 34], and [58] have been interpreted by the authors of the software platforms, we analysed the codes and highlighted the major differences that impacted on the performance of the algorithms. We classified these differences according to their type: (1) algorithmic differences, i.e. different interpretations of the text or pseudocode in the original publication; (2) software engineering differences, i.e. implementation choices that are not part of the algorithmic structure but are still important elements that affect the runs and the results.

Furthermore, there is a difference in programming style between PlatEMO and the other packages which appears to heavily affect the performance for the algorithms and problems considered in this study. In PlatEMO, the software parameters are mostly pre−defined without opportunity for user-specification outside of modifying the source code directly. Many of the parameters appear to be pre−tuned and orientated towards high performance.

In the following subsections, we highlight some of the software differences that we were able to observe by comparing the five software platforms under consideration.

NSGA-II

Simulated binary crossover (SBX) [10] is a popular and established recombination operator which was motivated by the binary crossover operators which were popular in early genetic algorithms. SBX enables the single−point crossover of two real-coded parent solutions to produce an offspring solution through exploitation of the existing information, with the benefit of using a probability distribution for selecting offspring solutions. In particular, NSGA-II employs the SBX operator when operating on problems consisting of real-coded decision variables, and any difference in its implementation will impact the convergence and search pressure throughout the optimisation process.

The software platforms under considerations give different interpretations of SBX and thus propose slightly different algorithms. In SBX, a random number determines whether SBX performs the recombination according to the crossover probability, but if this criterion is not satisfied then the offspring solution directly inherits the decision variable from the first parent. However, in jMetal, the offspring solution also inherits directly from the first parent if the absolute difference between the decision variable from both parents is greater than a pre−defined precision value. This extra swap mechanism does not occur in the MOEA Framework. The SBX operation in Platypus follows the same logic as MOEA Framework. An empirical comparison using identical decision variables (for two parent solutions) and pre−generated random numbers proved a difference in the output from both jMetal and MOEA. The results are presented in Table 13.

Table 13 The offspring solutions generated by SBX implementations in jMetal.NET and MOEA Framework using identical inputs
Full size table

An example of a software engineering difference is in the epsilon (EPS) value used for precision in the frameworks, where jMetal-Java and jMetal-.NET both use \(1.0e-14\), MOEAFramework uses \(1.0e-1\), and Platypus uses 2.220446049250313e-1 (provided by “sys.float_info.epsilon”). Additionally, the jMetal-.NET implementation of NSGA-II had hard-coded the seed used by the random number generators. This meant that every execution on a problem would produce identical results, so this was corrected for the experiments in this paper.

Finally, another difference is in the use random seeds, while jMetal implementations of NSGA-II make use of some hard-coded seeds, MOEA and Platypus generate new random numbers at each occurrence.

GDE3

The four software platform present a subtle different interpretation of the crossover in GDE3. To decide which design variables are copied from the parent solution, jMetal platforms use the condition rand\([0,1)<CR\) as mentioned in the original paper [34] whereas MOEA and Platypus platforms reinterpret the expressions as rand\([0,1) \le CR\). Although this difference does not impact most of the comparisons, it is performed many times in each run. Thus, it is likely to generate some different offspring solutions and modify the behaviour of the algorithm. For example, if we consider

$$\begin{aligned} \begin{array}{l} \mathbf {x^i}=\left( 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0\right) \\ \mathbf {x^{r1}}=\left( 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0 \right) \\ \mathbf {x^{r2}}=\left( 10.0, 9.0, 8.0, 7.0, 6.0, 5.0, 4.0, 3.0, 2.0, 1.0 \right) \\ \mathbf {x^{r3}}= \left( 2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0, 18.0, 20.0 \right) \\ \end{array} \end{aligned}$$

with \(F=CR=0.5\), the mutant vector is

$$\begin{aligned} \begin{array}{l} \mathbf {u}=\mathbf {x^{r3}}+F \left( \mathbf {x^{r1}}-\mathbf {x^{r2}}\right) =\left( -2.5, 0.5, 3.5, 6.5, 9.5, 12.5, 15.5, 18.5, 21.5, 24.5 \right) . \end{array} \end{aligned}$$

After a crossover where we have synthetically ensured that CR will equal 0.5 in some instances (highlighted) through pre-generated random numbers, jMetal and MOEA platforms produced the following, respectively,

$$\begin{aligned} \begin{array}{l} {\mathbf {u}_{\mathbf{jMetal}}}= \left( \mathbf {0.5}, 0.5, 1.5, 6.5, \mathbf {2.5}, 12.5, \mathbf {3.5}, 4.0, 4.5, 24.5 \right) \\ {\mathbf {u}}_{\mathbf{MOEA}}=\left( \mathbf {-2.5}, 0.5, 1.5, 6.5,\mathbf {9.5}, 12.5, \mathbf {15.5}, 4.0, 4.5, 24.5\right) \end{array} \end{aligned}$$

which then affects the final results.

MOEA/D-DRA

The first algorithmic difference in the MOEA/D-DRA implementations is in the way the decision whether solutions from the neighbourhood or from the entire population should be selected during the mating process. The comparison of a random number against a threshold \(\delta\) is coded as rand\((0,1] < \delta\) in jMetal and rand\((0,1] \le \delta\) in MOEA, respectively.

The main algorithmic difference is in the way sub-problems are selected. In MOEA sub-problem’s indices are randomly selected from the entire list of problems. Thus, the MOEA Framework allows the same subproblem to be selected multiple times. The jMetal platforms implement a very different logic: the selected sub-problems are “blacklisted” so that they cannot be selected twice.

Moreover, MOEA shuffles the indices before returning them whereas jMetal does not.

Conclusion

This article performs an experimental study on various interpretations and implementations of well-known algorithms. Numerical results clearly show that three popular heuristic algorithms for multi-objective optimisation, that is, NSGA-II, GDE3, and MOEA/D-DRA, have been subject to various interpretations by four popular software platforms, that is, the two versions of jMetal, MOEA Framework, Platypus, and PlatEMO. As expected, each of these platforms make software engineering decisions which may affect the results, such as the use of different precision values or random number generator. More importantly, the platforms propose different logical implementations of the algorithms. Effectively, these platforms run different algorithms under the same name.

Algorithmic and software engineering differences are evident in the presented Results section. Numerical results show that different implementations of the same algorithm lead to statistically different performance across the experimental setup used in this study. According to our position, the differences are due to two concurrent reasons. The first is that several articles in the field may not be explicit about some important details of an algorithm. This may be due to the complexity of the algorithm and the decision by authors to use references from other articles instead of detailed explanations to enhance the readability of the proposed method. The second is that software platforms may creatively change some of the details because they may be more convenient or for consistency across the platform, e.g. the use of “\(\le\)” in MOEA and “<” in jMetal.

We believe that the description of complex software and its explanation to a human is a difficult task which can easily lead to misinterpretations. Furthermore, we believe that this will have consequences not only in frameworks contributed by and for the scientific community, but also for commercial platforms such as KimemeFootnote 2 and ModeFRONTIERFootnote 3. Hence, we feel that the field of heuristic optimisation would greatly benefit from a standardised protocol to present new algorithms.