1 Introduction

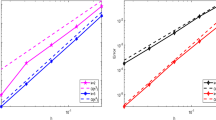
Application-driven developments of complex fluid flows at multiple scales can benefit from deep understanding of the mathematical aspects of multi-resolution analysis (MRA) combined with existing knowledge of accuracy enhancement. This allows for more accurate approximations when passing information between meshes of different resolutions. In this article, we combine a natural technique for simulations at multiple scales, that of multi-wavelet MRA, and that of accuracy enhancing post-processing. Specifically, the techniques introduced in this article reduce the error in the approximation when moving information between coarse and fine grids (and vice versa). This is accomplished by exploiting the underlying properties of the numerical scheme such as the superconvergence paired with the multi-wavelet/MRA. This ability to reduce the errors when moving information from coarse data to finer data is demonstrated in Fig. 1. In this figure, the \(L^2\) and \(L^\infty\) errors are presented in log-log scale for six different meshes. Specifically, the initial information is given on a mesh consisting of twenty elements, and the mesh is refined five times so that the final mesh consists of 640 elements. Errors are given for a simple \(L^2\) projection onto a finer grid as well as constructing an enhanced reconstruction before mesh refinement.

Fig. 1
figure 1

\(L^2\) and \(L^\infty\) errors on a series of six meshes. The initial information is given on a mesh consisting of twenty elements, and the mesh is refined five times so that the final mesh consists of 640 elements. Errors are given for a simple \(L^2\) projection onto a finer grid as well as constructing an enhance reconstruction before mesh refinement. Left: \(p=3\) approximation; right: \(p=4\) approximation

Full size image

The MRA is a useful technique for expressing the discontinuous Galerkin (DG) approximation. It is based on a series of papers by Alpert, Belykin, and collaborators [1, 9], and was introduced in the DG framework in [1]. It has since been used by Cheng, Gao, and collaborators for sparse representations [7, 15, 25, 26, 31], by Müller and collaborators for adaptivity [3, 6, 13], and by Vuik and Ryan for discontinuity detection [29, 30]. It is based on the idea that a DG approximation over a mesh consisting of 2N elements, denoted \(u_h^{2N}(x,t)\), and be written as a DG approximation over a mesh consisting of N elements, denoted \(u_{2h}^N(x,t)\), together with the multi-wavelet information. Mathematically, the expression is the following:

$$\begin{aligned} u_h^{2N}(x,t) = u_{2h}^N(x,t) + \sum _{j=1}^N\, \sum _{k=0}^p\, d_{k,j}^N(t)\psi ^N_{k,j}(x). \end{aligned}$$
(1)

Here, \(\psi ^N_{k,j}(x)\) are called multi-wavelets and are generally taken to be those defined by Alpert [1]. They are piecewise polynomials of degree p, defined on an element. \(d_{k,j}^N\) are the multi-wavelet coefficients that can be thought of as the detail coefficients between a mesh consisting of N elements and a mesh consisting of 2N elements, whereas the approximation on a mesh consisting of N elements is the average.

We can further improve the reconstruction by using the information from neighboring cells combined with the idea of superconvergence. This produces an alternative set of multi-wavelets that creates an improved reconstruction and reduces the error when passing the approximation from a coarse grid to a finer grid. It combines accuracy extraction techniques with the MRA. This combination creates an alternative set of multi-wavelets that allows for error reduction while allowing information to be passed from a fine scale to a coarse scale and vice versa.

The property of the superconvergence for Galerkin methods means that the solution is converging faster than the “optimal” convergence rate, which is tied to more accurate propagation of waves and allows for the physically relevant eigenvalue to dominate in long time simulations [8]. For the DG, the optimal rate is \(p+1\). In [4], it was shown that a specially designed post-processor can extract the higher order information of the dispersion and dissipation error and create an approximation that converges with \(2p+1\) order accuracy. This post-processing filtering has been further developed as the Smoothness-Increasing Accuracy-Conserving (SIAC) filtering [10,11,12, 14, 18,19,20, 22, 24]. The ability to extract the higher order information will be exploited to allow for accurate transfer of information between scales.

The SIAC kernel has mostly been developed for DG methods. In [20], it was demonstrated that the approximation properties of the SIAC procedure actually lend themselves to describing a family of filtering kernels. Specifically, the smoothness increasing the property of the SIAC filtering is a direct result of using the B-spline filtering, the accuracy preserving property (i.e., superconvergence) of the SIAC filtering is attained through choosing a specific number of B-splines and imposing a polynomial reproduction constraint. The authors in [20] also studied variations of the symmetric SIAC kernel that still attain superconvergence properties while having different computational costs and smoothness properties. From the application point of view, the results can help practitioners design new kernels of interest with different design criteria.

It should be noted that combining these ideas leads to a variant of the Nyström reconstruction [21]. The Nyström reconstruction provides for more accurate reconstruction using convolution. Here, we present these ideas for DG approximations, but expect that they can be translated to other areas as well. The outline of this paper is the following. In Sect. 2, we present the DG approximation as well as how it can be written in terms of a multi-wavelet MRA. We also discuss the SIAC kernel that will be used to generate an alternative set of wavelets. In Sect. 3, we show how to combine these ideas to generate an alternative set of multi-wavelets and multi-wavelet coefficients. Finally, numerical examples are presented in Sect. 4.

2 Background

In this section, the discussion will be limited to the important components that serve as the mathematical formulation of the DG method, the MRA, and a specific filtering that both extracts accuracy and maintains accurate wave propagation properties. That is, a discussion of the SIAC filtering.

2.1 MRA

To illustrate the usefulness of the DG-MRA, an example of translating from a coarse scale to a finer scale is given in Fig. 2. In this figure, the approximation space for the coarsest mesh (level 0) consisting of one element is given in the top left. The approximation space for a mesh consisting of two elements (level 1) is given in the top right. We can relate these two approximations spaces by adding the multi-wavelet information where the multi-wavelets are given on the bottom row. In other words, the DG approximation space on level 1 can be rewritten as a direct sum of the scaling function basis of the coarse level 0 together with multi-wavelets. The coefficients multiplying the multi-wavelets contain the details needed to go from level 0 to level 1. Hence,

$$\begin{aligned} \underbrace{u_h(x,t) = 2^{-\frac{1}{2}}\sum _{j=0}^{1} \sum _{\ell =0}^p u_j^{(\ell )}(t) \phi _{\ell j}^1(x) }_{\text {DG approximation on level } 1} = \underbrace{\sum _{\ell =0}^p s_{\ell 0}^{0} \phi _{\ell j}^{0}(x)}_{\text {DG approximation on level } 0} +\underbrace{\sum _{\ell =0}^p\, d_{\ell j}^{1}(t)\psi _{\ell j}^{1}(x)}_{\text {finer details required for level }1}, \end{aligned}$$
(2)

where \(d_{\ell j}^{0}\) are the detail coefficients.

The DG-MRA can be generalized for multiple levels. Here, \(\psi _{\ell j}^m(x)\) are multi-wavelets that allow for translation from one level to another. This means that by subtracting details, the approximation on a coarser level can be obtained. This knowledge has already been established for the DG approximation basis itself [29, 30].

Fig. 2
figure 2

The scaling functions on level 0 and level 1 for a \(p=4\) approximation. To produce the scaling functions on level 1, the \(\psi ^{(4)}_{k,1}(x),\, k=0,\cdots ,4\) multi-wavelets are added to the scaling functions on level 0

Full size image

To provide more details of how the MRA works in the general case, consider a DG approximation for a given equation. To construct such an approximation, it is necessary to first break the domain up into N elements. In one dimension, denote elements as \(I_j,\, j=1,\cdots ,N\) such that the domain can be written as \(\Omega = \mathop \cup \limits _{j=1}^N\, I_j\). On each element, the DG approximation is formed of piecewise polynomials of degree less than or equal to p,  denoted \(\mathbb {P}^p(I_j).\) The entire DG approximation space is then given by

$$\begin{aligned} V_h^p = \{ f: f \in \mathbb {P}^{p}(I_j^n), j = 1,\cdots , N \}, \end{aligned}$$
(3)

where h denotes the element size. However, this is directly related to a multi-resolution approximation. In Fig. 3, the DG space is given at level n with the element size \(h=\frac{|\Omega |}{N}\) and \(N=2^n\). The approximation itself is represented as

$$\begin{aligned} u_h^N(x,t) = 2^{-\frac{n}{2}}\sum _{j=0}^{2^n - 1} \sum _{\ell =0}^p u_j^{(\ell )}(t) \phi _{\ell j}^n(x), \end{aligned}$$
(4)

where \(\phi _{\ell j}^n(x) \in V_h^p\) are the basis functions in the approximation. The DG basis functions are also the scaling functions of the MRA on level n. The finer details are given by the multi-wavelet space, which is defined as the orthogonal complement of the scaling function space on a given level. For example, the DG approximation space on level n,  denoted \(V_h^p\), can be rewritten as a direct sum of the scaling function basis on level \(n-1\) (with the element size 2h) and its orthogonal complement:

$$\begin{aligned} V_h^p=V_{2h}^p\oplus W_{2h}^p. \end{aligned}$$
(5)

The coefficients multiplying the wavelets in the space \(W_{2h}^p\) contain the details needed to go from level \(n-1\) to level n. Hence,

$$\begin{aligned} u_h^N(x,t) =&2^{-\frac{n}{2}}\sum _{j=0}^{2^n - 1} \sum _{\ell =0}^p u_j^{(\ell )}(t) \phi _{\ell j}^n(x)\nonumber \\ =&\underbrace{\sum _{j=0}^{2^{n-1} - 1} \sum _{\ell =0}^p s_{\ell n-1}^{n-1} \phi _{\ell j}^{n-1}(x)}_{\text {DG approximation on level } n-1}+\underbrace{\sum _{j=0}^{2^{n-1}-1}\sum _{\ell =0}^p\, d_{\ell j}^{n}(t)\psi _{\ell j}^{n}(x)}_{\text {finer details required for level }n}. \end{aligned}$$
(6)

This means that by subtracting details, the approximation on a coarser level can be obtained. For example, to get from level n to level 0,  the coarsest level, the DG approximation at level 0 can be written as

$$\begin{aligned} \sum _{\ell =0}^{p}s_{\ell 0}^0(t) \phi _\ell (x) =u_h^N(x,t) - \sum _{m=0}^{n-1} \sum _{j = 0}^{2^m - 1} \sum _{\ell = 0}^p d_{\ell j}^m(t)\psi _{\ell j}^m(x), \end{aligned}$$
(7)

where \(d_{\ell j}^m\) are the detail coefficients and \(\psi _{\ell j}^m(x)\) are multi-wavelets that allow for translation from one level to another. A diagram of the different multi-resolution levels and their scaling function bases is given in Fig. 3. The extra information provided by the multi-wavelets allows for translation from one level to another.

Fig. 3
figure 3

Diagram of the approximation levels in the MRA. Level n represents the level at which a DG solution is given. Using the relation from the MRA, there exists an automatic and precise relation to coarsened levels

Full size image

2.2 SIAC Filtering

The symmetric SIAC kernel was originally introduced in [2, 4]. It was extended to include the superconvergent derivative information in [22, 27]. The utility for post-processing near the boundaries or shocks was addressed through one-sided SIAC kernels in [23, 28]. Recent investigations into nonlinear equations show that it may be possible to improve on the filtered solution by modifying the kernel to account for the reduced regularity assumptions [12, 16, 17]. Traditionally, introducing these filters in engineering applications can be challenging since a tensor product filter grows in support size as the field dimension increases, becoming computationally expensive. Recently, this was overcome with the introduction of the line SIAC filter [5]. This one-dimensional filter for multi-dimensional data preserves the properties of traditional tensor product filtering, including smoothness and improvement in the convergence rate, at a greatly reduced computational cost.

The SIAC filter uses the continuous convolution

$$\begin{aligned} u_h^\star (x,T)=K_H\star u_h =\int _{-\infty }^\infty K_H^{(r+1,\ell )}(x-y)u_h (y,T) \mathrm{d}y, \quad x \in \Omega \end{aligned},$$
(8)

where \(u_h\) denotes the approximation at final time and the kernel (symmetric) is a linear combination of central B-splines,

$$\begin{aligned} K^{(r+1,\ell )}(\eta )=\sum _{\gamma =0}^r c_\gamma \psi ^{(\ell )}\left( \eta -\left( \frac{r}{2}-\gamma \right) \right) . \end{aligned}$$
(9)

Here, \(\gamma\) denotes the B-splines centers and \(c_\gamma\) their weights. The kernel subindex H in (8) acts as a scaling factor, i.e., \(K_H(x-y)=\frac{1}{H} K\left( \frac{x-y}{H}\right) =\frac{1}{H}K(\eta ).\) To give an idea of the filter size, for uniform meshes, the usual scaling choice is \(H=h\), where h denotes the element size. The superindexes \((r+1,\ell )\) indicate the number of B-splines employed to build the kernel \((r+1)\) and the spline order (\(\ell\)). The convolution kernel then has a support of size \((2r+\ell )H\) around the point being post-processed. For typical DG solutions, the superconvergent extracting SIAC kernel employs \(r+1=2p+1\) B-Splines of order \(\ell =p+1\) (p denotes the highest polynomial degree employed for the numerical approximation). In multiple dimensions, computational costs can be saved by applying this filter as a line integral [5].

In this article, we take \(2p+1\) B-splines of order \(\ell =1.\) Using higher order splines will lead to over-smoothing, a decrease in accuracy, and a decrease in accuracy with refinement. In this instance, the first three kernels are

$$\begin{aligned} K^{(3,1)}(x)&= -\frac{1}{24}(\mathbb {1}_{[-3/2,-1/2)}+\mathbb {1}_{[1/2,3/2)})+\frac{13}{12}\mathbb {1}_{[-1/2,1/2)},\\ K^{(5,1)}(x)&= \frac{3}{640}(\mathbb {1}_{[-5/2,-3/2)}+\mathbb {1}_{[3/2,5/2)})-\frac{29}{480}(\mathbb {1}_{[-3/2,-1/2)}+\mathbb {1}_{[1/2,3/2)}) +\frac{1\,067}{960}\mathbb {1}_{[-1/2,1/2)},\\ K^{(7,1)}(x)&= -\frac{5}{7\,168}(\mathbb {1}_{[-7/2,-5/2)}+\mathbb {1}_{[5/2,7/2)})+\frac{159}{17\,920}(\mathbb {1}_{[-5/2,-3/2)}+\mathbb {1}_{[3/2,5/2)})\\&\quad -\frac{7\,621}{107\,520}(\mathbb {1}_{[-3/2,-1/2)}+\mathbb {1}_{[1/2,3/2)})+\frac{30\,251}{26\,880}\mathbb {1}_{[-1/2,1/2)}.\\ \end{aligned}$$

These kernels will be utilized to obtain more accurate approximations when refining coarse mesh information.

3 SIAC-MRA

In this section, we introduce an enhanced reconstruction using the SIAC-MRA. This provides a basis of alternative multi-wavelets as well as alternative multi-wavelet coefficients. To do so, we introduce the following notation:

$$\begin{aligned} V_h^{p^*} = \left\{ \sqrt{\frac{1}{2}} \cup \{\mathcal {X}_{\rm L}^{(k)}(\xi _j)\}_{k=0}^p,\, j=1,\cdots ,N\right\} \end{aligned}$$
(10)

with \(\xi _j = \frac{2}{\Delta x_j}(x-x_j)\) and

$$\begin{aligned} \mathcal {X}_{\rm L}^{(k)}(\eta ) = \frac{1}{2}\int _{-1}^\eta \, \phi ^{(k)}(\xi )\, \mathrm{d}\xi . \end{aligned}$$

This is the approximation space of the post-processed solution. There is a right counterpart to these functions defined as

$$\begin{aligned} \mathcal {X}_{\rm R}^{(k)}(\eta ) = \frac{1}{2}\int ^{1}_\eta \, \phi ^{(k)}(\xi )\, \mathrm{d}\xi . \end{aligned}$$

However, this expression can be further simplified if the basis functions are taken to be the orthonormal Legendre polynomials, \(\phi ^{(k)}(\xi ) = \sqrt{k+\frac{1}{2}}P^{k}(\xi )\) in \([-1,1]\). In this case, we can write \(\mathcal {X}_{\rm R}^{(k)}(\eta ) = - \mathcal {X}_{\rm L}^{(k)}(\eta ) = -\frac{\sqrt{k+1/2}}{2(2k+1)}\left( P^{(k+1)}(\eta )-P^{(k-1)}(\eta )\right)\) when \(k>0\). For \(k=0\), we have \(\mathcal {X}_{\rm L}^{(0)}(\eta ) = \frac{1}{2\sqrt{2}}(\eta +1)\) and \(\mathcal {X}_{\rm R}^{(0)}(\eta ) = \frac{1}{2\sqrt{2}}(1-\eta )\) which means that \(\mathcal {X}_{\rm R}^{(0)}(\eta ) = -\mathcal {X}_{\rm L}^{(0)}(\eta )+\sqrt{\frac{1}{2}}\). Plots of these functions are given in Fig. 4 (left).

Fig. 4
figure 4

Graphs of the left and right enhanced polynomials

Full size image

To describe the procedure of the enhanced reconstruction, we begin with the DG approximation represented by orthonormal Legendre polynomials:

$$\begin{aligned} u_h^N(x,t)\bigg |_{I_j} = \sum _{k=0}^p\, u_j^{(N,k)}\phi ^{(k)}(\xi _j) \end{aligned}$$

on a mesh consisting of N elements. Next, using a post-processor of \(2p+1\) B-Splines of order one we obtain the post-processed solution:

$$\begin{aligned} u_h^*(\bar{x})&= c_{-p}\sum _{k=0}^p\, u_{j-(p+1)}^{(N,k)}\mathcal {X}_{\rm R}^{(k)}(\zeta + 1) \nonumber \\&\quad +\sum _{\gamma = -p}^{p-1}\, \sum _{k=0}^p\, u_{j+\gamma }^{(N,k)}\left( c_\gamma \mathcal {X}_{\rm L}^{(k)}(\zeta + 1)+c_{\gamma +1}\mathcal {X}_{\rm R}^{(k)}(\zeta + 1)\right) \nonumber \\&\quad + c_{p}\sum _{k=0}^p\, u_{j+p}^{(N,k)}\mathcal {X}_{\rm L}^{(k)}(\zeta +1), \nonumber \\&= \sqrt{\frac{1}{2}}b_{j,{\rm R}}^{(0)}+\sum _{k=0}^p\, b_j^{(k)}\mathcal {X}_{\rm L}^{(k)}(\zeta +1), \end{aligned}$$
(11)

where \(\bar{x} = x_j + \frac{\Delta x}{2}\zeta\). The above is valid when \(\zeta \in (-1,0)\). Here,

$$\begin{aligned} b_{j,{\rm R}}^{(0)}= & {} \sum _{\gamma =-(p+1)}^{p-1}\, c_{\gamma +1}u_{j+\gamma }^{(N,k)} ,\end{aligned}$$
(12)
$$\begin{aligned} b_j^{(k)}= & {} -c_{-p}u_{j-(p+1)}^{(N,k)} + \sum _{\gamma =-p}^{p-1}(c_\gamma -c_{\gamma +1})u_{j+\gamma }^{(N,k)} +c_pu_{j+p}^{(N,k)},\quad k=0,\cdots ,p. \end{aligned}$$
(13)

Similarly, if \(\zeta \in (0,1)\), the post-processed solution can be written as

$$\begin{aligned} u_h^*(\bar{x}) = \sqrt{\frac{1}{2}}\widetilde{b}_{j,{\rm R}}^{(0)} +\sum _{k=0}^p\, \widetilde{b}_j^{(k)} \mathcal {X}_{\rm L}^{(k)}(\zeta -1), \end{aligned}$$
(14)

where

$$\begin{aligned} \widetilde{b}_{j,{\rm R}}^{(0)}&= \sum _{\gamma = -p}^p\, c_\gamma u_{j+\gamma }^{(N,0)},\\ \widetilde{b}_j^{(k)}&= -c_pu_{j-p}^{(N,k)}+\sum _{\gamma =-(p-1)}^p\, (c_{\gamma -1}-c_\gamma )u_{j+\gamma }^{(N,k)}+c_pu_{j+p}^{(N,k)}. \end{aligned}$$

We then need to obtain the approximation on the finer mesh, which can be expressed in terms of the following approximation space:

$$\begin{aligned} V_{h/2}^{p} = \left\{ \{\phi ^{(k)}(\xi _j)\}_{k=0}^p,\, j=1,\cdots ,2N\right\} . \end{aligned}$$
(15)

This gives the coefficients for the refined approximation as

$$\begin{aligned} u_{2j-1}^{(2N,m)}&= b_{j,{\rm R}}^{(0)} \left( \sqrt{\frac{1}{2}},\phi ^{(m)}\right) _{(-1,1)}+\sum _{k=0}^p\, b_j^{(k)}\left( \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi +1)\right) ,\phi ^{(m)}(\xi )\right) _{(-1,1)}, \end{aligned}$$
(16)
$$\begin{aligned} u_{2j}^{(2N,m)}&= \widetilde{b}_{j,{\rm R}}^{(0)} (\sqrt{\frac{1}{2}},\phi ^{(m)})_{(-1,1)}+\sum _{k=0}^p\, \widetilde{b}_j^{(k)}\left( \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi -1)\right) ,\phi ^{(m)}(\xi )\right) _{(-1,1)}\nonumber \\&\quad {j=1,\cdots ,N,\quad m=0,\cdots ,p.} \end{aligned}$$
(17)

The inner products used above are defined in the following way:

$$\begin{aligned} \left( \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi +1)\right) ,\phi ^{(m)}(\xi )\right) _{(-1,1)}&= \int _{-1}^1\, \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi +1)\right) \phi ^{(m)}(\xi )\, \mathrm{d}\xi ,\quad m=0,\cdots ,p,\\ \left( \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi -1)\right) ,\phi ^{(m)}(\xi )\right) _{(-1,1)}&= \int _{-1}^1\, \mathcal {X}_{\rm L}^{(k)}\left( \frac{1}{2}(\xi -1)\right) \phi ^{(m)}(\xi )\, \mathrm{d}\xi ,\quad m=0,\cdots ,p. \end{aligned}$$

Hence, an alternative multi-wavelet coefficient expression of

$$\begin{aligned} \sum _{j=1}^{2N}\, \left( \sum _{k=0}^p\, \widetilde{d}_j^{(k)}{\psi }^{(k)}(\xi _j)\right) = \mathcal {P}_{h/2}u_h^*-u_h^N \end{aligned}$$
(18)

can be obtained, where \(\mathcal {P}_{h/2}\) denotes the projection onto the piecewise polynomial approximation space (15) consisting of 2N elements, and \(\widetilde{d}_j^{(k)}\) are new multi-wavelets coefficients that may be inserted into (6).

Remark 1

(Errors) The enhanced reconstruction using the SIAC is of order \(p+2\). This allows for a reduced error constant when refining the mesh.

4 Numerical Results

In this section, we present the effectiveness of the enhanced reconstruction for a series of test problems involving both projections and time-evolution equations. We begin with an application to an analytical function and move on to a discontinuous function. Finally, we compare the time evolution of the usual MRA solution against the enhanced reconstruction.

4.1 Analytic Function

In this section, we consider

$$\begin{aligned} f(x) = \sin (2\pi x),\quad x \in [-1,1]. \end{aligned}$$

The function is first projected onto a mesh consisting of twenty elements using a piecewise orthonormal Legendre basis. This approximation is then further projected onto a series of five finer meshes, where the number of elements are doubled for every refinement. The projection using the standard orthonormal Legendre polynomials is compared with enhanced reconstructions that exploit the SIAC information. We compare using the enhanced reconstruction for every refinement versus the enhanced reconstruction only for the first refinement. The log-log plots of the errors for \(\mathbb {P}^1-\mathbb {P}^4\) are given in Fig. 5 and pointwise errors in Fig. 6. The corresponding error tables are given in Table 1. Figure 5 and Table 1 show that even if the enhanced reconstruction is used just for the first refinement, it is beneficial. The errors can be further reduced using the enhanced reconstruction for each refinement thereafter. In other words, the magnitude of the error decreases with the first refinement, and the errors continue to decrease if enhancement is done with each refinement. This is because the affect of the SIAC is the greatest on the original approximation. It should be noted that using the SIAC and then refining always produces better errors than refinement by itself.

Fig. 5
figure 5

The log-log plots of N vs. error for \(f(x)=\sin (2\pi x)\) on a series of six meshes. Using an enhanced reconstruction reduces the errors, even if it is done only for the first refinement

Full size image
Fig. 6
figure 6

Pointwise error plots \(f(x)=\sin (2\pi x)\) on the first three meshes. Using an enhanced reconstruction for every refinement reduces the errors and produces fewer oscillations in the errors

Full size image
Table 1 \(L^2\) and \(L^\infty\) errors for \(f(x)=\sin (2\pi x)\) for a series of projections onto finer meshes. Left: projection only. Middle: enhanced only for the first projection. Right: enhanced each refinement. Using an enhanced reconstruction reduces the errors, even if it is done only for the first refinement
Full size table

4.2 Two-Dimensional Analytic Function

We repeat the experiment in Sect. 4.1 for two dimensions, that is, we consider the two-dimensional function

$$\begin{aligned} f(x,y) = \sin (2\pi (x+y)),\quad (x,y) \in [-1,1]^2. \end{aligned}$$

The log-log plots of the errors are given in Fig. 7 and the corresponding error table is given in Table 2. Similar to the one-dimensional case, we find that using the enhanced reconstruction is beneficial, even if it is only performed for the first refinement.

Fig. 7
figure 7

The log-log plots of N vs. error for \(f(x)=\sin (2\pi (x+y))\) on a series of six meshes. Using an enhanced reconstruction reduces the errors, even if it is done only for the first refinement

Full size image
Table 2 \(L^2\) and \(L^\infty\) errors for \(f(x,y)=\sin (2\pi (x+y))\) for a series of projections onto finer meshes. Left: projection only. Middle: enhanced only for the first projection. Right: enhanced each refinement. Using an enhanced reconstruction reduces the errors, even if it is done only for the first refinement
Full size table

4.3 Discontinuous Function

In this section, we consider a simple box function,

$$\begin{aligned} f(x) =\mathbb {1}_{(-0.45,0.45)},\quad x \in [-1,1]. \end{aligned}$$

Note that the projections can achieve machine zero provided the discontinuities are at domain boundaries. For illustrative purposes, we only consider \(p=1, 2\). Plots of the function using a simple projection as well as enhanced reconstructions are given in Fig. 8. The log-log plots of N vs. error are given in Fig. 9. We see that it is still beneficial to use the enhanced reconstruction for the first refinement. However, continually using the enhanced reconstruction, while still better, may not be beneficial. The results can be seen in Table 3 and Fig. 10. The errors are calculated away from the discontinuities.

Fig. 8
figure 8

One-dimensional box function plots for \(p=1\). Left: approximation using simple projections. Middle: approximation using the enhanced reconstruction for each refinement. Right: approximation using the enhanced reconstruction only for the first refinement. Notice that the enhanced reconstruction reduces the oscillations at discontinuities

Full size image
Fig. 9
figure 9

The log-log plots of N vs. error for the one-dimensional box function using \(p=1\) (left) and \(p=2\) (right) polynomials. It is still beneficial to use the enhanced reconstruction for the first refinement. However, continually using the enhanced reconstruction, while still better, may not be beneficial

Full size image
Fig. 10
figure 10

Pointwise error plots for the one-dimensional box function for \(p=1,2\). In this case, we see that the enhanced reconstruction may create a pollution region around the discontinuity, while reducing the oscillations near a discontinuity

Full size image
Table 3 \(L^2\) and \(L^\infty\) errors for the one-dimensional box function using \(p=1\) and \(p=2\) polynomials. It is still beneficial to use the enhanced reconstruction for the first refinement. However, continually using the enhanced reconstruction, while still better, may not be beneficial
Full size table

4.4 Time Evolution

In this example, we consider the linear transport equation

$$\left\{\begin{aligned}u_t+u_x&=0,\quad x \in [-1,1],\, t>0,\nonumber \\ u(x,0)& = {} \sin (2\pi x). \end{aligned} \right.$$
(19)

The initial approximation is done for twenty elements and the errors are calculated after four periods in time (\(T=8\)). The same calculation is performed where the initialization uses the \(L^2\) projection onto twenty elements and then is refined either with or without the enhanced reconstruction. The log-log plots of the errors for \(p=1\), 2, 3, 4 is given in Fig.11. After the initial refinement, a better approximation is obtained using an enhanced reconstruction. This matches the corresponding \(L^2\) and \(L^\infty\) errors given in Table 4. Pointwise errors for \(p=3,\, 4\) are given in Fig. 12. The errors for the enhanced reconstruction have fewer oscillations.

Fig. 11
figure 11

Log-log plots of N vs. Error for the linear transport equation at time \(T=8\) for the initial condition \(u(x,0)=\sin(2\pi x)\) using \(p=1-4\) polynomials. it is beneficial to use the enhanced reconstruction after the first refinement

Full size image
Fig. 12
figure 12

Errors for the linear transport equation at time \(T=8\) for the initial condition \(u(x,0)=\sin (2\pi x)\) using approximations of polynomial degrees \(p=3\) (top), and \(p= 4\) (bottom). The enhanced reconstruction (right column) reduces oscillations in the error over a simple \(L^2\) projection

Full size image
Table 4 Errors for the linear transport equation at time \(T=8\) for the initial condition \(u(x,0)=\sin (2\pi x)\) using approximations of polynomial degrees \(p=1, 2, 3, 4.\) Left: errors using an \(L^2\) projection. Right: enhanced reconstruction for each refinement. The enhanced reconstruction reduces the \(L^2\) and \(L^\infty\) errors after the initial refinement
Full size table

5 Conclusions

In this article, we demonstrated that it is possible to construct a more accurate MRA that exploits the multi-scale structure of the underlying numerical approximation while taking advantage of the hidden accuracy of the approximation. This allows for reducing errors when passing numerical information from coarse scales to fine scales (and vice versa). We specifically utilized the SIAC filtering combined with multi-wavelets. Although this article presents the details of the SIAC filtering using the standard DG method, these techniques are easily extendable to other types of data.