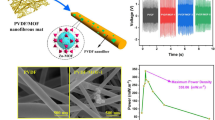
Abstract
Owing to the robust scalability, ease of control and substantial industrial applications, the utilization of electrospinning technology to produce piezoelectric nanofiber materials demonstrates a significant potential in the development of wearable products including flexible wearable sensors. However, it is unfortunate that the attainment of high-performance piezoelectric materials through this method remains a challenging task. Herein, a high-performance composite nanofiber membrane with a coherent and uniformly dispersed two-dimensional network topology composed of polyvinylidene fluoride (PVDF)/dopamine (DA) nanofiber membranes and ultrafine PVDF/DA nanofibers was successfully fabricated by the electrospinning technique. Based on the evidence obtained from simulations, experimental and theoretical results, it was confirmed that the unique structure of the nanofiber membrane significantly enhances the piezoelectric performance. The present PVDF/DA composite nanofibers demonstrated a remarkable piezoelectric performance such as a wide response range (1.5–40 N), high sensitivity to weak forces (0–4 N, 7.29 V N−1), and outstanding operational durability. Furthermore, the potential application of the present PVDF/DA membrane as a flexible wearable sensor for monitoring human motion and subtle physiological signals has also been validated. This work not only introduces a novel strategy for the application of electrospun nanofibers in sensors but also provides new insights into high-performance piezoelectric materials.
Graphical Abstract

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Owing to the unique properties, the flexible electronics offer significant advantages over traditional silicon-based electronic materials in various fields including bending. The flexible electronics are found to be well-suited for various potential applications, particularly, in space exploration, human–machine interaction, and wearable electronics [1,2,3,4]. As a core component of flexible electronics, flexible sensors are capable of acquiring and converting various types of information (e.g., strain, pressure, temperature), serving as a crucial interface between the system and the external environment. The accuracy of sensor data acquisition is paramount, particularly for flexible pressure sensors [5,6,7,8]. Currently, extensive research has been conducted on achieving high sensitivity, wide range, and high stretchability of the flexible sensors [9,10,11,12,13]. For example, Gao et al. [14] constructed a pressure sensor based on a skin-like structure, achieving a sensitivity greater than 1000 kPa−1. They found that the excellent flexibility and sensitivity of the developed pressure sensor can be achieved by tuning the materials design and structure. However, the method is highly limited due to it difficult fabrication and high costs.
In recent years, the electrospun nanofibers with high specific surface area and controllable-structure has provided an attractive platform for various potential applications [15,16,17]. As a relatively mature commercial technology, electrospinning has obvious advantages in the controllable and large-scale production of various kinds of electrospun nanofibers [18]. The feasible electrospun nanofiber-based sensors have remarkable attractiveness and dominance in designing and manufacturing of thin, soft, and comfortable wearable products [19,20,21,22]. According to the previous research, three main sensing principles (piezoelectric, piezoresistive and capacitive) are required for pressure sensors [23]. Among them, piezoelectric materials have the potential to be self-powering due to their ability to collect various mechanical movements and convert them effectively into electrical energy [24]. To this end, researchers have devoted considerable research efforts to develop high-performance piezoelectric sensors [25]. Park et al. [26] successfully embedded lead-free (Na, K)(Nb, Sb)O3-BaZnO3-(Bi, K)ZrO3 in polycrystalline silicon into P(VDF-TrFE) (poly(vinylidene fluoride-co-trifluoroethylene)) electrospun nanofiber matrix. The nanofibers maintained an open-circuit voltage, a high maximum generated power, and an output voltage of approximately 12.2 V, 33.2 nW, and 1.25 V, respectively, despite being bent for 10,000 cycles. Li et al. [27]. reported that PDA-coated BaTiO3 nanowires (BTNW) were introduced into P(VDF-TrFE) electrospun nanofibers to form coaxial composite nanofibers, which produced an optimal piezoelectric output of 18.2 V under an impact force of 5 N with excellent sensitivity of 4.3 V N−1. Frank K. et al. [28] used electrospinning to grow CsPbI2Br perovskite crystals in situ on polyvinylidene fluoride (PVDF) nanofibers. CsPbI2Br spread over the nanofiber, leading to a rough surface, and complementing piezoelectric nanocomposite formation with PVDF for superior stress excitation. The output voltage of 8.3 V and current of 1.91 μA and used to charge capacitors for powering electronics.
It is evident that despite the inherently low piezoelectric performance of electrospun nanofibers, the introduction of inorganic nanomaterials through embedding or in-situ growth can leverage interfacial polarization between organic and inorganic components or enhances the material stress induction, thereby achieving heightened piezoelectric performance [29]. Nevertheless, the presence of inorganic materials poses issues such as sensitivity to environmental conditions and biological toxicity, restricting their practical applications [30]. Currently, achieving excellent piezoelectric performance without introducing inorganic materials remains a difficult challenging endeavor for electrospun nanofibers. Ding et al. [31, 32]. have developed electrospinning-jetting and electrospun mesh techniques to fabricate 2D nanonets with a continuous topology Steiner tree structure and a diameter of 20–35 nm. Due to the unconstrained nature of polymer materials, these nanonets exhibit outstanding performance in air and water filtration. Nevertheless, in the solution systems capable of producing ultrafine nanofibers in current research, achieving satisfactory formation necessitates strict requirements not only on the choice of the receiving substrate material but also on the substrate thickness, which significantly hinders their application in other fields. But inspired by it, if similar ultrafine nanofibers are introduced into conventional electrospun nanofibers, the resulting hierarchical structure are expected to have distinctly different pressure effects that will impact piezoelectric properties generation from the nanofiber membrane.
This work investigates, for the first time, the effect of ultrafine nanofibers on the piezoelectric properties of electrospun nanofibers. By varying the spinning time, PVDF composite nanofiber with different structures are created. This structure was confirmed to correlate with piezoelectric properties through a combination of experiments and finite element simulations. Additionally, by introducing dopamine during the electrospinning process and benefiting from hydrogen bonding and dipole interactions, it successfully induces PVDF and ultrafine PVDF nanofibers to form a higher β-crystal orientation. Moreover, the core–shell structure formed by dopamine (DA) and PVDF electrospun nanofibers enhances the material stability, ensuring high piezoelectric output and sensitivity. This study highlights the fact that the piezoelectric voltage output can be improved by 66.7% and high sensitivity by constructing a composite nanofiber with uniformly dispersed two-dimensional network topology. It is anticipated that the results presented in this work propose a new door for electrospun nanofibers to be used in the field of piezoelectric sensors and provide new ideas for the design and development of electrospun nanofiber membranes with high-performance piezoelectric materials.
Experimental
Materials
PVDF granules (Mr = 275,000) were obtained from Sigma-Aldrich (Japan). PVDF powder (Mr = 500,000) were purchased from Arkema (Japan). Tetrabutylammonium chloride (TBAC), Dopamine (DA), N,N-dimethylformamide (DMF, ≥ 99.9%) and Acetone (≥ 99.9%) were supplied by Sigma-Aldrich (Japan). All the chemicals used were of analytical grade.
Formation of Electrospun Nanofibers and Ultrafine Nanofibers
To prepare the electrospun nanofiber solution, at first, a 16 wt% of PVDF (Mr = 275,000) solution was prepared in a mixture of DMF and acetone (3:2). To the above mixture, 0, 1, 2 and 3 wt% (solute mass) of DA was dissolved and a homogenous spinning solution was obtained by stirring continuously for 2 h at 60 °C. In case of the preparation of spinning solution for obtaining the ultrafine nanofiber, TBAC powders with 2.5 wt% was first dissolved in DMF by magnetically stirring for 2 h at 40 °C. Subsequently, the DA of 0, 0.5, 1 and 2 wt% (solute mass) was dispersed in the TBAC solution and the mixture was stirred for 2 h at 50 °C. Finally, 3 wt% of PVDF (Mr = 500,000) powder was dissolved in the DA/TBAC solution. Electrospinning process was performed by using the above 2 mixed solutions into a 5 mL plastic syringe fitted with a 18G/20G stainless steel nozzle. In the process of electrospun nanofibers, a high voltage power supply was set to 15 kV between the nozzle tip and the collector at 20 cm. When preparing ultrafine nanofiber, the voltage is 22 kV and the tip to collector distance of 22 cm. During the electrospinning process, the temperature was maintained at 25 °C and the humidity was controlled between 35 and 40%. For the preparation of nanofiber membranes with hierarchical structures, PVDF/DA nanofiber membranes were covered on the drum rotator, of which the roller speed was selected to be 100 rpm for collecting the ultrafine nanofiber. The flow chart for the fabrication of composite nanofiber piezoelectric sensor with hierarchical structure is shown in Fig. 1.
Configuration of the Sensor
A very lightweight, flexible, piezoelectric sensor (effective area of ~ 25 × 25 mm2) was fabricated by different structures and types of PVDF nanofiber membranes. PVDF nanofiber membranes was sandwiched between two copper (Cu) electrodes and two copper wires were soldered on the electrodes. The fabricated piezoelectric sensor, configured as Cu electrode/nanofiber membranes/Cu electrode, was encapsulated by PI (Polyimide) tapes to enhance its durability. For collecting biomechanical signals, the sensor was sealed with tape to make it fit better with human skin. Finally, the whole device was subjected to an appropriate compression, which helped to avoid the generation of triboelectric signal by eliminating the gap between different layers.
Characterizations and Measurements
The surface morphology of composite nanofiber piezoelectric sensors was observed using a JEOL JSM-6010 LA scanning electron microscope (FE-SEM). The FE-SEM was equipped with an energy-dispersive X-ray spectrometer (EDX), also from Japan called Inca Oxford, to image the surface morphology of individual nanofibers at an accelerating voltage of 10 kV. In addition, the internal and external structure and crystal orientation of the nanofibers were observed through transmission electron microscopy (TEM, JEOL JEM-2010). The attenuated total reflection-Fourier transform infrared (ATR-FTIR) spectroscopy was used to analyze the chemical structures of nanofiber membranes using a spectrometer (IR Prestige-21, Shimadzu, Japan). The crystalline structures were analyzed via X-ray diffraction (MiniFlex300 Rigaku, Japan) equipped with Cu Kα radiation. The crystallinity of the electrospun nanofibers was determined by differential scanning calorimetry (DSC, DSC-8500, PerkinElmer, USA) with the heating rate of 10 °C min−1 and temperature ranging from 35 to 300 °C. Chemical modification of nanofiber membranes was evaluated by X-ray photoelectron spectroscopy (XPS, Axis-Ultra HSA SV, Kratos Analytical Inc., U.K.). The thickness of all the fiber films was determined using a digital thickness gauge (YHT780, China) by putting the film sample between two fixtures. A quasi-static d33 meter (ZJ-3AN, Chinese Academy of Sciences) was used for d33 values. The dielectric properties were tested by precision impedance analyzer (1260/1296, Solartron Analytical Inc., U.K.) in range 102–106 Hz. Electrical outputs of the packaged devices were measured by Oscilloscope (DS-5414A ViewGoll, IWATSU, Japan) and Keithley 6514 electrometer and the corresponding data were recorded by Labview software.
Results and Discussion
Morphology of the Nanofiber Membranes
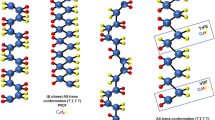
The morphology of PVDF/DA nanofibers with different DA concentrations (0, 1, 2, 3 wt%) is presented (Fig. S1 in the supporting information), hereinafter referred to as PDS-0, PDS-1, PDS-2, PDS-3. The Representative images of PVDF nanofiber morphology with different DA concentrations are shown in Fig. 2a. As the concentration of DA increases to 2 wt% (PDS-2), the adhesion between fibers becomes more pronounced, accompanied by an increase in the average fiber diameter from 236 to 268 nm. From the TEM results in Fig. 2b, it is evident that these phenomena are not only attributed to the increase in DA concentration but also to the formation of typical core–shell structures between DA and PVDF. However, as the DA concentration increases to 3 wt% (PDS-3), the fiber diameter decreases, as observed from TEM (Fig. 2b), primarily due to the substantial embedding of DA into the PVDF matrix. Feng et al. [33] research suggests that the formation of the core–shell structure may be attributed to interactions between –NH2 and –CF2. Nevertheless, the molecular dynamics (MD) simulations were employed to compare the radial distribution functions (RDF) of fluorine atoms near –NH2 groups (N–H–F) and –OH groups (O–H–F) in the absence of an electric field. It was observed that within the range of 2.4–3.1 Å, the RDF for O–H–F exhibited an initial peak followed by a decrease, contrasting with N–H–F interactions (Fig. 2c). Notably, hydrogen bonding interactions predominantly occurred within the range of 2–3 Å. This implies that both –OH and –NH2 moieties exert an influence on –CF2 in PVDF in a solution state (Fig. 2d (i)). In addition, during the characterization of PDS-2 fibers post-electrospinning, the results obtained from Energy-Dispersive X-ray Spectroscopy (EDS), as depicted in Fig. 2e, bore a striking resemblance to prior research. With the sole exception of fluorine, the distribution of nitrogen (N) appeared notably more even than that of oxygen (O) within the core region. Moreover, the XPS findings, detailed in Fig. 2f–g, not only unequivocally confirmed the presence of carbon (C), nitrogen (N), fluorine (F), and oxygen (O) elements within PDS but also revealed an intriguing facet. Specifically, in the N 1s peak deconvolution, in addition to the discernible N–H and –NH2 characteristic peaks of DA, a distinct N–F characteristic peak (406.8 eV) emerged. This observation implies a robust interaction between nitrogen in DA and the –CF2 moieties on polyvinylidene fluoride, underscoring their strong interplay within the nanofiber structure. When amalgamating prior research with the findings from the molecular motion simulations presented in this article, a predominant factor behind the formation of the core–shell structure emerges the positive charge carried by –NH2 in DA under the influence of an electric field. This positive charge compels these entities to migrate to more distant positions from the nozzle, driven by electrostatic repulsion. However, the compelling dipolar interaction between these positively charged –NH2 and –CF2 groups subsequently exerts an attractive force, making it more probable for a protective shell structure to take shape on the surface of the fibers. Significantly, the alignment of PVDF molecules under this long-range interaction exhibits a pronounced level of symmetry (Fig. 2d (ii)), making it more predisposed to the β-type structure of CH2–CF2 [34](in an all-trans conformation referred to as TTTT structure).
Characterization of PVDF/DA electrospun nanofibers. a SEM image of PVDF with 0, 1, 2, 3 wt% DA (PDS-0, PDS-1. PDS-2, PDS-3). b TEM image of the core/shell PDS-1, PDS-2, PDS-3. c RDFs between the –CF2 groups in PVDF and the –NH2 (black) and –OH (red) groups in DA. The inset is the MD simulations of a PVDF/DA molecular structure in equilibrium, showing the core (PVDF)–shell (DA) arrangement. d Schematic of the PVDF chain arrangement and orientation induced by intermolecular interactions during the electrospinning process for the fabrication of PVDF/DA core/shell nanofibers. e EDS mapping of F (brown), O (blue), and N (petrol) elements distribution in a PVDF/DA core/shell NF shown in the FE-SEM image. f XPS survey spectra of PDS-2 (red) and pure PVDF (black) nanofibers. g The XPS N 1s spectrum of the PDS-2. h Digital images of PDS-2
Figure 3a illustrates the X-ray diffraction (XRD) data of PDS. Notably, the prominent diffraction peak is positioned at 2θ = 20.5°, corresponding to the β (110) crystal plane. Additionally, relatively weaker diffraction peaks at 18.4° and 36° are attributed to the α (020) and α (200) crystal planes, respectively. XRD peak splitting (Fig. 3b–e) reveals that as the concentration of DA increases, the proportion of α characteristic peaks initially decreases and then rises, with PDS-2 displaying the lowest α characteristic peak ratio. This observation is also substantiated by ATR-FTIR data (Fig. 3f). Despite the presence of clear β-phase characteristic peaks at various DA concentrations, such as 840 cm−1 (–CH2 rocking), 1176 cm−1 (C–F stretching), and 1275 cm−1 (C–F out-of-plane deformation), the height of the α-phase characteristic peak at around 763 cm−1 (–CF2 bending and scissile bending) follows a pattern of initial reduction and subsequent increase. This is primarily attributed to the increased incorporation of DA into the PVDF matrix, which disrupts the orientation and arrangement of PVDF chains in the nanofibers (Fig. 1b), thereby diminishing crystallinity. By combining ATR-FTIR data, the β-phase content can be calculated using F(β) = Aβ/(1.26Aα + Aβ) (S2 in the Supporting Information), where Aα and Aβ represent the absorbance areas at 763 cm−1 and 840 cm−1, respectively (F(β)) [35,36,37]. Please note that a coefficient of 1.26 is assumed to be valid for electrospun nanofibers. The results indicate that PDS-2 boasts the highest β-phase content, reaching 89% (Fig. 3g). DSC analysis provides further validation of this outcome. PDS-2 exhibits the highest melting temperature peak (Fig. 3h), as the increase in β-phase content corresponds to a higher melting temperature of PDS. Additionally, the crystallinity content (Xc) of PVDF was computed from the DSC spectrum [38, 39], with PDS-2 achieving the highest value (Fig. 3i), totaling 67.5%. This PDS-2 is 22.14% greater than pure PVDF, making PDS-2 the preferred base to produce ultra-fine PVDF/DA nanofibers.
Crystallinity characteristics of PDS. a XRD spectra of PVDF/DA nanofibers with different DA contents. b–e Inset is the β-phase percentage as a function of the DA content, quantified from the XRD spectra by the curve deconvolution. f FTIR spectra and g β-phase contents (F(β)) of PVDF/DA nanofibers with different DA contents. h DSC thermograms and i the crystallinity contents (Xc) value as a function of the DA content, quantified from the FTIR spectra and the DSC thermograms, respectively. β-phase crystallinity (%) = Xc × F(β) × 100%
Figure 4a displays FE-SEM images of ultrafine nanofibers with varying DA concentrations (0, 0.5, 1, 2 wt%, hereafter referred to as PDU-0, PDU-1, PDU-2, PDU-3). With increasing DA concentration, there is a slight enlargement in fiber diameter, reaching approximately 35 nm. Notably, in comparison to the twisted ultrafine nanofiber network observed in PDU-0, the structure of the ultrafine nanofiber network becomes more stable after the addition of DA, but it also leads to the emergence of more droplets. Among them, both PDU-1 and PDU-2 showed good conditions (Fig. S3 in the Supporting Information), and it is exciting that the self-oriented β phase of ultrafine PVDF nanofibers was confirmed by TEM for the first time (Fig. 4d). PVDF polymeric chains were aligned and oriented in parallel to the PVDF/DA interface. The inter-chain distance was 4.28 Å (upper inset of Fig. 4d), corresponding to the (110) plane.
Characterization of PVDF/DA ultrafine nanofibers. a SEM image of PVDF with 0, 0.5%, 1%, 2 wt% DA (PDU-0, PDU-1, PDU-2, PDU-3). b and c TEM image of the PDU. d High resolution TEM (HRTEM), the enlarged view of HRTEM (top inset) and FFT images (lower inset) of PDU-1 showing aligned PVDF chains along the fiber axis. e FTIR spectra and f XRD spectra of PVDF/DA ultrafine nanofibers with different DA contents. g ultrafine nanofiber forming mechanism diagram. h EDS mapping results of single ultrafine nanofibers of PVDF/DA containing 0.5 wt% DA. i RDFs between the –CF2 groups in PVDF and the –NH2 (black), –OH (red) and –N+(blue) groups in DA and TBAC. The inset is the MD simulations of a molecular structure in equilibrium, showing the PVDF, DA and TBAC arrangement. j XPS survey spectra and k N 1s spectrum of the PDU-1
This can also be proven from the ATR-FTIR data (Fig. 4e) and XRD (Fig. 4f). Compared with PDS, the peak intensity of PDU at 1275 cm−1 is significantly higher, which is a unique characteristic peak of β. And the alpha phase peak intensity at 763 cm−1 is very weak. It can also be seen from XRD that the α characteristic peak at 36° disappears, and there is only the β (110) crystallization characteristic peak at 20.6°, reflecting the presence of a higher β phase in PDU. Through calculation, the β phase content of PDU-1 reaches the highest value of 98%, but with the DA content, the β phase content drops significantly to 88%, which is lower than the β phase content without adding DA. From the ATR-FTIR data (Fig. 4e), it is found that the main reason for the decrease is due to the increase in DA loading to an increase in the γ phase (intensity increase at 1234 cm−1) in the PDU. In addition, from the TEM data (Fig. 4b–c and Fig. S4 in the Supporting Information), no obvious core–shell structure was observed. The primary reason for the observed phenomenon may be closely related to the unique formation mechanism of an ultrafine nanofiber network (Fig. 4g). Presently, researchers posit that the critical factor for generating electrospun ultrafine nanofibers is the charge density in the solution, which must surpass the droplet threshold, denoted as Dc [40, 41], where \(Dc = \sqrt {288\varepsilon \gamma /\delta \rho^2 D^3 }\). Here, ε represents the ambient permittivity, γ is the surface tension of the fluid, δ is the correction factor, ρ denotes the fluid density, and D signifies the diameter of the charged fluid. Additionally, \(D = 1.46Q^{0.44} \varepsilon^{0.12} \eta^{0.32} K^{ - 0.12} \gamma^{ - 0.32} \) [42], where Q stands for the volumetric flow rate, η is the fluid viscosity, and K represents the fluid conductivity. Consequently, the formation of ultrafine nanofibers necessitates not only high electrical conductivity but also a low-concentration state in the solution. In this state, many droplets are ejected due to the high electrical conductivity and surface tension. These droplets disperse within the electric field and undergo a series of complex processes, including collision, stretching, and evaporation, which vary with changes in electric field intensity [43, 44]. This may result in the inability of DA to exist around PVDF ultrafine nanofiber stably and continuously.
Molecular dynamics simulations further validate the existence of this phenomenon. Analyzing the radial distribution function (RDF) reveals a similarity to the PDS process (Fig. 4i). Even though TBAC is present, the priority of DA is significantly higher than that of TBAC. This emphasizes that a core–shell structure will also form in the normal jet mode. Moreover, an examination of the highest β-phase PDU-1 surface scan and XPS data (Fig. 4j–k) indicates the presence of DA on the surface. However, the absence of N–F in the N 1s spectrum suggests that there is no strong bond between –NH2 and –CF2, demonstrating that the high β-phase of PVDF primarily relies on induction through high stretching and electrical fields. Nevertheless, due to the positive charge of –NH2 in DA, a small amount of DA may still promote the formation of the PVDF β-phase under the influence of hydrogen bonding and dipole forces. Moreover, an examination of the highest β-phase PDU-1 EDS and XPS data (Fig. 4h–k) indicates the presence of DA on the surface. However, the absence of N–F in the N 1s spectrum suggests that there is no strong bond between –NH2 and –CF2, demonstrating that the high β-phase of PVDF primarily relies on induction through high stretching and electrical fields. Nevertheless, due to the positive charge of –NH2 in DA, a small amount of DA may still promote the formation of the PVDF β-phase under the influence of hydrogen bonding and dipole forces. Nevertheless, due to the electric field inducing a positive charge on the –NH2 in DA, a small amount of DA can still promote the formation of the PVDF β-phase under the influence of hydrogen bonding and dipole forces. However, when the DA content within the droplets is excessive, leading to an uneven distribution, it may instead induce the formation of the γ phase.
Results and Analysis of Composite Nanofiber Piezoelectric Material
The high β-phase content in the NFs was expected to largely enhance their piezoelectricity. Using PDS-2 with the highest β phase as the base, PDU-1 was spun for 90 min, 180 min, and 240 min respectively, and three types of multi-scale PVDF/DA nanofiber membranes were prepared. For the convenience of recording, they are abbreviated as MPD-1 MPD-2 and MPD-3. From FE-SEM results (Fig. 5e, Fig. S5 in the Supporting Information), it was found that the density of the ultrafine fiber network in the pores of PDS-2 fibers did not increase with time. Specifically, after 240 min, numerous "film" and polymer spheres developed within the pores of PDS-2 fibers or adjacent to the fibers, without any increase in fiber density within the pores. It is crucial to emphasize that at the 180 min mark, a noticeable density of ultrafine nanofibers formed within the pores of the thicker nanofibers. These ultrafine nanofibers were closely interconnected with the thicker nanofibers, resulting in the formation of a complete two-dimensional topological network structure. Additionally, under higher magnification electron microscopy, it was observed that the thicker nanofibers and ultrafine nanofibers were closely connected, which was not only due to the adhesion of DA on the surface of the thicker nanofibers but also to Formation of "thin film" during spinning of ultrafine nanofibers. This helps to improve the mechanical properties of the composite nanofiber membrane (Fig. S6 in the Supporting Information).
a Dielectric constant, and b dielectric loss diagram of the PDS-2 and MPD. c Piezoelectric coefficient (d33) of the PDS-2 and MPD. d Optical photo and schematic diagram of flexible sensor structure. e typical FE-SEM images of PDU-1 with different spinning times (90 min, 180 min and 240 min) based on PDS-2 and corresponding output voltage. f Comparison of output voltages under different structures. g Output current and h data comparison under different structures
To assess the impact of PDU-1 spinning time on the encapsulated electrical properties of MPD, a comprehensive investigation of MPD dielectric and piezoelectric properties under varying spinning durations was conducted. The relative dielectric constant and dielectric loss of MPD were measured across frequencies ranging from 102 to 106 Hz and were compared with the performance of PDS-3, as illustrated in Fig. 5a–b. It is noteworthy that the dielectric constant of MPD initially increases and then decreases as the spinning time of PDU-1 is extended. The initial increase can be attributed to differences in dielectric properties between PDS and PDU, which lead to an increase in Maxwell–Wagner–Sillars interface polarization and, subsequently, an increase in the dielectric constant. The subsequent decrease is linked to the agglomeration of TBAC due to the increased presence of "film" in the fiber membrane. In addition, with the addition of ultrafine nanofibers, the dielectric loss of MPD remains in a low range, which is due to the polymer matrix. The piezoelectric coefficient (d33) of MPD was determined using a static d33 meter, as depicted in Fig. 5c. The d33 value of MPD is found to be influenced by the content of PDU-1. With an increase in the spinning time of PDU-1, the d33 value of MPD rises from 32 to 52 pC N−1, with MPD-2 displaying the highest piezoelectric coefficient. The improvement in d33 can be attributed to its higher beta phase content compared to PDU-1. Notably, this high d33 value surpasses that of other reported PVDF-based nanostructures (films, nanoribbons, and nanofibers) and is comparable to certain ceramic-based micro/nanofibers (Table S1, Supporting Information) [17, 45,46,47,48].
To display its piezoelectric properties more intuitively, a piezoelectric test unit was made from the above-mentioned multi-scale structural fiber membranes at different times. The structure of the test unit is shown in Fig. 5d, with a size of 25 × 25 mm2 and an automatic stepper. The motor controller tested the film piezoelectric properties by repeatedly pressing and releasing it at 1.5 N and a low frequency of about 1.2 Hz. The performance results are shown in Fig. 5f–h. The open-circuit voltage and short-circuit current have increased, and both show a similar trend with d33, verifying that VOC and ISC are directly related to the d33 value. Especially for MPD-2, the open-circuit voltage output reaches 14.3 ± 0.2 V and the short-circuit current reaches 1.01 ± 0.1 μA.
It is of significance to highlight that despite the increase in PDU-1 content, the electrical output performance of MPD did not exhibit improvement; in fact, it showed a decline. To gain a clear understanding, it is imperative to elucidate the factors influencing the electrical output of piezoelectric materials during electromechanical operation. Presently, researchers have developed multiple theoretical models to elucidate the factors impacting the electrical output of piezoelectric materials. These theoretical models broadly delineate the microstructure of piezoelectric materials into alternating material layers and air layers. Following Kirchhoff’s second law, the formula for output voltage can be expressed as follows [49, 50]:
where V represents the open-circuit voltage, Q denotes the total charge density, ε0 signifies the vacuum permittivity, S stands for the effective operational area of the device, de signifies the total thickness of the solid layer, εr represents the relative permittivity of the material layer, dgas corresponds to the total thickness of the air layer, εg symbolizes the relative permittivity of air. σj represents the charge captured at the solid–gas interface after polarization, where j is the layer number of the air layer, and n represents the total number of layers.
The following corresponding boundary condition can be obtained at time t = 0:
By combining Eqs. (1) and (2), the output voltage can be written as:
where dgas(t = 0) = dgas_0, Q0 represents the initial charge density at t = 0, Q(t) expresses the quantity of electric charge on each electrode at the instant when the top and bottom electrodes are approaching each other immediately after the stimulus commences at time t = 0.
Under short-circuit (SC) current conditions, ISC can be obtained from Equation:
Indeed, from the above formula, it is apparent that the electrical output performance of piezoelectric materials is positively correlated with the material charge density. In the case of organic materials, an elevation in the dielectric constant contributes to an increase in the peak of transferred charges after polarization [51], thus elucidating one of the factors behind the high electrical output performance of MPD-2.
Furthermore, apart from the inherent material properties, the enhancement of charge density in piezoelectric materials is also influenced by the distribution of mechanical stress. As the time duration of PDU-1 increases, the structural characteristics of MPD change, and this, in turn, affects the stress distribution within the material. To theoretically assess the impact of structure on piezoelectric performance, representative material models were established for stress and piezoelectric potential calculations using finite element simulations (COMSOL Multiphysics 6.1). The primary structure consisted of a 25 × 25 mm2 matrix of PVDF with a thickness of 30 mm and an 8 × 8 grid. Based on the structural variations within MPD, it was divided into three structures. In Fig. 6a, the top layer has no fine fibers within the pores, referred to as S-1. In Fig. 6b, the top layer exhibits an even distribution of fine fibers within the pores, known as S-2. In Fig. 6c, the top layer alternates between fine fibers and PVDF membranes within the pores denoted as S-3. All structures were anchored at the base and grounded, and an external force was applied parallel to the z-axis for stimulation. The corresponding schematic diagrams for the process are shown in Fig. S7 (in the Supporting Information).
The piezoelectricity can be elaborated by coupling the electrical behavior of dielectric material and Hooke law, as described in the following equations [52]:
where S is strain, s is compliance, T is applied stress, D is the electric charge density displacement, E is electric field strength and ε is permittivity; Their linear relations can be shown by the following equations [53]:
The above equations reveal the different piezoelectric outputs owing to strain variations. Based on the above concept, it is not difficult to find that the higher the internal the stress of the material, the higher the potential can be generated. In S-1, stress distribution is uniform. However, in S-2, due to the presence of fine fibers, stress within the pores of the thick fibers changes. Notably, stress concentration becomes prominent at the connections between the fine fibers and the thick fibers, resulting in significantly elevated stress levels (more than 30 times that of S-1). The stress concentration simultaneously promotes the piezoelectric response of the two-scale nanofibers and the stress-induced polarization under load, thereby feeding back the highest potential (Fig. 6d–f). In addition, although the content of fine fibers in S-3 (here it is assumed that the film is quite composed of fine fibers) is increased, the presence of the film weakens the stress concentration of the thin fibers and gives a lower potential than S-2. This also explains why MPD-2 has a higher piezoelectric constant.
Furthermore, structural changes induce different piezoelectric phenomena in MPD at different frequencies (2–10 Hz), as illustrated in Fig. 7a–c. Notably, when the frequency falls within the range of approximately 2–4 Hz, the voltage measured by the oscilloscope exhibits minimal fluctuations. As the frequency is increased to around 6–10 Hz, both MPD-2 and MPD-3 generate voltages that fluctuate regularly, with MPD-2 displaying shorter fluctuation periods. This change can be attributed to the differential response speed of ultrafine nanofibers compared to coarse fibers (Fig. 7d). In contrast to conventional piezoelectric materials, this periodic fluctuation is more conducive to providing feedback when the frequency changes under the same force [54].
Therefore, based on the results, it is concluded that MPD-2 exhibits the most favorable piezoelectric performance, and subsequent research has been focused on the sensing applications of MPD-2.
Practical Application and Stability of the MPD-2
When considering piezoelectric sensors, it is crucial to assess sensitivity and the linear pressure range. The sensitivity (S) is defined as \(S = (\Delta V/V_0 )\Delta P\), where \(\Delta V/V_0\) represents the relative variation in voltage [46], while \(\Delta P\) indicates the applied pressure. Figure 8a illustrates the sensitivity of the MPD-2 sample under applied pressure. The data reflects voltage stepwise changes in response to forces ranging from 1.5 N to 40 N. Notably, a substantial change in voltage amplitude is observed in the 1.5–10 N region, while the voltage change amplitude decreases in the 16.5–40 N range. Linear fitting (Fig. 8b) reveals that MPD-2 exhibits high sensitivity in both the low-pressure region (below 10 N) and the high-pressure region (above 10 N). Specifically, the sensitivity values in the low-pressure (0–4 N) region reach 7.29 V N−1, in the medium-pressure (5–10 N) region reach 4.11 V N−1, and in the high-pressure (30–40 N) region also reach 1.41 V N−1. These values demonstrate higher sensitivity and a broader pressure range when compared to PVDF-based piezoelectric materials and previously reported polymer composites (Table 1). Additionally, due to the stable structural network formed by DA adhesion between ultrafine nanofibers and thick fibers, consistent voltage output is maintained even after 10,000 taps at 2 Hz (Fig. 8c).
a Output voltage signals under different pressures. b Directional sensing behavior of MPD-1. c Long-term stability and durability of MPD-1 during 10,000 working cycles at the same location (4 Hz, 1.5 N). Real-time monitoring of human motions and subtle physiological activities, including d speaking, e wrist pulse, f finger tapping, g elbow bending, h knee bending and i foot stamping
Certainly, besides its exceptional sensing capabilities and stability, its performance in practical applications must be taken into account. Thanks to the flexibility and lightweight nature of the nanofiber membrane, it finds utility as a wearable film sensor for detecting human movements and subtle physiological activities. When comfortably affixed to a speaker’s throat, it can capture delicate and intricate weak force signals, such as muscle movements and epidermal deformations during speech. In Fig. 8d, the output voltage curve is depicted as the word "Hello" is spoken five times in various languages. Consistent characteristic peaks are recorded for each pronunciation method, demonstrating that the sensor exhibits high sensitivity and reliability for speech recognition. This capability can be utilized for rehabilitating the speech abilities of individuals with damaged vocal cords. Additionally, Fig. 8e displays the real-time pulse signal when the sensor is attached to the wrist. In addition to detecting a wrist pulse frequency of 65 beats per minute, it's essential to note that, due to the presence of ultra-fine nanofibers, the single signal waveform of the wrist pulse reveals two distinct peaks, P1 and P2 [55]. Among these, P1 represents the pulse wave, while P2 corresponds to the reflected wave from the hand. Based on this parameter, the arterial augmentation index (AIr = P2/P1) can be computed, with an average value of 0.448, which aligns with that of a healthy 26-year-old woman [56, 57]. This pulse information can be harnessed for hypertension and cardiovascular disease detection. The MPD-1, with its exceptional sensitivity to weak force signals, holds significant potential in the realms of health monitoring and clinical diagnosis.
Additionally, with its exceptional sensitivity to weak force signals, the MPD-1 sensor is proficient in discerning variations in pressure, including those induced by finger, elbow movements, and foot joint motions. As exemplified in Fig. 8f, when the MPD-1 sensor is directly affixed to the fingertip, it can accurately capture real-time tapping actions across different contexts. Gentle taps yield an output voltage of 3.4 V, while forceful strikes result in an increased output voltage of 7.5 V. For the above sensing applications, the finger motion amplitude and speed can be extracted by decoupling the force and frequency dependences of the electric signal. Meanwhile, when the sensor is affixed to the elbow, as depicted in Fig. 8g, it can detect the bending of the elbow from a straight position to 45° and 90°, generating peak voltages of 7.1 V and 9.8 V, respectively. The positive and negative voltage values correspond to the bending [58] and angle of the elbow, respectively. Similarly, when the sensors are attached to corresponding body parts, such as the knee and foot, they can detect bending and movement, as shown in Fig. 8h–i. Therefore, the MPD-1 sensor exhibits rapid response and can be employed for motion capture and tactile perception, presenting potential applications in remote human–computer interaction and control.
To further, owing to the high piezoelectric performance of the MPD-1, it can be integrated into piezoelectric nanogenerator systems. When connected to a designated module, as delineated in Fig. 9a, and leveraging the internal rectification circuit, the MPD-1 alternating current (AC) output is efficiently converted into direct current (DC). This allows for the illumination of small LED lights through tapping actions on the MPD-1. It is worth noting that distinct tapping intensities yield varying numbers of illuminated LED lights, as exemplified in Fig. 9b and supplementary materials. In fact, under vigorous tapping, it can simultaneously power more than 20 LED bulbs (Movie S1 in Supporting Information).
Moreover, the 33 μF capacitor within the module can be charged, reaching a voltage of 3 V in 280 s at a tapping frequency of 2 Hz, as illustrated in Fig. 9c. After the charging process, the timer can be activated through capacitor discharge via a switch within the module (Movie S2 in Supporting Information). Given the MPD-1’s impressive power generation capacity, particularly considering its effective working area of 2.5 × 2.5 cm2 square centimeters, it underscores its potential as a sustainable power source for portable electronic devices.
Conclusions
In summary, the electrospinning technique was effectively utilized to fabricate a composite nanofiber membrane with a coherent and uniformly dispersed two-dimensional network topology composed of PVDF/DA nanofiber membranes and ultrafine PVDF/DA nanofibers. This innovative configuration lays the foundation for the development of high-performance PVDF piezoelectric sensors. Initially, the PVDF/DA nanofiber membrane with a high β-phase content (89%) was prepared, which provides a suitable base material with excellent piezoelectric properties. A complete and homogeneous two-dimensional topology composed of ultrafine PVDF/DA nanofibers was successfully constructed. Experimental data and theoretical modeling analysis have demonstrated that the unique structure of the composite nanofiber membrane effectively enhances the material piezoelectric performance. Under a force of 1.5 N, the output voltage reaches 14.3 ± 0.2 V, while the output current reaches 1.01 ± 0.1 μA. Furthermore, the existence of this hierarchical structure enables systematic voltage fluctuations under varying impact frequencies, aiding in signal feedback amidst frequency changes. Additionally, due to the close distribution of DA and ultrafine nanofibers within the pores of electrospun PVDF/DA nanofibers, the material maintains the voltage stability even after approximately 10,000 cycles, demonstrating excellent durability. Benefiting from its exceptional piezoelectric performance, the sensor exhibits good sensitivity in the range of 0–4 N, 5–10 N and 30–40 N, which are 7.29 V N−1, 4.11 V N−1 and 1.41 V N−1. As a result, it can be utilized for detecting various pressure stimuli in the human body, including speech, pulse, and movement. Additionally, we further demonstrate its potential applications for energy harvesting devices. Overall, due to the simple fabrication and high piezoelectric performance, we believe that the present work would provide a beneficial idea for the construction of PVDF-nanofiber membranes based piezoelectric sensors for various wearable electronic products.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files. Should any data files be needed in another format they are available from the corresponding author upon reasonable request.
References
Xiong J, Chen J, Lee PS. Functional fibers and fabrics for soft robotics, wearables, and human-robot interface. Adv Mater. 2021;33:2002640.
Zhao Y, Gao W, Dai K, Wang S, Yuan Z, Li J, Zhai W, Zheng G, Pan C, Liu C, Shen C. Bioinspired multifunctional photonic-electronic smart skin for ultrasensitive health monitoring, for visual and self-powered sensing. Adv Mater. 2021;33:2102332.
Rich SI, Wood RJ, Majidi C. Untethered soft robotics. Nat Electron. 2018;1:102.
Peng B, Zhao F, Ping J, Ying Y. Recent advances in nanomaterial-enabled wearable sensors: material synthesis, sensor design, and personal health monitoring. Small. 2020;16:2002681.
Hong SY, Lee YH, Park H, Jin SW, Jeong YR, Yun J, You I, Zi G, Ha JS. Stretchable active matrix temperature sensor array of polyaniline nanofibers for electronic skin. Adv Mater. 2016;28:930.
Yao C, Yin X, Yu Y, Cai Z, Wang X. Chemically functionalized natural cellulose materials for effective triboelectric nanogenerator development. Adv Funct Mater. 2017;27:1700794.
Iqbal SMA, Mahgoub I, Du E, Leavitt MA, Asghar W. Advances in healthcare wearable devices. Npj Flex Electron. 2021;5:9.
Zhang Z, Wang L, Yu H, Zhang F, Tang L, Feng Y, Feng W. Highly transparent, self-healable, and adhesive organogels for bio-inspired intelligent ionic skins. ACS Appl Mater Inter. 2020;12:15657.
Karan SK, Bera R, Paria S, Das AK, Maiti S, Maitra A, Khatua BB. An approach to design highly durable piezoelectric nanogenerator based on self-poled PVDF/AlO-rGO flexible nanocomposite with high power density and energy conversion efficiency. Adv Energy Mater. 2016;6:1601016.
Li J, Bao R, Tao J, Peng Y, Pan C. Recent progress in flexible pressure sensor arrays: from design to applications. J Mater Chem C. 2018;6:11878.
Zhang Y, Zhou L, Gao X, Liu C, Chen H, Zheng H, Gui J, Sun C, Yu L, Guo S. Performance-enhanced flexible piezoelectric nanogenerator via layer-by-layer assembly for self-powered vagal neuromodulation. Nano Energy. 2021;89: 106319.
Zhang Z, Yu Y, Yu H, Feng Y, Feng W. Water-resistant conductive organogels with sensation and actuation functions for artificial neuro-sensory muscular systems. SmartMat. 2022;3:632.
Yu Y, Feng Y, Liu F, Wang H, Yu H, Dai K, Zheng G, Feng W. Carbon dots-based ultrastretchable and conductive hydrogels for high-performance tactile sensors and self-powered electronic skin. Small. 2023;19:2204365.
Gao L, Han Y, Surjadi JU, Cao K, Zhou W, Xu H, Hu X, Wang M, Fan K, Wang Y, Wang W, Espinosa HD. Magnetically induced micropillar arrays for an ultrasensitive flexible sensor with a wireless recharging system. Sci China Mater. 1977;2021:64.
Wang Y, Yokota T, Someya T. Electrospun nanofiber-based soft electronics. Npg Asia Mater. 2021;13:22.
Sharma S, Chhetry A, Maharjan P, Zhang S, Shrestha K, Sharifuzzaman M, Bhatta T, Shin Y, Kim D, Lee S, Park JY. Polyaniline-nanospines engineered nanofibrous membrane based piezoresistive sensor for high-performance electronic skins. Nano Energy. 2022;95: 106970.
Wang S, Tong W, Li Y, Zhang P, Liu Y, Chen Y, Zhang Y. Contributions of piezoelectricity and triboelectricity to a hydroxyapatite/PVDF–HFP fiber-film nanogenerator. Nano Energy. 2023;105: 108026.
Chinnappan A, Baskar C, Baskar S, Ratheesh G, Ramakrishna S. An overview of electrospun nanofibers and their application in energy storage, sensors and wearable/flexible electronics. J Mater Chem C. 2017;5:12657.
Jin T, Pan Y, Jeon GJ, Yeom HI, Zhang S, Paik KW, Park SK. Ultrathin nanofibrous membranes containing insulating microbeads for highly sensitive flexible pressure sensors. ACS Appl Mater Inter. 2020;12:13348.
Li Y, Xu M, Xia Y, Wu J, Sun X, Wang S, Hu G, Xiong C. Multilayer assembly of electrospun/electrosprayed PVDF-based nanofibers and beads with enhanced piezoelectricity and high sensitivity. Chem Eng J. 2020;388: 124205.
Li J, Yin J, Wee MGV, Chinnappan A, Ramakrishna S. A self-powered piezoelectric nanofibrous membrane as wearable tactile sensor for human body motion monitoring and recognition. Adv Fiber Mater. 2023;5:1417.
Zhang J, Yang T, Tian G, Lan B, Deng W, Tang L, Ao Y, Sun Y, Zeng W, Ren X, Li Z, Jin L, Yang W. Spatially confined MXene/PVDF nanofiber piezoelectric electronics. Adv Fiber Mater. 2023. https://doi.org/10.1007/s42765-023-00337-w.
Dong K, Peng X, Wang ZL. Fiber/fabric-based piezoelectric and triboelectric nanogenerators for flexible/stretchable and wearable electronics and artificial intelligence. Adv Mater. 2020;32:1902549.
Su Y, Chen C, Pan H, Yang Y, Chen G, Zhao X, Li W, Gong Q, Xie G, Zhou Y, Zhang S, Tai H, Jiang Y, Chen J. Muscle fibers inspired high-performance piezoelectric textiles for wearable physiological monitoring. Adv Funct Mater. 2021;31:2010962.
Sultana A, Ghosh SK, Alam MM, Sadhukhan P, Roy K, Xie M, Bowen CR, Sarkar S, Das S, Middya TR, Mandal D. Methylammonium lead iodide incorporated poly(vinylidene fluoride) nanofibers for flexible piezoelectric-pyroelectric nanogenerator. ACS Appl Mater Inter. 2019;11:27279.
Kim SR, Yoo JH, Kim JH, Cho YS, Park JW. Mechanical and piezoelectric properties of surface modified (Na, K)NbO3-based nanoparticle-embedded piezoelectric polymer composite nanofibers for flexible piezoelectric nanogenerators. Nano Energy. 2021;79: 105445.
Wan X, Wang Z, Zhao X, Hu Q, Li Z, Lin Wang Z, Li L. Flexible and highly piezoelectric nanofibers with organic–inorganic coaxial structure for self-powered physiological multimodal sensing. Chem Eng J. 2023;451: 139077.
Wu S, Zabihi F, Yeap RY, Darestani MRY, Bahi A, Wan Z, Yang S, Servati P, Ko FK. Cesium lead halide perovskite decorated polyvinylidene fluoride nanofibers for wearable piezoelectric nanogenerator yarns. ACS Nano. 2023;17:1022.
Vijayakanth T, Liptrot DJ, Gazit E, Boomishankar R, Bowen CR. Recent advances in organic and organic-inorganic hybrid materials for piezoelectric mechanical energy harvesting. Adv Funct Mater. 2022;32:2109492.
Chen S, Zhu P, Mao L, Wu W, Lin H, Xu D, Lu X, Shi J. Piezocatalytic medicine: an emerging frontier using piezoelectric materials for biomedical applications. Adv Mater. 2023;35:2208256.
Zhang S, Liu H, Tang N, Ge J, Yu J, Ding B. Direct electronetting of high-performance membranes based on self-assembled 2D nanoarchitectured networks. Nat Commun. 2019;10:1458.
Gong X, Ding M, Gao P, Liu X, Yu J, Zhang S, Ding B. High-performance liquid-repellent and thermal-wet comfortable membranes using triboelectric nanostructured nanofiber/meshes. Adv Mater. 2023;35:2305606.
Li T, Qu M, Carlos C, Gu L, Jin F, Yuan T, Wu X, Xiao J, Wang T, Dong W, Wang X, Feng ZQ. High-performance poly(vinylidene difluoride)/dopamine core/shell piezoelectric nanofiber and its application for biomedical sensors. Adv Mater. 2021;33:2006093.
Luo J, Fang CC, Wu NL. High polarity poly(vinylidene difluoride) thin coating for dendrite-free and high-performance lithium metal anodes. Adv Energy Mater. 2017;8:1701482.
Jaleh B, Jabbari A. Evaluation of reduced graphene oxide/ZnO effect on properties of PVDF nanocomposite films. Appl Surf Sci. 2014;320:339.
Wang C, Zhang J, Gong S, Ren K. Significantly enhanced breakdown field for core-shell structured poly(vinylidene fluoride-hexafluoropropylene)/TiO2 nanocomposites for ultra-high energy density capacitor applications. J Appl Phys. 2018;124: 154103.
Zhang J, Du X, Wang C, Ren K. Poly(vinylidene fluoride-hexafluoropropylene) based blend film for ultrahigh energy density capacitor applications. J Phys D Appl Phys. 2018;51: 255306.
Soin N, Shah TH, Anand SC, Geng J, Pornwannachai W, Mandal P, Reid D, Sharma S, Hadimani RL, Bayramol DV, Siores E. Novel “3-D spacer” all fibre piezoelectric textiles for energy harvesting applications. Energy Environ Sci. 2014;7:1670.
Maji S, Sarkar PK, Aggarwal L, Ghosh SK, Mandal D, Sheet G, Acharya S. Self-oriented beta-crystalline phase in the polyvinylidene fluoride ferroelectric and piezo-sensitive ultrathin Langmuir–Schaefer film. Phys Chem Chem Phys. 2015;17:8159.
Wang X, Ding B, Sun G, Wang M, Yu J. Electro-spinning/netting: a strategy for the fabrication of three-dimensional polymer nano-fiber/nets. Prog Mater Sci. 2013;58:1173.
Zhang S, Chen K, Yu J, Ding B. Model derivation and validation for 2D polymeric nanonets: origin, evolution, and regulation. Polymer. 2015;74:182.
Sahay R, Teo CJ, Chew YT. New correlation formulae for the straight section of the electrospun jet from a polymer drop. J Fluid Mech. 2013;735:150.
Wilm M. Principles of electrospray ionization. Mol Cell Proteomics. 2011;10(M111): 009407.
Han Y, Koplik J, Maldarelli C. Surfactant and dilatational viscosity effects on the deformation of liquid droplets in an electric field. J Colloid Interface Sci. 2022;607:900.
Soin N, Boyer D, Prashanthi K, Sharma S, Narasimulu AA, Luo J, Shah TH, Siores E, Thundat T. Exclusive self-aligned beta-phase PVDF films with abnormal piezoelectric coefficient prepared via phase inversion. Chem Commun (Camb). 2015;51:8257.
Li H, Lim S. High-performance piezoelectric nanogenerators featuring embedded organic nanodroplets for self-powered sensors. J Mater Chem A. 2022;10:14894.
Liu Z, Li S, Zhu J, Mi L, Zheng G. Fabrication of beta-phase-enriched PVDF sheets for self-powered piezoelectric sensing. ACS Appl Mater Inter. 2022;14:11854.
Yuan M, Ma R, Ye Q, Bai X, Li H, Yan F, Liu C, Ren Y, Wang Z. Melt-stretched poly(vinylidene fluoride)/zinc oxide nanocomposite films with enhanced piezoelectricity by stress concentrations in piezoelectric domains for wearable electronics. Chem Eng J. 2023;455: 140771.
Sessler GM, Hillenbrand J. Electromechanical response of cellular electret films. Appl Phys Lett. 1999;75:3405.
Li W, Wu N, Zhong J, Zhong Q, Zhao S, Wang B, Cheng X, Li S, Liu K, Hu B, Zhou J. Theoretical study of cellular piezoelectret generators. Adv Funct Mater. 1964;2016:26.
Mo X, Zhou H, Li W, Xu Z, Duan J, Huang L, Hu B, Zhou J. Piezoelectrets for wearable energy harvesters and sensors. Nano Energy. 2019;65: 104033.
He L, Lu J, Han C, Liu X, Liu J, Zhang C. Electrohydrodynamic pulling consolidated high-efficiency 3D printing to architect unusual self-polarized beta-PVDF arrays for advanced piezoelectric sensing. Small. 2022;18:2200114.
Lee JH, Yoon HJ, Kim TY, Gupta MK, Lee JH, Seung W, Ryu H, Kim SW. Micropatterned P(VDF-TrFE) film-based piezoelectric nanogenerators for highly sensitive self-powered pressure sensors. Adv Funct Mater. 2015;25:3203.
Xu F, Yang J, Dong R, Jiang H, Wang C, Liu W, Jiang Z, Zhang X, Zhu G. Wave-shaped piezoelectric nanofiber membrane nanogenerator for acoustic detection and recognition. Adv Fiber Mater. 2021;3:368.
Ghosh SK, Park J, Na S, Kim MP, Ko H. A fully biodegradable ferroelectric skin sensor from edible porcine skin gelatine. Adv Sci. 2021;8:2005010.
Nichols WW. Clinical measurement of arterial stiffness obtained from noninvasive pressure waveforms. Am J Hypertens. 2005;18:3S.
Huang CM, Chang HC, Kao ST, Li TC, Wei CC, Chen C, Liao YT, Chen FJ. Radial pressure pulse and heart rate variability in heat- and cold-stressed humans. Evid-based Compl Alt. 2011;2011: 751317.
Cao X, Xiong Y, Sun J, Zhu X, Sun Q, Wang ZL. Piezoelectric nanogenerators derived self-powered sensors for multifunctional applications and artificial intelligence.pdf. Adv Funct Mater. 2021;31:2102983.
Faraz M, Singh HH, Khare N. A progressive strategy for harvesting mechanical energy using flexible PVDF-rGO-MoS2 nanocomposites film-based piezoelectric nanogenerator. J Alloys Compd. 2022;890: 161840.
Garain S, Jana S, Sinha TK, Mandal D. Design of in situ poled Ce(3+)-doped electrospun PVDF/graphene composite nanofibers for fabrication of nanopressure sensor and ultrasensitive acoustic nanogenerator. ACS Appl Mater Inter. 2016;8:4532.
Yi J, Song Y, Cao Z, Li C, Xiong C. Gram-scale Y-doped ZnO and PVDF electrospun film for piezoelectric nanogenerators. Compos Sci Technol. 2021;215: 109011.
Panda S, Hajra S, Jeong H, Panigrahi BK, Pakawanit P, Dubal D, Hong S, Kim HJ. Biocompatible CaTiO3-PVDF composite-based piezoelectric nanogenerator for exercise evaluation and energy harvesting. Nano Energy. 2022;102: 107682.
Yan M, Liu S, Xu Q, Xiao Z, Yuan X, Zhou K, Zhang D, Wang Q, Bowen C, Zhong J, Zhang Y. Enhanced energy harvesting performance in lead-free multi-layer piezoelectric composites with a highly aligned pore structure. Nano Energy. 2023;106: 108096.
Acknowledgements
This work was supported by JST SPRING, Grant Number JPMJSP2144 (Shinshu University).
Funding
Open Access funding partially provided by Shinshu University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file2 (MP4 2801 KB)
Supplementary file3 (MP4 6416 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xiong, J., Wang, L., Liang, F. et al. Flexible Piezoelectric Sensor Based on Two-Dimensional Topological Network of PVDF/DA Composite Nanofiber Membrane. Adv. Fiber Mater. 6, 1212–1228 (2024). https://doi.org/10.1007/s42765-024-00415-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42765-024-00415-7