1 Introduction

The ability to efficiently and accurately model a dataset, even without full knowledge of why a model is the way it is, is a valuable tool for understanding complex systems. Machine learning (ML), the field of data analysis algorithms that create models of data, is experiencing a renaissance due to the availability of data, increased computational resources, and algorithm innovations, notably in deep neural networks (The R. S. 2017; Silver et al. 2016). Of particular interest are unsupervised algorithms that train generative models. These models are useful because they can be used to generate new examples representative of a dataset.

A Generative Adversarial Network (GAN) is an algorithm which trains a latent variable generative model with a range of applications including image or signal synthesis, classification and upscaling. The algorithm has been demonstrated in a range of architectures, now well over 300 types and applications, from the GAN zoo (Isola et al. 2017; Radford et al. 2015; Ledig et al. 2017). Two problems in GAN learning are non-convergence, oscillating and unstable parameters in the model, and mode collapse, where the generator only provides a small variety of possible samples. These problems have been addressed previously in existing work including energy-based GANs (Zhao et al. 2016) and the Wasserstein GAN (Arjovsky et al. 2017; Gulrajani et al. 2017). Another proposed solution involves replacing the canonical uniform noise prior of a GAN with a prior distribution modelling low-dimensional feature representation of the dataset. Using this informed prior may alleviate the learning task of the generative network, decrease mode-collapse, and encourage convergence (Arici and Celikyilmaz 2016).

This feature distribution is a rich and low-dimensional representation of the dataset extracted by the discriminator in a GAN. A generative probabilistic graphical model can learn this feature distribution. However, given the intractability of calculating the exact distribution of the model, classical techniques often use approximate methods for sampling from restricted topologies, such as contrastive divergence, to train and sample from these models. Novel means for sampling efficiently and accurately from less restricted topologies could further broaden the application and increase the effectiveness of these already powerful approaches.

Quantum computing can provide proven advantages for some sampling tasks; for example, it is known that under reasonable complexity theory assumptions, quantum computers can sample more efficiently from certain classical distributions (Lund et al. 2017; Bremner et al. 2016). It is an open question in quantum computing as to the extent to which quantum computers provide a more efficient means of sampling from other, more practically useful, distributions. On gate model quantum computers, quantum sampling for machine learning has been explored by a number of groups for arbitrary distributions (Benedetti et al. 2019; Farhi and Neven 2018; Schuld et al. 2017) and Boltzmann distributions (Verdon et al. 2019; Shingu et al. 2020; Zoufal et al. 2020). In a quantum annealing framework, there is literature on sampling from Boltzmann distributions (Benedetti et al. 2017; Amin et al. 2016). Here, we extend this exploration to the use of quantum processors for Boltzmann sampling to the powerful framework of adversarial learning. Specifically, we model the latent space with a Boltzmann machine trained via samples from a quantum annealer, though any classical or quantum system for sampling from a parameterized distribution could be used. Our experiments used the D-Wave 2000Q quantum annealer, but the work is relevant for near-term quantum processors in general.

Quantum annealing has been shown to sample from a Boltzmann-like distribution on near-term hardware (Benedetti et al. 2017; Amin et al. 2016) effectively enough to train Boltzmann machines and to exhibit learning. In the future, quantum annealing may decrease the cost of this training by decreasing the computation time (Biamonte et al. 2017), energy usage (Ciliberto et al. 2018), or improve performance as quantum models (Kappen 2018) may better represent some datasets.

Here, we demonstrate the Quantum Assisted Associative Adversarial Network (QAAAN) algorithm (Fig. 1), a hybrid quantum-assisted GAN in which a Boltzmann Machine (BM) trains, using samples from a quantum annealer, a model of a low-dimensional feature distribution of the dataset as the prior to a generator. The model learned by the algorithm is a latent variable implicit generative model p(x∣z) and an informed prior p(z), where z are latent variables and x are data space variables. The prior will contain useful information about the features of the data distribution and this information will not need to be learned by the generator. Put another way, the prior will be a model of the feature distribution containing the latent variable modes of the dataset.

Fig. 1
figure 1

The inputs to the generator network are samples from a Boltzmann distribution. A BM trains a model of the feature space in the generator network, indicated by the Learning. Samples from the quantum annealer, the D-Wave 2000Q, are used in the training process for the BM, and replace the canonical uniform noise input to the generator network. These discrete variables z are reparameterized to continuous variables ζ before being processed by transposed convolutional layers. Generated and real data are passed into the convolutional layers of the discriminator which extracts a low-dimensional representation of the data. The BM learns a model of this representation. An example flow of information through the network is highlighted in green. In the classical version of this algorithm, MCMC sampling is used to sample from the discrete latent space; otherwise, the architectures are identical

Full size image

2 Contributions

The core contribution of this work is the development of a scalable quantum-assisted GAN which trains an implicit latent variable generative model. This algorithm fulfills the criteria for inclusion of near-term quantum hardware in deep learning frameworks that can learn continuous variable datasets: resistant to noise, small number of variables, in a hybrid architecture. Additionally, in this work, we explore different topologies for the latent space model. The purpose of the work is to:

  • Compare different topologies to appropriately choose a graphical model, restricted by the connectivity of the quantum hardware, to integrate with the deep learning framework,

  • Design a framework for using sampling from a quantum processor in generative adversarial networks, which may lead to architectures that encourage convergence and decrease mode collapse,

  • And lastly design a hybrid quantum-classical framework which successfully tackles the problems of integrating a quantum processor into scalable deep learning frameworks, while exploiting the strengths of classical elements (handling a large number of continuous variables) and the quantum processor (sampling hard distributions).

These contributions extend previous work for integrating quantum processors into deep learning frameworks (Khoshaman et al. 2018; Perdomo-Ortiz et al. 2017; Benedetti et al. 2018; Benedetti et al. 2018). The Quantum-Assisted Helmholtz Machine (QAHM) (Perdomo-Ortiz et al. 2017; Benedetti et al. 2018) was one of the first attempts to integrate quantum models into the latent space of deep learning architectures. However, the QAHM is based on the wake-sleep algorithm, which faces two challenges: the loss function is not well defined and the gradients do not propagate between the inference and generative networks. The quantum variational autoencoder (Khoshaman et al. 2018) tackles both of these challenges. We introduce another algorithm which also handles these challenges and has additional advantages, including high-fidelity images, for which GANs are generally known to perform well. Finally, after completing the work, a preprint was posted that covers similar ideas on quantum-classical associative adversarial networks that was performed independently from ours. In this work, the authors investigate a quantum-classical associative model and sample the latent space with quantum Monte Carlo (Anschuetz and Zanoci 2019).

3 Outline

First, there is a short background section, specifically GANs, quantum annealing, and Boltzmann machines. Then, Section 5 describes closely related work. In Section 6, an algorithm is developed to learn a latent variable generative model using samples from a quantum processor to replace the canonical uniform noise input. We explore different models, specifically complete, symmetric bipartite, and Chimera topologies, tested on a reduced stochastically binarized version of MNIST, for use in the latent space. In Section 7, the results are detailed, including application of the QAAAN and a classical version of the algorithm to the MNIST dataset. The architectures are evaluated using the Inception Score and the Frechét Inception Distance. The algorithm is also implemented on the LSUN bedrooms dataset using classical sampling methods, demonstrating the scalability.

4 Background

4.1 Generative Adversarial Networks

Implicit generative models are those which specify a stochastic procedure with which to generate data. In the case of a GAN, the generative network maps latent variables z to images which are likely under the real data distribution, for example x = G(z), G is the function represented by a neural network, x is the resulting image with \(\mathbf {z} \sim q(\mathbf {z})\), and q(z) is typically the uniform distribution between 0 and 1, \(\mathcal {U}[0,1]\).

Training a GAN can be formulated as a minimax game where the discriminator attempts to maximize the cross-entropy of a classifier that the generator is trying to minimize. The cost function of this minimax game is

$$ \begin{array}{@{}rcl@{}} V(D,G)&=& \mathbb{E}_{x \sim p(x)} [\log(D(x))] \\ &&+ \mathbb{E}_{z \sim q(z)} [\log(1 - D(G(z)))]. \end{array} $$
(1)

\(\mathbb {E}_{x\sim p(x)}\) is the expectation over the distribution of the dataset, \(\mathbb {E}_{z \sim q(z)}\) is the expectation over the latent variable distribution, and D and G are functions instantiated by a discriminative and generative neural network, respectively, and we are trying to find \(\underset {G}{\min \limits } \underset {D}{\max \limits } V(D, G)\). The model learned is a latent variable generative model Pmodel(x∣z).

The first term in Eq. 1 is the \(\log \)-probability of the discriminator predicting that the real data is genuine and the second the \(\log \)-probability of it predicting that the generated data is fake. In practice, ML engineers will instead use a heuristic maximizing the likelihood that the generator network produces data that trick the discriminator instead of minimizing the probability that the discriminator label them as real. This has the effect of stronger gradients earlier in training (Goodfellow et al. 2014).

GANs are lauded for many reasons: The algorithm is unsupervised; the adversarial training does not require direct replication of the real dataset resulting in samples that are sharp (Wang et al. 2017); and it is possible to perform the weight updates through efficient backpropagation and stochastic gradient descent. There are also several known disadvantages. Primarily, the learned distribution is implicit. It is not straightforward to compute the distribution of the training set (Mohamed and Lakshminarayanan 2016) unlike explicit, or prescribed, generative models which provide a parametric specification of the distribution specifying a \(\log \)-likelihood \(\log P(\textbf {x})\) that some observed variable x is from that distribution. This means that simple GAN implementations are limited to generation.

4.2 Boltzmann machines and quantum annealing

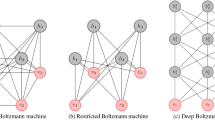
A BM is an energy-based graphical model composed of stochastic nodes, with weighted connections between and biases applied to the nodes. The energy of the network corresponds to the energy function applied to the state of the system. BMs represent multimodal and intractable distributions (Roux and Bengio 2008), and the internal representation of the BM, the weights and biases, can learn a generative model of a distribution (Ackley et al. 1987).

A graph \(\mathcal {G} = (\mathcal {V}, \mathcal {E})\) with cardinality N describing a Boltzmann machine with model parameters λ = {ω,b} over logical variables \(\mathcal {V} = \{z_{1}, z_{2}, ... z_{N}\}\) connected by edges \(\mathcal {E}\) has energy

$$ E_{\boldsymbol{\lambda}} (\textbf{z}) = -\sum\limits_{z_{i} \in \mathcal{V}} b_{i} z_{i} - \sum\limits_{(z_{i},z_{j}) \in \mathcal{E}} \omega_{ij} z_{i} z_{j} $$
(2)

where weight ωij is assigned to the edge connecting variables zi and zj, bias bi is assigned to variable zi and possible states of the variables are zi ∈ {− 1,1} corresponding to “off” and “on,” respectively. We refer to this graph as the logical graph. The distribution of the states z is

$$ P(\textbf{z}) = \frac{e^{-\beta E_{\boldsymbol{\lambda}} (\textbf{z})}}{Z} $$
(3)

with β a parameter recognized by physicists as the inverse temperature in the function defining the Boltzmann distribution and \(Z = {\sum }_{\textbf {z}} e^{-\beta E_{\boldsymbol {\lambda }}(\textbf {z})}\) the partition function, where the sum is over all possible states.

BM training requires sampling from the distribution represented by Eq. 3. For fully connected variants, it is an intractable problem to calculate the probability of the state occurring exactly (Koller et al. 2007) and is computationally expensive to approximate. Exact inference of complete graph BMs is generally intractable and approximate methods including Gibbs sampling are slow. Generally, applications will use deep stacked Restricted Boltzmann Machine (RBM) architectures, which can be efficiently trained with approximate methods, notably contrastive divergence. Contrastive divergence and Gibbs sampling are examples of Markov chain Monte Carlo (MCMC) methods.

A Markov chain describes a sequence of stochastic states where the probability of any state in the chain occuring is only dependent on the previous state. A Monte Carlo method is one which uses repeated sampling to make numerical approximations. For example, Gibbs sampling involves taking some random initial state of nodes, stochastically updating the state of a random node zn given the current states of other nodes \(P(z_{n}=1|\mathcal {V} \setminus z_{n}) = S(2\beta ({\sum }_{z_{i} \in \mathcal {V} \setminus z_{n}} \omega _{ni}z_{i} + b_{n}))\), where

$$ S(x) = \frac{1}{1+e^{-x}}. $$
(4)

Repeating this procedure many times evolves the Markov chain to some equilibrium where samples of states are approximately from the Boltzmann distribution (Eq. 3).

An RBM is a symmetric bipartite BM, shown in Fig. 2c. It is possible to efficiently learn the distribution of some input data spaces through approximate methods, e.g., contrastive divergence (Carreira-Perpinan and Hinton 2005). Stacked RBMs form a Deep Belief Net (DBN) and can be greedily trained to learn the generative model of datasets with higher-level features with applications in a wide range of fields from image recognition to finance (Li et al. 2014). Training these types of models requires sampling from the Boltzmann distribution.

Fig. 2
figure 2

a Complete, b chimera, and c symmetric bipartite graphical models. These graphical models are embedded into the hardware and the nodes in these graphs are not necessarily representative of the embeddings

Full size image

Quantum annealing (QA) has been proposed as a method for sampling from complex Boltzmann-like distributions. It is an optimization algorithm exploiting quantum phenomena to find the ground state of a cost function. QA has been demonstrated for a range of optimization problems (Biswas et al. 2017); however, defining and detecting speedup, especially in small and noisy hardware implementations, is challenging (Rønnow et al. 2014; Katzgraber et al. 2014).

In order to achieve this, the framework outlined in Eq. 2 can be mapped to an Ising model for a quantum system represented by the Hamiltonian

$$ \hat{H}_{\boldsymbol{\lambda}} = - \sum\limits_{\hat{\sigma}^{z}_{i} \in \mathcal{V}} h_{i} \hat{\sigma}^{z}_{i} - \sum\limits_{(\hat{\sigma}^{z}_{i},\hat{\sigma}^{z}_{j}) \in \mathcal{E}} J_{ij} \hat{\sigma}^{z}_{i} \hat{\sigma}^{z}_{j}. $$
(5)

where now variables z have been replaced by the Pauli-z operators, \(\hat {\sigma }_{i}\), which return eigenvalues in the set {− 1,1} when applied to the state of variable zi, physically corresponding to spin-up and spin-down, respectively. Parameters bi and ωij are replaced with the Ising model parameters hi and Jij which are conceptually equivalent. In the hardware, these parameters are referred to as the flux bias and the coupling strength, respectively.

The full Hamiltonian describing the dynamics of the D-Wave 2000Q, equivalent to the time-dependent transverse field Ising model, is

$$ \hat{H}(t) = A(t) \hat{H}_{\perp} + B(t) \hat{H}_{\boldsymbol{\lambda}}. $$
(6)

The transverse field term H⊥ is

$$ \hat{H}_{\perp} = \sum\limits_{\hat{\sigma}_{i}^{x} \in \mathcal{V}} \hat{\sigma}_{i}^{x}. $$
(7)

\(\hat {\sigma }^{x}\) are the Pauli-x operators in the Hilbert space \(\mathbb {C}^{2^{N}}\). A(t) and B(t) are monotonic functions defined by the total annealing time \(t_{\max \limits }\) (Biswas et al. 2017). Generally, at the start of an anneal, A(0) ≈ 1 and B(0) ≈ 0. A(t) decreases and B(t) increases monotonically with t until, at the end of the anneal, \(A(t_{\max \limits })\approx 0\) and \(B(t_{\max \limits }) \approx 1\). When B(t) > 0, the Hamiltonian contains terms that are not possible in the classical Ising model, that is those that are normalized linear combinations of classical states.

Each state found after an anneal comes from a distribution, although it is not clear what distribution the quantum annealer is sampling from. For example, in some cases, the distribution is hypothesized to follow a quantum Boltzmann distribution up to the “freeze-out region”—where for some value of t the dynamics of the system slow down and diverge from the model (Eq. 8) (Amin 2015). If the freeze-out region is narrow then the distribution can be modelled as the classical distribution of problem Hamiltonian, \(\hat {H}_{\boldsymbol {\lambda }}\), at a higher unknown effective temperature β∗,

$$ \rho_{t_{\max}} = \frac{e^{-\beta^{*} \hat{H}_{\boldsymbol{\lambda}}}}{Z} $$
(8)

where \(Z= \text {Tr}[e^{-\beta ^{*} \hat {H_{\boldsymbol {\lambda }}}}]\) and we have performed matrix exponentiation. \(\rho _{t_{\max \limits }}\) is the model for the distribution. In the case where the dynamics of the distribution do not slow down and \(\hat {H}(t_{\max \limits }) = \hat {H}_{\lambda }\) the Hamiltonian contains no off-diagonal terms and Eq. 8 is equivalent to the classical Boltzmann distribution, Eq. 3, at some temperature. β is a dimensionless parameter which depends on the temperature of the system, the energy scale of the superconducting flux qubits, and open system quantum dynamics. However, it is an open question as to when the freeze-out hypothesis holds (Albash et al. 2012; Marshall et al. 2017).

5 Related work

This work can be framed as a quantum-classical hybrid implementation of the associative adversarial network (Arici and Celikyilmaz 2016). In this work, the authors note, as outlined in the introduction, the training of a GAN is prone to non-convergence (Barnett 2018), and mode collapse (Thanh-Tung et al. 2018). This stability of GAN training is an issue and there are many hacks to encourage convergence, discourage mode collapse, and increase sample diversity including using spherical input space (White 2016), adding noise to the real and generated samples (Arjovsky et al. 2017) and minibatch discrimination (Salimans et al. 2016). We hypothesize that using an informed prior will decrease mode collapse and encourage convergence.

With respect to quantum classical models, QA has been proposed, and in some cases demonstrated, as a sampling subroutine in ML algorithms: a quantum Boltzmann machine (Amin et al. 2016); training a quantum variational autoencoder (QVAE) (Khoshaman et al. 2018); a quantum-assisted Helmholtz machine (Benedetti et al. 2018); deep belief nets of stacked RBMs (Adachi and Henderson 2015). Though related, this framework can be distinguished from other efforts to incorporate gate-model quantum devices into machine learning algorithms (Benedetti et al. 2019; Farhi and Neven 2018; Schuld et al. 2017).

6 Quantum-assisted associative adversarial network

In this section, the QAAAN algorithm and related methods are outlined, including a novel way to learn the feature distribution generated by the discriminator network via a BM using sampling from a quantum annealer. The QAAAN architecture is similar to the classical Associative Adversarial Network proposed in Ref. Arici and Celikyilmaz (2016), as such the minimax game played by the QAAAN is

$$ \begin{array}{@{}rcl@{}} V(D, G, \rho) &=& {\mathbb{E}}_{x \sim p_{\mathsf{data}}(x)}[\log D(x)]\\ &&+ {{\mathbb{E}}}_{z \sim \rho(z)} [\log(1 - D(G(z)))]\\ &&+ {{\mathbb{E}}}_{f \sim \rho_{f}(f)} [\log \rho], \end{array} $$
(9)

where the aim is now to find \(\underset {\mathcal {G}}{\textsf {min}} \underset {\rho }{\textsf {max}} \underset {\mathcal {D}}{\textsf {max}} V(D, G, \rho )\), with equivalent terms to Eq. 1 plus an additional term to describe the optimization of the model ρ (Eq. 8). This term conceptually represents the probability that samples generated by the model ρ are from the feature distribution ρf. ρf is the feature distribution extracted from the interim layer of the discriminator. This distribution is assumed to be Boltzmann, a common technique for modelling a complex distribution.

The algorithm used for training ρ, a probabilistic graphical model, is a BM. Sampling from the quantum annealer, the D-Wave 2000Q, replaces a classical sampling subroutine in the BM. ρ is used in the latent space of the generator (Fig. 1), and samples from this model, also generated by the quantum annealer, replace the canonical uniform noise input to the generator network. Samples from ρ are restricted to discrete values, as the measured values of qubits are z ∈{− 1,+ 1}. These discrete variables z are reparameterized to continuous variables ζ before being processed by the layers of the generator network, producing “generated” data. Generated and real data are then passed into the layers of the discriminator which extracts the low-dimensional feature distribution ρf. This is akin to a variational autoencoder, where an approximate posterior maps the evidence distribution to latent variables which capture features of the distribution (Doersch 2016). The algorithm for training the complete network is detailed in Fig. 3.

Fig. 3
figure 3

QAAAN training algorithm. ρ represents the distribution sampled by the quantum annealer; therefore, \(\rho \rightarrow \phi \) represents sampling a set of vectors zi from distribution ρ. The training samples, X, are sampled from the datasets MNIST or LSUN bedrooms. Steps 5 and 8 are typical of GAN implementation, G(⋅) and D(⋅) are the functions representing the generator and discriminator networks, respectively. For clarity, we have omitted implementation details arising from the embedding a logical graph into the quantum annealer. Further details on mapping to the logical space for samples from the quantum annealer can be found in Section 6

Full size image

Below, we outline the details of the BM training in the latent space, reparameterization of discrete variables, and the networks used in this investigation. Additionally, we detail an experiment to distinguish the performance of three different topologies of probabilistic graphical models to be used in the latent space.

6.1 Latent space

As in Fig. 1, samples from an intermediate layer of the discriminator network are used to train a model for the latent space of the generator network. Here, a BM trains this model. The cost function of this BM is the quantum relative entropy

$$ S(\rho || \rho_{f} ) = \text{Tr}[\rho \ln \rho] - \text{Tr}[\rho \ln \rho_{f}] $$
(10)

equivalent to the classical Kullback-Leibler divergence when all off-diagonal elements of ρ and ρf are 0. This measure quantifies the divergence of distribution ρ from ρf where ρf is the target feature distribution of features extracted by the discriminator network and ρ is the model trained by the BM, from Eq. 9. Though the distributions used here are modelled classically, this framework can be extended to quantum models using the quantum relative entropy. Given this, it can be shown that the updates to the weights and biases of the model are

$$ \begin{array}{@{}rcl@{}} {\varDelta} J_{ij} &=& \eta \beta [{\langle{z_{i} z_{j}}\rangle}_{\rho_{f}} - {\langle{z_{i} z_{j}}\rangle}_{\rho}] \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} {\varDelta} h_{i} &=& \eta \beta [{\langle{z_{i}}\rangle}_{\rho_{f}} - {\langle{z_{i}}\rangle}_{\rho}]. \end{array} $$
(12)

η is the learning rate, β is an unknown parameter, and 〈z〉ρ is the expectation value of z in distribution ρ.

Other implementations compute of similar models compute the unknown β (Benedetti et al. 2016), the instance dependent effective temperature. In this work to get around the problem of using the unknown effective temperature for training a probabilistic graphical model, we use a gray-box model approach proposed in Benedetti et al. (2017). In this approach, full knowledge of the effective parameters, dependent on β, are not needed to perform the weight updates as long as the projection of the gradient is positive in the direction of the true gradient. The gray-box approach ties the model generated to the specific device used to train the model, though is robust to noise and is not required to estimate β (Raymond et al. 2016). We find that under this approach performance remains good enough for deep learning applications.

Though we do not have full knowledge of the distribution the quantum annealer samples from, we have modelled it as a classical Boltzmann distribution at an unknown temperature. This allows us to train models without the having to estimate the temperature of the system, providing a simple approach to integrating probabilistic graphical models into deep learning frameworks.

We set β = 1 and tune the learning rate without knowledge of the true value of β. z are the logical variables of the graphical model and the expectation values 〈z〉ρ are estimated by averaging 1000 samples from the quantum annealer. The quantum relative entropy is minimized by stochastic gradient descent.

6.2 Topologies

We explored three different topologies of probabilistic graphical models: complete, symmetric bipartite, and Chimera, for the latent space. Their performance on learning a model of a reduced stochastically binarized version of MNIST (Fig. 4) was compared, in both sampling via quantum annealing and classical sampling cases. The complete topology is self-explanatory (Fig. 2a), restricted refers to a symmetric bipartite graph (Fig. 2c), and the sparse is the graph native to the D-Wave 2000Q, or Chimera graph, where the connectivity of the model is determined by the available connections on the hardware (Fig. 2b).

Fig. 4
figure 4

Left to right: 28×28 continuous, 6×6 continuous, 6×6 stochastically binarized example from the MNIST dataset

Full size image

The models were trained by minimizing the quantum relative entropy (Eq. 10), and evaluated with the L1-norm,

$$ L_{1}\text{-norm} = \sum\limits_{z_{i},z_{j} \in \mathcal{V}}\left|{ {\langle z_{i}z_{j} \rangle}_{\rho_{f}} - {\langle z_{i}z_{j} \rangle}_{\rho}}\right|. $$
(13)

The algorithm did not include temperature estimation as discussed in the previous section, or methods to adjust intra-chain coupling strengths for the embedding (Benedetti et al. 2017). The method used here makes a comparison between the different topologies, though for best performance one would want to account for the embedding and adjust algorithm parameters, such as the learning rate, to each topology.

This Hamiltonian was embedded in the D-Wave 2000Q, a system with 2048 qubits, each with degree 6, i.e., other than qubits on the edge of the graph each qubit is connected to 6 other qubits. Embedding is the process of mapping the logical graph, represented by Eq. 5, to hardware. If the logical graph has degree > 6 or a structure that is not native to the hardware, the logical graph can still be embedded in the hardware via a 1-many mapping, that means one variable zi is represented by more than one qubit. These qubits are arranged in a “chain” (this term is used even when the set of qubits forms a small tree). A chain is formed by setting the coupling strength Jij between these qubits to a strong value to encourage them to take a single value by the end, but not so strong that it overwhelms the Jij and hi in the original problem Hamiltonian or has a detrimental effect on the dynamics. There is a sweet spot for this value. In our case, we used the maximum value available on the D-Wave 2000Q, namely − 1. At the end of the anneal, to determine the value of a logical variable expressed as a qubit chain in the hardware a majority vote is performed: The logical variable takes the value corresponding to the state of the majority of qubits. If there is no majority, a coin is flipped to determine the value of the logical variable.

In addition to these requirements, there are several non-functioning, “dead,” qubits and couplers in the hardware. These qubits or couplers were removed in all embeddings, which had a negligible effect on the final performance. The complete topology embedding was found using a heuristic embedder (Cai et al. 2014). A better choice would be a deterministic embedder, resulting in shorter chain lengths, though when adjusting for the dead qubits the symmetries are broken and the embedded graph chain length increases to be comparable to that returned by the heuristic embedder. The restricted topology was implemented using the method detailed by Adachi and Henderson (2015). At a high level, qubits corresponding to visible nodes are mapped to vertical chains and qubits corresponding to hidden nodes are mapped to horizontal chains . The Chimera topology was implemented on a 2×2 grid of unit cells, avoiding dead qubits. Learning was run over 5 different embeddings for each topology and the results averaged. For topologies requiring chains of qubits, the couplers in the chains were set to − 1.

6.3 Reparameterization

Samples from the latent space come from a discrete space. These variables are reparameterized to a continuous space, using standard techniques. There are many potential choices for reparameterization functions and a simple example case is outlined below. We chose a probability density function pdf(x) which rises exponentially and can be scaled by parameter α:

$$ \mathrm{p}(x) = \frac{\alpha \exp(-\alpha(1-x))}{1 - \exp(-2\alpha)}. $$
(14)

The cumulative distribution function of this probability density function is

$$ F(r) = \begin{cases} 1 &\quad r > 1 \\ {\int}^{r}_{-1} p(x) dx &\quad -1 < r \leq 1 \\ 0 &\quad \mathrm{otherwise,} \end{cases} $$
(15)

and

$$ {\int}^{r}_{-1} p(x) dx = \frac{\exp(-\alpha(1-r))-\exp(-2\alpha)}{1 - \exp(-2\alpha)} $$
(16)

Discrete samples can be reparameterized by sampling F(r) from \(\mathcal {U}(0,1]\) solving Eq. 16 for r. In the method implemented in this work, the continuous variables ζi, Fig. 1, are − 1 in the case when zi = − 1 and sampled from pdf(x) (Eq. 6.3), when zi = 1. Then, the continuous variables are input to the generator of the network.

The value of α was set to 4 the pdf for this and other α are shown in Figure 5. The uncertainty in the evaluation of performance was not accurate enough to determine meaningful differences in the setting of α. We chose α to intuitively set ζi close to the discrete variables zi. Certainly, further investigation into the type of reparameterization, e.g., different functions and methods developed in other works (Amin et al. 2016), will be needed to determine best practices in the field for these types of models.

Fig. 5
figure 5

The probability density function, p(x), for different values of α. In this investigation, α = 4 was used, to distinguish strongly from the uniform noise case

Full size image

6.4 Networks

The generator network consists of dense and transpose convolutional, stride 2 kernel size 4, layers with batch normalization, and ReLU activations. A ReLU activation is a standard activation function used to avoid vanishing gradients, where the derivative is 0 when the input is less than 0 and 1 otherwise. The output layer is implemented with a tanh activation. These components are standard deep learning techniques found in textbooks, for example (Goodfellow et al. 2016).

The discriminator network consists of dense, convolutional layers, stride 2 kernel size 4, LeakyReLU activations. The dense layer corresponding to the feature distribution was chosen to have tanh activations in order that outputs could map to the BM. The hidden layer representing ρf was the fourth layer of the discriminator network with 100 nodes. When sampling the training data for the BM from the discriminator, the variables given values from the set {− 1,1} as in the Ising model, dependent on the activation of the node being greater or less than the threshold, set at 0, respectively.

We found the stability of the network was dependent on the structure of the model and followed best practices (Arjovsky et al. 2017; Goodfellow et al. 2014) to guide the development. Though this model worked well, there is scope to understand if there are alternate best practices for models incorporating quantum devices into the latent space.

The networks were trained with an Adam optimizer with learning rate 0.0002. The learning rate was set by performing two sweeps. The first over the set {0.01, 0.001, 0.0001, 0.00001} and the second in the region around the best performing (0.001). The best performing was determined by evaluating the Inception Score and the Frechét Inception Distance (FID), described further in Section 7, after 100 iterations. High learning rates (0.01) were unstable and the training diverged, whereas low learning rates (0.00001) the training was stable but slow. The labels were smoothed with noise.

For the sparse graph latent space used in learning the MNIST dataset in Section 7, the BM was embedded in the D-Wave hardware using a heuristic embedder. As there is a 1-1 mapping for the sparse graph, it was expressed in hardware using 100 qubits. An annealing schedule of 1 μs and a learning rate of 0.0002 were used. The classical architecture that was compared with the QAAAN was identical other than replacing sampling via quantum annealing with MCMC sampling techniques.

We used D-Wave Systems Inc. provided Python API to interact with the device. Qubits, biases, and weights can be assigned through this API, which can be used to implement details such as the embedding. Other experimental hyperparameters (number of samples/annealing schedule) can be set with high-level functionality.

7 Results and discussion

For this work, we performed several experiments. First, we compared three topologies of graphical models, trained using both classical and quantum annealing sampling methods. They were evaluated for performance by measuring the L1-norm over the course of the learning a reduced stochastically binarzied version of the MNIST dataset (Fig. 4). Second, the QAAAN and the classical associative adversarial network described in Section 6 were both used to generate new examples of the MNIST dataset. Their performance was evaluated used the inception score and the FID. Finally, the classical associative adversarial network was used to generate new examples of the LSUN bedrooms dataset.

In the experiment comparing topologies, as expected, the BM trains a better model faster with higher connectivity, but when trained via sampling with the quantum annealer, the picture is less intuitive (Figs. 6, 7). All topologies learned a model to the same accuracy, at similar rates. This indicates that there is a noise floor preventing the learning of a better model in the more complex graphical topologies. For the purposes of this investigation, the performance of the sparse graph was demonstrated to be enough to learn an informed prior for use in the QAAAN algorithm.

Fig. 6
figure 6

Comparison of the convergence of different graphical topologies trained using samples from a quantum annealers on a reduced stochastically binarized MNIST dataset. The learning rate used was 0.03. This learning rate produced the fastest learning with no loss in performance of the final model. The learning was run 5 times over different embeddings and the results averaged. The error bars describe the variance over these curves

Full size image
Fig. 7
figure 7

Comparison of different graphical topologies trained using MCMC sampling on a reduced stochastically binarized MNIST dataset. The learning rate used was 0.001. This learning rate was chosen such that the training was stable for each topology; we found that the error diverged for certain topologies at other learning rates. The learning was run 5 times and the results averaged. The error bars describe the variance over these curves

Full size image

Given the results of the first experiment, the classical associative adversarial network and the quantum-assisted algorithm were evaluated with a sparse topology latent space. The generated images are shown for both classical and quantum versions in Figs. 8a and b, respectively.

Fig. 8
figure 8

Example MNIST characters generated by a classical and b quantum-assisted associative adversarial network architectures, with sparse topology latent spaces

Full size image

We evaluated classical and quantum-assisted versions of the associative adversarial network with sparse latent spaces via two metrics, the inception score and the FID. Both metrics required an inception network, a network trained to classify images from the MNIST dataset, which was trained to an accuracy of \(\sim 95\%\). The Inception Score (Eq. 17) attempts to quantify realism of images generated by a model. For a given image, p(y|x) should be dominated by one value of y, indicating a high probability that an image is representative of a class. Secondly, over the whole set, there should be a uniform distribution of classes, indicating diversity of the distribution. This is expressed

$$ \text{IS} = \exp({\mathbb{E}}_{x\sim\rho_{\mathrm{D}}} \mathrm{D}_{\text{KL}}(p(y | x) || p(y))). $$
(17)

The first criterion is satisfied by requiring that image-wise class distributions should have low entropy. The second criterion implies that the entropy of the overall distribution should be high. The method is to calculate the KL distance between these two distributions: A high value indicates that both the p(y|x) is distributed over one class and p(y) is distributed over many classes. When averaged over all samples, this score gives a good indication of the performance of the network. The inception scores of the classical and quantum-assisted versions (with sparse latent spaces) were \(\sim 5.7\) and \(\sim 5.6\), respectively.

The FID measures the similarity between features extracted by an inception network from the dataset X and the generated data G. The distribution of the features is modelled as a multivariate Gaussian. Lower FID values mean the features extracted from the generated images are closer those for the real images. In Eq. 18, μ are the means of the activations of an interim layer of the inception network and Σ are the covariance matrices of these activations. The classical and quantum-assisted algorithms (with sparse latent spaces) scored \(\sim 29\) and \(\sim 23\), respectively.

$$ \text{FID}(X, G) = ||\mu_{X} - \mu_{G}||^{2}_{2} + \text{Tr}({\Sigma}_{X} + {\Sigma}_{G} - 2\sqrt{{\Sigma}_{X} {\Sigma}_{G}}) $$
(18)

The classical implementation, with a sparse latent space, was also used to generate images mimicking the LSUN bedrooms dataset (Fig. 9). The Large Scale scene UNderstanding (LSUN) (Yu et al. 2015) dataset are images of 10 scenes, where there are on average a million examples of each scene. From this dataset, we only took examples of one scene: bedrooms. This image set had around 300,000 images. This final experiment was only performed as a demonstration of scalability, and no metrics were used to evaluate performance.

Fig. 9
figure 9

Bedrooms from the LSUN dataset generated with an associative adversarial network, with a fully connected latent space sampled via MCMC sampling

Full size image

7.1 Discussion

Though it is trivial to demonstrate a correlation between the connectivity of a graphical model and the quality of the learned model (Fig. 7), it is not immediately clear that the benefits of increasing the complexity of the latent space can be detected easily in deep learning frameworks, such as the quantum-assisted Helmholtz machine (Benedetti et al. 2018) and those looking to exploit quantum models (Khoshaman et al. 2018). The effect of the complexity of the latent space model on the quality of the final latent variable generative model was not apparent in our investigations. Deep learning frameworks looking to exploit quantum hardware supported training in the latent spaces need to truly benefit from this application, and not iron out any potential gains with backpropagation. For example, if exploiting a quantum model gives improved performance on some small test problem, it is an open question as to whether this improvement will be detected when integrated into a deep learning framework, such as the architecture presented here.

Here, given the nature of the demonstration and a desire to avoid chaining we use a sparse connectivity model. Avoiding chaining allows for larger models to be embedded into near-term quantum hardware. Given the O(n2) scaling of qubits to logical variables for a complete logical graph (Choi 2011), future applications of sampling via quantum annealing will likely exploit restricted graphical models. Though the size of near-term quantum annealers has followed Moore’s law trajectory, doubling in size every 2 years, it is not clear what size of probabilistic graphical models will find mainstream usage in machine learning applications and exploring the uses of different models will be an important theme of research as these devices grow in size.

There are two takeaways from the results presented here. Though these values are not comparable to state-of-the-art GAN architectures and are on a simple MNIST implementation, they serve the purpose of highlighting that the inclusion of a near-term quantum device is not detrimental to the performance of this algorithm. Secondly, we have demonstrated the framework on the larger, more complex, dataset LSUN bedrooms (Fig. 9). This indicates that the algorithm can be scaled.

8 Conclusions

8.1 Summary

In this work, we have presented a novel and scalable quantum-assisted algorithm, based on a GAN framework, which can learn an implicit latent variable generative model of complex datasets, such as LSUN, and compared performance of different topologies

This work is a step in the development of algorithms that use quantum phenomena to improve the learning generative models of datasets. This algorithm fulfills the requirements of the three areas outlined by Perdomo-Ortiz et al. (Perdomo-Ortiz et al. 2017): Generative problems, data where quantum correlations may be beneficial, and hybrid. This implementation also allows for use of sparse topologies, removing the need for chaining, requires a relatively small number of variables (allowing for near-term quantum hardware to be applied), and is resistant to noise. However, there are aspects of this implementation and model that limit the performance and increase the cost. These are discussed below.

8.2 Limitations

Throughout the paper, several limitations to quantum annealing devices and this method of integrating quantum annealing devices to neural network models have been mentioned. We collect these ideas here to highlight the areas in which quantum annealers, and this implementation of a hybrid quantum-classical model, may have to improve to increase the usefulness of these methods.

Applications of quantum computing to quantum machine learning have well-recognized limitations, such as benchmarking these models against classical counterparts (Vinci et al. 2020; Rønnow et al. 2014; King et al. 2015; Vinci and Lidar 2016). The approach presented in this paper has several more specific limitations.

Firstly, the cost of embedding a logical graph in a quantum annealer may be large in terms of the performance of the model (Marshall et al. 2020). Specifically, it is not clear whether how close the model of the distribution sampled by the quantum annealer is to the real distribution for an embedded graph. This problem may become more obvious at larger model sizes. Higher connectivity of quantum annealing devices will most likely be needed to continue improving quantum-assisted model performance. This is related to the problem proposed by the freeze-out hypothesis (Amin 2015), where the samples may not come from the distribution modelled.

Secondly, we did not determine the temperature of the quantum annealer, under the gray-box assumption (Benedetti et al. 2018). Better models for the behavior of the device and potentially heurisitics for mitigating their effects would help further improve and understand these methods.

Finally, the key feature of this model is the learning of the intermediate distribution between the discriminator and the generator. Although we have highlighted this as a potential avenue to solve some problems associated with GANs, it is not clear if the integration of the discrete space of the Boltzmann machine and the continuous space of the classical aspects of the model will be able to match state-of-the-art performance. Additionally, we chose a relatively simple mapping of discrete to continuous variables, whereas other methods, such as those described in related work (Rolfe 2016; Amin et al. 2016), will most likely improve the performance.

These effects, along with the noise of the quantum device, result in the overall decreased performance of the Boltzmann machine (as compared with classical MCMC sampling) and the indistinguishability of the three topologies (Fig. 6). Although the architecture still performs well enough to model the higher dimensional LSUN bedrooms dataset, they must be further understood and addressed for these methods to continue to improve.

8.3 Further work

There are many avenues to use quantum annealing for sampling in machine learning, topologies, and GAN research. Here, we have outlined a framework that works on simple (MNIST) and more complex (LSUN) datasets. We highlight several areas of interest that build on this work.

The first is an investigation into how the inclusion of quantum hardware into models such as this can be detected. There are two potential improvements to the model: Quantum terms improve the model of the data distribution; or graphical models, which are classically intractable to learn for example fully connected, integrated into the latent spaces, may improve the latent variable generative model learned. Before investing extensive time and research into integrating quantum models into latent spaces, it will be important to note that these improvements are reflected in the overall model of the dataset. That is, that backpropagation does not erase any latent space performance gains.

There are still outstanding questions as to the distribution the quantum annealer samples. The pause and reverse anneal features on the D-Wave 2000Q gives greater control over the distribution output by the quantum annealer, and can be used to explore the relationship between the quantum nature of that distribution and the quality of the model trained by a quantum Boltzmann machine (Marshall et al. 2018). It is also not clear what distribution is the “best” for learning a model of a distribution. It could be that efforts to decrease the operating temperature of a quantum annealer to boost performance in optimization problems will lead to decreased performance in ML applications, as the diversity of states in a distribution decreases and probabilities accumulate at a few low-energy states. There are interesting open questions as to the optimal effective temperature of a quantum annealer for ML applications. This question fits within a broad area for research in ML asking which distributions are most useful for ML and why. As larger gate model quantum processors become available, it will be interesting to evaluate a variety of quantum algorithms beyond quantum annealing for sampling in this framework.

For this simple implementation, the quantum sampling sparse graph performance is comparable to the complete and restricted topologies. Though in optimized implementations we expect divergent performance, the sparse graph serves the purpose of demonstrating the QAAAN architecture. Additionally, we have highlighted sparse classical graphical models for use in the architecture demonstrated on LSUN bedrooms. Though they have reduced expressive power, there are many more applications for current quantum hardware; for example, a fully connected graphical model would require in excess of 2048 qubits (the number available on the D-Wave 2000Q) to learn a model of a standard MNIST dataset, not to mention the detrimental effect of the extensive chains. A sparse D-Wave 2000Q native graph (Chimera) conversely would only use 784 qubits. This is a stark example of how sparse models might be used in lieu of models with higher connectivity. Investigations finding the optimal balance between the complexity of a model, resulting overhead required by embedding, and the affect on both on performance are needed to understand how future quantum annealers might be used for applications in ML. More generally, understanding how the architectural, as well as algorithmic, choices in near-term gate model devices affect performance will enhance our understanding of quantum computings impact on machine learning in the decades ahead.