1 Introduction

Ionic liquids (ILs) are being explored for a wide range of applications including but not limited to portable energy storage devices such as lithium ion batteries (LIBs). Conventional electrolytes based on organic solvents, despite their higher ionic conductivity pose safety concerns and this limits their operative temperature range [1, 2]. For these reasons, therefore, ILs are being explored an alternative promising electrolytes for LIBs mainly because of thier negligible vapour pressure, high chemical and thermal stability [3,4,5]. ILs, on the other hand, have higher viscosity which induces low wettability of the electrode surface and lower ionic conductivity. There have been several continued researchs efforts to mitigate these problems.Due to the excellent dissolving properties of ILs, for example, ILs can be modified into hybrid electrolytes, either with lithium salts and/or organic solvents, which can effectively reduce the viscosity and ionic transferring resistance, which thereby improves the ion transport and interfacial properties of battery electrolytes [6,7,8]. While ionic liquids have promising potential applications, predicting their chemical and physical properties, however, requires understanding of their isolated and bulk structures [9]. To this end, therefore, a useful starting point to understand the full chemical and physical properties of ILs is to determine the microscopic structure of the individual cation–anion pairs.

The transport properties of ILs (e.g. viscosity, diffusion and ionic conductivity) are controlled by the intermolecular interactions among the constituent ions. From ab initio first principles perspective, it is the molecular interactions between cations and anions, and the interplay between the short-range and long-range interactions which govern the details of ILs’ physicochemical properties [10]. It is thus, imperative to understand these interionic interactions, including coulombic and specific hydrogen bonding interactions, which enable a task-specific design and optimization of ILs. Both experimental [11, 12] and theoretical calculations [13] have been carried out to investigate the interactions between cations and anions among a series of imidazolium-based ILs. Although experiments [14] may provide valuable information about the structures of ILs, determining the exact structure of cation and anion ion pairs, however, requires the use of quantum mechanical calculations [15]. This was highlighted, for example, in the difficulty of determining whether a hydrogen bond exists between the cation and anion ion pairs in 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (EMI[TFSI]) [16]. The presence of H-bonding in ILs has been shown to affect the viscosity of these ILs [17, 18].

Among the different ILs investigated, those based on the anion [TFSI]− have been very popular because of their high thermal and electrochemical stabilities [19]. Thus, the [TFSI]− anion has been extensively studied for electrochemical applications. Therefore, it appears useful in our study to critically investigate the molecular and electronic interactions in [EMI][TFSI] ion pairs, and the impact of such molecular interactions on the achievable transport properties of the corresponding ILs. Previous scientific reports about the structural and electronic properties of imidazolium-based ILs paid particular emphasis on simple imidazolium-based halide ion pairs with the single atomic anions. For example, ab initio DFT calculations were used to explore the geometric and electronic structures of [EMI][BF4] and [BMI][PF6] ion pairs [20]. Dong et al. investigated the interactions in imidazolium tetrafluoroborate salt and hexafluorophosphate salt by DFTcalculations and have shown that there exists C–H…F H-bonds between cations and anions [21]. Furthermore, there has been extensive reviews on the structural characteristics of H-bonds in the different ILs, relationship with the properties and roles in applications in recent publications [22]. Seddon et al. [23] investigated the interactions of ions in a series of representative hexafluorophosphate salts, and found that there were specific directional H-bonds in [PF6]− anions. Ludwig et al. [24, 25] found that the H-bonds in imidazolium-based ILs perturb the Coulomb forces to deviate from charge symmetry which resulted in the decreased viscosities and enhanced fluidization of the ILs. The melting point and enthalpy of vaporization was also correlated with the H-bonds [26, 27]. In the imidazolium-based salts, it has been shown that the hydrogen atoms on imidazolium ring (C2–H) were mainly involved in the formation of H-bonds. [28, 29].

Although there has been extensive previous scientific reports about the structural and electronic properties of simple imidazolium-based halide ion pairs, relatively fewer studies were devoted to the detailed structural and electronic studies of imidazolium-based ILs with polyatomic anions such as [TFSI]−. There have been some vibrational and spectroscopic studies about [EMI][TFSI] and its analogs. Many other groups have also investigated inter- and intramolecular interactions in bulk [EMI][TFSI] by probing liquid and solid samples with techniques such as IR and Raman spectroscopy, and NMR [30,31,32,33,34,35,36]. Roth etal. observed the presence of C2–H stretch and several overtone frequencies on [EMI][TFSI] ion pairs, a study which was further corroborated by the work of Grondin et al. [35]. Many ab initio DFT calculations [21, 28] and ab initio molecular dynamics have been performed to investigate the structures and interactions, which show that the H-bonds and the local H-bonded network are the essential structural features for the behavior of ILs. Although numerous structural studies about [EMI][TFSI] ion pair conformers have been reported so far, however, there are relatively fewer detailed structural analysis of [EMI][TFSI] ion pair conformers that have multiple interactions sites for the anion. The current work, therefore, gives detailed analysis of the [EMI][TFSI] ion pair conformers through analysis of the interaction energies, stabilization energies and natural orbital analysis of the ion pair conformers.

Both molecular dynamics (MD) and Monte Carlo simulations (MC) methods are commonly used to investigate the thermodynamic properties as well as ions arrangements in ILs [13, 37]. A key drawback of these simulations, however, is the strong dependence on the quality of potential functions and the charges associated with each atom or group.Therefore, the investigations based on electronic level provide more direct understanding about the intra- and intermolecular interactions of the molecules or ions [38]. The KohnSham (KS) density functional theory (DFT) is the most widely used method for electronic structure calculations in condensed matter physics and quantum chemistry. However, in general, the drawback of all the common functionals is their inability to describe long-range electron correlations responsible for noncovalent interactions [39,40,41]. Coupled cluster theory with singles, doubles, and perturbatively connected triple excitations [CCSD(T)], in conjunction with large basis sets, can accurately describe these effects [42,43,44,45,46]. Unfortunately, CCSD(T) calculations are computationally very demanding and therefore can be applied for systems with few atoms. Second-order Møller Plesset perturbation theory (MP2) has a much lower computational cost, and is seen as a suitable method to partly account for dispersive interactions in large systems. However, it tends to overestimate binding energies for π-stacked systems [47]. Due to the high cost of Coupled cluster methods, there has been considerable effort to capture the long-range correlation effects at a much reduced cost by nonempirical DFT based approaches such as symmetry-adapted intermolecular perturbation theory (SAPT). However, since this representation of dispersion interactions is nonempirical in nature, the computational cost still represents a serious bottleneck. Therefore, the method of choice has been the use of DFT-D based description of non-covalent interactions, leading to several dispersion-corrected methods [48, 49]. The simplest approach, normally designated as DFT-D, introduces dispersion interactions using an empirical potential [50]. The DFT-D has been applied to calculate the intermolecular interactions energies for large benchmark sets of noncovalent molecules with very satisfactory results. The ωB97X-D functional has been shown to have the best performance in treating π-π intermolecular interactions and charge transfer excitations [47,48,49,50]. For large molecular systems where Coupled cluster is very expensive to use, the ωB97X-D functional can provide accurate description of intermolecular distances. Therefore, we believe that the ωB97X-D functional approach can also be an excellent alternative to deal with ionic liquids containing immidazolium based systems where the effect of dispersion interactions leads to ring stacking interactions and delicate intermolecular interactions like H-bonding occur predominantly.

Besides the functionals, the quality of the basis set is another important factor that affects the speed and accuracy of calculations. Since large basis sets, in general, yield more accurate results than smaller basis sets, triple-zeta basis sets or even larger have been routinely employed to compare different functionals. However, large basis sets make the calculations too slow for large systems. Smaller basis sets, such as those of double-zeta quality, could make the calculations faster but may not describe noncovalent interactions accurately, such as halogen bonding [47, 48]. Therefore, small basis sets, which could combine high computational speed and accuracy, are in great demand. It has been shown that for halogen-bonded complexes for which the complexation energies have been previously calculated with more accurate CCSD(T)/CBS method, the DGDZVP basis set performed far better than other double-zeta basis sets, and it even outperformed the triple-zeta basis sets. Due to its small size, it is well suited for studying halogen bonding in large systems. The DGDZVP basis set in combination with ωB97XD functional has been shown to perform better than other double-zeta basis sets, and at least as good as triple-zeta basis sets and is well-suited for calculating halogen bond strengths on large complexes [46,47,48]. The DGDZVP basis set has been used in our work in combination with ωB97XD functional and results were compared against previously reported experimental results as well as other basis sets such as 6–311 +  + G(d,p), 6–311 +  + G(3df,2dp).

In this article, we present a detailed analysis of molecular interactions and conformational states of 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMI][TFSI]) via the ab initio methods at the density functional theory (DFT). The article is structured as follows. First, we give a brief overview over the computational methods employed in this work. This is followed by the discussion of the structures of single cations, anions, and cation–anion ion-pairs of [EMI][TFSI] based ionic liquids. The interaction energies, stabilization energies and natural orbital analysis of the ion pair conformers are thoroughly analyzed and discussed.

2 Calculation methods

DFT calculations have been carried out with the Gaussian 09 suite of programs [51]. Using the density functional theory with the hybrid B3LYP functional [52, 53] and with Grimme’s B97D functional including dispersion [54]. All monomeric ion calculations at the B3LYP and ω97X-D levels have been carried out with the 6-311++G(d,p), 6–311++G(3df,2dp), and DGDZVD basis sets. All structures have been fully optimized both in the gas phase and using the polarizable continuum model (PCM) implemented in the Gaussian program. Electrostatic interactions of the ion pair with surrounding ions were effectively accounted for by introducing apparent dielectric constant ε for the RTIL environment. Previous reports show that this approach, originally introduced for quadrupolar solvents, such as benzene and supercritical carbon dioxide, was able to describe solvation effects in nondipolar solvents [55]. In the present study, we employed acetonitrile (ε = 36) to model [EMI][TFSI] in the PCM framework. The use of polarizable continuum model (PCM) is based on MD simulation results [56] that imidazolium-based ILs show somewhat larger solvatochromic shifts. Each structure has been individually optimized for each method. Natural bond orbital analysis (NBO) analyses for all the ILs was made at ω97X-D levels with the DGDZVD basis set using the polarizable continuum model (PCM). This analysis helps us to identify specific orbital interactions, NBO charges and also to obtain the descriptions of orbital hybridization. Vibrational frequencies of all the optimized structures have also been calculated to ensure that the optimized structure represents the true minimum. The absence of imaginary vibrational frequency confirms that the optimized geometry represents the stable structure. Basis set superposition error (BSSE) correction was not employed as its contribution to the interaction energy for an ionic salt are already reported to be insignificant [57].

3 Result and discussion

3.1 Geometric analysis

3.1.1 Structures of isolated cation and anion

In order to give a visual understanding of the cation–anion interaction before designing initial geometries for the ion pairs (dimers), the most stable geometries of the isolated [EMI]+ cation, and [TFSI]− anion conformers were revised and analyzed first. The atomic numbering scheme employed in the present work is displayed in Fig. 1. The geometries of both [EMI]+ cation and [TFSI]− anion were optimized directly at the B3LYP/6-311++G(d,p), B3LYP/6-311++G(3df,2dp), B3LYP/DGDZVP, ω97X-D/6-311++G(d,p), ω97X-D/6–311++G(3df,2dp) and ω97X-D/DGDZVP level both in gas phase and the presence of polarizable dielectric continuum medium using acetonitrile as a solvent. Vibrational frequencies of all the optimized structures have also been calculated to ensure that the optimized structure represents the true minimum. The absence of imaginary vibrational frequency confirms that the optimized geometry represents the stable structure. The structures of the fully optimized [TFSI]− anion and [EMI]+ cation, respectively, are shown in Figs. 2 and 3. Selected structural parameters for [EMI]+ cation and [TFSI]− anion are compiled in Tables S1–S6.

Fig. 1
figure 1

The atomic numbering scheme employed in the present work: a [EMI]+ b [TFSI]−

Full size image
Fig. 2
figure 2

Gas phase structures of a cis and b trans conformers of [TFSI]−) optimized at ω97XD/6-311++(3df,2dp)

Full size image
Fig. 3
figure 3

Gas phase structures of a planar and b nonplanar conformers of EMI optimized at ω97X-D/6-311++(3df,2dp)

Full size image

The results of our calculated structural parameters of the cis and trans conformers of [TFSI]− anion are compiled in Tables S1–S3. Similar to previously reported results [58,59,60,61,62,63], we obtained two optimized minimum energy structures without imaginary frequencies. According to our results, the [TFSI]− anion exists in two different conformations: one with trans-symmetry where the CF3 group are on opposite sides of the C–S–N–S dihedral angle, and another with cis-symmetry where the CF3 groups are on the same side of the C–S–N–S dihedral (see Fig. 2). On the basis of ωB97X-D/6-311++G(3df,2dp) functional and in the presence polarizable dielectric continuum medium, we found that the conformers with the C–S–N–S dihedral angles 95.35°, 95.35° (trans-[TFSI]−) and 87.6716, − 128.195) (cis-[TFSI]−) give the global and local minima, respectively, with the SCF energy difference of 3.025 kJ mol−1 (Table S2 and S4). Our results show slight difference to previous results by Takamuku and coworkers where on the basis of B3LYP/6-311+G(d) calculations [63], the values of the dihedral angles were (90.9°, 90.9°) for the trans geometry and (− 81.2°, 120.2°) for the cis geometry, with the SCF energy difference of 2.3 kJ mol−1. The deviations of the dihedral angles for B3LYP calculations compared to our results on the basis of the ωB97X-D functional stems from the description of dispersion forces for which B3LYP density functional fails [51].

As can be seen from Tables S1–S4, bond lengths, angles and dihedrals of the conformers calculated using the ω97X-D level of theory are in good agreement among the various basis sets and the ω97X-D/6-311++(3df,2dp) level of theory and basis set gives calculated results that best agree with those in crystals [59]. On the other hand, bond lengths calculated using the B3LYP level of theory show some variations larger than those in the crystals [59] as well as than that of ω97X-D results. These imply that the wB97X-D functional with a larger basis set with polarization functions show good performance for such molecules involving fluorine or sulfur atoms [47]. The energy of the cis-[TFSI]− conformer relative to that of the trans-[TFSI]− conformer calculated using ω97X-D/6-311++(3df,2dp) levels of theory and the basis set and in the presence of dielectric continuum medium employed here is 3.025 kJ mol−1. The small value, relative to the RT value at 298 K implies that the conformers are present in equilibrium. The dipole moment of the conformers is also shown. According to the ω97X-D/6-311++(3df,2dp) levels of theory and basis set and in the presence of dielectric continuum medium, the dipole moment of the cis-[TFSI]− (µ = 6.0640) conformer is significantly larger than that of the trans-[TFSI]− (µ = 0.1107) one, implying that the cis-[TFSI]− geometry is preferred around small sized cations.

Selected structural parameters of the planar-cis and non-planar staggered conformers are compiled in Tables S5-S8. The optimized geometrical structures of [EMI]+ cation are shown in Fig. 3. According to our results, the most stable geometry ω97X-D/6-311++G(3df,2dp) level of theory showed a non-planar staggered with the dihedral angles N7–C5–N8–C13 and C9–N7–C5–H6 of 177.684° and 0.334° respectively (Table S8). Our results show agreement with previously reported results [64].

As can be seen from Tables S5–S8, bond lengths, angles and dihedrals of the conformers calculated using the ω97X-D level of theory are in good agreement among the various basis sets and the ω97X-D/6-311++(3df,2p) level of theory and basis set, and gives calculated results that best agree with those in the crystals [59]. The energy of the planar-cis [EMI]+ conformer relative to that of the non-planar staggered [EMI]+ conformer calculated using the ω97X-D/6-311++(3df,2p) levels of theory and basis set and in the presence of dielectric continuum medium is 9.8 kJ mol−1. According to the ω97X-D/6-311++(3df,2p) levels of theory and basis set and in the presence of dielectric continuum medium, the dipole moment of the non-planar staggered [EMI]+ (µ = 2.0550) conformer is slightly larger than that of the planar-cis [EMI]+ one (µ = 1.3131), implying that the non-planar staggered [EMI]+ geometry is preferred around more small sized anions.

3.1.2 Structures of isolated ion pairs

After analyzing the influence of the level of theory and basis sets for the monomeric ions, to further investigate the molecular interactions and conformational states of 1-ethyl-3 methylimidazolium bis(trifluoromethylsulfonyl)imide ion-pairs ([EMI][TFSI]), geometry optimization of each ion pair conformer was done on isolated ion pair with ωB97X-D/DGDZVP level of theory and basis set. Electrostatic interactions of the ion pair with surrounding ions were effectively accounted for by introducing apparent dielectric constant (acetonitrile) for the RTIL environment. To avoid the effect of change of basis sets, all calculations are performed using the same basis set. Concentrating now on the ωB97x-D/ DGDZVP results only, the intra- and interionic bond lengths, angles, dihedral angle in different ion pair conformations are compiled in Table 1. For convenience, the atomic numbering scheme employed in the present work is displayed in Fig. 1. There are six different minimum energy different conformations available for [EMI][TFSI] ion pair that could be connected via the most acidic proton (H1) of the cation or via the other protons of the methyl and ethyl group hydrogen’s of the cation (see Figs. 4 and 5). Vibrational frequencies of all the optimized structures have also been calculated to ensure that the optimized structure represents the true minimum.

Table 1 Bond distance, bond angle and dihedral angles of between [EMI]+ cation and [TFSI]− anion in dielectric continuum using ωB97x-D/ DGDZVP level of theory and basis set
Full size table
Fig. 4
figure 4

The optimized geometrical structures of cation–anion pairs in dielectric continuum medium using ωB97x-D/DGDZVP level of theory and basis set. C1(Planar cis[EMI]-cis [TFSI]), C2 (Staggered nonplanar[EMI]-cis [TFSI]), C3(Staggered nonplanar[EMI]-cis [TFSI]), C4 (Planar cis[EMI]-trans [TFSI]), C5(Staggered nonplanar[EMI] (syn)-trans [TFSI]), C6(Staggered nonplanar[EMI](anti)-trans [TFSI

Full size image
Fig. 5
figure 5

[EMI]+ cation showing the possible interaction sites for the [TFSI]− anion (represented as X); anticlockwise these are front-me, alkyl-me, side-me, back, side-but, alkyl-me and front-but

Full size image

Previous computational reports by Tsuzuki et al. on ion pair conformers of [EMI][TFSI] (at the Møller−Plesset (MP) level of theory) showed the existence of 17 configurations which were within 2.4 kcal/mol [29]. Further studies by Obi and coworkers using the same theoretical manifold as Tsuzuki et al., but with a larger basis set, obtained 23 possible configurations of the ion pair [EMI][TFSI] which were within 0.5 kcal/mol [32]. In another study by Shubham and coworkers, both DFT calculations using B3LYP/aug-cc-pVTZ and experimental techniques using experimental IR and UV−vis were used to characterize [EMI][TFSI] ion pairs [64]. In those studies, they identified several configurations for the ion pair that were within 10 kcal/mol and 6 configurations that were within 0.5 kcal/mol at the B3LYP/aug-cc-pVTZ level of theory. In the solution phase, however, the authors identified three unique minima using the implicit solvation model which were significantly different geometrically than what was observed in the gas phase. Lassegues and co-workers [65] carried out an extensive conformational search for the [TFSI]− anion and found that the transoid rotamer of the anion was more stable than the cisoid rotamer by about 0.5 kcal/mol. Previous studies by Umebayashi et al. [63] on the molecular conformations of [EMI][TFSI] by Raman and infrared spectroscopy showed that the [TFSI]− anion in the trans conformation was favored over the cis-[TFSI]− anion. Tsuzuki et al. [29] have noted in their ab initio study that the magnitude and directionality of ion pair interactions are important to the dissociation and association behaviors of the ions in RTILs. The most recent studies on the conformational states of [EMI][TFSI] were performed via the ab initio methods at the density functional theory (DFT) and via experimental Raman and FT-IR spectroscopy [66]. In those studies, the different conformers of the [EMI][TFSI] cation−anion pairs were optimized at B3LYP level and found that the anion in the lowest energy ion pair state adopted a trans conformation. Those studies showed that, in the gas phase, the lowest energy conformer exhibited a characteristically strong C1−H1–N1 interaction through the C1−H1 cation bond, accompanied by a substantial red shift of C1−H1 stretching vibrational frequency.

However, those studies reported so far have focused only on the conformational preferences of the [TFSI]− anion (as either cis-[TFSI]− and/or trans-[TFSI]−) while no indications were made on the conformational preference of the [EMI]+ cation (as either non-planar staggered [EMI]+ and/or planar cis [EMI]+). The B3LYP functional fails to represent dispersion interaction (i.e., optimized structure may result in saddle point instead of global minimum), and thus the hybrid functional B3LYP offers poor description of the electronic structure of [EMI][TFSI] and is clearly inferior to ωB97X -D functional [51] which has not been given due consideration by those studies mentioned above. For example, the optimized geometries of [EMI][TFSI] ion pair at B3LYP/aug-cc-pVTZ level by Shubham and coworkers (Figs. 2 and 3 of reference [64]) involve [TFSI]− anion in between cisoid and the transoid configuration which when re-optimized at ωB97X-D functional resulted in the [EMI][TFSI] ion pair with the TFSI anion in the cis-configuration. Furthermore, optimized geometries of the [EMI][TFSI] ion pairs reported by Tsuzuki et al. (Fig. 9 of reference [29]) and Umebayashi et al. (Fig. 2 of reference [63]) involve unstable ion pair configurations which when re-optimized at ωB97X -D functional resulted in optimized structures as shown in Fig. 4 of our study.The present work, therefore, focuses on the molecular interactions and conformational analysis of [EMI][TFSI], by making use of detailed NBO analysis and multiple interaction sites (in addition to the C1–H1–N1 and C1–H1–O1 interactions) and the conformational preferences of the cation as either non-planar staggered and/or planar cis [EMI]+ cation. As shown in Fig. 5, the starting geometries for the optimization of the [EMI][TFSI] ion pair conformers were taken from all poosible sites btween the [EMI]+ cation and the [TFSI]− anion.

In the current study, all possible combinations of planar cis [EMI]+-cis [TFSI]−, planar cis [EMI]+-trans [TFSI]−, non-planar staggered [EMI]+-cis [TFSI]− and non-planar staggered [EMI]+–trans [TFSI]− were analyzed and discussed. As shown in Fig. 4, a total of six minimum energy different stable ion pair conformers (C1−C6) were obtained. The energetic difference relative to the lowest energy ion pair conformer ranges from 0.676 to 5.170 kJ/mol. The selected optimized structural parameters of the stable conformers, C1–C6, are shown in Table 1. According to our results, the C6 ion pair conformer was found to be the lowest energy conformer. From our closer inspection of the C6 ion pair conformer, we found that the C6 ion pair conformer constitutes the staggerd anti [EMI]+-trans [TFSI]− ion pair configuration with the [TFSI]− anion on top position. Overall, the [TFSI]− anion in the C4, C5 and C6 states was found to adopt a trans conformation for the C−S−S−C dihedral angle, whereas a cis conformation was predicted for C1, C2 and C3 ion pair conformers. The values of the dihedral angles N1–C1–H1–O1 for the ion pair conformers of C1, C2, C3 and C4, respectively, are 132.14°, 122.08° and 135.73° indicating that the [TFSI]− anion is on top position with respect to the imidazolium rings. On the other hand, the value of the dihedral angle N1–C1–H1–O1 for the C5 ion pair conformer is 171.15° indicating that the [TFSI]− anion is nearly coplanar with the imidazolium rings. Minimum energy structures of [EMI]][TFSI] obtained in this study also support the notion that both cis and trans conformations can exist for the [TFSI]− anion, which is also in excellent agreement with previously published work on geometries of ILs. The above/below configurations is energetically relevant to the π electrons that delocalize on the imidazolium ring and the π interaction which increase the absolute value of the interaction energy and makes the configurations more stable, which is further dicussed in Sect. 3.3.

The study of H-bonds in ILs is multifaceted with a range of experimental and computational methods employed. A traditional H-bond involves complex intermolecular interactions represented by X–H–Y, where a H-atom intercedes between two electronegative species X and Y, such as O or N. Standard H-bonds are primarily electrostatic interactions with covalent and dispersion contributions [15]. The concept of X–H–Y hydrogen bonds may be extended to ionic liquids. Nevertheless, the characteristics and features of H-bonding in ILs cover an extremely wide and diverse range which is still the subject of scientific debate, and are thus not fully understood. H-bonding is not a binary on–off phenomenon but occurs in a graduated scale which makes quantifying and clearly demarking H-bonding difficult. To differentiate the H-bond in IL from other ionic H-bonds, we refer to the H-bond between [EMI]+ and [TFSI]− species as the doubly ionic H-bond. Doubly ionic H-bonds are very common and occur within a large range of ILs. There are best reviews available in this topic [15]. The doubly ionic H-bond between [EMI]+ and [TFSI]− species is bifurcated, and unlike many molecular liquids, a significant variety of distinct H-bonds are formed between different types and numbers of donor and acceptor sites within the [EMI]+[TFSI]− ion pair. Aprotic imidazolium based ILs typically exhibit weak H-bonds. However, Large anions such as the [TFSI]− anion typically have multiple H-bonding interaction sites within different ion pair conformers, increasing the overall energy contribution from H-bonds and π-type interactions [15].

Following the recommendations and naming conventions of Hunt et al. [15] and coworkers, the possible interaction sites of the [EMI]+ cation with the [TFSI]− anion are indicated in Fig. 5. As shown in Fig. 5, there are different association sites for the [TFSI]− anion within the [EMI]+ cation: front-me, front-but and alkyl-me positions. The C1, C2 and C5 ion pair conformers have front-me, front-but and terminal methyl H-bond interactions. The C3 and C4 ion pair conformers, on the other hand, exhibit front-me, front-but, methylene and terminal methyl H-bond interactions. The ion pairs in C1, C3 and C4 conformations exhibit bifurcated C−H–N1 inter ion interactions through the primary C1−H1 and terminal methyl C6−H9 cation H-bonds. The ion pairs in C1, C2, C4 and C5 conformations exhibit bifurcated C−H–O1 inter ion interactions through the primary C1−H1 and terminal methyl group C5−H8 cation H-bonds (see Figure S1). In addition to the primary front-me C−H–O1 inter ion interactions, there also exist a secondary front-but C−H–O3 inter ionic interactions for C3, C4 and C5 ion pair conformers through the methylene group C2−H2 cation bond. Very weak C−H–F interactions have also been observed for all conformers except for the C2 ion pair conformer through terminal methyl C5−H8 and C6−H9 cation H-bonds.

The values of the distances of Cl−H1–O1 for the ion pair conformers C1, C2, C4 and C5, respectively, are 2.30 Å, 2.45 Å, 2.51 Å and 2.18 Å which are shorter than the sum of the corresponding van der Waals radii for H (1.20 Å) and O (1.52 Å); and the corresponding respective values for angles for Cl−H1–O1 are 134.91°, 122.62°, 130.00° and 145.73°, which are within the accepted criteria of the C1−H1–Ol H-bonds, which implies that the [TFSI]− anion forms H-bonds with Cl−H1–O1 and Cl−H1–N1 fragments of the [EMI]+ ring cation (see Table 1). The type, number and strength of the different cation−anion molecular interactions play a crucial role in the overall conformer stability. According to Gilli et al. [67], it is possible to relate the strength of the H-bond (and hence the stability of conformers) to the donor–acceptor distance as a first estimate. The stability of C4 ion pair conformer can be attributed to the favorable orientations of the O and N atoms in [TFSI]− anion towards the proton-donating groups of the terminal methyl and methylene hydrogen atoms of the [EMI]+ cation. In the C4 conformer, there exist bifurcated hydrogen bond interactions through primary front-me C1−H1–O1 (with a distance 2.50 Å and an angle of 130.00°), front-me C5−H8–O1 (with a distance 2.42 Å and an angle of 149.80°) and through the terminal methyl group hydrogen atoms of C6−H9–N1 (with a distance 2.55 Å and an angle of 144.15°) cation bond. Thus, by relating the strength of the H-bond (and thus the stability of the conformer) to the donor–acceptor distance as a first estimate, there are multiple shorter and more linear hydrogen bonding interaction sites in the C4 ion pair conformer and hence is more stable than the least stable C2 ion pair conformer by 5.17 kJ mol−1. In the least stable ion pair conformer (C2), the terminal methyl group hydrogens are in the anti-position with respect to the position of the O and N atoms of the [TFSI]− anion in the imidazolium ring, and thus the approaching oxygen (C2−H2–O3) and nitrogen atoms (C6−H9–N1) cannot make favorable H-bonding interactions to the terminal group hydrogen atoms of the cation and thus making it the least stable of all other conformers. The distance between the hydrogen atom at the C1 position of the cation and the hydrogen bond acceptor atom of the anion for primary C1−H1–O1 interaction is shorter for conformers C1, C2, C4 and C5 than similar distances for C1−H1–N1 and C1−H1–F interactions (see Table 1). This suggests that the interionic H-bond interaction of the former is stronger than the latter two. When imidazolium cations are associated with large anionic groups, like [TFSI]− anion [79], there exist multiple H-bond interaction sites within the liquid environment and exhibit varying levels of H-bond strength and directionality. Additionally, these large anions take preferential on-top distributions above and below imidazolium rings, leading to π-type interactions. The delicate interplay of H-bond and π-type interactions in [EMI][TFSI] ionic species becomes more complicated than this and requires further investigation.

3.2 Interaction energies of isolated ion pairs

ILs are dominated by columbic and weak intermolecular interactions that gives rise to the unique physical and chemical environment present in each IL. Aiming at investigating the molecular interactions and the occurrence of H-bonding in [EMI][TFSI] ion pairs, the interaction energy of the different ion pair conformations were calculated using ωB97x-D/ DGDZVP level of theory and basis set and the results are shown in Fig. 6. The interaction energy between the cation and the anion of the ILs was calculated according to the following expression (Eq. 1):

$${\text{E}}\left(\frac{{\text{kJ}}}{{\text{mol}}}\right)=\mathrm{ E}\left({\text{IP}}\right) -({\text{E}}\left({\text{cation}}\right) +\mathrm{ E}\left({\text{anion}}\right))$$
(1)

where E(IP) is the energy of the ion pair, and E(cation) and E(anion) are the energy of the cation and anion, respectively. For the ion pair [EMI][TFSI], the absolute value of the interaction energies is lower than the normal hydrogen bond energies (50 kJ.mol−1), which indicates that there exist weak electrostatic attractions between the imidazolium cations and TFSI anions.

Fig. 6
figure 6

Correlation between interaction and relative conformer energies of the different ion pair conformers of [EMI][TFSI] ion pairs in dielectric continuum medium using ωB97x-D/DGDZVP level of theory and basis set

Full size image

The correlations between interaction and relative conformer energies of the different [EMI][TFSI] conformers are shown in Fig. 6. The C4 ion pair conformer has the maximum and C2 and C5 conformers have the minimum absolute interaction energies. Comparison between interaction and relative conformer energies reveals that there are very important variations between the ordering of calculated relative and interaction energy values. According to Fig. 6, the relative stabilities among the five conformers changes in the following order: C6 > C4 > C2 > C3 > C1 > C5 whereas the absolute interaction energies change in the order: C4 > C1 > C6 > C2 > C3 > C5. The absolute values of the interaction energies of the conformers C1, C3 and C4 are in the range 47.9–48.64 kJ mol−1 which are higher than those of C2 (43.4 kJ/mol) and C5 (41.22 kJ/mol). The relative energy of the C5 ion pair conformer (3.53 kJ.mol) is lower than that of the ion pair conformers of C1 (4.03 kJ/mol) and C2 (5.17 kJ/mol) and thus is expected to be more stable than the other two. However, the question why the C5 ion pair conformer has less absolute interaction energy than C1 and C2 ion pair conformers is likely to be raised. Previous studies indicated that the total interaction energy (ΔE) was a measure of the stability of an ion pair conformers, and it has been shown that the values of the interaction energies were not closely relevant to the sizes and symmetries of the anions. However, the charge distribution was found to be responsible for order in the values of the interaction energies [68]. Ludwig and co-workers [69] have shown that agreement with experimental data could only be obtained by choosing conformers which hold higher absolute interaction energies than the global minimum. Thus, the sole importance of the global minimum structure for the condensed phase is highly questionable [69]. Apparently from the results in Fig. 6, for the ion pair [EMI][FSI], the absolute value of the interaction energies is lower than the normal hydrogen bond energies (50 kJ/mol), which indicates that there exist very weak electrostatic interaction between the [EMI]+ cations and [TFSI]− anions. The weaker attraction between the [EMI]+ and [TFSI]− ions suggests as one contributor to the larger value of diffusion coefficients of the ions.

From Table 1, it is obvious that the C1 ion pair conformer, has multiple shorter and more linear H-bond interactions such as front-me C1−H1–O1 (with a distance 2.33 Å and an angle of 134.91°), terminal methyl C5–H8–O1 (with a distance 2.57 Å and an angle of 140.09°), terminal methyl C6−H9–N1 (with a distance 2.58 Å and an angle of 142.77°) interactions whereas the C3 ion pair conformer has longer and nonlinear hydrogen bonds such as front-me C1−H1–O1 (with a distance 2.79 Å and an angle of 97.45°), terminal methyl C5−H8–O1 (with a distance of 2.55 Å and an angle of 137.24°), terminal methyl C6−H9–N1 (with a distance 2.64 Å and an angle of 130.27°) H-bond interactions. In C5 ion pair conformer, the strongest H-bond is made between front-me C1−H1–O1 (with a distance 2.18 Å and an angle of 145.72°), terminal methyl C5−H8–O1 (with a distance 2.42 Å and an angle of 150.03°), front-but C1−H1–O3 (with a distance 2.39 Å and an angle of 118.63°), methylene C2−H2–O3 (with a distance 2.63 Å and an angle of 114.59°), terminal methyl C5−H8–F1 (with a distance 2.89 Å and an angle of 155.72°) H-bond interactions. Using IR/UV double resonance spectroscopy, it has been shown that there are multiple conformers of the [EMI][TFSI] ion pair present in the gas phase and each conformer has a characteristic red shift in the frequency of its C1–H group that reveals the variation in strength of a hydrogen bond between the cation and anion [70]. Our results show that the greater the number of multiple H-bond interactions, the greater the absolute value of the interaction energy.

3.3 The stabilization energies of isolated ion pairs

Natural bond orbital analysis (NBO) [84] provides good information regarding the change in charge densities of donor and acceptor ions. While the interaction energy is defined as the difference between the energy of the ion pairs and the sum of the energies of the purely cationic and anionic species (Eq. 1) however, for each donor NBO(i) and acceptor NBO(j), the stabilization energy E(2) (Eq. 2) associated with delocalization of electron pair from donor orbital (i) to acceptor orbital (j) and is estimated as:

$${\text{E}}\left(2\right) = {\Delta {\text{E}}}_{{\text{ij}}}= \frac{{q}_{i}{\text{F}}{({\text{i}},{\text{j}})}^{2}}{{\varepsilon }_{i} -{\varepsilon }_{j}}$$
(2)

where qi is the donor orbital occupancy, εi and εj are the diagonal elements (orbital energies) and F(i,j) is the interaction element between donor and acceptor orbitals and is known as diagonal NBO Fock matrix element. In this case, the electronic wave function is interpreted in terms of a set of occupied Lewis and a set of unoccupied non-Lewis localized orbital and the delocalization effects can be identified by means of off-diagonal elements of the Fock matrix. The forces of these delocalization interaction, E(2) (kcal/mol), are estimated by second order perturbation theory [75]. When electrons are shared via the Ylp \(\to\) σ*C–H (Y = N, O, or F) bonding and anti-bonding interaction, this is equivalent to transferring electron density from the lone pair of N and/or O atoms into the σ*C–H orbital. Typically Yn(lp)\(\to\) σ*X–H is strongest for a linear or near linear H-bond. In particular, the H-bond strength has been related to the charge transfer component E(2)n \(\to\) σ* of the NBO analysis. E(2)n \(\to\) σ* is proportional to the amount of electron density (qi) donated from the filled donor lone-pair orbital into the empty σ* orbital, moderated by the energy difference between these two fragment orbitals (Δε), and thus the NBO analysis on the DFT optimized structure allows the analysis of intermolecular donor–acceptor orbitals interactions [15, 71].

NBO analysis of the structure of various alkyl-imidazolium derivatives with simple mono-atomic anions were studied at B3LYP level with DGDZVP basis set [71]. However, there are no prior reported studies on the detailed NBO analysis of [EMI][TFSI] ion pair conformers that have multiple interactions sites for the anion. The current work gives detailed analysis of the stabilization energy obtained from NBO analysis of different ion pair conformers of [EMI][TFSI], and broadly discusses the nature of orbital interactions between the empty σ*C–H fragment orbital (FO) of the [EMI]+ cation and the occupied lone pair FO on N and O of the [TFSI]− anion. Imidazolium based ion pairs with weak H-bond acceptor anions such as [BF4]− and [PF6]− have E(2)n \(\to\) σ* = 50–60 kJ/mol while those with strong hydrogen acceptor anions such as Cl− and [NO3]− have E(2)n \(\to\) σ* = 110–180 kJ/mol. The much stronger hydrogen bonds of protic ion pairs with strong hydrogen acceptor anions of [NO3]− have E(2)n \(\to\) σ* = 250–320 kJ/mol [14, 72]. Generally speaking, weak H-bonds have E(2)n \(\to\) σ* < 30 kJ/mol and strong hydrogen bonds have E(2)n \(\to\) σ* > 150 kJ/mol [76] and those lying between these extremes are moderate hydrogen bonds. However, it is still the subject of scientific debate an ongoing research to establish a more robust level of knowledge relating to the E(2)n \(\to\) σ* parameter with respect hydrogen bonds in ionic liquids. In particular, a large range of IL ion pair conformers need to be examined, geometric influences and the impact of multiple concomitant hydrogen bonds need be better understood.

From the Tables S10–S14, we observed that in general, for [EMI][TFSI] ion pair conformers, charge transfer occurs mainly from the lone pairs of oxygen and nitrogen atom to the σ-type anti-bonding orbital of the C–H and π-type anti-bonding orbitals of N–C bonds. This was evident from the values of the stabilization energy E(2) associated with each electron delocalization from the donor to acceptor orbitals. Apparently, from the above results, it is noticeable that there exist large numbers of multiple concomitant hydrogen bonds but the values of the stabilization energy E(2) are generally small (E(2)n \(\to\) σ* < 3 kcal/mol) for the individual H-bond interactions. The shorter the C–H–-O and/or C–H–N bond is, the larger charge transfer, and the larger the stabilization energy E(2) associated with electron delocalization from donor to acceptor anti-bonding orbital.

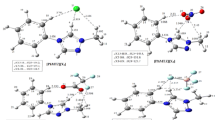
We can see from Fig. 7 and Table S9 that there is a strong linear correlation between H-bond length and the value of the stabilization energy (E(2)). The ion pair conformer C5 has the shortest C1–H1–O1 bond (2.18 Å) and more linear angle (145.72°), and thus with greater value of second-order perturbation energy for O1 \(\to\) σ*C1-H1 (E(2) = 2.15 kcal/ mol) among all ion pair conformers investigated. The ion pair conformer C1 (with C1–H1–O1 bond length 2.33 Å and angle 134.91°) has the second largest stabilization energy for O1 \(\to\) σ*C1-H1 (E(2) = 2.15 kcal/ mol) followed by C2 (with C1–H1–O1 bond length 2.40 Å and angle 122.62125°) and C4 (with C1–H1–O1 bond length 2.51 Å and angle 130.00°). NBO analysis of [EMI][TFSI] ion pair conformers also revealed that the lone pairs of nitrogen donate its electrons to the σ-type and π-type anti-bonding orbital for N1−C1 bonds. The weak NBO interactions of N1 \(\to\) σ*N1-C1 and N1 \(\to\) π*N1-C1 imply the existence of anion donor-π* interactions. Other non-bonded interactions that also contribute significantly to stabilization of the compound are O1 \(\to\) σ*C5-H8, O3 \(\to\) σ*C2-H2, and N1 \(\to\) σ*C6-H9 interactions.

Fig. 7
figure 7

Correlations between H-bond length (C1–H1–O1), H-bond angle (< C1–H1–O1) and stabilization energies (E(2)) of the different ion pair conformers

Full size image

The [EMI][TFSI] ion pair conformers tend to form multiple but bent H bonds, reducing the strength of the individual H bonds from a potential (linear) maximum. Generally speaking, they form a major H-bond with the C1−H1 and a minor one with Calkyl−H bonds. The relative contribution from each of these is not easily resolved via the association energy which includes the ionic as well as a combined H-bond contribution. Moreover, [EMI][TFSI] ion pairs are not symmetric and thus cannot reach the maximum covalent contribution, which is possible only for symmetric H-bonds. From Table S9, it is clear that the most significant E(2) values for C1 ion pair conformer are for the LP(2)O1 (donor NBO)\(\to\) BD*(1)C1−H1 (acceptor NBO) interaction with an E(2) of 1.66 kcal/mol that shows the presence of weak C1−H1–O1 H-bond interaction; LP(1)N1(donor NBO)\(\to\) BD*(1)C6−H9 (acceptor NBO) interaction with an E(2) of 1.28 kcal/mol that shows the presence of weak C1–H1–N1 H-bond interaction; and LP(2)N1 (donor NBO)\(\to\) BD*(2)N1-C1 (acceptor NBO) interactions with an E(2) of 1.78 kcal/mol indicating the presence of anion donor-π* acceptor interactions while the rest are less significant in comparison to this value. For the C1 ion pair conformer, the stabilization energies that arise from LP(2)O1(donor NBO)\(\to\) BD*(1)C1–H1(acceptor NBO) is only with an E(2) value of 0.61 kcal/mol and LP(1) N1(donor NBO)\(\to\) BD*(1) N1–C1 (acceptor NBO) interaction with an E(2) of 2.32 kcal/mol indicating the presence of anion donor-π* acceptor interactions. For the C4 ion pair conformer, however, the E(2) values have much smaller values for C1–H1 and C6–H9 interaction indicating the absence of appreciable C–H–O1 H-bond interaction. In the C4 ion pair conformer, the E(2) value for anion donor-π* acceptor interactions is much larger than other interactions. The C2 ion pair conformer which has the cation ethyl group in anti-position with respect to the position of the anion in the imidazolium ring, has LP(2)O1(donor NBO)\(\to\) BD*(1)C1–H1(acceptor NBO) interaction with an E(2) of 0.64 kcal/mol indicating the absence of appreciable C1–H1–O1 H-bonding interaction; LP(2)N1 (donor NBO)\(\to\) BD*(2)N1–C1 (acceptor NBO) interactions with an E(2) of 1.38 kcal/mol indicating the presence of anion donor-π* acceptor interaction. The C3 ion pair conformer which has the cation ethyl group in syn-position with respect to the position of the anion in the imidazolium ring, has LP(2)O3 (donor NBO)\(\to\) BD*(1) C2–H2 (acceptor NBO) interactions with an E(2) of 1.24 kcal/mol indicating the presence of C2–H2–O3 H-bonding interaction through the ethyl group hydrogen of the cation. The C5 ion pair conformer has LP(1) O1(donor NBO)\(\to\) BD*(1)C1–H1(acceptor NBO) interactions with an E(2) of 2.15 kcal/mol and LP(2)O1(donor NBO)\(\to\) BD*(1)C1–H1(acceptor NBO) interactions with an E(2) of 1.34 kcal/mol indicating the presence of C1–H1–O1 H-bonding interaction.

The NBO method has also been employed to characterize the natural orbital coefficients and hybridization on H-bond formation. The main listing of NBOs, displaying occupancy, natural atomic hybrids, polarization coefficient, and spλ composition of the different conformers of [EMI][TFSI] ion pair for a selected set of NBOs are shown in Table S15 and Fig. 8. For the ion pair conformer C1, the σ*C1–H1 NBO is formed from an sp1.63 hybrid (61.95% p-character) on carbon interacting with an s orbital (100% s-character) on hydrogen corresponding to linear combination of atomic orbitals 0.609C(sp1.63)–0.794H(s) comprising 61.95% p-character and larger polarization coefficient of H. This result can be substantiated by the extent of orbital interaction between lone pair orbitals LP(1) and LP(2) of O1 and the anti-bonding orbitals of σ*C1-H1. The lone pair electron of LP(2) (sp1.00 hybride orbital with 99.72% p-character) is actually oriented along the direction of the O1–H1 H-bond axis. The LP(1) of O1 (which has sp0.34 hybrid orbital with 74.79% s character and 25.19% p characer) possesses a vintage overlap with the σ*C1-H1 orbital, while the interaction of the LP(2) orbital of O1 with the σ*C1-H1 anti-bonding orbital is relatively larger. Furthermore, the percentage of”s” character of the lone pair orbital is another factor that determines the strength of H-bond interaction. The NBO analysis indicates that the”s” character of LP(1) of O1 (74.79%) is greater than that of LP(2) orbital. While, the “p” character of LP(2) are higher than that of LP(1) on O1. Hence, the LP(1) should be more tightly held by the nucleus and reduced tendency for hyper conjugative charge transfer. Similarly, the π*N1-C1 NBO is formed from an sp99.99d26.92 hybrid (99.69% p-character) on carbon interacting with an sp1.00 hybrid orbital (99.93% p-character) on nitrogen corresponding to the linear combination of the orbitals 0.8461C(sp99.99d26.92)–0.5330N(sp1.00) comprising sp1.00 hybrids (99.93% p-character) and larger polarization coefficient of C. The NBO analysis indicates that the”s” character of LP(1) (43.15%) is greater than that of the”s” character LP(2) of N1 (0.00%) (see Table S10). The “p” characters of LP(2) are higher than that of LP(1) on N1 indicating that the LP(1) should be more tightly held by the nucleus and reduced tendency of hyper conjugative charge transfer.

Fig. 8
figure 8

Selected natural bond orbital (NBO) interactions between different single ion pair conformers of [EMI][TFSI] pairs in dielectric continuum medium using ωB97x-D/ DGDZVP level of theory and basis set a C1 b LP(1)N1, LP(2)N1 and BD*(1) C6–H9 for C1 c LP(1)O1, LP(2)O1 and BD*(1)C1–H1 for C1 d LP(1)N1, LP(2)N1 and BD*(1)N1–C1 for C2 e LP(1)O3, LP(2)O3 and BD*(1)C2–H2 for C3 f LP(1)N1, LP(2)N1 and BD*(1)N1–C1 for C4. “LP” for 1-center valence lone pair, “BD” for 2-center bond, “BD*” for 2-center antibond, and, the unstarred and starred labels corresponding to Lewis and non-Lewis NBOs, respectively), a serial number (1, 2, if there is a single, double,… bond between the pair of atoms), and the atom(s) to which the NBO is affixed

Full size image

NBO analyses for [EMI][TFSI] ion pair conformers were performed to obtain the NBO charge distribution (Tables S10–S14). The general feature of charge distribution on the cation is that the positive charges are located on the peripheral hydrogen atoms and the negative charges are located on the nitrogen atoms, while the C4/5 carbon atoms remain essentially neutral. For the C1 ion pair conformer, the NBO charge of H1 (0.25476) is more positive than that of other hydrogen atoms, while the NBO charges of O1 (-0.98636) is more negative than that of other oxygen/fluorine atoms, which is ascribed stronger to C1–H1–O1 H-bond interactions (E(2) = 1.66 kcal/mol). Similarly, for the C3 ion pair conformer, the most negative charge of O3 (-0.97992) and the C2–H2–O3 interaction leads to the more positive charge of H2 (0.23535). The C5 ion pair conformer has the most positive H atom (0.25638) which is ascribed to the shorter distance of C1–H1–O1 H-bond interactions (E(2) = 2.15 kcal/mol). Analysis of NBO charges show that the positive charge of H and negative charge of O atoms increase when they are involved in C–H···O interactions. The shorter the H-bond length of C–H···O, the larger the increase of positive charges of hydrogen atoms and negative charges of oxygen. The anion donor π-type anti-bonding interaction between the most electronegative N1 atom of the [TFSI]− anion with the π*N1-C1 anti-bonding orbital of the [EMI]+ cation leads to more positive charges on C1 atoms of the C1( 0.3303), C2 (0.34646) and C4 (0.34389) ion pair conformers. The greater the magnitude of the anion donor π*N1–C1 anti-bonding interaction, the higher the values of the positive charges on C1 atoms of the [EMI]+ cation.

4 Conclusion

The electronic strucures of [EMI][TFSI] ion pair conformers were investigated by DFT calculations. A total of six stable single ion pair conformers of [EMI][TFSI] were obtained. Minimum energy structures of [EMI]][TFSI] obtained in this study also support the notion that both cis and trans conformations can exist for the [TFSI]− anion, which is also in excellent agreement with previously published work on geometries of ILs. According to our results, the C6 ion pair conformer, which constitutes the staggerd anti [EMI]+-trans [TFSI]− ion pair configuration was found to be the lowest energy conformer. Overall, the [TFSI]− anion in the C4, C5 and C6 states was found to adopt a trans conformation for the C−S−S−C dihedral angle, whereas a cis conformation was predicted for C1, C2 and C3 ion pair conformers. The [TFSI]− anion prefers to be close to the upper part of the ring and located near C1-H1 group of immidazolium cation. The [TFSI]− anion forms hydrogen bonds with Cl–H1–O1 and Cl–H1–N1 fragments of the [EMI]+ cation. The greater the number of multiple H-bond interactions, the greater the absolute value of the interaction energy. From the NBO analysis, for [EMI][TFSI] ion pair conformers, charge transfer occurs mainly from the lone pairs of oxygen and nitrogen atom to the σ-type anti-bonding orbital of the C–H and π-type anti-bonding orbitals of N–C bonds. This is evident from the values of the stabilization energy E(2) associated with each electron delocalization from the donor to acceptor orbitals. From the NBO results, there exist large numbers of multiple concomitant hydrogen bonds, but the values of the stabilization energy E(2) are generally small (E(2)n \(\to\) σ* < 3 kcal/mol) for the individual H-bond interactions. The shorter the C–H···O and/or C–H···N bond is, the larger charge transfer, and the larger the stabilization energy E(2) associated with electron delocalization from donor to acceptor. The [EMI][TFSI] ion pair conformers tend to form multiple but bent H bonds, reducing the strength of the individual H bonds from a potential (linear) maximum. They form a major H-bond with the C1-H1 and a minor one with Calkyl-H bonds.