On the rub-impact force, bifurcations analysis, and vibrations control of a nonlinear rotor system controlled by magnetic actuator integrated with PIRC-control algorithm

Abstract

This article presents the Proportional Integral Resonant Controller (PIRC-controller) as a novel control strategy to suppress the lateral vibrations and eliminate nonlinear bifurcation characteristics of a vertically supported rotor system. The proposed control algorithm is incorporated into the rotor system via an eight-pole electromagnetic actuator. The control strategy is designed such that the control law (PIRC-controller) is employed to generate eight different control currents depending on the air-gap size between the rotor and the electromagnetic poles. Then, the generated electrical currents are utilized to energize the magnetic actuator to apply controllable electromagnetic attractive forces to suppress the undesired lateral vibrations of the considered rotor system. According to the suggested control strategy, the whole system can be represented as a mathematical model using classical mechanics' principle and electromagnetic theory, in which, the rub-impact force between the rotor and the stator is included in the derived model. Then, the obtained discrete dynamical model is analyzed using perturbation techniques and validated numerically through bifurcation diagrams, frequency spectrums, Poincare maps, time responses, and steady-state whirling orbit. The obtained results illustrate that the proposed control algorithm can mitigate the nonlinear vibration and eliminate the catastrophic bifurcations of the rotor system when the control gains are designed optimally. In addition, the system dynamics are analyzed when the rub-impact occurrence between the rotor and the pole housing is unavoidable. The acquired results revealed that the system may perform periodic-1, periodic-n, or quasiperiodic motion with one of two oscillation modes depending on both the impact stiffness coefficient and the dynamic friction coefficient.

Article Highlights

• Nonlinearity dominates the uncontrolled rotor response, where it suffers from the jump phenomenon and multiple solutions.

• The proposed controller forces the Jeffcott rotor to respond as a linear system with small oscillation amplitudes.

• The rotor oscillates with full-annular-rub or partial-rub-impact mode when rub-impact occurs between the rotor and stator.

1 Introduction

Rotating machinery is an essential part of several industries such as machine tools, automotive industries, aerospace engines, military industries, and autonomous power engineering. Ensuring safe working conditions and avoiding the catastrophic failure of these types of machines is the main task of scientists and engineers. One of the important reasons for the failure of the rotating machines and sometimes destruction are the nonlinear vibrations. Several causes can induce undesired vibrations for the rotating machines such as the rotating shafts eccentricity, the propagation of the cracks, the improper alignment in the case of a multi-rotor system, the wear of the bearing system, the occurrence of rub and/or impact between the rotor and its housing, and the asymmetric rotors. Therefore, many research articles regarding vibration analysis and control of rotating machinery are published annually as an indication of the importance of this issue, where Yamamoto [1] discussed the influence of the bearings' clearance on the rotor dynamics at the primary resonance more than sixty years ago. Ehrich [2] investigated the dynamical behaviors of the rotor system at subharmonic response conditions more than thirty years ago when the bearings' clearance is considered. In addition, Ganesan [3] studied the asymmetry of the bearings system on the oscillatory behaviors of the rotating machines more than twenty years ago. Moreover, Chávez et al. [4] investigated both theoretically and experimentally the motion bifurcation of an asymmetric Jeffcott system having radial clearance and subject to rub-impact force, where the theoretical and experimental results demonstrated that the considered system could perform period-1, period-2, or period-3 motion depending on the rotor angular speed. The nonlinear dynamics of the rotor systems with nonlinear stiffness behaviors have been studied extensively [5,6,7,8,9,10,11,12,13], where Kim and Noah [5], and Adiletta et al. [6] investigated analytically and experimentally the dynamical characteristics of the Jeffcott system having a nonlinear restoring force. They reported that the studied system may perform either a chaotic motion or a quasiperiodic one according to the damping magnitude beside the periodic solution. Yamamoto et al. [7,8,9] studied the motion bifurcation and the corresponding dynamical behaviors of a Jeffcott rotor model having cubic nonlinear stiffness coefficients at $\frac{1}{2}-$ and $\frac{1}{3}-$ order subharmonic resonance case. Ishida et al. [10] studied the nonstationary oscillation of a Jeffcott system having nonlinear stiffness coefficients when subjected to acceleration through the first critical speed. In addition, the dynamical behaviors of the Jeffcott rotor with nonlinear spring characteristics have been investigated when the angular speed is one, two, and three times the rotor critical speed in the case of 1:1 internal resonance [11], where the authors reported the complex dynamics of the system at the case of the combined resonance condition. Cveticanin [12] analyzed the free vibration of a rotor system having cubic nonlinear restoring force. where the obtained results showed that the system may perform circular motion or vibrate along a straight line depending on the initial position and velocity. The horizontally suspend rotor with nonlinear spring properties has been studied by Yabuno et al. [13]. The authors demonstrated that the considered rotor system is governed by two coupled second-order differential equations comprising both cubic and quadratic nonlinear terms. They utilized the normal form analysis to prove that the system exhibits either forward or backward whirling depending on the rotor angular speed. On the other hand, the propagation of the cracks over the shaft surfaces due to either concentration of the stresses or the material imperfections may cause undesired chaotic motion for the rotating machines [14, 15]. In addition, the rub-impact forces that occur between the rotor and the stator parts are one of the main destruction reasons for the machine structure [16,17,18,19,20,21]. The rub-impact occurs when the lateral vibration amplitude exceeds the air-gap size between the rotors and their housing. However, the main source of these undesired lateral vibrations is the imbalance [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21], the shaft asymmetry [22, 23], or both.

Accordingly, many research articles have been dedicated to suppressing or at least mitigating these destructive oscillations in rotating machinery either by active or passive control strategies [24,25,26,27,28]. Ishida and Inoue [24] introduced a passive vibration absorber to mitigate the unwanted vibrations of a rotor system having a nonlinear restoring force. The authors used four electromagnetic poles to couple the rotor system to the designed absorber, where the authors have succeeded to reduce the rotor lateral vibrations to a small vibration level as well as eliminating the catastrophic bifurcation. Ji et al. [25], and Xiu-yan and Wei-hua [26] applied two different time-delayed active control techniques to eliminate the rotor unwanted vibrations that arise due to the shaft imbalance. In addition, Saeed et al. [27, 28] introduced two different active control techniques to eliminate the rub-impact impact force between the Jeffcott rotor and stator using 4-pole as active actutor.

The nonlinear dynamics for different configurations of the electromagnetic actuators (i.e., 6-pole [29], 8-pole [30,31,32], 12-pole [33], and 16-pole [34,35,36]) have been extensively investigated with different control techniques, but they have not been applied as active actuators before to suppress the nonlinear oscillation of the rotating machinery. Moreover, the 4-pole magnetic actuator only has been applied extensively with different control algorithms as an active actuator to mitigate the undesired nonlinear vibrations of the Jeffcott rotor systems. However, the 8-pole magnetic actuator has many advantages over the 4-pole system such as better suspension characteristics and high dynamic stiffness coefficients.

Accordingly, the 8-pole active magnetic bearings system with a novel PIRC-control algorithm is integrated as a single unit to suppress the undesired lateral vibration and eliminate the catastrophic bifurcation of a vertically suspend nonlinear Jeffcott rotor system for the first time within this article. Based on the introduced control strategy, the system mathematical model is obtained as a discontinuous two-degree-of-freedom dynamical system coupled linearly to two first-order differential equations. The system mathematical model is analyzed both analytically and numerically. The obtained results illustrated that the PIRC-control algorithm can mitigate the nonlinear vibration and eliminate the catastrophic bifurcations of the rotor system when the control gains are designed optimally. Furthermore, the system dynamics are explored numerically when the rub-impact force is unavoidable. The acquired results reveal that the system may oscillate either with a full-annular rub or partial rub-impact mode according to the impact stiffness and the dynamic friction coefficients.

This article is organized such that Sect. 2 is dedicated to derive the whole system mathematical model. Sect. 3 is intended to explore the system dynamics when the rub-impact force between the rotor and stator is neglected, while in Sect. 4 the nonlinear dynamics of the controlled system are simulated when the rub-impact force between the rotor and stator is considered. Finally, the main obtained results are concluded in Sect. 5.

2 Equations of motion

2.1 Jeffcott-rotor system

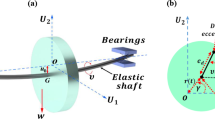
The equations of motion that govern the nonlinear lateral vibrations of the considered Jeffcott-rotor system shown in Fig. 1 can be expressed as follows [13, 24, 37]:

$$m\ddot{x}(t) + c\dot{x}(t) + F_{RX} = m\,f\omega^{2} \cos (\omega t)$$

(1)

$$m\ddot{y}(t) + c\dot{y}(t) + F_{RY} = m\,f\omega^{2} \sin (\omega t)$$

(2)

where $m$ is the mass (in $kilogram$) of the rotating disc, $c$ represents the linear damping parameter in $Newton.second/meter$, ${F}_{RX}$ and ${F}_{RY}$ denote the restoring forces (in $Newton$) of the shaft carrying the disc in $X$ and $Y$ directions, respectively, $f$ denote the eccentricity (in $meter$) of the rotating disc, $\omega$ is the angular speed (in $secon{d}^{-1}$) of the Jeffcott-rotor system, and $t$ represents the time variable (in $second$). According to Refs. [13, 24]. It is considered that the Jeffcott-rotor restoring force ${F}_{R}$ is a cubic nonlinear function of the radial displacement ($R=\overline{OC }$) of the rotating disc away from the origin $O$ as shown in Fig. 1b. accordingly, ${F}_{R}$ can be expressed as follows:

$$F_{R} = k_{l} R(t) + k_{n} R^{3} (t),\;R(t) = \sqrt {x^{2} (t) + y^{2} (t)}$$

(3)

where ${k}_{L}$ denote the shaft linear stiffness coefficient (in $Newton/meter$), and ${k}_{N}$ represents the nonlinear stiffness coefficient of the shaft (in $Newton/{meter}^{3}$). Based on Eq. (3), ${F}_{R}$ can be resolved into its normal components in $X$ and $Y$ directions (i.e., ${F}_{RX}$ and ${F}_{RY}$) as follows:

$$F_{RX} = \left[ {k_{L} R + k_{N} R^{3} } \right]cos(\beta ) = k_{L} x(t) + k_{N} \left[ {x^{3} (t) + x(t)y^{2} (t)} \right]$$

(4)

$$F_{RY} = \left[ {k_{L} R + k_{N} R^{3} } \right]\sin (\beta ) = k_{L} y(t) + k_{N} \left[ {y^{3} (t) + x^{2} (t)y(t)} \right]$$

(5)

Fig. 1

Schematic diagram of a vertically supported Jeffcott system with nonlinear restoring forces

Inserting Eqs. (4) and (5) into Eqs. (1) and (2), yields

$$m\ddot{x}(t) + c\dot{x}(t) + k_{L} x(t) + k_{N} \left( {x^{3} (t) + x(t)y^{2} (t)} \right) = mf\omega^{2} \cos (\omega t)$$

(6)

$$m\ddot{y}(t) + c\dot{y}(t) + k_{L} y(t) + k_{N} \left( {y^{3} (t) + x^{2} (t)y(t)} \right) = mf\omega^{2} \sin (\omega t)$$

(7)

To control the undesired nonlinear oscillations $x(t)$ and $y(t)$ of the studied nonlinear model given by Eqs. (6) and (7), It is proposed to control these lateral vibrations utilizing both the Proportional Integral Resonant Controller (PIRC) that integrated to the rotor system via 8-pole magnetic actuator as shown in Fig. 2. The suggested control strategy will apply the control forces ${F}_{11}$ and ${F}_{21}$ on the rotor system in $X$ and $Y$ directions, respectively, which will be obtained in Sect. 2.2. In addition, if the applied controller fails to prevent the rub-impact force between the rotor and the 8-pole housing an additional force ${F}_{12}$ and ${F}_{22}$ will be developed on the rotor-housing interface. Accordingly, the equations of motion of the controlled Jeffcott-rotor system should be modified to:

$$m\ddot{x}(t) + c\dot{x}(t) + k_{L} x(t) + k_{N} \left( {x^{3} (t) + x(t)y^{2} (t)} \right) = mf\omega^{2} \cos (\omega t) + F_{11} + F_{12} ,$$

(8)

$$m\ddot{y}(t) + c\dot{y}(t) + k_{L} y(t) + k_{N} \left( {y^{3} (t) + x^{2} (t)y(t)} \right) = mf\omega^{2} \sin (\omega t) + F_{21} + F_{22} .$$

(9)

Fig. 2

Jeffcott rotor system controlled via 8-pole magnetic actuator and PIRC controller: a the rotating disc at its nominal position with air-gap size ${s}_{0}$, and b the rotating disc with small displacements $x\left(t\right)$ and $y(t)$ and actual air-gap sizes ${H}_{j}, (j=\mathrm{1,2},\dots ,8)$

where ${F}_{11}$ and ${F}_{21}$ represent the resultant control force components in $X$ and $Y$ directions that will be applied by the proposed $PIRC$ controller via the 8-pole magnetic actuator, while ${F}_{12}$ and ${F}_{22}$ denote the normal components of the rub-impact forces that develop between the rotor and the pole-housing interface when the $PIRC$ fails to mitigate the rotor oscillation as explained in Sects. 2.2 and 2.3.

2.2 Control forces ${{\varvec{F}}}_{11}$ and ${{\varvec{F}}}_{21}$

According to Fig. 2a, the applied electromagnetic attractive force ${f}_{j} (j=\mathrm{1,2},\dots ,8)$ of each pole on the Jeffcott-rotor system can be computed relying on the electromagnetic theory as follows [38]:

$$f_{j} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\frac{{I_{j}^{2} }}{{H_{j}^{2} }},\;j = 1,2, \ldots 8$$

(10)

where ${\mu }_{0}$ is the air-gab magnetic permeability, $n$ the winding number of each coil of the eight poles, $Acos(\psi )$ is the effective cross-sectional area of the electromagnetic pole, ${I}_{j}$ is the ${j}^{th}$ pole electrical current, and ${H}_{j}$ is the effective air-gap size. Based on the geometry of Fig. 2b, for the small lateral displacements $x(t)$ and $y\left(t\right)$ of the rotor system in $X$ and $Y$ directions, the effective air-gap size can be expressed as follows

$$\left. \begin{gathered} H_{j} = s_{0} \mp x,\quad j = 1,5 \hfill \\ H_{j} = s_{0} \mp y,\quad j = 3,7 \hfill \\ H_{j} = s_{0} \mp x\cos (\alpha ) \mp y\cos (\alpha ),\quad j = 2,6 \hfill \\ H_{j} = s_{0} \pm x\cos (\alpha ) \mp y\,\cos (\alpha )\quad j = 4,8 \hfill \\ \end{gathered} \right\}$$

(11)

Based on Eq. (10), the control forces ${f}_{j} (j=\mathrm{1,2},\dots ,8)$ can be adjusted to control the undesired lateral oscillation of the Jeffcott rotor via adjusting the electrical current ${I}_{j}$ of the eight poles according to predefined control law. Within this article, the Proportional Integral Resonant Controller (PIRC) is suggested to generate the control currents ${I}_{j} (j=\mathrm{1,2},\dots ,8)$ based on the rotor states $x(t)$ and $y(t)$, and the controller states $u(t)$ and $v(t)$ as follows:

$$\left. \begin{aligned} I_{1} =\, I_{0} - k_{1} x + k_{2} u, \\ I_{2} =\, I_{0} - k_{1} x\,\cos (\alpha ) + k_{2} u\cos (\alpha ) - k_{3} y\cos (\alpha ) + k_{4} v\cos (\alpha ), \\ I_{3} =\, I_{0} - k_{3} y + k_{4} v, \\ I_{4} =\, I_{0} + k_{1} x\,\cos (\alpha ) - k_{2} u\cos (\alpha ) - k_{3} y\cos (\alpha ) + k_{4} v\cos (\alpha ), \\ I_{5} =\, I_{0} + k_{1} x - k_{2} u, \\ I_{6} =\, I_{0} + k_{1} x\,\cos (\alpha ) - k_{2} u\cos (\alpha ) + k_{3} y\cos (\alpha ) - k_{4} v\cos (\alpha ), \\ I_{7} =\, I_{0} + k_{3} y - k_{4} v, \\ I_{8} =\, I_{0} - k_{1} x\,\cos (\alpha ) + k_{2} u\cos (\alpha ) + k_{3} y\cos (\alpha ) - k_{4} v\cos (\alpha ). \\ \end{aligned} \right\}$$

(12)

where the equations of motion of the proposed controller are given as follows [39]:

$$\dot{u} + \rho_{1} u = \gamma_{1} x,$$

(13)

$$\dot{v} + \rho_{2} v = \gamma_{2} y.$$

(14)

where $\dot{u}, \dot{v}$ denote the velocities of the IRC- controller, $u, v$ are the displacements of the IRC- controller, ${\rho }_{1}, {\rho }_{2}$ are constants represent the internal feedback gains, and ${\gamma }_{1}, {\gamma }_{2}$ denote the feedback control gains. Now, substituting Eqs. (11) and (12) into Eq. (10), we have

$$f_{1} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\frac{{I_{1}^{2} }}{{H_{1}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\left( {\frac{{I_{0} - k_{1} x + k_{2} u}}{{s_{0} - x}}} \right)^{2} ,$$

(15)

$$f_{2} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\frac{{I_{2}^{2} }}{{H_{2}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\left( {\frac{{I_{0} - k_{1} x\,\cos (\alpha ) + k_{2} u\cos (\alpha ) - k_{3} y\cos (\alpha ) + k_{4} v\cos (\alpha )}}{{s_{0} - x\,\cos (\alpha ) - y\cos (\alpha )}}} \right)^{2} ,$$

(16)

$$f_{3} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\frac{{I_{3}^{2} }}{{H_{3}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A{\text{cos}}(\psi )\left( {\frac{{I_{0} - k_{3} y + k_{4} v}}{{s_{0} - y}}} \right)^{2} ,$$

(17)

$$f_{4} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\frac{{I_{4}^{2} }}{{H_{4}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left( {\frac{{I_{0} + k_{1} x\,\cos (\alpha ) - k_{2} u\cos (\alpha ) - k_{3} y\cos (\alpha ) + k_{4} v\cos (\alpha )}}{{s_{0} + x\,\cos (\alpha ) - y\,\cos (\alpha )\,}}} \right)^{2} ,$$

(18)

$$f_{5} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\frac{{I_{5}^{2} }}{{H_{5}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left( {\frac{{I_{0} + k_{1} x - k_{2} u}}{{s_{0} + x}}} \right)^{2} ,$$

(19)

$$f_{6} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\frac{{I_{6}^{2} }}{{H_{6}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left( {\frac{{I_{0} + k_{1} x\,\cos (\alpha ) - k_{2} u\cos (\alpha ) + k_{3} y\cos (\alpha ) - k_{4} v\cos (\alpha )}}{{s_{0} + x\,\cos (\alpha ) + y\cos (\alpha )}}} \right)^{2} ,$$

(20)

$$f_{7} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\frac{{I_{7}^{2} }}{{H_{7}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left( {\frac{{I_{0} + k_{3} y - k_{4} v}}{{s_{0} + y}}} \right)^{2} ,$$

(21)

$$f_{8} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\frac{{I_{8}^{2} }}{{H_{8}^{2} }} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left( {\frac{{I_{0} - k_{1} x\,\cos (\alpha ) + k_{2} u\cos (\alpha ) + k_{3} y\cos (\alpha ) - k_{4} v\cos (\alpha )}}{{s_{0} - x\,\cos (\alpha ) + y\,\cos (\alpha )}}} \right)^{2} .$$

(22)

According to the system structure shown in Fig. (2), one can express the resultant control forces ${F}_{11}$ and ${F}_{21}$ in $X$ and $Y$, respectively as follows:

$$F_{11} = f_{1} - f_{5} + (f_{2} + f_{8} - f_{4} - f_{6} )\cos (\alpha ),$$

(23)

$$F_{21} = f_{3} - f_{7} + (f_{2} + f_{4} - f_{6} - f_{8} )\cos (\alpha ).$$

(24)

Substituting Eqs. (15) to (22) into Eqs. (23) and (24), with expanding the resulting equations using Maclurin series up to third-order approximation, yields

$$\begin{aligned} F_{11} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\Big(\Big(\frac{{4I_{0}^{2} }}{{s_{0}^{3} }} - \frac{{8I_{0} k_{1} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{8I_{0}^{2} \cos^{2} (\alpha )}}{{s_{0}^{3} }} - \frac{{4I_{0} k_{1} }}{{s_{0}^{2} }}\Big)x + \Big(\frac{{8I_{0} k_{2} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{4I_{0} k_{2} }}{{s_{0}^{2} }}\Big)u \\ \; + \Big(\frac{{8k_{3}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{48I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }} + \frac{{16k_{1} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }} - \frac{{48I_{0} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{24I_{0} k_{1} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)xy^{2} \\ \; + \Big(\frac{{8k_{2}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{4k_{2}^{2} }}{{s_{0}^{3} }}\Big)xu^{2} + \frac{{8k_{4}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}xv^{2} + \Big(\frac{{12I_{0} k_{2} }}{{s_{0}^{4} }} - \frac{{8k_{1} k_{2} }}{{s_{0}^{3} }} - \frac{{16k_{1} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} \\ \; + \frac{{24I_{0} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)x^{2} u + \Big(\frac{{24I_{0} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{2} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)y^{2} u +\Big (\frac{{48I_{0} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{3} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }} \\ \; - \frac{{16k_{1} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)xyv + \frac{{16k_{2} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}yuv + \Big(\frac{{4k_{1}^{2} }}{{s_{0}^{3} }} + \frac{{8I_{0}^{2} }}{{s_{0}^{5} }} - \frac{{24I_{0} k_{1} \cos^{4} (\alpha )}}{{s_{0}^{4} }} + \frac{{16I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }} \\ \; - \frac{{12I_{0} k_{1} }}{{s_{0}^{4} }} + \frac{{8k_{1}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)x^{3} \Big), \\ \end{aligned}$$

(25)

$$\begin{aligned} F_{21} = \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\Big(\Big(\frac{{4I_{0}^{2} }}{{s_{0}^{3} }} - \frac{{4I_{0} k_{3} }}{{s_{0}^{2} }} - \frac{{8I_{0} k_{3} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{8I_{0}^{2} \cos^{2} (\alpha )}}{{s_{0}^{3} }}\Big)y +\Big(\frac{{8I_{0} k_{4} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{4I_{0} k_{4} }}{{s_{0}^{2} }}\Big)v \\ \; + \Big(\frac{{16k_{1} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }} - \frac{{24I_{0} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{48I_{0} k_{1} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)x^{2} y + \Big(\frac{{8k_{1}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{48I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }}\Big)x^{2} y \\ \; +\Big (\frac{{24I_{0} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{1} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)x^{2} v + \frac{{8k_{2}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}yu^{2} + \Big(\frac{{12I_{0} k_{4} }}{{s_{0}^{4} }} - \frac{{8k_{3} k_{4} }}{{s_{0}^{3} }} - \frac{{16k_{3} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }} \\ \; + \frac{{24I_{0} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)y^{2} v + \Big(\frac{{8k_{4}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{4k_{4}^{2} }}{{s_{0}^{3} }}\Big)yv^{2} + \Big(\frac{{48I_{0} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{2} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }} \\ \; - \frac{{16k_{1} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)xyu + \frac{{16k_{2} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}xuv + \Big(\frac{{16I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }} + \frac{{8k_{3}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} - \frac{{12I_{0} k_{3} }}{{s_{0}^{4} }} \\ \; - \frac{{24I_{0} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{4} }} + \frac{{4k_{3}^{2} }}{{s_{0}^{3} }} + \frac{{8I_{0}^{2} }}{{s_{0}^{5} }}\Big)\Big)y^{3} . \\ \end{aligned}$$

(26)

2.3 Rub-impact forces ${{\varvec{F}}}_{12}$ and ${{\varvec{F}}}_{22}$

When the control forces ${F}_{11}$ and ${F}_{21}$ fail to suspend the Jeffcott rotor system in its hovering position, the rotating shaft may contact the magnetic poles housing that is resulting in the development of both the normal impact and the tangent forces (i.e., ${F}_{N}$ and ${F}_{T}$) between the rotor–stator interface as shown in Fig. 3. Therefore, when the radial oscillation amplitude $R\left(t\right)=\sqrt{{x}^{2}\left(t\right)+{y}^{2}(t)}$ of the rotor system exceeds the nominal air-gap size ${s}_{0}$ (i.e., if $R\left(t\right)\ge {s}_{0}$), the forces ${F}_{N}$ and ${F}_{T}$ appears between the rotor–stator interface, otherwise, they become zeros. Accordingly, using the unit-step function $U$, one can express the forces ${F}_{N}$ and ${F}_{T}$ as follows [27, 28]:

$$F_{N} (t) = k_{h} (R(t) - s_{0} )\,U(R(t) - s_{0} ),$$

(27)

$$F_{T} (t) = \mu_{d} F_{N} (t) = \mu_{d} k_{H} (R(t) - s_{0} )U(R(t) - s_{0} ).$$

(28)

Fig. 3

Jeffcott rotor system with rub-impact force between the rotating disc and the 8-pole housing

where ${k}_{h}$ is the linear stiffness coefficient of the pole housing, ${\mu }_{d}$ denote the dynamic frictional coefficient between the rotating disc and the inner surface of the pole housing, and $R\left(t\right)-{s}_{0}>0$ represents the displacement of the pole housing away from its nominal position due to the impact of the rotor system. Based on the geometry of Fig. 3, one can resolve the forces ${F}_{N}$ and ${F}_{T}$ into their horizontal and vertical component (i.e., ${F}_{12}$ and ${F}_{22}$) using the relations $\mathrm{cos}\left(\omega t\right)=\frac{x}{R}$ and $\mathrm{sin}\left(\omega t\right)=\frac{y}{R}$ as follows:

$$F_{12} = F_{T} \sin (\omega t) - F_{N} \cos (\omega t) = \frac{{k_{h} }}{R}(R - s_{0} )(\mu_{f} y - x)U(R - s_{0} ),$$

(29)

$$F_{22} = - F_{T} \cos (\omega t) - F_{N} \sin (\omega t) = - \frac{{k_{h} }}{R}(R - s_{0} )(\mu_{f} x + y)\,U(R - s_{0} ).$$

(30)

2.4 Controlled Jeffcott-rotor system

Inserting Eqs. (25), (26), (29), and (30) into Eqs. (8) and (9), one can obtain the following discontinuous differential equations that govern the nonlinear dynamics of the controlled Jeffcott system as follows:

$$\begin{aligned} m\ddot{x}(t) + & c\dot{x}(t) + k_{L} x(t) + k_{N} \left( {x^{3} (t) + x(t)y^{2} (t)} \right) = mf\omega^{2} \cos (\omega t) \\ & \; + \frac{1}{4}\mu_{0} n^{2} A\cos (\psi )\left[ {\Big(\frac{{4I_{0}^{2} }}{{s_{0}^{3} }}} \right. - \frac{{8I_{0} k_{1} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{8I_{0}^{2} \cos^{2} (\alpha )}}{{s_{0}^{3} }} - \frac{{4I_{0} k_{1} }}{{s_{0}^{2} }}\Big)x \\ & \; + \Big(\frac{{8I_{0} k_{2} \cos^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{4I_{0} k_{2} }}{{s_{0}^{2} }}\Big)u + \Big(\frac{{8k_{3}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{48I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }} + \frac{{16k_{1} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }} \\ & \; - \frac{{48I_{0} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{24I_{0} k_{1} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)xy^{2} + \Big(\frac{{8k_{2}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{4k_{2}^{2} }}{{s_{0}^{3} }}\Big)xu^{2} + \frac{{8k_{4}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}xv^{2} \\ & \; + \Big(\frac{{12I_{0} k_{2} }}{{s_{0}^{4} }} - \frac{{8k_{1} k_{2} }}{{s_{0}^{3} }} - \frac{{16k_{1} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{24I_{0} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{4} }}\Big)x^{2} u + \Big(\frac{{24I_{0} k_{2} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{2} k_{3} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)y^{2} u \\ & \; + \Big(\frac{{48I_{0} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{3} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }} - \frac{{16k_{1} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)xyv + \frac{{16k_{2} k_{4} \cos^{4} (\alpha )}}{{s_{0}^{3} }}yuv \\ & \; +\Big (\frac{{4k_{1}^{2} }}{{s_{0}^{3} }} + \frac{{8I_{0}^{2} }}{{s_{0}^{5} }} - \frac{{24I_{0} k_{1} \cos^{4} (\alpha )}}{{s_{0}^{4} }} + \frac{{16I_{0}^{2} \cos^{4} (\alpha )}}{{s_{0}^{5} }} - \frac{{12I_{0} k_{1} }}{{s_{0}^{4} }}\left. { + \frac{{8k_{1}^{2} \cos^{4} (\alpha )}}{{s_{0}^{3} }}\Big)x^{3} } \right] \\ & \; + \frac{{k_{h} }}{R}(R - s_{0} )(\mu_{f} y - x)U(R - s_{0} ), \\ \end{aligned}$$

(31)

$$\begin{gathered} m\ddot{y}(t) + c\dot{y}(t) + k_{L} y(t) + k_{N} \left( {y^{3} (t) + x^{2} (t)y(t)} \right) = mf\omega ^{2} \sin (\omega t) + \frac{1}{4}\mu _{0} n^{2} A\cos (\psi )\left[ {\Big(\frac{{4I_{0}^{2} }}{{s_{0}^{3} }}} \right. \hfill \\ - \frac{{4I_{0} k_{3} }}{{s_{0}^{2} }} - \frac{{8I_{0} k_{3} \cos ^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{8I_{0}^{2} \cos ^{2} (\alpha )}}{{s_{0}^{3} }}\Big)y + \Big(\frac{{8I_{0} k_{4} \cos ^{2} (\alpha )}}{{s_{0}^{2} }} + \frac{{4I_{0} k_{4} }}{{s_{0}^{2} }}\Big)v +\Big (\frac{{16k_{1} k_{3} \cos ^{4} (\alpha )}}{{s_{0}^{3} }} \hfill \\ - \frac{{24I_{0} k_{3} \cos ^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{48I_{0} k_{1} \cos ^{4} (\alpha )}}{{s_{0}^{4} }}\Big)x^{2} y +\Big(\frac{{8k_{1}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{48I_{0}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{5} }}\Big)x^{2} y + \Big(\frac{{24I_{0} k_{4} \cos ^{4} (\alpha )}}{{s_{0}^{4} }} \hfill \\ - \frac{{16k_{1} k_{4} \cos ^{4} (\alpha )}}{{s_{0}^{3} }}\Big)x^{2} v + \frac{{8k_{2}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{3} }}yu^{2} + \Big(\frac{{12I_{0} k_{4} }}{{s_{0}^{4} }} - \frac{{8k_{3} k_{4} }}{{s_{0}^{3} }} - \frac{{16k_{3} k_{4} \cos ^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{24I_{0} k_{4} \cos ^{4} (\alpha )}}{{s_{0}^{4} }}\Big)y^{2} v \hfill \\ + \Big(\frac{{8k_{4}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{3} }} + \frac{{4k_{4}^{2} }}{{s_{0}^{3} }}\Big)yv^{2} + \Big(\frac{{48I_{0} k_{2} \cos ^{4} (\alpha )}}{{s_{0}^{4} }} - \frac{{16k_{2} k_{3} \cos ^{4} (\alpha )}}{{s_{0}^{3} }} - \frac{{16k_{1} k_{2} \cos ^{4} (\alpha )}}{{s_{0}^{3} }}\Big)xyu \hfill \\ + \frac{{16k_{2} k_{4} \cos ^{4} (\alpha )}}{{s_{0}^{3} }}xuv + \Big(\frac{{4k_{3}^{2} }}{{s_{0}^{3} }} + \frac{{8I_{0}^{2} }}{{s_{0}^{5} }} - \frac{{24I_{0} k_{3} \cos ^{4} (\alpha )}}{{s_{0}^{4} }} + \frac{{16I_{0}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{5} }} - \frac{{12I_{0} k_{3} }}{{s_{0}^{4} }} \hfill \\ \left. { + \frac{{8k_{3}^{2} \cos ^{4} (\alpha )}}{{s_{0}^{3} }}\Big)y^{3} } \right] - \frac{{k_{h} }}{R}(R - s_{0} )(\mu _{f} x + y)U(R - s_{0} ) \hfill \\ \end{gathered}$$

(32)

where $u$ and $v$ are given by Eqs. (13) and (14). Introducing the dimensionless quantities${q}_{1}=\frac{x}{{s}_{0}}, {q}_{2}=\frac{y}{{s}_{0}}, {q}_{3}=\frac{u}{{s}_{0}}, {q}_{4}=\frac{v}{{s}_{0}}, r=\sqrt{{q}_{1}^{2}+{q}_{2}^{2}}=\sqrt{{\left(\frac{x}{{s}_{0}}\right)}^{2}+{\left(\frac{y}{{s}_{0}}\right)}^{2}}=\frac{R}{{s}_{0}}, \tau ={\omega }_{n}t, {\dot{q}}_{1}=\dot{\frac{x}{{\omega }_{n}{s}_{0}}}, {\dot{q}}_{2}=\dot{\frac{y}{{\omega }_{n}{s}_{0}}}, {\dot{q}}_{3}=\dot{\frac{u}{{\omega }_{n}{s}_{0}}}, {\dot{q}}_{4}=\dot{\frac{v}{{\omega }_{n}{s}_{0}}}, {\ddot{q}}_{1}=\frac{\ddot{x}}{{\omega }_{n}^{2}{s}_{0}}, {\ddot{q}}_{2}=\frac{\ddot{y}}{{\omega }_{n}^{2}{s}_{0}}, \mu =\frac{c}{m{\omega }_{n}}, {\delta }_{1}=\frac{{s}_{0}}{{I}_{0}}{k}_{1}, {\delta }_{2}=\frac{{s}_{0}}{{I}_{0}}{k}_{2}, {\delta }_{3}=\frac{{s}_{0}}{{I}_{0}}{k}_{3}, {\delta }_{4}=\frac{{s}_{0}}{{I}_{0}}{k}_{4} , \lambda =\frac{{k}_{N}}{m{\omega }_{n}^{2}}, k=\frac{{k}_{h}}{m{\omega }_{n}^{2}}, E=\frac{f}{{s}_{0}},\Omega =\frac{\omega }{{\omega }_{n}} , {\lambda }_{1}=\frac{{\rho }_{1}}{{\omega }_{n}}, {\lambda }_{2}=\frac{{\rho }_{2}}{{\omega }_{n}}, {\eta }_{1}=\frac{{\gamma }_{1}}{{\omega }_{n}}, {\eta }_{2}=\frac{{\gamma }_{2}}{{\omega }_{n}}$, and ${\omega }_{n}=\sqrt{\frac{{k}_{L}}{m}}=\sqrt{\frac{\mu {I}_{0}^{2}{n}^{2}Acos(\theta )}{4m{s}_{0}^{3}}}$ into Eqs. (13), (14), (31), and (32), one can derive the following dimensionless equations of motion of the whole system:

$$\begin{aligned} \frac{{d^{2} q_{1} }}{{d\tau^{2} }} + & \mu \frac{{dq_{1} }}{d\tau } + q_{1} + \lambda (q_{1}^{3} + q_{1} q_{2}^{2} ) = E\Omega^{2} \cos (\Omega \tau ) + \rho_{10} q_{1} + \rho_{11} q_{3} + \rho_{12} q_{1} q_{2}^{2} + \rho_{13} q_{1} q_{3}^{2} + \rho_{14} q_{1} q_{4}^{2} \\ & + \rho_{15} q_{1}^{2} q_{3} + \rho_{16} q_{2}^{2} q_{3} + \rho_{17} q_{1} q_{2} q_{4} + \rho_{18} q_{2} q_{3} q_{4} + \rho_{19} q_{1}^{3} \\ & + \frac{k}{r}(r - 1)(\mu_{f} q_{2} - q_{1} )U(r - 1), \\ \end{aligned}$$

(33)

$$\begin{aligned} \frac{{d^{2} q_{2} }}{{d\tau^{2} }} +& \mu \frac{{dq_{2} }}{d\tau } + q_{2} + \lambda (q_{2}^{3} + q_{2} q_{1}^{2} ) = E\Omega^{2} \sin (\Omega \tau ) + \rho_{20} q_{2} + \rho_{21} q_{4} + \rho_{22} q_{2} q_{1}^{2} + \rho_{23} q_{2} q_{4}^{2} + \rho_{24} q_{2} q_{3}^{2} \\ & \; + \rho_{25} q_{2}^{2} q_{4} + \rho_{26} q_{1}^{2} q_{4} + \rho_{27} q_{1} q_{2} q_{3} + \rho_{28} q_{1} q_{3} q_{4} + \rho_{29} q_{2}^{3} \\ & \; - \frac{k}{r}(r - 1)(\mu_{f} q_{1} + q_{2} )U(r - 1), \\ \end{aligned}$$

(34)

$$\frac{{dq_{3} }}{d\tau } + \lambda_{1} \,q_{3} = \eta_{1} q_{1} ,$$

(35)

$$\frac{{dq_{4} }}{d\tau } + \lambda_{2} \,q_{4} = \eta_{2} q_{2} .$$

(36)

Equations (33) and (34) represent the equation of motion of the controlled Jeffcott system, while Eqs. (35) and (36) are the equations of motion of the coupled IRC controller. The coefficients of Eqs. (33) to (36) are given in Appendix A.

3 Continuous dynamical system

It is clear from Eqs. (33) and (34) that the controlled Jeffcott system is governed by a discontinues nonlinear dynamical system due to including the rub-impact force between the rotor and the 8-pole housing, where no straightforward method to investigate this system analytically. Therefore, Eqs. (33) to (36) are analyzed within this work in two stages. In the first stage, Eqs. (33) to (36) are analyzed as a continuous nonlinear dynamical system via neglecting the rub-impact force between the rotor and the poles housing when letting $k=0$ to determine the conditions at which the rub-impact can occur. Secondly, the whole system model is analyzed numerically as a discontinuous nonlinear system to explore the rotor dynamics when the rub-impact force between the rotor and stator surely occurred.

3.1 Analytical solution

To obtain an analytical solution to the nonlinear dynamical system given by Eqs. (33) to (36) when the rub-impact force between the rotor and stator is neglected (i.e., when $+\frac{k}{r}\left(r-1\right)\left({\mu }_{f}{q}_{2}-{q}_{1}\right)U\left(r-1\right)=-\frac{k}{r}\left(r-1\right)\left({\mu }_{f}{q}_{1}+{q}_{2}\right)U\left(r-1\right)=0$), an approximate solution to Eqs. (33)- (36) can be derived using perturbation methods as follows [40, 41]:

$$q_{1} (\tau ,\varepsilon ) = q_{10} (T_{0} ,T_{1} ) + \varepsilon q_{11} (T_{0} ,T_{1} ),$$

(37)

$$q_{2} (\tau ,\varepsilon ) = q_{20} (T_{0} ,T_{1} ) + \varepsilon q_{21} (T_{0} ,T_{1} ),$$

(38)

$$q_{3} (\tau ,\varepsilon ) = \varepsilon q_{30} (T_{0} ,T_{1} ) + \varepsilon^{2} q_{31} (T_{0} ,T_{1} ),$$

(39)

$$q_{4} (\tau ,\varepsilon ) = \varepsilon q_{40} (T_{0} ,T_{1} ) + \varepsilon^{2} q_{41} (T_{0} ,T_{1} ).$$

(40)

where $\varepsilon \ll 1$ is a book-keeping parameter, ${T}_{0}=\tau$, and ${T}_{1}=\varepsilon \tau$ are the fast and slow time scales, respectively. Using the chain role for differentiation, one can express the ordinary derivatives $\frac{d}{d\tau }$ and $\frac{{d}^{2}}{d{\tau }^{2}}$ in term of ${T}_{0}$ and ${T}_{1}$ as follows:

$$\frac{d}{d\tau } = D_{0} + \varepsilon D_{1} {, }\frac{{d^{2} }}{{d\tau^{2} }} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} , \quad D_{j} = \frac{\partial }{{\partial T_{j} }},\quad j = 0,1$$

(41)

To start the solution procedure, the system parameters should be scaled as follows [40, 41].

$$\mu = \varepsilon \tilde{\mu },\lambda = \varepsilon \tilde{\lambda },E = \varepsilon \tilde{E},\eta_{1} = \varepsilon \tilde{\eta }_{1} ,\eta_{2} = \varepsilon \tilde{\eta }_{2} ,\rho_{jk} = \varepsilon \tilde{\rho }_{jk} ,j = 1,2,k = 0,1,...,9.$$

(42)

Substituting Eqs. (37) to (42) into Eqs. (33) to (36) considering that $k=0,$ one can obtain the following set of differential equations after comparing the coefficients of the same power of $\varepsilon$:

O (${\varepsilon }^{0}$):

$$(D_{0}^{2} + 1)q_{10} = 0,$$

(43)

$$(D_{0}^{2} + 1)q_{20} = 0,$$

(44)

O ($\varepsilon$):

$$\left( {D_{0} + \lambda_{1} } \right)q_{30} = \tilde{\eta }_{1} q_{10} ,$$

(45)

$$\left( {D_{0} + \lambda_{2} } \right)q_{40} = \tilde{\eta }_{2} q_{20} ,$$

(46)

$$\begin{aligned} (D_{0}^{2} + 1)q_{11} = & - 2D_{0} D_{1} q_{10} - \tilde{\mu }D_{0} q_{10} - \tilde{\lambda }q_{10}^{3} - \tilde{\lambda }q_{10} q_{20}^{2} + \tilde{\rho }_{10} q_{10} + \tilde{\rho }_{11} q_{30} + \tilde{\rho }_{12} q_{10} q_{20}^{2} + \tilde{\rho }_{13} q_{10} q_{30}^{2} \\ & \; + \tilde{\rho }_{14} q_{10} q_{40}^{2} + \tilde{\rho }_{15} q_{10}^{2} q_{30} + \tilde{\rho }_{16} q_{20}^{2} q_{30} + \tilde{\rho }_{17} q_{10} q_{20} q_{40} + \tilde{\rho }_{18} q_{20} q_{30} q_{40} + \tilde{\rho }_{19} q_{10}^{3} + \tilde{E}\Omega^{2} \cos (\Omega \tau ), \\ \end{aligned}$$

(47)

$$\begin{aligned} (D_{0}^{2} + 1)q_{21} = & - 2D_{0} D_{1} q_{20} - \tilde{\mu }D_{0} q_{20} - \tilde{\lambda }q_{20}^{3} - \tilde{\lambda }q_{20} q_{10}^{2} + \tilde{\rho }_{20} q_{20} + \tilde{\rho }_{21} q_{40} + \tilde{\rho }_{22} q_{20} q_{10}^{2} + \tilde{\rho }_{23} q_{20} q_{40}^{2} \\ & \; + \tilde{\rho }_{24} q_{20} q_{30}^{2} + \tilde{\rho }_{25} q_{20}^{2} q_{40} + \tilde{\rho }_{26} q_{10}^{2} q_{40} + \tilde{\rho }_{27} q_{10} q_{20} q_{30} + \tilde{\rho }_{28} q_{10} q_{30} q_{40} + \tilde{\rho }_{29} q_{20}^{3} + \tilde{E}\Omega^{2} \sin (\Omega \tau ). \\ \end{aligned}$$

(48)

The solution of Eqs. (43) to (46) can be expressed as follows:

$$q_{10} (T_{0} ,T_{1} ) = A(T_{1} )e^{{iT_{0} }} + \overline{A} (T_{1} )e^{{ - iT_{0} }} ,$$

(49)

$$q_{20} (T_{0} ,T_{1} ) = B(T_{1} )e^{{iT_{0} }} + \overline{B} (T_{1} )e^{{ - iT_{0} }} ,$$

(50)

$$q_{30} (T_{0} ,T_{1} ) = \delta_{1} A(T_{1} )e^{{iT_{0} }} + \overline{\delta }_{1} \overline{A} (T_{1} )e^{{ - iT_{0} }} ,$$

(51)

$$q_{40} (T_{0} ,T_{1} ) = \delta_{2} B(T_{1} )e^{{iT_{0} }} + \overline{\delta }_{2} \overline{B} (T_{1} )e^{{ - iT_{0} }} .$$

(52)

where $i=\sqrt{-1}, A({T}_{1})$ and $B({T}_{1})$ are unknown functions that will be defined next, and${\delta }_{1}=\frac{{\lambda }_{1}-i}{{\lambda }_{1}^{2}+1}{\widetilde{\eta }}_{1} , {\delta }_{2}=\frac{{\lambda }_{2}-i}{{\lambda }_{2}^{2}+1}{\widetilde{\eta }}_{2}$. Inserting Eqs. (49) to (52) into Eqs. (47) and (48), yields

$$\begin{gathered} (D_{0}^{2} + 1)q_{11} = [ - i\tilde{\mu }A + \tilde{\rho }_{10} A + \delta_{1} \tilde{\rho }_{11} A - 3\tilde{\lambda }A^{2} \overline{A} - \tilde{\lambda }B^{2} \overline{A} + \tilde{\rho }_{12} B^{2} \overline{A} + 2\overline{\delta }_{1} \delta_{1} \tilde{\rho }_{13} A^{2} \overline{A} + \delta_{1}^{2} \tilde{\rho }_{13} A^{2} \overline{A} \\ + \delta_{2}^{2} \tilde{\rho }_{14} B^{2} \overline{A} + \overline{\delta }_{1} \tilde{\rho }_{15} B^{2} \overline{A} + 2\delta_{1} \tilde{\rho }_{15} B^{2} \overline{A} + \overline{\delta }_{1} \tilde{\rho }_{16} B^{2} \overline{A} + \delta_{2} \tilde{\rho }_{17} B^{2} \overline{A} + \overline{\delta }_{1} \delta_{2} \tilde{\rho }_{18} B^{2} \overline{A} + 3\tilde{\rho }_{19} A^{2} \overline{A} \\ - 2\tilde{\lambda }AB\overline{B} + 2\rho_{12} AB\overline{B} + 2\delta_{2} \overline{\delta }_{2} \rho_{14} AB\overline{B} + 2\delta_{1} \rho_{16} AB\overline{B} + \overline{\delta }_{2} \rho_{17} AB\overline{B} + \delta_{2} \rho_{17} AB\overline{B} \\ + \delta_{1} \overline{\delta }_{2} \tilde{\rho }_{18} AB\overline{B} + \delta_{1} \delta_{2} \tilde{\rho }_{18} AB\overline{B} - 2iD_{1} A]e^{{iT_{0} }} + [ - \tilde{\lambda }A^{3} - \tilde{\lambda }AB^{2} + \tilde{\rho }_{12} AB^{2} + \delta_{1}^{2} \tilde{\rho }_{13} A^{3} \\ + \delta_{2}^{2} \tilde{\rho }_{14} AB^{2} + \delta_{1} \tilde{\rho }_{15} A^{3} + \delta_{1} \tilde{\rho }_{16} AB^{2} + \delta_{2} \tilde{\rho }_{17} AB^{2} + \delta_{1} \delta_{2} \tilde{\rho }_{18} AB^{2} + \tilde{\rho }_{19} A^{3} ]e^{{3iT_{0} }} \\ + \frac{1}{2}\tilde{E}\Omega^{2} e^{{i\Omega T_{0} }} + cc, \\ \end{gathered}$$

(53)

$$\begin{gathered} (D_{0}^{2} + 1)q_{21} = [ - i\tilde{\mu }B + \tilde{\rho }_{20} B + \delta_{2} \tilde{\rho }_{21} B - 2\tilde{\lambda }A\overline{A}B + 2\tilde{\rho }_{22} A\overline{A}B + 2\overline{\delta }_{1} \delta_{1} \tilde{\rho }_{24} A\overline{A}B + 2\delta_{2} \tilde{\rho }_{26} A\overline{A}B \\ + \overline{\delta }_{1} \tilde{\rho }_{27} A\overline{A}B + \delta_{1} \tilde{\rho }_{27} A\overline{A}B + \overline{\delta }_{1} \delta_{2} \tilde{\rho }_{28} A\overline{A}B + \delta_{1} \delta_{2} \tilde{\rho }_{28} A\overline{A}B - \tilde{\lambda }A^{2} \overline{B} - 3\tilde{\lambda }B^{2} \overline{B} + \tilde{\rho }_{22} A^{2} \overline{B} \\ + 2\delta_{2} \overline{\delta }_{2} \tilde{\rho }_{23} B^{2} \overline{B} + \delta_{2}^{2} \tilde{\rho }_{23} B^{2} \overline{B} + \delta_{1}^{2} \tilde{\rho }_{24} A^{2} \overline{B} + \overline{\delta }_{2} \tilde{\rho }_{25} B^{2} \overline{B} + 2\delta_{2} \tilde{\rho }_{25} B^{2} \overline{B} + \overline{\delta }_{2} \tilde{\rho }_{26} A^{2} \overline{B} \\ + \delta_{1} \tilde{\rho }_{27} A^{2} \overline{B} + \delta_{1} \overline{\delta }_{2} \tilde{\rho }_{28} A^{2} \overline{B} + 3\tilde{\rho }_{29} B^{2} \overline{B} - 2iD_{1} B]e^{{iT_{0} }} + [ - \tilde{\lambda }A^{2} B - \tilde{\lambda }B^{3} + \tilde{\rho }_{22} A^{2} B \\ + \delta_{2}^{2} \tilde{\rho }_{23} B^{3} + \delta_{1}^{2} \tilde{\rho }_{24} A^{2} B + \delta_{2} \tilde{\rho }_{25} B^{3} + \delta_{2} \tilde{\rho }_{26} A^{2} B + \delta_{1} \tilde{\rho }_{27} A^{2} B + \delta_{1} \delta_{2} \tilde{\rho }_{28} A^{2} B + \tilde{\rho }_{29} B^{3} ]e^{{3iT_{0} }} \\ - \frac{1}{2}i\tilde{E}\Omega^{2} e^{{i\Omega T_{0} }} + cc. \\ \end{gathered}$$

(54)

where $cc$ refers to the complex conjugate terms. Equations (53) and (54) should have bounded solutions to have a stable controlled system. Accordingly, the small divisor and the coefficients of ${e}^{i{T}_{0}}$ in Eqs. (53) and (54) should be vanished. Therefore, to obtain the solvability condition Eqs. (53) and (54) at the primary resonance case (i.e., when $\Omega \to 1$), let us use the parameter $\sigma$ to represent the closeness of $\Omega$ to the system natural frequency $\omega =1$ as follows:

$$\Omega = 1 + \sigma = 1 + \varepsilon \tilde{\sigma }$$

(55)

Inserting Eqs. (55) into Eqs. (53) and (54), one can drive the solvability conditions of Eqs. (53) and (54) as follows:

$$\begin{aligned} - i\tilde{\mu }A + & \tilde{\rho }_{10} A + \delta_{1} \tilde{\rho }_{11} A - 3\tilde{\lambda }A^{2} \overline{A} - \tilde{\lambda }B^{2} \overline{A} + \tilde{\rho }_{12} B^{2} \overline{A} + 2\overline{\delta }_{1} \delta_{1} \tilde{\rho }_{13} A^{2} \overline{A} + \delta_{1}^{2} \tilde{\rho }_{13} A^{2} \overline{A} + \delta_{2}^{2} \tilde{\rho }_{14} B^{2} \overline{A} \\ & + \overline{\delta }_{1} \tilde{\rho }_{15} B^{2} \overline{A} + 2\delta_{1} \tilde{\rho }_{15} B^{2} \overline{A} + \overline{\delta }_{1} \tilde{\rho }_{16} B^{2} \overline{A} + \delta_{2} \tilde{\rho }_{17} B^{2} \overline{A} + \overline{\delta }_{1} \delta_{2} \tilde{\rho }_{18} B^{2} \overline{A} + 3\tilde{\rho }_{19} A^{2} \overline{A} - 2\tilde{\lambda }AB\overline{B} + 2\tilde{\rho }_{12} AB\overline{B} \\ & + 2\delta_{2} \overline{\delta }_{2} \tilde{\rho }_{14} AB\overline{B} + 2\delta_{1} \tilde{\rho }_{16} AB\overline{B} + \overline{\delta }_{2} \tilde{\rho }_{17} AB\overline{B} + \delta_{2} \tilde{\rho }_{17} AB\overline{B} + \delta_{1} \overline{\delta }_{2} \tilde{\rho }_{18} AB\overline{B} + \delta_{1} \delta_{2} \tilde{\rho }_{18} AB\overline{B} - 2iD_{1} A \\ & + \frac{1}{2}\tilde{E}(1 + \sigma )^{2} e^{{i\varepsilon \tilde{\sigma }T_{0} }} = 0, \\ \end{aligned}$$

(56)

$$\begin{aligned} - i\tilde{\mu }B + & \tilde{\rho }_{20} B + \delta_{2} \tilde{\rho }_{21} B - 2\tilde{\lambda }A\overline{A}B + 2\tilde{\rho }_{22} A\overline{A}B + 2\overline{\delta }_{1} \delta_{1} \tilde{\rho }_{24} A\overline{A}B + 2\delta_{2} \tilde{\rho }_{26} A\overline{A}B + \overline{\delta }_{1} \tilde{\rho }_{27} A\overline{A}B \\ & + \delta_{1} \tilde{\rho }_{27} A\overline{A}B + \overline{\delta }_{1} \delta_{2} \tilde{\rho }_{28} A\overline{A}B + \delta_{1} \delta_{2} \tilde{\rho }_{28} A\overline{A}B - \tilde{\lambda }A^{2} \overline{B} - 3\tilde{\lambda }B^{2} \overline{B} + \tilde{\rho }_{22} A^{2} \overline{B} + 2\delta_{2} \overline{\delta }_{2} \tilde{\rho }_{23} B^{2} \overline{B} \\ & + \delta_{2}^{2} \tilde{\rho }_{23} B^{2} \overline{B} + \delta_{1}^{2} \tilde{\rho }_{24} A^{2} \overline{B} + \overline{\delta }_{2} \tilde{\rho }_{25} B^{2} \overline{B} + 2\delta_{2} \tilde{\rho }_{25} B^{2} \overline{B} + \overline{\delta }_{2} \tilde{\rho }_{26} A^{2} \overline{B} + \delta_{1} \tilde{\rho }_{27} A^{2} \overline{B} + \delta_{1} \overline{\delta }_{2} \tilde{\rho }_{28} A^{2} \overline{B} \\ & + 3\tilde{\rho }_{29} B^{2} \overline{B} - 2iD_{1} B - \frac{1}{2}i\tilde{E}(1 + \sigma )^{2} e^{{i\varepsilon \tilde{\sigma }T_{0} }} = 0. \\ \end{aligned}$$

(57)

To analyze Eqs. (56) and (57), let us express the functions $A({T}_{1})$ and $B({T}_{1})$ in their polar forms as follows [40, 41].

$$A(T_{1} ) = \frac{1}{2}a(T_{1} )e^{{i\theta_{1} (T_{1} )}} ,\;B(T_{1} ) = \frac{1}{2}b(T_{1} )e^{{i\theta_{2} (T_{1} )}} .$$

(58)

By substituting Eqs. (58) into Eqs. (56) and (57), one can derive the following autonomous dynamical system after separating the real and imaginary parts and restoring the parameters into their original form (i.e.,$\widetilde{\mu }=\frac{\mu }{\varepsilon },\widetilde{\lambda }=\frac{\lambda }{\varepsilon } , \widetilde{E}=\frac{E}{\varepsilon },{\widetilde{\eta }}_{1}=\frac{{\eta }_{1}}{\varepsilon }, {\widetilde{\eta }}_{2}=\frac{{\eta }_{2}}{\varepsilon }, {\widetilde{\rho }}_{jk}=\frac{{\rho }_{jk}}{\varepsilon } , (j=\mathrm{1,2}, k=\mathrm{1,2},\dots ,9)$):

$$\begin{aligned} \frac{da}{{d\tau }} = & - \frac{1}{2}a\mu + \frac{1}{8}ab^{2} \lambda \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{2}\frac{{a\eta_{1} \rho_{11} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}ab^{2} \rho_{12} \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{4}\frac{{a^{3} \eta_{1}^{2} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{1}{8}\frac{{ab^{2} \eta_{2}^{2} \rho_{14} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{ab^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{8}\frac{{ab^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{a^{3} \eta_{1} \rho_{15} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{4}\frac{{ab^{2} \eta_{1} \rho_{16} }}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{ab^{2} \eta_{1} \rho_{16} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}\frac{{ab^{2} \eta_{1} \lambda_{1} \rho_{16} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{2} \rho_{17} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{8}\frac{{ab^{2} \eta_{2} \lambda_{2} \rho_{17} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{2}E\Omega^{2} \sin (\phi_{1} ), \\ \end{aligned}$$

(59)

$$\begin{aligned} \frac{db}{{d\tau }} = & - \frac{1}{2}b\mu - \frac{1}{8}a^{2} b\lambda \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{2}\frac{{b\eta_{2} \rho_{21} }}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}a^{2} b\rho_{22} \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{4}\frac{{b^{3} \eta_{2}^{2} \lambda_{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{a^{2} b\eta_{1}^{2} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a^{2} b\eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{a^{2} b\eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{b^{3} \eta_{2} \rho_{25} }}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a^{2} b\eta_{2} \rho_{26} }}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{2} \rho_{26} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{a^{2} b\eta_{1} \rho_{27} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{2} \rho_{28} (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{2}E\Omega^{2} \cos (\phi_{2} ), \\ \end{aligned}$$

(60)

$$\begin{aligned} \frac{{d\varphi_{1} }}{d\tau } = & \sigma - \frac{3}{8}a^{2} \lambda - \frac{1}{4}b^{2} \lambda - \frac{1}{8}b^{2} \lambda \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{2}\rho_{10} + \frac{1}{2}\frac{{\eta_{1} \lambda_{1} \rho_{11} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}b^{2} \rho_{12} \\ & \; + \frac{1}{8}b^{2} \rho_{12} \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{3}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \rho_{14} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{3}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{15} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{b^{2} \eta_{1} \lambda_{1} \rho_{16} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \lambda_{1} \rho_{16} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \rho_{16} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{17} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{17} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{b^{2} \eta_{2} \rho_{17} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{3}{8}a^{2} \rho_{19} - \frac{1}{2a}E\Omega^{2} \cos (\phi_{1} ), \\ \end{aligned}$$

(61)

$$\begin{aligned} \frac{{d\varphi_{2} }}{d\tau } = & \sigma - \frac{3}{8}b^{2} \lambda - \frac{1}{4}a^{2} \lambda - \frac{1}{8}a^{2} \lambda \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{2}\rho_{20} + \frac{1}{2}\frac{{\eta_{2} \lambda_{2} \rho_{21} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}a^{2} \rho_{22} \\ & c + \frac{1}{8}a^{2} \rho_{22} \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{3}{8}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1} \lambda_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & - \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1}^{2} \lambda_{1} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & + \frac{3}{8}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{25} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a^{2} \eta_{2} \lambda_{2} \rho_{26} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{2} \lambda_{2} \rho_{26} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{a^{2} \eta_{2} \rho_{26} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} \\ & + \frac{1}{4}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{27} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \rho_{27} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{27} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} sin(2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & - \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} sin(2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{3}{8}b^{2} \rho_{29} + \frac{1}{2b}E\Omega^{2} \sin (\phi_{2} ). \\ \end{aligned}$$

(62)

where ${\phi }_{1}=\sigma \tau -{\theta }_{1}, {\phi }_{2}=\sigma \tau -{\theta }_{2}$. Substituting Eqs. (49), (50), (51), (52), and (58) into Eqs. (37) to (40), yields

$$q_{1} (\tau ) = a(\tau )\cos \left( {\Omega \tau - \phi_{1} (\tau )} \right),$$

(63)

$$q_{2} (\tau ) = b(\tau )\cos \left( {\Omega \tau - \phi_{2} (\tau )} \right),$$

(64)

$$q_{3} (\tau ) = \frac{{\eta_{1} a(\tau )}}{{\lambda_{1}^{2} + 1}}\left[ {\lambda_{1} \cos (\Omega \tau - \phi_{1} (\tau )) + sin(\Omega \tau - \phi_{1} (\tau ))} \right] = a_{1} (\tau )\sin \left( {\Omega \tau - \phi_{1} (\tau ) + \psi_{1} } \right)$$

(65)

$$q_{4} (\tau ) = \frac{{\eta_{2} b(\tau )}}{{\lambda_{2}^{2} + 1}}\left[ {\lambda_{2} \cos (\Omega \tau - \phi_{2} (\tau )) + sin(\Omega \tau - \varphi_{2} (\tau ))} \right] = b_{1} (\tau )\sin \left( {\Omega \tau - \phi_{2} (\tau ) + \psi_{2} } \right)$$

(66)

where ${a}_{1}\left(\tau \right)=\frac{{\eta }_{1}}{\sqrt{{\lambda }_{1}^{2}+1 } }a\left(\tau \right), {b}_{1}\left(\tau \right)=\frac{{\eta }_{2}}{\sqrt{{\lambda }_{2}^{2}+1 } }b\left(\tau \right), {\psi }_{1}={\mathrm{tan}}^{-1}({\lambda }_{1}), {\psi }_{2}={\mathrm{tan}}^{-1}({\lambda }_{2})$. Equations (63) to (66) represent the periodic solution of the dynamical system given by Eqs. (33) to (36) when the rub-impact force is neglected. Based on Eqs. (63) to (66), one can deduce that $a(\tau )$ and $b(\tau )$ are the oscillation amplitudes of the controlled Jeffcott system, while and ${\phi }_{1}\left(\tau \right)$ and ${\phi }_{2}\left(\tau \right)$ denote the corresponding phase angles. In addition, ${a}_{1}\left(\tau \right)$ and ${b}_{1}\left(\tau \right)$ represent the vibration amplitudes of the IRC-controller that is coupled to the rotor system, where ${a}_{1}\left(\tau \right)$ and ${b}_{1}\left(\tau \right)$ are a constant multiple of the rotor vibration amplitudes (i.e., ${a}_{1}\left(\tau \right)=\left({\eta }_{1}/\sqrt{{\lambda }_{1}^{2}+1 } \right)a\left(\tau \right)$ and ${b}_{1}\left(\tau \right)=\left({\eta }_{2}/\sqrt{{\lambda }_{2}^{2}+1 }\right)b\left(\tau \right)$). Moreover, the evolution of rotor vibration amplitudes (i.e., $a(\tau )$ and $b(\tau )$) are governed by the autonomous dynamical system given by Eqs. (59) to (62). Accordingly, one can explore the steady-state vibration amplitudes of the controlled system by setting $\dot{a}\left(\tau \right)=\dot{b}\left(\tau \right)=\dot{{\phi }_{1}}\left(\tau \right)={\dot{\phi }}_{2}\left(\tau \right)=0$ into Eqs. (59) to (62) to obtain the following nonlinear algebraic system:

$$\begin{aligned} g_{1} (a,b,\phi_{1} ,\phi_{2} ) = & - \frac{1}{2}a\mu + \frac{1}{8}ab^{2} \lambda \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{2}\frac{{a\eta_{1} \rho_{11} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}ab^{2} \rho_{12} \sin (2\phi_{1} - 2\phi_{2} ) \\ & \; - \frac{1}{4}\frac{{a^{3} \eta_{1}^{2} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{ab^{2} \eta_{2}^{2} \rho_{14} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{ab^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{8}\frac{{a^{3} \eta_{1} \rho_{15} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{4}\frac{{ab^{2} \eta_{1} \rho_{16} }}{{\lambda_{1}^{2} + 1}} \\ & \; + \frac{1}{8}\frac{{ab^{2} \eta_{1} \rho_{16} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}\frac{{ab^{2} \eta_{1} \lambda_{1} \rho_{16} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{2} \rho_{17} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{8}\frac{{ab^{2} \eta_{2} \lambda_{2} \rho_{17} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{ab^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{2}E\Omega^{2} \sin (\phi_{1} ) = 0, \\ \end{aligned}$$

(67)

$$\begin{aligned} g_{2} (a,b,\phi_{1} ,\phi_{2} ) = & - \frac{1}{2}b\mu - \frac{1}{8}a^{2} b\lambda \sin (2\phi_{1} - 2\phi_{2} ) - \frac{1}{2}\frac{{b\eta_{2} \rho_{21} }}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}a^{2} b\rho_{22} \sin (2\phi_{1} - 2\phi_{2} ) \\ & \; - \frac{1}{4}\frac{{b^{3} \eta_{2}^{2} \lambda_{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{8}\frac{{a^{2} b\eta_{1}^{2} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a^{2} b\eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{1}{8}\frac{{a^{2} b\eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{8}\frac{{b^{3} \eta_{2} \rho_{25} }}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a^{2} b\eta_{2} \rho_{26} }}{{\lambda_{2}^{2} + 1}} \\ & \; + \frac{1}{8}\frac{{a^{2} b\eta_{2} \rho_{26} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{2}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{a^{2} b\eta_{1} \rho_{27} \cos (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{a^{2} b\eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{1} - 2\phi_{2} )}}{{\lambda_{1}^{2} + 1}} \\ & \; + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{2} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} b\eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{2}E\Omega^{2} \cos (\phi_{2} ) = 0, \\ \end{aligned}$$

(68)

$$\begin{aligned} g_{3} (a,b,\varphi_{1} ,\varphi_{2} ) = & \sigma - \frac{3}{8}a^{2} \lambda - \frac{1}{4}b^{2} \lambda - \frac{1}{8}b^{2} \lambda \cos (2\varphi_{1} - 2\varphi_{2} ) + \frac{1}{2}\rho_{10} + \frac{1}{2}\frac{{\eta_{1} \lambda_{1} \rho_{11} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}b^{2} \rho_{12} \\ & \; + \frac{1}{8}b^{2} \rho_{12} \cos (2\varphi_{1} - 2\varphi_{2} ) + \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{3}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \rho_{14} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \sin (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{3}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{15} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{b^{2} \eta_{1} \lambda_{1} \rho_{16} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \lambda_{1} \rho_{16} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \rho_{16} \sin (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{17} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{17} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{b^{2} \eta_{2} \rho_{17} \sin (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \rho_{18} \cos (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \sin (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \sin (2\varphi_{1} - 2\varphi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{3}{8}a^{2} \rho_{19} \\ & \; - \frac{1}{2a}E\Omega^{2} \cos (\varphi_{1} ) = 0, \\ \end{aligned}$$

(69)

$$\begin{aligned} g_{4} (a,b,\phi_{1} ,\phi_{2} ) = & \sigma - \frac{3}{8}b^{2} \lambda - \frac{1}{4}a^{2} \lambda - \frac{1}{8}a^{2} \lambda \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{2}\rho_{20} + \frac{1}{2}\frac{{\eta_{2} \lambda_{2} \rho_{21} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}a^{2} \rho_{22} \\ & \; + \frac{1}{8}a^{2} \rho_{22} \cos (2\phi_{1} - 2\phi_{2} ) + \frac{1}{8}\frac{{b^{2} \eta_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{3}{8}\frac{{b^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1} \lambda_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; - \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a^{2} \eta_{1}^{2} \lambda_{1} \rho_{24} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{a^{2} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{3}{8}\frac{{b^{2} \eta_{2} \lambda_{2} \rho_{25} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a^{2} \eta_{2} \lambda_{2} \rho_{26} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{2} \lambda_{2} \rho_{26} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{a^{2} \eta_{2} \rho_{26} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{27} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \rho_{27} \sin (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \lambda_{1} \rho_{27} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} sin(2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \rho_{28} \cos (2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{a^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} sin(2\phi_{1} - 2\phi_{2} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{3}{8}b^{2} \rho_{29} \\ & \; + \frac{1}{2b}E\Omega^{2} \sin (\phi_{2} ) = 0. \\ \end{aligned}$$

(70)

Based on Eqs. (67) to (70), one can explore the performance of the proposed control strategy (i.e., $PIRC-$ controller) in reducing the oscillation amplitudes of the rotor system (i.e. $a, b$) via solving the nonlinear algebraic system ${g}_{j}\left(a,b, {\phi }_{1}, {\phi }_{2}\right)=0 (j=1, 2, 3, 4)$ in terms of the system and control parameters (i.e., $\sigma , E, {\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}, {\eta }_{1}, {\eta }_{2}, {\lambda }_{1}, {\lambda }_{2}$) as given in Sect. 3.2. In addition, the solution stability of Eqs. (67) to (70) can be checked by exploring the eigenvalues of the linear dynamical system corresponding to the nonlinear system (59)-(62). To obtain the linearized dynamical system corresponding to Eqs. (59) to (62), let (${a}_{10}, {b}_{10},{\phi }_{10}, {\phi }_{20}$) be the equilibrium point of the autonomous system (59) to (62) and suppose (${a}_{11}, {b}_{11},{\phi }_{11}, {\phi }_{21}$) be a small perturbation about this equilibrium point. Therefore, one can write

$$\left. \begin{gathered} a = a_{10} + a_{11} ,b = b_{10} + b_{11} ,\phi_{1} = \phi_{10} + \phi_{11} ,\phi_{2} = \phi_{20} + \phi_{21} , \hfill \\ \dot{a} = \dot{a}_{11} \dot{b} = \dot{b}_{11} \dot{\phi }_{1} = \dot{\phi }_{11} ,\dot{\phi }_{2} = \dot{\phi }_{21} . \hfill \\ \end{gathered} \right\}$$

(71)

Inserting Eqs. (71) into Eqs. (59) to (62) with expanding for ${a}_{11}, {b}_{11},{\varphi }_{11}, {\varphi }_{21}$ and keeping the linear terms only yields the following linearized model

$$\dot{a}_{11} = \frac{{\partial g_{1} }}{{\partial a_{11} }}a_{11} + \frac{{\partial g_{1} }}{{\partial b_{11} }}b_{11} + \frac{{\partial g_{1} }}{{\partial \varphi_{11} }}\phi_{11} + \frac{{\partial g_{1} }}{{\partial \varphi_{21} }}\phi_{21} ,$$

(72)

$$\dot{b}_{11} = \frac{{\partial g_{2} }}{{\partial a_{11} }}a_{11} + \frac{{\partial g_{2} }}{{\partial b_{11} }}b_{11} + \frac{{\partial g_{2} }}{{\partial \varphi_{11} }}\phi_{11} + \frac{{\partial g_{2} }}{{\partial \varphi_{21} }}\phi_{21} ,$$

(73)

$$\dot{\varphi }_{11} = \frac{{\partial g_{3} }}{{\partial a_{11} }}a_{11} + \frac{{\partial g_{3} }}{{\partial b_{11} }}b_{11} + \frac{{\partial g_{3} }}{{\partial \varphi_{11} }}\phi_{11} + \frac{{\partial g_{3} }}{{\partial \varphi_{21} }}\phi_{21} ,$$

(74)

$$\dot{\varphi }_{21} = \frac{{\partial g_{4} }}{{\partial a_{11} }}a_{11} + \frac{{\partial g_{4} }}{{\partial b_{11} }}b_{11} + \frac{{\partial g_{4} }}{{\partial \varphi_{11} }}\phi_{11} + \frac{{\partial g_{4} }}{{\partial \varphi_{21} }}\phi_{21} .$$

(75)

where the coefficients of Eqs. (72)–(75) are given in Appendix B. The above linear dynamical system (i.e., Eqs. (72) to (75)) is topologically equivalent to the nonlinear system given by Eqs. (59) to (62) (see Ref. [42]). Accordingly, the stability of the nonlinear system (59)–(62) can be investigated by checking the eigenvalues of the linear system (72)–(75).

3.2 Sensitivity analysis and numerical validation

Relying on the analytical investigation given in Sect. 3.1, the performance of the purposed control technique (i.e., $PIRC$-controller) is studied within this section via solving the nonlinear algebraic system (67)-(70) (using Newton–Raphson algorithm [43]) in terms of the different control gains (i.e.,${\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}, {\eta }_{1}, {\eta }_{2}, {\lambda }_{1}, {\lambda }_{2}$) utilizing $\sigma$ or $E$ as the main bifurcation parameter. The control performance can be evaluated via plotting the steady-state vibration amplitude ($a,b$) of the Jeffcott system versus $\sigma$ or $E$ at the different control gains. In addition, the whirling direction of the rotor system either forward or backward can be determined by plotting the steady-state phase-angles (${\phi }_{1}, {\phi }_{2}$) versus the same bifurcation parameter (i.e., $\sigma$ or$E$). Relying on Eqs. (63) and (64) the Jeffcott system may perform forward whirling oscillation as long as${\phi }_{1}>{\phi }_{2}$, but when ${\phi }_{2}>{\phi }_{1}$ this implies that the rotor system exhibits backward whirling motion. Moreover, the rotor system performs vibration along a straight line with a slope ${\phi }_{1}$ when${\phi }_{1}={\phi }_{2}$. The dimensionless system parameters that are used in the current analysis are adopted as follows: $E=0.03, \mu =0.015, \lambda =0.05, {\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1, \alpha =4{5}^{o}, \sigma =0,\Omega =1+\sigma , k=5,$ and ${\mu }_{f}=0.2$ [13, 24, 39]. The following subsections are organized such that the dynamical behaviors of the uncontrolled Jeffcott system are discussed in Sect. 3.2.1 when letting ${\rho }_{1j}= {\rho }_{2j}=0 \left(j=\mathrm{0,1},\dots ,9\right)$ into Eqs. (67) to (70), while Sects. 3.2.2 is intended to explore the influences of the different control gains (i.e.,${\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}, {\eta }_{1}, {\eta }_{2}, {\lambda }_{1}, {\lambda }_{2}$) on the steady-steady vibration amplitudes and the whirling direction (either forward or backward) of the considered Jeffcott system.

3.2.1 Uncontrolled rotor system

Based on the derived Eqs. (67)–(70), the oscillation amplitudes ($a, b$) of the uncontrolled Jeffcott system and the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$) are plotted versus $\sigma$ at three different magnitudes of the disc eccentricity $E$ as shown in Fig. 4. It is clear from Fig. 4A and B that the rotor lateral vibrations are symmetric in $X$ and $Y$ directions, and a monotonic increasing function in $E$. In addition, the figures demonstrate that the nonlinear characteristics dominate the system response when $\sigma >0$ (i.e., when the rotor angular speed $\Omega$ is higher than the system natural frequency $\omega =1$, where $\sigma =\Omega -1$), where the rotor system may have a bistable periodic solution. Moreover, Fig. 4C, D, and E confirm that the steady-state phase difference between the lateral vibrations in $X$ and $Y$ directions is always constant (i.e., ${\phi }_{1}-{\phi }_{2}=\pi /2$) regardless of the rotor angular speed and the eccentricity magnitudes, which confirm the forward circular whirling motion of the considered rotor system.

Fig. 4

A, B oscillation amplitudes ($a, b$) of the uncontrolled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}$

To demonstrate the accuracy of the angular speed response curve given in Fig. 4, numerical simulation for the equations of motion of uncontrolled Jeffcott system (i.e., Eqs. (33) and (34) when $k={\rho }_{1j}= {\rho }_{2j}=0 \left(j=\mathrm{0,1},\dots ,9\right)$) are illustrated in Fig. 5 according to Fig. 4 when $E=0.03, \sigma =0.05$ at the two initial sets ${q}_{1}\left(0\right)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$ and ${q}_{1}\left(0\right)={q}_{2}\left(0\right)=1.0, =\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$. Figure 5A, B, and C show the steady-state temporal lateral vibrations and the corresponding whirling motion, and Fig. 5D and E illustrate the instantaneous radial oscillations $r\left(\tau \right)$ at the considered initial conditions. By examining Fig. 5, one can deduce that the rotor system is sensitive to the initial conditions, where the system can oscillate by one of two periodic solutions depending on the initial conditions.

Fig. 5

Numerical simulation of the rotor temporal oscillations according to Fig. 4 when $E=0.03, \sigma =0.05$: A, B, C steady-state lateral temporal vibrations and the corresponding whirling orbit of the rotor system at the initial conditions ${q}_{1}\left(0\right)={q}_{2}\left(0\right)=1.0, \dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$ and ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$, (D, E) the corresponding radial oscillation $r\left(\tau \right)=\sqrt{{q}_{1}\left(\tau \right)+{q}_{2}(\tau )}$

Accordingly, the main target of this article is to control the undesired lateral vibrations of the considered Jeffcott system and eliminate the catastrophic nonlinear characteristics via designing a novel control strategy (i.e., $\mathrm{PIRC}$-controller).

3.2.2 Controlled rotor system

Based on Eqs. (12), (33), (34), (35), and (36), the dimensionless parameters ${\delta }_{1}=\frac{{s}_{0}}{{I}_{0}}{k}_{1},\, {\delta }_{2}=\frac{{s}_{0}}{{I}_{0}}{k}_{2},\, {\delta }_{3}=\frac{{s}_{0}}{{I}_{0}}{k}_{3},\, {\delta }_{4}=\frac{{s}_{0}}{{I}_{0}}{k}_{4},\, {\lambda }_{1}=\frac{{\rho }_{1}}{{\omega }_{n}}, {\lambda }_{2}=\frac{{\rho }_{2}}{{\omega }_{n}},\, {\eta }_{1}=\frac{{\gamma }_{1}}{{\omega }_{n}},$ and ${\eta }_{2}=\frac{{\gamma }_{2}}{{\omega }_{n}}$ represent the control gains of the suggested $\mathrm{PIRC}$-controller. Therefore, this section is dedicated to explore the effect of these control parameters on the oscillation amplitudes and the whirling direction of the considered rotor system via solving the nonlinear algebraic system given by Eqs. (67) to (70).

The influence of the proportional gain (i.e., ${\delta }_{1}$ and ${\delta }_{3}$) on the rotor oscillation amplitudes ($a, b$), and the whirling direction (i.e., ${\phi }_{1}, {\phi }_{2}$) is depicted in Fig. 6. The figure illustrates the evolution of $a, b, {\phi }_{1},$ and ${\phi }_{2}$ against $\sigma$ at the three different values of the proportional gains ${\delta }_{1}={\delta }_{3}=0.95, 1.0,$ and $1.05$. It is clear from the figure that the increase of the proportional gains to ${\delta }_{1}={\delta }_{3}=1.05$, shifts the Jeffcott system response curves to the right leading to avoiding the high oscillation amplitude at the perfect resonance (perfect resonance means that $\sigma =0.0$). However, the rotor system may oscillate with strong vibration amplitudes when the angular speed is higher than the system's natural frequency (i.e., when $\sigma =0.2$). In addition, the figure demonstrates that the decrease of ${\delta }_{1}={\delta }_{3}=1.05$ to ${\delta }_{1}={\delta }_{3}=0.95$, shifts the response curve to the left. Accordingly, one can deduce that the control gains ${\delta }_{1}$ and ${\delta }_{3}$ act as a proportional gain that can be utilized to avoid the resonance vibrations of the considered system via shifting the resonant peaks either to the right or the left at the perfect resonance conditions. Moreover, Fig. 6C, D, and E demonstrate that the phase difference ${\phi }_{1}-{\phi }_{2}= \pi /{2}^{o}$, which confirms that the rotor system always performs a circular forward whirling motion.

Fig. 6

A, B oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$), when ${\delta }_{1}={\delta }_{3}=0.95, 1.0,$ and $1.05$

The effect of the control gains ${\delta }_{2}$ and ${\delta }_{4}$ on the steady-state vibration amplitudes and the corresponding phase angles of the controlled rotor system are depicted in Fig. 7. It is clear from Fig. 7A and B that the increase of the control gains (${\delta }_{2}$ and ${\delta }_{4}$) from ${\delta }_{2}={\delta }_{4}=0.001$ to ${\delta }_{2}={\delta }_{4}=0.015$ has decreased the vibration amplitudes along $\sigma -$ axis and forced the nonlinear rotor system to respond as a linear system. In addition, Fig. 7C–E demonstrated that the rotor system can perform circular forward whirling motion only along $\sigma -$ axis, where the phase differences ${\phi }_{1}-{\phi }_{2}$ is always $\pi /{2}^{o}$ regardless of the control gain. Figure 8 shows the evolution of the rotor oscillation amplitudes and the corresponding phase-angles versus $\sigma$ at the different values of the feedback gains ${\eta }_{1}$ and ${\eta }_{2}$ (i.e., ${\eta }_{1}={\eta }_{2}=0.1, 0.5,$ and $1.0$). It is clear from Fig. 8A and B that the system steady-state lateral vibrations are a monotonic decreasing function of the feedback gains ${\eta }_{1}$ and ${\eta }_{2}$. Moreover, Fig. 8C–E depict that the phase difference ${\phi }_{1}-{\phi }_{2}$ is $\pi /{2}^{o}$ along the $\sigma -$ axis regardless of the magnitudes of the feedback gains ${\eta }_{1}$ and ${\eta }_{2}$. By examining Figs. 7 and 8 one can demonstrate that the control gains (${\delta }_{2}, {\delta }_{4}$) and feedback gains (${\eta }_{1}, {\eta }_{2}$) of the proposed $PIRC-$ controller act as damped controllers, where the increasing of ${\delta }_{2}={\delta }_{4}$ and ${\eta }_{1}={\eta }_{2}$ increases the damping coefficients of the Jeffcott system, which ultimately reduce the undesired vibration amplitudes of the rotor system.

Fig. 7

A, B oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$), when ${\delta }_{2}={\delta }_{4}=0.001, 0.005,$ and $0.015$

Fig. 8

A, B oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$), when ${\eta }_{1}={\eta }_{2}=0.1, 0.5,$ and $1.0$

Figure 9 shows the lateral vibration amplitudes ($a$ and $b$) of the controlled Jeffcott system at three different values of the control parameters ${\lambda }_{1}$ and ${\lambda }_{2}$ of the $\mathrm{PIRC}$-controller (see Eqs. (35) and (36)). By examining Fig. 9A and B, one can note that the rotor vibration amplitudes are a monotonic increasing function of ${\lambda }_{1}$ and ${\lambda }_{2}$. In addition, Fig. 9C–E show that the rotor system can only perform forward whirling motion along $\sigma -$ axis regardless of the magnitudes of the control parameters ${\lambda }_{1}$ and ${\lambda }_{2}$, where the phase-difference ${\phi }_{1}-{\phi }_{2}$ is $\pi /{2}^{o}$.

Fig. 9

A, B oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$), when ${\lambda }_{1}={\lambda }_{2}=1.0, 2.5,$ and $5.0$

Finally, Fig. 10 shows the evolution of the lateral vibration amplitudes ($a, b$) and the corresponding phase-angles (${\phi }_{1}, {\phi }_{2}$) at three high levels of the disc eccentricity $E$ (i.e. $E=0.05, 0.1,$ and $0.15$) when the control parameters are selected such as ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0$. by comparing Figs. 4 and 10, we can conclude that the proposed control technique has suppressed the nonlinear behaviors and forced the rotor system to respond as a linear one regardless of the strong excitation force. In addition, the sensitivity of the uncontrolled system has been avoided after control. Relying on the acquired results from Figs. 6, 7, 8, 9 and 10, it is possible to reshape the undesired nonlinear dynamical characteristics of the considered rotor system using the proposed $PIRC-$ controller.

Fig. 10

A, B oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C, D, E the corresponding phase angles (${\phi }_{1}, {\phi }_{2}$), when ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0$ at three different values of the disc eccentricity $E=0.05, 0.1,$ and $0.15$

4 Discontinuous dynamical system and rub-impact force

When the rotor lateral displacements $x(t)$ and/or $y(t)$ are larger than the nominal air-gap size ${s}_{0}$ between the rotating disc and the 8-pole housing as shown in Fig. 2a a rub-impact force develops between the rotating disc and 8-pole housing interface as shown in Fig. 3. These rub and impact forces may be resulting in different catastrophic dynamical behaviors of the considered system. Therefore, this section is intended to investigate the nonlinear dynamics of the Jeffcott system when the controller fails to keep the rotor lateral displacements $x(t)$ and/or $y(t)$ smaller than the nominal air-gap size ${s}_{0}$ via solving the discontinuous dynamical system given by Eqs. (33) to (36) when $k\ne 0$ and ${\mu }_{f}\ne 0$.

Based on the introduced dimensionless variables ${q}_{1}=\frac{x}{{s}_{0}}$ and ${q}_{2}=\frac{y}{{s}_{0}}$ given before Eq. (33), where ${q}_{1}\left(\tau \right)=a\left(\tau \right)\mathrm{cos}(\Omega \tau -{\phi }_{1}\left(\tau \right))$ and ${q}_{2}\left(\tau \right)=b\left(\tau \right)\mathrm{cos}(\Omega \tau -{\phi }_{2}\left(\tau \right))$ as given by Eqs. (63) and (64). Accordingly, one can deduce that the rub and/or impact forces between the Jeffcott rotor and the pole housing occur when the oscillation amplitudes $a(\tau )$ and/or $b(\tau )$ are larger than unity (i.e., when $a\left(\tau \right)\ge 1$ and/or $b\left(\tau \right)\ge 1$). Relying on this condition, it is possible to predict the rub-impact force between the rotor and stator utilizing the response curves given in Sect. 3 as in Figs. 4, 6, 7, 8, 9 and 10.

For example, Fig. 10A and B depict that the proposed $\mathrm{PIRC}$-controller failed to prevent the rub-impact occurrence between the rotating disc and the pole housing at a specific interval of the parameter $\sigma$ (i.e., at $-0.08\le \sigma \le 0.04$) when the disc eccentricity $E=0.15$, where $a>1$ and $b>1$. According to Figs. 10A and B, 11 is established when ${\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}= {\lambda }_{1}={\lambda }_{2}=1, k=5, {\mu }_{f}=0.2$ and $E=0.15$, where Fig. 11A and B are obtained via solving Eqs. (67)–(70). On the other hand, Fig. 11C is obtained via plotting the steady-state Poincare-map of the radial oscillation $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}\left(\tau \right)}$ for the discontinuous system given by Eqs. (33)–(36) utilizing $\sigma$ as the main bifurcation parameter on the interval $-0.1\le \sigma \le 0.1$. It is clear from Fig. 11A and B that the Jeffcott system may be subjected to rub and impact force when the rotor angular speed within the range $\Omega =1+\sigma , \sigma \in [-0.08, 0.04]$ because $a>1$ and $b>1$ on the interval $-0.08\le \sigma \le 0.04$. Therefore, the system bifurcation diagram has been established in Fig. 11C according to Fig. 11A and B on the interval $-0.1\le \sigma \le 0.1$ at $k=5.0$ and ${\mu }_{f}=0.2$ to explore the nature of the rotor motion when the rub-impact force occurs between the rotor and stator.

Fig. 11

A, B steady-state oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $\sigma$, C the corresponding bifurcation diagrams when the rub-impact force between the rotor and stator is included, ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0, k=5.0, {\mu }_{f}=0.2,$ and $E=0.15$

By examining Fig. 11C, one can notice that the Jeffcott system exhibits aperiodic motion as long as $\sigma \in \left[-0.08, 0.04\right]\cup [0.04, 0.069]$, otherwise the rotor system will oscillate with periodic motion. It is clear from Fig. 11C that the rotor performs aperiodic oscillation on the interval $-0.08\le \sigma \le 0.04$ due to the rub-impact occurrences between the rotor and stator, where $a>1$ and $b>1$ on this interval as shown in Fig. 11A and B. However, Fig. 11C demonstrates that the Jeffcott system performs aperiodic motion also on the interval $0.04\le \sigma \le 0.069$ despite $a<1$ and $b<1$ on this interval shown in Fig. 11A and B. The main reason for these aperiodic oscillations can be interpreted as “strong transient vibration induces a sustained rub-impact force between the rotor and stator”, where this phenomenon will be explained next in detail through Figs.14, and 15.

Figures 12, 13, 14, and 15 visualize the temporal oscillations and the corresponding whirling motion of the considered Jeffcott system according to Fig. 11C at the three different values of the rotor angular speed $\Omega =1+\sigma , \sigma = -0.1, 0,$ and $0.06$ via solving the discontinuous dynamical system (33)–(36) numerically with zero initial conditions. Figure 12 illustrates the instantaneous lateral vibrations, the radial oscillation, and the corresponding steady-state whirling motion of the controlled rotor at $\sigma = -0.1$. It is clear from Fig. 12 that the transient and the steady-state vibration amplitudes are smaller than unity (i.e., ${q}_{1}\left(\tau \right)<1, {q}_{2}\left(\tau \right)<1$, and $r\left(\tau \right)<1$ along the interval $0\le \tau <\infty$). Therefore, the controlled rotor system can oscillate safely with circular forward whirling motion without rub-impact occurrence between the rotating disc and the 8-pole housing as demonstrated in Fig. 12D. On the other hand, Fig. 13 simulates the system's instantaneous lateral vibrations, the radial oscillation, and the corresponding steady-state whirling motion when $\sigma = 0$. The figure demonstrates that the Jeffcott system exhibits a quasiperiodic oscillation due to the rub-impact force occurrence between the rotor and the 8-pole housing, which agrees with Fig. 11A and B where $a>1$ and $b>1$ at $\sigma = 0$.

Fig. 12

Numerical simulation of the rotor temporal oscillations according to Fig. 11 when $\sigma =-0.1$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A, B temporal lateral vibrations ${q}_{1}(\tau )$ and ${q}_{2}(\tau )$, C temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and D the corresponding steady-state whirling orbit

Fig. 13

Numerical simulation of the rotor temporal oscillations according to Fig. 11 when $\sigma =0.0$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A, B temporal lateral vibrations ${q}_{1}(\tau )$ and ${q}_{2}(\tau )$, C temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and D the corresponding steady-state whirling orbit

Fig. 14

Numerical simulation of the rotor temporal oscillations according to Fig. 11 when $\sigma =0.06$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$ when the rub-impact force is set to be zero: A, B temporal lateral vibrations ${q}_{1}(\tau )$ and ${q}_{2}(\tau )$, (C) temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and D the corresponding steady-state whirling orbit

Fig. 15

Numerical simulation of the rotor temporal oscillations according to Fig. 11 when $\sigma =0.06$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A, B temporal lateral vibrations ${q}_{1}(\tau )$ and ${q}_{2}(\tau )$, C temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and D the corresponding steady-state whirling orbit

It is clear from Figs. 11A and B that the steady-state vibration amplitudes $a$ and $b$ are smaller than unity on the interval $0.04\le \sigma <0.069$ (i.e., $a \& b<1$ as long as $0.04<\sigma <0.069$), which means that the rotor system can oscillate safely without rub-impact occurrence between the rotor and stator. However, Fig. 11C demonstrates that the system performs aperiodic motion on the interval $0.04\le \sigma <0.069$ due to the rub-impact occurrence between the rotor and stator. To explain the contradiction between Fig. 11A, B, and C on the interval$0.04\le \sigma <0.069$, the system temporal Eqs. (33)–(36) are numerically simulated according to Figs. 11 when $\sigma =0.06$ (i.e.$\sigma =0.06\in [0.04, 0.069]$) as shown in Figs. 14 and 15, where Fig. 14 depicts the system motion when the rub impact force is neglected (i.e. when $k={\mu }_{f}=0.0$), but Fig. 15 illustrates the system dynamics when $k=5.0$ and${\mu }_{f}=0.2$. By examining Fig. 14, one can notice that the rotor system exhibits strong transient lateral vibrations (i.e., ${q}_{1}\left(\tau \right)>1, {q}_{2}\left(\tau \right)>1, r\left(\tau \right)>1$ on short time interval), where these instantaneous vibrations reach the steady-state with oscillation amplitudes smaller than unity when the rub-impact force is neglected (i.e., when $k={\mu }_{f}=0.0$). On the other hand, Fig. 15 demonstrates that the strong transient oscillations shown in Fig. 14 may cause a sustained rub-impact force between the rotor and stator when the rub impact force is considered. Accordingly, one can conclude that $a>1$ and/or $b>1$ is not the only sufficient condition for the occurrence of a rub-impact force between the rotor and stator, but also the strong transient oscillations may be resulting in a sustained rub-impact occurrence between the rotor and stator even if the steady state amplitude of this transient oscillation is smaller than unity as depicted in Figs. 14 and 15.

To investigate the system dynamics at a wide range of the rotor eccentricity $E$, the steady state vibration amplitudes ($a, b$) of the controlled Jeffcott system are plotted against $E$ via solving Eqs. (67)–(70) when $\sigma =0.0, {\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1$ as shown in Fig. 16A and B. It is clear from Fig. 16A and B that the controlled system can oscillate safely with oscillation amplitude smaller than the air-gap size as long as the eccentricity magnitude $E<0.1045$. But the increase of $E$ beyond $0.1045$ may increase the system's lateral vibration amplitudes to become larger than the air-gap size, which ultimately leads to rub-impact occurrence between the rotor and stator. To confirm the accuracy of the analytical results obtained in Fig. 16A and B, the corresponding bifurcation diagram of the discontinuous system (33)–(36) is established via plotting the steady-state Poincare-map of the radial oscillation $r\left(\tau \right)$ versus the disc eccentricity when $\sigma =0.0, {\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1, k=5.0, {\mu }_{f}=0.2$ at zero initial conditions as shown in Fig. 16C. By examining Fig. 16C, one notices that the rotor system can perform periodic motion as long as $0<E<0.1045$, otherwise, the system will oscillate with rub-impact mode to perform aperiodic oscillation, which exactly agrees with the same results drawn From Fig. 16A and B.

Fig. 16

A, B steady-state oscillation amplitudes ($a, b$) of the controlled Jeffcott system versus $E$, C the corresponding bifurcation diagram when the rub-impact force between the rotor and stator is included, ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0, k=5.0, {\mu }_{f}=0.2,$ and $\sigma =0.0$

Based on Figs. 16, 17 and 18 demonstrate the effect of a small increase of the rotor eccentricity from $E=0.1$ to $E=0.106$ on the oscillatory behaviors of the considered discontinuous system (33)–(36. It is clear from Fig. 17 that the Jeffcott system exhibits periodic oscillation with forward circular motion when $E=0.1$. However, Fig. 18 demonstrates that the periodic motion of the rotor system at $E=0.1$ has been bifurcated to a quasiperiodic motion when $E$ became $0.106.$

Fig. 17

Numerical simulation of the rotor temporal oscillations according to Fig. 16 when $E=0.1$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and B the corresponding steady-state whirling orbit

Fig. 18

Numerical simulation of the rotor temporal oscillations according to Fig. 16 when $E=0.106$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and B the corresponding steady-state whirling orbit

The influence of the impact stiffness coefficient $k$ on the bifurcation of the rotor motion is investigated as shown in Fig. 19 via plotting the system bifurcation diagram utilizing $k$ as the main bifurcation parameter when $E=0.15, \sigma =0.0, {\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1, {\mu }_{f}=0.2$ along the interval$0\le k\le 50$. Based on the established bifurcation diagram, it was found that the Jeffcott system can oscillate by one of two vibration modes (which are full-annular-rub mode and partial-rub-impact mode) depending on the magnitude of the impact stiffness coefficient $k$, where Fig. 19 illustrates that the rotating disc can perform forward whirling motion in continuous contact with the 8-pole housing as long as the impact stiffness coefficient $0\le k<1$ (i.e., the rotor performs full-annular-rub motion when$0\le k<1$). However, as soon as $k$ exceeds 1, the rotor system escapes to the partial-rub-impact mode to perform quasiperiodic motion along$1\le k<50$.

Fig. 19

Controlled rotor system bifurcation diagram utilizing the impact stiffness coefficient ($k$) as the bifurcation control parameters when ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0, {\mu }_{f}=0.2,\sigma =0.0$ and $E=0.015$

The temporal motions of the considered Jeffcott system have been simulated in Fig. 20 according to the two vibration modes that are reported in Fig. 19. The figure shows the steady-state whirling motion and the corresponding frequency-spectrum of the Jeffcott system according to Fig. 19 at the three values of the impact stiffness coefficient $k=0.5, 25$, and $50$. It seems from the numerical simulations shown in Fig. 20A and B that the Jeffcott system performs periodic motion outside the boundary of the 8-pole housing when $k=0.5$. This means that the rotor system moves along a circular path in continuous contact with the 8-pole housing, which is known as a full-annular-rub mode. On the other hand, Fig. 20C and D illustrate that the rotor system performs periodic-n motion with partial-rub-impact mode when $k=25.0$, while Fig. 20E and F demonstrate that the Jeffcott system exhibits a quasiperiodic motion with partial-rub-impact mode when $k=50.0$.

Fig. 20

Controlled Jeffcott system whirling-orbit and the corresponding frequency-spectrum according to Fig. 19 at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A, B periodic motion with full-annular-rub mode when $k=0.5$, C, D Periodic-n motion with partial-rub-impact mode when $k=25.0$, and E, F quasi-periodic motion with partial-rub-impact mode when $k=50.0$

The nonlinear dynamics of the controlled Jeffcott system have been explored for a wide range of the dynamic friction coefficient ${\mu }_{f}$ via obtaining the system bifurcation diagram utilizing ${\mu }_{f}$ as the bifurcation parameter on the interval $0\le {\mu }_{f}\le 0.55$ as shown in Fig. 21 when $E=0.15, \sigma =0.0, {\delta }_{1}={\delta }_{3}=1, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1, k=5.0$. It is clear from the figure that the system will oscillate with a full-annular-rub mode as long as $0<{\mu }_{f}<0.044$. However, the increase of ${\mu }_{f}$ beyond $0.044$ resulting in a partial-rub-impact mode for the rotating shaft. Relying on Fig. 21, the temporal oscillations of the controlled rotor system are numerically simulated as shown in Figs. 22 and 23 at ${\mu }_{f}=0.01$ and $0.55,$ respectively. Figure 22 demonstrates the full-annular-rub mode, while Fig. 23 depicts the partial rub-impact oscillation of the Jeffcott system. Finally, Fig. 24 illustrates the temporal vibrations and the corresponding whirling motion of the controlled rotor system according to Fig. 21 but when ${\mu }_{f}=0.6$. It is clear from the figure that the rotor may lose its stability to respond with unbounded motion, which implies practically the destruction of the considered system if the interface between the rotor and stator is a rough surface with a dynamic friction coefficient ${\mu }_{f}=0.6$.

Fig. 21

Controlled rotor system bifurcation diagram utilizing the dynamic friction coefficient (${\mu }_{f}$) as the bifurcation control parameters when ${\delta }_{1}={\delta }_{3}=1.0, {\delta }_{2}={\delta }_{4}=0.015, {\eta }_{1}={\eta }_{2}={\lambda }_{1}={\lambda }_{2}=1.0, k=5.0,\sigma =0.0$ and $E=0.015$

Fig. 22

Numerical simulation of the rotor temporal oscillations according to Fig. 21 when ${\mu }_{f}=0.01$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and B the corresponding steady-state whirling orbit

Fig. 23

Numerical simulation of the rotor temporal oscillations according to Fig. 21 when ${\mu }_{f}=0.55$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and B the corresponding steady-state whirling orbit

Fig. 24

Numerical simulation of the rotor temporal oscillations according to Fig. 21 when ${\mu }_{f}=0.6$ at the initial conditions ${q}_{1}(0)={q}_{2}\left(0\right)=\dot{{q}_{1}}\left(0\right)=\dot{{q}_{2}}\left(0\right)=0$: A temporal radial vibrations $r\left(\tau \right)=\sqrt{{q}_{1}^{2}\left(\tau \right)+{q}_{2}^{2}(\tau )}$, and B the corresponding steady-state whirling orbit

5 Conclusions

Nonlinear vibration control of a vertically supported Jeffcott rotor has been investigated in this article utilizing the Proportional Integral Resonant Controller ($\mathrm{PIRC}$). The proposed controller has been integrated into the considered rotor system via an eight-pole electromagnetic actuator. The control strategy is designed such that the PIRC-controller generates control currents according to the instantaneous lateral displacements of the rotating shaft, which are measured using suitable displacement sensors. These control currents are used to energize the 8-pole electromagnetic actuator in order to generate controllable electromagnetic attractive forces in the air-gap between the 8-pole housing and the rotating shaft in such a way that mitigates the undesired nonlinear vibrations of the considered rotor system. Relying on the electromagnetic and mechanical coupling between the Jeffcott system, the magnetic actuator, and the PIRC-controller, the whole system mathematical model is derived with the aid of both the classical mechanics' principle and the electromagnetic theory, where the rub-impact force between the rotating shaft and the 8-pole housing is included in the obtained model. Then, the derived discontinuous dynamical system has been investigated analytically and numerically. Sensitivity analysis for the different control parameters has been explored. In addition, the dynamical characteristics of the considered system have been investigated when the proposed control algorithm fails to prevent the rub-impact force between the rotor and stator. According to the above discussions, the following important remarks can be concluded:

• 1. The nonlinearity dominates the response of the uncontrolled Jeffcott system, where the system may suffer from the jump phenomenon, sensitivity to the initial conditions, and the existence of multiple periodic solutions at a specific range of the rotor angular speed.

• 2. The coupling of the PIRC-controller to the considered rotor system can reshape the rotor dynamics and modify its bifurcation characteristics according to the designed control gains. (${\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}, {\eta }_{1}, {\eta }_{2}, {\lambda }_{1}, {\lambda }_{2}$).

• 3. The controller's proportional gains (${\delta }_{1}, {\delta }_{3}$) can be used to avoid the strong oscillation amplitudes at the perfect resonance conditions via shifting the resonant peaks either to the right or the left of $\sigma =0$

• 4. The control gains (${\delta }_{2}, {\delta }_{3}$) and/or the feedback gains (${\eta }_{1}, {\eta }_{2}$) of the proposed PIRC- controller can be used to eliminate the catastrophic nonlinear bifurcation behaviors via increasing the linear and nonlinear damping parameters of the considered rotor system.

• 5. The optimal design for the control gains of the PIRC-controller can force the Jeffcott rotor to respond as a linear dynamical system with a single periodic attractor regardless of the rotor angular speed and disc eccentricity.

• 6. The failure of the PIRC-controller to keep the rotor vibration amplitudes smaller than the nominal air-gap size between the rotor and the 8-pole housing makes the rub and/or impact between the rotor and stator inevitable.

• 7. Strong transient oscillations may be resulting in a sustained rub-impact occurrence between the rotor and stator even if the steady-state amplitudes of these transient oscillations are smaller than the air-gap size between the rotor and stator.

• 8. The rotor system may oscillate with one of two vibration modes when the rub and/or impact occur depending on the magnitude of both the impact stiffness coefficient and dynamic friction coefficient with fixing the other parameters, where these modes are the full-annular-rub and the partial-rub-impact.

• 9. In general, the rotor system performs periodic-n or quasiperiodic motion in the case of the partial-rub-impact mode, otherwise, the system exhibits a periodic lateral vibration with circular forward whirling motion.

• 10. The controlled rotor system may lose its stability to respond with unbounded motion, which implies practically the destruction of the considered system if the interface between the rotor and stator is a rough surface with a dynamic friction coefficient ${\mu }_{f}\ge 0.6$.

Based on the above discussion, it is recommended to verify the above results experimentally soon. In addition, the application of this type of controller on the muti-degree-of-freedom rotor system will remain under the scope of future research work.

Appendices

Appendix A:

$$\rho_{10} = 4 + 8\cos^{2} (\alpha ) - 8\delta_{1} \cos^{2} (\alpha ) - 4\delta_{1} ,$$

$$\rho_{11} = 8\delta_{2} \cos^{2} (\alpha ) + 4\delta_{2} ,$$

$$\rho_{12} = 8\delta_{3}^{2} \cos^{4} (\alpha ) + 48\cos^{4} (\alpha ) + 16\delta_{1} \delta_{3} \cos^{4} (\alpha ) - 48\delta_{3} \cos^{4} (\alpha ) - 24\delta_{1} \cos^{4} (\alpha ),$$

$$\rho_{13} = 8\delta_{2}^{2} \cos^{4} (\alpha ) + 4\delta_{2}^{2} ,$$

$$\rho_{14} = 8\delta_{4}^{2} \cos^{4} (\alpha ),$$

$$\rho_{15} = 12\delta_{2} - 8\delta_{1} \delta_{2} - 16\delta_{1} \delta_{2} \cos^{4} (\alpha ) + 24\delta_{2} \cos^{4} (\alpha ),$$

$$\rho_{16} = 24\delta_{2} \cos^{4} (\alpha ) - 16\delta_{2} \delta_{3} \cos^{4} (\alpha ),$$

$$\rho_{17} = 48\delta_{4} \cos^{4} (\alpha ) - 16\delta_{3} \delta_{4} \cos^{4} (\alpha ) - 16\delta_{1} \delta_{4} \cos^{4} (\alpha ),$$

$$\rho_{18} = 16\delta_{2} \delta_{4} \cos^{4} (\alpha ),$$

$$\rho_{19} = 4\delta_{1}^{2} + 8 - 24\delta_{1} \cos^{4} (\alpha ) + 16\cos^{4} (\alpha ) - 12\delta_{1} + 8\delta_{1}^{2} \cos^{4} (\alpha ),$$

$$\rho_{20} = 4 + 8\cos^{2} (\alpha ) - 8\delta_{3} \cos^{2} (\alpha ) - 4\delta_{3} ,$$

$$\rho_{21} = 8\delta_{4} \cos^{2} (\alpha ) + 4\delta_{4} ,$$

$$\rho_{22} = 8\delta_{1}^{2} \cos^{4} (\alpha ) + 48\cos^{4} (\alpha ) + 16\delta_{1} \delta_{3} \cos^{4} (\alpha ) - 48\delta_{1} \cos^{4} (\alpha ) - 24\delta_{3} \cos^{4} (\alpha ),$$

$$\rho_{23} = 8\delta_{4}^{2} \cos^{4} (\alpha ) + 4\delta_{4}^{2} ,$$

$$\rho_{24} = 8\delta_{2}^{2} \cos^{4} (\alpha ),$$

$$\rho_{25} = 12\delta_{4} - 8\delta_{3} \delta_{4} - 16\delta_{3} \delta_{4} \cos^{4} (\alpha ) + 24\delta_{4} \cos^{4} (\alpha ),$$

$$\rho_{26} = 24\delta_{4} \cos^{4} (\alpha ) - 16\delta_{1} \delta_{4} \cos^{4} (\alpha ),$$

$$\rho_{27} = 48\delta_{2} \cos^{4} (\alpha ) - 16\delta_{1} \delta_{2} \cos^{4} (\alpha ) - 16\delta_{2} \delta_{3} \cos^{4} (\alpha ),$$

$$\rho_{28} = 16\delta_{2} \delta_{4} \cos^{4} (\alpha ),$$

$\rho_{29} = 4\delta_{3}^{2} + 8 - 24\delta_{3} \cos^{4} (\alpha ) + 16\cos^{4} (\alpha ) - 12\delta_{3} + 8\delta_{3}^{2} \cos^{4} (\alpha )$.

Appendix B:

$$\begin{aligned} \frac{{\partial g_{1} }}{{\partial a_{11} }} = & - \frac{1}{2}\mu + \frac{1}{8}b_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{2}\frac{{\eta_{1} \rho_{11} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}b_{10}^{2} \rho_{12} \sin (2\phi_{10} - 2\phi_{20} ) - \frac{3}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{1}{8}\frac{{b_{10}^{2} \eta_{2}^{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{8}\frac{{b_{10}^{2} ab^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{3}{8}\frac{{a_{10}^{2} \eta_{1} \rho_{15} }}{{\lambda_{1}^{2} + 1}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \rho_{16} }}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{b_{10}^{2} \eta_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} - \frac{1}{8}\frac{{b_{10}^{2} \eta_{1} \lambda_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} \\ & \; - \frac{1}{8}\frac{{b_{10}^{2} \eta_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{8}\frac{{b_{10}^{2} \eta_{2} \lambda_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{8}\frac{{b_{10}^{2} ab^{2} \eta_{1} \eta_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{8}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{8}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{1} }}{{\partial \varphi_{11} }} = & \frac{1}{4}a_{10} b_{10}^{2} \lambda \cos (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}a_{10} b_{10}^{2} \rho_{12} \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{1}{2}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} \\ & \; - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \lambda_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2} \lambda_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} \\ & \; - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{2}E\Omega^{2} \cos (\phi_{10} ), \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{1} }}{{\partial \varphi_{21} }} = & - \frac{1}{4}a_{10} b_{10}^{2} \lambda \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}a_{10} b_{10}^{2} \rho_{12} \cos (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{2}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \lambda_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{2} \lambda_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a_{10} b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{2} }}{{\partial a_{11} }} = & - \frac{1}{4}a_{10} b_{10} \lambda \sin (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}a_{10} b_{10} \rho_{22} (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; - \frac{1}{2}\frac{{a_{10} b_{10} a^{2} b\eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{2}\frac{{a_{10} b_{10} \eta_{2} \rho_{26} }}{{\lambda_{2}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{2}\frac{{a_{10} b_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} cos(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} b_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{gathered} \frac{{\partial g_{2} }}{{\partial b_{11} }} = - \frac{1}{2}\mu - \frac{1}{8}a_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{2}\frac{{\eta_{2} \rho_{21} }}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}a_{10}^{2} \rho_{22} \sin (2\phi_{10} - 2\phi_{20} ) - \frac{3}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} \\ - \frac{1}{8}\frac{{a_{10}^{2} \eta_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{8}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ - \frac{3}{8}\frac{{b_{10}^{2} \eta_{2} \rho_{25} }}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{2} \rho_{26} }}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}\frac{{a_{10}^{2} \eta_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{8}\frac{{a_{10}^{2} \eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} \\ - \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ + \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} cos(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ + \frac{1}{8}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{gathered}$$

$$\begin{aligned} \frac{{\partial g_{2} }}{{\partial \varphi_{11} }} = & - \frac{1}{4}a_{10}^{2} b_{10} \lambda \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}a_{10}^{2} b_{10} \rho_{22} \cos (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{1}{2}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \lambda_{1} \rho_{24} sin(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{2} \rho_{26} sin(2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{2} \lambda_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \rho_{27} sin(2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \lambda_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} }}{{\lambda_{1}^{2} + 1}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} sin(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} sin(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{gathered} \frac{{\partial g_{2} }}{{\partial \varphi_{21} }} = \frac{1}{4}a_{10}^{2} b_{10} \lambda \cos (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}a_{10}^{2} b_{10} \rho_{22} \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ - \frac{1}{2}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \lambda_{1} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} \\ - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{2} \lambda_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{2}^{2} + 1}} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \lambda_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{\lambda_{1}^{2} + 1}} \\ - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} b_{10} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ - \frac{1}{4}\frac{{a_{10}^{2} b_{10} a^{2} b\eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{2}E\Omega^{2} \sin (\phi_{20} ), \\ \end{gathered}$$

$$\frac{{\partial g_{3} }}{{\partial a_{11} }} = - \frac{3}{4}a_{10} \lambda + \frac{1}{4}\frac{{a_{10} \eta_{1}^{2} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{3}{4}\frac{{a_{10} \eta_{1} \lambda_{1} \rho_{13} }}{{(\lambda_{1}^{2} + 1)^{2} }} + + \frac{3}{4}\frac{{a_{10} \eta_{1} \lambda_{1} \rho_{15} }}{{(\lambda_{1}^{2} + 1)}} + \frac{3}{4}a_{10} \rho_{19} + \frac{1}{{2a_{10}^{2} }}E\Omega^{2} \cos (\phi_{10} ),$$

$$\begin{aligned} \frac{{\partial g_{3} }}{{\partial b_{11} }} = & - \frac{1}{2}b_{10} \lambda - \frac{1}{8}b^{2} \lambda \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{2}b_{10} b^{2} \rho_{12} + \frac{1}{4}b_{10} \rho_{12} \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{2}\frac{{b_{10} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{1}{2}\frac{{b_{10} \eta_{2}^{2} \rho_{14} }}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b_{10} \eta_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{2}\frac{{b_{10} \eta_{2}^{2} \lambda_{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{1}{4}\frac{{b_{10} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{2}\frac{{b_{10} \eta_{1} \lambda_{1} \rho_{16} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10} \eta_{1} \lambda_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b_{10} \eta_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{2}\frac{{b_{10} \eta_{2} \lambda_{2} \rho_{17} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10} \eta_{2} \lambda_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{b_{10} \eta_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{2}\frac{{b_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b_{10} \eta_{1} \eta_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{3} }}{{\partial \varphi_{11} }} = & \frac{1}{4}b_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}b_{10}^{2} \rho_{12} \sin (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; - \frac{1}{2}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \sin \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \lambda_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{2} \lambda_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{{2a_{10} }}E\Omega^{2} \sin (\phi_{10} ), \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{3} }}{{\partial \varphi_{21} }} = & - \frac{1}{4}b_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}b_{10}^{2} \rho_{12} \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} \\ & \; + \frac{1}{2}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2} \rho_{14} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{2}^{2} \lambda_{2}^{2} \rho_{14} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \lambda_{1} \rho_{16} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \rho_{16} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{2} \lambda_{2} \rho_{17} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{2} \rho_{17} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \rho_{18} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{b_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{18} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}, \\ \end{aligned}$$

$$\begin{gathered} \frac{{\partial g_{4} }}{{\partial a_{11} }} = - \frac{1}{2}a_{10} \lambda - \frac{1}{4}a_{10} \lambda \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{2}a_{10} \rho_{22} + \frac{1}{4}a_{10} \rho_{22} \cos (2\phi_{10} - 2\phi_{20} ) + \frac{1}{2}\frac{{a_{10} \eta_{1} \lambda_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} \\ + \frac{1}{2}\frac{{a_{10} \eta_{1}^{2} \rho_{24} }}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10} \eta_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{2}\frac{{a_{10} \eta_{1}^{2} \lambda_{1} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ + \frac{1}{4}\frac{{a_{10} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{2}\frac{{a_{10} \eta_{2} \lambda_{2} \rho_{26} }}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} \eta_{2} \lambda_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ - \frac{1}{4}\frac{{a_{10} \eta_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{2}\frac{{a_{10} \eta_{1} \lambda_{1} \rho_{27} }}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} \eta_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} \eta_{1} \lambda_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ + \frac{1}{2}\frac{{a_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} }}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} sin(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ + \frac{1}{4}\frac{{a_{10} \eta_{1} \eta_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} sin(2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}. \\ \end{gathered}$$

$$\frac{{\partial g_{4} }}{{\partial b_{11} }} = \frac{3}{4}b_{10} \lambda + \frac{1}{4}\frac{{b_{10} \eta_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{3}{4}\frac{{b_{10} \eta_{2}^{2} \lambda_{2}^{2} \rho_{23} }}{{(\lambda_{2}^{2} + 1)^{2} }} + \frac{3}{4}\frac{{b_{10} \eta_{2} \lambda_{2} \rho_{25} }}{{(\lambda_{2}^{2} + 1)}} + \frac{3}{4}b_{10} \rho_{29} - \frac{1}{{2b_{10}^{2} }}E\Omega^{2} \sin (\phi_{20} ).$$

$$\begin{aligned} \frac{{\partial g_{4} }}{{\partial \varphi_{11} }} = \; + \frac{1}{4}a_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}a_{10}^{2} \rho_{22} \sin (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; + \frac{1}{2}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{a_{10}^{2} \eta_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}}. \\ \end{aligned}$$

$$\begin{aligned} \frac{{\partial g_{4} }}{{\partial \varphi_{21} }} = & - \frac{1}{4}a_{10}^{2} \lambda \sin (2\phi_{10} - 2\phi_{20} ) + \frac{1}{4}a_{10}^{2} \rho_{22} \sin (2\phi_{10} - 2\phi_{20} ) - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} \\ & \; - \frac{1}{2}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1} \rho_{24} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1}^{2} \lambda_{1}^{2} \rho_{24} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)^{2} }} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{2} \lambda_{2} \rho_{26} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} \eta_{2} \rho_{26} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \rho_{27} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \lambda_{1} \rho_{27} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \lambda_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} - \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{2} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \rho_{28} \sin (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} \\ & \; + \frac{1}{4}\frac{{a_{10}^{2} \eta_{1} \eta_{2} \lambda_{1} \rho_{28} \cos (2\phi_{10} - 2\phi_{20} )}}{{(\lambda_{1}^{2} + 1)(\lambda_{2}^{2} + 1)}} + \frac{1}{{2b_{10} }}E\Omega^{2} \cos (\phi_{20} ). \\ \end{aligned}$$