Parametric instability of a Jeffcott rotor with rotationally asymmetric inertia and transverse crack

Abstract

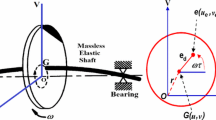
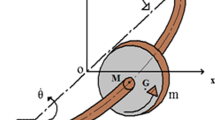
Both the rotationally asymmetric inertia and transverse crack frequently appear in the rotor system. The parametric excitations induced by this two features cause instability and severe vibration under certain operating conditions. Thus, the parametric instability of a Jeffcott rotor with asymmetric disk and open transverse crack is studied analytically. The vibration equations of four degrees-of-freedom of the system are established, and the stiffness coefficients of cracked rotor shaft are derived based upon the compliance method and strain energy release rate method. Then, utilizing the harmonic balance method and Taylor expansion technique, the unstable widths of simple and combination instability regions (SIR and CIR) are solved approximately. For a practical rotor system, the approximate unstable widths are verified by the Floquet numerical analysis. The effects of crack depth and position upon the unstable widths are discussed, and the conditions for zero unstable points (ZUPs) are given: Besides the asymmetric angle should be π/2 (for SIR) or 0 (for CIR), the relationships between the inertia asymmetry and crack parameters (depth and position) are also presented analytically. These results would be useful for crack detection and instability control of the asymmetric rotor-bearing system.

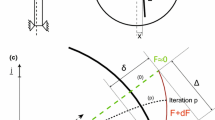
Appendix: Numerical determination of unstable regions based upon the Floquet theory

By taking $\mathbf{y}(t)=[\dot{\mathbf{q}}(t)\ \mathbf{q}(t)]^{T}$, Eq. (11) could be transformed into the state space as

$$ \mathbf{A}(t)\dot{\mathbf{y}}=\mathbf{B}(t)\mathbf{y} $$

(33)

in which the coefficient matrices A(t) and B(t) are expressed as

(34)

(35)

where

(36a)

(36b)

(36c)

The classical method to study the parametric stability uses the Floquet theory. To avoid the additional time domain processing and to keep the inherent advantages of the frequency method (low computational cost and speed compared with the direct integration), it is recommended to use a frequency method for the determination of the stability. According to the Floquet theory, a solution of Eq. (33) can be written as a product of an exponential part and 2π/(2Ω)=π/Ω periodic part. Representing the periodic part by its complex Fourier series expansion, this solution can be written as

$$ \mathbf{y}(t)=\textrm{e}^{2\rho\varOmega t} \sum_{k=-\infty}^{\infty}\textbf {y}_k \textrm{e}^{2\textrm{i}k\varOmega t} $$

(37)

where $\textrm{i}=\sqrt{-1}$, ρ represents the Floquet (or characteristic) exponent and y _k are the complex Fourier coefficients’ vectors. Considering the coefficient matrices A(t) and B(t) are periodic with single harmonic frequency 2Ω, thus they could be rewritten by finite complex Fourier series

(38)

(39)

Substituting Eqs. (37)–(39) into Eq. (33), and simplifying by setting the same harmonic coefficients zero, then one can obtain the following infinite-dimensional eigenvalue problems about ρ as

$$ (\boldsymbol{\varLambda}+\rho\boldsymbol{\varUpsilon})\textbf{Y}=\mathbf{0} $$

(40)

in which

$$\textbf{Y}= \bigl[\cdots\quad\mathbf{y}_{-4}^T\quad \mathbf{y}_{-3}^T\quad\mathbf{y}_{-2}^T\quad\mathbf{y}_{-1}^T\quad \mathbf{y}_{0}^T\quad\mathbf{y}_{1}^T\quad\mathbf{y}_{2}^T\quad \mathbf{y}_{3}^T\quad\mathbf{y}_{4}^T\quad\cdots \bigr]^T, $$

and

(41)

(42)

where $\boldsymbol{\varLambda}^{(0)}_{k}=-\mathbf{B}_{0}+\textrm{i}2k\varOmega \mathbf{A}_{0}$, $\boldsymbol{\varLambda}^{(1)}_{k}=-\mathbf{B}_{-2} + \textrm{i}2k\varOmega\mathbf{A}_{-2}$ and $\boldsymbol{\varLambda}^{(2)}_{k}=- \mathbf{B}_{2}+\textrm{i}2k\varOmega\mathbf{A}_{2}$ (k=…,−1,0,1,…). In order to get approximate numerical eigenvalues for the stability analysis, Eq. (40) should be truncated into a finite-dimensional one. In practice, the first few harmonics are needed to meet the precision requirements. The eigenvalues of Eq. (40) are complex. If the system is stable, the real part of all eigenvalues ρ is negative and the exponential part diminishes as the time passes. On the other hand, if at least one of the eigenvalues has a positive part, the system is unstable.