1 Introduction

Superfluidity in liquid \(^{4}\)He was reported in 1938 by Kapitza [1] and independently by Allen and Misener [2] who for the first time found that the viscosity of \(^{4}\)He drops below \(T_{\lambda }=2.17\) K. Almost 20 years before the Bardeen–Cooper–Schrieffer (BCS) [3] theory, Kapitza also found that this phenomenon is analogous to that of a superconductor (SC). In turn, London [4] proposed that \(^{4}\)He is in a phase II, i.e., below \(T_{\lambda }\), and has a Bose–Einstein condensation (BEC) behavior. The calculated BEC critical temperature of He II is \(T_{BEC}=3.1\) K and so is thus slightly higher than \(T_{\lambda }\). Landau [5,6,7] introduced the concept of two fluids for \(^{4}\)He but with no connection with a BEC. Bogoliubov [8] had already shown that in a degenerate Bose gas with weak interactions there is really a BEC. Also, the existence of superfluidity turns out to be linked with BEC [9] —and indeed with Bose statistics.

In the early 1970s Leggett [10, 11], based on experiments by Osheroff et al. [12], noted that \(^{3}\)He atoms could in fact form BCS-like pairs. He concluded that the liquid \(^{3}\)He phase must show [13] all phenomena associated with a BCS-like phase; he later derived [14] two basic crossover equations at \(T=0\) for any many-fermion system. In 1964 Schrieffer [15] was apparently the first to state that one must solve two equations, a gap-like and a number equation. This was perhaps the first BCS-Bose crossover theory. It was further developed by Keldysh [16] (1965), Popov [17] (1966), Labbé et al. [18] (1967), Eagles [19] (1969), Miyake [20] (1983), Nozières [21] (1985), Ranninger et al. [22] (1988), Randeria et al. [23, 24] (1989), Van der Marel [25] (1990), Bar-Yam [26, 27] (1991), Drechsler and Zwerger [28] (1992), Haussmann [29] (1993), Pistolesi and Strinati [30] (1996) among others.

The London penetration depth \(\lambda _{L}=(m_{e}/\mu _{0}n_{s}e^{2})^{1/2}\) is the distance below a SC surface where an external magnetic field B vanishes like \(B=B_{0}\exp (-x/\lambda _{L})\) where x is the depth inside the SC. Here \(m_{e}\) is the electron mass, e the elementary electron charge, \(\mu _{0}\) the magnetic susceptibility and \(n_{s}\) the superconducting electron-number density. The latter is linked with the “superelectrons”[31] of the Landau theory. In 1989 Uemura et al. [32] found a linear relationship between the critical temperature \(T_{c}\) of a SC and its superfluid number density \(n_{s}\). It was concluded [33] that, in general, the magnitude of \(T_{c}\) depends on \(n_{s}(T)\) rather than on the interelectronic coupling strength as long claimed to be true. Later, in 2016 Božović et al. [34] came to agree with these conclusions. The well-known Uemura graph [32, 33] relates the \(T_{c}\) of a SC with its superfluid number-density as \(n_{s}^{2/3}/(m^{*}/m_{e})\) where \(m^{*}\) is the effective electron mass and \(m_{e}\) its bare mass. Uemura et al. [32] [33] then suggested a crossover theory to correctly describe SCs. We refer to the crossover “BCS-Bose” [35, 36] instead of the more common “BCS-BEC” since a BEC cannot occur in either two dimensions (2D) nor in one dimension (1D) while bosons can form in both instances.

Here we corroborate the Kapitza concept that superfluidity is analogous with superconductivity, by calculating the SC superfluid density \(n_{s}(T)\) for \(T\le T_{c}\) based on the generalized Bose–Einstein condensation (GBEC) theory [37,38,39,40,41] that includes as a special case the BCS-Bose crossover theory and also an extended version with two-hole Cooper pairs (2hCPs) [42] along with the more common two-electron Cooper pairs (2eCPs) ones.

In Sect. 2 the GBEC theory is recalled as it leads to the BCS-Bose extended crossover equations as a special case; in Sect. 3 the superfluid density \(n_{s}(T)\) is introduced for two kinds of superfluids, one for 2eCPs and another for 2hCPs, the latter with an opposite charge carrier sign with respect to 2eCPs. Here we report calculated \(n_{s}(T)\) results in 3D with a boson quadratic-dispersion relation and in 2D with a linear-dispersion one. Comparisons are made with experimental data in 3D and 2D for some elemental and cuprate SCs. In Sect. 4 some discussion and our conclusions with future work are mentioned.

2 Generalized Bose–Einstein condensation theory

The GBEC theory starts from an ideal, noninteracting boson-fermion (BF) ternary gas mixture of free/unbound fermions (here electrons) plus 2eCPs and 2hCPs as bosons. To this one adds specific BF vertex interactions [37, 38] leading to a fully-interacting gas defined by the hamiltonian \(H=H_{0}+H_{int}\) where \(H_{0}\) stands for the ideal ternary gas and \(H_{int}\) for the BF interactions.

The ideal ternary gas hamiltonian is

$$\begin{aligned} H_{0}=\sum _{{\mathbf {k}}_{1},s_{1}}\epsilon _{{\mathbf {k}}_{1}}a_{{\mathbf {k}} _{1},s_{1}}^{\dagger }a_{{\mathbf {k}}_{1},s_{1}}^{{}}+\sum _{{\mathbf {K}} }E_{+}(K)b_{{\mathbf {K}}}^{\dagger }b_{{\mathbf {K}}}^{{}}-\sum _{{\mathbf {K}} }E_{-}(K)c_{{\mathbf {K}}}^{\dagger }c_{{\mathbf {K}}}^{{}} \end{aligned}$$
(1)

here \({\mathbf {K}}\equiv {\mathbf {k}}_{1}+{\mathbf {k}}_{2}\) is the center-of-mass momentum (c.m.m.) wavevector of two fermions, where \(K \equiv \vert {\mathbf {K}}\vert\), and \({\mathbf {k}}\equiv \frac{1}{2}({\mathbf {k}}_{1}-{\mathbf {k}}_{2})\) as their relative wavevector while \(\epsilon _{k_{1}}\equiv \hbar ^{2}k_{1}^{2}/2m\) is the energy of a single fermion and \(E_{\pm }(K)=E_{\pm }(0)+\hbar ^{2}K^{2}/4m\) the bosonic 2e/2hCPs phenomenological energies with \(E_{\pm }(0)\) the bosonic energies for \(K=0\). Here \(a_{{\mathbf {k}} _{1},s_{1}}^{\dagger }(a_{{\mathbf {k}}_{1},s_{1}}^{{}})\) are the creation (annihilation) fermion operators, and \(b_{{\mathbf {K}}}^{\dagger }\)(\(b_{ {\mathbf {K}}}^{{}}\)) and \(c_{{\mathbf {K}}}^{\dagger }\)(\(c_{{\mathbf {K}}}^{{}}\)) the boson operators for 2e/2hCPs. CPs are treated here as actual bosons in contrast with the BCS [3] “correlated” pairs which depend on their relative wavevector \({\mathbf {k}}\) and also on their total \({\mathbf {K}}\) wavevector whereas the original CPs [43] depend only on \({\mathbf {K}}\) [40, 41]. The former do not satisfy Bose commutation relations [3] but the latter are consistent with Bose statistics [40, 41]. The interaction hamiltonian \(H_{int}\) has four BF interaction vertices, one with two-fermion/one boson creation-annihilation operators representing how the unbound electrons (subindex \(+\)) or holes (subindex −) combine to form 2e/2hCPs in any d-dimensional system of size L. Thus

$$\begin{aligned} H_{int}= \,& {} L^{-d/2}\sum _{{\mathbf {k}},{\mathbf {K}}}f_{+}(k)\{a_{{\mathbf {k}}+\frac{ 1}{2}{\mathbf {K}},\uparrow }^{\dagger }a_{-{\mathbf {k}}+\frac{1}{2}{\mathbf {K}} ,\downarrow }^{\dagger }b_{{\mathbf {K}}}+a_{-{\mathbf {k}}+\frac{1}{2}{\mathbf {K}} ,\downarrow }^{{}}a_{{\mathbf {k}}+\frac{1}{2}{\mathbf {K}},\uparrow }^{{}}b_{ {\mathbf {K}}}^{\dagger }\} \nonumber \\&\quad +\,&L^{-d/2}\sum _{{\mathbf {k}},{\mathbf {K}}}f_{-}(k)\{a_{{\mathbf {k}}+\frac{1}{2} {\mathbf {K}},\uparrow }^{\dagger }a_{-{\mathbf {k}}+\frac{1}{2}{\mathbf {K}} ,\downarrow }^{\dagger }c_{{\mathbf {K}}}^{\dagger }+a_{-{\mathbf {k}}+\frac{1}{2} {\mathbf {K}},\downarrow }^{{}}a_{{\mathbf {k}}+\frac{1}{2}{\mathbf {K}},\uparrow }^{{}}c_{{\mathbf {K}}}^{{}}\}. \end{aligned}$$
(2)

where \(f_{\pm }(k)\) are the BF interaction functions defined in Refs. [37, 38] for electrons/holes. Note that \(H_{int}\) is reminiscent of the Fröhlich interaction hamiltonian (or Dirac in QED [44] p. 36) involving two-fermion operators with a one-boson operator, but with two kinds of CPs instead of phonons/photons. Contrasting with Fröhlich and Dirac, there is no conservation law for the number of unbound electrons, i.e., \([H_{int},\sum _{{\mathbf {k}}_{1},s_{1}}\epsilon _{{\mathbf {k}}_{1}}a_{ {\mathbf {k}}_{1},s_{1}}^{\dagger }a_{{\mathbf {k}}_{1},s_{1}}^{{}}]\ne 0\).

One can consider a simpler reduced \(H_{red}\) that may be written by neglecting nonzero K values and ignoring those bosons with \(K\ne 0\) in \(H_{int}\)—but not also in \(H_{0}\) as assumed in BCS theory. Applying the Bogoliubov recipe of replacing the zero-K creation operators \(b_{{\mathbf {0}}}^{\dagger }\) and \(c_{{\mathbf {0}}}^{\dagger }\) for the 2e/2hCP bosons by c-numbers \(\sqrt{N_{0}}\) and \(\sqrt{M_{0}}\) with \(N_{0}\) and \(M_{0}\) the numbers of 2e/2hCP \(K=0\) bosons. Then, using the Bogoliubov-Valatin transformation [45, 46] allows exactly diagonalizing [39] the reduced dynamical operator \({\hat{H}}_{red}-\mu {\hat{N}}\) with \({\hat{N}}\) the total-electron-number operator and \(\mu\) a Lagrange multiplier. Bringing the neglected c.m.m. \(K\ne 0\) terms back into the picture was recently implemented with two-time-Green-function techniques [47,48,49,50].

The thermodynamic (or Landau) potential of the grand-canonical statistical ensemble is now \(\Omega (T,L^{d},\mu ,N_{0},M_{0}) = -k_{B}T\ln \left[ \mathrm {Tr}(\exp \{-\beta ({\hat{H}}_{red}-\mu {\hat{N}})\})\right]\) where Tr means “trace,” \(L^{d}\) is the system volume with d = 3, 2, 1 and \(\beta \equiv 1/k_{B}T\) with \(k_{B}\) the Boltzmann constant and \(\mu\) the electronic chemical potential. Thus \(\Omega\) can now be evaluated explicitly. The Helmholtz free energy is then \(F(T,L^{d},\mu ,N_{0},M_{0})\equiv \Omega (T,L^{d},\mu ,N_{0},M_{0})+\mu N\). Taking the negative partial derivative of \(\Omega\) with respect to \(\mu\), and also minimizing the Helmholtz free energy wrt \(N_{0}\) and \(M_{0}\), gives

$$\begin{aligned} -\frac{\partial \Omega }{\partial \mu }=N, \qquad\frac{\partial F}{ \partial N_{0}}=0, \qquad \frac{\partial F}{\partial M_{0}}=0. \end{aligned}$$
(3)

The first equation is familiar from quantum-statistical mechanics and ensures net-charge conservation, i.e., gauge invariance [51], not guaranteed in BCS theory. The last two equations of (3) are needed to have a stable thermodynamic state.

From (3) the GBEC theory [37] gives three coupled, transcendental equations for three unknown T-dependent functions, the \(\mu (T)\) and the 2eCP and 2hCP Bose–Einstein (BE) condensate (i.e., with \(K=0\)) number densities \(N_{0}(T)/L^{3}\equiv n_{0}(T)\) and \(M_{0}(T)/L^{3}\equiv m_{0}(T)\) for 3D. The first equation of (3) leads to a number equation for the ternary-gas mixture in terms of the total electron-number density \(N/L^{3}\equiv n\) and is

$$\begin{aligned} n=2\left[ n_{0}(T)+n_{B+}(T)-m_{0}(T)-m_{B+}(T)\right] +n_{f}(T) \end{aligned}$$
(4)

where \(n_{B+}(T)\) and \(m_{B+}(T)\) refer to the number densities of excited 2eCP and 2hCP bosons with \(K>0\). The free/unbound electron-number density \(n_{f}(T)\) turns out to be

$$\begin{aligned} n_{f}(T)\equiv & {} \int _{0}^{\;\infty }d\epsilon N(\epsilon )\left[ 1-\frac{ \epsilon -\mu }{E(\epsilon )}\tanh \{{\tfrac{1}{2}}\beta E(\epsilon )\} \right] \nonumber \\&\xrightarrow [{T \rightarrow 0}]{}&\left( 2mE_{f}\right) ^{3/2}/3\pi ^{2}\hbar ^{3}\equiv n_{f}. \end{aligned}$$
(5)

Here, \(E_{f}\) is viewed as a “pseudo-Fermi” energy as it refers only to free electrons at T = 0 and \(E(\epsilon )\equiv \sqrt{(\epsilon -\mu )^{2}+\Delta ^{2}(T)}\) is the gapped Bogoliubov fermion-dispersion relation containing the electronic energy gap

$$\begin{aligned} \Delta (T)\equiv f_{+}(\epsilon )\sqrt{n_{0}(T)}+f_{-}(\epsilon )\sqrt{m_{0}(T)} \end{aligned}$$
(6)

where \(f_{\pm }(\epsilon )\) are BF vertex-interaction constants. For condensed 2eCPs

$$f_{ + } (\epsilon) = \left\{ {\begin{array}{*{20}l} {f\;} \hfill & {{\text{if}}\;{\text{E}}_{{\text{f}}} < \epsilon < {\text{E}}_{{\text{f}}} + \delta \epsilon } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(7)

and for condensed 2hCPs

$$f\_(\epsilon) = {\text{ }}\left\{ {\begin{array}{*{20}l} f \hfill & {{\text{if}}\;{\text{E}}_{{\text{f}}} - \delta\epsilon {\text{ < }} \epsilon {\text{ < E}}_{{\text{f}}} } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(8)

as originally defined in Refs. [37, 38]. Here f was taken as \(f\equiv f_{+}=f_{-}\). Here \(E_f\) and \(\delta \epsilon\) are phenomenological energies associated with the free/unbound electrons in the BF gas mixture. \(E_f\) is related with the number density of the unbound fermions of the system \(n_f(T=0) \equiv n_f\) just as in (5). This number of unbound fermions is necessary in the calculation of the energy gap as well as in the chemical potential to obtain the superfluid density. While \(\delta \epsilon\) is the energy range where the BF interactions occur and can be identified with the Debye energy of the lattice. Note that \(E_{f}\) coincides exactly with the Fermi energy \(E_{F}\) of an ideal fermion gas when \(n_{0}(T)=m_{0}(T)\) and \(n_{B+}(T)=m_{B+}(T)\), i.e., for a 50%–50% gas mixture of 2eCPs/2hCPs. For unbound electrons in 3D the density of states (DOS) is \(N(\epsilon )=\left( m^{3/2}/2^{1/2}\pi ^{2}\hbar ^{3}\right) \epsilon ^{1/2}\) and for 2D it is the constant \(N(\epsilon )=m/2\pi \hbar ^{2}\).

References [52, 53] introduce a generalized energy dispersion relation for the bosonic CPs. In the weak-coupling limit the dispersion relation can be expanded for small K in a series around K. In 2D one has \(\varepsilon _{K}\underset{K\rightarrow 0}{\longrightarrow } \varepsilon _{0}+\tfrac{2}{\pi }\hbar v_{F}K+O(K^{2})\) where \(v_{F}\) is the Fermi velocity. If \(\delta \epsilon \ll E_{F}\) is the energy range over which the BF interaction acts in 3D and gives \(\varepsilon _{K}\underset{ K\rightarrow 0}{\longrightarrow }\varepsilon _{0}+\tfrac{1}{2}\hbar v_{F}K+O(K^{2})\).

For an ideal Bose gas (IBG) consisting of pairs of fermions \(T_{c}\) is nonzero if \(d>s\) [54] where d is the gas dimensionality and s the exponent of the bosonic CP dispersion-relation energy. As in Ref. [54] in 3D one has \(s=2\) and in 2D \(s=1\). With this one recovers the results of an IBG of two bound electrons as CPs if all electrons are assumed paired [55], i.e., with no unbound fermions left in the gas.

The excited (or noncondensed) boson number densities then become

$$\begin{aligned}&n_{B+}(T)\equiv \int _{0+}^{\infty }d\varepsilon M(\varepsilon )\big [\exp \beta [{\mathcal {E}}_{+}(\varepsilon )]-1\big ]^{-1} \end{aligned}$$
(9)
$$\begin{aligned}&m_{B+}(T)\equiv \int _{0+}^{\infty }d\varepsilon M(\varepsilon )\big [\exp \beta [{\mathcal {E}}_{-}(\varepsilon )]-1\big ]^{-1} \end{aligned}$$
(10)

where \(M(\varepsilon )\) is the bosonic DOS and \({\mathcal {E}}_{\pm }(\varepsilon )=\pm 2E_{f}+\delta \varepsilon \mp 2\mu +\varepsilon\) the energy of excited 2e/2hCPs. For the 3D IBG with \(s=2\) one has

$$\begin{aligned} M(\varepsilon )=(2m^{3/2}/\pi ^{2}\hbar ^{3})\sqrt{\varepsilon } \end{aligned}$$
(11)

and in 2D with \(s=1\) [54]

$$\begin{aligned} M(\varepsilon )=2\pi \left( \delta \epsilon /2{\tilde{G}}_{2D}\hbar v_{F}\right) ^{2}\varepsilon +{\mathcal {O}}(\varepsilon ^{2}). \end{aligned}$$
(12)

We introduce \({\tilde{G}}\) a BF dimensionless strength interaction in 2D which in turn is related with the BF vertex-interaction constants f as

$$\begin{aligned} {\tilde{G}}_{2D}\equiv f^{2}m_{e}/8\pi \hbar ^{2}E_{F} \qquad \qquad {\tilde{G}}_{3D}\equiv f^{2}m_{e}^{3/2}/2^{5/2}\pi ^{2}\hbar ^{3}E_{F}^{1/2} \end{aligned}$$
(13)

where the second equation is in 3D, last defined in Refs. [37, 38]. The Bose distributions in (9) and (10) are clear indications of the bosonic nature of both kinds of CPs. In 3D the BF strength interaction can be related with the BCS dimensionless coupling paremeter \(\lambda _{BCS}\) as \(G_{3D} = \lambda _{BCS}\delta\epsilon_{3D}/2\) and in 2D as \(G_{2D} = \lambda_{BCS}\delta\epsilon_{2D}/4\).

The second equation in (3) gives a gap-like equation for 2eCPs

$$\begin{aligned} 2\sqrt{n_{0}(T)}[2E_{f}+\delta \epsilon -2\mu (T)]=\int _{0}^{\infty }d\epsilon N(\epsilon )\frac{\Delta (\epsilon )f_{+}(\epsilon )}{E(\epsilon ) }\tanh \left[ \tfrac{1}{2}\beta E(\epsilon )\right] \end{aligned}$$
(14)

and the third equation in (3) the same, but for 2hCPs

$$\begin{aligned} 2\sqrt{m_{0}(T)}[2\mu (T)-2E_{f}+\delta \epsilon ]=\int _{0}^{\infty }d\epsilon N(\epsilon )\frac{\Delta (\epsilon )f_{-}(\epsilon )}{E(\epsilon ) }\tanh \left[ \tfrac{1}{2}\beta E(\epsilon )\right] . \end{aligned}$$
(15)

We then have three special cases, namely

  1. (i)

    50%–50% proportions between 2eCPs and 2hCPs, i.e., \(n_0(T) = m_0(T)\) and \(n_{B+}(T) = m_{B+}(T)\) solving simultaneously (14) plus (15) with (4),

  2. (ii)

    100%–0%, i.e., \(m_0(T)=0\) solving simultaneously (14) with (4) and

  3. (iii)

    0%–100%, i.e., \(n_0(T)=0\) solving simultaneously (15) with (4).

The set of equations (14), (15) and (4) are called as the extended BCS-Bose crossover equations with explicit inclusion of 2hCPs [42] and contains a dimensionless coupling parameter \(n/n_f\) with n the total number density and \(n_f\) that for unbound electrons at zero absolute temperature. We found two distinct coupling regimes, namely i) weak coupling for \(n/n_{f}=1\) when all electrons are unbound, albeit like “correlated ”pairs as in BCS theory, with \(\mu (T=0)=E_{F}\); ii) strong coupling when \(n/n_{f} \rightarrow \infty\) as when, e.g., \(n_{f} \rightarrow 0\), meaning that all electrons are paired into CPs implying an IBG consisting of 2eCPs when \(\mu (T)/E_{F}\rightarrow 0\). Here \(n/n_{f}=10^{6}\) is virtually the strong-coupling extreme; and iii) an intermediate regime between weak- and strong-coupling when \(1<n/n_{f}<\infty\). Varying this parameter from \(n/n_f = 1\) one can describe elemental superconductors. Changing \(n/n_f\) slightly from unity one can address SCs like Pb and Hg which are known as “bad actors” [56] in BCS theory.

In the extended BCS-Bose crossover one calculates [57] the ratio \(T_{c}/T_{F}\equiv k_{B}T_{c}/E_{F}\) for several elemental superconductors including the BCS theory “bad actors”  Hg and Pb. This was reported in Ref. [57] for the energy gap in the 50%–50% case and found to agree to with the data, whereas the 100%–0% case [i.e., when \(m_{0}(T)=0\)] lies too far below data trends and likewise for the 50%–50% case. This already suggests that condensed 2hCPs might be necessary to correctly describe any SC. Recall that from Ref. [37] 2hCPs are indispensable in a BCS condensate which must be a 50%–50% mixture to give the BCS gap equation exactly for all couplings and all Ts as well as the full condensation energy for \(T=0\).

3 Superconductor superfluid density

In the extended-crossover theory the T-dependent superfluid number density \(n_{s}(T)\) involves only those CPs either in the ground/excited state for \(T\le T_{c}\). One can then define \(n_{s}(T)\) as

$$\begin{aligned} n_{s}(T)\equiv & {}\, n-n_{f}(T) \nonumber \\=\, & {} 2\left[ n_{0}(T)+n_{B+}(T)-m_{0}(T)-m_{B+}(T) \right] \end{aligned}$$
(16)

where n is the total number density (4) and \(n_{f}(T)\) that of unbound electrons (5). Here, the superfluid density (SFD) (16) resembles the SFD of the Landau two-fluid model [5,6,7] where the total mass density is \(\rho =\rho _{s}+\rho _{n}\) with \(\rho _{s}\) the superfluid mass density and \(\rho _{n}\) SFD with Bose statistics since in (16) there are only CPs as bosons.

There are two special cases: i) \(m_{0}(T)\) = 0, i.e., there are no condensed 2hCPs, so one has the 100%–0% case and the SFD is

$$\begin{aligned} n_{s,2e}(T)=2\left[ n_{0}(T)+n_{B+}(T)-m_{B+}(T)\right] \end{aligned}$$
(17)

and ii) \(n_{0}(T)=0\), i.e., there are no condensed 2eCPs, one has in the 0%–100% case

$$\begin{aligned} n_{s,2h}(T)=2\left[ -m_{0}(T)+n_{B+}(T)-m_{B+}(T)\right] . \end{aligned}$$
(18)

The more general case (16) includes both kind of CPs, while 100%–0% and 0%–100% cases one have ignored one kind of condensed CPs. To find the superfluid density in this extended crossover one must solve the set equations (14), (15) and (4) to have the energy gap as well as the chemical potential, both dependent of temperature. These values must be substituted in (16), (17) and (18).

Figure 1a shows a phase diagram of the dimensionless superfluid density \(n_s(0)/n\) vs. the dimensionless number density \(n/n_f\) for the 100%–0% case using (17) and for the 0%–100% case using (18) in 3D with a quadratic energy-dispersion relation as well as in 2D with linear relation. If one takes the 50%–50% proportions in (16) one sees that \(n_s(T) = 0\) implying that both kinds of CPs cannot contribute to SFD in any coupling regime while the 100%–0% and 0%–100% cases can do. Taking the weak-coupling extreme, i.e., when \(n/n_f = 1\) the 100%–0% and 0%–100% cases cannot contribute to SFD, one must take \(n/n_f \ne 1\). Taking \(n/n_f \simeq 10^{3}\) one sees that the 100%–0% case in 3D as well as in 2D all electrons are paired, i.e., one has an ideal Bose gas composed of 2eCPs. The 0%–100% case with \(n/n_f = 0.5\) all holes paired into 2hCPs. Thus \(n/n_f\) becomes our interest here since taking \(n/n_f =1\) all particles are unbound, implying that \(n/n_f > 1\) electrons paired into CPs and taking \(n/n_f <1\), holes paired into 2hCP. However, the proper interpretation of \(n < n_f\) is that the number density of unbound fermions are greater than the total number density, but this leads to a disagreement, instead one might suppose that occurs an insertion of particles to the system, in this case a finite number of 2hCPs, this suggests that the system can be doped with holes.

Fig. 1
figure 1

(Color online) a Dimensionless superfluid density \(n_s(0)/n\) vs. \(n/n_f\) for 100%–0% (black full) curve, 0%–100% (gray-dashed) curve using (17) and (18), respectively, for 3D and 100%–0% (red dashed) curve, 0%–100% (gray dashed) curve using the same equations for 2D. When \(n/n_f \simeq 10^3\) one have \(n_{s,2e}(0)/n \simeq 1\) and when \(n/n_f \simeq 0.5\) one has \(n_{s,2h}(0)/n \simeq -1\). One has the negative sign in the superfluid density of 0%–100% case, this is consistent with 2hCPs charge carriers sign in (4). Inset shows the behavior of superluid density near \(n/n_f = 1\) (weak coupling) extreme. Also there is a sign symmetry with respect this point between 100%–0% and 0%–100% cases. b Critical temperature \(T_{c}\) vs \(n_{s}(0)/n\) from the extended crossover theory for the 100%–0% and 0%–100% cases in 3D and 2D, \(m_{B+}(T)=0\) indicate that excited 2hCPs have been ignored and \(n_{B+}(T)=0\) that excited 2eCPs have also been ignored. Note that the mere presence of 2hCPs enhance critical temperatures. One can see a linear behavior still holds at relatively high superfluid densities, this linear behavior holds in the strong-coupling regime as Božović et al. [34] found in their Fig. 2d. Here \({\tilde{G}}=10^{-4}\) and \(\delta {\tilde{\epsilon }}=10^{-3}\) were used; “tilde” meaning made dimensionless with the Fermi energy \(E_{F}\)

Full size image

In Fig. 1b the critical temperature \(T_{c}\) is plotted for the 100%–0% and 0%–100% cases vs \(n_{s}(0)/n\) in both 2D and 3D. Shows the 100%–0% case with a special case where \(m_{B+}(T)=0\), i.e., the excited 2hCPs bosons has been ignored, with a linear energy-dispersion relation in 2D and with a quadratic relation in 3D. The 0%–100% case enhances the critical temperature at relatively low SFD. Note that \(n_{s}(0)/n\) has a linear behavior in the strong-coupling regime as reported in Ref. [34, Fig. 2d] for \(T_{c}\) vs \(\rho _{s0}\) SFD of data where \(\rho _{s0}\equiv \rho _{s}(T\rightarrow 0)\) from this reference. The mere presence of excited 2hCPs enhances the value of \(T_{c}\) [40, 41]. This is exactly analogous to the increase, at higher and higher temperatures, of antibosons (here 2hCPs) in the relativistic IBG [58].

As mentioned above, the weak-coupling (BCS) regime is when one considers the 50%–50% proportions. Thus in (4) at \(T=0\) one has \(n/n_f = 1\) meaning that the rest of fermions remain unbound. This limit resembles a fermion system interacting via an attractive potential [21] when \(N=N_f\), i.e., sufficiently high fermion densities [59]. The BEC regime is achieved when all fermions are bound as pairs, i.e., the fermion density decrease while boson density increase, namely, the number density ratio changes as \(1 \le n/n_f < \infty\). These properties are described in the phase diagram \(T_c/T_F\) vs \(n/n_f\) in but is here extended with the dimensionless SFD \(n_s(0)/n\), which is illustrated in Fig. 2 in 3D. The phase diagram of Fig. 2 describes the behavior of the dimensionless SFD at \(T=0\) when the dimensionless number density varies as function of \(T_c/T_F\). For 100%–0% case in the strong-coupling regime when \(n/n_f > 10^2\) almost all fermions as pairs are in the superfluid state, while for 0%–100% case this occur when \(n/n_f \rightarrow 1/2\), but the 50%–50% case the dimensionless SFD is zero as shown before. Also, note that \(T_c/T_F\) increases linearly as the dimensionless SFD increases in the strong-coupling regime as Uemura et al. [32, 33] and independently Božović et al. [34] found. The region of arbitrary proportions between 2eCPs and 2hCPs may lie between the white-orange (100-0) surface and light-blue (0-100) surface.

Fig. 2
figure 2

Phase diagram \(n/n_f\) vs \(T_c/T_F\) vs \(n_s(0)/n\) for the 100%–0% (white-red surface) and 0%–100% (light-blue surface) cases in 3D of the extended BCS-Bose crossover. The weak-coupling regime is when \(n/n_f = 1\) there is a high unbound fermion density, while the strong-coupling regime occurs when \(n/n_f > 10^2\) for the 100%–0% case and \(n/n_f \rightarrow 1/2\) for the 0%–100% case with high boson density. Note that \(T_c/T_F\) increases linearly as the dimensionless SFD increases just as Uemura et al. [32, 33] and, independently, Božović et al. [34] found

Full size image

Table 1 lists superfluid density \(n_{s}(T=0)\) experimental values and also calculated with the extended-crossover set of equations (17) and (18) for 100%–0% and 0%–100% cases, respectively, taking specifically \(n/n_f = 1.00001\) for 100%–0%, meaning that the number density of unbound electrons is 0.001% smaller than the total number density. For 0%–100% \(n/n_f = 0.99999\) was used meaning that the number density of unbound holes is 0.001% greater than of that total number density, i.e., it has been inserted as finite number of 2hCP. These values of the dimensionless number density are near the weak coupling extreme (BCS theory) for elemental superconductors. They are compared with data from Ref. [33] in 2D. In 3D as \(n_{s,3D}^{2/3}(T=0)\) with a quadratic energy-dispersion relation and in 2D simply as \(n_{s,2D}(T=0)\) and with a linear relation. Note that the 3D results agree with data trends, while in 2D results have some orders of magnitude below even from the 3D case.

Also shown is the penetration depth \(\lambda ^{2} \propto m^{\star } / n_s\) results in 3D. Results of the 100%–0% case for Zn are near the data while the 0%–100% case is so for Al, Sn and Nb, while the 2D cases are not reported since the SFD are too far below of data. But it needs the Pippard coherence length of the 2e/2hCPs to have a complete picture of the penetration depth. Here we used the effective electron mass in 3D for the calculations in 3D and 2D. Also listed are the BF parameters as \(\delta {\tilde{\epsilon }}\) and \({\tilde{G}}\) for each SC. Future work will be to use the effective mass tensor.

For an ultracold bosonic atomic gas one must solve the 100%–0% case, i.e., with \(m_{0}(T)=m_{B+}(T)=0\). This is analogous to an IBG gas when \(n/n_{f}\rightarrow \infty\), e.g., when \(n_{f}=0\). Here 2hCPs contributions can be neglected as their numbers are likely negligible at the very low densities associated with a shallow Fermi sea is expected [60] to accommodate only a tiny number of holes. Ignoring them, one recovers the limits of \(T_{c}/T_{F}\) when \(n/n_{f}\rightarrow \infty\). For the extended crossover in 3D giving \(T_{c}/T_{F}\rightarrow 0.204\) and in 2D \(T_{c}/T_{F}\rightarrow 0.034\) so that \(n_{s}(0)/n\rightarrow 1\) as expected [55]. Results in Table 1 suggest again the connection between superfluid density and Bose statistics. The \(_{2}^{4}\)He case is worth mentioning too because all fermions are supposed to be paired for extremely strong coupling, viz., \(n/n_{f}\rightarrow \infty\), leaving essentially an IBG so that the calculated superfluid density agrees with the data. This suggests that this BF mixture with the 100%–0% case can describe successfully ultracold fermionic atomic clouds.

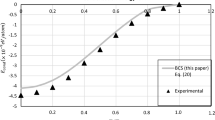
Table 1 Values of \(n_{s3D}(T=0)^{2/3}/(m^{*}/m_{e})\) with a quadratic energy dispersion relation and \(n_{s2D}(T=0)/(m^{*}/m_{e})\) with a linear relation, calculated with the extended BCS-Bose crossover theory using (17) for the 100%–0% case with \(n/n_{f}=1.00001\) and (18) for the 0%–100% case with \(n/n_{f}=0.99999\) in 2D and 3D
Full size table

Figure 3a shows calculated 2D superfluid density \(n_{s}(T)/n_{s}(0)\) vs \(T/T_{c}\) curves with a linear dispersion relation using (17) and (18) compared with HTSC data [63,64,65]. Also plotted is the 100%–0% case near weak coupling with \(n/n_f = 1.00005\) and the intermediate coupling with \(n/n_f = 100\). The former approximates better the data trends but the latter is too far below the data. Also plotted is the 0%–100% case near weak coupling with \(n/n_f = 0.99999\) and \(n/n_f = 0.997\). The former appears to mean that 0.001% of unbound holes have been inserted while the latter with 0.3%. If one varies \(n/n_1 \ne 1\) with 2hCPs one can adjust to data trends. This suggests that this HTSC cannot be correctly described by a 50%–50% mix of 2eCPs/2hCPs in the weak-coupling regime.

Figure 3b shows the 3D superfluid density \(n_{s}(T)/n_{s}(0)\) vs T/Tc with a quadratic relation compared with the same HTSCs data [63,64,65] previously shown. Shows the weak-coupling regime solving (17) and (18), these two cases are so far from data but they are near of the SFD curve of BCS theory, this suggesting that this HTSC cannot be explained by weak-coupling BCS theory, as long suspected. But if one changes \(n/n_f \ne 1\) both curves come together with the general behavior but not adjust to data. This suggests that the 3D case cannot describe at all the HTSC data.

Fig. 3
figure 3

(Color online) a 2D superfluid density \(n_{s}(T)/n_{s}(0)\) vs \(T/T_{c}\) from the extended crossover for 100%–0% case using (17) black-full curve with \(n/n_f = 1.00005\) near weak coupling and the black-dashed curve with \(n/n_f = 100\) strong-coupling regime. For 0%–100% case using (18) gray-full curve with \(n/n_f=0.99999\) and gray-dashed curve with \(n/n_f=0.997\) each compared with HTSC data of YBa\(_{3}\)CuO\(_{\delta -7}\) ab-plane [63] (open circles); La\(_{2-x}\)Sr\(_{x}\)CuO\(_{4}\) [64] (gray squares) \(x=0.15\) (blue-online diamonds) \(x=0.21\); YBa\(_{2}\)Cu\(_{4}\)O\(_{8}\) [65], Ca \(=0.06\) (open triangles) and La \(=0.075\) (red online circles). There is two important cuprate-SC results shown here between the 100%–0% and 0%–100% cases near the weak coupling regime and between the 100%–0% strong-coupling regime and 0%–100% gray-dashed case suggesting that these SCs might be correctly described by bosonic 2hCPs in 2D. b 3D superfluid density \(n_{s}(T)/n_{s}(0)\) vs. \(T/T_{c}\) from the extended-crossover theory for 100%–0% case using (17) black-full curve with \(n/n_f = 1.00001\) near weak coupling and the black-dashed curve with \(n/n_f = 2\) intermediate coupling. For the 0%–100% case using (18) gray-full curve with \(n/n_f=0.99999\) and gray-dashed curve with \(n/n_f=0.999\) each compared with HTSC data and BCS (dotted-gray) curve is included for comparison purposes only. Finally, near weak-coupling regime the 3D case is far from data trends

Full size image

In 3D, the 100–0% as well as the 0%–100% cases near weak-coupling regime, i.e., with \(n/n_f=1\) is too far from the data and also from the BCS curve. Thus, these cuprates cannot be correctly described with weak-coupling assumptions. However, for these SC cuprates occurs in cuasi-2D as in La\(_{2-x}\)Sr\(_{x}\)CuO\(_{4}\) with \(x=0.21\) [64]. In 2D, the 100%–0% as well as 0%–100% curves with \(n/n_{f} \simeq 1\) does describe the general behavior, although the 0%–100% case changing as \(0.997 \le n/n_{f} \le 0.99999\) can adjust the data, suggesting that charge carriers are 2hCPs. This suggests that this SC might lie between a BF mixture with \(n/n_{f}=1\) and \(n/n_{f}=10^{2}\), i.e., in the intermediate-coupling regime.

4 Discussion

From Kaptiza’s arguments on the superfluid density and from definitions of (17) and (18), the 2eCPs and the 2hCPs contribute to the superfluid density. The extended crossover leads to the important concept of “three components” since one here deals with a ternary gas. Taking the 50%–50% mixture of 2eCPs/2hCPs, i.e., \(n_{0}(T)=m_{0}(T)\) and \(n_{B+}(T)=m_{B+}(T)\) implying that \(n_{s}(T) = 0\); this result drastically contrasts with the results of the energy gap or the critical temperature [42]. This result is quite different, even for the BCS-theory superfluid density it was assumed to be a symmetrical distribution between 2eCPs and 2hCPs, this symmetry remains unclear in their superfluid density. Furthermore, in the London penetration depth related with superconductor density there is no mention on what kind of charge carriers are involved, even as it’s supposed to be negative charge carriers, i.e., electrons. We have considered this kind of symmetry and obtained good results [57]. Thus, in definitions given in (17) and (18) there are two kinds of specific contributions of condensed 2eCPs/2hCPs as well as excited 2e/2hCPs. The main advantage of the extended crossover theory seems to be the explicit inclusion of 2hCPs. This addition of 2hCPs might be interpreted as doping since the number density has been increased.

Two independent groups, Uemura et al. [32, 33] and Božović et al. [34], have found that the critical temperature \(T_{c}\) has a linear relationship with the superfluid density, rather than with the coupling strength as commonly held. This is illustrated in Fig. 1b showing \(T_{c}\) vs superfluid density of 2eCPs after using (17) for 100%–0% cases. It’s worth mentioning here that the 0%–100% case enhanced \(T_c\)s with relatively low SFDs. Also, one sees that in the range of intermediate- to strong-coupling regime clearly showing that regardless of the pair-coupling strength the linear relationship between superfluid density and \(T_{c}\) can, in fact, be explained by an increase of the number of 2eCPs as many have long claimed, at least in 2D, and also with the explicitly inclusion of excited 2hCPs.

5 Conclusions

The superfluid density \(n_{s}(T)\) was calculated with the extended-crossover theory from the GBEC theory. In the weak-coupling regime, in 3D \(n_{s}(T=0)\) agrees with the Uemura et al. [32] data for the elemental SCs like Zn, Al, Sn and Nb. However, the quadratic energy-dispersion relation in 3D gives a better approach to the superfluid density reported, at least for the elemental SCs since here can be addressed with a BF gas mixture in 3D. Regarding all of this, there are at least five thermodynamic scenarios, e.g., see Ref. [57], which show that a lack of 2hCPs decreases the energy-gap size and also that of the gap-to-\(T_{c}\) ratio from well-known data, leading one to conclude unequivocally that condensed 2hCPs are indeed indispensable to correctly describe SCs. However, in the strong-coupling regime \(n_{s}(T)\) for ultracold-bosonic-atomic clouds of, e.g., \(_{2}^{4}\)He, in the 100%–0% case [i.e., with \(m_{0}(T)=m_{B+}(T)=0\) and \(n/n_{f}\simeq 10^{6}\)] agrees remarkably well with the data, indicating that condensed ultracold bosonic gases behave like ordinary BE condensates. Also, the superfluid density \(n_{s}(0)/n\) in strong coupling is seen to have a linear behavior with \(T_{c}\) just as Božović et al. [34] found. Hence, HTSC data can be described reasonably well with a BF mixture using the 100%–0% and the 0%–100% cases between weak- and strong-coupling in 2D by changing the number density of the unbound fermions.

Future work will focus on \(n_{s}(T)\) using the 0%–100% case for some other HTSCs and for ultracold-fermionic-atomic clouds [66, 67] including BF gas mixtures like \(_{2}^{4}\)He / \(_{2}^{3}\)He and also with the critical magnetic field \(H_{c}^{2}(T,n)/8\pi\) of the superfluid density from the extended-crossover theory. Also, the dimensionless number density that we used since a coupling parameter has been changed slightly and is not big enough to note any singular phenomena. This will be dealt with in another paper. However, it seems to us necessary to address the electronic structure in this BF theory; this might improve the results shown here. The electronic structure study will be discussed elsewhere as part of future work.