Exact Liquid-Solid Transition from the Laughlin Liquid State to the Wigner Crystal in the Lowest Landau Level

Abstract

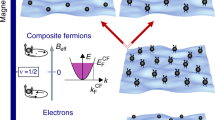
In this work, we study the exact liquid-solid transition between the Laughlin liquid and the Wigner crystal states in the lowest Landau level at low filling factors. The incompressible quantum fluid consists of strongly correlated electrons interacting with a strong magnetic field and cooled at a low temperature. According to composite fermions theory, in principle all fractions are possible. The Laughlin wave function is not particularly accurate at $\upsilon$ $\le 1/7$ where the transition from the liquid to crystal occurs. Independent of the model used to estimate the transition temperature, we note that the Wigner crystal phase is expected to exist at such low filling factors based on analytical calculation, into the series of fractional quantum Hall effect (FQHE) liquids prescribed by the composite fermions model.

Appendix

1.1 The Coulomb Interaction Potential

The wave functions in the lowest Landau level are simple monomials in $z_{j}$. Thus, let us apply the change $r_{j}$ $\rightarrow$ $z_{j}=x_{j}-i y_{j}=r_{j}$e$^{-i\varphi _{j}}, j=1,...,N$. The electron-electron interaction potential

$$\begin{aligned} \widehat{V}_{ee}=\sum _{i<j}^{N}\ \frac{e_{0}^{2}}{|\overrightarrow{r}_{i}-\overrightarrow{r}_{j}|}, \end{aligned}$$

(12)

where ${r}_{i}$ (or ${r}_{j}$) indicates the electron vector position. For a given wave function $\mathit{\Psi}$, these energies are determined using the following formulae:

$$\begin{aligned} \left\langle \widehat{V}_{ee}\right\rangle = \frac{\left\langle \mathit{\Psi} |{V}_{ee}| \mathit{\Psi} \right\rangle }{ \left\langle \mathit{\Psi} \mathit{\Psi} \right\rangle }, \end{aligned}$$

(13)

The term $\left\langle \widehat{V}_{ee}\right\rangle$ is written as follows:

$$\begin{aligned} \left\langle \widehat{V}_{ee}\right\rangle =\frac{N(N-1)}{2}\frac{\int d^{2}r_{1}\cdot \cdot \cdot d^{2}r_{N}\frac{e_{0}^{2}}{|r_{1}-r_{2}|}|\mathit{\Psi} (r_{1},\dots ,r_{N})|^{2}}{\int d^{2}r_{1}\cdot \cdot \cdot d^{2}r_{N}|\mathit{\Psi} (r_{1},\dots ,r_{N})|^{2}}. \end{aligned}$$

(14)

The electron-background interaction potential

$$\begin{aligned} \widehat{V}_{eb}=-\rho \sum _{i<j}^{N}\int _{S_{N}}^{{}}d^{2}r\frac{e_{0}^{2}}{|\overrightarrow{r}_{i}-\overrightarrow{r}|}, \end{aligned}$$

(15)

$\overrightarrow{r}_{i}$ and $\overrightarrow{r}$ are background coordinates. $S_{N}$ is the area of the disk and $\rho$ is the density of the system defined by

$$\begin{aligned} \rho = \frac{\upsilon }{2 \pi l_{0}^{2}}, \end{aligned}$$

(16)

$$\begin{aligned} \left\langle \widehat{V}_{eb}\right\rangle = \frac{\left\langle \mathit{\Psi} |{V}_{eb}| \mathit{\Psi} \right\rangle }{ \left\langle \mathit{\Psi} \mathit{\Psi} \right\rangle }, \end{aligned}$$

(17)

is the electron-background interaction energy and

$$\begin{aligned} \left\langle \widehat{V}_{eb}\right\rangle =-\rho N \frac{\int d^{2}r_{1}\cdot \cdot \cdot d^{2}r_{N} |\mathit{\Psi} (r_{1},\dots ,r_{N})|^{2}\int _{S_{N}}^{{}}d^{2}r\frac{e_{0}^{2}}{|r_{1}-r|}}{\int d^{2}r_{1}\cdot \cdot \cdot d^{2}r_{N}|\mathit{\Psi} (r_{1},\dots ,r_{N})|^{2}}. \end{aligned}$$

(18)

with

$$\begin{aligned} \int _{S_{N}}^{{}}d^{2}r\frac{e_{0}^{2}}{|r_{1}-r|}=2 \pi R_{N}\int _{0}^{\infty }\frac{dq}{q}J_{1}(q)J_{0}(\frac{q}{R_{N}}r_{1}), \end{aligned}$$

(19)

where is the $J_{n}(x)$ n-th order Bessel functions [21].

The background-background interaction potential

$$\begin{aligned} \widehat{V}_{bb}=\frac{\rho ^{2}}{2}\sum _{i<j}^{N}\int _{S_{N}}^{{}}d^{2}r\int _{S_{N}}^{{}}d^{2}r^{\prime }\frac{e_{0}^{2}}{|\overrightarrow{r}-\overrightarrow{r}^{\prime }|}, \end{aligned}$$

(20)

$$\begin{aligned} \left\langle \widehat{V}_{bb}\right\rangle = \frac{\left\langle \mathit{\Psi} |{V}_{bb}| \mathit{\Psi} \right\rangle }{ \left\langle \mathit{\Psi} \mathit{\Psi} \right\rangle }, \end{aligned}$$

(21)

$$\begin{aligned} \left\langle \widehat{V}_{bb}\right\rangle =\frac{8N}{3\pi }\frac{\sqrt{\upsilon N}}{2}\frac{e_{0}^{2}}{l_{0}}. \end{aligned}$$

(22)