1 Introduction

In polymer fabrication at high temperature [1, 2], radiative heat distribution takes place in addition to heat convection and heat conduction. The solution of integro-differential equation of heat radiation is most general, computationally it is very challenging. In the presence of other effects such as magnetohydro-dynamics, rheology are the effortless pragmatic approach that frequently features an approximation algebraic flux that can be of the Traugott P1 flux model, Milne-Eddington type, Rosseland type, six flux Hamaker formulation, Schuster-Schwartzchild type etc. In coating flows of multi-physical, high radiation optical thicknesses are practically and correctly presented using the Rosseland model. Though it does not permit the stimulation of spectal effects or optical viscosity, but provides an evaluating mechanism for the relative role of heat flux radiation and heat conduction. Numerous scholars have investigated radiative heat transfer in materials processing including Shamshuddin et al. [3] (bio convection nanofluid), Kadir et al. [4] (thermal stress analysis), Liu et al. [5] (multi laser processing) and Yue and Reitz [6] (internal combustion energies).

In recent years, nanofluids have been increasingly deployed in industrial and technological systems. They constitute a unique subset of nanomaterials. ethylene glycol, engine oil and water are common fluids that constrained heat transfer due to their low heat conductivity capacity, while metals have remarkably heat conductivities strength than those fluids. Therefore, scattering high thermal conductivity solid particles augments heat conductivity of the subsequent fluid suspension. The idea of nanoliquids was initiated by Choi et al. [7] at Argonne Energy Lab, USA. As noted, thermal conductivity is the magnificent attribute of nanofluids [8]. Carbides (SiC), Nitrides (AlN, SiN), Metallic oxides (Al2O3, TiO2), Metallic (Al, Cu) or nanotubes carbon with diameter ranges from 10 to 100 nm are the nanoparticles used in synthesis of nanofluids. Hamid et al. [9] studied transient convective radiation of nanofluid flow past a vertical medium. It was observed that changing in the shape of nanoparticle encourages the rate of heat transfer. Pandey and Kumar [10] investigated Cu-water nanoliquid heat transfer in a moving cylinder boundary layer with slip condition. Many robust mathematical formualtions have been developed for flow of nanoparticles through demanding foundational experimental data. Amanullah et al. [11] examined computationally, the non-Newtonian nanofluid with different nanoparticles. Anwar et al. [12] studied experimentally, the drilling lubricant fluids with nano particles and Bio convection lubricants [13]. Several researchers have studied nanofluid flow with different nanoparticles applying different geometries which has applications in material processing including Shamshuddin et al. [14] (squeezing flow), Anwar Beg et al., [15] (magnetic nanoploymer flow), Rashidi et al. [16] (triangular obstacle), Akar et al. [17] (rotating cylinder), Hamid et al. [18] (duct equipped with porous baffels), Eid [19] (Riga surface), Eid and Mabood [20] (cross nano material flow), Eid and Mabood [21] (micropolar dusty CNTs), Mohebbi et al., [22] (extended surface channel), Mohebbi nd Rashidi [23] (L-shaped heating obstacle enclosure) and Armaghani et al. [24] (baffled L-shaped caviity).

The present article is inspired to provide a more broad understanding of the processes involving heat generating at high temperature. A mathematical equation is formulated for viscous radiative flow fluid from a flat plate with heat source. This formulated equation strengthens the former report of Gangadhar [25] to examine the transfer of thermal radiation and IHG impacts. The modelled partial derivative boundary value equation reduces to an ordinary non-linear derivative boundary value equation with applicable transformation variables. A vigorous numerical solution is gotten with the uses of MATLAB package bvp4c and validation with the non-IHG case Gangadhar [25] is considered. A complete parametric analysis of the impact of suction, velocity slip, Eckert number and thermal radiation on the velocity magnitude, temperature component and skin friction coefficients results are conducted with graphical representation.

1.1 Mathematical model

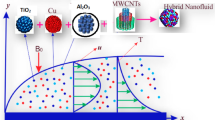
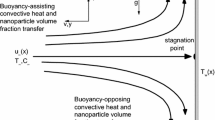
Examine the flow of conducting viscous incompressible liquid of heat transport over a flat moving plate with magnetic effect been ignored. We consider a Cartesian system of coordinate such that the plate corresponds with the xy-coordinate and the liquid fills the space \(z \ge 0\) as defined in Fig. 1. Taken \(u = U_{w} (x)\) while \(v = V_{0} (x)\) describe the plate velocities in the direction of x, y. The fluid velocity is maintained with velocity U, and Velocity of the far field and the flat sheet are assumed as \(U_{\infty } ,U_{w}\) respectively. It is considered that plate temperature is \(T_{w}\), while free stream uniform temperature is \(T_{\infty }\).

Fig. 1
figure 1

Boundary layer of 2D laminar flow

Full size image

Under the specified assumptions, the associated equations defining the viscous two-dimensional fluid momentum are stated as an extension of the model presented by Gangadhar [25] with IHG and radiative heat flux terms, leading to:

Continuity Equation:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(1)

Momentum Equation:

$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \upsilon_{nf} \frac{{\partial^{2} u}}{{\partial y^{2} }},$$
(2)

Energy Equation:

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho C_{p} } \right)_{nf} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{\mu_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \frac{{q^{\prime } }}{{\left( {\rho C_{p} } \right)_{nf} }},$$
(3)

Here, u and v denote the component of velocities in the x and y axes.\(\rho c_{p}\) is the nanoliquid heat capacity.\(q_{r} = - \frac{{4\sigma^{ * } }}{{3k^{ * } }}\frac{{\partial T^{4} }}{\partial y}\) is net radiative heat flux, expanding \(T^{4}\) using Taylor’s series assuming temperature difference and higher order terms neglecting, thus

$$T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4}$$
(4)

Boundary conditions are subjected to be:

$$\left. {\begin{array}{*{20}l} {u = U_{w} ,v = v_{0} ,} \hfill & {T = T_{w} } \hfill & {at\;y = 0} \hfill \\ {u = U_{\infty } ,} \hfill & {T = T_{\infty } } \hfill & {as\;y \to \infty } \hfill \\ \end{array} } \right\}$$
(5)

The nanofluid modified properties are simulated according to Gangadhar [25], the nanoparticles thermophysical characteristics and the base liquid are given in the Table 1.

$$\left. \begin{gathered} \alpha_{nf} = \frac{{k_{nf} }}{{(\rho C_{p} )_{nf} }},\rho_{nf} = \rho_{f} - \phi \rho_{f} + \phi \rho_{s} ,\mu_{nf} = \frac{{\mu_{f} }}{{(1 - \phi )^{2.5} }}, \hfill \\ (\rho C_{p} )_{nf} = \left[ {\left( {\rho C_{p} } \right)_{f} - \phi \left( {\rho C_{p} } \right)_{f} } \right],k_{nf} = k_{f} \left\{ {\frac{{(k_{s} /k_{f} ) + (n - 1) - (n - 1)\phi \left( {1 - (k_{s} /k_{f} )} \right)}}{{(k_{s} /k_{f} ) + (n - 1)\phi \left( {1 - (k_{s} /k_{f} )} \right)}}} \right\} \hfill \\ \end{gathered} \right\}$$
(6)
Table 1 Nanoparticle thermophysical properties and the base liquid at 20 °C (293 K)
Full size table

1.2 Transformations

We have to reframe the boundary layer equations to a non-dimensional system of equations using similarity variable. The objective of similarity conversion is to reduce the independent variable in the governing equations by quantities of transformation. The parlance quantities is worn because of the widening of the boundary layer with distance x from the major edge, both velocity and temperature profile remain geometrically similar [25, 26]. Similarity variable of the form [27, 28];

Here,

$$\left. {\psi (x,y) = (U_{\infty } \upsilon_{nf} x)^{1/2} f(\eta ),\;\theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\;\;\eta = y\left( {\frac{{U_{\infty } }}{{\upsilon_{nf} x}}} \right)^{1/2} ,S = v_{o} (x)\sqrt {\frac{x}{{\nu_{n\;f} U_{\infty } }}} } \right\}$$
(7)

where ψ (x, y) is the stream function that is described as,

$$u = \frac{\partial \psi }{{\partial y}},v = - \frac{\partial \psi }{{\partial y}}$$
(8)

In terms of these new variables

$$u = U_{\infty } f^{\prime } (\eta ),v = \frac{1}{2}\left( {\frac{{\upsilon_{nf} U_{\infty } }}{x}} \right)^{1/2} \left( {nf^{\prime } (\eta ) - f(\eta )} \right)$$
(9)

Finally, we get the similarity results for the velocity and temperature modules as:

$$2L_{0} f^{{\prime \prime \prime }} + ff^{{\prime \prime }} = 0$$
(10)
$$\left[ {1 + Nr} \right]L_{1} \theta^{\prime \prime } + \frac{{\left( {\Pr } \right)_{nf} }}{2}f\theta^{\prime } + L_{2} \left( {\Pr } \right)_{nf} \left( {Ec} \right)_{nf} f^{\prime \prime 2} + L_{3} Ce^{ - n} = 0$$
(11)

The transmuted boundary conditions are found as:

$$\left. {\begin{array}{*{20}c} {f(0) = S,f^{\prime } (0) = \lambda ,\;\theta (0) = 1} & {at\;\eta = 0} \\ {f^{\prime } (\eta ) = 1,\theta (\eta ) = 0} & {as\;\eta \to \infty } \\ \end{array} } \right\}$$
(12)

where (′) represents derivative with respect to \(\eta\), \(\lambda\) is the slip velocity term, the term \(Nr\) denotes thermal radiation, Ec represents Eckert number, Pr stands for Prandtl number, and S is the local injection parameter (< 0), or the local suction parameter (> 0) or these terms are respectively denoted as follows

$$Nr = \frac{{k_{f} k^{ * } }}{{4\sigma^{ * } T_{\infty }^{3} }},Ec = \frac{{U^{2} }}{{\left( {C_{p} } \right)_{f} (T_{w} - T_{\infty } )}},\left( {\Pr } \right)_{nf} = \frac{{\upsilon_{nf} }}{{\alpha_{nf} }},\lambda = \left( {\frac{{U_{\infty }^{3} }}{{x\upsilon_{f} }}} \right)^{1/2} ,S = \left( {\frac{x}{{\nu_{nf} U_{\infty } }}} \right)^{1/2} v_{0} (x)$$
(13)

C mentioned in Eq. (11) must be constant and independent on x and it is defined as \(C = \left[ {e^{n} /k_{nf} {\text{Re}}_{x} (T_{w} - T_{\infty } )} \right]\) which is the scale of the strength of the internal heat generation (IHG). Furthermore, to have similarity solution for ordinary differential equations, the terms \(\lambda .\;S\) is independent of \(x\). These conditions are gratified when \(\lambda \propto x^{1/2}\) and \(v_{0} \propto x^{ - 1/2}\) i.e., \(\lambda = Ax^{1/2}\) \(v_{0} = Bx^{ - 1/2}\) Where A, B are constants. The terms are the local similarity variables which are used to obtain the dimensionless equations. This gives an invariant transformation that has been adopted by several researches including magneto-fluid dynamics and heat transfer. It gives the required physics validity and the results offered in this study are locally self-sufficient as seen in Sparrow and Yu [29]

Hence

$$\left. {\lambda = A\left( {\frac{{U_{\infty }^{3} }}{{\nu_{nf} }}} \right)^{1/2} ,S = B\left( {\frac{1}{{\nu_{nf} U_{\infty } }}} \right)^{1/2} } \right\}$$
(14)

In addition to that \(L_{0} ,L_{1} ,L_{2}\) and \(L_{4}\) are constants which are defined as follows

$$\begin{array}{*{20}c} {L_{0} = \frac{1}{{(1 - \phi )^{2.5} \left[ {(1 - \phi ) + \phi \;(\rho_{s} /\rho_{f} )} \right]}},} & {L_{1} = \frac{{k_{nf} /k_{f} }}{{\left[ {(1 - \phi ) + \phi \;(\left( {\rho C_{p} } \right)_{s} /\left( {\rho C_{p} } \right)_{f} )} \right]}},} \\ {L_{2} = \frac{1}{{(1 - \phi )^{2.5} \left[ {(1 - \phi ) + \phi \;(\left( {\rho C_{p} } \right)_{s} /\left( {\rho C_{p} } \right)_{f} } \right]}},} & {L_{4} = \frac{1}{{(1 - \phi ) + \phi \;(\left( {\rho C_{p} } \right)_{s} /\left( {\rho C_{p} } \right)_{f} )}}} \\ \end{array}$$
(15)

In material processing, important engineering design quantities are the skin friction coefficient \(C_{f}\) and local Nusselt number \(Nu_{x}\) are defined as

$$C_{f} = \frac{{\tau_{w} }}{{\rho_{nf} U_{\infty }^{2} /2}},Nu_{x} = \frac{{xq_{w} }}{{k_{nf} (T_{w} - T_{\infty } )}},$$
(16)

where the shear stress \(\tau_{w} = \mu \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} ,q_{w} = - \left( {k_{nf} + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}} \right)\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} ,\)where \(\mu\) is the dynamic viscosity.

The skin friction is taken as,

$$C_{f} \sqrt {{\text{Re}}_{x} } = \frac{{f^{\prime \prime } (0)}}{{(1 - \phi )^{2.5} }}$$
(17)

For this present paper the skin friction has no impact on the result. Therefore, the focus is on the local Nusselt number,

$$Nu_{x} {\text{Re}}_{x}^{ - 1/2} = - \left( {\frac{{k_{nf} }}{{k_{f} }} + \frac{4}{3Nr}} \right)\theta^{\prime } (0),$$
(18)

where \({\text{Re}}_{x} = \left( {U_{\infty } x} \right)/\upsilon\) is the local Reynolds number.

2 Numerical procedure

The coupled system of Eqs. (10) and (11) in combination with conditions (12) was numerically solved using the bvp4c package from Matlab. The package is built on boundary value procedures. The conditions (12) are substituted by utilizing the similarity variable \(\eta_{\max }\) of value 8 which is taken at the infinity (∞) value (assumed) of \(\eta\). The chosen of \(\eta_{\max } = 8\) shows that the far stream boundary conditions satisfies correctly. Solutions for the values of Ec, Pr, Nr, C and S are nevertheless suitable since they demonstrate the core features of the response boundary layers. Here we have taken the values of Prandtl number, \(\Pr = 2.37\)(for copper water nanofluid), \(\Pr = 6.38\)(for alumina water nanofluid). Eckert number, \(Ec = 0.5,1.0\), radiation parameter, \(Nr = 0.0,1.0,2.0\), \(C = 0.0\)(for without heat generation), \(C = 1.0\)(for heat generation), suction parameter, \(S = 0.0,0.2,0.4\) and velocity ratio parameter, \(\lambda = - 0.4,0.0,0.4\).

3 Results and discussion

After solving the governing system of equations numerically, the results obtained are illustrated in figures and tables. The influence of various dimensionless terms on the linear velocity and energy components is demonstrated. Computed results for the skin friction and heat gradient number in the considered nanofluids (alumina and copper liquid) are presented in tables. The missing slops for varying parameters are also calculated for various examined nanofluids and compared with previous studies.

In Table 2, the computed results for the skin friction is presented for different nanofluids. As shown is the table, the skin friction coefficient has no substantial influence on the variation of Prandtl number, but the Nusselt number shows an impactful effect. More also, the computed values are verified for \(f^{\prime \prime } (0) = 0.332\) at \(\phi = 0,\lambda = 0\) and \(S = 0\) which is found to be in agreement with what was obtained in other studies. Hence, our presented results are valid for further study.

Table 2 Values of skin friction for various nanofluids
Full size table

From Tables 3 and 4, the computational results for the missing slops is depicted for the heat gradient \(\theta^{\prime } (0)\) and nanofluids wall effect \(f^{\prime \prime } (0)\) for different parameter values. It is seen that the values of the missing slope for \(\theta^{\prime } (0)\) is decreasing while \(f^{\prime \prime } (0)\) is increasing as the values of the term suction (S) rises for both ‘Alumina water and Copper water’. Variation of suction number shows no momentous effect for \(f^{\prime \prime } (0)\) in both nanofluids considered. However, the decreasing rate of \(\theta^{\prime } (0)\) is slower in alumina water than copper water nanofluids. These agreed well with the report of Gangadhar [16].

Table 3 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying S with constant \(\Pr ,Ec,Nr,\lambda\)
Full size table
Table 4 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying S with constant\(\Pr ,Ec,Nr,\lambda\)
Full size table

In Tables 5 and 6, the computed values for the missing slops is presented for the Nusselt number \(\theta^{\prime } (0)\) and skin friction \(f^{\prime \prime } (0)\) for constant values of terms \(\Pr ,Ec,Nr,\lambda\). As observed in the tables, the heat gradient is decreasing while the nanofluid wall friction is increasing as the values of velocity slip (\(\lambda\)) is increased for both ‘Alumina water and Copper nanoliquids’. Meanwhile, varying of velocity slip shows no substantial effect for \(f^{\prime \prime } (0)\) in the two cases of the examined nanofluids. Therefore, diminishing rate of \(\theta^{\prime } (0)\) is lesser for copper water than alumina water nanofluid as obtained from the investigation.

Table 5 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime}(0)\) calculation for varying \(\lambda\) with constant\(\Pr ,Ec,Nr,s\)
Full size table
Table 6 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime}(0)\) calculation for varying \(\lambda\) with constant\(\Pr ,Ec,Nr,s\)
Full size table

From Tables 7 and 8, the impact of variation in the term Ec on \(\theta^{\prime } (0)\) and \(f^{\prime \prime } (0)\) is numerically demonstrated for some fixed parameter values. The value of \(\theta^{\prime } (0)\) is increasing and \(f^{\prime \prime } (0)\) decreasing for the different values of Ec for both ‘Alumina and Copper Nano-water’, this is found to be in alliance with the work of Gangadhar [16]. For varying Eckert number (Ec), the impact is not significant for \(f^{\prime \prime } (0)\) as depicted in the tables. Therefore, increasing rate of \(\theta^{\prime } (0)\) is reduced for copper nano-water than alumina nano-water. Hence, Nano-structure is enhanced in the alumina nanofluid than copper nanofluid.

Table 7 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying \(Ec\) with constant \(\Pr ,\lambda ,Nr,s\)
Full size table
Table 8 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying \(Ec\) with constant\(\Pr ,\lambda ,Nr,s\)
Full size table

Tables 9 and 10 show the calculated values for missing slopes with varying values of the term Nr in the physical wall effect \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\). Evaluation of \(\theta^{\prime } (0)\) shows a decreasing in the numerical values, but \(f^{\prime \prime } (0)\) is increasing as the values of radiation (Nr) is encouraged for both ‘Alumina and Copper Nano-liquid. Variation of radiation number has no influence on \(f^{\prime \prime } (0)\) as presented in the tables. Here, decreasing rate of \(\theta^{\prime } (0)\) is reduced for copper nanofluid than alumina nanoliquid. This is in agreement with the report of a reference [16] in the absence of heat generation.

Table 9 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying \(Nr\) with constant \(\Pr ,\lambda ,s\)
Full size table
Table 10 Missing slops \(f^{\prime \prime } (0)\) and \(\theta^{\prime } (0)\) calculation for varying \(Nr\) with constant \(\Pr ,\lambda ,s\)
Full size table

Figure 2a and b depict the reaction of alumina water nanofluid flow rate and energy distribution in a horizontal motioning plate with different values of suction (S). As obtained from the graphs, the velocity field of the alumina nano-water is encouraged as the suction term values is increased as presented in the Fig. 2a. The rise in the flow magnitude is due to an increase in the nanoparticles colloidal suspension that enhanced the particle dispersion of alumina water. The nanofluid mixture does not settle, this leads to free collision of nanoparticles that in turn raised the velocity profile. In Fig. 2b, either in the existence or absence of heat generation, it is seen that the heat field magnitude reduces. The diminishing in the overall energy dispersion is as a result of thinner in the energy boundary layer that causes more heat to leave the system. This resulted in a decline in the quantity of heat transfer in the flow medium, the outcome supported the claim by Amanullah et al. [11]. Figure 3a and b for the flow field and heat distribution demonstrate the same behaviour for copper water nanofluid with an increasing suction term (S). The flow velocity rises in the presence of heat generation, this is because the fluid temperature increases as the soluble nanofluids mixture reacted which breaks the fluid bonding force and cause the nanoparticle to move freely. Therefore, the nanofluid flow rate increases in the flow medium due to reduction in the fluid viscosity resulting in free flow of the fluid. Meanwhile, the temperature distribution within the system is discouraged as more heat diffused out of the colloidal suspension mixture. This is possible due to diminish in the heat limiting layer that leads to decline in the energy transfer component as seen in Fig. 3b. An increase in the overall heat transfer to the surroundings assists in reducing the quantity of heat within the nanofluid reaction system. Hence, this prevent excessive heat that can cause blow up and low performance of industrial thermal technology, this agreed well with what was reported by Okedoye and Salawu [30].

Fig. 2
figure 2

a velocity behaviour for S with Alumina-Water for \(Nr = 0.1,\lambda = - 0.3\) b Temperature behaviour for S with Alumina-Water for \(Nr = 0.1,\lambda = - 0.3\)

Full size image
Fig. 3
figure 3

a Velocity behaviour for S with Copper–Water for \(Nr = 0.1,\lambda = - 0.3\) b. Temperature behaviour for S with Copper–Water for \(Nr = 0.1,\lambda = - 0.3\)

Full size image

The response of the alumina nanofluid velocity and heat field to rising in the velocity slip term (\(\lambda\)) are illustrated in the Figs. 4a and b. As the slip velocity of the porous plate is increased, the nanofluid velocity profile momentously rises close to the moving plate, but the flow rate gets reduced as it moves steadily away from the moving surface to the far boundary layer. This is normal since the considered nanofluids flow is only being propelled by the moving surface as no pressure or thermal convection exists in the system. Nevertheless, the temperature field is discouraged as depicted in Fig. 4b. As the slip velocity is raised, a noteworthy reduction in the temperature is noticed close to the slip wall. This is as a result of heat being released through the porous plate, its decreases gradually further away from the surface until it becomes uniform in the system as achieved in [17, 22]. Similarly, copper nanofluid exhibited the same characteristic for the heat and velocity components as represented in Fig. 5a and b. In Fig. 5a, the fluid thermal conductivity is enhanced that in turn discourages the copper liquid bonding force. This allows free nanoparticles motion in the mixture that leads to a boost in the velocity magnitude as the slip term is increased. Therefore, the parameter will assist in raising industrial fluid flow in order to enhance productivity. Meanwhile, with or without internal heat generation the copper nanofluid temperature decreases regularly until it attains a uniform heat distribution as observed in Fig. 5b. Thus, more heat diffusion occurs near the slip porous wall due to shrinking in the heat boundary viscosity. However, parameter that decrease heat production in a nanofluid mixture should be encouraged because it will support and help in maintaining viscoelastic material viscosity as reported by Salawu et al. [31].

Fig. 4
figure 4

a Velocity behaviour for \(\lambda\) with Alumina-Water for \(Nr = 1.0,S = 0.5,Ec = 0.1\) b Temperature behaviour for \(\lambda\) with Alumina-Water for \(Nr = 1.0,S = 0.5,Ec = 0.1\)

Full size image
Fig. 5
figure 5

a Velocity behaviour for \(\lambda\) with Copper–Water with \(Nr = 1.0,S = 0.5,Ec = 0.1\) b Temperature behaviour for \(\lambda\) with Copper–Water for \(Nr = 1.0,S = 0.5,Ec = 0.1\)

Full size image

Figure 6a and b depict respectively, the heat profiles for the rising effect of heat dissipation term (Ec) on the alumina and copper water nanofluid temperature dispersion. As seen, the heat component increases for both considered nanoliquids. The effect is significant near the velocity slip plate, this is due to the difference between the boundary layer enthalpy and the nanofluids kinetic energy. The local specific heat is enhanced as the variance between the local heat and plate heat is increased. Hence, this enhanced the thickness of the boundary layer that resulted in high heat distribution in the nano-species mixture. Therefore, the temperature profiles is encouraged. Moreover, rising in the radiation term (Nr) values causes overall reduction in the alumina and copper water temperature fields as presented in Fig. 7a and b. The decreasing effect is lowered close to the slip plate, but reduces progressively as it travels towards the far stream layer. The release of energy to the surroundings is strengthened as moving subatomic nanoparticles carries heat from the slip plate to the far boundary layer. Thus, the magnitude of temperature distribution is generally discouraged in the nanoliquids as the values of (Nr) is raised. The influence of volume friction in wall coefficient heat transfer (Nusselt number) is demonstrated in Fig. 8 for the alumina nanoliquid and copper water nanoliquid. The plot shows the temperature gradient for the nanofluid volume friction at the plate surface.

Fig. 6
figure 6

a Temperature behaviour for \(Ec\) with Alumina-Water for \(Nr = 0.1,S = 0.5,\lambda = - 0.35\) b Temperature behaviour for \(Ec\) with Copper–Water for \(Nr = 0.1,S = 0.5,\lambda = - 0.35\)

Full size image
Fig. 7
figure 7

a Temperature behaviour for \(Nr\) with Alumina-Water for \(Ec = 0.1,S = 0.5,\lambda = - 0.3\). b Temperature behaviour for \(Nr\) with Copper–Water for \(Ec = 0.1,S = 0.5,\lambda = - 0.3\)

Full size image
Fig. 8
figure 8

The Impact of volume Fraction \(\phi\) in Nusselt number for Alumina-water nanofluids and Copper–water nanofluids

Full size image

4 Conclusions

In the present study, a detailed mathematical formulation of incompressible fluid has been offered for steady-state heat transport boundary layer flow of a nanofluid past a flat motioning plate, stimulated by nanomaterial coating applications. Two different nanoparticles (Cu, Al) have been examined to simulate nanoscale impacts. The radiation and IHG influences have been included. With applicable similarity quantities for the momentum and energy transformation, the main dimensional model has been changed to a couple of ordinary derivative equations. These equations under appropriate wall and free stream boundary conditions have been computationally solved through the MATLAB package bvp4c. Validation of solutions with earlier distinct case of the overall model available in the literature has been performed. A detailed analysis of the impact of suction, velocity slip, Eckert number and thermal radiation on the momentum and thermal characteristics (including coefficient of skin dragging and energy gradient) has been conducted. The present numerical simulations have shown that:

  • The rates of change of velocity in both water-based nanoparticles are aided with improving values of \(S,\lambda\). Whereas reverse orientation is perceived in rates of change of temperature.

  • Increasing values of the Ec, raises the temperature changes rate in both water-based nanoparticles are intensified.

  • Rising values of the Nr, increases the temperature changes rate for both water-based nanoparticles are intensified.

  • Nusselt number accelerates as nanoparticle volume fraction for both water-based nanoparticles raise.

It is predicted that this analysis carried out here will motivate additional attention in more realist industrial electro conductive magneto nano-polymers. The present investigation is valid for nanofluid flow of free convection over a flat plate, complex geometries mixed convective flow including non-Newtonian fluids like Casson, Williamson and Sisko fluid are underway and will be communicated imminently. The study is limited to heat transfer of nanofluid without considering chemical reaction.